Моделирование. Введение

1.

Кафедра вычислительной техники
МОДЕЛИРОВАНИЕ

2.

Лекция
ВВЕДЕНИЕ

3.

Сущность понятия «модель» и
моделирование.
Роль моделей в процессе
познания.

4.

Модель есть упрощенное
отображение объекта

5.

Определения модели
Модель (лат. modulus — мера) — это
объект-заместитель объекта-оригинала,
обеспечивающий изучение некоторых свойств
оригинала
Модель представляет собой систему,
исследование которой служит средством
получения информации о другой системе

6.

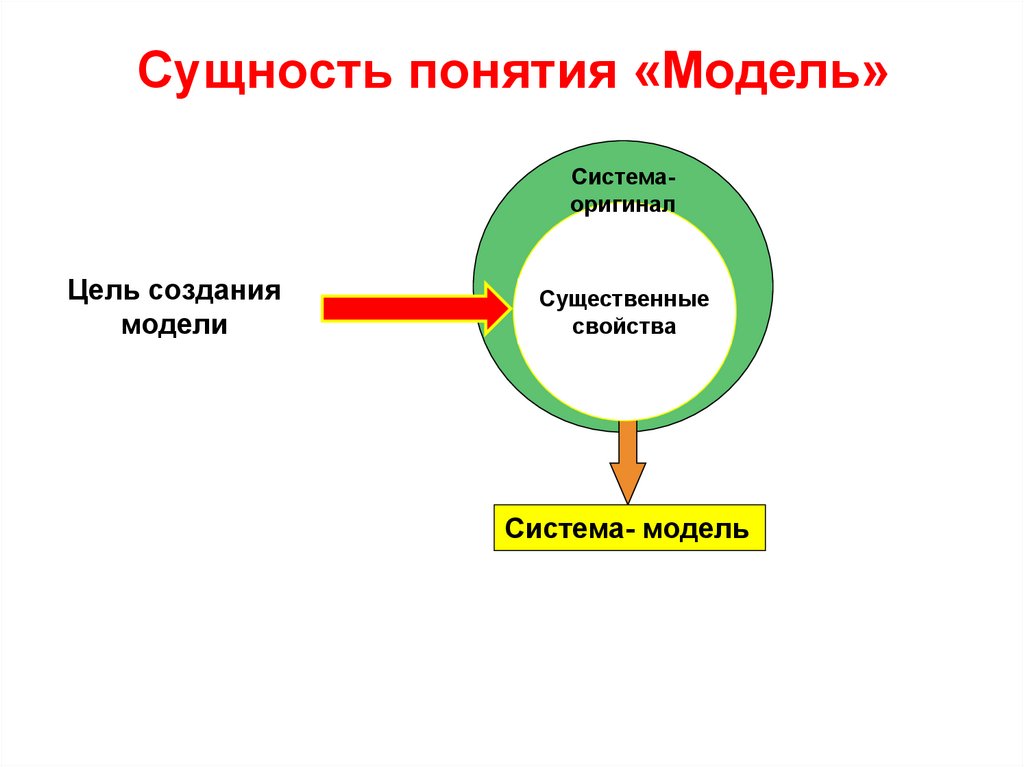
Сущность понятия «Модель»
Системаоригинал
Цель создания
модели
Существенные
свойства
Система- модель

7.

Модель есть созданная или
выбранная субъектом система,
воспроизводящая существенные для
данной цели познания стороны
(элементы, свойства, отношения,
параметры) изучаемого объекта и в
силу этого находящаяся с ним в
таком отношении замещения и
сходства, что исследование ее
служит опосредованным способом
получения знания об этом объекте

8.

Признаки модели:
между моделью и оригиналом имеется отношение
сходства, форма которого явно выражена
и точно зафиксирована
(условия отражения или уточненной аналогии)
модель в процессе научного познания является
заместителем изучаемого объекта
(условие репрезентации)
изучение модели позволяет получить информацию
(сведения) об оригинале
(условие экстраполяции)

9.

Методологические выводы:
1. Модель строится для
решения конкретных задач
исследования
2. Характеристика системы
должна даваться с помощью
нескольких моделей
(многомодельный подход)

10.

Моделированием называется
замещение одного объекта
другим с целью получения
информации о важнейших
свойствах объекта-оригинала
с помощью объекта-модели

11.

Роль моделей в процессе познания
Наблюдения
Используются для сбора фактов
Описательная
Дают описание объектов
или процессов
Экспериментальная
Обеспечивают проведение
экспериментов

12.

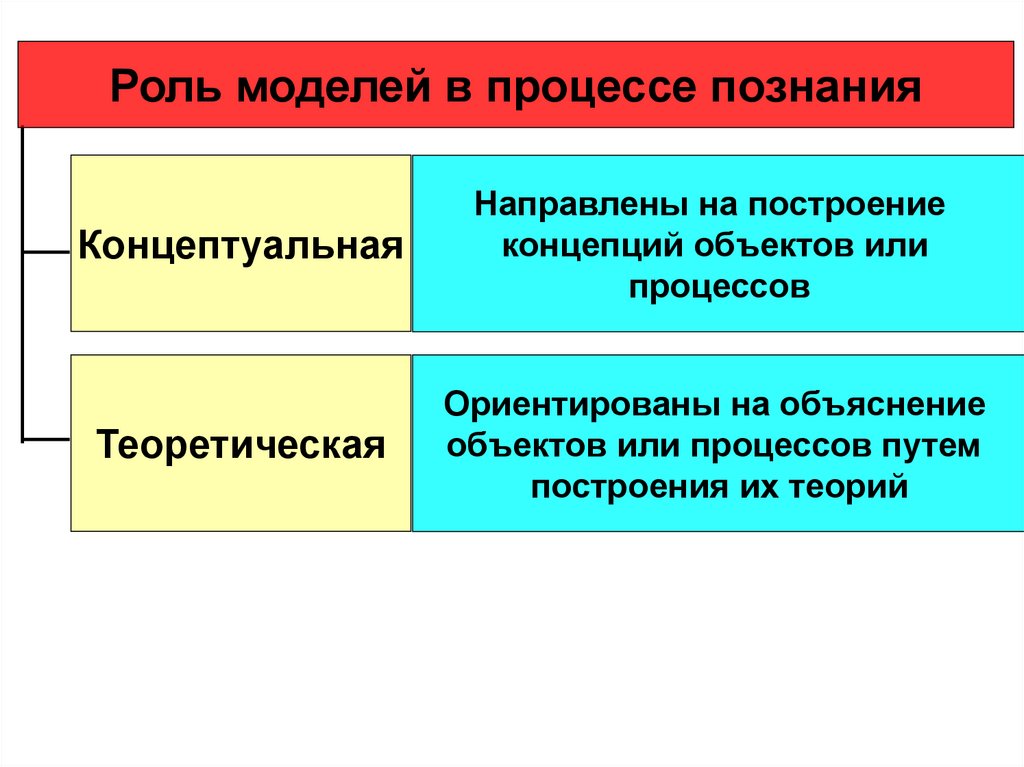
Роль моделей в процессе познания
Концептуальная
Направлены на построение
концепций объектов или
процессов
Теоретическая
Ориентированы на объяснение
объектов или процессов путем
построения их теорий

13.

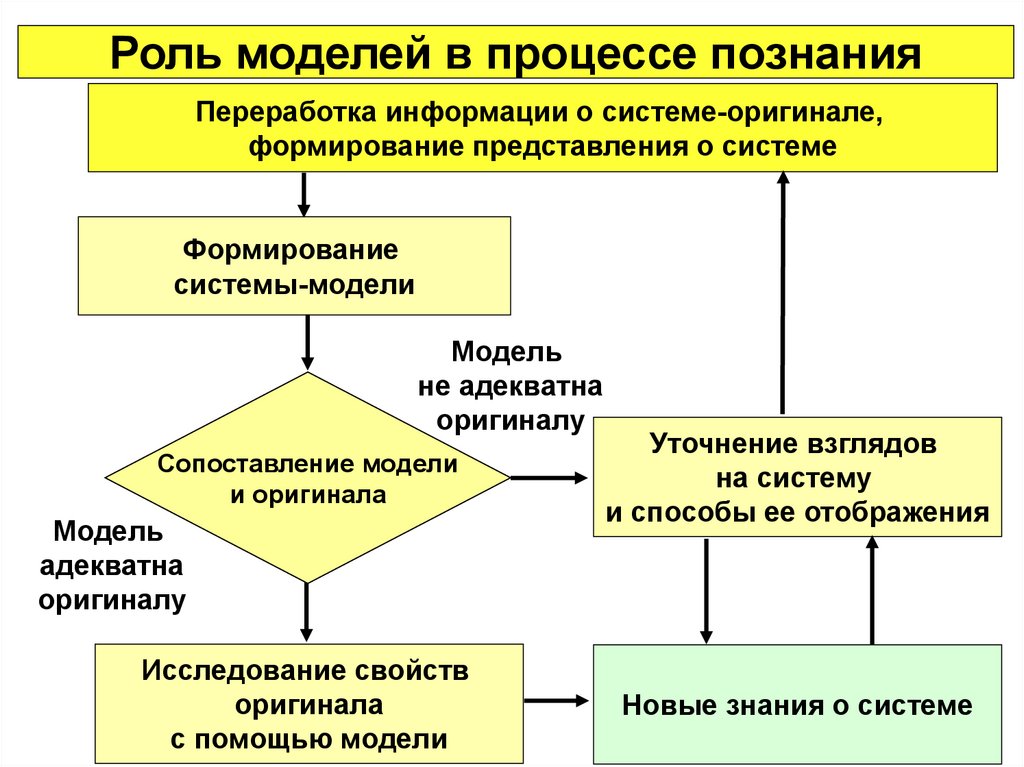
Роль моделей в процессе познания
Переработка информации о системе-оригинале,
формирование представления о системе
Формирование
системы-модели
Модель
не адекватна
оригиналу
Сопоставление модели
и оригинала
Модель
адекватна
оригиналу
Исследование свойств
оригинала
с помощью модели
Уточнение взглядов
на систему
и способы ее отображения
Новые знания о системе

14.

15.

Требования к моделям
1. полнота модели - должна предоставлять
пользователю возможность получения
необходимого набора оценок характеристик
системы с требуемой точностью и достоверностью;
2. гибкость модели - должна давать возможность
воспроизведения различных ситуаций при
варьировании структуры, алгоритмов и параметров
системы;

16.

Требования к моделям
3. длительность разработки и реализации модели
большой системы - должна быть по возможности
минимальной при учёте ограничений на имеющиеся
ресурсы;
4. структура модели - должна быть блочной, то есть
допускать возможность замены, добавления и
исключения некоторых частей без переделки всей
модели;
5. информационное обеспечение - должно
предоставлять возможность эффективной работы
модели с базой данных определённого класса;

17.

Требования к моделям
6. программные и технические средства - должны
обеспечивать эффективную машинную реализацию
модели и удобное общение с ней пользователя;
7. должно быть обеспечено проведение
целенаправленных (планируемых) экспериментов
с моделью.
Процесс моделирования является итерационным
и продолжается до получения модели, которую
можно считать адекватной.

18.

Формальная модель системы
S - система;
E - внешняя среда;
xi X , i 1, nx
- совокупность входных
воздействий на систему;
vl V , l 1, nv
- совокупность воздействий
внешней среды;
hk H , k 1, nH - совокупность внутренних
y j Y , j 1, nY
(собственных) параметров
системы;
- совокупность выходных
характеристик системы;

19.

Формальная модель системы
независимые переменные:
x (t ) ( x1 (t ), x2 (t ), ..., xnX (t ));
v (t ) (v1 (t ), v2 (t ), ..., vnV (t ));
h (t ) (h1 (t ), h2 (t ), ..., hnH (t ));
зависимые переменные:
y (t ) ( y1 (t ), y2 (t ), ..., ynY (t ));
y(t ) FS ( x, v , h , t )
- закон функционирования системы;

20.

Формальная модель системы
AS - алгоритм функционирования системы;
Состояние системы в момент времени t , t (t0 , T )
z ( z1 (t ), z2 (t ), ..., zk (t ))
Начальные условия: z ( z1 (t0 ), z2 (t0 ), ..., zk (t0 ));
0
z (t ) Ф( z , x , v , h , t ).
y (t ) F ( z , t ).
y (t ) F Ф( z 0 , x, v , h , t ) .
0

21.

Математическая модель системы –
конечное подмножество переменных
x(t ), v (t ), h (t )
вместе с математическими связями
между ними и характеристиками
y (t ).

22.

23.

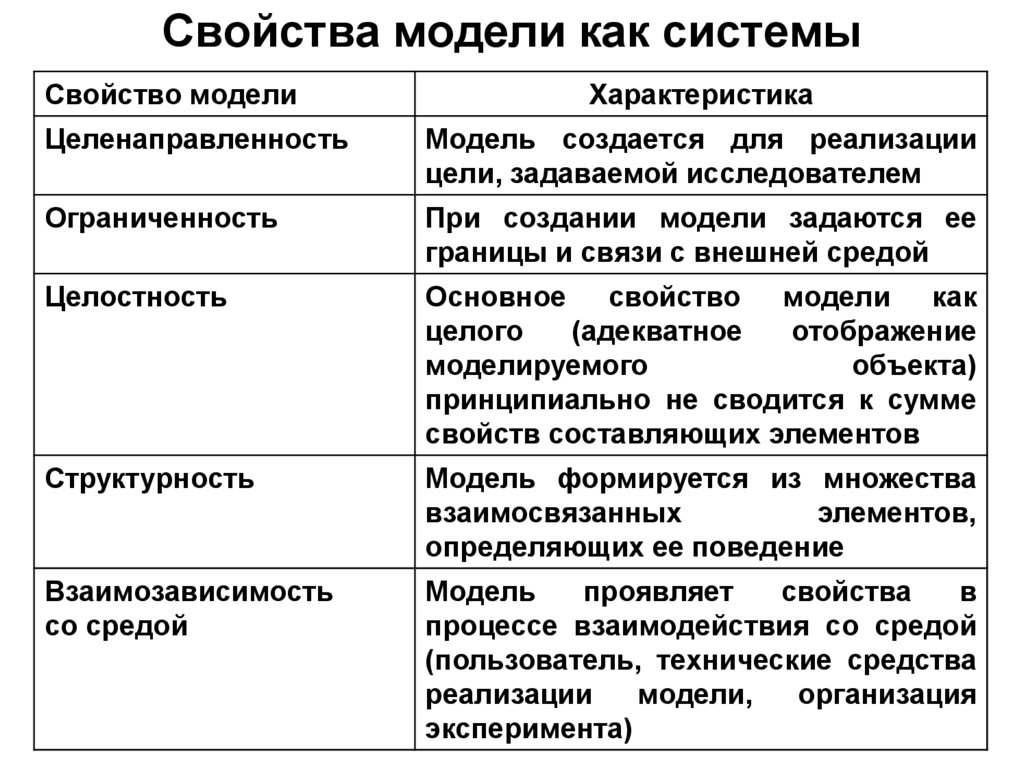
Свойства модели как системы
Свойство модели
Характеристика
Целенаправленность
Модель создается для реализации
цели, задаваемой исследователем
Ограниченность
При создании модели задаются ее
границы и связи с внешней средой
Целостность
Основное свойство модели как
целого
(адекватное
отображение
моделируемого
объекта)
принципиально не сводится к сумме
свойств составляющих элементов
Структурность
Модель формируется из множества
взаимосвязанных
элементов,
определяющих ее поведение
Взаимозависимость
со средой
Модель
проявляет
свойства
в
процессе взаимодействия со средой
(пользователь, технические средства
реализации
модели,
организация
эксперимента)

24.

Свойства модели как системы
Свойство модели
Характеристика
Иерархичность
Соподчиненность
элементов
модели
(модульная конструкция модели)
Множественность
описаний
Характеристика
модели
требует
множественности
ее
описаний
(концептуальное,
формальное,
алгоритмическое и т.д.)
Адаптивность
Модель должна иметь возможность
адаптации к новым задачам, условиям и
методам
исследования
(открытый
характер
модели,
возможность
ее
развития)
Управляемость
Модель должна обеспечивать управление
со стороны экспериментаторов для
получения возможности рассмотрения
протекания
процесса
в
различных
условиях (широкий спектр управляемых
параметров, вмешательство человека в
процесс моделирования)

25.

26.

Любая классификация методов
моделирования обречена на
неполноту ввиду того, что
терминология в этой области
опирается не столько на
"строгие" правила, сколько на
языковые, научные и
практические традиции

27.

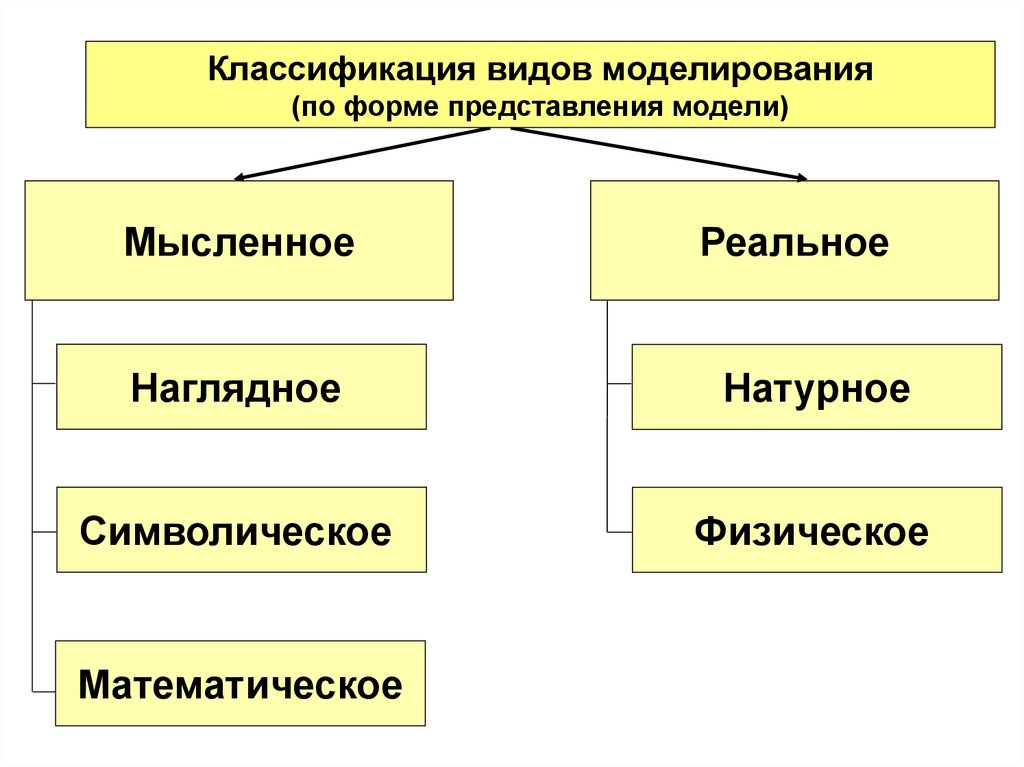
Классификация видов моделирования
(по форме представления модели)
Мысленное
Реальное
Наглядное
Натурное
Символическое
Физическое
Математическое

28.

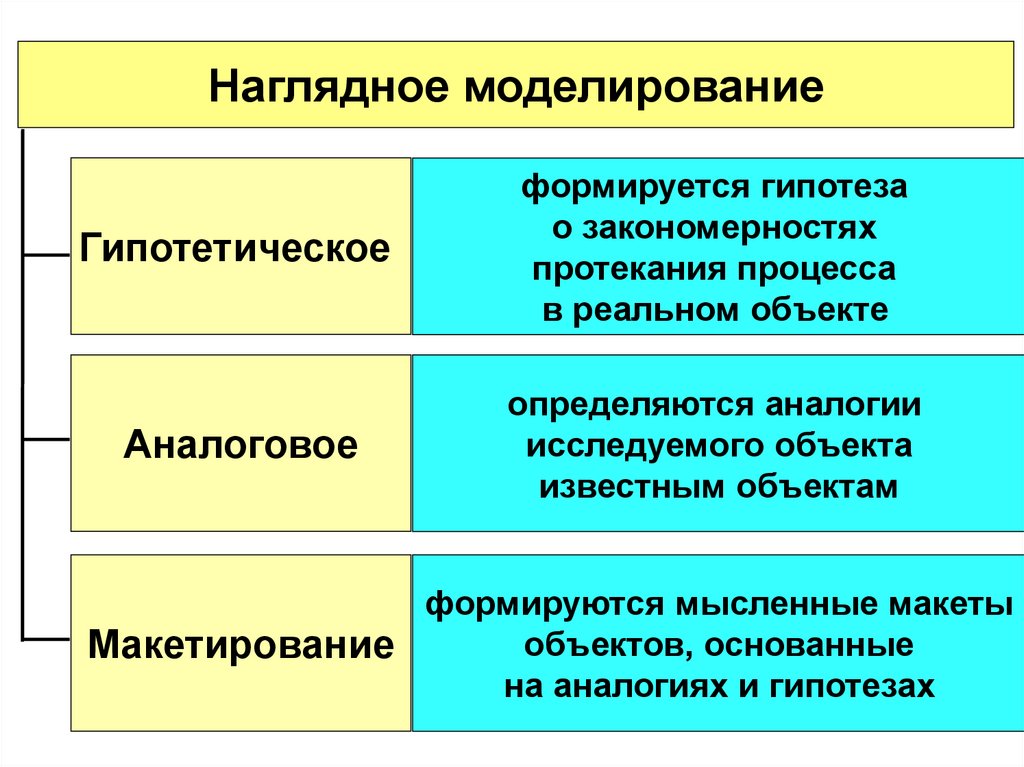
Наглядное моделирование
Гипотетическое
формируется гипотеза
о закономерностях
протекания процесса
в реальном объекте
Аналоговое
определяются аналогии
исследуемого объекта
известным объектам
формируются мысленные макеты
объектов, основанные
Макетирование
на аналогиях и гипотезах

29.

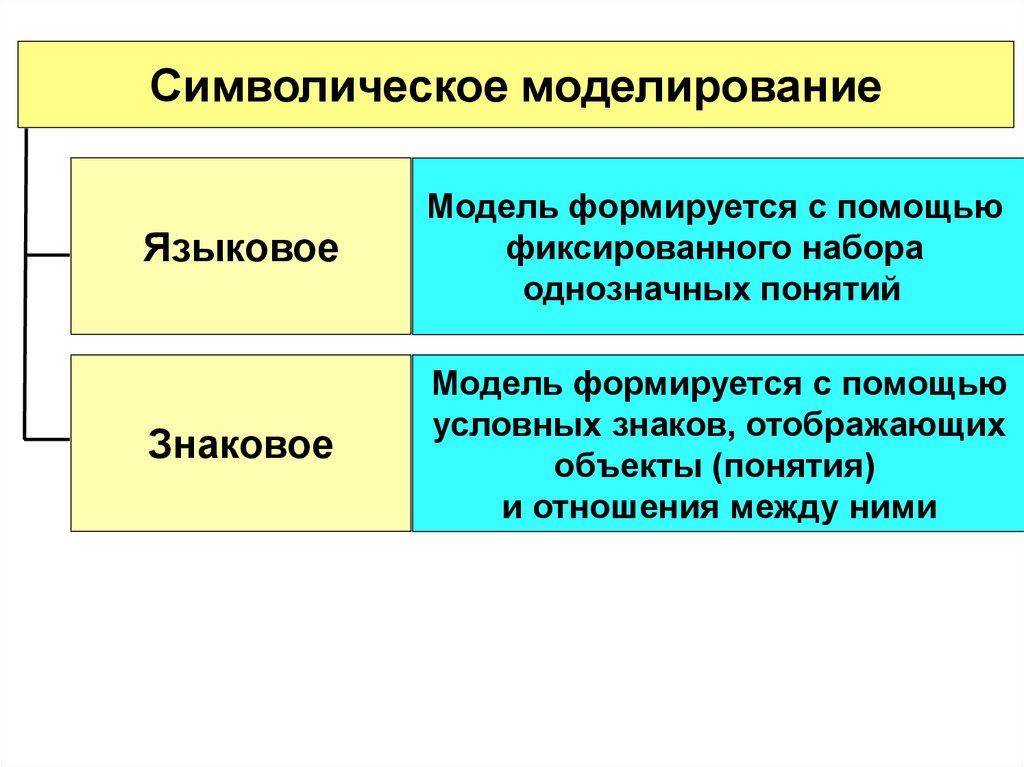
Символическое моделирование
Языковое
Модель формируется с помощью
фиксированного набора
однозначных понятий
Знаковое
Модель формируется с помощью
условных знаков, отображающих
объекты (понятия)
и отношения между ними

30.

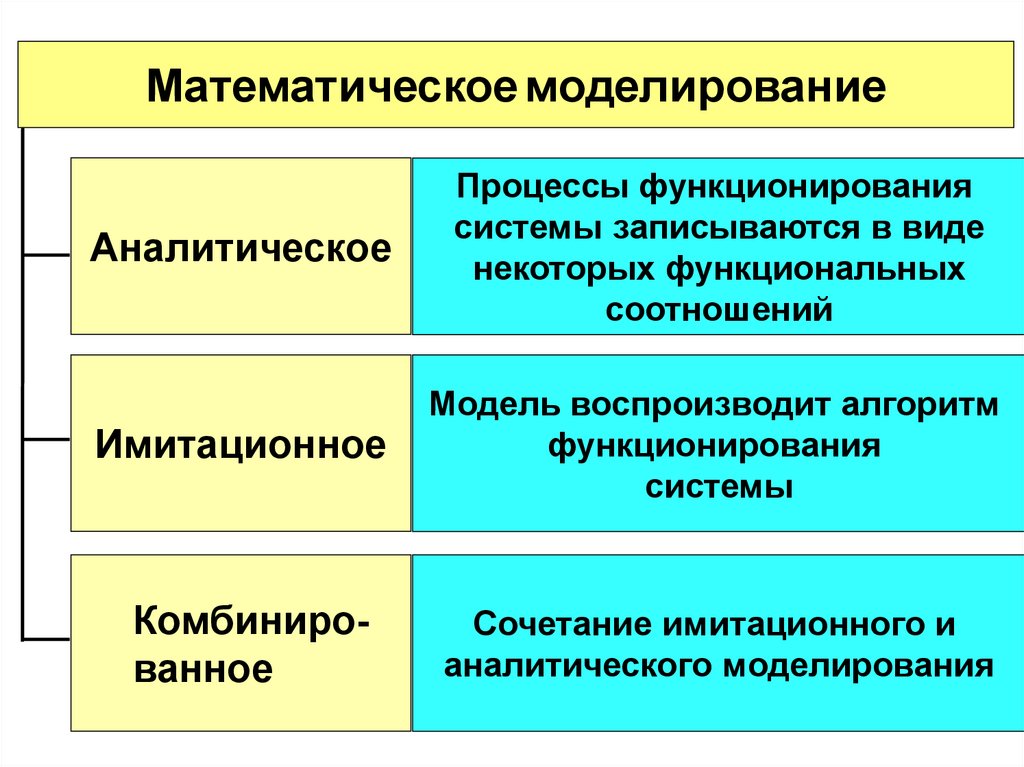
Математическое моделирование
Аналитическое
Процессы функционирования
системы записываются в виде
некоторых функциональных
соотношений
Имитационное
Модель воспроизводит алгоритм
функционирования
системы
Комбинированное
Сочетание имитационного и
аналитического моделирования

31.

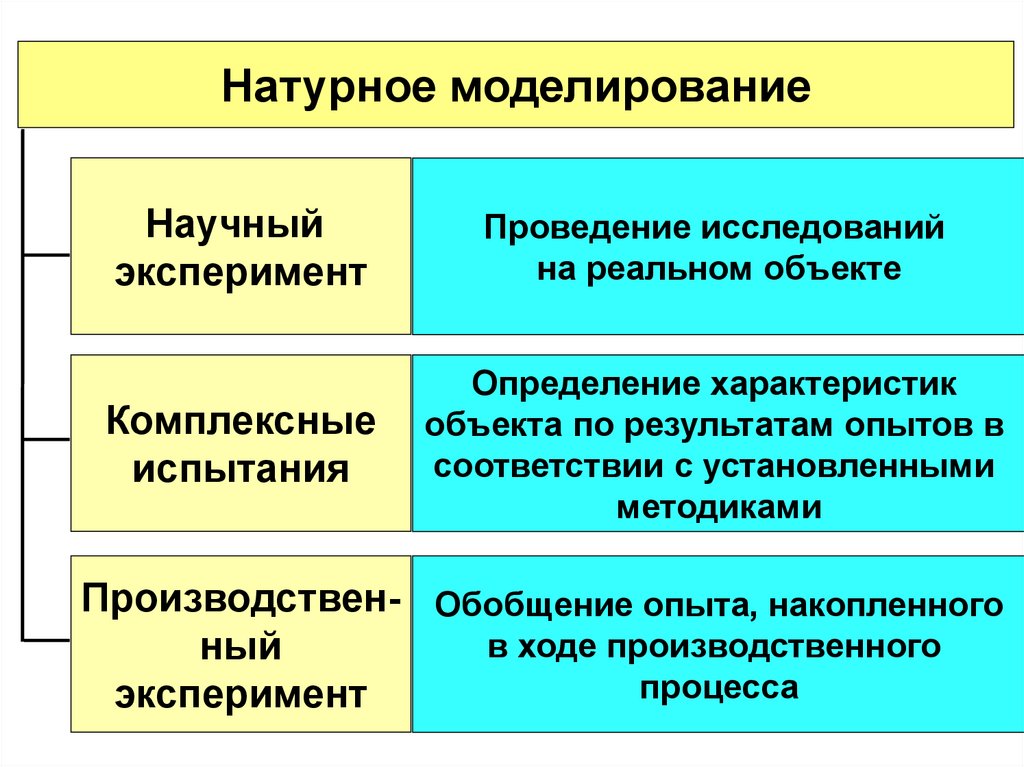
Натурное моделирование
Научный
эксперимент
Проведение исследований
на реальном объекте
Комплексные
испытания
Определение характеристик
объекта по результатам опытов в
соответствии с установленными
методиками
Производствен- Обобщение опыта, накопленного
в ходе производственного
ный
процесса
эксперимент

32.

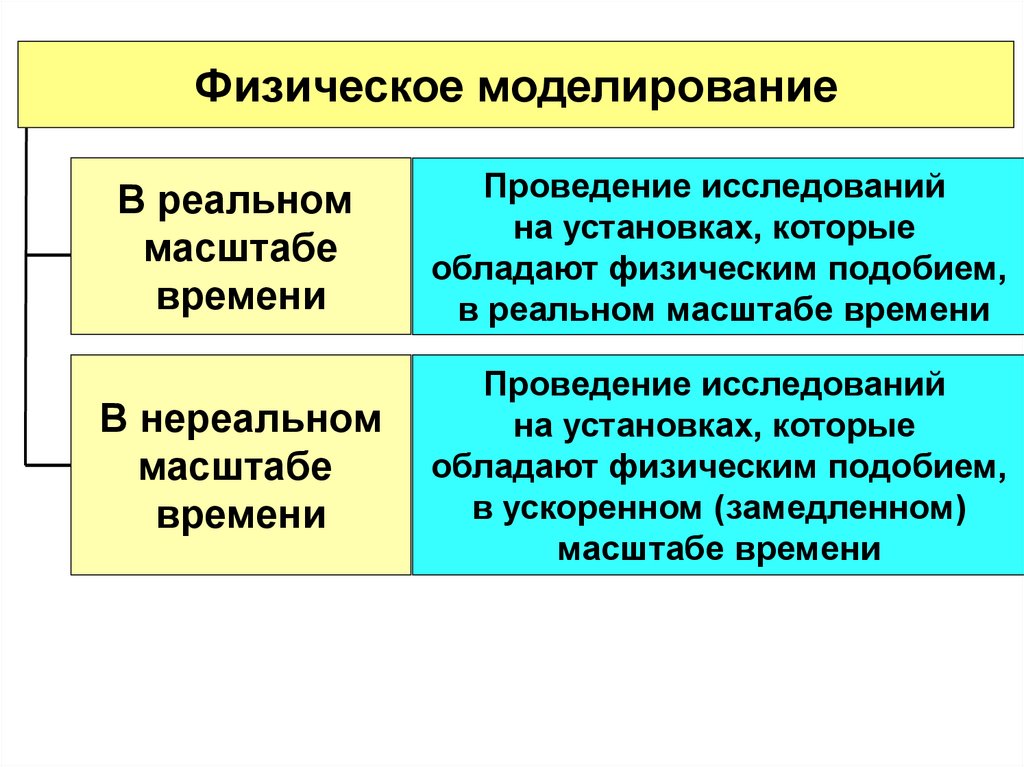
Физическое моделирование
В реальном
масштабе
времени
Проведение исследований
на установках, которые
обладают физическим подобием,
в реальном масштабе времени
В нереальном
масштабе
времени
Проведение исследований
на установках, которые
обладают физическим подобием,
в ускоренном (замедленном)
масштабе времени

33.

34.

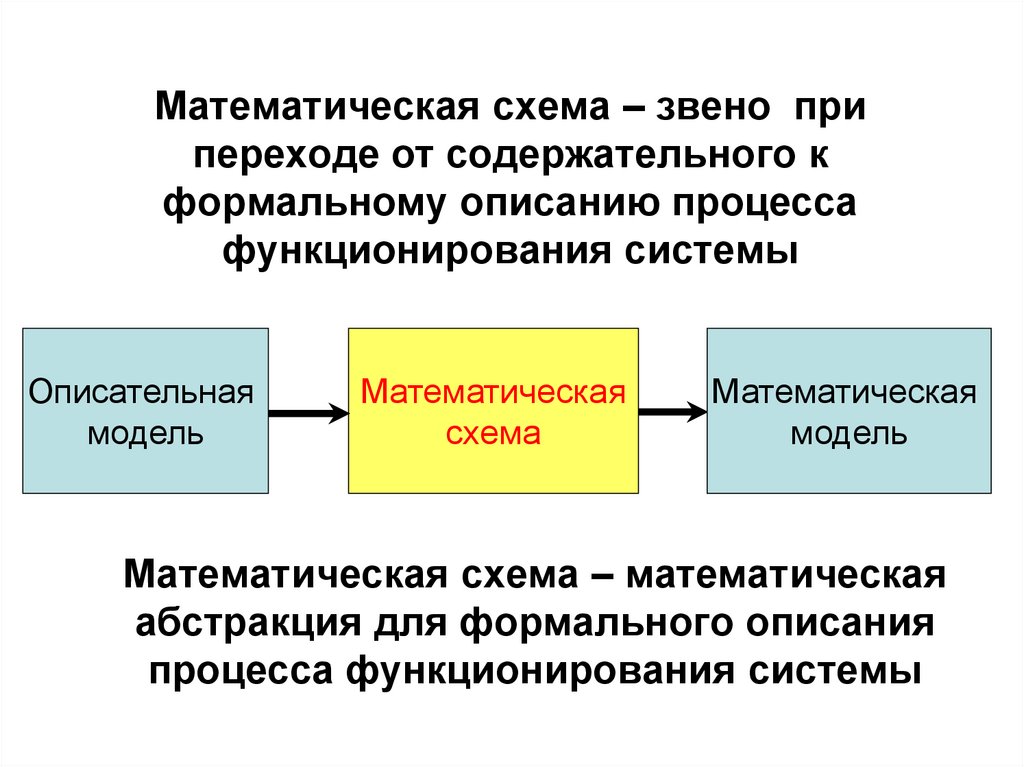
Математическая схема – звено при
переходе от содержательного к
формальному описанию процесса
функционирования системы
Описательная
модель
Математическая
схема
Математическая
модель
Математическая схема – математическая
абстракция для формального описания
процесса функционирования системы

35.

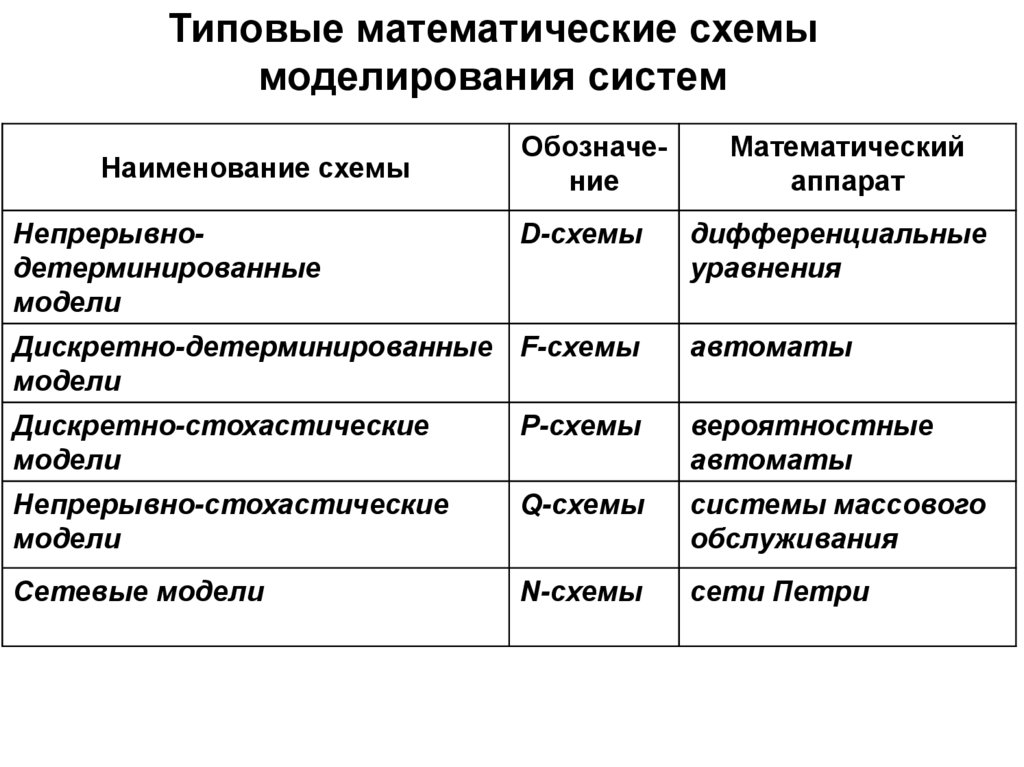
Типовые математические схемы
моделирования систем
Наименование схемы
Непрерывнодетерминированные
модели
Обозначение
Математический
аппарат
D-схемы
дифференциальные
уравнения
Дискретно-детерминированные F-схемы
модели
автоматы
Дискретно-стохастические
модели
P-схемы
вероятностные
автоматы
Непрерывно-стохастические
модели
Q-схемы
системы массового
обслуживания
Сетевые модели
N-схемы
сети Петри