Основные функции и законы алгебры логики

1.

Составитель:
Учитель информатики
МБОУ «СОШ №18»
Пестрецова Л.А.

2.

Основные понятия
Логические выражения
Логическое отрицание
Логическое сложение
Логическое умножение
Логическое следование
Эквивалентность
Составление таблиц истинности
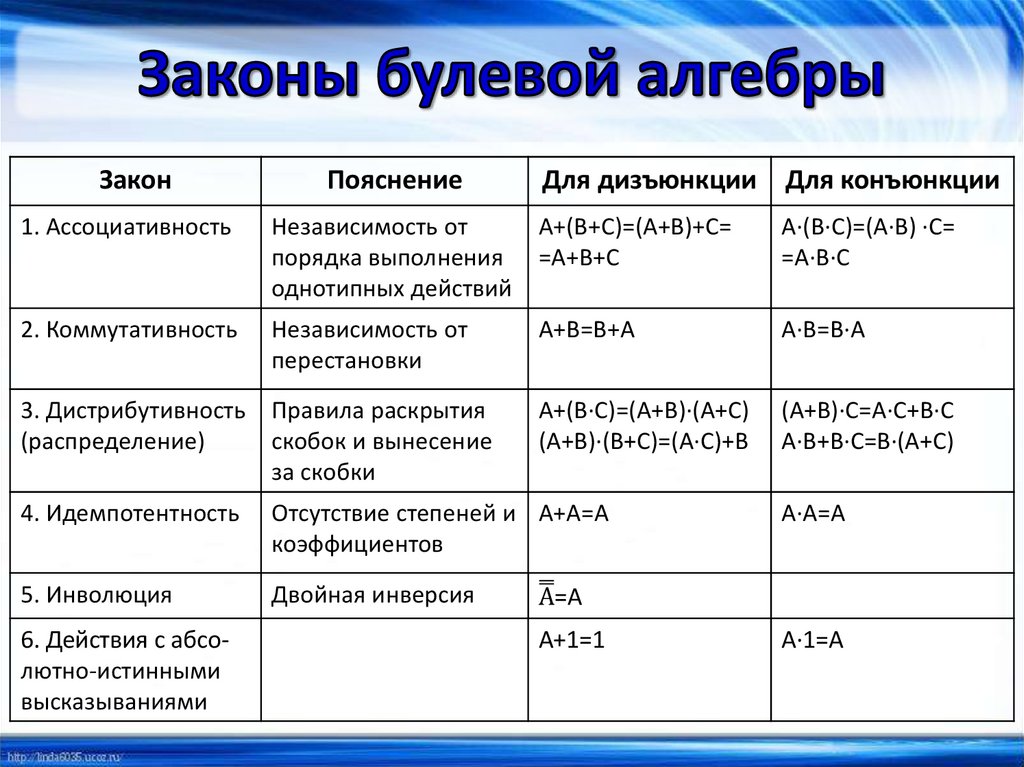
Законы булевой алгебры

3.

Алгебра логики – это аппарат, который позволяет выполнять
действия над высказываниями.
Высказывание – это предложение относительно которого имеет
смысл говорить истинно оно или ложно.
Основы алгебры логики (Булевой алгебры)
разработаны в XIX веке английским
математиком Джорджем Булем.
Высказывание
Значение
Все кошки серы
Ложь
Париж – столица Франции
Истина
5 х 5 = 25
Истина
Н + О = Н2О
Ложь

4.

Уберите предложения не являющиеся высказываниями

5.

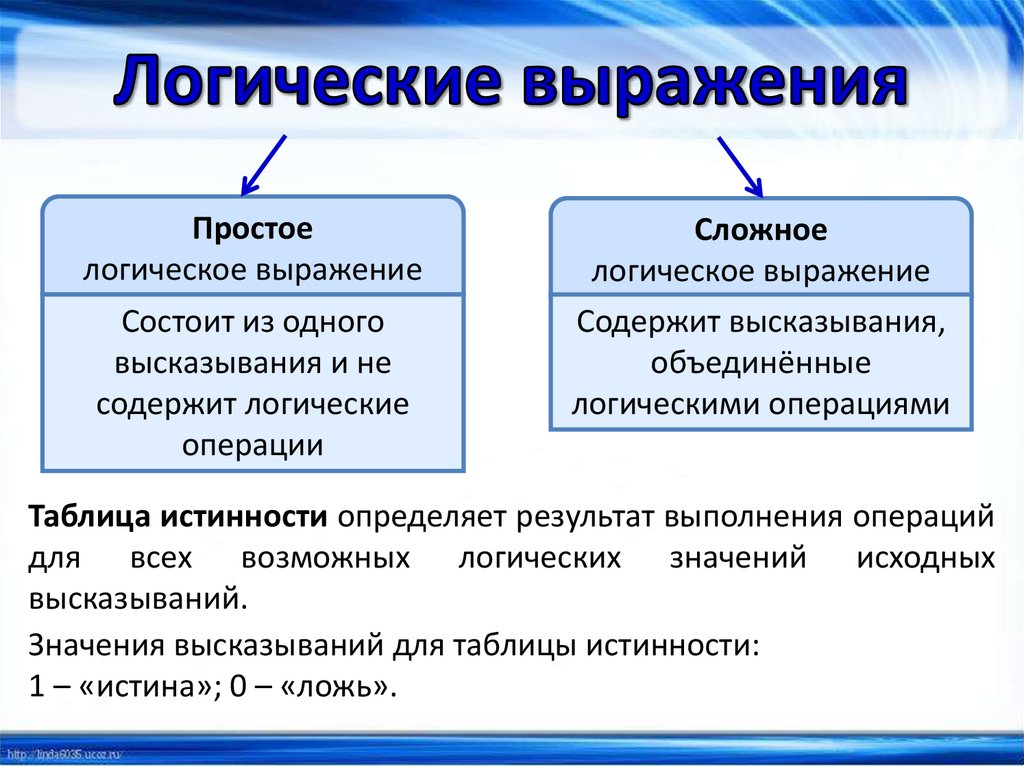
Простое
логическое выражение
Состоит из одного
высказывания и не
содержит логические
операции
Сложное
логическое выражение
Содержит высказывания,
объединённые
логическими операциями
Таблица истинности определяет результат выполнения операций
для всех возможных логических значений исходных
высказываний.
Значения высказываний для таблицы истинности:
1 – «истина»; 0 – «ложь».

6.

Логическая операция НЕ (логическое отрицание, инверсия)
применяется к одному аргументу, простому или сложному.
Таблица истинности для логического отрицания:
Результат
операции
логического
отрицания истинен, когда исходное
высказывание ложно, и наоборот.
Операция логического отрицания аналогична
работе переключателя настольной лампы.
A
0
1
1
0

7.

Логическая операция ИЛИ (логическое сложение, дизъюнкция)
выполняет функцию объединения двух высказываний, простых
или сложных.
Условные обозначения: A или B; A + B; A v B; A|B; A or B.
Таблица истинности для логического сложения:
Результат
операции
логического
сложения истинен, когда истинно хотя
бы
одно
входящее
в
него
высказывание.
Операция логического сложения аналогична
работе параллельного соединения лампочек.
A
В
АvВ
0
0
0
0
1
1
1
0
1
1
1
1

8.

Логическая операция И (логическое умножение, конъюнкция)
выполняет функцию пересечения двух высказываний, простых
или сложных.
Условные обозначения: A и B; A · B; A ^ B; A & B; A and B.
Таблица истинности для логического умножения:
Результат
операции
логического
умножения истинен, когда истинны
все входящее в него высказывание.
Операция логического умножения аналогична
работе
последовательного
соединения
лампочек.
A
В
А^В
0
0
0
0
1
0
1
0
0
1
1
1

9.

Приведите примеры сложных высказываний, используя рисунки:

10.

Количество строк в таблице истинности = 2N, где N – число
высказываний в логическом выражении.
Приоритет выполнения действий:
1) Действия в скобках
2) Инверсия (отрицание)
3) Конъюнкция (логическое умножение)
4) Дизъюнкция (логическое сложение)
Правила-подсказки:
А+1=1
А·0=0

11.

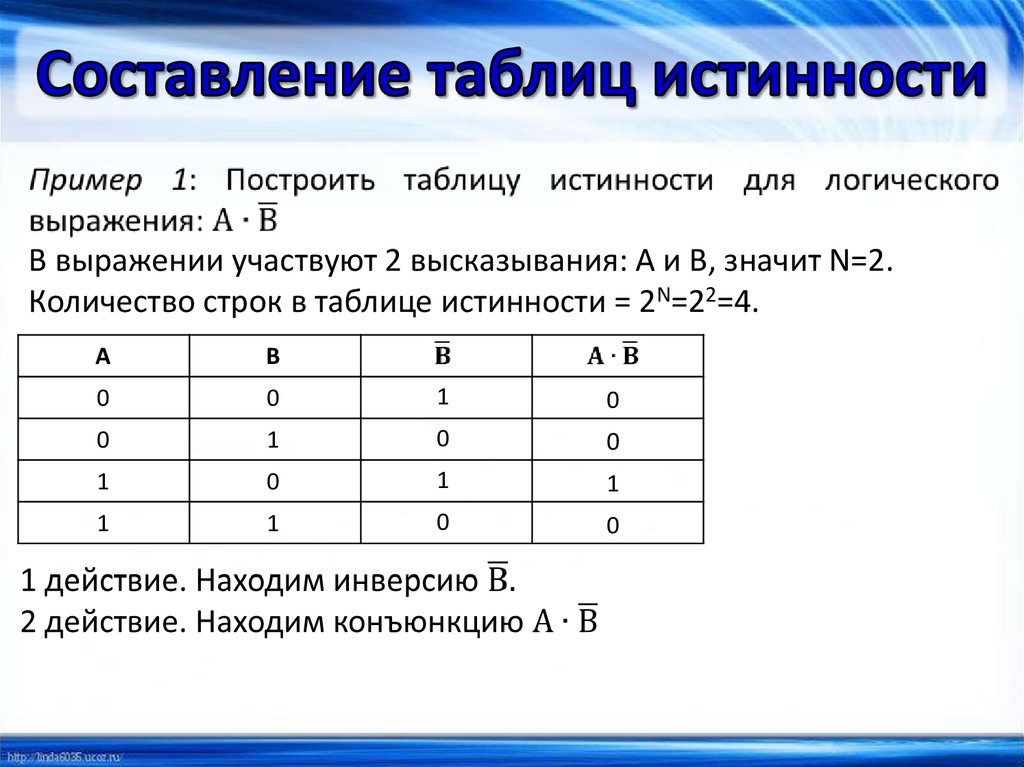
В выражении участвуют 2 высказывания: А и В, значит N=2.
Количество строк в таблице истинности = 2N=22=4.
A
B
0
0
1
0
0
1
0
0
1
0
1
1
1
1
0
0

12.

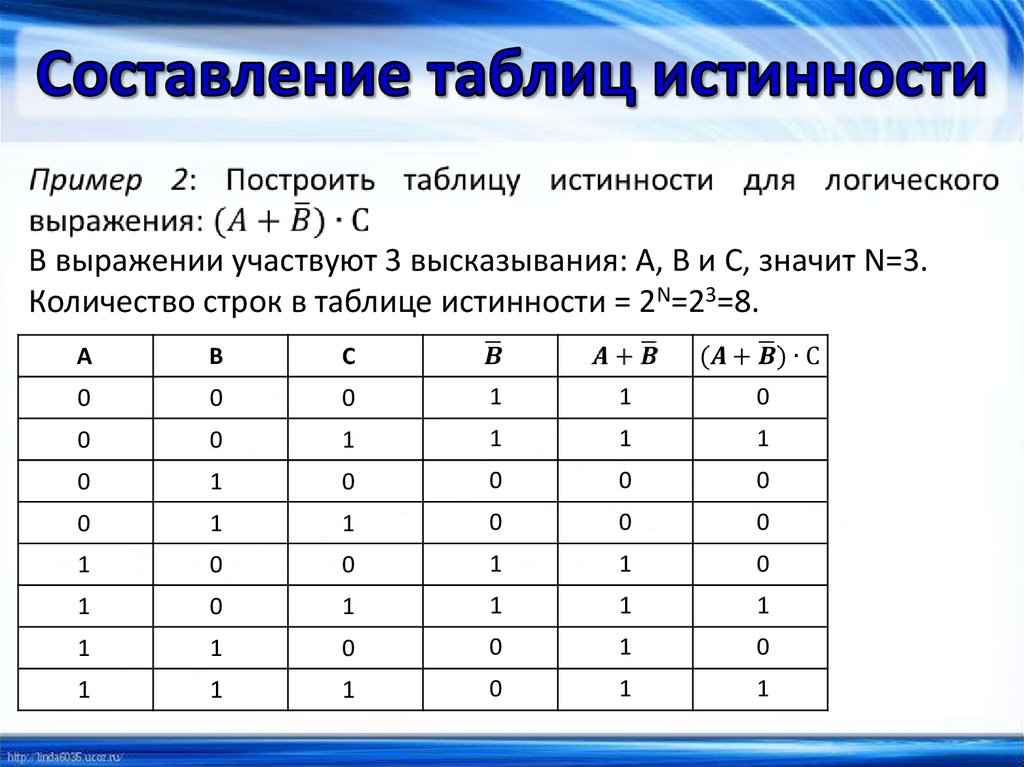
В выражении участвуют 3 высказывания: А, В и С, значит N=3.
Количество строк в таблице истинности = 2N=23=8.
A
B
С
0
0
0
1
1
0
0
0
1
1
1
1
0
1
0
0
0
0
0
1
1
0
0
0
1
0
0
1
1
0
1
0
1
1
1
1
1
1
0
0
1
0
1
1
1
0
1
1

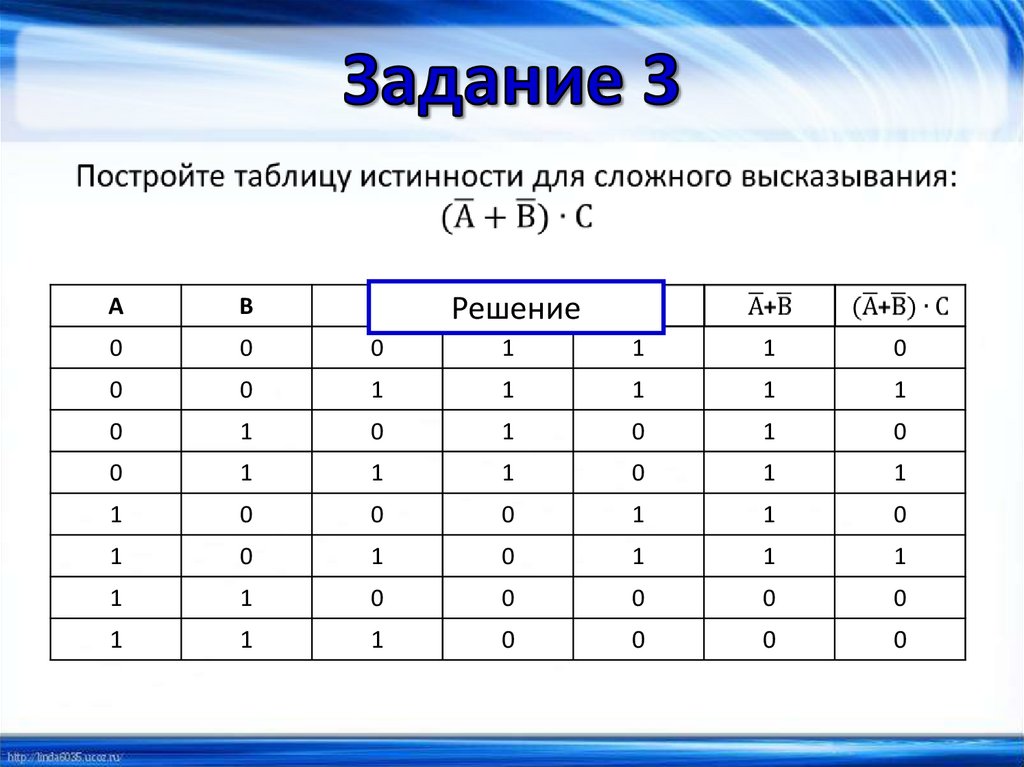
13.

А
В
С
Решение
0
0
0
1
1
1
0
0
0
1
1
1
1
1
0
1
0
1
0
1
0
0
1
1
1
0
1
1
1
0
0
0
1
1
0
1
0
1
0
1
1
1
1
1
0
0
0
0
0
1
1
1
0
0
0
0

14.

Закон
Пояснение
1. Ассоциативность
Независимость от
порядка выполнения
однотипных действий
А+(В+С)=(А+В)+С=
=А+В+С
А·(В·С)=(А·В) ·С=
=А·В·С
2. Коммутативность
Независимость от
перестановки
А+В=В+А
А·В=В·А
А+(В·С)=(А+В)·(А+С)
(А+В)·(В+С)=(А·С)+В
(А+В)·С=А·С+В·С
А·В+В·С=В·(А+С)
3. Дистрибутивность Правила раскрытия
(распределение)
скобок и вынесение
за скобки
Для дизъюнкции Для конъюнкции
4. Идемпотентность
Отсутствие степеней и А+А=А
коэффициентов
5. Инволюция
Двойная инверсия
6. Действия с абсолютно-истинными
высказываниями
А+1=1
А·А=А
А·1=А

15.

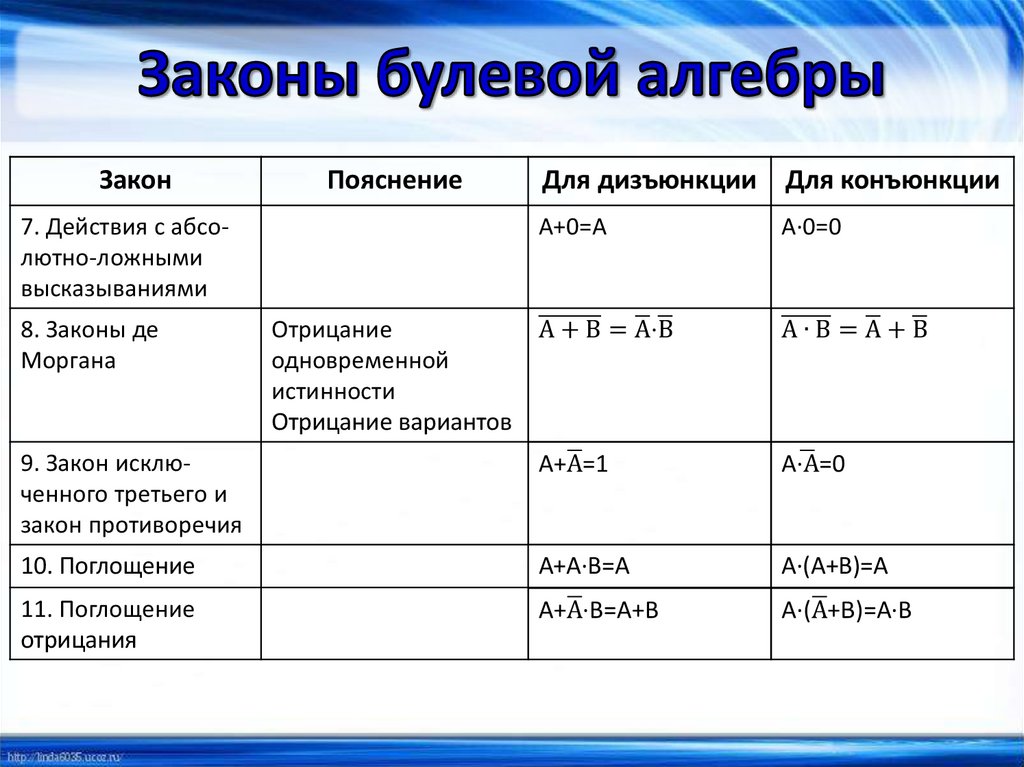
Закон
Пояснение
7. Действия с абсолютно-ложными
высказываниями
8. Законы де
Моргана
Для дизъюнкции Для конъюнкции
А+0=А
А·0=0
А+А·В=А
А·(А+В)=А
Отрицание
одновременной
истинности
Отрицание вариантов
9. Закон исключенного третьего и
закон противоречия
10. Поглощение
11. Поглощение
отрицания

16.

Решение

17.

§п.3.1 (изучить)