Множество прямых параллельных данной прямой

1. ВЕРНО - НЕВЕРНО ?

1. Верно ли, что через любую точку
пространства можно провести
множество прямых параллельных
данной прямой?

2. ОТВЕТЫ И ПОДСКАЗКИ

• Ответ: Неверно.
По теореме о существовании прямой, параллельной
данной прямой, через точку пространства можно
провести единственную прямую.
b
a
B

3. ВЕРНО - НЕВЕРНО ?

2. Верно ли, что если одна из двух
параллельных прямых пересекает
плоскость, то и другая тоже пересекает
эту плоскость?

4. ОТВЕТЫ И ПОДСКАЗКИ

Ответ: Верно.
По лемме о пересечении плоскости двумя
параллельными прямыми, если одна из
параллельных прямых пересекает данную
плоскость, то и другая прямая пересекает эту
плоскость.
b
a
M

5. ВЕРНО - НЕВЕРНО ?

3. Верно ли, что две непересекающиеся
прямые в пространстве параллельны?

6. ОТВЕТЫ И ПОДСКАЗКИ

3. Ответ: неверно.
В пространстве не имеют общих точек
параллельные и скрещивающиеся
прямые.
c и d - скрещиваются
a // b
d
b
a
с

7. ВЕРНО – НЕВЕРНО?

4. Верно ли, что если две прямые
параллельны некоторой плоскости, то
они параллельны друг другу?

8. ОТВЕТЫ И ПОДСКАЗКИ

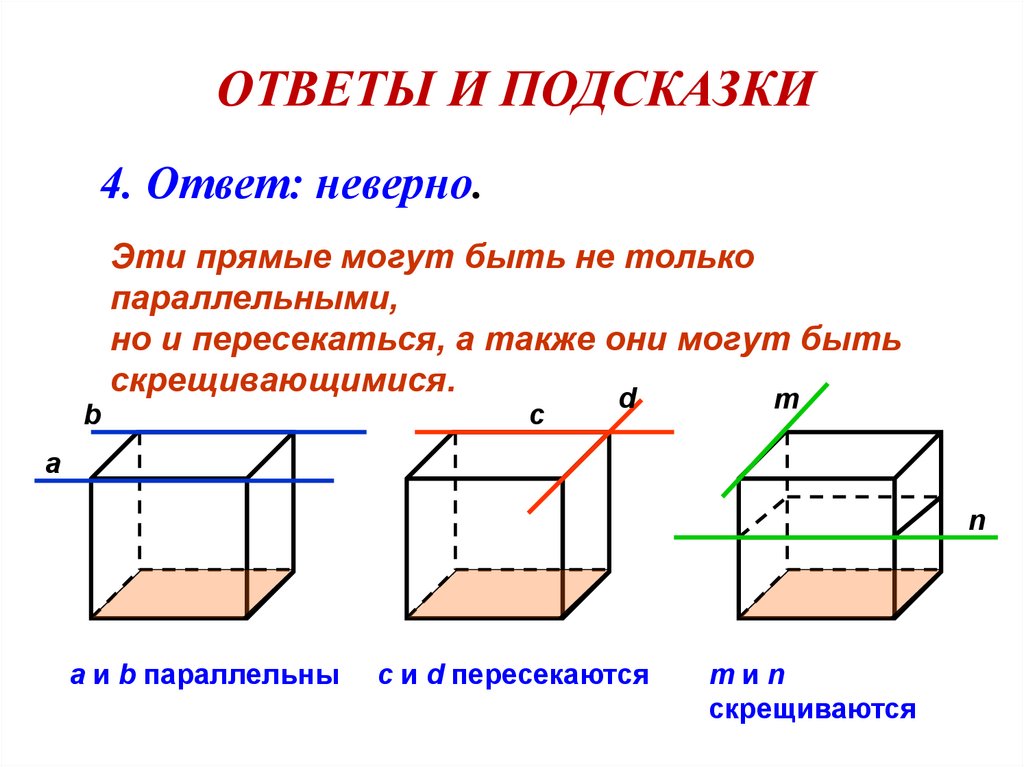
4. Ответ: неверно.
b
Эти прямые могут быть не только
параллельными,
но и пересекаться, а также они могут быть
скрещивающимися.
d
m
c
a
n
a и b параллельны
с и d пересекаются
mиn
скрещиваются

9. ВЕРНО – НЕВЕРНО?

5. Верно ли, что если две плоскости
пересечены двумя параллельными
прямыми и отрезки данных прямых,
заключённых между ними равны, то
плоскости параллельны?

10. ОТВЕТЫ И ПОДСКАЗКИ

5. Ответ: Неверно.
Это утверждение неверно , так как нет
условий для выполнения признака
параллельности плоскостей.
Если a // b и
АА1=BВ1,
то плоскости
могут
быть
параллельны, а
могут
пересекаться
а
А
b
А
B
В
D1
C1
В1
C
А1
А1
B1

11. Ортогональная проекция плоской фигуры на плоскость и ее площадь

12. Итак, мы приступили к изучению стереометрии – геометрии в пространстве. Как всегда нам необходимо уметь изображать

геометрические фигуры, причем все чертежи мы по-прежнему
выполняем на плоскости (на странице тетради, на доске и т.д.).
Каким образом пространственную фигуру (например, куб)
можно «уложить» в плоскость?
Для решения этой задачи применяется метод параллельного
проектирования.

13. ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ

косоугольное
прямоугольное

14. ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ

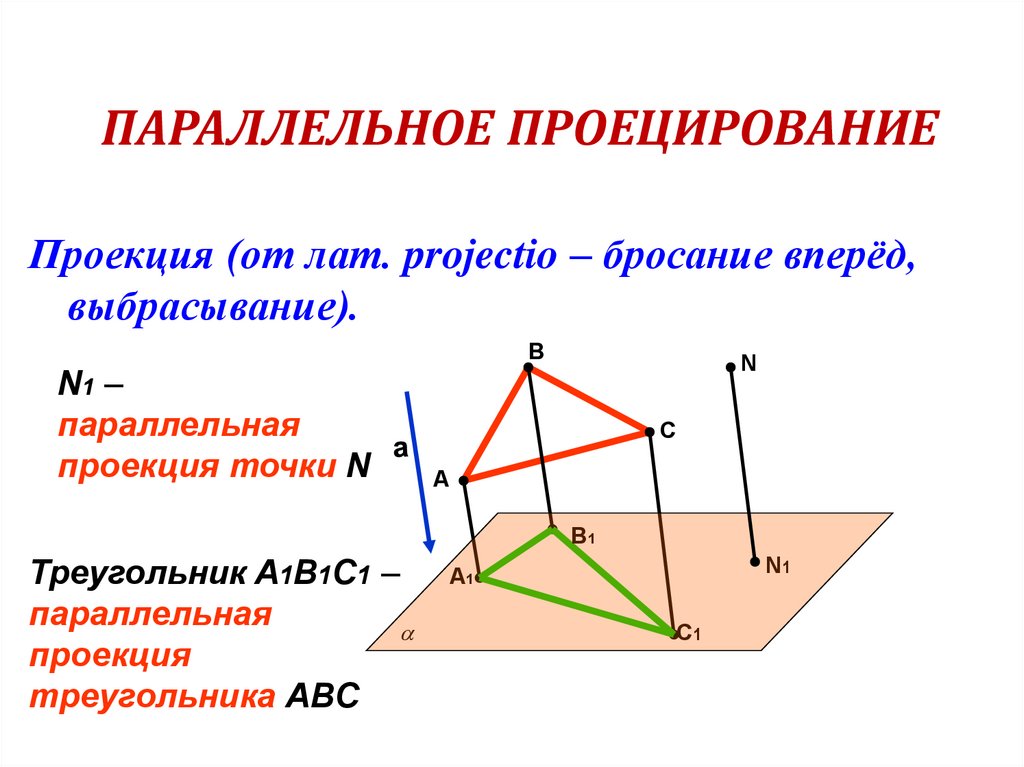
Проекция (от лат. projectio – бросание вперёд,
выбрасывание).
N1 –
параллельная
проекция точки N
B
N
C
A
B1
Треугольник A1B1C1 –
параллельная
проекция
треугольника ABC
N1
A1
C1

15.

А
Выясним суть этого метода
геометрической фигуры – точки.
на
примере
простейшей
Итак, у нас есть геометрическая фигура в пространстве – точка А.

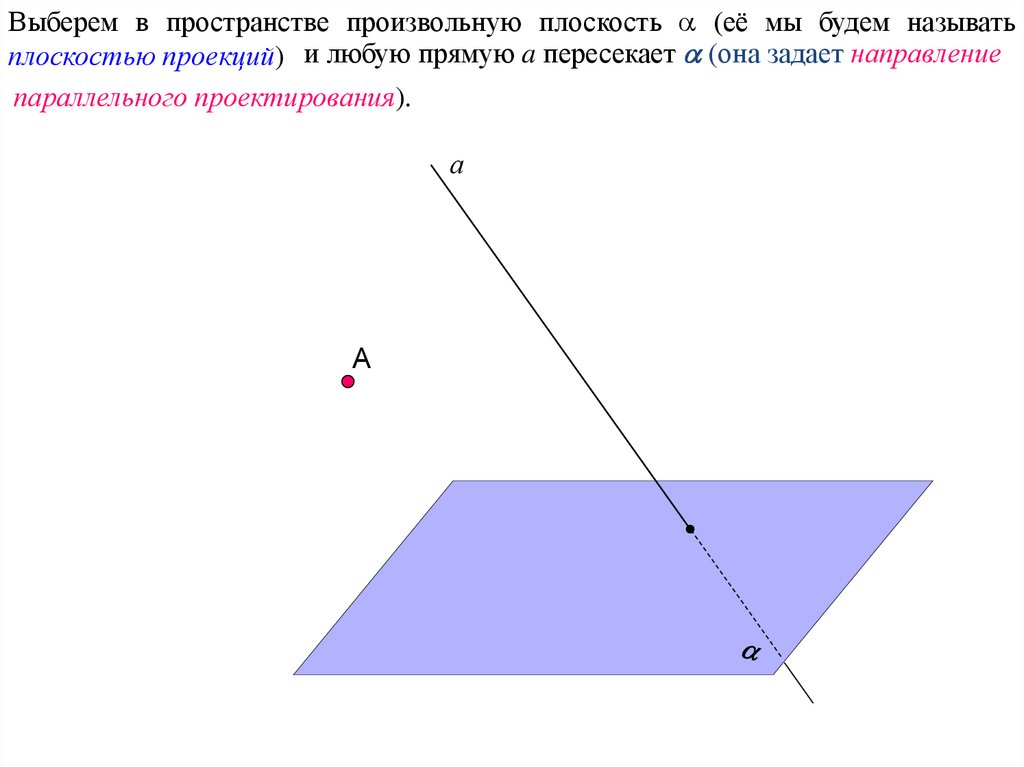
16.

Выберем в пространстве произвольную плоскость (её мы будем называть
плоскостью проекций) и любую прямую a пересекает (она задает направление
параллельного проектирования).
а
А

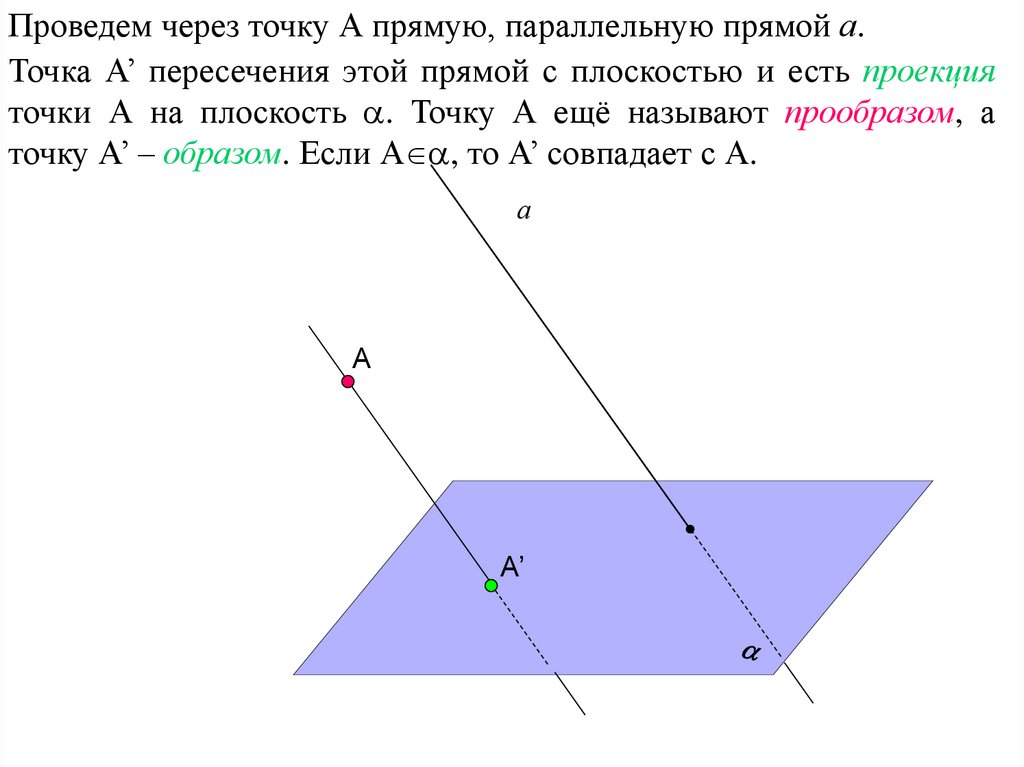
17.

Проведем через точку А прямую, параллельную прямой а.
Точка А’ пересечения этой прямой с плоскостью и есть проекция
точки А на плоскость . Точку А ещё называют прообразом, а
точку А’ – образом. Если А , то А’ совпадает с А.
а
А
А’

18. Рассматривая любую геометрическую фигуру как множество точек, можно построить в заданной плоскости проекцию данной фигуры.

Таким образом
можно получить изображение (или «проекцию») любой плоской или
пространственной фигуры на плоскости (см.рис.).
а
Наглядным примером параллельного проектирования является отбрасываемая
любым объектом(прообраз) в пространстве тень(образ) от солнечных
лучей(направление параллельного проектирования) на Земле(плоскость
проекций).

19. ПАРАЛЛЕЛЬНОЕ ПРОЕЦИРОВАНИЕ

Параллельную проекцию
реальной фигуры
представляет, например, её
тень, падающая на плоскую
поверхность при солнечном
освещении, поскольку
солнечные лучи можно
считать параллельными.

20.

Примечание 1. При параллельном проектировании не
выбирают направление параллельного проектирования
параллельно плоскости проекции (самостоятельно
обоснуйте почему).
а
А

21.

Примечание 2. При параллельном проектировании плоских фигур не выбирают
направление параллельного проектирования параллельно плоскости, которой
принадлежит эта плоская фигура, т.к. получающаяся при этом проекция не
отражает свойства данной плоской фигуры.
B
а
А
C
B’
C’
А’

22.

Примечание
3.
Если
направление
параллельного
проектирования
перпендикулярно плоскости проекций, то такое параллельное проектирование
называется ортогональным (прямоугольным) проектированием.
B
а
А
C
А’
C’
B’

23.

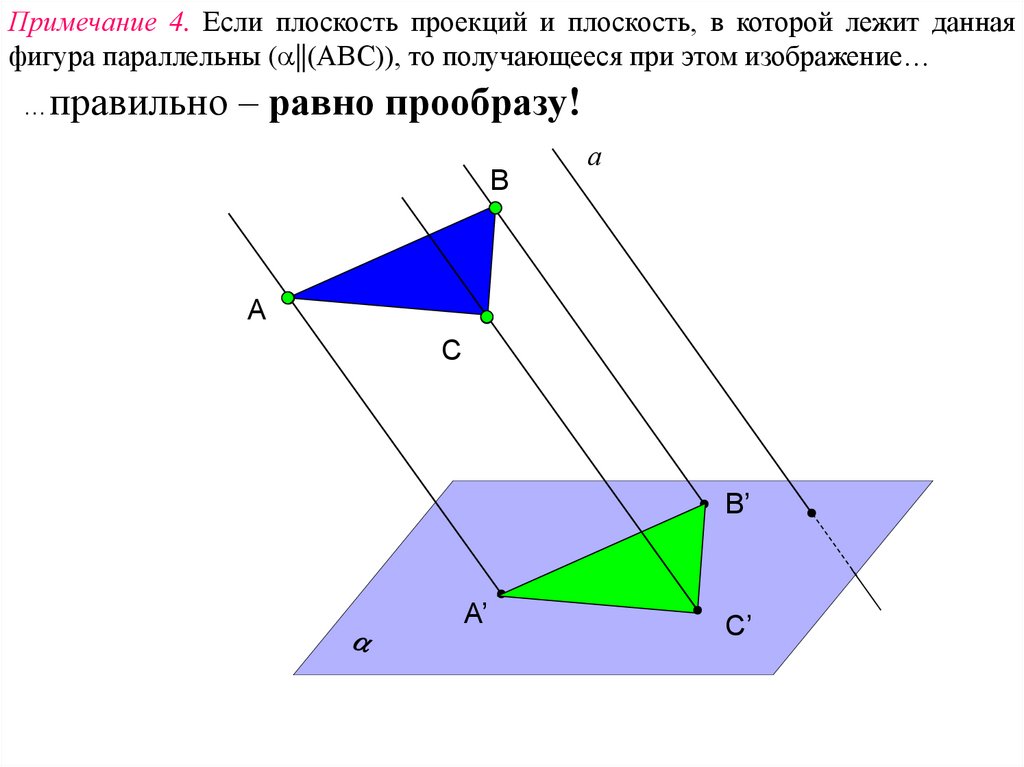
Примечание 4. Если плоскость проекций и плоскость, в которой лежит данная
фигура параллельны ( ||(АВС)), то получающееся при этом изображение…
…правильно – равно прообразу!
B
а
А
C
B’
А’
C’

24.

Параллельное проектирование обладает свойствами:
1) параллельность прямых (отрезков, лучей) сохраняется;
B
а
D
A
C
B’
D’
A’
C’

25.

Параллельное проектирование обладает свойствами:
1) параллельность прямых (отрезков, лучей) сохраняется;
2) отношение длин отрезков, лежащих на параллельных или на одной
B
прямой сохраняется;
а
М
D
A
C
B’
М’
D’
A’
C’
Если, например, АВ=2CD, то А’В’=2C’D’ или
AM A' M '
MB M ' B'

26.

Параллельное проектирование обладает свойствами:
1) параллельность прямых (отрезков, лучей) сохраняется;
2) отношение длин отрезков, лежащих на параллельных или на одной прямой
сохраняется;
3) Линейные размеры плоских фигур(длины отрезков, величины
углов) не сохраняются (исключение – см. примечание 4).
а
B
C
A
C’
A’
B’

27.

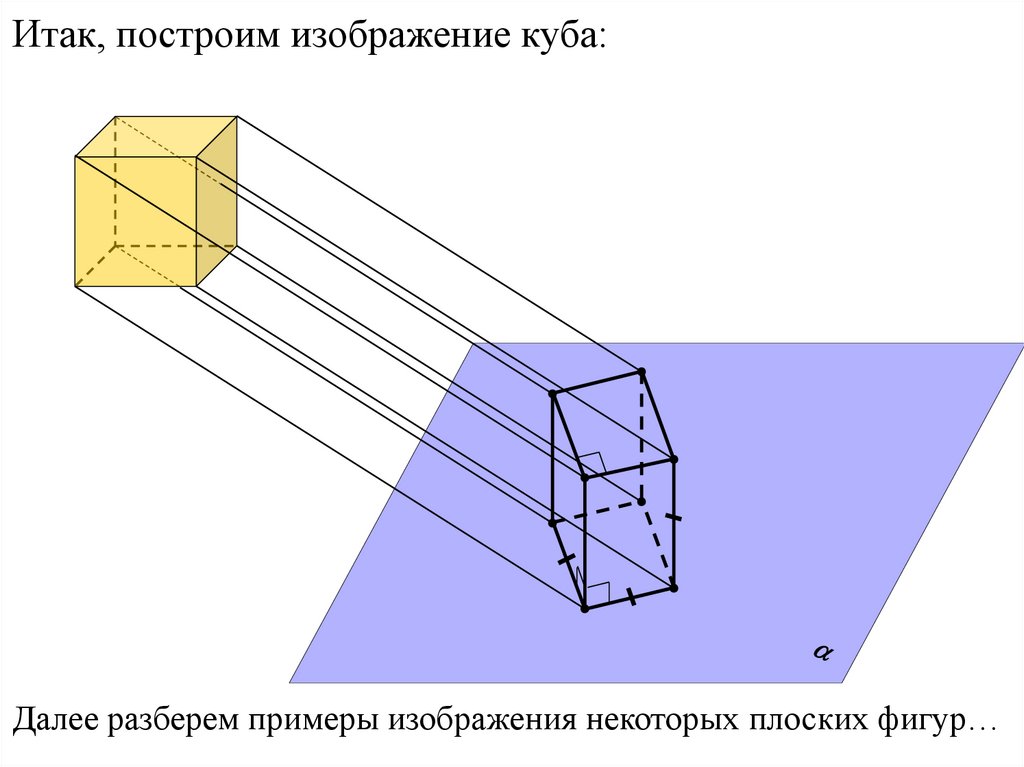
Итак, построим изображение куба:
Далее разберем примеры изображения некоторых плоских фигур…

28.

Ортогональная проекция точки
l
А
a
α
А’
Ортогональной проекцией
точки А на данную плоскость
называется проекция точки
на эту плоскость параллельно
прямой, перпендикулярной
этой плоскости.
a┴α, l//a

29.

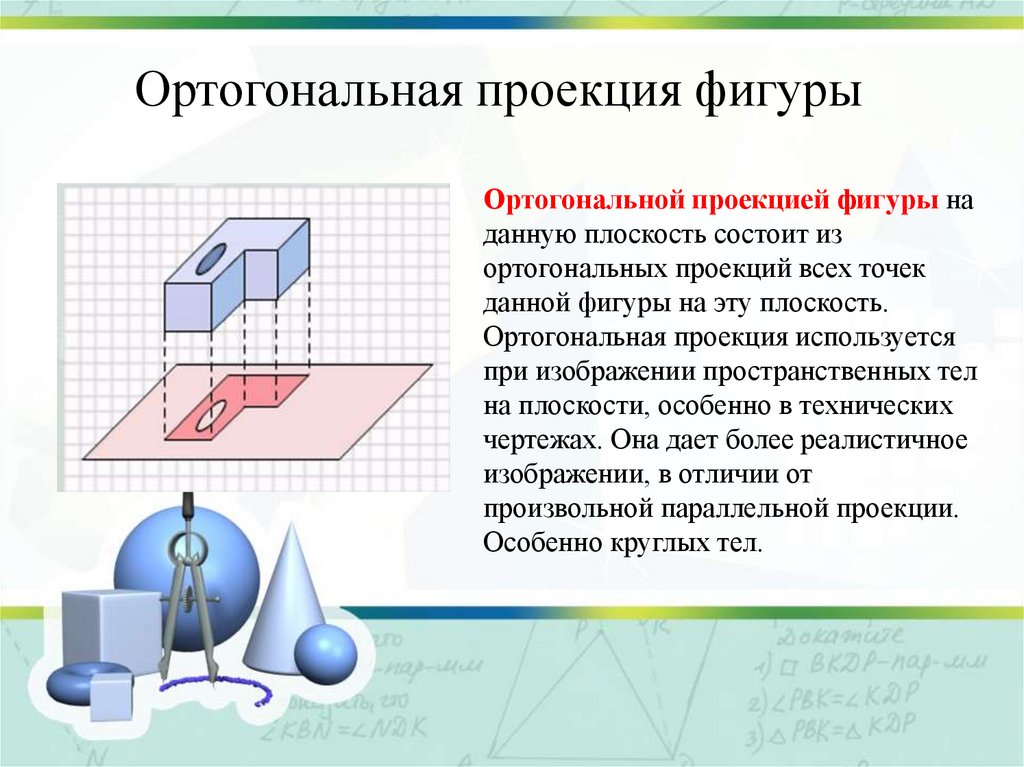
Ортогональная проекция фигуры
Ортогональной проекцией фигуры на
данную плоскость состоит из
ортогональных проекций всех точек
данной фигуры на эту плоскость.
Ортогональная проекция используется
при изображении пространственных тел
на плоскости, особенно в технических
чертежах. Она дает более реалистичное
изображении, в отличии от
произвольной параллельной проекции.
Особенно круглых тел.

30.

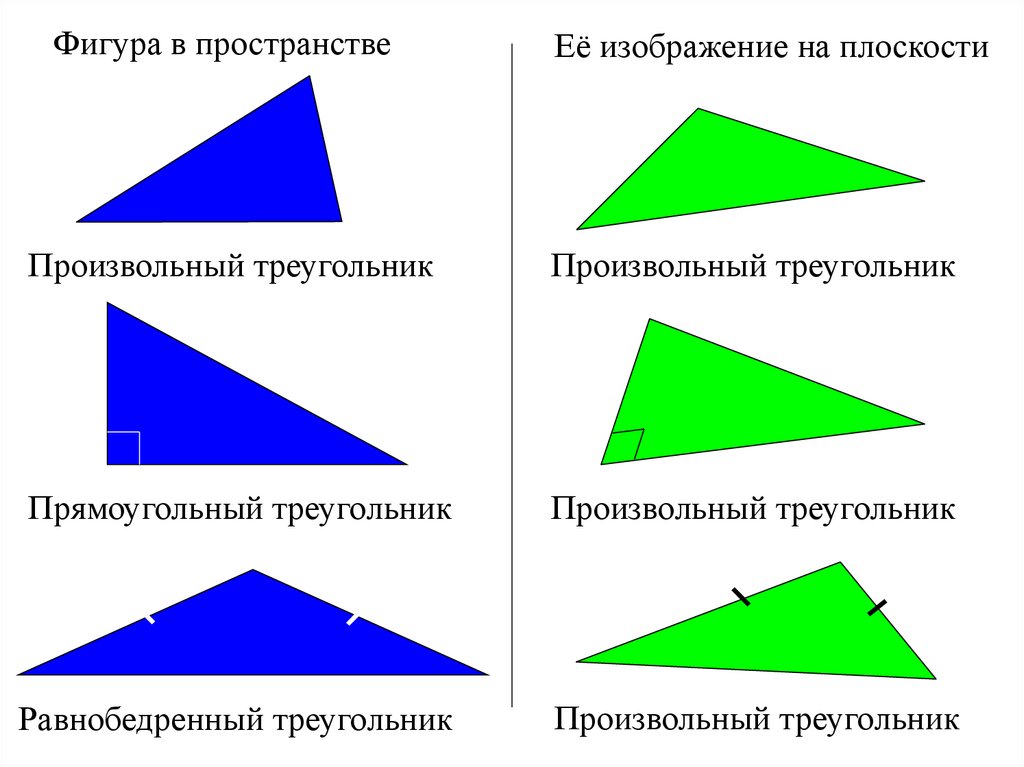
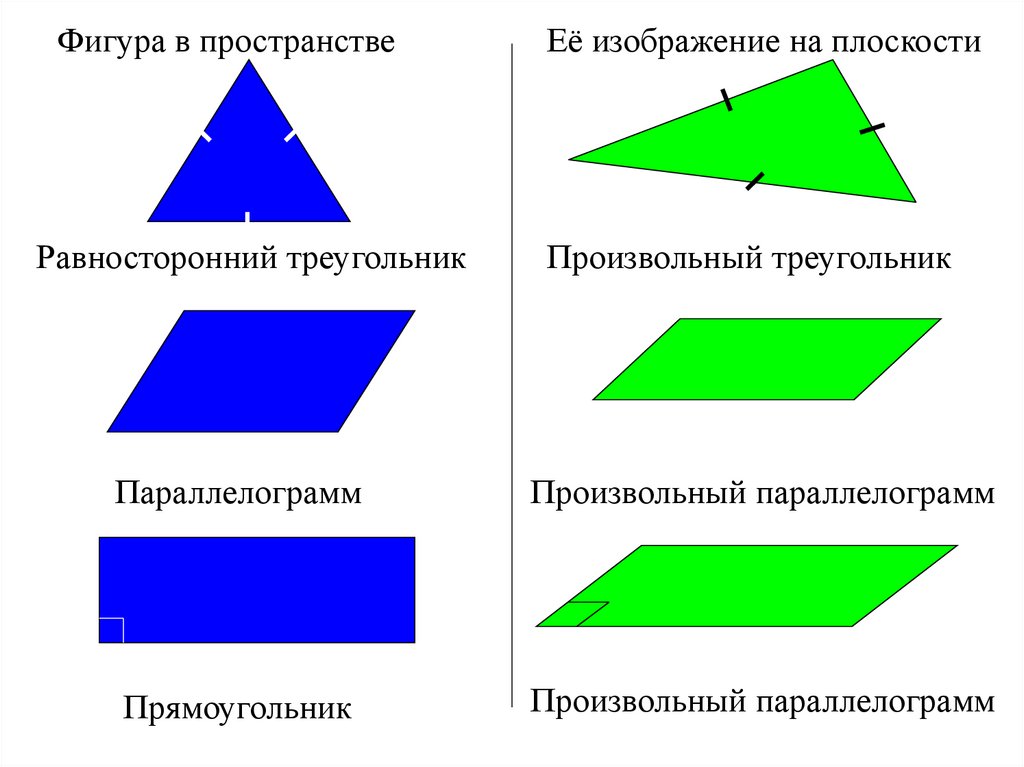
Фигура в пространстве
Её изображение на плоскости
Произвольный треугольник
Произвольный треугольник
Прямоугольный треугольник
Произвольный треугольник
Равнобедренный треугольник
Произвольный треугольник

31.

Фигура в пространстве
Её изображение на плоскости
Равносторонний треугольник
Произвольный треугольник
Параллелограмм
Произвольный параллелограмм
Прямоугольник
Произвольный параллелограмм

32.

Фигура в пространстве
Квадрат
Ромб
Трапеция
Её изображение на плоскости
Произвольный параллелограмм
Произвольный параллелограмм
Произвольная трапеция

33.

Фигура в пространстве
Её изображение на плоскости
Равнобокая трапеция
Произвольная трапеция
Прямоугольная трапеция
Произвольная трапеция
Круг
(окружность)
Овал (эллипс)

34.

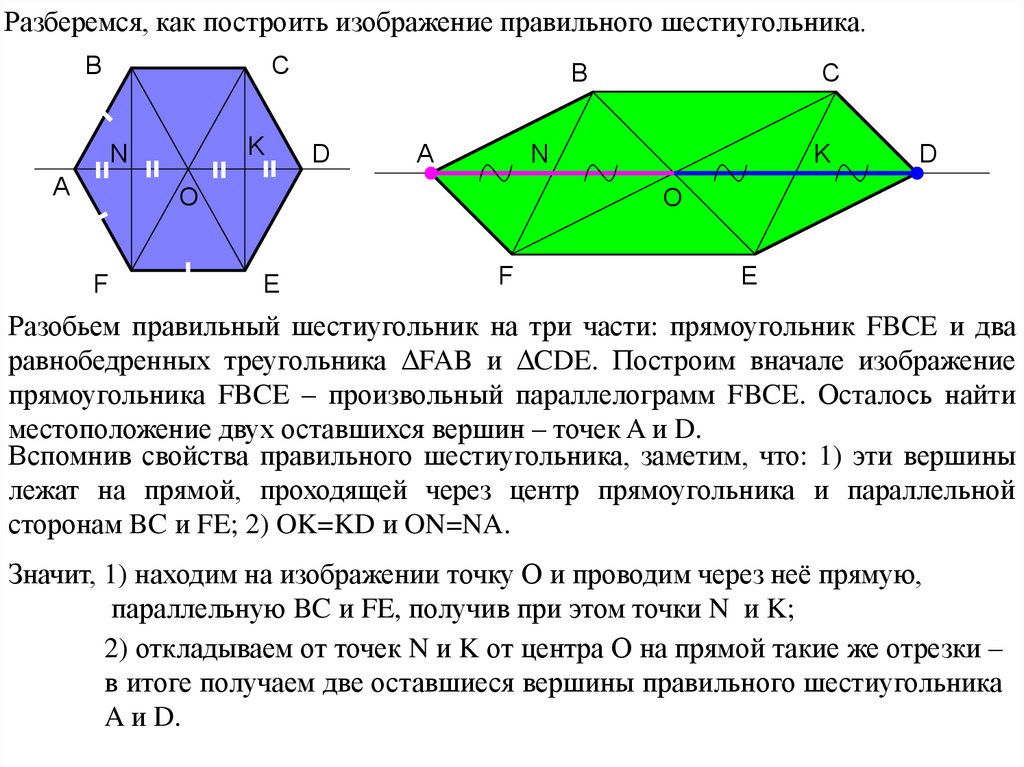
Разберемся, как построить изображение правильного шестиугольника.
B
C
K
N
A
B
D
A
N
O
F
C
K
D
O
E
F
E
Разобьем правильный шестиугольник на три части: прямоугольник FBCE и два
равнобедренных треугольника ΔFAB и ΔCDE. Построим вначале изображение
прямоугольника FBCE – произвольный параллелограмм FBCE. Осталось найти
местоположение двух оставшихся вершин – точек A и D.
Вспомнив свойства правильного шестиугольника, заметим, что: 1) эти вершины
лежат на прямой, проходящей через центр прямоугольника и параллельной
сторонам BC и FE; 2) OK=KD и ON=NA.
Значит, 1) находим на изображении точку О и проводим через неё прямую,
параллельную BC и FE, получив при этом точки N и K;
2) откладываем от точек N и K от центра О на прямой такие же отрезки –
в итоге получаем две оставшиеся вершины правильного шестиугольника
A и D.

35.

B
B
C
A
A
E
D
C
E
D
Попробуйте самостоятельно построить изображение правильного
пятиугольника.
Подсказка: разбейте фигуру на две части – равнобокую трапецию и
равнобедренный треугольник, а затем воспользуйтесь некоторыми
свойствами этих фигур и ,конечно же, свойствами параллельного
проектирования.
Решение. Просмотрите ход построения…

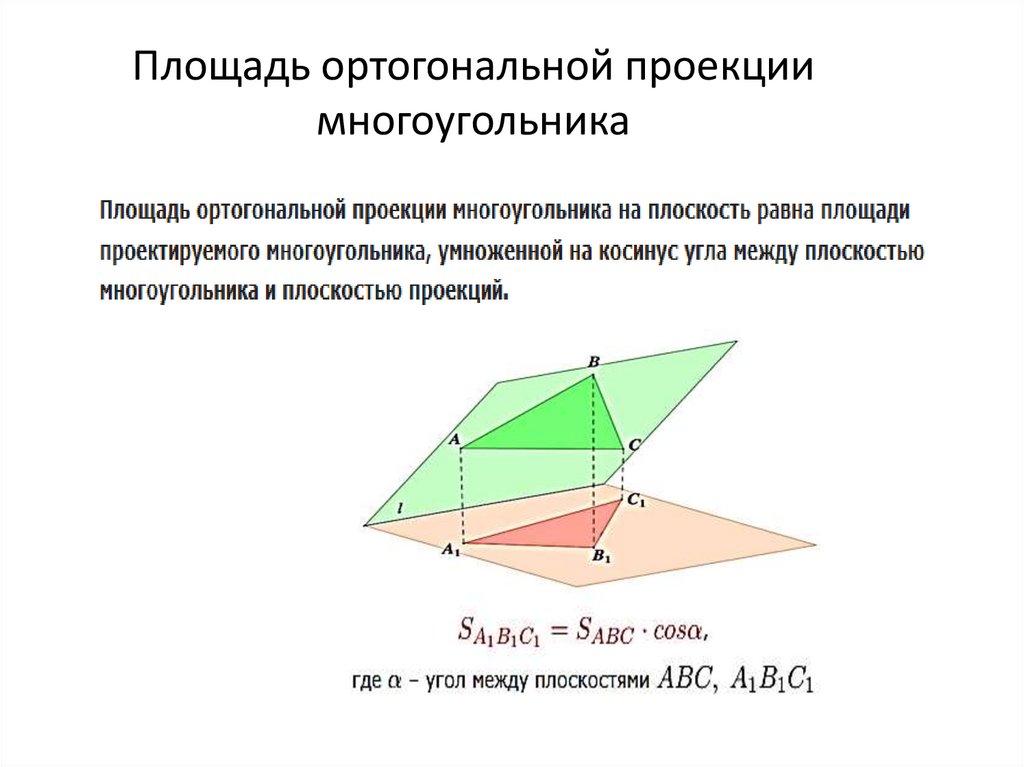
36. Площадь ортогональной проекции многоугольника

37.

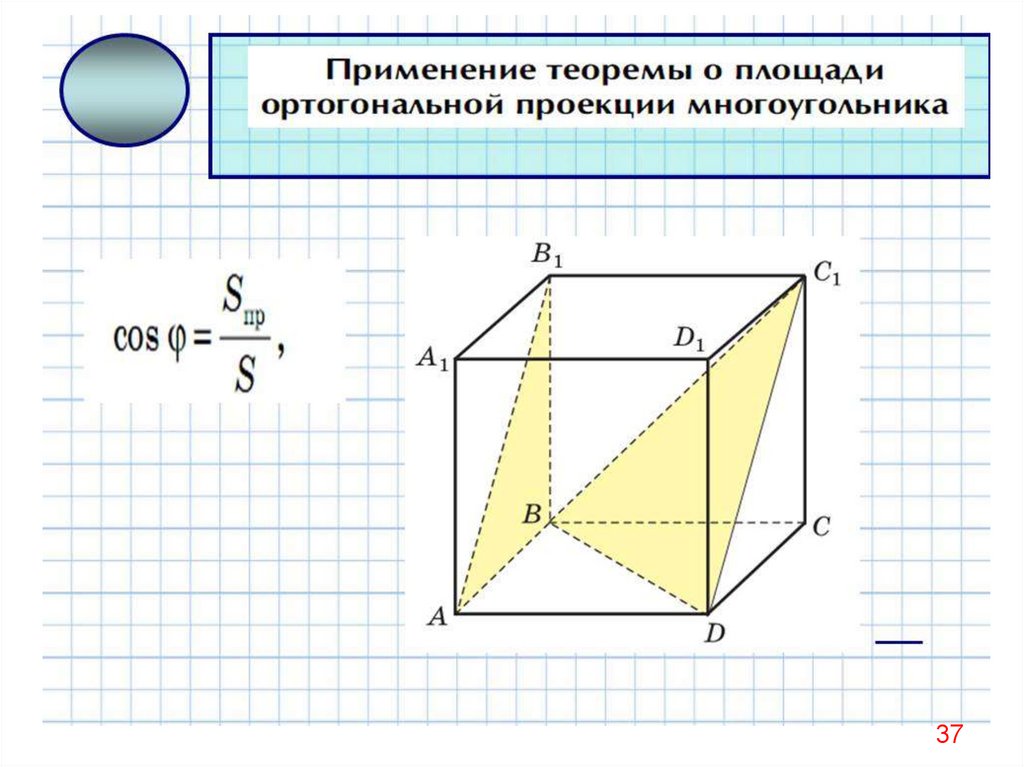
37

38. Задача

• Дано: АВ = ВС = АС = 12 см
А1В1 = В1С1 = 10 см
H
А1С1 = 12 см
• Найти: Угол между АВС и А1В1С1
38

39.

39

40.

в аудитории
№2.89,№2.95

41.

домашнее задание
№2.96(1),2.97(2)