Методика подготовки учащихся к ЕГЭ по информатике. С чего начинать…

1. Методика подготовки учащихся к ЕГЭ по информатике

LOGO

2. С чего начинать…

Создание коллекции ссылок на
Интернет ресурсы
Формирование методической
копилки подготовки к ЕГЭ
Выработать свою систему работы
www.themegallery.com
Company Logo

3. Распределение заданий по разделам курса информатики и ИКТ

Моделирование
Технология обработки графической информации
Обработка числовой информации и баз данных
Телекоммуникационные технологии
Системы счисления
Информация и е кодирование
Логика и алгоритмы
Алгоритмизация и
программирование
www.themegallery.com
1 задание -2,5%
1 задание-2,5%
3 задания-7,5%
3 задания-7,5%
3 задания-7,5%
5 заданий-12,5%
7 заданий-25%
9 заданий-35%
Company Logo

4. Работа по подготовке к экзамену в формате ЕГЭ

Первая часть состоит в том, что начиная с 8го класса в планы уроков вносятся
изменения, ориентированные на подготовку к
ЕГЭ практически на каждом уроке.
Вторая часть предполагает разработку
программы по подготовке выпускников
непосредственно к сдаче экзамена:
www.themegallery.com
Company Logo

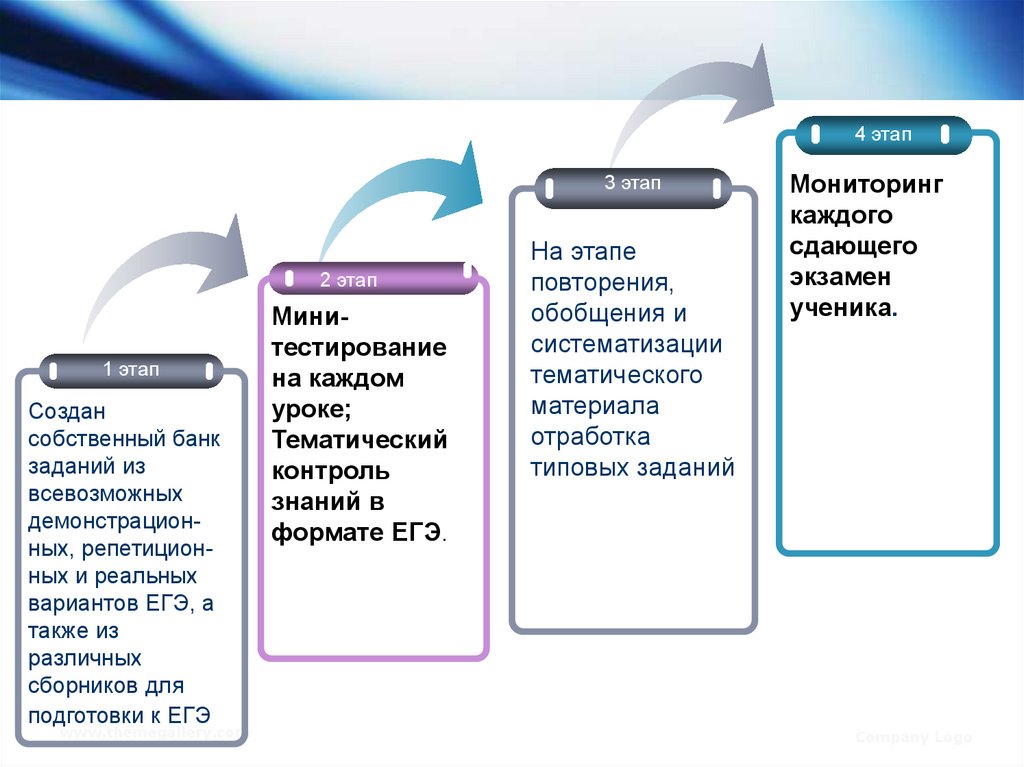
5.

4 этап
3 этап
2 этап
1 этап
Создан
собственный банк
заданий из
всевозможных
демонстрационных, репетиционных и реальных
вариантов ЕГЭ, а
также из
различных
сборников для
подготовки к ЕГЭ
www.themegallery.com
Минитестирование
на каждом
уроке;
Тематический
контроль
знаний в
формате ЕГЭ.
На этапе
повторения,
обобщения и
систематизации
тематического
материала
отработка
типовых заданий
Мониторинг
каждого
сдающего
экзамен
ученика.
Company Logo

6. Интернет-ресурсы

-
Ссылки универсального назначения
http://www.edu.ru/. Российское образование. Федеральный портал.
http://katalog.iot.ru/. Каталог образовательных ресурсов сети Интернет, раздел
“Информационная поддержка ЕГЭ”.
http://standart.edu.ru. Наш ориентир на будущее. Проект стандарта второго
поколения.
http://www.fipi.ru/view/sections/136/docs/202.html. Перечень учебных изданий,
допущенных ФИПИ к использованию в учебном процессе в образовательных
учреждениях для подготовки к ЕГЭ
http://ege.edu.ru/. Портал информационной поддержки единого
государственного экзамена, форум.
http://www.egeinfo.ru. Все о ЕГЭ, форум “Все о ЕГЭ”.
http://www.it-n.ru/. Сеть творческих учителей. Сообщество учителей
информатики
-
.
http://kpolyakov.narod.ru Сайт К.Полякова Методические материалы и
программное обеспечение для школьников и учителей.
Интернет-подготовка к экзамену, тесты, тесты on-line
- http://www.intuit.ru. Интернет-университет информационных технологий.
- http://www.fipi.ru. Главная > Единый государственный экзамен > Открытый
сегмент ФБТЗ > Информатика (on-line).
- http://www.egeinfo.ru. Сайт “Все о ЕГЭ”.
- http://www.hi-edu.ru/CentrDovusBooks/xbook616/01/index.html?part005.htm#i699 Онлайн-тренажер по подготовке к ЕГЭ
www.themegallery.com
Company Logo

7.

8.

5 заданий (12,5% от максимального первичного балла за всю работу )
3 с выбором ответа
2 с кратким ответом
Разделы ЕГЭ, где есть вопросы, связанные с темой «Основы логики»:
Алгоритмизация и
программирование
Технология хранения,
поиска и сортировки
информации в базах
данных
Телекоммуникацион
ные технологии
Обработка
информации в
электронных таблицах

9.

А9. Умение строить таблицы истинности и логические
схемы.
(Б – 2 мин)
А10. Умение строить и преобразовывать логические
выражения.
(Б – 1 мин)
А15. Знание основных понятий и законов
математической логики.
(П – 2 мин)
В7. Умение строить и преобразовывать логические
выражения
(П – 8 мин)
В10. Умение строить и преобразовывать логические
выражения
(В – 10 мин)
В9. Составление запросов для поисковых систем с
использованием логических выражений (П – 3 мин)
Уровни сложности заданий: Б (базовый), П (повышенный), В (высокий)

10.

В КИМ по информатике не включены
задания, требующие простого
воспроизведения знания терминов, понятий,
величин, правил.
Осуществляется проверка сформированности:
умений применять свои знания в
стандартной ситуации (создание и
преобразование логических выражений;
формирование для логической функции
таблицы истинности и логической схемы);
умений применять свои знания в новой
ситуации (решение логических задач).

11.

решение может быть достаточно
громоздким, это трудоемко, легко ошибиться;
можно перепутать значение операций «И» и
«ИЛИ», а также порядок выполнения цепочки
операций;
часто
представляет трудность длинное
запутанное условие задачи, из которого нужно
выделить
действительно
существенную
информацию и формализовать ее;

12.

решая логическое уравнение, нужно
проверять,
что
среди
найденных
решений нет одинаковых;
есть риск потерять какие-то решения
при переборе вариантов;
при решении логических уравнений не
всегда удается догадаться, что
неверных комбинаций меньше;
легко
по
невнимательности
перепутать порядок букв в ответе или
дать ответ не по форме;

13.

нужно
внимательно читать условие,
так как в некоторых задачах требуется
перечислить запросы в порядке
убывания количества результатов, а в
некоторых – в порядке возрастания;
в некоторых заданиях требуется
применить знания не только из курса
информатики, но и математики;
нужно знать таблицы истинности
логических операций и помнить
правила преобразования логических
выражений.

14.

А9. Символом F обозначено одно из указанных
ниже логических выражений от трех
аргументов: X, Y, Z. Дан фрагмент таблицы
истинности выражения F. Какое выражение
соответствует F?
¬X ¬Y ¬Z
2. X Y Z
3. X Y Z
4. ¬X ¬Y ¬Z
1.
X Y Z
X Y Z
X Y Z
X Y Z
X
1
0
1
Y
0
0
1
Z
0
0
1
F
1
1
0

15.

А10. Укажите, какое логическое выражение
равносильно выражению A ¬(¬B C).
1) ¬A ¬B ¬C
2) A ¬B ¬C
3) A B ¬C
4) A ¬B C
A ¬(¬B C) = A ( B C) А В С
1)
A B C
3)
A B C
2)
A B C
4)
A B C

16.

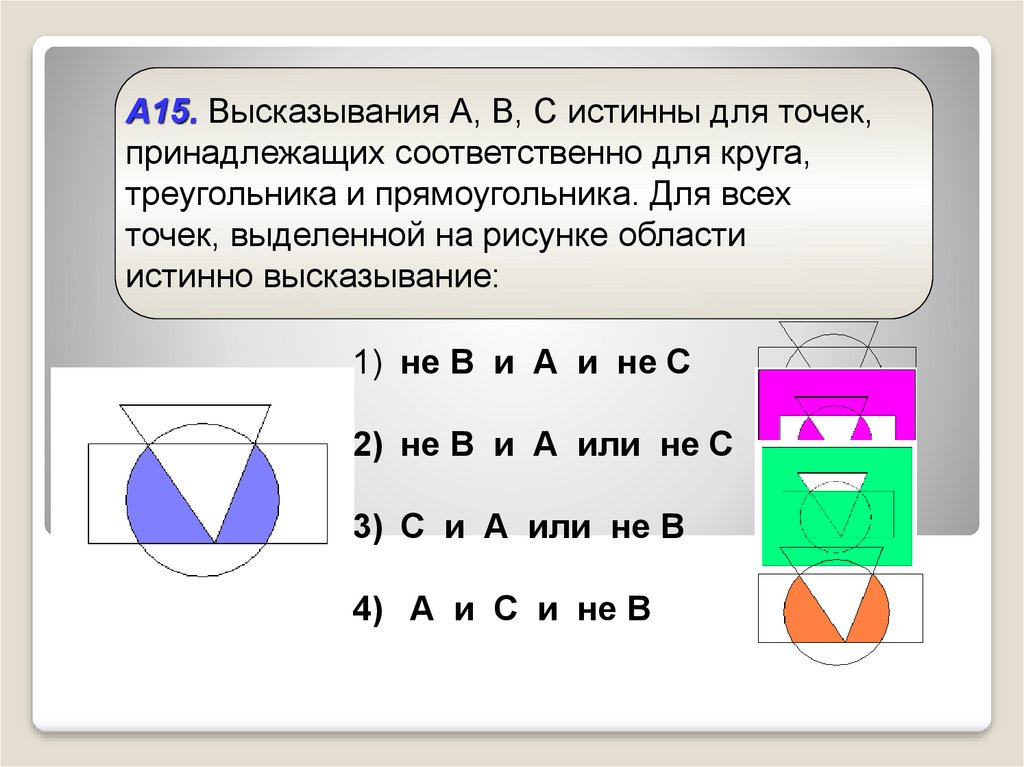
А15. Высказывания А, В, С истинны для точек,
принадлежащих соответственно для круга,
треугольника и прямоугольника. Для всех
точек, выделенной на рисунке области
истинно высказывание:
1) не В и А и не С
2) не В и А или не С
3) С и А или не В
4) А и С и не В

17.

(X Для
2) (X 5)какого
(X 3) 1
А15.
из указанных значений X
истинно высказывание
(X > 2) (X > 5)→(X < 3)
1) 5
2) 2
3) 3
4) 4
(X 2) (X 3) 1
( X 2 X 5) ( X 3) 1
((X 2) (X 5)) (X 3) 1
Из набора значений
подходит только
число 2.

18.

А15. Для
какого
1С
ПГ 2С имени истинно высказывание:
¬ (Первая буква согласная → Последняя буква
гласная) Вторая буква согласная?
а) ИРИНА
б) СТЕПАН
в) МАРИНА
г) ИВАН
1С ПГ 2С
1С ПГ 2С
1С ПС 2С

19.

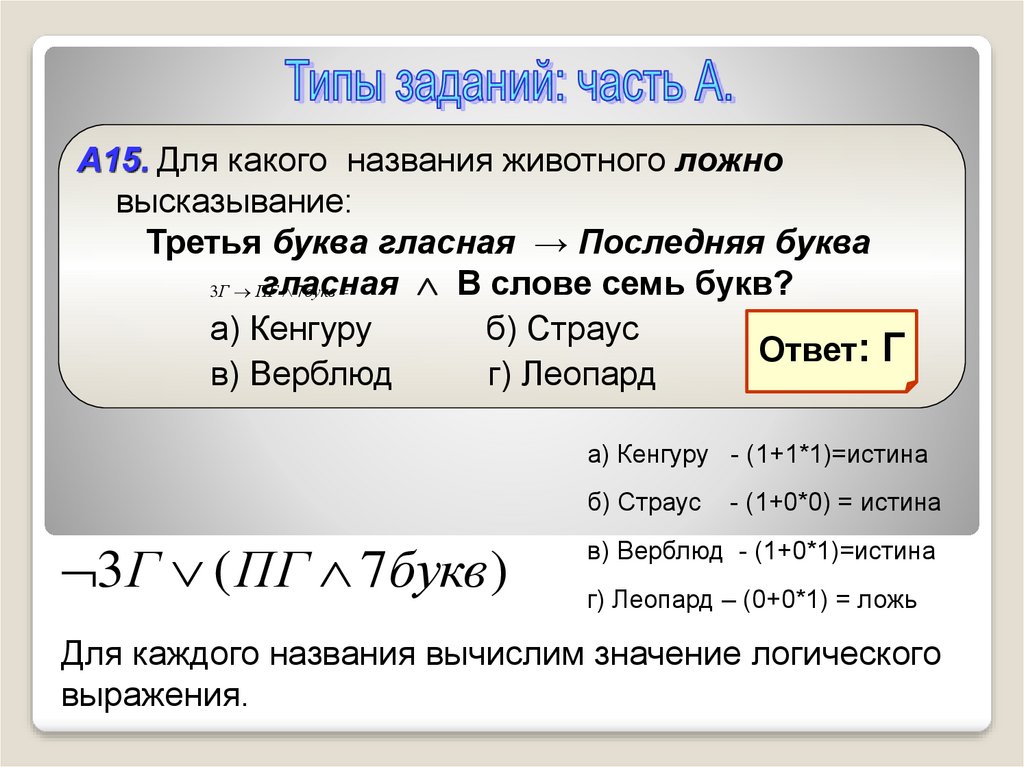
А15. Для какого названия животного ложно
высказывание:
Третья буква гласная → Последняя буква
гласная
В слове семь букв?
3 Г ПГ
7букв
а) Кенгуру
б) Страус
Ответ: Г
в) Верблюд
г) Леопард
а) Кенгуру - (1+1*1)=истина
б) Страус
3 Г ( ПГ 7букв )
- (1+0*0) = истина
в) Верблюд - (1+0*1)=истина
г) Леопард – (0+0*1) = ложь
Для каждого названия вычислим значение логического
выражения.

20.

В10. Каково наибольшее целое число X, при
котором истинно высказывание:
(50 < X·X) → (50 > (X+1)·(X+1))?
50 X X 50
2
,
А
50
В
50 (X 1)2 X 1 50
50 1
50 1
50
X
A → B истинно, если
1) А=0 и В=0
2) А=0 и В=1
3) А=1 и В=1
50 -1 <x<
50 , т.е. хмах=7
50 <x< 50 -1, т.е. хmax=6
50 -1<x<- 50 , т.е. хmax=-7
Xmax=7

21.

В10. Укажите значения переменных К, L, M, N, при
которых логическое выражение
(¬(М L) К) → (¬К ¬М) N) ложно. Ответ
запишите в виде строки из 4 символов: значений
переменных К, L, М и N. Так, например, строка 1101
соответствует тому, что К=1, L=1, M=0, N=1.
(( M L ) K ) ( K M N ) 0
((M L) K ) K M N 0
M L K K M N 0
M L K N 0
Ответ - 1000
M L N 0, K 1

22.

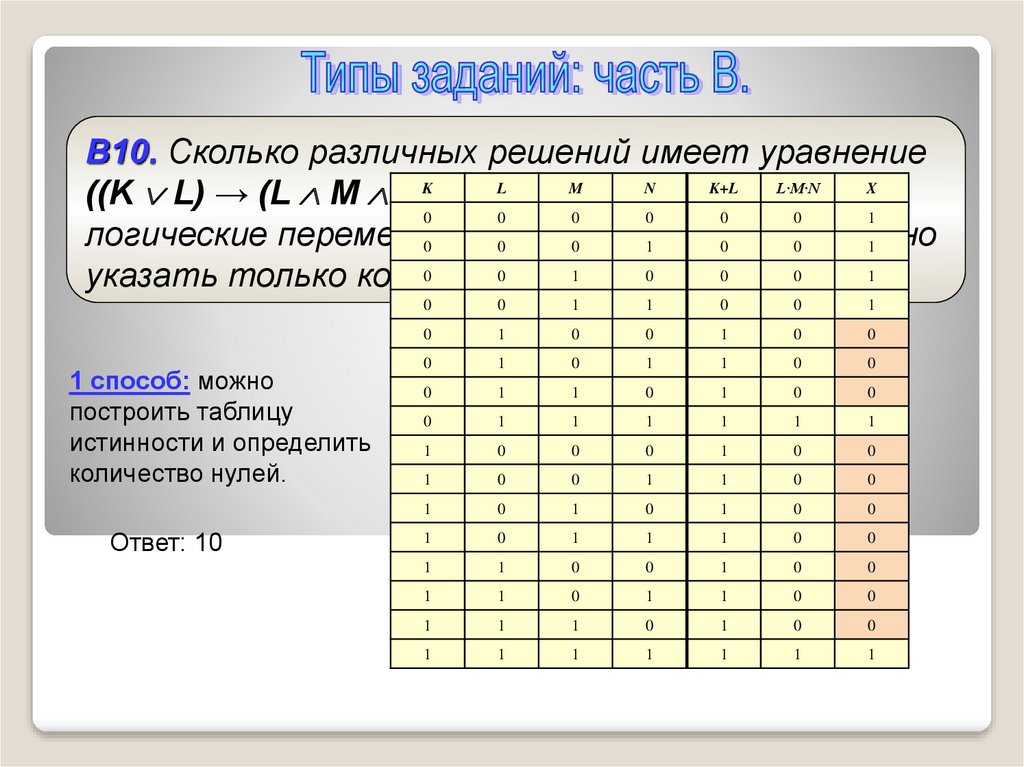
В10. Сколько различных решений имеет уравнение
K
M
N
((K L) → (L M N))
= 0L , где
K, L,
M,K+LN –L·M·N X
0
0
0
0
0
0
1
логические переменные?
ответа
нужно
0
0В качестве
0
1
0
0
1
0
0
1
0 наборов.
0
0
1
указать только количество
таких
1 способ: можно
построить таблицу
истинности и определить
количество нулей.
Ответ: 10
0
0
1
1
0
0
1
0
1
0
0
1
0
0
0
1
0
1
1
0
0
0
1
1
0
1
0
0
0
1
1
1
1
1
1
1
0
0
0
1
0
0
1
0
0
1
1
0
0
1
0
1
0
1
0
0
1
0
1
1
1
0
0
1
1
0
0
1
0
0
1
1
0
1
1
0
0
1
1
1
0
1
0
0
1
1
1
1
1
1
1

23.

2 способ:
В10. Сколько различных решений имеет уравнение
((K L) → (L M N)) = 0 , где K, L, M, N –
логические переменные? В качестве ответа нужно
указать только количество таких наборов.
((K + L) → (L · M · N)) = 0
Из первого уравнения следует:
K=1, L=0
L·M·N=0
выполняется при
любых М и N (00,
01, 10 и 11).
4 решения
K+L=1
L·M·N=0
K=0, L=1
L·M·N=0
Выполняется, если
М · N = 0;
(00, 01, 10).
3 решения
Ответ: 10 решений
K=1, L=1
L·M·N=0
Выполняется, если
М · N = 0;
(00, 01, 10).
3 решения

24.

В10. Сколько различных решений имеет уравнение
J /\ ¬K /\ L /\ ¬M /\ (N \/ ¬N) = 0 , где J,K, L, M, N –
логические переменные? В качестве ответа нужно
указать только количество таких наборов.
J /\ ¬K /\ L /\ ¬M /\ (N \/ ¬N) = 0
1
J /\ ¬K /\ L /\ ¬M = 0
Решения:
K
0
0
L
1
1
M
0
0
N
0
1
J
1
1
Рассмотрим количество решений,
когда выражение равно 1.
Чтобы ответить на вопрос задания,
необходимо из общего количества
решений (25=32) вычесть 2 решения,
когда выражение принимало
значение 1.
Ответ: 30

25.

В10. A, B и С – целые числа, для которых истинно
высказывание
¬(А = B) ((A > B)→(B > C)) ((B > A)→(С > B))
Чему равно В, если A = 45 и C = 43?
1) ¬(А = B) =1 , следовательно А B
2) (A > B)→(B > C) =1
3) (B > A)→(С > B)=1
Предположим, что
A < B.
Тогда из
Ответ
В=44
уравнения (3) получаем, что
1→(С > B)=1.
Предположим, что A > B, тогда из
уравнения
(2) может
получаем,
Это
выражение
бытьчто
истинно,
C > B.если
А значит
1→(B > C)=1. Это выражение может
бытьесли
истинно,
B > C.
C >соответствует
B > A - противоречие
условию
А значит A > B > C, этому условию
только число
44.
задачи.

26.

В10. Сколько различных решений имеет уравнение
(((¬K→ M) → (M/\¬L/\¬N)) \/ ((¬K/\ ¬M) → (¬M\/ L \/ N))) /\ (L/\M) = 1,
где K, L, M, N – логические переменные?
В качестве ответа нужно указать количество
таких наборов.
(((¬K→ M) → (M/\¬L/\¬N)) \/ ((¬K/\ ¬M) → (¬M\/ L \/ N))) /\ (L/\M) = 1
А
А
((( K M ) A) ( ( K M ) A)) ( L M ) 1
[( ( K M ) A) (( K M ) A)] ( L M ) 1

27.

[( ( K M ) A) (( K M ) A)] ( L M ) 1
[ ( K M ) A ( K M ) A] ( L M ) 1
[ ( K M ) ( K M ) 1] ( L M ) 1
Первая скобка будет равна 1 при любых
значениях входящих переменных.
L/\M=1
L=1, M=1 –
одно решение
Так как переменные K и N могут
принимать различные значения, то
Ответ:
4 решения

28.

В10. Сколько различных решений имеет уравнение
((J → K) →(M N L)) ((M N L) → (¬J K)) (M → J) = 1,
где J, K, L, M, N – логические переменные?
В качестве ответа нужно указать количество
таких наборов.
J K M N L M N L ( J K ) (M J ) 1
( J K ) M N L M N L ( J K ) (M J ) 1
.
А
В
( A B) ( B A) ( M J ) 1

29.

( A B) ( B A) ( M J ) 1
( А B) ( В A) ( M J ) 1
( А В A В) ( M J ) 1
( А В A В) 1
По таблице
истинности можно
доказать, что А=В.
J K M N L
(M J ) 1
a) M=0, J=0
b) M=0, J=1
c) M=1, J=1

30.

a) M=0, J=0
J K M N L
b) M=0, J=1
c) M=1, J=1
Рассмотрим различные варианты значений M и J:
а) 1+K=0 – нет решений.
b) 0+K=0 при любых значениях N и L. Следовательно –
4 решения.
c) K N L
Если K=0, то три решения (N=0, L=0; N=0, L=1; N=1, L=0)
Если K=1, то одно решение N=1, L=1.
Следовательно – 4 решения.
Совпадающих решений в пунктах b) и c) нет.
Ответ: 4+4=8 решений

31.

В10. Найти единственное решение системы
логических уравнений. Ответ записать в виде
четырех символов: значений переменных А, B, C, D.
A B ( D B) ( A C ) ( B D) ( A C )
A C ( B D)
Воспользуемся законом де Моргана:
A B ( D B) ( A C ) B D A C
A C B D

32.

A B ( D B) ( A C ) B D A C
A C B D
A B ( D B) ( B D) B D A C
( A B D A B B) ( B D) B D A C
Произведем замену в первом уравнении:
Воспользуемся распределительным законом дважды для левой
части уравнения:
0 B D A C
Ответ:
0011

33.

В7. В симфонический оркестр приняли на работу трёх
музыкантов: Брауна, Смита и Вессона, умеющих
играть на скрипке, флейте, альте, кларнете, гобое и
трубе. Известно, что:
Смит самый высокий;
играющий на скрипке меньше ростом играющего на
флейте;
играющие на скрипке и флейте и Браун любят пиццу;
когда между альтистом и трубачом возникает ссора,
Смит мирит их;
Браун не умеет играть ни на трубе, ни на гобое.
На каких инструментах играет каждый из музыкантов,
если каждый владеет двумя инструментами?

34.

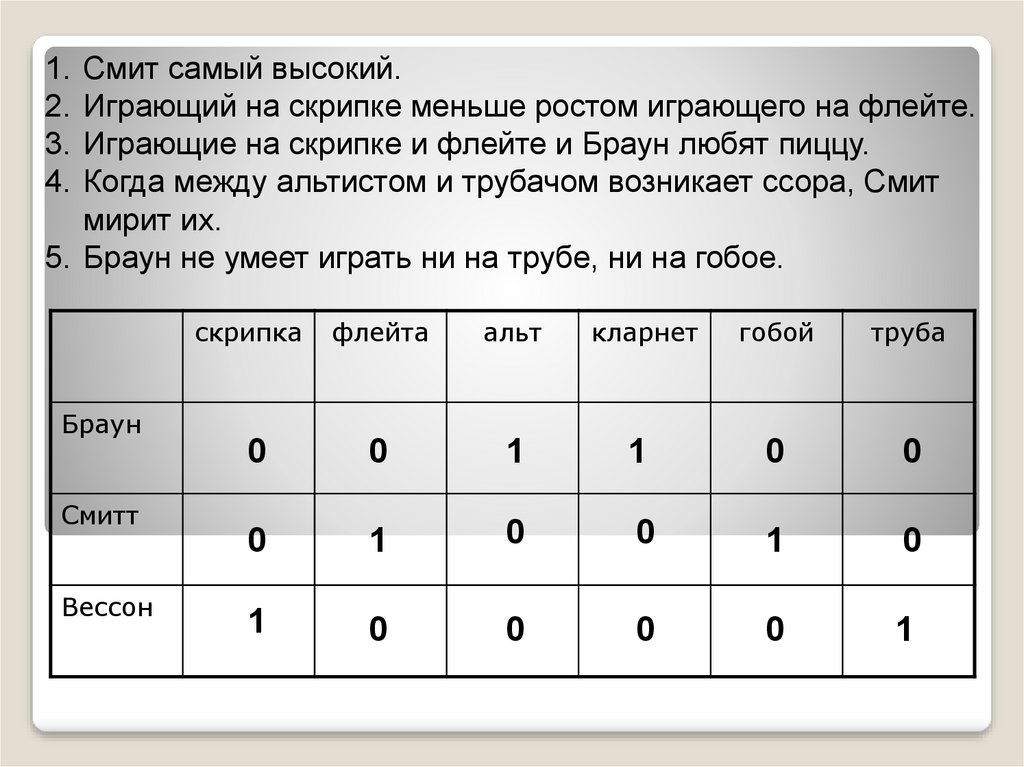
Смит самый высокий.
Играющий на скрипке меньше ростом играющего на флейте.
Играющие на скрипке и флейте и Браун любят пиццу.
Когда между альтистом и трубачом возникает ссора, Смит
мирит их.
5. Браун не умеет играть ни на трубе, ни на гобое.
1.
2.
3.
4.
скрипка
Браун
Смитт
Вессон
флейта
альт
кларнет
гобой
труба
0
0
1
1
0
0
0
1
0
0
1
0
1
0
0
0
0
1

35.

В7. Министры иностранных дел России, США и Китая обсудили
за закрытыми дверями проекты договора, представленные
каждой из стран. Отвечая затем на вопрос журналистов: «Чей
именно проект был принят?», министры дали следующие
ответы:
Россия «Проект не наш (1), проект не США (2)»;
США
«Проект не России (1), проект Китая (2)»;
Китай «Проект не наш (1), проект России (2)».
Один из них оба раза говорил правду; второй – оба раза
говорил неправду, третий один раз сказал правду, а другой
раз — неправду. Чей проект был принят?
Проект
США (?)
Россия
(1)
+
+
(2)
Проект
Китая (?)
–
–
США
Противоречие
Китай
условию!
(1)
(2)
Проект
России (?)
(1)
(2)
Россия
+
+
Россия
–
+
США
+
+
США
–
+
–
+
Китай
Противоречие
условию!
Китай

36.

В7. Кто из девочек посещает секцию
фигурного катания, если известно, что:
1. Света посещает.
2. Если Вика не посещает, то посещают
Света и Даша.
3. Если Аня или Вика посещает, то Света
не посещает.
С (В C D) ((A B) C) 1

37.

С ( В C D) (( A B) C )
С ( B (C D)) (( A B) C )
C (( B A B) ( B C )
(C D A B) (C D С )
( B C C ) (C C D A B)
C D A B 1
Посещают
Света и Даша

38.

В7. Виктор, Роман, Леонид и Сергей заняли
на математической олимпиаде четыре
первых места. Когда их спросили о
распределении мест, они ответили так:
Сергей – первый, Роман - второй.
Сергей – второй, Виктор – третий..
Леонид – второй, Виктор – четвертый.
Известно, что в каждом ответе только одно
утверждение верно. Как распределились
места?
(С1 Р 2) (С 2 В3) ( Л 2 В 4) 1

39.

(С1 Р 2) (С 2 В3) ( Л 2 В 4) 1
Воспользуемся
((С1 С 2) (Сраспределительным
1 В3) (Р2 С 2)
законом для первых двух скобок.
(Р2 В3)) ( Л 2 В4)
((С1 В3) ( Р 2 В3)) ( Л 2 В 4)
(С1 В3 Л 2) (С1 В 3 В 4)
(Р 2 В 3 Л 2) (Р 2 В 3 В 4)
С1 В3 Л2 1
1 место - Сергей
2 место - Леонид
3 место - Виктор
4 место - Роман

40.

В7. Восемь школьников, оставшиеся в классе на
перемене, были вызваны к директору. Один из
них разбил окно. На вопрос директора, кто это
сделал, были даны следующие ответы :
Егор
«Разбил Андрей».
Оля
«Света разбила».
Миша «Это кто-то с улицы».
Коля «Это Вика или Света».
Андрей «Ни Вика, ни Света этого не делали».
Надя «Оля права».
Вика «Андрей не бил».
Света «Вика разбила».
Известно, что только три высказывания были
истинными.
Кто разбил окно?

41.

Е О М К А Н В С А С
1
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
1
0
0
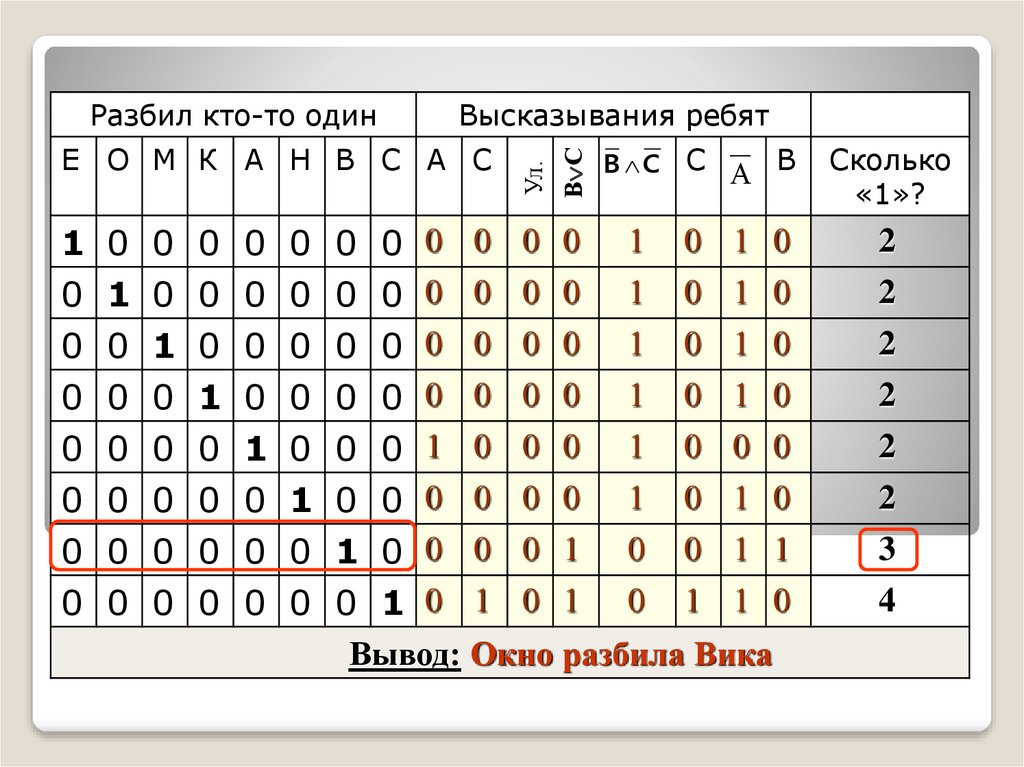
В С
Высказывания ребят
Ул.
Разбил кто-то один
В С
С А В
0 0 0 0 0 0 1 0 1 0
0 0 0 0 0 0 1 0 1 0
0 0 0 0 0 0 1 0 1 0
0 0 0 0 0 0 1 0 1 0
0 0 1 0 0 0 1 0 0 0
0 0 0 0 0 0 1 0 1 0
1 0 0 0 0 1 0 0 1 1
0 1 0 1 0 1 0 1 1 0
Вывод: Окно разбила Вика
Сколько
«1»?
2
2
2
2
2
2
3
4

42.

В7. На одной улице стоят в ряд 4 дома, в каждом из них живет
по одному человеку. Их зовут Василий, Семен, Геннадий и Иван.
Известно, что все они имеют разные профессии: скрипач,
столяр, охотник и врач. Известно, что
(1) Столяр живет правее охотника.
(2) Врач живет левее охотника.
(3) Скрипач живет с краю.
(4) Скрипач живет рядом с врачом.
(5) Семен не скрипач и не живет рядом со скрипачом.
(6) Иван живет рядом с охотником.
(7) Василий живет правее врача.
(8) Василий живет через дом от Ивана.
Определите, кто где живет, и запишите начальные буквы имен
жильцов всех домов слева направо.
№1
№2
№3
скрипач
врач
охотник
№4
столяр
скрипач

43.

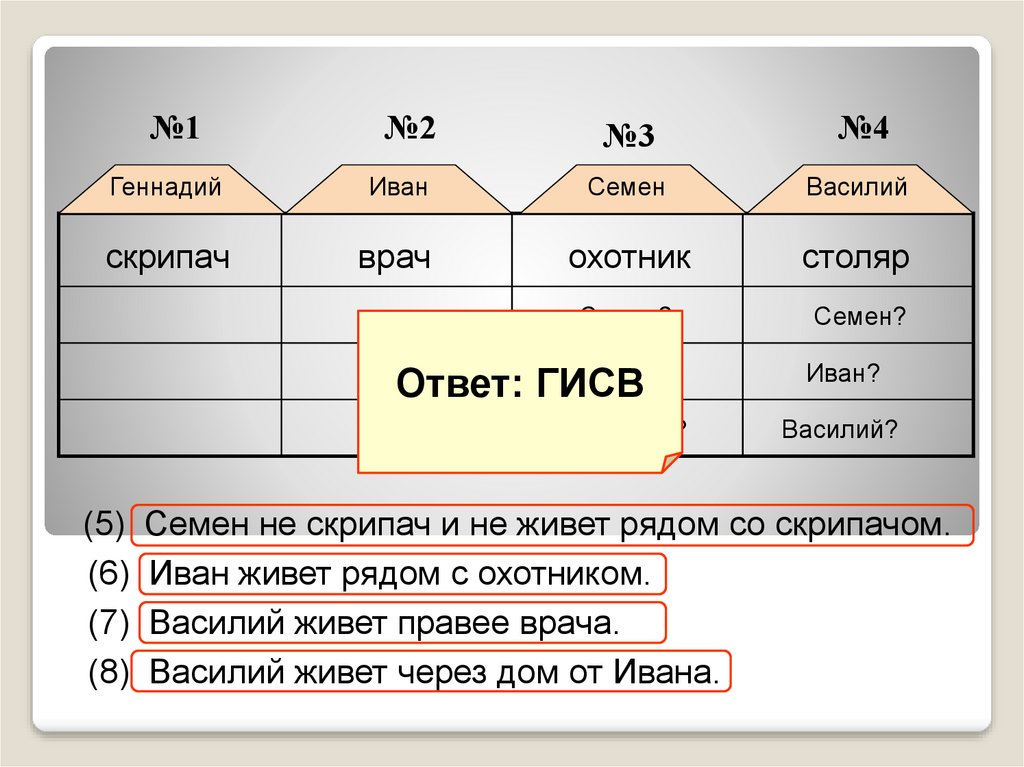
№1
№2
№3
№4
Геннадий
Иван
Семен
Василий
скрипач
врач
охотник
столяр
Семен?
Семен?
Иван?
Ответ: ГИСВ
Василий?
(5)
(6)
(7)
(8)
Иван?
Василий?
Семен не скрипач и не живет рядом со скрипачом.
Иван живет рядом с охотником.
Василий живет правее врача.
Василий живет через дом от Ивана.

44.

В7. После зимних каникул классный
руководитель спросил, кто из ребят ходил в
кино, театр или цирк? Оказалось, что из 36
учеников класса двое не были ни в кино, ни
в театре, ни в цирке. В кино побывали 25
человек, в театре – 11, в цирке - 17.
И в кино и в театре – 6, и в кино и в цирке
– 10, в театре и в цирке – 4. Сколько
человек из класса побывали и в кино, и в
театре, и в цирке?
Всего=36
Обозначим: Нигде=2
КТЦ - х
К=25
Т=11
Ц=17
КТ=6
КЦ=10
ТЦ=4

45.

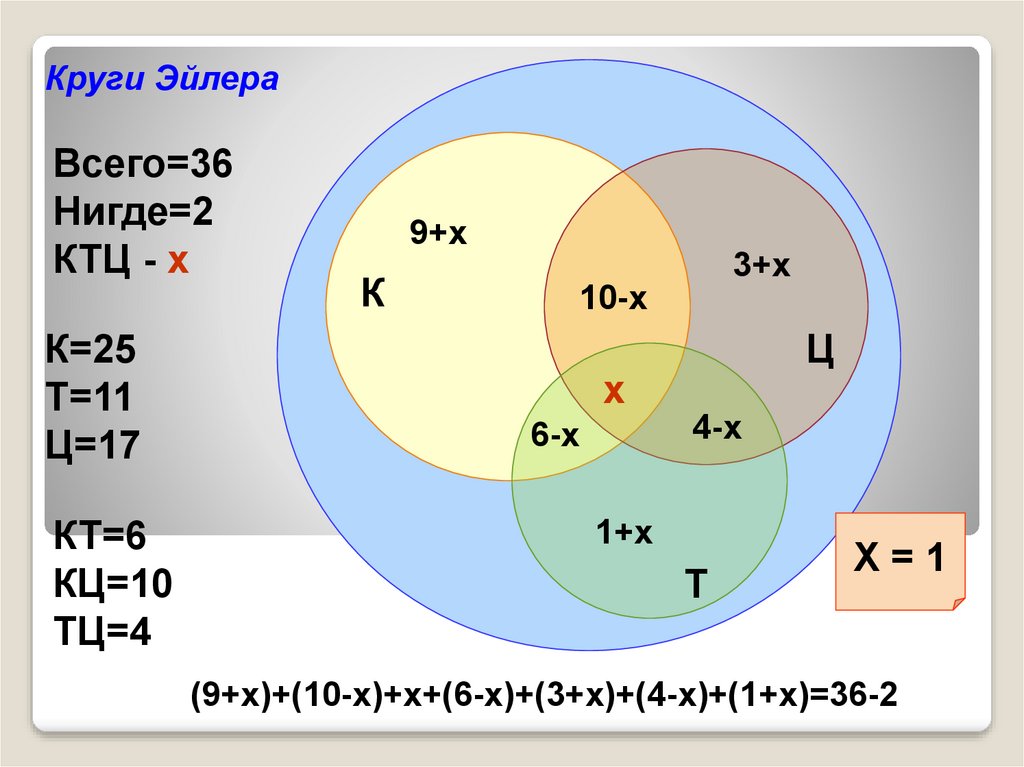
Круги Эйлера
Всего=36
Нигде=2
КТЦ - х
К=25
Т=11
Ц=17
КТ=6
КЦ=10
ТЦ=4
9+х
К
3+х
10-х
Ц
х
4-х
6-х
1+х
Т
Х=1
(9+х)+(10-х)+х+(6-х)+(3+х)+(4-х)+(1+х)=36-2

46.

В9. В таблице приведены запросы к поисковому
X A B
X A B C
X A B
X A B C
3
1
4порядке
2
серверу. BРасположите
номера
запросов
в
A
A
A
A
B
С
B
возрастания количества страниц, которые найдет
поисковый сервер по каждому запросу. Для
обозначения логической операции «ИЛИ» в
С
С
В
С
запросе используется символ |, а для логической
операции «И» – &.
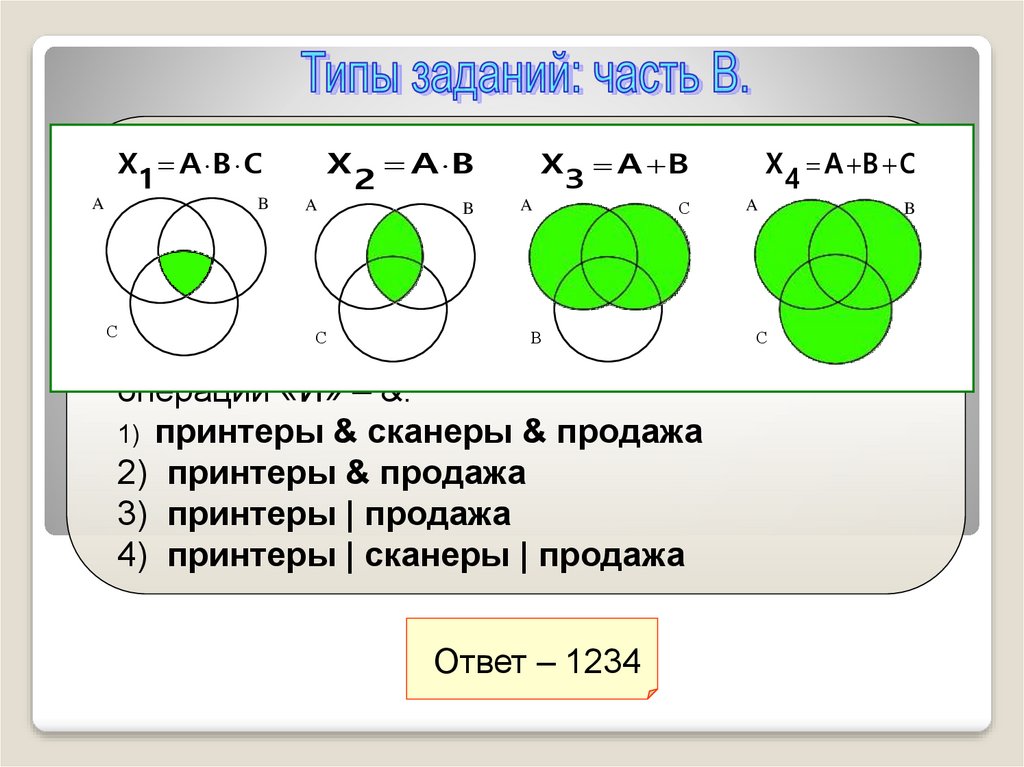
1) принтеры & сканеры & продажа
2) принтеры & продажа
3) принтеры | продажа
4) принтеры | сканеры | продажа
Ответ – 1234

47.

В9. Некоторый сегмент сети Интернет состоит из 1000 сайтов.
Поисковый сервер в автоматическом режиме составил таблицу
ключевых слов для сайтов этого сегмента. Вот ее фрагмент:
Ключевое слово
Количество сайтов, для которых
данное слово является ключевым
сканер
200
принтер
250
монитор
450
Сколько сайтов будет найдено по запросу
(принтер | сканер) & монитор,
если по запросу принтер | сканер было найдено 450 сайтов,
по запросу
принтер & монитор – 40,
а по запросу
сканер & монитор – 50.

48.

Решение с помощью кругов Эйлера:
1) Запросу (П | C) & M соответствует
объединение областей 4, 5 и 6 («зеленая
зона» на рисунке)
2) Ni - количество сайтов, удовлетворяющих
запросу в области i:
сканер
N1 + N2 + N4 + N5 = 200
принтер
N2 + N3 + N5 + N6 = 250
принтер | сканер
N1 + N2 + N4 + N5 + N3 + N6 = 450
3) Из первого и третьего уравнений следует
200 + N3 + N6 = 450 N3 + N6 = 250
4) Из второго уравнения
N2 + N5 + 250 = 250 N2 + N5 = 0
(П | С) & M
С
П
2
1
3
5
4
М
6
7
N5 + N6 = 40 N6 = 40
6) сканер & монитор
N4 + N5 = 50 N4 = 50
7) Окончательный результат:
Ответ : 90
(принтер | сканер) & монитор N4 + N5 + N6 = N4 + N6 = 40 + 50 = 90
5) принтер & монитор