Похожие презентации:
Измерение информации. Информативность сообщений
1.
2. Разбейте сообщения на 2 группы:
1. Столица России – Москва.2. Двери тибетских монастырей не зарывались
ни днем, ни ночью, т.к. их охраняли
сиамские кошки.
3. Теорема: Абсолютно сходящийся ряд
сходится.
4. Эйфелева башня имеет высоту 300м и вес
9000 т.
3. Тема урока: Измерение информации.
Цель урока:• научиться определять количество
информации, учитывая вероятность событий.
4.
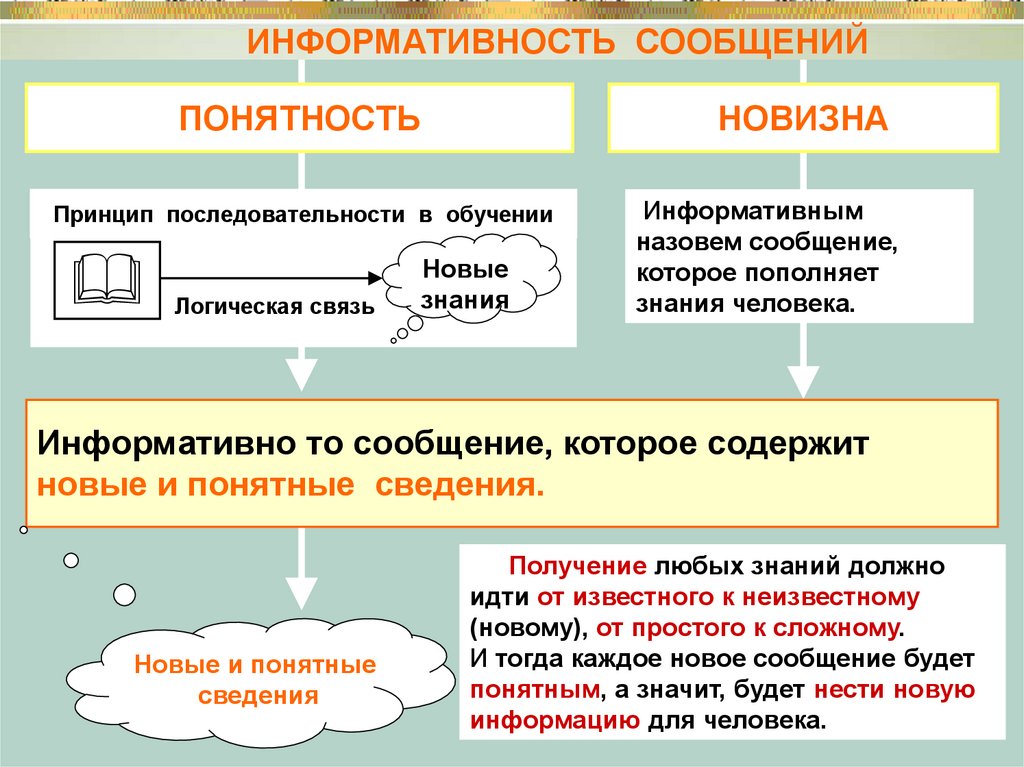
ИНФОРМАТИВНОСТЬ СООБЩЕНИЙПОНЯТНОСТЬ
НОВИЗНА
Принцип последовательности в обучении
Логическая связь
Новые
знания
Информативным
назовем сообщение,
которое пополняет
знания человека.
Информативно то сообщение, которое содержит
новые и понятные сведения.
Новые и понятные
сведения
Получение любых знаний должно
идти от известного к неизвестному
(новому), от простого к сложному.
И тогда каждое новое сообщение будет
понятным, а значит, будет нести новую
информацию для человека.
5. Подходы к измерению информации:
1. Неизмеримость информации в быту6.
СОДЕРЖАТЕЛЬНЫЙ ПОДХОД К ИЗМЕРЕНИЮ ИНФОРМАЦИИСообщение о том, что произошло одно событие из двух
равновероятных (неопределенность знания уменьшилась в два раза),
несет 1 бит информации.
8 цветных шаров в корзине –
8 равновероятных событий
Неопределенность
знания о том, что из
корзины может быть
извлечен шар красного
цвета, равна 8.
СОДЕРЖАТЕЛЬНЫЙ ПОДХОД к измерению информации
заключается в том, что количество информации связывается с
содержанием (смыслом) полученного человеком сообщения.
Количество информации, заключенное в сообщении, тем больше, чем
более оно пополняет наши знания (уменьшает неопределенность
наших знаний).
7. Подходы к измерению информации:
1. Неизмеримость информации в быту2. Содержательный подход
3. Алфавитный подход
8. Основные понятия
Вероятность события количественно характеризуетвозможность (шанс) осуществления этого события в
ходе случайного эксперимента.
События равновероятны, если ни одно из них не имеет
преимущества перед другими
Теория вероятностей является теоретической базой
статистики, она дает возможность рационального,
обоснованного выбора решений в условиях
неопределенности.
Неопределенность, объективно имеет место в
реальной жизни.
Например, объем будущего спроса на производимую продукцию,
размер процентной ставки, курсы валют могут быть оценены с
некоторой долей уверенности. Теория вероятностей
предоставляет средства для создания методов такого
оценивания.
9. Формула Ричарда Хартли (1928)
• Информация - это снятая неопределенность.• 1 бит - это сообщение, уменьшающее
неопределенность нашего знания в 2 раза.
Формула Ричарда Хартли (1928)
N
2i =N
или
log2 N = i
i
Количество равновероятных событий
Количество информации в сообщении о
том, что произошло одно из N
равновероятных событий.
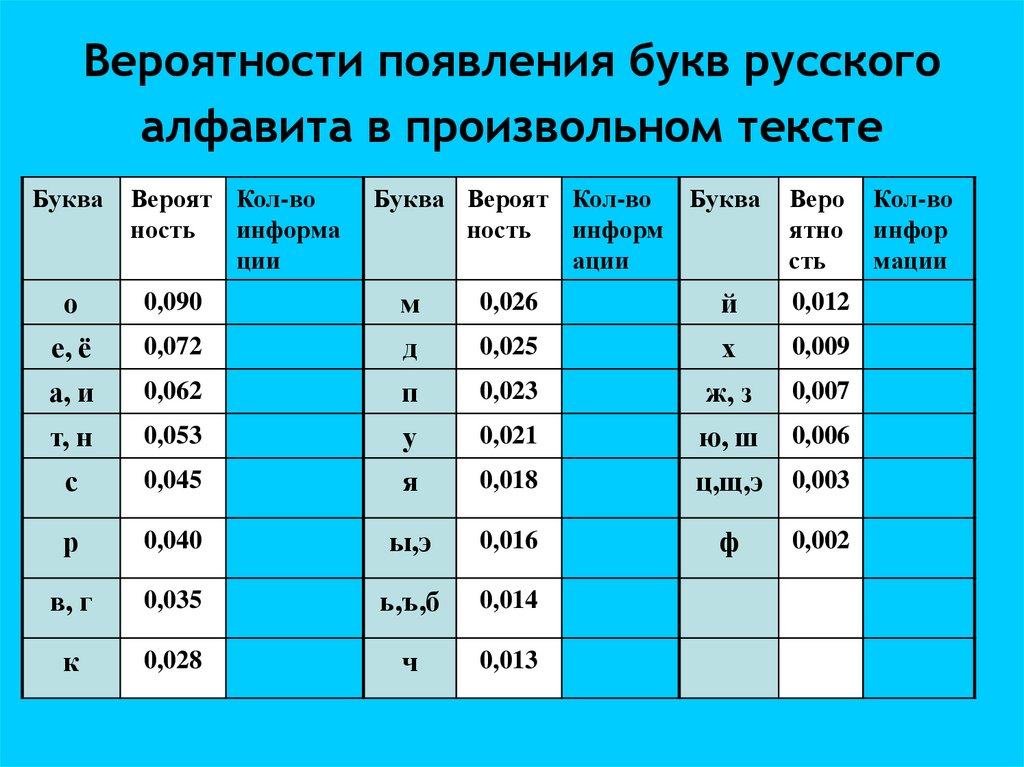
10. Вероятности появления букв русского алфавита в произвольном тексте
БукваВероят Кол-во
ность
информа
ции
Буква Вероят Кол-во
ность
информ
ации
Буква
Веро
ятно
сть
о
0,090
м
0,026
й
0,012
е, ё
0,072
д
0,025
х
0,009
а, и
0,062
п
0,023
ж, з
0,007
т, н
0,053
у
0,021
ю, ш
0,006
с
0,045
я
0,018
ц,щ,э
0,003
р
0,040
ы,э
0,016
ф
0,002
в, г
0,035
ь,ъ,б
0,014
к
0,028
ч
0,013
Кол-во
инфор
мации
11.
При работе технических средств связи не учитываетсяновизна и понятность этой информации.
Количество информации пропорционально количеству
символов, переданных по каналу связи.
Чтобы посчитать количество переданной информации,
надо знать информационный вес одного символа.
12.
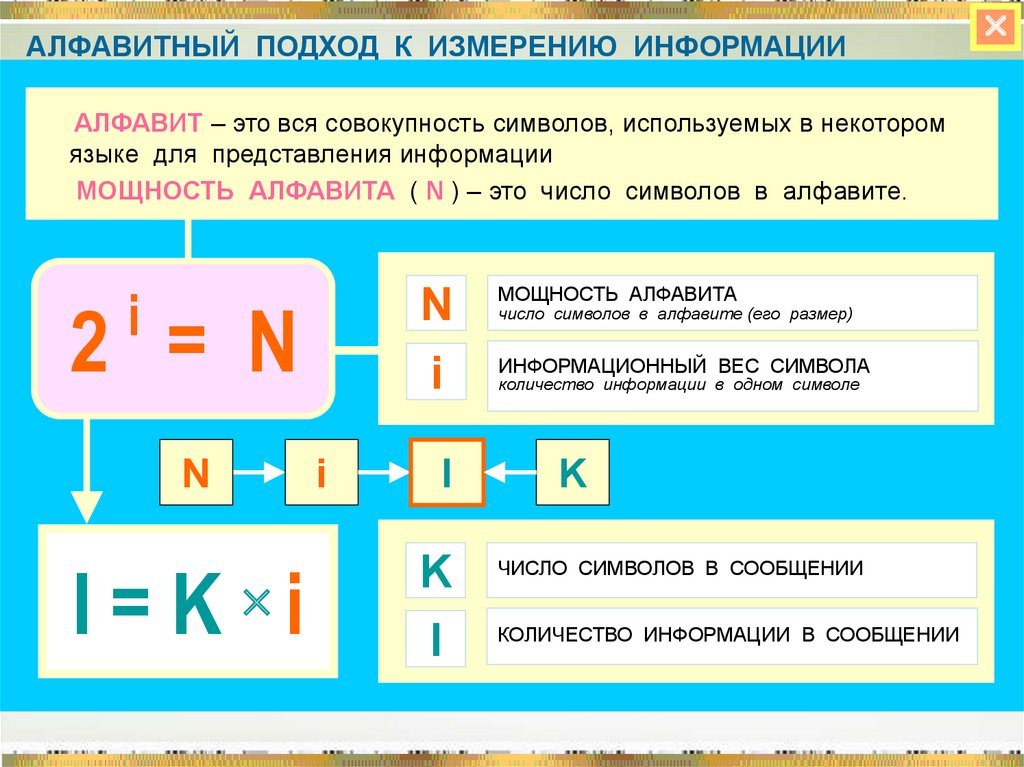
АЛФАВИТНЫЙ ПОДХОД К ИЗМЕРЕНИЮ ИНФОРМАЦИИАЛФАВИТ – это вся совокупность символов, используемых в некотором
языке для представления информации
МОЩНОСТЬ АЛФАВИТА ( N ) – это число символов в алфавите.
i
N
i
2 = N
N
I = K i
i
I
K
I
МОЩНОСТЬ АЛФАВИТА
число символов в алфавите (его размер)
ИНФОРМАЦИОННЫЙ ВЕС СИМВОЛА
количество информации в одном символе
K
ЧИСЛО СИМВОЛОВ В СООБЩЕНИИ
КОЛИЧЕСТВО ИНФОРМАЦИИ В СООБЩЕНИИ
13.
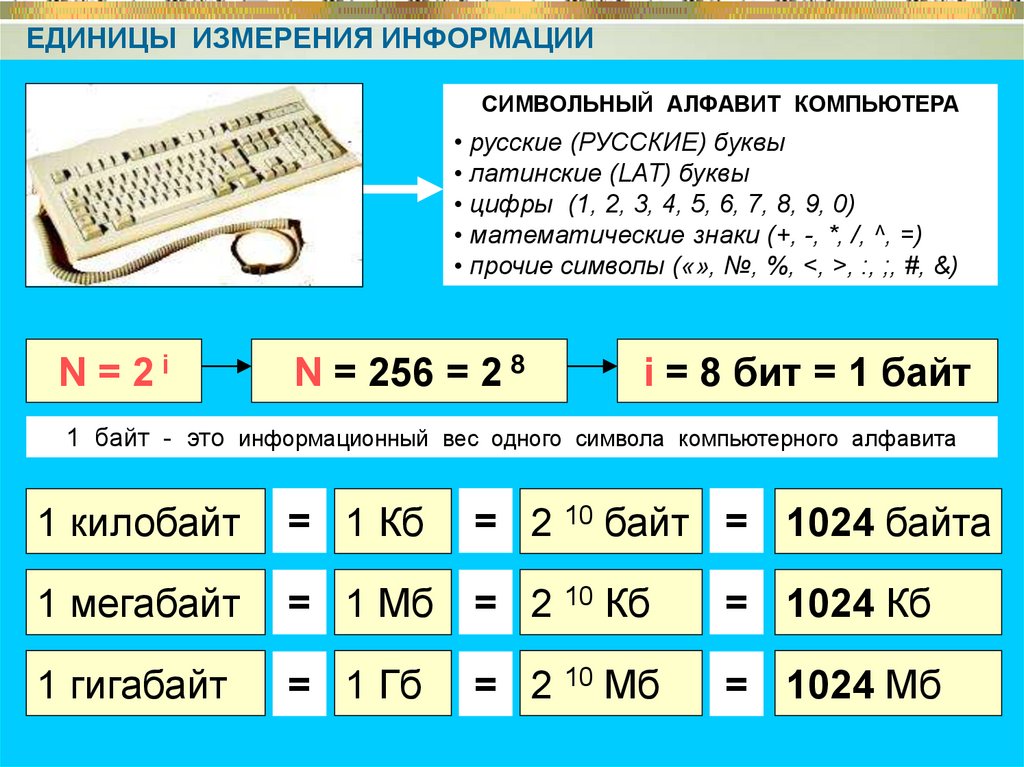
ЕДИНИЦЫ ИЗМЕРЕНИЯ ИНФОРМАЦИИСИМВОЛЬНЫЙ АЛФАВИТ КОМПЬЮТЕРА
• русские (РУССКИЕ) буквы
• латинские (LAT) буквы
• цифры (1, 2, 3, 4, 5, 6, 7, 8, 9, 0)
• математические знаки (+, -, *, /, ^, =)
• прочие символы («», №, %, <, >, :, ;, #, &)
N = 2i
N = 256 = 2 8
i = 8 бит = 1 байт
1 байт - это информационный вес одного символа компьютерного алфавита
1 килобайт
= 1 Кб
= 2 10 байт = 1024 байта
1 мегабайт
= 1 Мб = 2 10 Кб
= 1024 Кб
1 гигабайт
= 1 Гб
= 1024 Мб
= 2 10 Мб
14.
ИНФОРМАЦИОННЫЙ ОБЪЕМ ТЕКСТАЗАДАЧА
Книга, подготовленная с помощью компьютера, содержит 150 страниц. На
каждой странице – 40 строк, в каждой строке – 60 символов (включая пробелы
между словами). Каков объем информации в книге?
РЕШЕНИЕ
Мощность компьютерного алфавита равна 256, поэтому один символ несет 1 байт
информации. Значит, страница книги содержит 40 60 = 2400 байт информации.
[кол-во символов в строке] [кол-во строк] = [информационный объем страницы]
Объем всей информации в книге (в разных единицах):
[информационный объем страницы] [кол-во страниц] = [информационный объем книги]
2400 150 = 360 000 байт / 1024 = 351,5625 Кбайт / 1024 = 0,34332275 Мбайт
15. Пример 1
Компьютерный алфавит содержит 256 символов.По каналу связи было послано сообщение из 20
символов. Какое количество информации было
передано по каналу связи?
Решение
Определим информационный вес символа «i» из
решения уравнения 256 = 2 i
i = 8 бит
Если 1 символ несет 8 бит, то 20 символов в 20 раз
больше.
8бит * 20 = 160 бит
16. Пример 2
Какова мощность алфавита, с помощью которогопередано сообщение из 2048 символов. Известно,
что объем такого сообщения составил 1,25 Кб.
Решение
1. Сначала определим по формуле сколько бит
несет каждый символ.
1,25 Кб = 1,25*1024 байт = 1280 байт = 1280 * 8
бит = 10240 бит
10240 бит / 2048 = 5 бит
2. Теперь можно по формуле N=2i определить
мощность алфавита N=25 =32












 Информатика
Информатика








