Определение арифметической и геометрической прогрессий

1.

Тема урока:
Определение арифметической
и геометрической прогрессий.
Формулы n – го члена арифметической и геометрической
прогрессий.
( На уроке использованы элементы УДЕ -укрупнённая
дидактическая единица. Совместное и одновременное
изучение родственных разделов- параллельная запись
контрастных суждений, двухэтажная запись.)

2.

Оборудование урока:
Компьютер.
Мультимедиапроектор .
Карточки с заданиями.

3.

Цель урока:
• - Ввести понятие арифметической и
геометрической прогрессий;
• - вывести формулы n –го члена
арифметической и геометрической прогрессий;
• - закрепить умения и навыки применять
изучаемые формулы;
• - развитие логического мышления,
познавательного интереса учащихся.
• - воспитание настойчивости, воли для
достижения конечных результатов.

4.

ХОД УРОКА:
• 1. Организационный момент.
• 2. Изучение нового материала.
• При объяснении применяются элементы
УДЕ.
• 3. Тренировочные упражнения.

5.

1. Составим две числовые
последовательности с а1 = 5.
В первом случае будем прибавлять, во
втором случае – умножать на одно и то
же число.
5; 8; 11; 14; 17;20…
5; 15; 45; 135; 405…
- арифметическая
прогрессия.
-геометрическая
прогрессия.

6.

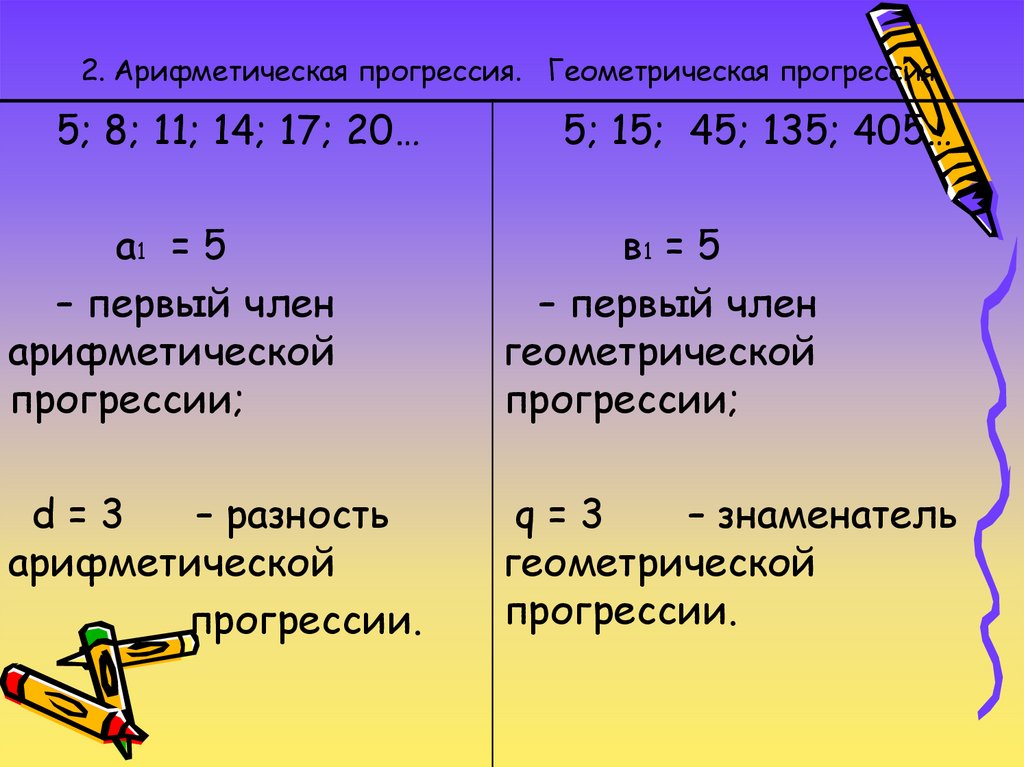
2. Арифметическая прогрессия. Геометрическая прогрессия.
5; 8; 11; 14; 17; 20…
5; 15; 45; 135; 405…
а1 = 5
– первый член
арифметической
прогрессии;
в1 = 5
– первый член
геометрической
прогрессии;
d=3
– разность
арифметической
прогрессии.
q=3
– знаменатель
геометрической
прогрессии.

7.

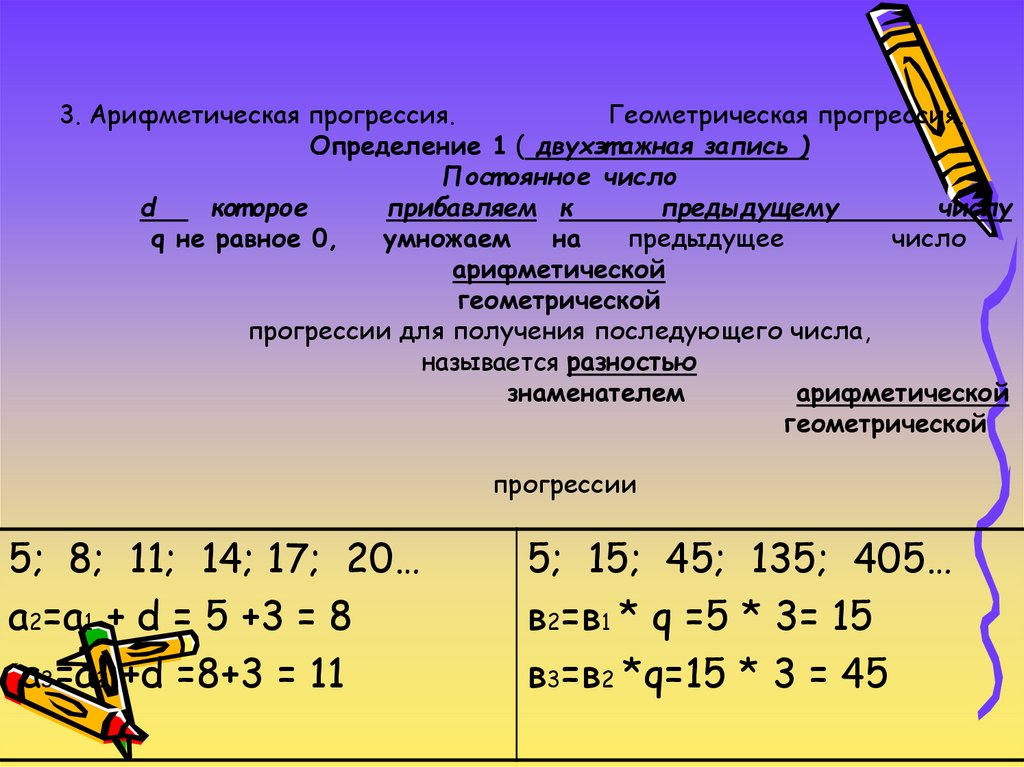
3. Арифметическая прогрессия.
Геометрическая прогрессия.
Определение 1 ( двухэт ажная запись )
Пост оянное число
d
кот орое
прибавляем к
предыдущему
числу
q не равное 0,
умножаем
на
предыдущее
число
арифметической
геометрической
прогрессии для получения последующего числа,
называется разностью
знаменателем
арифметической
геометрической
прогрессии
5; 8; 11; 14; 17; 20…
а2=а1 + d = 5 +3 = 8
а3=а2 +d =8+3 = 11
5; 15; 45; 135; 405…
в2=в1 * q =5 * 3= 15
в3=в2 *q=15 * 3 = 45

8.

4. Арифметическая прогрессия.
Геометрическая прогрессия.
Определение 2.
Арифмет ической
___________________
геомет рической
ПРОГРЕССИЕЙ НАЗЫВАЕТСЯ
такая последовательность, в
которой каждый последующий член равен предыдущему,
сложенному
________________
умноженному
С РАЗНОСТЬЮ
_________________
НА ЗНАМЕНАТЕЛЬ

9.

Формула n – го члена
арифметической
/ геометрической прогрессии.
параллельная запись конт раст ных суждений
а1
а2 = а1 + d
а3 = а2+d =а1 + 2 d
а4 = а3 +d = а1+3 d
-----------------------а n=а1 + d ( n - 1)
в1
в2 =в1 *q
2
в3 = в2 *q = в1* q
3
в4 =в3 * q = в1 * q
-----------------------n-1
вn = в1 * q
(

10.

ТРЕНИРОВОЧНЫЕ УПРАЖНЕНИЯ.
1. Устная работа.
НАЙТИ ЧЛЕНЫ
АРИФМЕТИЧЕСКОЙ / ГЕОМЕТРИЧЕСКОЙ
ПРОГРЕССИЙ:
1)-6; -4; а3; а4; а5;…
1) 6; 3; в3;в4; в5;…
2)14, а2; 20; а4;…
2) 20; в2; 80;в4;…

11.

Тренировочные упражнения.
2. Математический диктант.
1.У арифметической
1.У геометрической
прогрессии первый член
прогрессии первый
равен 4, второй 6. Найти
член равен 8, второй
разность d.
4. Найти знаменатель
q.
2. У геометрической
2.У арифметической
прогрессии первый
прогрессии первый член
член равен 9, второй
равен 6, второй 2. Найти
3. Найти третий член.
третий член.

12.

Математический диктант.
3.Найти десятый член
арифметической
прогрессии, если её
первый член равен 1, а
разность d равна 4.
4. ( аn) - арифметическая
прогрессия. Выразите
через а1 и d
а10.
3. Найти четвёртый
член геометрической
прогрессии, если её
первый член равен 1, а
знаменатель
q = -2.
4. (вn)геометрическая
прогрессия.
Выразите
через в1 и q
в10.

13.

Физкультминутка:
• Гимнастика для глаз.
• 1. Медленно переводить взгляд с пола на
потолок и обратно (8-12 раз).
• 2. Медленно переводить взгляд справа
налево и обратно.
• При выполнении всех упражнений голова
должна быть неподвижна.

14.

Решение задач в тестовой форме.
Самостоятельная работа обучающего характера
с последующей проверкой.
1 вариант
2 вариант
1.В арифметической
прогрессии а5= 8,7
и а8 = 12,3.
Найдите d и а1
а) d = 1,6 и а1 = 2,3;
1.В арифметической
прогрессии а3 = 7,5
и а7 = 14,3.
Найдите d и а1.
а) d = 6,8 и а1 = -6,1;
б) d= 3,6 и а1 = -5,7;
б) d= 3,4 и а1 = 0,7;
в) d = 1,2 и а1 = 3,9;
в) d= 1,7 и а1 = 4,1;
г) d = 1,4 и а1 = 3,1.
г) d= 1,4 и а1 = 4,7

15.

Решение:
а1+4d=
• 8,7
а1+7d = 12,3
Составим систему
уравнений и решим её.
а1+2d=7,5
а1+6d =14,3
Составим систему
уравнений и решим её.

16.

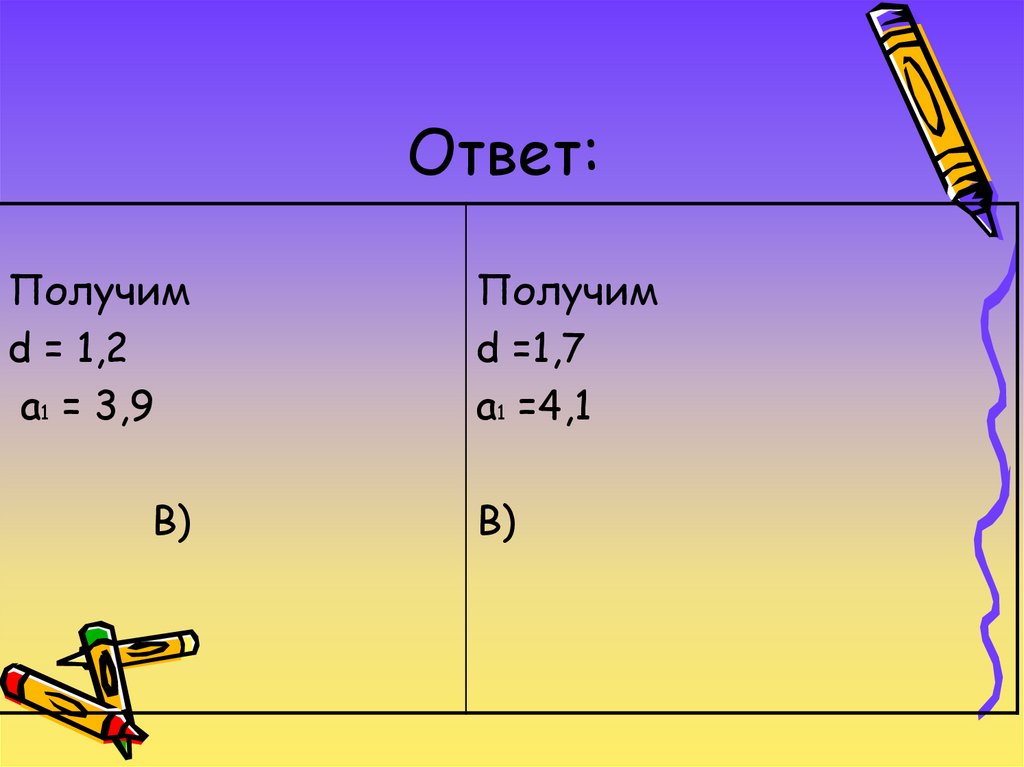
Ответ:
Получим
d = 1,2
а1 = 3,9
В)
Получим
d =1,7
а1 =4,1
В)

17.

2. Решите:
В арифметической
прогрессии а1=-7,3 и а2=6,4.
На каком месте
( укажите номер)
находится число 26?
а) 39,
б) 38,
в) 27)
г) 28
В арифметической
прогрессии а1 = -5,6 и а2=
-4,8.
На каком месте
( укажите номер)
находится число16?
а)14,
б) 13,
в) 27)
г) 28.

18.

Решение:
а1=-7,3
а2=-6,4
d=-6,4+7,3=0,9
26=-7,3+0,9(n-1).
Решая данное
уравнение,
получим:
а1=-5,6
а2= -4,8
d=-4,8+5,6=0,8
16=-5,6+0,8(n-1).
Решая данное
уравнение, получим:

19.

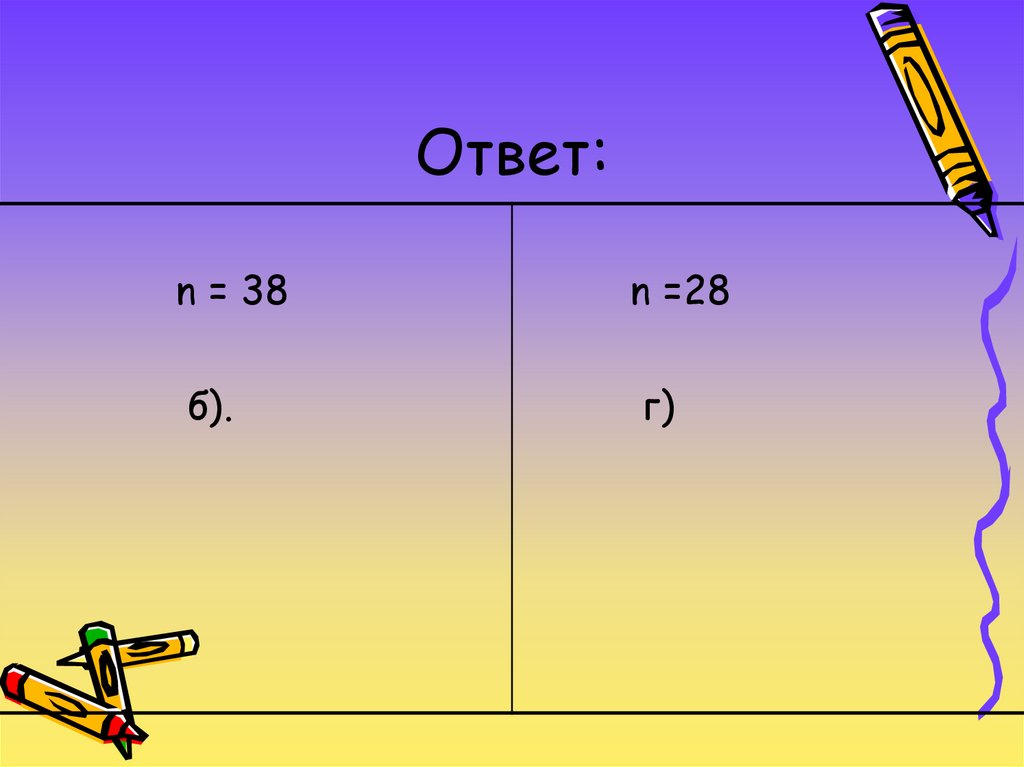
Ответ:
n = 38
б).
n =28
г)

20.

1 вариант
3. Решите:
В геометрической
прогрессии а1=1/6 и а2=
1/3.
Найдите шестой член
этой прогрессии.
а)1/384
б)16/3
в)1/192
г)32/3
2 вариант
В геометрической
прогрессии а1=-1/6,
а2=½.
Найдите пятый член
этой прогрессии.
а) 40/3,
б)40,5,
в)-13,5,
г)-1/486.

21.

Решение:
а1= 1/6,
а2= 1/3
q =2
5
а6=1/6*2
а1=-1/6;
а2=1/2
q=-3
4
а5=-1/6*(-3)

22.

Ответ:
Получим 16/3
Б)
Получим -13,5
В)

23.

Задание на дом:
Решение задач в тестовой форме
по карточкам.

24.

Подведение итогов урока:
• 1. Приведите примеры арифметической
прогрессии.
• 2. Приведите примеры геометрической
прогрессии.
• 3. Назовите формулы n-го члена
арифметической и геометрической
прогрессий.

25.

Использованная литература:
• П.М. Эрдниев. Технология УДЕ
(укрупнение дидактических
единиц)
• Алгебра, 9 класс, Ю.Н. Макарычев,
Н.Г. Миндюк, К.И. Нешков,
• С.Б. Суворова