Похожие презентации:
Математическая логика
1. Математическая логика
2. Математическая логика
Математическая логика— это разделматематики, изучающий
высказывания, рассматриваемые со
стороны их логических значений
(истинности или ложности) и
логических операций над ними.
3.
Математическая логикаразработана в середине
ХIХ века английским
математиком Джорджем
Булем. Ее создание
представляло собой
попытку решать
традиционные
логические задачи
алгебраическими
методами.
4.
Логическое высказывание — этолюбое повествовательное
пpедложение, в oтнoшении кoтopoгo
мoжно oднoзначнo сказать, истиннo
oнo или лoжнo.
Пример:
– "6 — четное число"
– "Рим — столица Франции"
5.
• Каждому логическому высказываниюсопоставляется логическая
переменная.
6.
Не всякое предложение являетсялогическим высказыванием.
Пример:
– ученик десятого класса;
– информатика — интересный предмет;
– в городе A более миллиона жителей ;
– у нее голубые глаза.
7.
• Употребляемые в обычной речи слова исловосочетания
"не", "и", "или", "если... ,
то", "тогда и только тогда" и другие
позволяют из уже заданных
высказываний строить новые
высказывания. Такие слова и
словосочетания
называются логическими связками.
8.
• Высказывания, образованные из другихвысказываний с помощью логических
связок, называются составными.
Высказывания, не являющиеся
составными,
называются элементарными.
9. Примеры
Элементарные высказывания:– Петров — врач;
– Солнце светит.
Составные высказывания :
– Петров — врач и шахматист ;
– Петров — врач или шахматист
10. Логические операции
Основными логическими операциямиявляются операции И, ИЛИ, НЕ.
Им соответствуют связки И, ИЛИ, НЕ
естественного языка.
11. Операция НЕ
выражаемая словом "не", называетсяотрицанием и обозначается чертой над
высказыванием (или знаком ).
Высказывание истинно, когда A ложно, и ложно,
когда A истинно.
Пример. "Луна — спутник Земли" (А); "Луна —
не спутник Земли" ().
12. Операция И
Операция Ивыражаемая связкой "и", называется конъюнкцией
(лат. conjunctio — соединение) или логическим
умножением и обозначается точкой " . " (может
также обозначаться знаками или &).
• Высказывание А В истинно тогда и только тогда,
когда оба высказывания А и В истинны.
• Например, высказывание "10 делится на 2 и 5
больше 3" истинно, а высказывание "10 делится
на 2 и 5 не больше 3",
— ложно.
13. Операция ИЛИ
выражаемая связкой "или" (в
неисключающем смысле этого слова),
называется дизъюнкцией (лат. disjunctio —
разделение) или логическим сложением и
обозначается знаком v (или плюсом).
• Высказывание А v В ложно тогда и только
тогда, когда оба высказывания А и В ложны.
• Например, высказывание "10 не делится на
2 или 5 не больше 3" ложно, а
высказывание "10 делится на 2 или 5
больше 3", — истинно.
14. Операция ЕСЛИ-ТО
выражаемая связками "если ..., то", "из... следует", "... влечет ...", называется
импликацией (лат. implico — тесно
связаны) и обозначается знаком .
Высказывание А В ложно тогда и только
тогда, когда А истинно, а В ложно.
15. Замечание
• В обычной речи связка "если ..., то"описывает причинно-следственную связь
между высказываниями. Но в логических
операциях смысл высказываний не
учитывается. Рассматривается только их
истинность или ложность. Поэтому
импликации, образоваться
высказываниями, совершенно не
связанными по содержанию.
16. Примеры импликаций
если президент США — демократ, то вАфрике водятся жирафы;
если арбуз — ягода, то в бензоколонке
есть бензин.
17. Операция РАВНОСИЛЬНО
• выражаемая связками "тогда и толькотогда", "необходимо и достаточно",
"... равносильно ...", называется
эквиваленцией или двойной
импликацией и обозначается
знаком или ~. Высказывание А
В истинно тогда и только тогда, когда
значения А и В совпадают.
18. Примеры
• высказывания "24 делится на 6тогда и только тогда, когда 24
делится на 3", "23 делится на 6
тогда и только тогда, когда 23
делится на 3" истинны;
• высказывания "24 делится на 6 тогда
и только тогда, когда 24 делится на
5", "21 делится на 6 тогда и только
тогда, когда 21 делится на 3" ложны.
19.
• Высказывания А и В, образующие составноевысказывание A B , могут быть
совершенно не связаны по содержанию,
например: "три больше двух" (А), "пингвины
живут в Антарктиде" (В). Отрицаниями
этих высказываний являются высказывания
"три не больше двух" ( A), "пингвины не
живут в Антарктиде" ( B). Образованные
из высказываний А и В составные
высказывания A B и A B истинны, а
высказывания A B и A B — ложны.
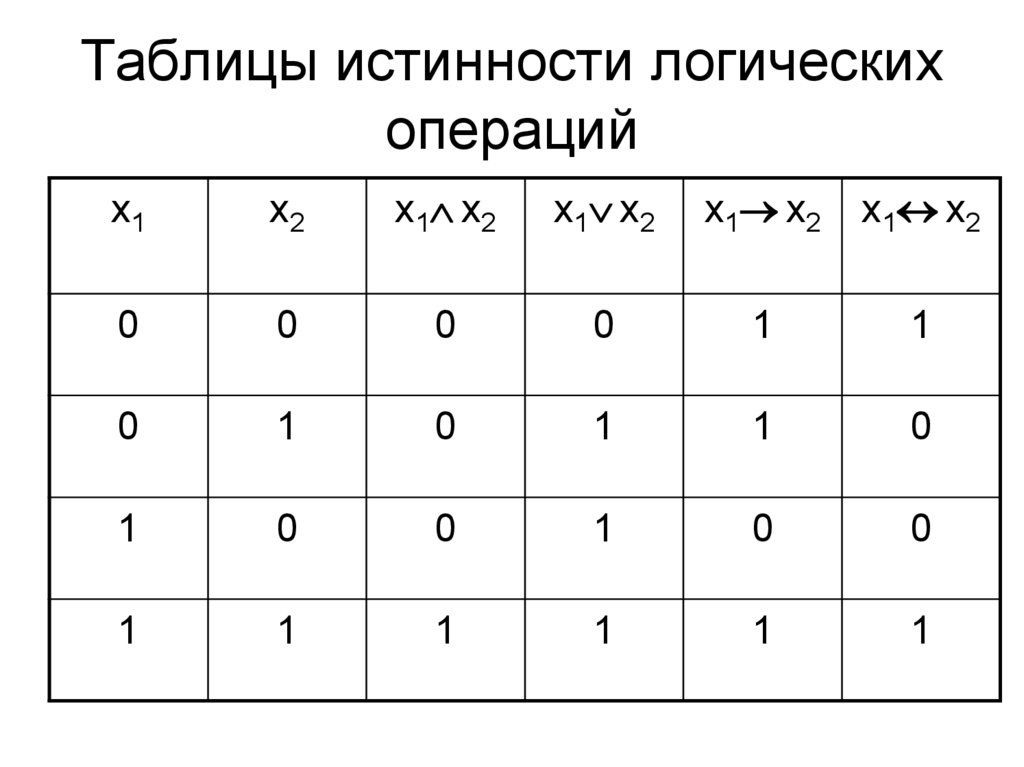
20. Таблицы истинности логических операций
x1x2
x 1 x 2
x 1 x 2
x 1 x 2
x1 x2
0
0
0
0
1
1
0
1
0
1
1
0
1
0
0
1
0
0
1
1
1
1
1
1
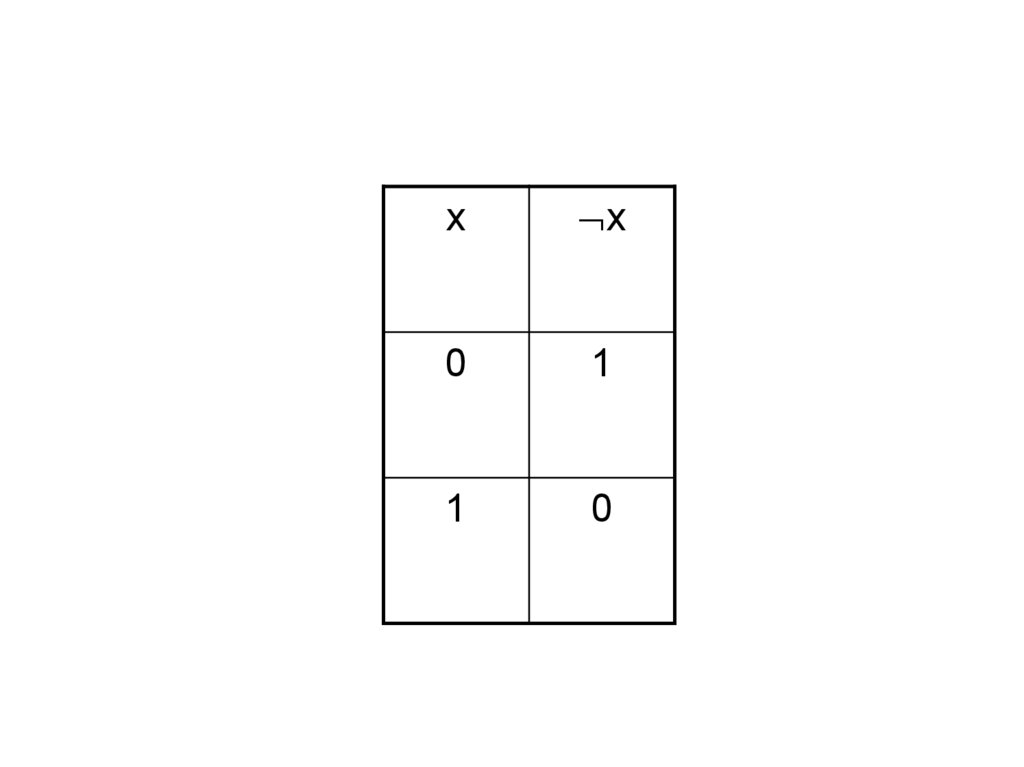
21.
xx
0
1
1
0
22.
• Число различныхбинарных функций =
23. Логическая формула
• С помощью логических переменных исимволов логических операций любое
высказывание можно формализовать,
то есть заменить логической формулой.
• Можно говорить о вычислении
логического высказывания в смысле
вычисления эквивалентной ему
логической формуле.
24. Порядок вычисления логических операций
1. Отрицание2. Конъюнкция
3. Дизъюнкция
4. Импликация, эквивалентность.
25. ОСНОВНЫЕ ЗАКОНЫ АЛГЕБРЫ ЛОГИКИ
ЗаконПереместительный
Сочетательный
Распределительный
Правила де Моргана
Идемпотенции
Поглощения
Склеивания
Операция переменной с
ее инверсией
Операция с
константами
Двойного отрицания
Для ИЛИ
Для И
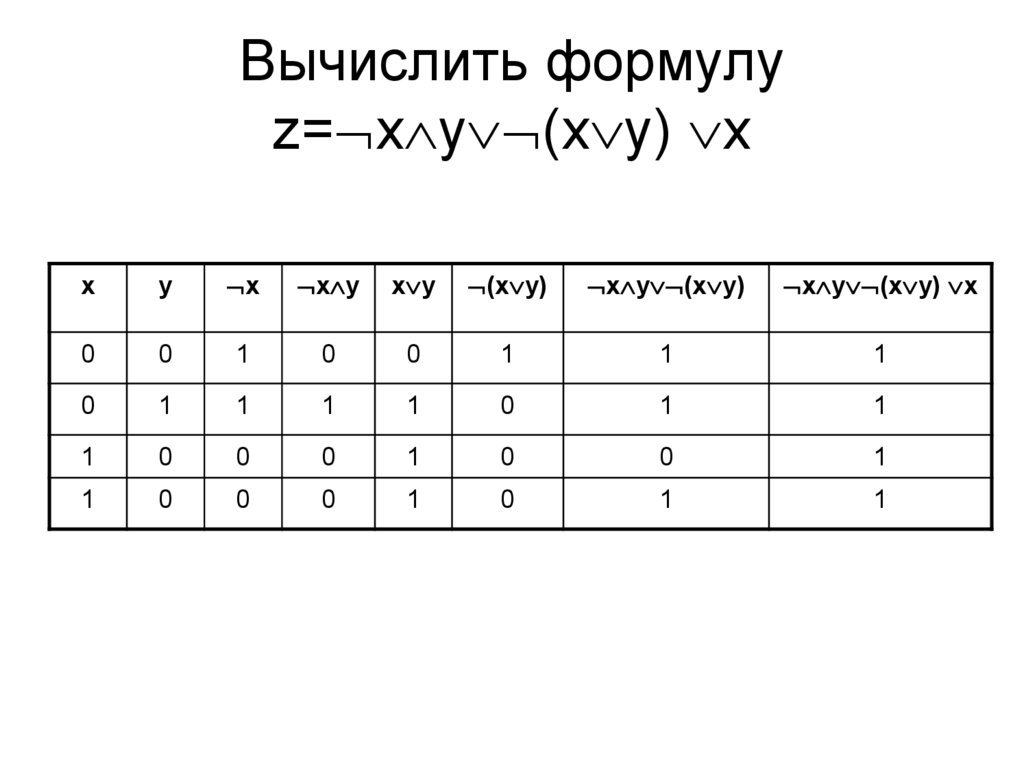
26. Вычислить формулу z=xy(xy) x
Вычислить формулуz= x y (x y) x
x
y
x
x y
x y
(x y)
x y (x y)
x y (x y) x
0
0
1
0
0
1
1
1
0
1
1
1
1
0
1
1
1
0
0
0
1
0
0
1
1
0
0
0
1
0
1
1
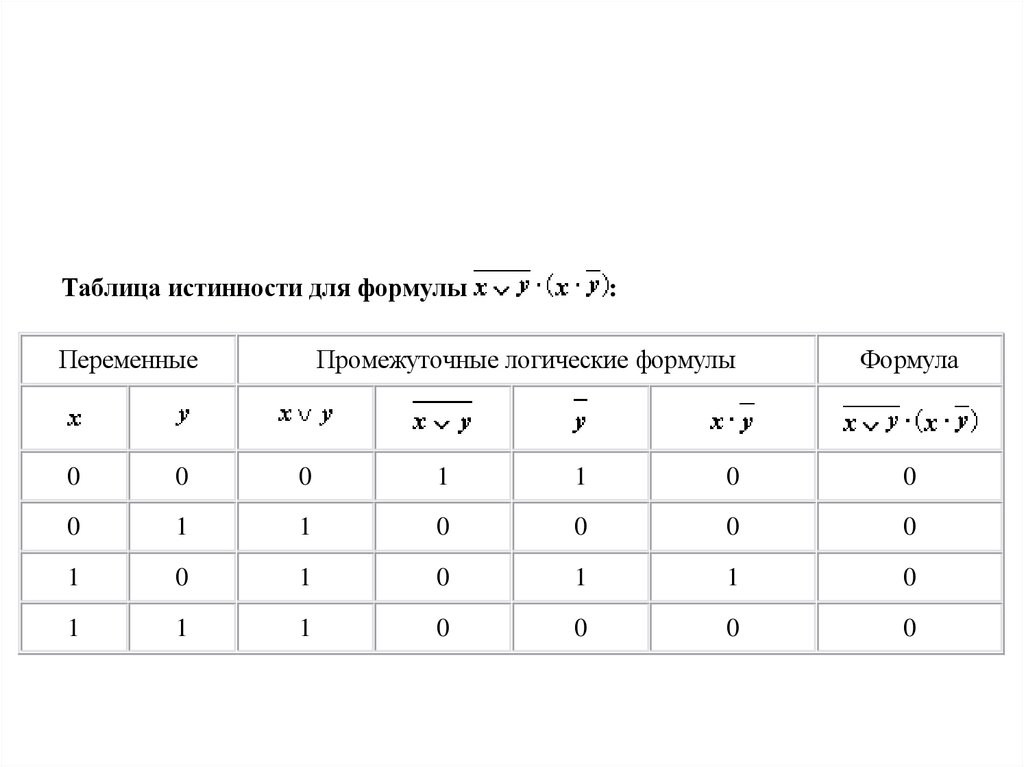
27.
Таблица истинности для формулыПеременные
:
Промежуточные логические формулы
Формула
0
0
0
1
1
0
0
0
1
1
0
0
0
0
1
0
1
0
1
1
0
1
1
1
0
0
0
0
28. Упрощение формул алгебры логики
1)(законы алгебры логики применяются в следующей последовательности: правило де
Моргана, сочетательный закон, правило операций переменной с её инверсией и правило
операций с константами);
2)
(применяется правило де Моргана, выносится за скобки общий множитель, используется
правило операций переменной с её инверсией);
3)
(повторяется второй сомножитель, что разрешено законом идемпотенции; затем
комбинируются два первых и два последних сомножителя и используется закон
склеивания);
4)
(вводится вспомогательный логический сомножитель (
); затем комбинируются
два крайних и два средних логических слагаемых и используется закон поглощения);
29. Связь между алгеброй логики и двоичным кодированием
• Математический аппарат алгебры логики описываетфункционирование аппаратных средств компьютера.
• Из этого следует два вывода:
• одни и те же устройства компьютера могут
применяться для обработки и хранения как числовой
информации, представленной в двоичной системе
счисления, так и логических переменных;
• на этапе конструирования аппаратных средств
алгебра логики позволяет значительно упростить
логические функции, описывающие
функционирование схем компьютера, и,
следовательно, уменьшить число элементарных
логических элементов.
30.
Дизъюнктивная нормальнаяформа (ДНФ).
Конъюнктивная нормальная
форма (КНФ).
30
31. Пусть функция от трех переменных задана следующей таблицей:
3132. тогда
Каждый из трех дизъюнктивных членов (слагаемых)записанной формулы соответствует набору значений
аргументов, для которого функция принимает значение 1.
32
33.
Легко видеть, что описанный способ построения формулы потаблице применим к любой функции, не равной тождественно
нулю.
Получаемые при этом формулы называются совершенными
дизъюнктивными нормальными формами, (СДНФ).
Считается, что СДНФ тождественного нуля– это «пустая»
дизъюнкция, не содержащая ни одного дизъюнктивного
слагаемого.
33
34.
Двойственная конструкция приводит к представлению функциив так называемой совершенной конъюнктивной нормальной
форме, сокращенно СКНФ.
СКНФ рассмотренной ранее функции имеет следующий вид:
Каждый из пяти конъюнктивных членов (множителей)
соответствует набору значений аргументов, для которого
функция принимает значение 0.
34
35.
Описанный выше способ построения СДНФ и СКНФ опираетсяна следующую теорему о разложении функции по переменной.
Теорема. Пусть
– произвольная булева
функция.
Тогда
35
36.
Доказательство. Докажем первую формулу. Чтобы незагромождать выкладки индексами и многоточиями,
ограничимся случаем функции от двух переменных.
Доказываемая формула принимает следующий вид:
При любом y подстановка в правую часть x=1 и x=0 дает
соответственно
36
37.
Таким образом, левая и правая части доказываемогоравенства совпадают на любом наборе значений аргументов.
Следовательно, функции слева и справа от знака равенства
равны. На общий случай доказательство распространяется
практически без изменений. Достаточно считать, что y
обозначает не одну переменную, а набор переменных. Второе
равенство из формулировки теоремы доказывается аналогично
(кроме того, его справедливость следует из принципа
двойственности).
37
38.
Последовательно применяя несколько раз (по числупеременных) разложение из предыдущей теоремы, можно
получить СДНФ булевой функции. Например,
38
39.
Функцияпредставлена в виде дизъюнкции четырех
дизъюнктивных членов. Те из них, для которых коэффициент
равен нулю, можно отбросить. В результате получится
СДНФ. Например, для функции
и
имеем
,
поэтому
39
40.
Элементарной конъюнкцией (конъюнктом) называют конъюнкциюпеременных и/или их отрицаний, в которой каждая переменная
встречается не более одного раза.
Пустой дизъюнкт считается равным 0.
Конъюнктивной нормальной формой называется конъюнкция
конечного числа дизъюнктов.
40




































 Математика
Математика








