Похожие презентации:
Формирование читательской и математической грамотности на уроках информатики
1.
Формирование читательской иматематической грамотности
на уроках информатики
Учитель информатики и ИКТ
МБОУ «Школа№3 города
Дебальцево»
Шкурко Л.А.
1
2.
23.
34.
Читательская грамотность —способность человека понимать и
использовать письмен-ные тексты,
размышлять о них и заниматься
чтением для того, чтобы достигать
своих целей, расширять свои знания и
возможности, участвовать в
социальной жизни.
4
5.
Использованиестратегий
смыслового
чтения
на
уроках
информатики позволяет осуществлять развитие читательской
грамотности.
Существует ряд
читательских
наработок по формированию различных
стратегий, освоение
которых
значительно
улучшит качество обработки прочитанного текста. Овладение
стратегиями происходит преимущественно в группах или
парах, что
позволяет
выработать у
учеников не только
речевую, но и коммуникативную компетентность.
5
6.
Стратегия № 1. Направленное чтение.Цель: сформировать умение целенаправленно читать учебный текст. Задавать проблемные
вопросы, вести обсуждения в группе.
1. Актуализация.
Прием «Ассоциативный куст»: учитель пишет
ключевое
слово или заголовок текста,
учащиеся один за другим высказывают свои ассоциации, учитель записывает. Использование
этого
приема
деятельность,
позволяет
актуализировать
знания,
мотивировать последующую
активизировать познавательную деятельность учащихся, настроить их на
работу.
2. Ученики про себя читают небольшой по объему текст или часть текста, останавливаясь на
указанных местах.
3. Учитель задает проблемный вопрос по прочитанному материалу.
4. Ответы нескольких учеников обсуждают в классе.
5. Ученики делают предположение относительно дальнейшего развития события
6
7.
Стратегия № 2. СинквейнЦель: развить умение учащихся
выделять
ключевые
понятия в
прочитанном, главные идеи, синтезировать полученные знания, проявлять
творческие способности.
Учитель предлагает написать Синквейн по ключевому слову поработанного
текста.
Синквейн – «белый стих», слоган
в
из
пяти
строк (от фр. Cing – пять),
котором синтезирована основная информация.
Структура Синквейна:
Существительное (тема).
Два прилагательных (описание).
Три глагола (действие).
Фраза из четырех слов (описание).
Существительное (перефразировка темы).
7
8.
Стратегия №3 «Верные и неверные утверждения»Универсальный прием, способствующий актуализации знаний учащихся и
активизации мыслительной деятельности. Данный прием дает возможность
быстро включить детей в мыслительную деятельность и логично перейти к
изучению темы урока.
Стратегия формирует умение оценивать ситуацию или факты, умение
анализировать информацию, умение отражать свое мнение. Детям предлагается
выразить свое отношение к ряду утверждений по правилу: верно – «+», не
верно – «-».
Стратегия №4 «Верите ли вы…»
Проводится с целью вызвать интерес к изучению темы и создать
положительную мотивацию самостоятельного изучения текста по этой теме.
Проводится в начале урока, после сообщения темы.
8
9.
Учитывая стратегии современных подходов к чтению, на уроках информатики можно:выбирать наиболее рациональные виды чтения для усвоения учащимися нового
материала;
формировать у учащихся интерес к чтению путем внедрения нестандартных форм и
методов работы с текстом;
предвидеть
возможные
затруднения
учащихся в тех или иных видах учебной
деятельности;
повышать уровень самостоятельности учащихся в чтении по мере их продвижения
вперед;
организовывать
различные виды деятельности учащихся с целью развития у них
творческого мышления;
9
10.
Математическая грамотность – это способностьчеловека мыслить математически, формулировать,
применять и интерпретировать математику для решения
задач в разнообразных практических контекстах.
10
11.
Содержательные областиматематической грамотности
пространство и
форма
изменения и
отношения
количество
неопределенность
11
12.
üü
ü
ü
ü
ü
ü
Подходы к подбору или составлению заданий
Предлагаются не учебные задачи, а практические
проблемные ситуации, разрешаемые средствами
математики.
Для выполнения задания требуется «холистическое», а
не фрагментарное применение математики.
В описании ситуации достаточно информации для
решения поставленной проблемы.
Дополнительная информация сообщается в
формулировке вопроса.
Структура задания: дается описание ситуации, к
которому предлагаются от 1 до 4 вопросов.
Объективность оценки обеспечивается
независимостью вопросов.
Содержание задания ориентировано на
требования к обязательной математической
12
подготовке (ФГОСНОО, ФГОСООО, предметные и
метапредметные планируемые результаты обучения).
13.
üü
ü
ü
ü
ü
ü
Подходы к подбору и составлению заданий
Решение проблемы может быть рассчитан она
привлечение жизненного опыта школьника.
Осознанность применения знаний и умений
обеспечивается отсутствием прямых указаний на
способ, правило или алгоритм выполнения (решения).
Уменьшение влияния вычислительных ошибок на
результат решения обеспечивается отсутствием
громоздких вычислений.
Информация предлагается в различном виде (рисунок,
текст, таблица и др.).
Используются возможности компьютера (построения,
заполнение свободных полей, перетаскивания и др.).
Используются возможности разной формы записи
ответа (выбор, краткий, развернутый).
Приоритет заданий, решаемых разными способами. 13
14.
1415.
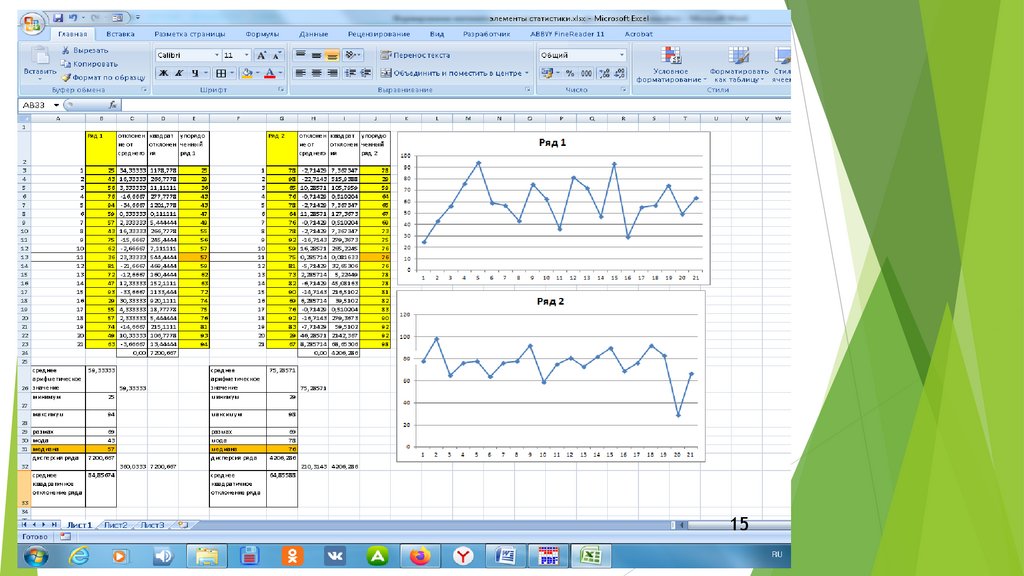
1516.
Логические задания на урокахинформатики
16
17.
Числовые ряды24,21,19,18,15,13,
,
,7
1,4,9,16, , ,49,64,81,100
16,17,15,18,14,19, ,
1,3,6,8,16,18, , ,76,78
17
18.
Темы уроков, на которых прослеживаетсяформирование математических представлений
на разных ступенях обучения 18
19.
5 класс19
20.
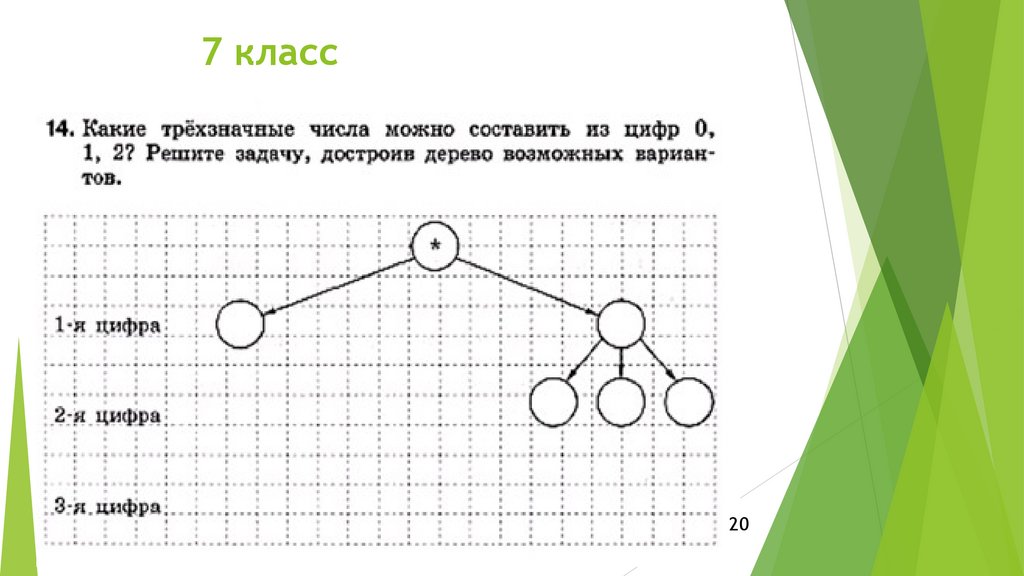
7 класс20
21.
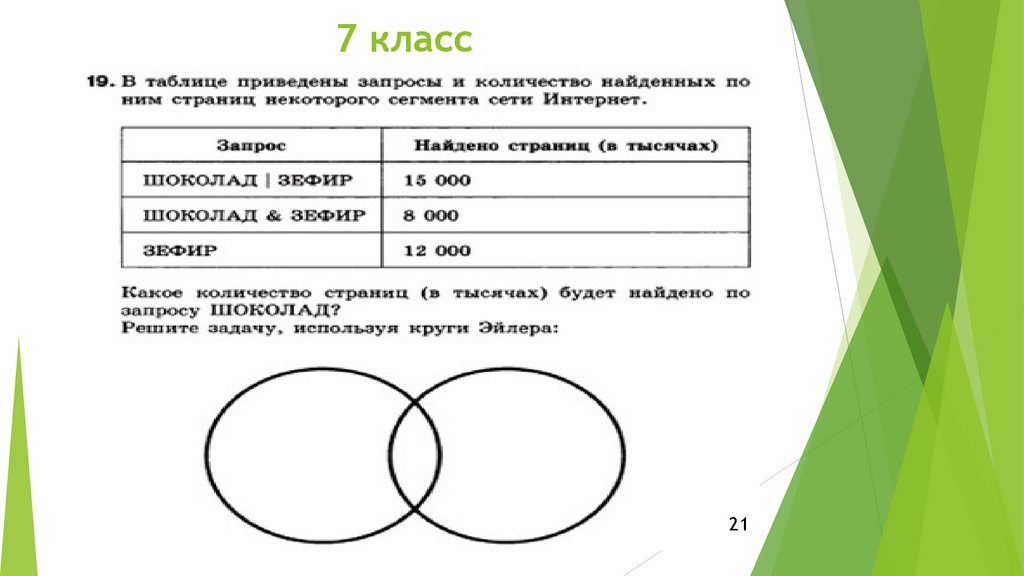
7 класс21
22.
8-9 класс8 класс
9 класс
22
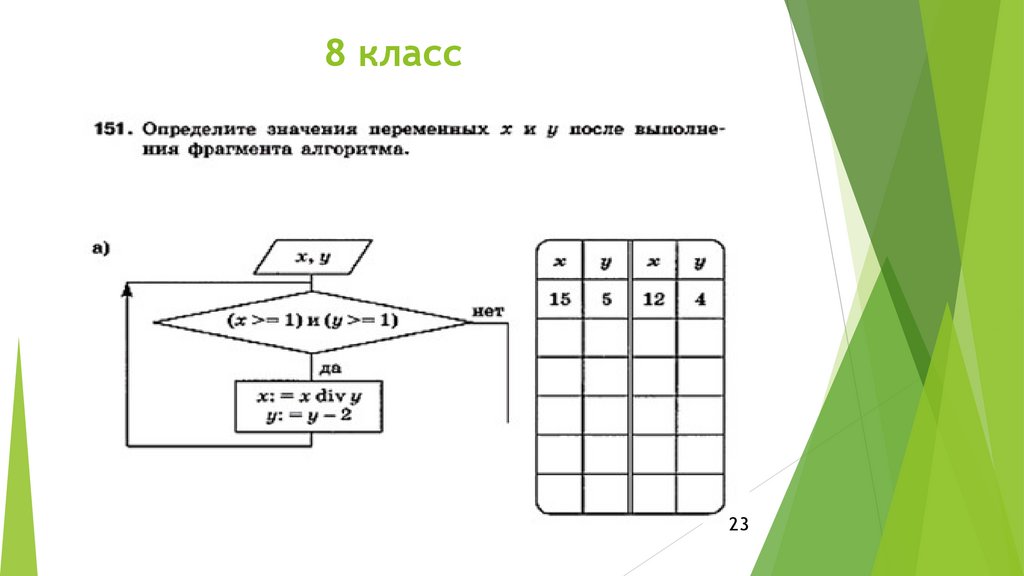
23.
8 класс23
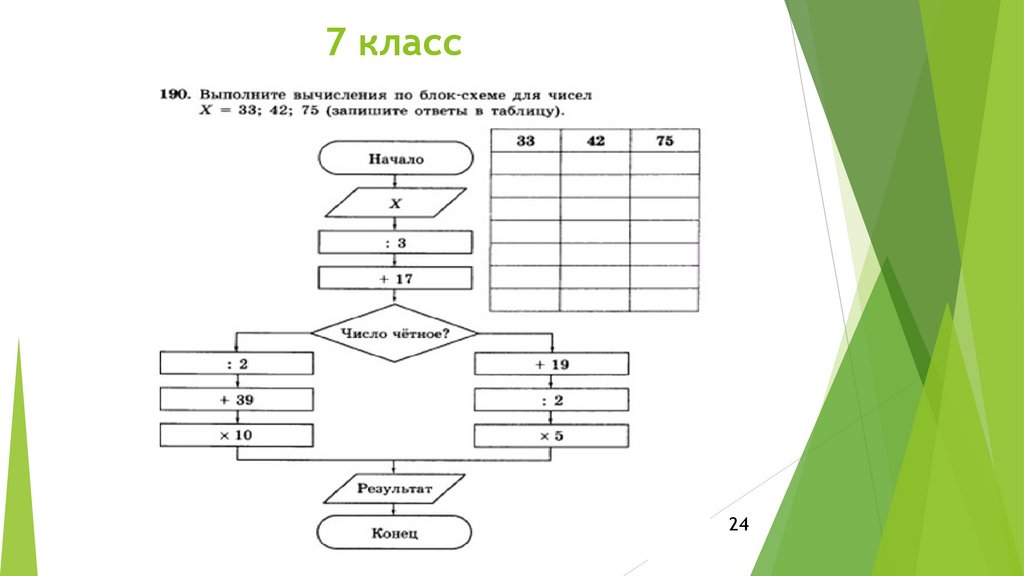
24.
7 класс24
25.
2526.
Спасибо за внимание!26




















 Математика
Математика Информатика
Информатика








