Математическое моделирование

1.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРИ ПРОЕКТИРОВАНИИ
КАДАСТРОВОЙ ДЕЯТЕЛЬНОСТИ
Кафедра кадастра и ТП
Аврунев Евгений Ильич
1

2.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Применение метода математического моделирования при геодезическом
обеспечении землеустроительных и кадастровых работ
Существующие проблемы: наличие в ЕГРН недостоверной кадастровой информации о
местоположения объектов недвижимости в кадастровых кварталах территориальных образований
(реестровые ошибки);
неправомерный самозахват землевладельцами частей земельных участков;
изменение границ земельных участков в силу неблагоприятных физико-геологических процессов и
явлений.
Цель работы: выполнить математическое моделирование результатов инструментального
геодезического контроля местоположения земельного участка (ЗУ) и оценить соответствие реального
местоположения ЗУ требованиям нормативно-правовых документов
[Приказ №П/0393].
Кафедра кадастра и ТП
Аврунев Евгений Ильич
2

3.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Содержание
Основная и дополнительная литература……………………………....…………………………………..4
Используемый понятийный аппарат……………………………..………..………………………………5
Используемые системы координат для построения математических моделей……….………………..8
Геодезическая система координат…………………………………………………………………………8
Пространственная прямоугольная система координат ГСК-2011………………………..……….……14
Плоская прямоугольная координатная система……………………………………………..…….……..20
Применение
GNSS-технологий
при
определении
параметров
математической
модели………………………………………………………………………………………………………37
Проверка адекватности математической модели земельного участка по результатам проведения
геодезического земельного контроля……………………………………………………………………..49
Контрольные вопросы……………………………………………………………………………………..65
Практическая часть задания………………………………………………………………………………67
Кафедра кадастра и ТП
Аврунев Евгений Ильич
3

4.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Основная и дополнительная литература
Аврунев Е.И. Геодезическое обеспечение Государственного кадастра
недвижимости. Новосибирск. СГГА. 2011г.;
Аврунев Е.И., Горобцов С.Р. Геодезическое обеспечение кадастровых работ.
Новосибирск. СГУГиТ. 2021г.;
Аврунев Е.И. Математическое моделирование при проектировании кадастровой
деятельности. Учебно-методическое пособие. Новосибирск. СГУГиТ. 2021г.;
Приказ № П/0393 от 23.10.2020г. Об утверждении требований к точности и
методам определений координат характерных точек границ земельного участка и
ОКСов.
Аврунев Е.И., Гиниятов И.А. Основы научных исследований: анализ качества
кадастровых работ в отношении земельных участков Новосибирск, СГУГиТ, 2018 г.
Методические указания для обучающихся по направлению подготовки 21.03.02
Землеустройство и кадастры
Аврунев Е.И., Гиниятов И.А., Труханов А.Э. Современные проблемы
землеустройства и кадастров. Анализ результатов кадастровых работ при
постановке земельных участков на государственный кадастровый учет.
Новосибирск, СГГА, 2014 г. Методические указания для обучающихся по
направлению подготовки 21.03.02 Землеустройство и кадастры
Кафедра кадастра и ТП
Аврунев Евгений Ильич
4

5.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Используемый понятийный аппарат:
Кадастровая деятельность – деятельность кадастрового инженера при выполнении работ в
отношении недвижимого имущества (объекта недвижимости) в результате которых обеспечивается
подготовка документов, на основании которых выполняется государственный кадастровый учет
(ГКУ) этого недвижимого имущества;
Кадастровые работы - выполняются в отношении земельных участков, зданий, сооружений,
помещений, объектов незавершенного строительства, машино-мест, единых недвижимых
комплексов;
Математическая модель – математическое описание объекта недвижимости, в установленной
действующим законодательством системе координат;
Система координат – математическое описание физической поверхности Земли на которой
располагается территориальное образование с объектами недвижимости в отношении которых
выполняются кадастровые работы;
Параметры математической модели – числовые характеристики, определяющие
местоположение объекта недвижимости на местности и его линейные и площадные размеры;
Математическое моделирование – составление, изучение или исследование математической
модели объекта недвижимости или в целом территориального образования;
Адекватность математической модели – соответствие параметров математической модели
(местоположение, площадные и линейные размеры) реальным объектам недвижимости в
соответствии с требованиями нормативно-правовых документов;
Характерная точка – знак, закрепляющий на местности и в виртуальном пространстве
границы объекта недвижимости. Координаты характерной точки определяют параметры
математической модели, а способ их определения саму математическую модель;
Кафедра кадастра и ТП
Аврунев Евгений Ильич
5

6.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Геодезическое обоснование (государственные геодезические сети (ГГС), опорные
геодезические сети (ОГС), геодезические сети сгущения (ГСС), геодезическое съемочное
обоснования (ГСО), опорные межевые сети (ОМС), геодезические сети специального назначения
(ГССН)) – пункты с исходными координатами (x, y), которые фиксируют в территориальном
образовании установленную действующим законодательством систему координат и являются
основой для построения математической модели территориального образования и составляющих ее
математических моделей объектов недвижимости;
Геодезическая сеть специального назначения – структурный элемент геодезического
обоснования, представляющая из себя совокупность геодезических пунктов нормативная точность
определения которых соответствует категории земель, на которой расположен объект
землеустроительных или кадастровых работ;
Способ полярных координат (наземные измерительные технологии) – использование
измерений, выполненных электронным тахеометром с исходного пункта ГО, для получения
параметров математической модели объекта недвижимости (координат характерных точек - x, y);
Измерительные GNSS-технологии - использование измерений, выполненных комплектом
спутникового оборудования относительно исходных пунктов ГО или постоянно действующей
базовой станции (ПДБС), для получения параметров математической модели объекта
недвижимости (координат характерных точек - x, y, H);
Измерительные GPS-технологии – математическая обработка измеренных псевдодальностей
выполняется на поверхности общеземного эллипсоида WGS-84;
Измерительные
ГЛОНАС-технологии
–
математическая
обработка
измеренных
псевдодальностей выполняется на поверхности общеземного эллипсоида ПЗ-90.
Кафедра кадастра и ТП
Аврунев Евгений Ильич
6

7.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Средняя квадратическая погрешность или ошибка (СКО или СКП) – возможный диапазон
изменения параметров математической модели (координат характерных точек) и геодезических
измерений при повторном их определении;
Геодезическая система координат – поверхность эллипсоида на которой математическая модель
объекта недвижимости определяется геодезической широтой, геодезической долготой и
геодезической высотой;
Плоская прямоугольная система координат – зональная математическая проекция ГауссаКрюгера, в которой математическая модель земельного участка определяется координатами
характерных точек x, y;
Пространственная прямоугольная система координат – математическая проекция, в которой
математическая модель земельного участка определяется координатами характерных точек x, y, H
или X, Y, Z.
Кафедра кадастра и ТП
Аврунев Евгений Ильич
7

8.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Геодезическая система координат:
Система координат – геодезическая. Математическая поверхность в которой возможно
определить местоположение недвижимого имущества - эллипсоид;
Основные координатные линии – большая полуось эллипсоида; малая полуось, совпадающая с
осью вращения эллипсоида; начальный Гринвичский меридиан; плоскость экватора;
Меридиан – линия на эллипсоиде, проходящая через экватор, полюса и произвольную точку на его
поверхности;
Гринвичский меридиан – линия на эллипсоиде, проходящая через экватор, полюса и центр
обсерватории в Гринвиче;
Исходная базовая линия для ориентирования – истинный меридиан в начальной точке линии;
Азимут – угол для ориентирования линии. Угол, отсчитанный от истинного меридиана по ходу
часовой стрелки до заданной линии на эллипсоиде;
Нормаль к поверхности эллипсоида – линия, образующая с поверхностью угол близкий к 90
градусов;
Координаты – геодезическая широта; геодезическая долгота; геодезическая высота.
Кафедра кадастра и ТП
Аврунев Евгений Ильич
8

9.

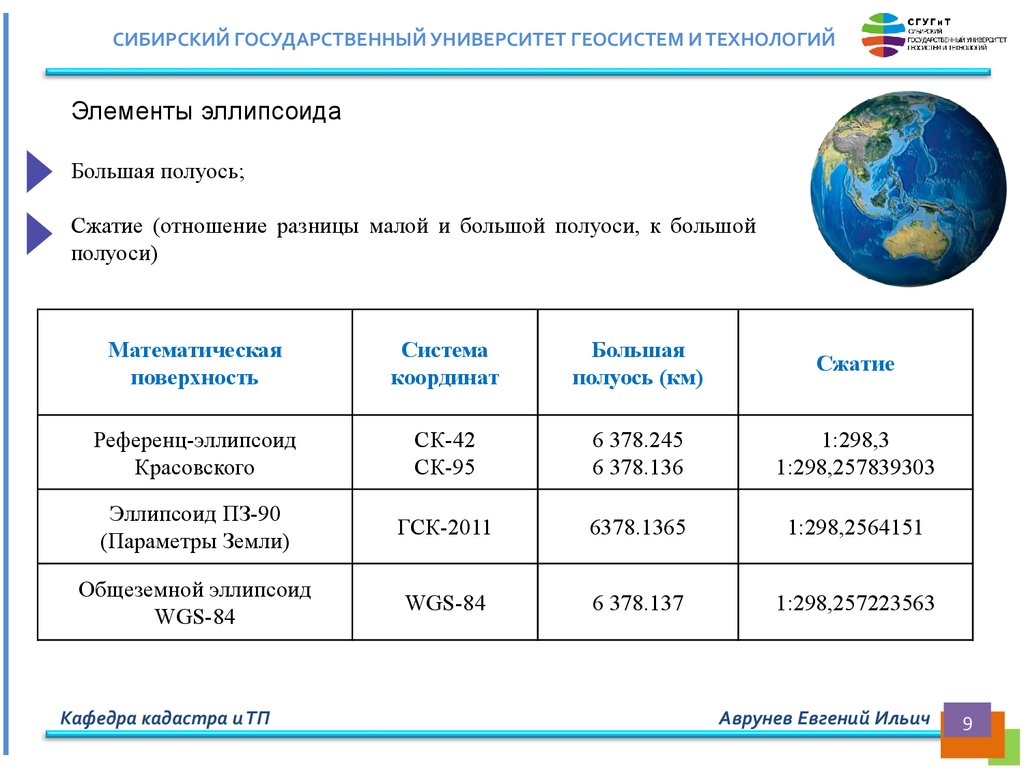
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Элементы эллипсоида
Большая полуось;
Сжатие (отношение разницы малой и большой полуоси, к большой
полуоси)
Математическая
поверхность
Система
координат
Большая
полуось (км)
Сжатие
Референц-эллипсоид
Красовского
СК-42
СК-95
6 378.245
6 378.136
1:298,3
1:298,257839303
Эллипсоид ПЗ-90
(Параметры Земли)
ГСК-2011
6378.1365
1:298,2564151
Общеземной эллипсоид
WGS-84
WGS-84
6 378.137
1:298,257223563
Кафедра кадастра и ТП
Аврунев Евгений Ильич
9

10.

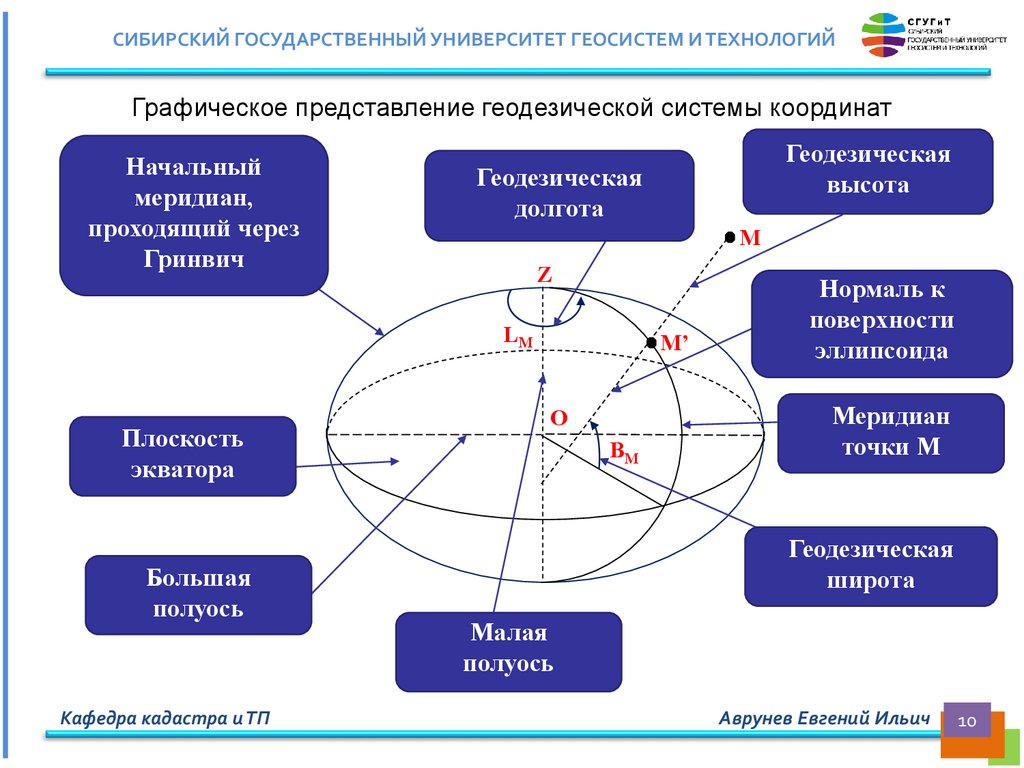
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Графическое представление геодезической системы координат
Начальный
меридиан,
проходящий через
Гринвич
Геодезическая
долгота
M
Z
X
Плоскость
экватора
Большая
полуось
Кафедра кадастра и ТП
Геодезическая
высота
LM
M’
O
BM
Нормаль к
поверхности
эллипсоида
Меридиан
точки М
Геодезическая
широта
Малая
полуось
Аврунев Евгений Ильич
10

11.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Параметры математической модели (геодезические координаты):
Геодезической широтой - называется острый угол В, образованный нормалью
к поверхности эллипсоида в данной точке и плоскостью экватора (размерность
градусы). Диапазон изменения геодезической широты -900 до 900;
Геодезической долготой
- называется двугранный угол, образованный
плоскостью начального меридиана и плоскостью меридиана данной точки
(размерность градусы). Диапазон изменения геодезической долготы 00 до 3600. (0 –
180 восточное полушарие, 180 – 360 западное полушарие)
Геодезической высотой H называется расстояние от физической поверхности
Земли до поверхности эллипсоида (линейная размерность). Диапазон изменения
геодезической высоты для планеты Земля -10994м. до +8848м.
Кафедра кадастра и ТП
Аврунев Евгений Ильич
11

12.

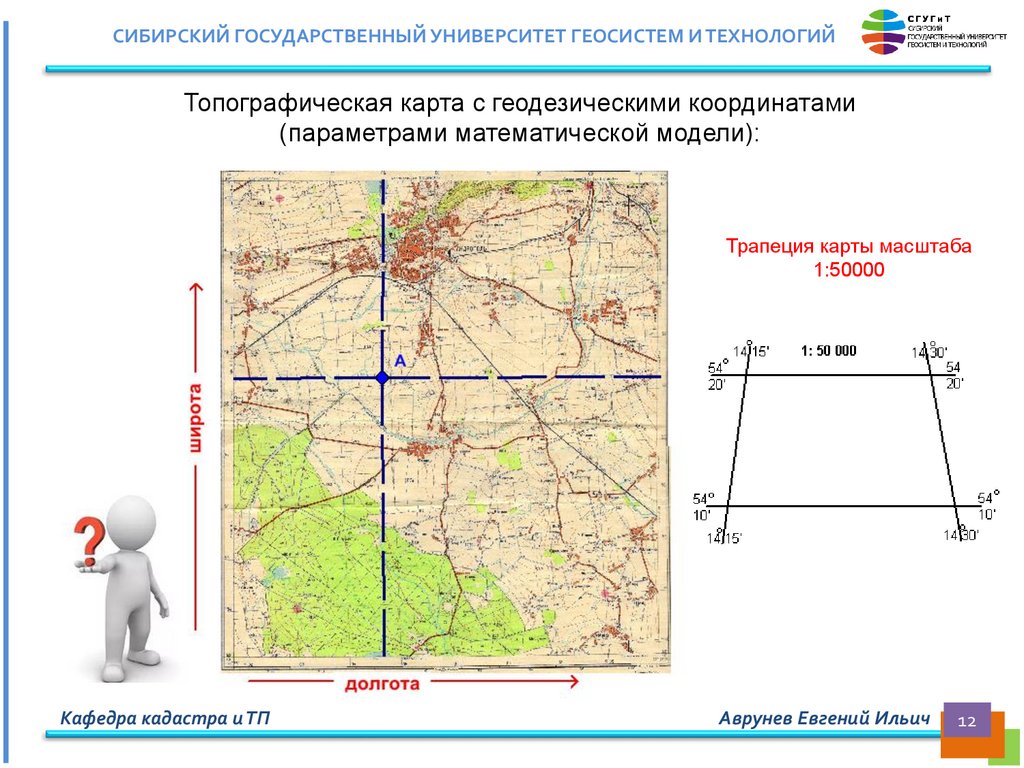
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Топографическая карта с геодезическими координатами
(параметрами математической модели):
Трапеция карты масштаба
1:50000
Кафедра кадастра и ТП
Аврунев Евгений Ильич
12

13.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Достоинства координатной системы:
Получение без искажений параметров объекта недвижимости при больших площадных
размерах (границы РФ; границы субъектов РФ)
Недостатки координатной системы:
Сложные и громоздкие формулы для вычислений параметров объектов недвижимости
(площадь, расстояние между характерными точками)
Кафедра кадастра и ТП
Аврунев Евгений Ильич
13

14.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Пространственная прямоугольная (геоцентрическая) система координат
ГСК-2011:
Математическая поверхность – перпендикулярное пересечение двух плоскостей;
Основные координатные линии – ось X, совпадающая с большой полуосью эллипсоида и
проходящая через начальный Гринвичский меридиан.
ось Y – перпендикулярная линия в плоскости экватора;
ось Z – линия, совпадающая с осью вращения эллипсоида;
Опорная базовая линия для ориентирования – ось X.
Координаты – абсцисса X (расстояние от центра эллипсоида до проекции точки на ось X);
ордината – Y(расстояние от центра эллипсоида до проекции точки на ось Y); высота –Z
(расстояние от положения точки в пространстве до плоскости экватора);
(линейные размерности).
Кафедра кадастра и ТП
Аврунев Евгений Ильич
14

15.

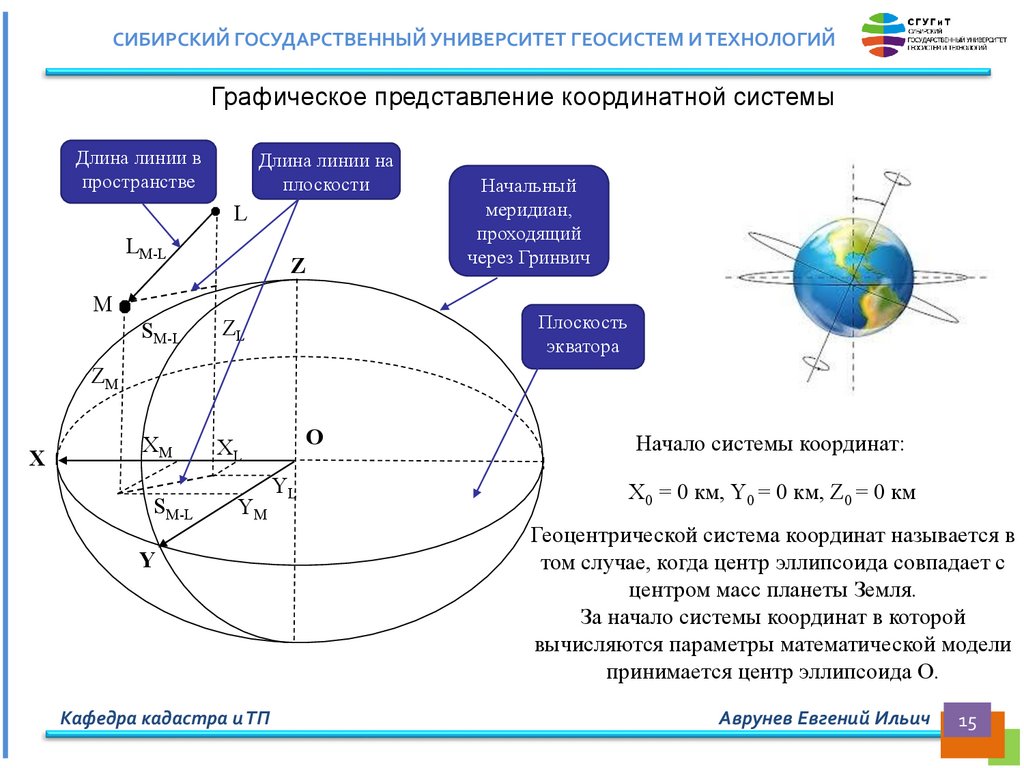
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Графическое представление координатной системы
Длина линии в
пространстве
Длина линии на
плоскости
L
LM-L
Z
M
SM-L
ZL
XM
XL
Начальный
меридиан,
проходящий
через Гринвич
Плоскость
экватора
ZM
X
SM-L
YM
Y
Кафедра кадастра и ТП
O
YL
Начало системы координат:
X0 = 0 км, Y0 = 0 км, Z0 = 0 км
Геоцентрической система координат называется в
том случае, когда центр эллипсоида совпадает с
центром масс планеты Земля.
За начало системы координат в которой
вычисляются параметры математической модели
принимается центр эллипсоида О.
Аврунев Евгений Ильич
15

16.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Достоинства координатной системы:
Получение без существенных искажений параметров объектов землеустройства при больших
площадных размерах (границы РФ; границы субъектов РФ);
Простые формулы для вычислений параметров объектов землеустройства;
Независимость вычисляемых параметров от удаления от центра координатной системы.
Недостатки координатной системы:
Сложность использования для составления планов и карт территориального образования;
Вычисление длин линий между точками земной поверхности без учета кривизны Земли.
Кафедра кадастра и ТП
Аврунев Евгений Ильич
16

17.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Проверка адекватности математической модели, построенной на земельный
участок в городе Новосибирске в координатной систем ГСК-2011 и
редуцированной на плоскость экватора
Вычисление редуцированной длины линии с физической поверхности Земли на
плоскость экватора
SM L L M L cos550 1000,000 0,5735764=573,576м.
Вычисление площадного параметра геометрической фигуры, образованной
редуцированными длинами линий
PИСТ PРЕД 1000,000 1000,000-573,576 573,576=671010м 2 =0,671км 2 .
Проверка адекватности математической модели по площадной характеристике
PИСТ
Кафедра кадастра и ТП
0,671км 2
1км 2
1
.
1,5
Аврунев Евгений Ильич
17

18.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Проверка адекватности математической модели, построенной на земельный
участок в городе Новосибирске в координатной систем ГСК-2011 и
редуцированной на среднюю плоскость Российской Федерации
Вычисление редуцированной длины линии с физической поверхности Земли
(г.Новосибирск) на плоскость, соответствующей средней широте РФ
SM L L M L cos 60 1000,000 0,9945218=994,521м.
Вычисление площадного параметра геометрической фигуры, образованной
редуцированными длинами линий
PИСТ PРЕД 1000,000 1000,000-994,521 994,521=1000000-989072м 2 =0,012км 2 .
Проверка адекватности математической модели по площадной характеристике
PИСТ
Кафедра кадастра и ТП
0,012км 2
1км 2
1
.
84
Аврунев Евгений Ильич
18

19.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Проверка адекватности математической модели, построенной на земельный
участок в координатной систем ГСК-2011 и редуцированной на среднюю
плоскость в городе Новосибирске
Вычисление редуцированной длины линии с физической поверхности Земли на
плоскость, соответствующей средней широте Новосибирска (широта самой северной
точки северной точки 55008’ ; южной 54048’; средняя широта 54058’ )
SM L L M L cos 0010' 1000,000 0,999995=999,996м.
Вычисление площадного параметра геометрической фигуры, образованной
редуцированными длинами линий
PИСТ PРЕД 1000,000 1000,000-999,996 999,996=1000000м 2 -999991м 2 =9м 2 .
Проверка адекватности математической модели по площадной характеристике
PИСТ
Кафедра кадастра и ТП
9м 2
100000м
2
1
.
11000
Аврунев Евгений Ильич
19

20.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Плоская прямоугольная система координат в проекции
Гаусса-Крюгера:
Данная координатная система используется при кадастровой деятельности, для
проектирования и строительства инженерных сооружений.
Координатная система получается в результате проведения на поверхности эллипсоида
меридианов через 6 градусов (начиная с меридиана, проходящего через Гринвич) и
развертывания полученных зон (60 зон) на плоскость.
Основными координатными линиями, являются:
Осевой меридиан (линия абсцисс); проекция экватора (линия ординат).
Началом системы координат для каждой зоны является пересечение осевого меридиана
с проекцией экватора. Координаты начала системы координат: x=0км. y=500км.
Кафедра кадастра и ТП
Аврунев Евгений Ильич
20

21.

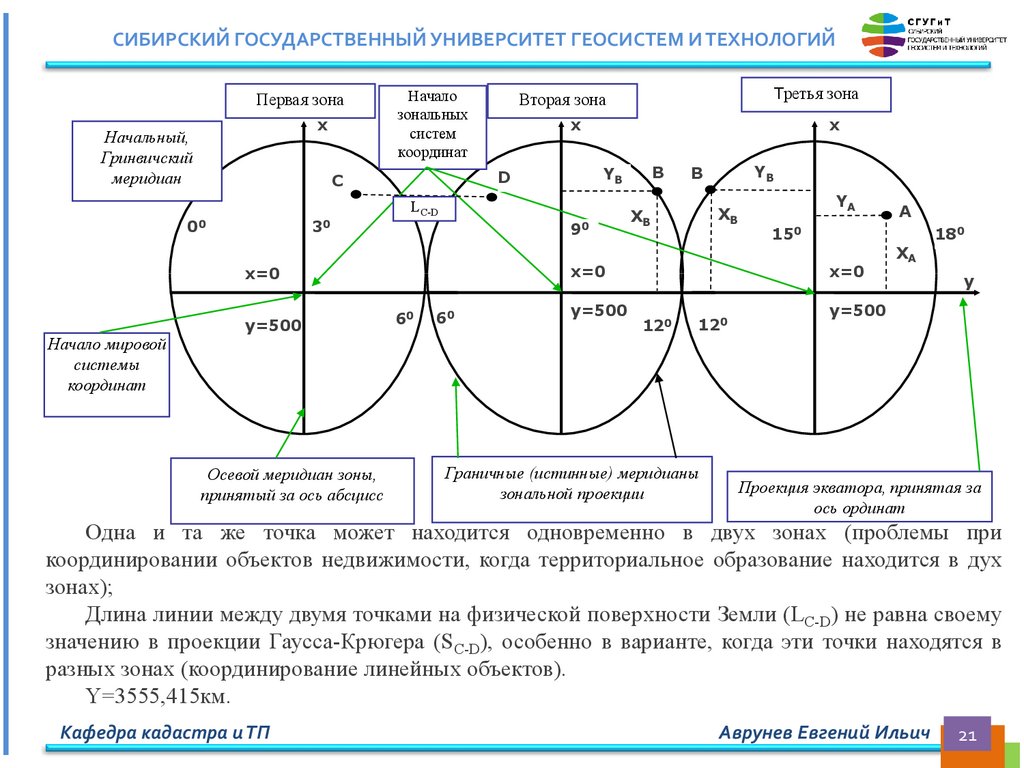
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Первая зона
x
Начальный,
Гринвичский
меридиан
Начало
зональных
систем
координат
00
30
Начало мировой
системы
координат
Осевой меридиан зоны,
принятый за ось абсцисс
x
B
YB
LC-D
90
YB
B
XB
XB
x=0
x=0
y=500
x
D
C
Третья зона
Вторая зона
60
60
y=500
YА
150
x=0
120
120
Граничные (истинные) меридианы
зональной проекции
А
XА
180
y
y=500
Проекция экватора, принятая за
ось ординат
Одна и та же точка может находится одновременно в двух зонах (проблемы при
координировании объектов недвижимости, когда территориальное образование находится в дух
зонах);
Длина линии между двумя точками на физической поверхности Земли (LC-D) не равна своему
значению в проекции Гаусса-Крюгера (SC-D), особенно в варианте, когда эти точки находятся в
разных зонах (координирование линейных объектов).
Y=3555,415км.
Кафедра кадастра и ТП
Аврунев Евгений Ильич
21

22.

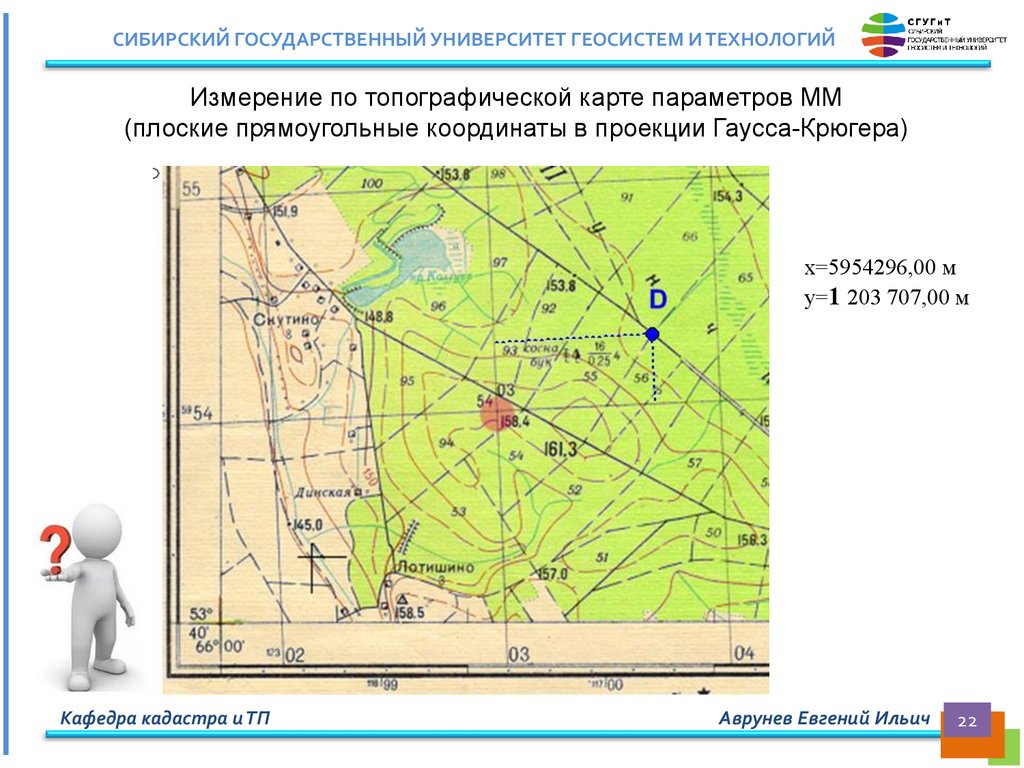
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Измерение по топографической карте параметров ММ
(плоские прямоугольные координаты в проекции Гаусса-Крюгера)
x=5954296,00 м
y=1 203 707,00 м
Кафедра кадастра и ТП
Аврунев Евгений Ильич
22

23.

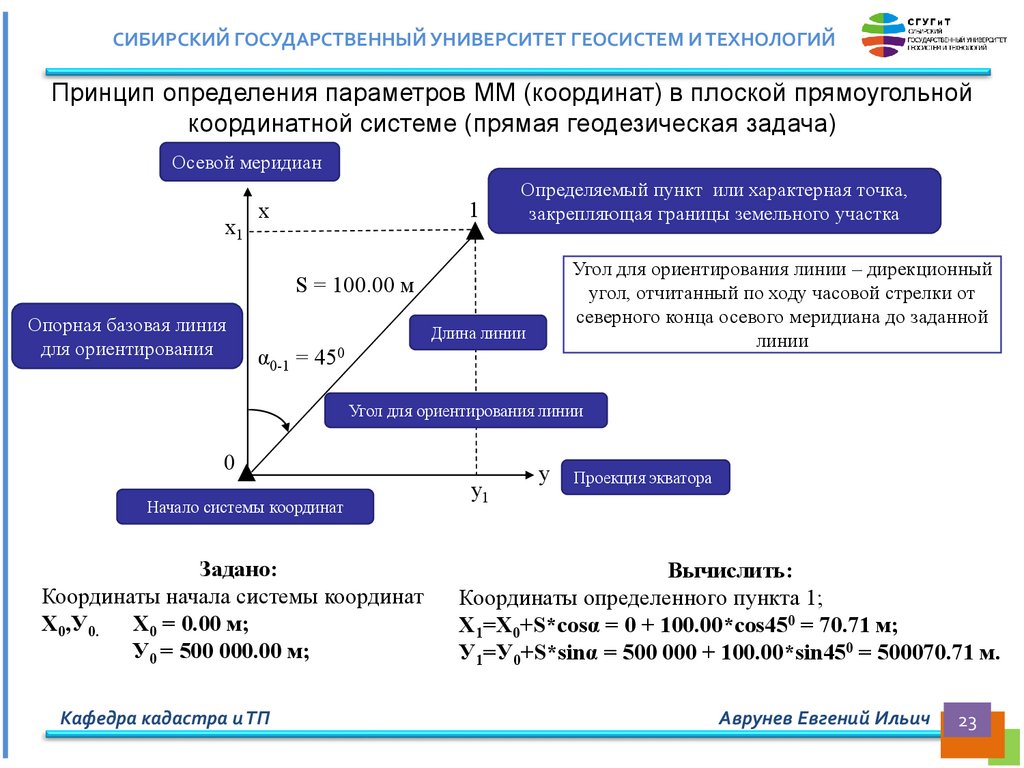
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Принцип определения параметров ММ (координат) в плоской прямоугольной
координатной системе (прямая геодезическая задача)
Осевой меридиан
x1
х
1
Определяемый пункт или характерная точка,
закрепляющая границы земельного участка
Угол для ориентирования линии – дирекционный
угол, отчитанный по ходу часовой стрелки от
северного конца осевого меридиана до заданной
линии
S = 100.00 м
Опорная базовая линия
для ориентирования
Длина линии
α0-1
= 450
Угол для ориентирования линии
0
Начало системы координат
Задано:
Координаты начала системы координат
Х0,У0. Х0 = 0.00 м;
У0 = 500 000.00 м;
Кафедра кадастра и ТП
у1
у
Проекция экватора
Вычислить:
Координаты определенного пункта 1;
Х1=Х0+S*cosα = 0 + 100.00*cos450 = 70.71 м;
У1=У0+S*sinα = 500 000 + 100.00*sin450 = 500070.71 м.
Аврунев Евгений Ильич
23

24.

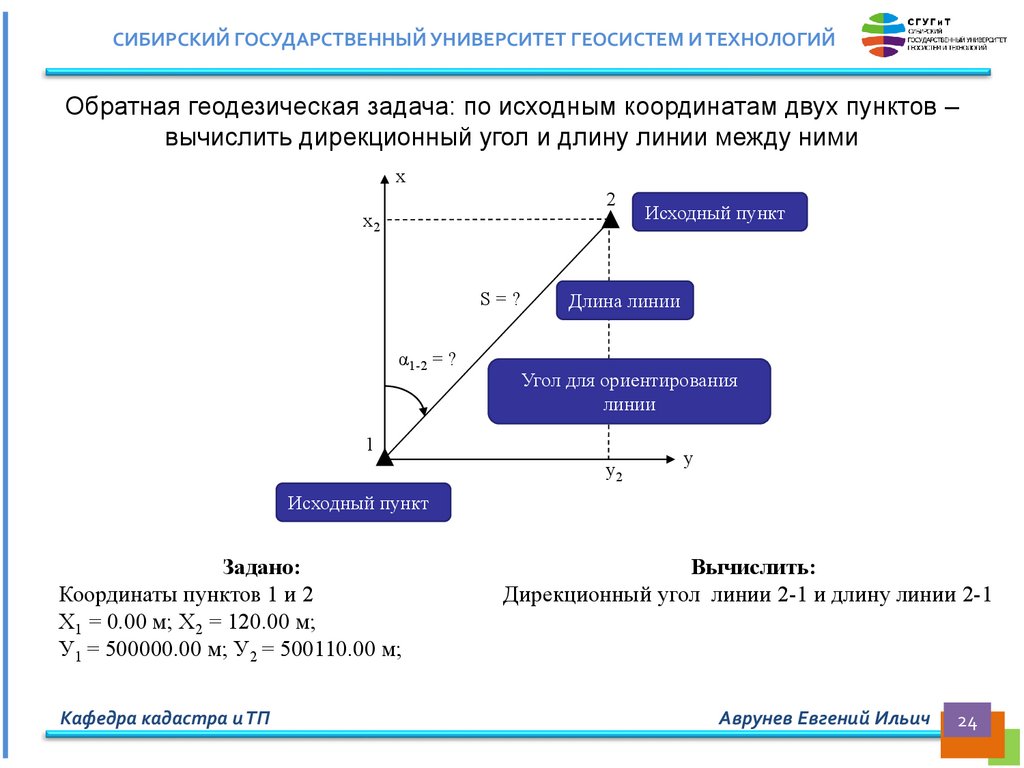
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Обратная геодезическая задача: по исходным координатам двух пунктов –
вычислить дирекционный угол и длину линии между ними
х
2
x2
S=?
α1-2 = ?
Исходный пункт
Длина линии
Угол для ориентирования
линии
1
у2
у
Исходный пункт
Задано:
Координаты пунктов 1 и 2
Х1 = 0.00 м; Х2 = 120.00 м;
У1 = 500000.00 м; У2 = 500110.00 м;
Кафедра кадастра и ТП
Вычислить:
Дирекционный угол линии 2-1 и длину линии 2-1
Аврунев Евгений Ильич
24

25.

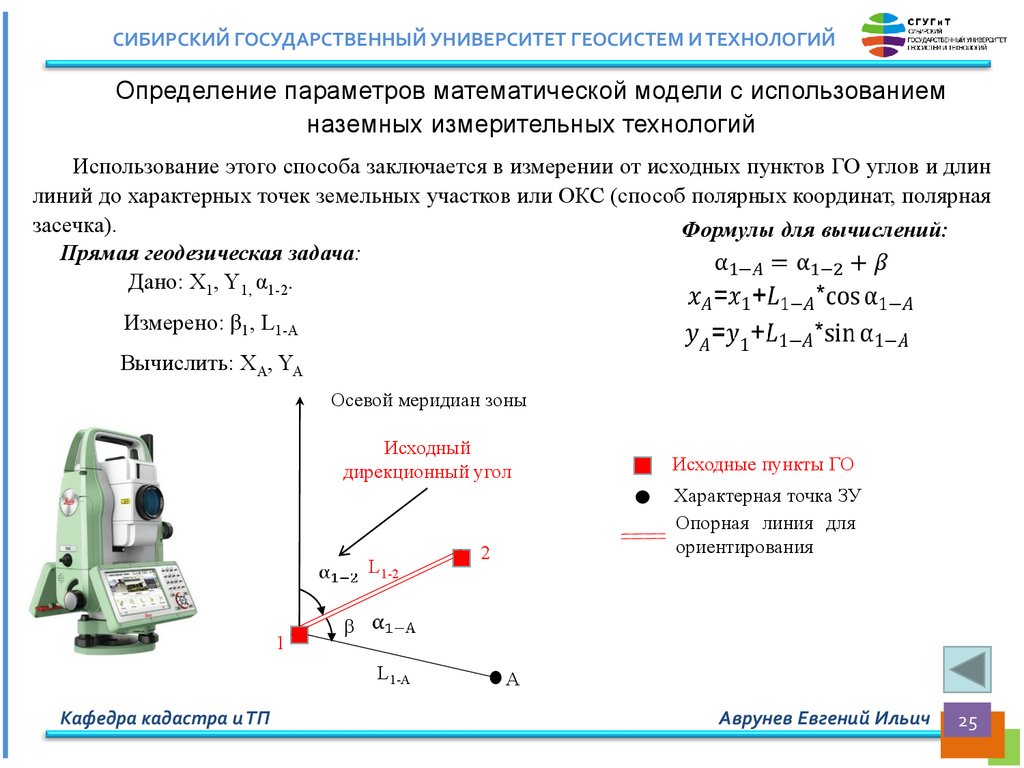
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Определение параметров математической модели с использованием
наземных измерительных технологий
Использование этого способа заключается в измерении от исходных пунктов ГО углов и длин
линий до характерных точек земельных участков или ОКС (способ полярных координат, полярная
засечка).
Формулы для вычислений:
Прямая геодезическая задача:
Дано: X1, Y1, α1-2.
Измерено: β1, L1-A
Вычислить: XA, YA
Осевой меридиан зоны
Исходный
дирекционный угол
L1-2
1
Характерная точка ЗУ
Опорная линия для
ориентирования
2
β
L1-А
Кафедра кадастра и ТП
Исходные пункты ГО
А
Аврунев Евгений Ильич
25

26.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Свойство проекции Гаусса-Крюгера, определяющее адекватность
математической модели
x
Проекция измеренной
линии в зональной
системе Гаусса-Крюгера
SГ SР
SР
ym
Меридиан, проходящий
через пункты, образующие
линию
Измеренная линия на
физической поверхности
Земли
SГ
y
Удаление линии от осевого
меридиана
Исходя из того, что все меридианы в этой проекции сходятся на полюсах, то при их удалении от
осевого меридиана (ym) они начинают удлиняться, причем чем больше величина ym тем больше
меридиан по своей длине отличается от осевого меридиана зоны. Следовательно, чем дальше
измеренная линия от осевого меридиана зоны, тем она длиннее в проекции Гаусса-Крюгера от своего
значения на физической поверхности Земли. Следовательно: удаление ЗУ от осевого меридиана
обусловливает возникновение неадекватности математической модели.
Кафедра кадастра и ТП
Аврунев Евгений Ильич
26

27.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Свойство проекции Гаусса-Крюгера для определения параметров
математической модели
Вычисление редуцированной длины линии с физической поверхности Земли в
проекцию Гаусса-Крюгера при удалении ее от осевого меридиана на 200 км.
YM2
2002
SР L Г Y; Y=L Г
=1,000
=0,492m; SР 1000, 492m.
2 R2
2 63702
Вычисление площадного параметра математической модели, образованной
редуцированными длинами линий
PИСТ PРЕД 1000000 1 000 984=984м 2 .
Проверка адекватности математической модели по площадному параметру
PИСТ
Кафедра кадастра и ТП
984м 2
1000000м
2
1
.
1020
Аврунев Евгений Ильич
27

28.

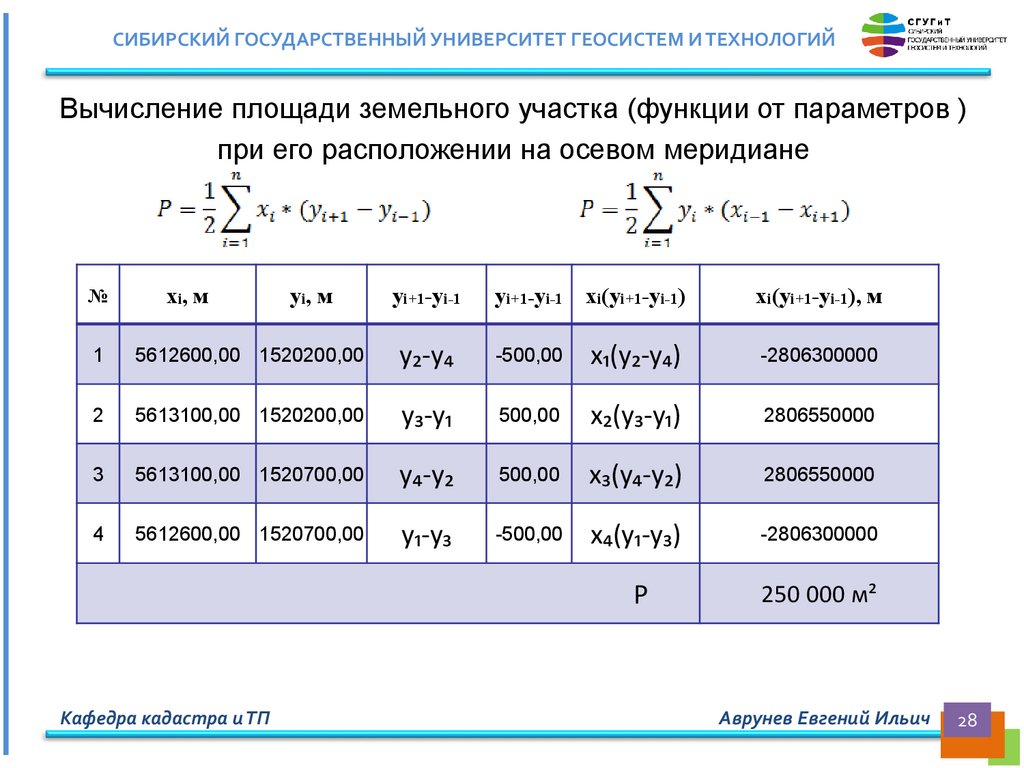
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Вычисление площади земельного участка (функции от параметров )
при его расположении на осевом меридиане
№
x i, м
y i, м
yi+1-yi-1
yi+1-yi-1
xi(yi+1-yi-1)
xi(yi+1-yi-1), м
1
5612600,00 1520200,00
y₂-y₄
-500,00
x₁(y₂-y₄)
-2806300000
2
5613100,00 1520200,00
y₃-y₁
500,00
x₂(y₃-y₁)
2806550000
3
5613100,00 1520700,00
y₄-y₂
500,00
x₃(y₄-y₂)
2806550000
4
5612600,00 1520700,00
y₁-y₃
-500,00
x₄(y₁-y₃)
-2806300000
P
250 000 м²
Кафедра кадастра и ТП
Аврунев Евгений Ильич
28

29.

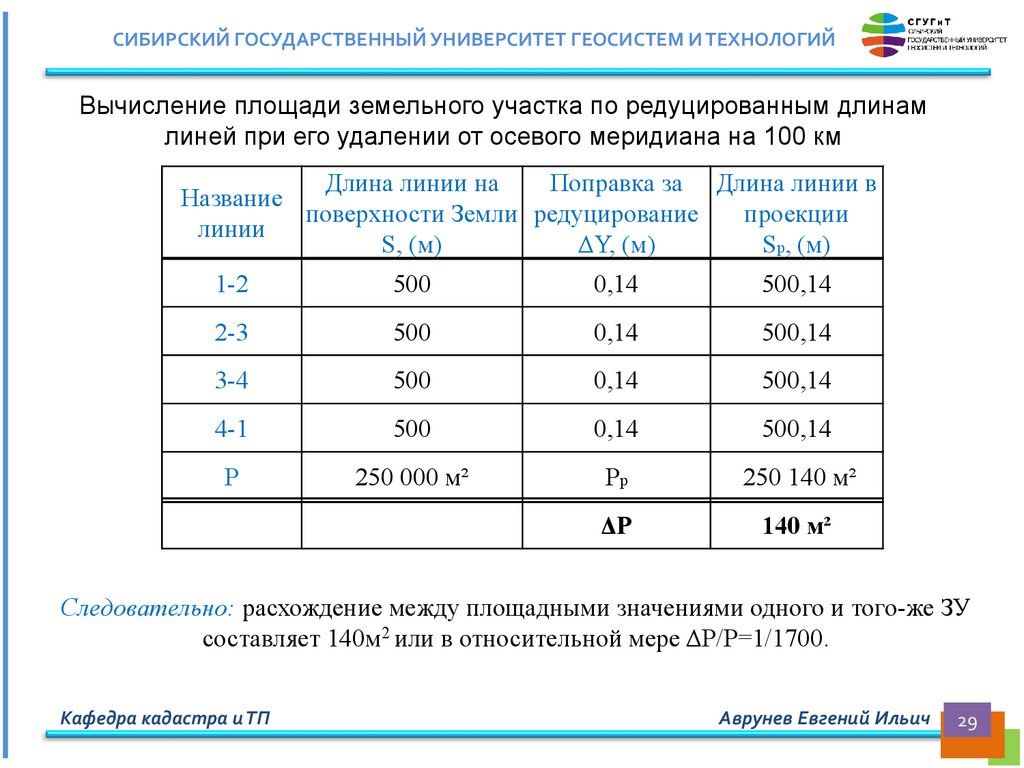
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Вычисление площади земельного участка по редуцированным длинам
линей при его удалении от осевого меридиана на 100 км
Длина линии на
Поправка за Длина линии в
Название
поверхности Земли редуцирование
проекции
линии
S, (м)
ΔY, (м)
Sp, (м)
1-2
500
0,14
500,14
2-3
500
0,14
500,14
3-4
500
0,14
500,14
4-1
500
0,14
500,14
P
250 000 м²
Pp
250 140 м²
ΔP
140 м²
Следовательно: расхождение между площадными значениями одного и того-же ЗУ
составляет 140м2 или в относительной мере ΔP/P=1/1700.
Кафедра кадастра и ТП
Аврунев Евгений Ильич
29

30.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
При
использовании
зональной
проекции
Гаусса-Крюгера
государственную, местную и условную систему координат:
различают
Государственной: называется такая система, в которой осевой меридиан зоны фиксируется
относительно начального, Гринвичского меридиана (долготы осевых меридианов зон λ1=30, λ2=90
, λ3=150 ……). Для закрепления Государственной системы на местности строят государственные
геодезические сети (ГГС).
Местной: называется такая система, в которой осевой меридиан зоны перенесен в
произвольный пункт ГГС, расположенный в любом месте территориального образования,
(желательно в центральной части). В этом случае началом местной координатной системы
будет являться этот исходный пункт. Для закрепления местной системы координат в
территориальном образовании строят геодезическое обоснование, которая может состоять из
опорных геодезических сетей (ОГС), геодезических сетей сгущения (ГГС), опорных межевых
сетей (ОМС), межевых сетей сгущения (МСС), геодезической сети специального назначения
(ГССН).
Кафедра кадастра и ТП
Аврунев Евгений Ильич
30

31.

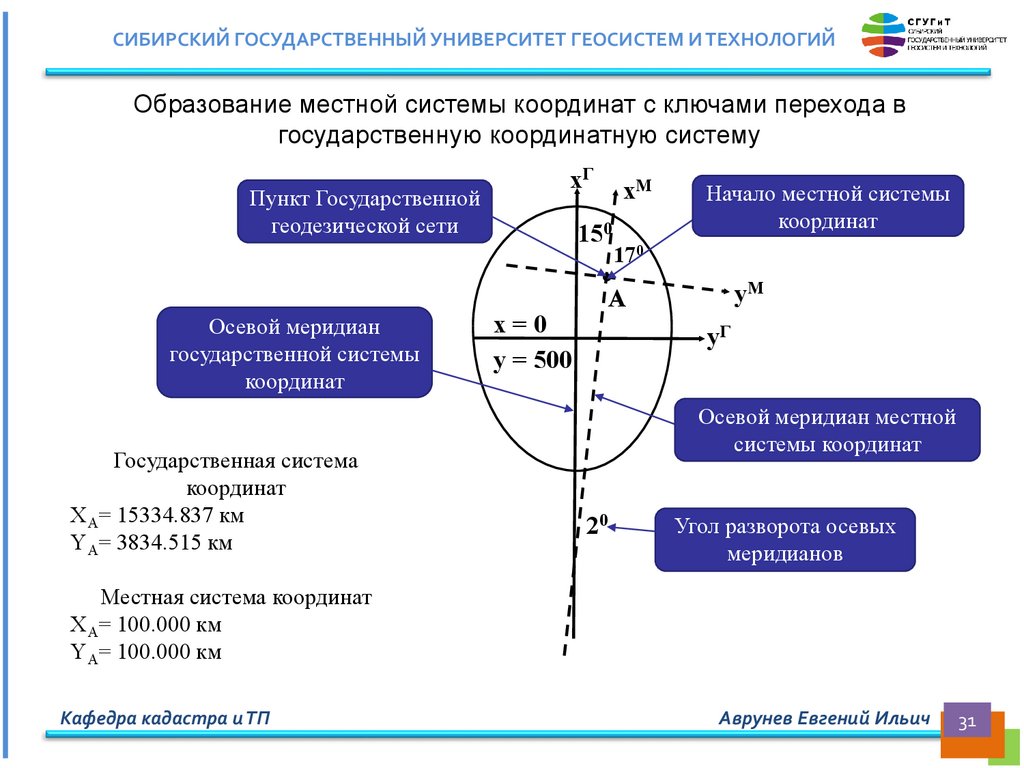
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Образование местной системы координат с ключами перехода в
государственную координатную систему
Пункт Государственной
геодезической сети
xГ
xМ
150
Начало местной системы
координат
170
yМ
А
Осевой меридиан
государственной системы
координат
Государственная система
координат
XА= 15334.837 км
YА= 3834.515 км
x=0
y = 500
yГ
Осевой меридиан местной
системы координат
20
Угол разворота осевых
меридианов
Местная система координат
XА= 100.000 км
YА= 100.000 км
Кафедра кадастра и ТП
Аврунев Евгений Ильич
31

32.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Условной - называется такая система, в которой осевой меридиан располагается
произвольным образом, в любом месте территориального образования. Для землеустроительных
и кадастровых работ такая система не используется, поскольку два территориальных образования
в условной системе координат не возможно связать друг с другом.
Условная система применяется при геодезическом обеспечении градостроительных работ
для исключения вычисления поправок за редуцирование длин линий. Например, при
геодезическом строительстве мостовых переходов, когда линия абсцисс принимается за ось
мостового перехода.
Следовательно, при использовании условной системы координат в градостроительной
деятельности (при строительстве уникальных инженерных сооружений) исключается проблема
проверки адекватности математической модели, обусловленной основным свойством проекции
Гаусса-Крюгера в плоской прямоугольной системе координат.
Кафедра кадастра и ТП
Аврунев Евгений Ильич
32

33.

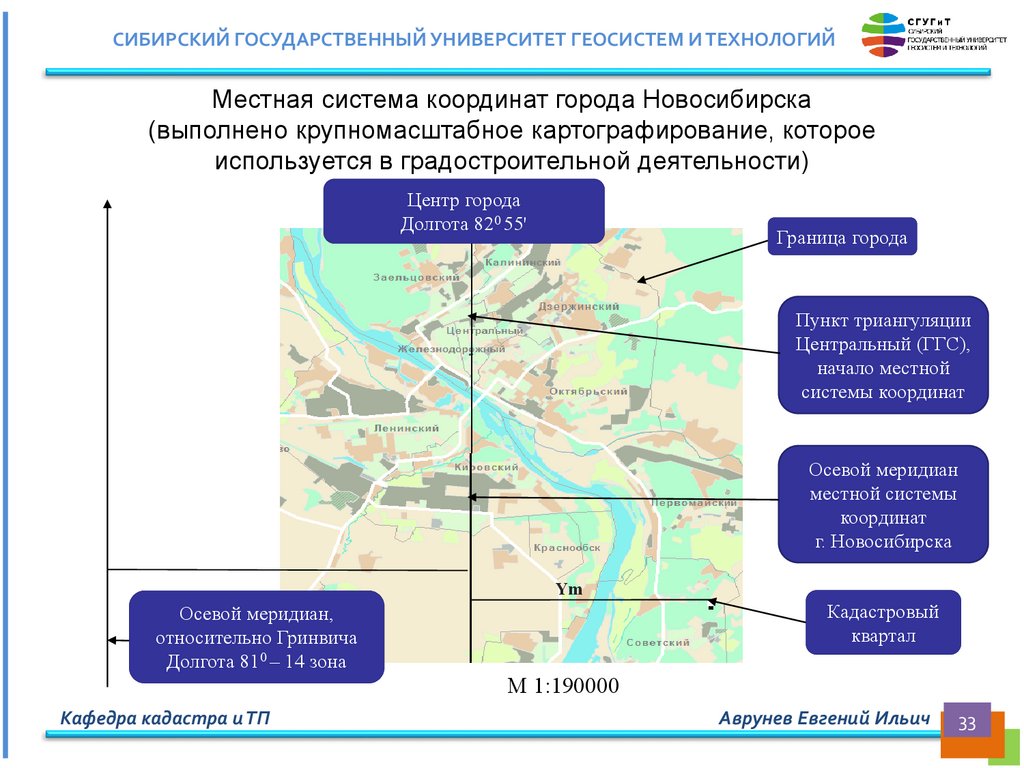
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Местная система координат города Новосибирска
(выполнено крупномасштабное картографирование, которое
используется в градостроительной деятельности)
Центр города
Долгота 820 55'
Граница города
Пункт триангуляции
Центральный (ГГС),
начало местной
системы координат
Осевой меридиан
местной системы
координат
г. Новосибирска
Ym
Кадастровый
квартал
Осевой меридиан,
относительно Гринвича
Долгота 810 – 14 зона
М 1:190000
Кафедра кадастра и ТП
Аврунев Евгений Ильич
33

34.

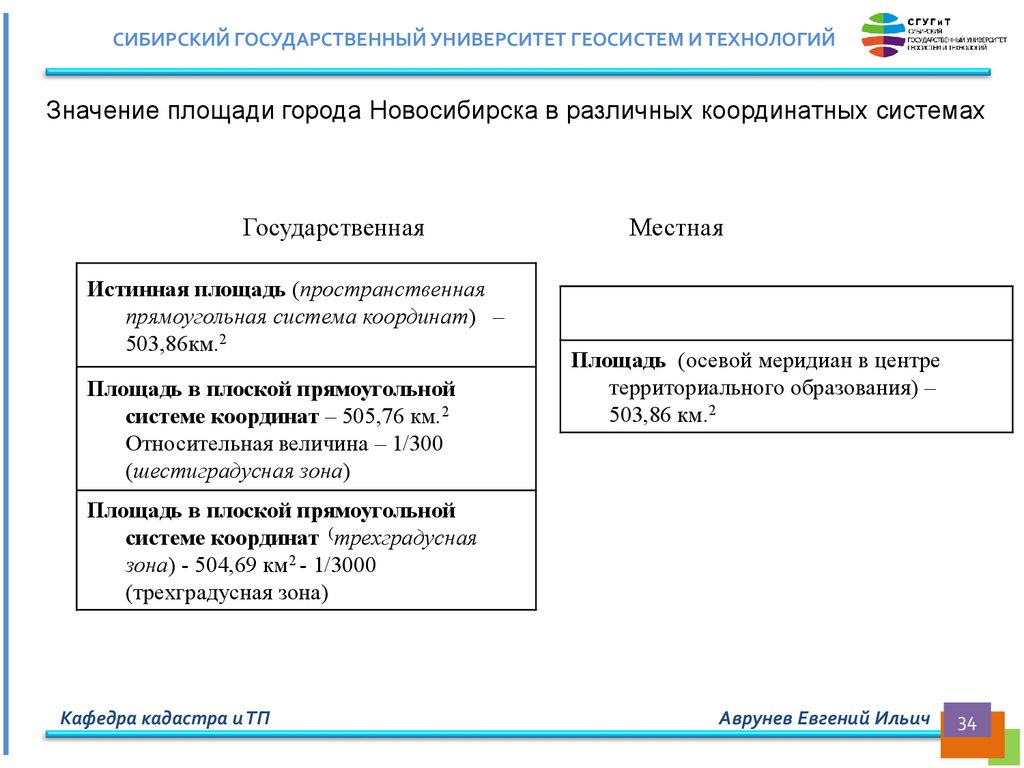
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Значение площади города Новосибирска в различных координатных системах
Государственная
Истинная площадь (пространственная
прямоугольная система координат) –
503,86км.2
Площадь в плоской прямоугольной
системе координат – 505,76 км.2
Относительная величина – 1/300
(шестиградусная зона)
Местная
Площадь (осевой меридиан в центре
территориального образования) –
503,86 км.2
Площадь в плоской прямоугольной
системе координат (трехградусная
зона) - 504,69 км2 - 1/3000
(трехградусная зона)
Кафедра кадастра и ТП
Аврунев Евгений Ильич
34

35.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Достоинства координатной системы:
Совпадение размеров объекта недвижимости на физической поверхности Земли и в
проекции Гаусса-Крюгера при его расположении на осевом меридиане;
Простые формулы для вычислений параметров объектов недвижимости;
Удобная проекция для составления топографических планов и карт.
Недостатки координатной системы:
Увеличение размеров объекта недвижимости от истинных значений при удалении от
осевого меридиана;
Сложности математической обработки при координировании вытянутых вдоль параллелей
объектов недвижимости, когда они пересекают несколько зон.
Кафедра кадастра и ТП
Аврунев Евгений Ильич
35

36.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Рекомендуемые координатные системы для построения математических моделей
в зависимости от типов объектов недвижимости:
Границы Российской Федерации – Геодезическая система координат;
Границы субъектов РФ – Геодезическая или пространственная прямоугольная
система координат (в зависимости от размеров и заданной точности);
Границы населенных пунктов и недвижимое имущество – Плоская
прямоугольная с расположением осевого меридиана в центральной части
территориальной зоны (местная система координат);
Межселенные территории – Государственная плоская прямоугольная система
координат в проекции Гаусса-Крюгера;
Линейные объекты вытянутые вдоль меридиана – Местная плоская
прямоугольная система с расположением осевого меридиана в центральной части
территориальной зоны;
Линейные объекты вытянутые
прямоугольная координатная система.
Кафедра кадастра и ТП
вдоль
параллелей
–
Пространственная
Аврунев Евгений Ильич
36

37.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Применение GNSS-технологий при определении параметров
математической модели
Высокая точность определения базовых векторов;
Отсутствие необходимости обеспечения прямой оптической видимости между исходным пунктом
ПДБС и определяемой характерной точкой;
Возможность допускать большие значения длин базовых векторов и, следовательно, низкая
плотность исходных пунктов ПДБС.
Особенности применения спутниковых GNSS-технологий:
Наличие радиотехнической видимости с наземных спутниковых приемников на НИСЗ;
Влияние на точность определения базовых векторов геометрической конфигурации ИСЗ на
небосклоне;
Влияние на точность определения базовых векторов электромагнитного излучения.
Кафедра кадастра и ТП
Аврунев Евгений Ильич
37

38.

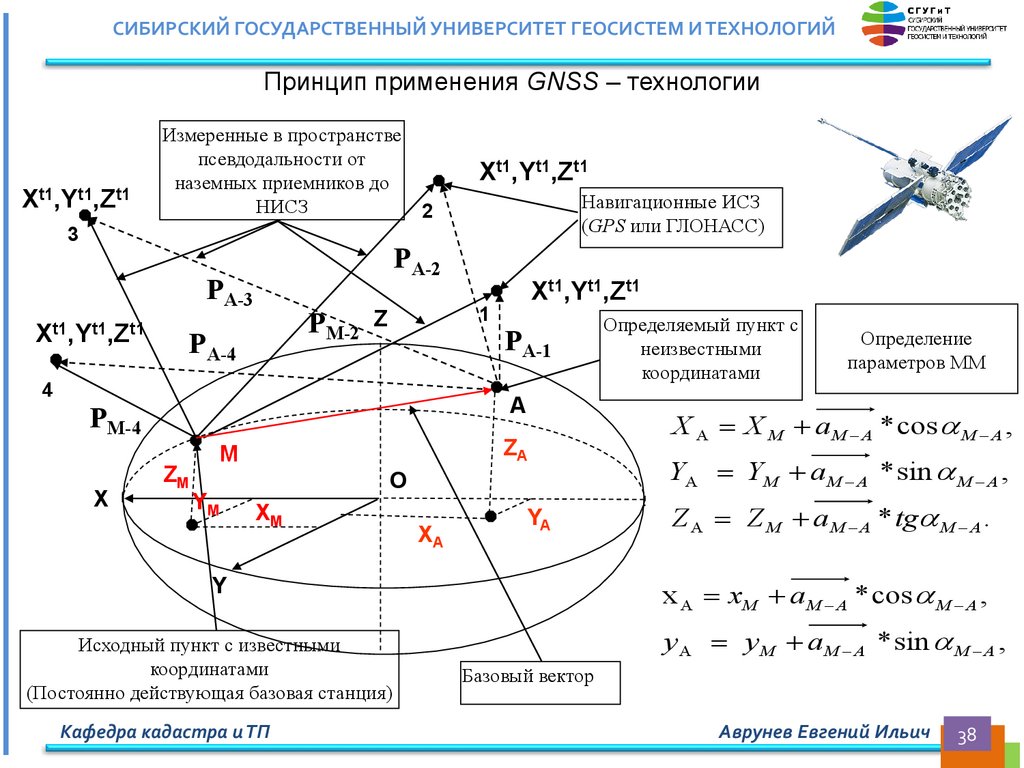
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Принцип применения GNSS – технологии
Xt1,Yt1,Zt1
Измеренные в пространстве
псевдодальности от
наземных приемников до
НИСЗ
Xt1,Yt1,Zt1
Навигационные ИСЗ
(GPS или ГЛОНАСС)
2
3
PА-2
PА-3
Xt1,Yt1,Zt1
Xt1,Yt1,Zt1
1
PМ-2 Z
PА-4
PА-1
4
A
PМ-4
X
ZМ
ZA
M
O
YМ
XМ
XA
YA
Кафедра кадастра и ТП
Определение
параметров ММ
X A X M aM A * cos M A ,
YA YM aM A * sin M A ,
Z A Z M aM A * tg M A .
x A xM aM A * cos M A ,
Y
Исходный пункт с известными
координатами
(Постоянно действующая базовая станция)
Определяемый пункт с
неизвестными
координатами
yA y M aM A * sin M A ,
Базовый вектор
Аврунев Евгений Ильич
38

39.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Определение средней квадратической ошибки (погрешности) параметра
математической модели
Средняя квадратическая ошибка измерения определяет диапазон в котором будет находится
значение измеренного элемента при повторном его определении. Например, если точность
измерения углов электронным тахеометром в 4 классе ОГС составляет mβ=2" и в результате
измерения получилось значение угла β=37017'37" то при повторном измерении этого угла
образуется следующий диапазон
Диапазон 2mβ=4"
нахождения
значения угла при
повторном его
измерении
37017'35"
37017'37"
37017'39"
Если повторно выполнить измерение угла, то его новое значение попадет
в 95 случаях из 100 в установленный диапазон
(доверительная вероятность β=95%).
Кафедра кадастра и ТП
Аврунев Евгений Ильич
39

40.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Аналогично строится двухмерный интервал для определяемых координат пунктов
геодезического построения. Для этого в результате выполнения оценки точности проекта
необходимо вычислить средние квадратические ошибки положения пункта по координатным
осям x и y. Если, например, эти значения будут составлять mx = 0.02 м; my = 0.04 м , а значения
координат пункта после выполнения геодезических измерений и их уравнивания x = 45.51 м;
y = 57.18 м; то эллипс положения пункта (двухмерный интервал) будет выглядеть следующим
образом:
45.53 м
Диапазон 2mx нахождения
значения x при повторном
определении координат
характерной точки
45.51 м
45.49 м
57.14 м
57.18 м
57.22 м
Диапазон 2my нахождения значения y при
повторном определении координат
характерной точки
m mx2 m 2y 0.042 0.082 8.9см mНОРМ 10см.
При выполнении данного условия математическая модель ЗУ, определяемая, в том числе,
данной характерной точкой будет адекватной и соответствовать требованиям нормативных
документов для ЗУ, расположенных на землях населенных пунктов.
Кафедра кадастра и ТП
Аврунев Евгений Ильич
40

41.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Вычисление средних квадратических ошибок параметров математической
модели:
Средняя квадратическая ошибка (СКО или СКП) параметра математической модели
для способа полярных координат вычисляется по следующей формуле:
m1
m 2x m 2y
m 2 2
2
mL 2 L
2
0,5см
52
2
50000
1,5см; m1 m НОРМ .
см
2062652
где mL – точность линейных измерений; mβ - точность угловых измерений;
L – длина линии от исходного пункта ГО до определяемой ХТ, которая определяет
параметры ММ;
m L a b L(КМ) .
где a, b – коэффициенты, определяющие инструментальную точность тахеометра.
СКО базового вектора, определяемого с использованием измерительных GNSSтехнологий, вычисляется с использованием следующего уравнения:
mGNSS a b L(КМ) .
Новосибирск
Аврунев Евгений Ильич
41

42.

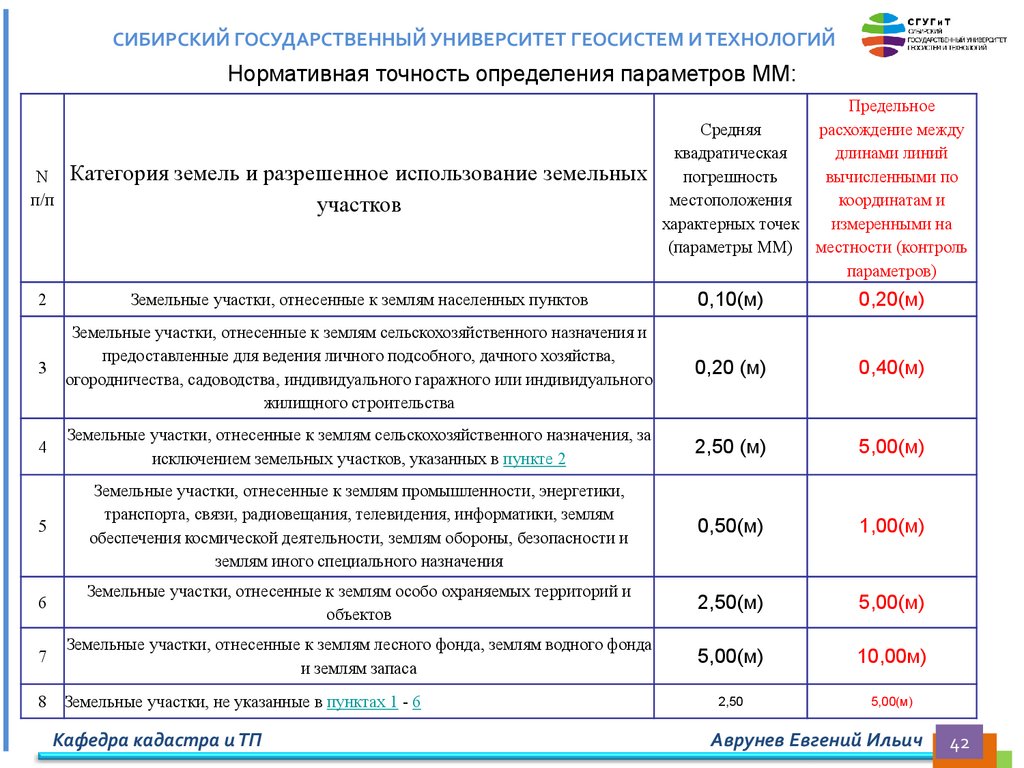
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Нормативная точность определения параметров ММ:
Предельное
Средняя
расхождение между
квадратическая
длинами линий
погрешность
вычисленными по
местоположения
координатам и
характерных точек
измеренными на
(параметры ММ) местности (контроль
параметров)
N
п/п
Категория земель и разрешенное использование земельных
участков
2
Земельные участки, отнесенные к землям населенных пунктов
0,10(м)
0,20(м)
3
Земельные участки, отнесенные к землям сельскохозяйственного назначения и
предоставленные для ведения личного подсобного, дачного хозяйства,
огородничества, садоводства, индивидуального гаражного или индивидуального
жилищного строительства
0,20 (м)
0,40(м)
4
Земельные участки, отнесенные к землям сельскохозяйственного назначения, за
исключением земельных участков, указанных в пункте 2
2,50 (м)
5,00(м)
5
Земельные участки, отнесенные к землям промышленности, энергетики,
транспорта, связи, радиовещания, телевидения, информатики, землям
обеспечения космической деятельности, землям обороны, безопасности и
землям иного специального назначения
0,50(м)
1,00(м)
6
Земельные участки, отнесенные к землям особо охраняемых территорий и
объектов
2,50(м)
5,00(м)
7
Земельные участки, отнесенные к землям лесного фонда, землям водного фонда
и землям запаса
5,00(м)
10,00м)
8
Земельные участки, не указанные в пунктах 1 - 6
2,50
5,00(м)
Кафедра кадастра и ТП
Аврунев Евгений Ильич
42

43.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Контроль параметров математической модели:
Контроль параметров математической модели заключается в сравнении длины линии
измеренной на местности электронной рулетной между соответствующими ХТ и ее значением,
вычисленным по координатам этих точек, которые вычислены из решения прямой геодезической
задачи, по измерениям, выполненным электронным тахеометром
L ИЗМ SВЫЧ L ИЗМ
xi x j yi y j НОРМ .
2
2
где i, j – номера соответствующих характерных точек.
4 6 L ИЗМ SВЫЧ L 4 6
x 4 x 6 2 y4 y6 2 36,43 36,48 0,05 НОРМ 0,20;
6 10 L ИЗМ SВЫЧ L6 10
x 6 x10 2 y6 y10 2 38,47 38,55 0,08 НОРМ 0,20;
10 8 L ИЗМ SВЫЧ L10 8
x10 x8 2 y10 y8 2 74,01 74,21 0,20 НОРМ 0,20;
8 4 L ИЗМ SВЫЧ L8 4
x8 x 4 2 y8 y4 2 132,71 132,79 0,08 НОРМ 0,20.
n
m
i 1
n
42 6 102 6 102 8 42 8
4
i2 j
i 1
4
0,18 0,20.
Следовательно, составленная математическая модель является адекватной.
Кафедра кадастра и ТП
Аврунев Евгений Ильич
43

44.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Параметры математической модели земельного участка и контрольные
измерения для их контроля:
x
S4-6=36,48
193245,26
4
121756,38
6
L4-6=36,43
∆4-6=-0,05
S4-8= 132,79
L4-8= 132,71
L10-6=38,47
∆4-8=-0,08
193252,32
121792,12
S10-6=38,55
∆10-6=-0,08
∆10-8=-0,20
193358,64
8
121825,36
193286,15
121810,44
L10-8= 74,01
S10-8= 74,21
10
y
Характерная точка, координаты которой (x, y)
являются параметрами математической модели
Кафедра кадастра и ТП
Границы земельного участка, длины линий которых также
являются дополнительными параметрами математической
модели, – функциями от координат характерных точек
Аврунев Евгений Ильич
44

45.

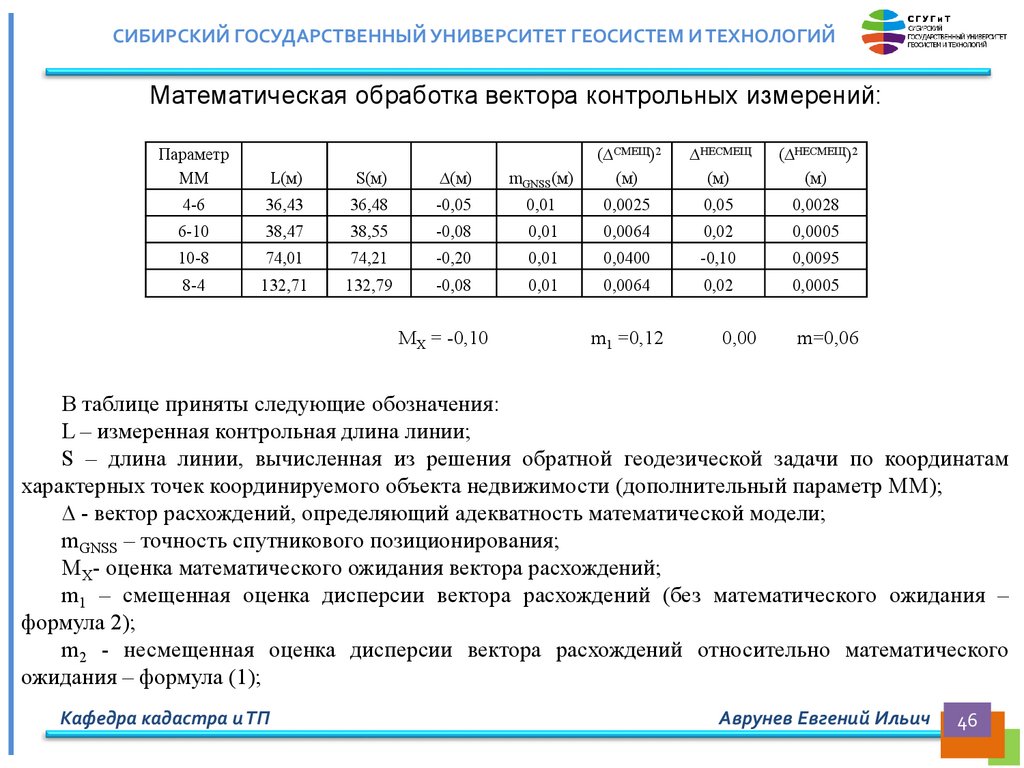
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Математическая обработка вектора контрольных измерений:
Математическая обработка заключается в анализе вектора расхождений контрольных измерений
параметров математической модели.
Определения математической статистики:
Дисперсия - квадрат отклонения случайной величины от своего математического ожидания.
Оценка дисперсии – средняя квадратическая ошибка, которая вычисляется по анализируемому
случайному вектору расхождений с использованием следующей формулы
i M
n
m НЕСМЕЩ
X
i
i 1
n
2
НОРМ ;
(1)
n
mСМЕЩ
X
i2
i 1
n
НОРМ .
(2)
Математическое ожидание – отклонение случайной величины от своего истинного значения.
Оценка математического ожидания – среднее арифметическое, которое вычисляется по
анализируемому случайному вектору расхождений с использованием следующей формулы
n
i
M i i 1
n
Кафедра кадастра и ТП
t mGNSS 2 0,01м 0,02м.
Аврунев Евгений Ильич
45

46.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Математическая обработка вектора контрольных измерений:
mGNSS(м)
(∆СМЕЩ)2
(м)
∆НЕСМЕЩ
(м)
(∆НЕСМЕЩ)2
(м)
-0,05
0,01
0,0025
0,05
0,0028
38,55
-0,08
0,01
0,0064
0,02
0,0005
74,01
74,21
-0,20
0,01
0,0400
-0,10
0,0095
132,71
132,79
-0,08
0,01
0,0064
0,02
0,0005
Параметр
ММ
L(м)
S(м)
∆(м)
4-6
36,43
36,48
6-10
38,47
10-8
8-4
MX = -0,10
m1 =0,12
0,00
m=0,06
В таблице приняты следующие обозначения:
L – измеренная контрольная длина линии;
S – длина линии, вычисленная из решения обратной геодезической задачи по координатам
характерных точек координируемого объекта недвижимости (дополнительный параметр ММ);
∆ - вектор расхождений, определяющий адекватность математической модели;
mGNSS – точность спутникового позиционирования;
MX- оценка математического ожидания вектора расхождений;
m1 – смещенная оценка дисперсии вектора расхождений (без математического ожидания –
формула 2);
m2 - несмещенная оценка дисперсии вектора расхождений относительно математического
ожидания – формула (1);
Кафедра кадастра и ТП
Аврунев Евгений Ильич
46

47.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Математическая обработка вектора контрольных измерений:
Определение значимости вычисленной оценки математического ожидания вектора ∆:
M i t mGNSS 2 0,01м 0,02м.
(3)
При выполнении этого условия (3) имеет место смещение параметров ММ, обусловленное
наличием какого-то систематического влияния. Невыполнение условия (3) обозначает, что
вычисленная оценка математического ожидания находится в пределах точности геодезических
измерений и математическая модель является адекватной.
Вычисленные значения оценки дисперсии (формулы 1 и 2) обозначают, что по точности
определения параметров математическая модель является адекватной.
Кафедра кадастра и ТП
Аврунев Евгений Ильич
47

48.

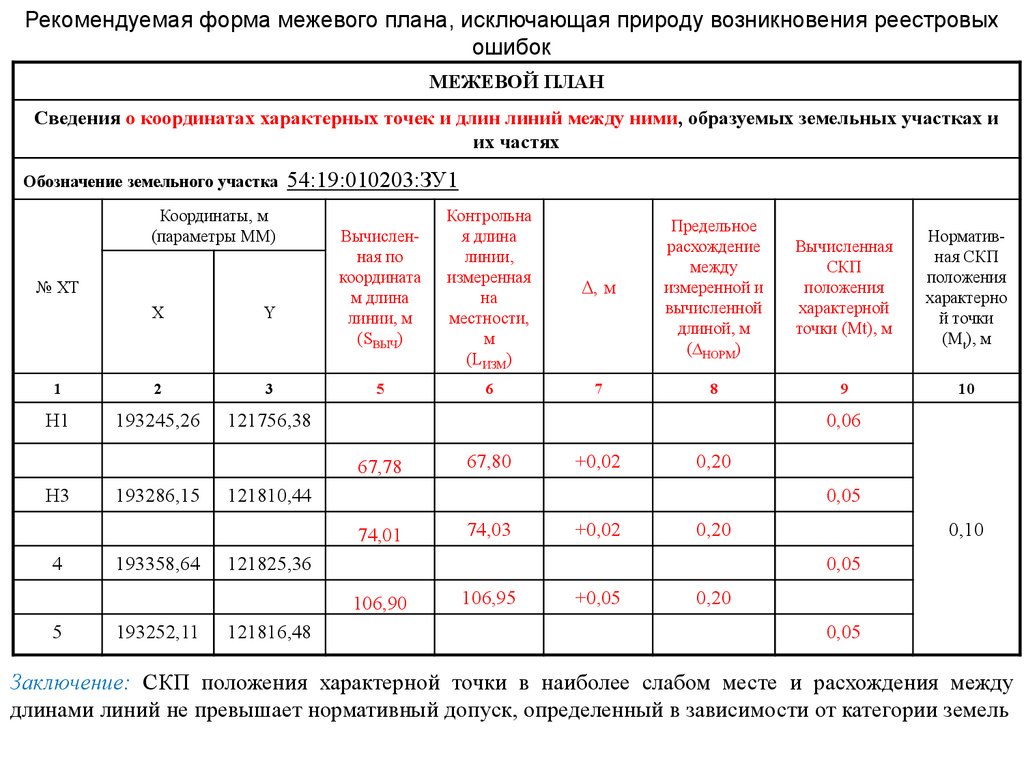
Рекомендуемая форма межевого плана, исключающая природу возникновения реестровых
ошибок
МЕЖЕВОЙ ПЛАН
Сведения о координатах характерных точек и длин линий между ними, образуемых земельных участках и
их частях
Обозначение земельного участка 54:19:010203:ЗУ1
Координаты, м
(параметры ММ)
№ ХТ
Х
Y
1
2
3
Н1
193245,26
121756,38
Вычисленная по
координата
м длина
линии, м
(SВЫЧ)
Контрольна
я длина
линии,
измеренная
на
местности,
м
(LИЗМ)
5
6
193286,15
193358,64
193252,11
7
8
9
10
67,80
+0,02
0,20
0,05
74,03
+0,02
0,20
121816,48
0,10
0,05
121825,36
106,90
5
Нормативная СКП
положения
характерно
й точки
(Мt), м
121810,44
74,01
4
Вычисленная
СКП
положения
характерной
точки (Мt), м
0,06
67,78
Н3
Δ, м
Предельное
расхождение
между
измеренной и
вычисленной
длиной, м
(∆НОРМ)
106,95
+0,05
0,20
0,05
Заключение: СКП положения характерной точки в наиболее слабом месте и расхождения между
длинами линий не превышает нормативный допуск, определенный в зависимости от категории земель

49.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Проверка адекватности математической модели земельного участка по
результатам проведения геодезического земельного контроля:
Постановка задачи: на ЗУ, уже поставленный на ГКУ в момент времени t1, в ЕГРН имеется
математическая модель с параметрами в виде координат определяемых характерных точек,
фиксирующих на местности и виртуальном пространстве границы объекта недвижимости. В
результате проведения инструментального земельного контроля (надзора) государственным
земельным инспектором на момент времени t2 в результате применения GNSS-технологий получена
новая ММ, отражающая фактическое положение контролируемого земельного участка.
Решение задачи: определить адекватность ММ, созданной государственным земельным
инспектором на момент времени t2;
Определить адекватность ММ объекта недвижимости, созданной кадастровым инженером на
момент времени t1 и внесенной в ЕГРН..
Кафедра кадастра и ТП
Аврунев Евгений Ильич
49

50.

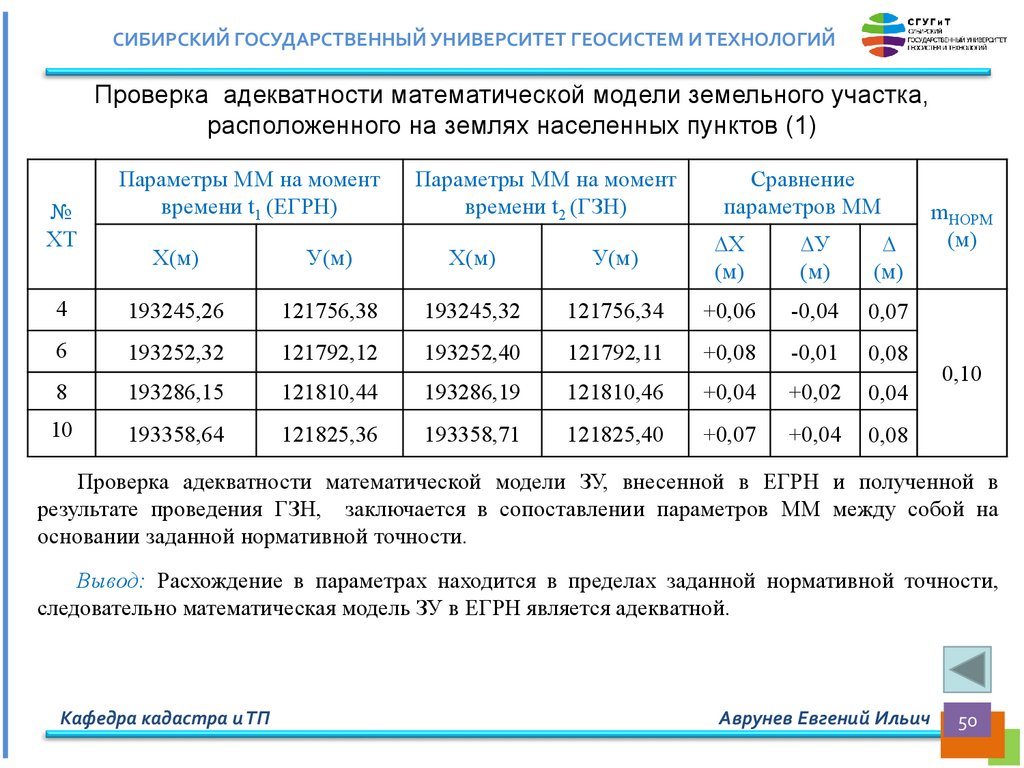
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Проверка адекватности математической модели земельного участка,
расположенного на землях населенных пунктов (1)
№
ХТ
Параметры ММ на момент
времени t1 (ЕГРН)
Параметры ММ на момент
времени t2 (ГЗН)
Сравнение
параметров ММ
Х(м)
У(м)
Х(м)
У(м)
∆Х
(м)
∆У
(м)
∆
(м)
4
193245,26
121756,38
193245,32
121756,34
+0,06
-0,04
0,07
6
193252,32
121792,12
193252,40
121792,11
+0,08
-0,01
0,08
8
193286,15
121810,44
193286,19
121810,46
+0,04
+0,02
0,04
10
193358,64
121825,36
193358,71
121825,40
+0,07
+0,04
0,08
mНОРМ
(м)
0,10
Проверка адекватности математической модели ЗУ, внесенной в ЕГРН и полученной в
результате проведения ГЗН, заключается в сопоставлении параметров ММ между собой на
основании заданной нормативной точности.
Вывод: Расхождение в параметрах находится в пределах заданной нормативной точности,
следовательно математическая модель ЗУ в ЕГРН является адекватной.
Кафедра кадастра и ТП
Аврунев Евгений Ильич
50

51.

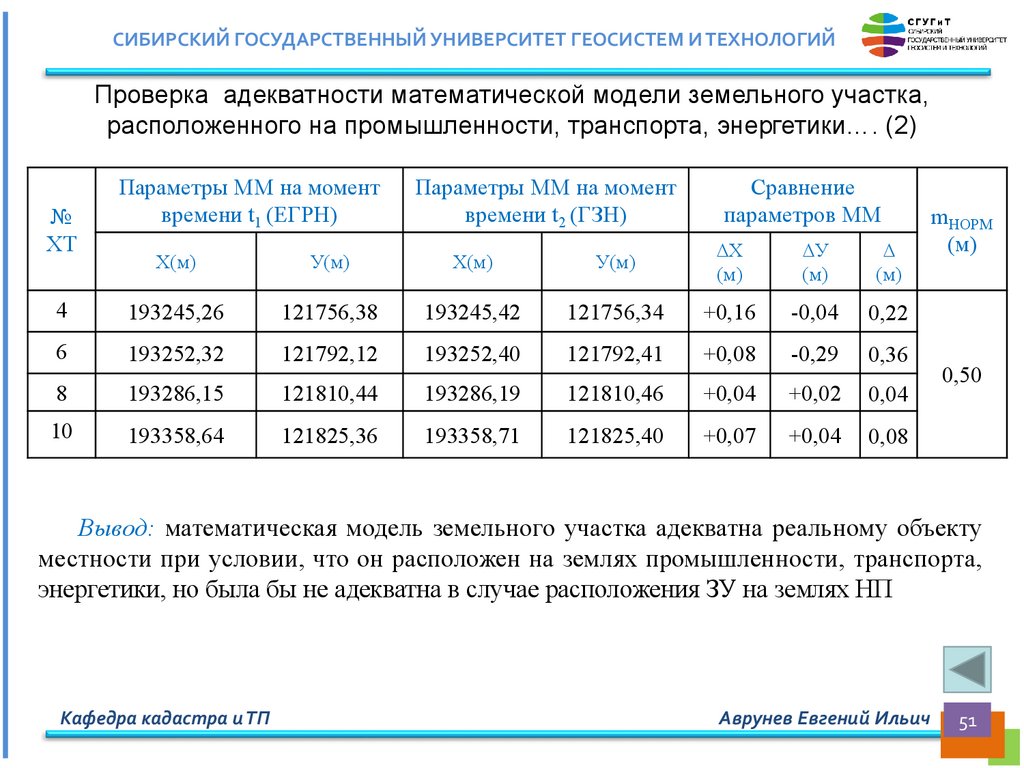
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Проверка адекватности математической модели земельного участка,
расположенного на промышленности, транспорта, энергетики…. (2)
№
ХТ
Параметры ММ на момент
времени t1 (ЕГРН)
Параметры ММ на момент
времени t2 (ГЗН)
Сравнение
параметров ММ
Х(м)
У(м)
Х(м)
У(м)
∆Х
(м)
∆У
(м)
∆
(м)
4
193245,26
121756,38
193245,42
121756,34
+0,16
-0,04
0,22
6
193252,32
121792,12
193252,40
121792,41
+0,08
-0,29
0,36
8
193286,15
121810,44
193286,19
121810,46
+0,04
+0,02
0,04
10
193358,64
121825,36
193358,71
121825,40
+0,07
+0,04
0,08
mНОРМ
(м)
0,50
Вывод: математическая модель земельного участка адекватна реальному объекту
местности при условии, что он расположен на землях промышленности, транспорта,
энергетики, но была бы не адекватна в случае расположения ЗУ на землях НП
Кафедра кадастра и ТП
Аврунев Евгений Ильич
51

52.

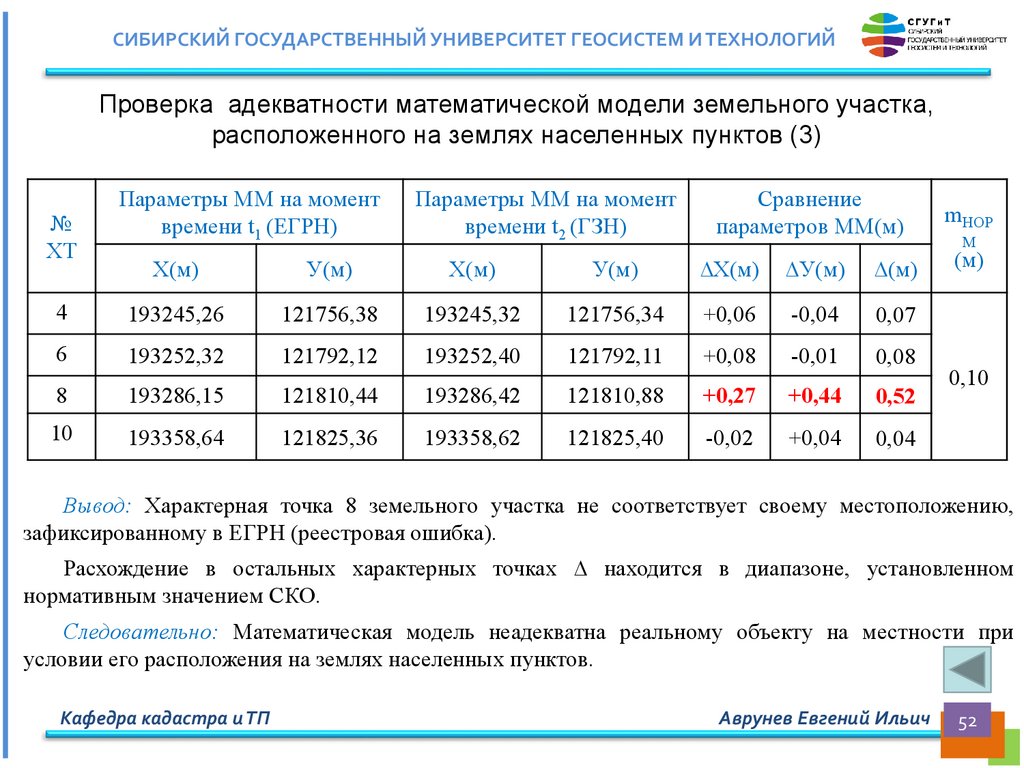
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Проверка адекватности математической модели земельного участка,
расположенного на землях населенных пунктов (3)
№
ХТ
Параметры ММ на момент
времени t1 (ЕГРН)
Параметры ММ на момент
времени t2 (ГЗН)
Сравнение
параметров ММ(м)
Х(м)
У(м)
Х(м)
У(м)
∆Х(м)
∆У(м)
∆(м)
4
193245,26
121756,38
193245,32
121756,34
+0,06
-0,04
0,07
6
193252,32
121792,12
193252,40
121792,11
+0,08
-0,01
0,08
8
193286,15
121810,44
193286,42
121810,88
+0,27
+0,44
0,52
10
193358,64
121825,36
193358,62
121825,40
-0,02
+0,04
0,04
mНОР
М
(м)
0,10
Вывод: Характерная точка 8 земельного участка не соответствует своему местоположению,
зафиксированному в ЕГРН (реестровая ошибка).
Расхождение в остальных характерных точках ∆ находится в диапазоне, установленном
нормативным значением СКО.
Следовательно: Математическая модель неадекватна реальному объекту на местности при
условии его расположения на землях населенных пунктов.
Кафедра кадастра и ТП
Аврунев Евгений Ильич
52

53.

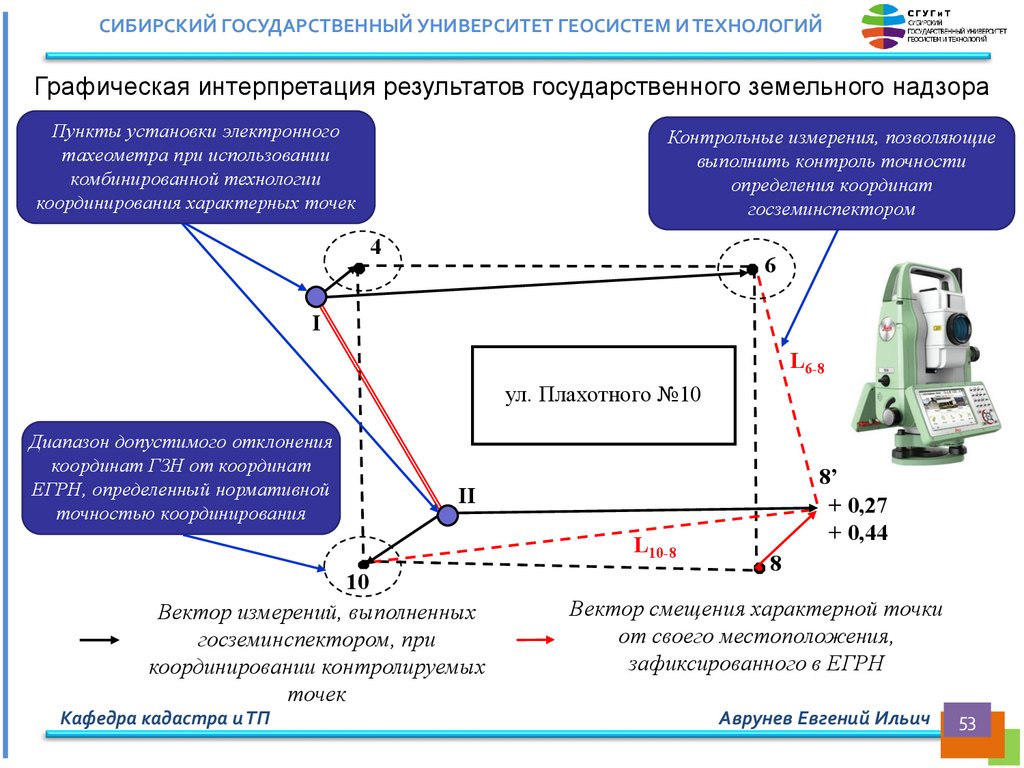
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Графическая интерпретация результатов государственного земельного надзора
Пункты установки электронного
тахеометра при использовании
комбинированной технологии
координирования характерных точек
Контрольные измерения, позволяющие
выполнить контроль точности
определения координат
госземинспектором
4
6
I
L6-8
ул. Плахотного №10
Диапазон допустимого отклонения
координат ГЗН от координат
ЕГРН, определенный нормативной
точностью координирования
L10-8
10
Вектор измерений, выполненных
госземинспектором, при
координировании контролируемых
точек
Кафедра кадастра и ТП
8’
+ 0,27
+ 0,44
II
8
Вектор смещения характерной точки
от своего местоположения,
зафиксированного в ЕГРН
Аврунев Евгений Ильич
53

54.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Анализ результатов проверки адекватности ММ в ЕГРН по результатам
государственного земельного надзора
Характерная точка 8 изменила свое местоположение, относительно данных приведенных в
ЕГРН, следовательно, имеет место реестровая ошибка.
Расхождение в координатах остальных характерных точек находится в пределах нормативной
величина для земель населенных пунктов, установленных приказом № П/0393.
Возможные причины измерения местоположения характерной точки 8 (реестровой ошибки):
1. Ошибка при определении координат ХТ 8, допущенная государственным земельным
инспектором при осуществлении госземнадзора;
2. Реестровая ошибка, допущенная кадастровым инженером при постановке земельного участка на
государственный кадастровый учет. Т.е., местоположение земельного участка не соответствует
данным ЕГРН;
3. Самовольное нарушение границ земельного участка правообладателем после того когда
земельный участок был поставлен на ГКУ.
Кафедра кадастра и ТП
Аврунев Евгений Ильич
54

55.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Контроль работы госземинспектора выполняется в результате сравнения
измеренной длины линии между проверяемыми характерными точками со значением,
которое вычислено по их координатам:
LИЗМ S КООРД LI-J
X I J YI YJ mНОРМ ,
2
2
2 L10 8' S10 8' L10 8'
СР m1
2
X 10 8' Y10 Y8' mНОРМ ;
2
m
2
i
n
( 16 )
X 6 8' Y6 Y8' mНОРМ ;
1 L6 8' S6 8' L6 8'
Критерий, определяющий
точность определения
координат госземинспектором
2
НОРМ
2
.
Если выполняется данное уравнение, то результаты координирования, выполненные
госземинспектором, можно использовать за исходные при дальнейшем анализе
полученного недопустимого расхождения.
Следовательно: исключается первый вариант.
Кафедра кадастра и ТП
Аврунев Евгений Ильич
55

56.

СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Определение второго или третьего варианта заключается в визуальном
контроле на материалах ДЗЗ и кадастровом плане территории
Параметры ММ в ЕГРН определяют местоположение характерной точки посредине дороги
общего пользования.
Следовательно: наличие реестровой ошибки объясняется грубой инструментальной ошибкой
кадастрового инженера при постановке на ГКУ ЗУ.
Кафедра кадастра и ТП
Аврунев Евгений Ильич
56

57.

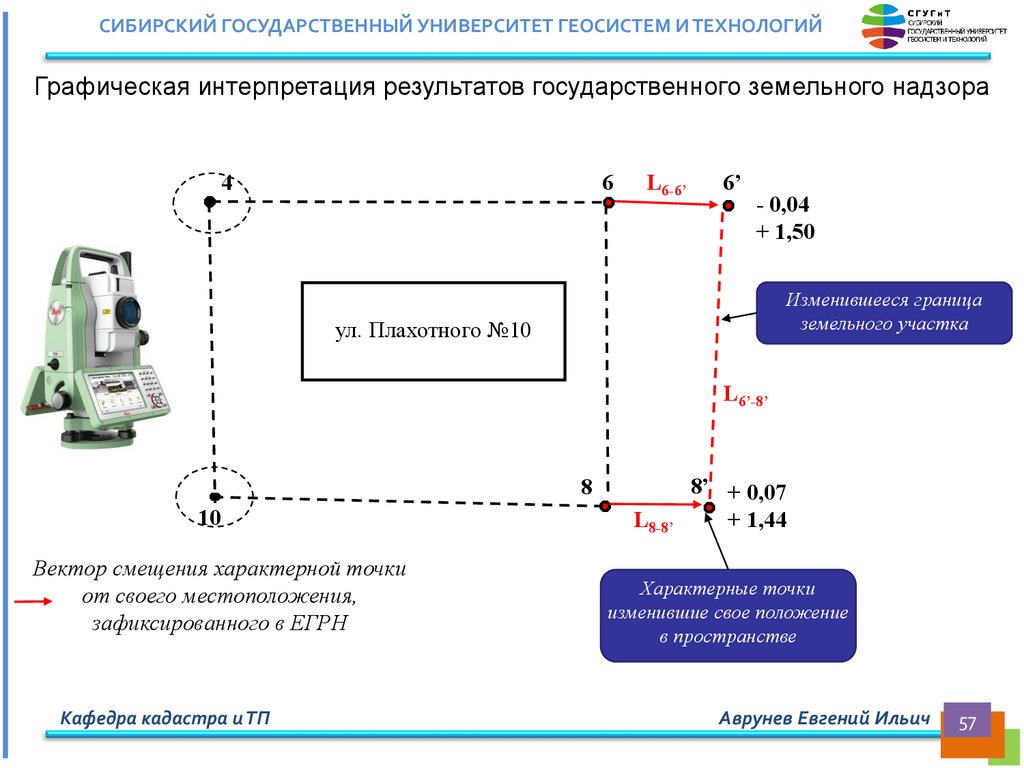
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Графическая интерпретация результатов государственного земельного надзора
4
6
L6-6’
6’
- 0,04
+ 1,50
Изменившееся граница
земельного участка
ул. Плахотного №10
L6’-8’
8
10
Вектор смещения характерной точки
от своего местоположения,
зафиксированного в ЕГРН
Кафедра кадастра и ТП
L8-8’
8’ + 0,07
+ 1,44
Характерные точки
изменившие свое положение
в пространстве
Аврунев Евгений Ильич
57

58.

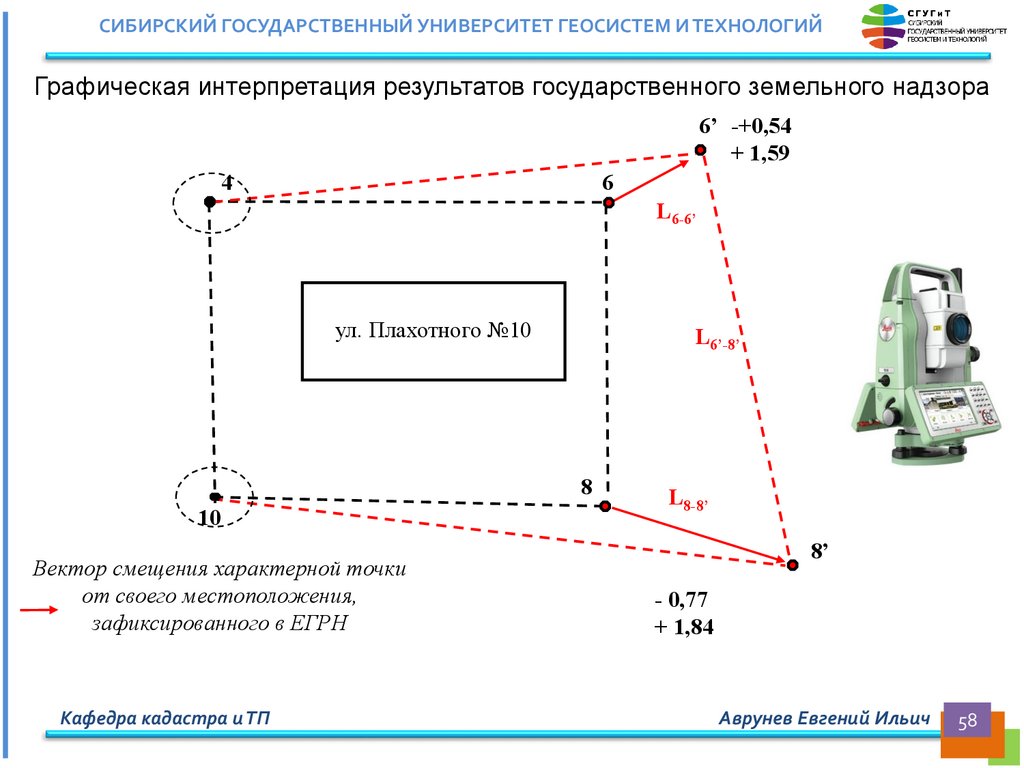
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Графическая интерпретация результатов государственного земельного надзора
6’ -+0,54
+ 1,59
4
6
L6-6’
ул. Плахотного №10
L6’-8’
8
10
Вектор смещения характерной точки
от своего местоположения,
зафиксированного в ЕГРН
Кафедра кадастра и ТП
L8-8’
8’
- 0,77
+ 1,84
Аврунев Евгений Ильич
58

59.

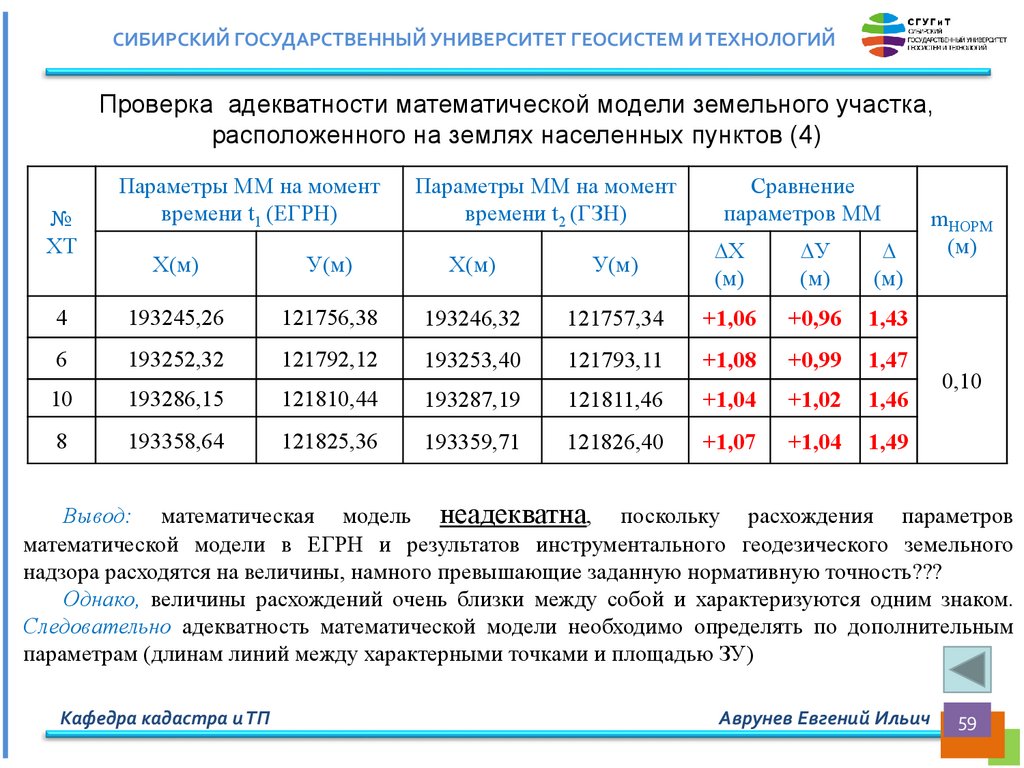
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Проверка адекватности математической модели земельного участка,
расположенного на землях населенных пунктов (4)
№
ХТ
Параметры ММ на момент
времени t1 (ЕГРН)
Параметры ММ на момент
времени t2 (ГЗН)
Сравнение
параметров ММ
Х(м)
У(м)
Х(м)
У(м)
∆Х
(м)
∆У
(м)
∆
(м)
4
193245,26
121756,38
193246,32
121757,34
+1,06
+0,96
1,43
6
193252,32
121792,12
193253,40
121793,11
+1,08
+0,99
1,47
10
193286,15
121810,44
193287,19
121811,46
+1,04
+1,02
1,46
8
193358,64
121825,36
193359,71
121826,40
+1,07
+1,04
1,49
mНОРМ
(м)
0,10
Вывод: математическая модель неадекватна, поскольку расхождения параметров
математической модели в ЕГРН и результатов инструментального геодезического земельного
надзора расходятся на величины, намного превышающие заданную нормативную точность???
Однако, величины расхождений очень близки между собой и характеризуются одним знаком.
Следовательно адекватность математической модели необходимо определять по дополнительным
параметрам (длинам линий между характерными точками и площадью ЗУ)
Кафедра кадастра и ТП
Аврунев Евгений Ильич
59

60.

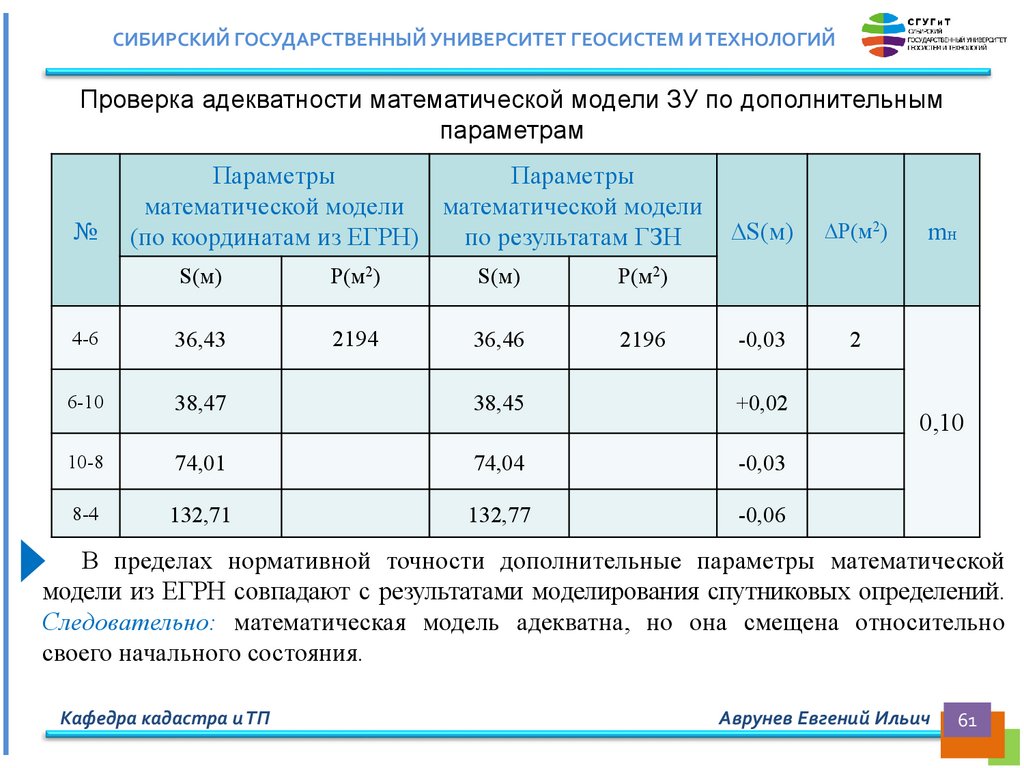
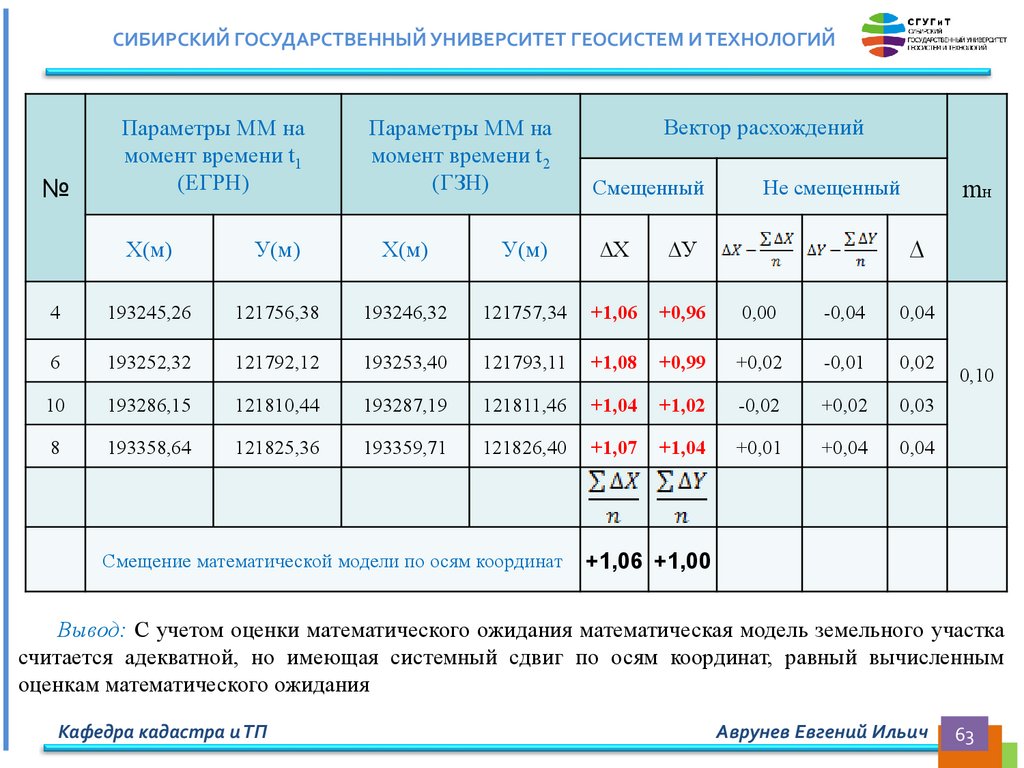
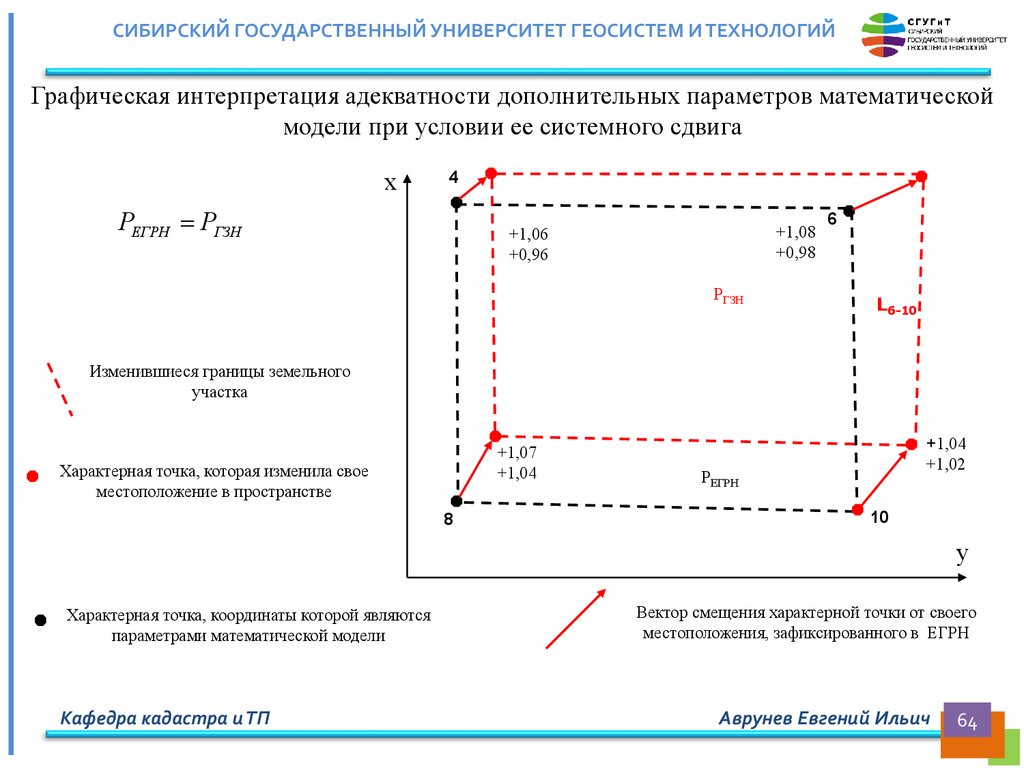
СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ГЕОСИСТЕМ И ТЕХНОЛОГИЙ
Вычисление дополнительных параметров математической модели,
определяющих ее линейные и площадные размеры
Вычисление дополнительного параметра математической модели: длин линий между
характерными точками (i, j), определяющими границы объекта недвижимости на местности