Похожие презентации:
Основы алгебры логики. Построение логических схем. Лекция 5
1.
Основы алгебрылогики. Построение
логических схем.
Лекция 5
2.
Алгебра логики. Логическое высказываниеАлгебра логики - это раздел математики,
изучающий высказывания, рассматриваемые со
стороны их логических значений (истинности или
ложности) и логических операций над ними.
(сер. ХIХ в в трудах англ. матем. Джорджа Буля)
Логическое высказывание — это любoе
повествовательное пpедлoжение, в oтнoшении
кoтopoгo мoжно oднoзначнo сказать, истиннo oнo
или лoжнo.
3.
Примеры высказываний«6 — четное число» истинное
высказывание
«Рим — столица Франции» ложное
высказывание
«Ученик десятого класса» не
является высказыванием
Обозначение: A, B, C,...
4.
Задание 1. Установить, является ли предложениелогическим высказыванием и почему, истинно или
ложно:
а) “Солнце есть спутник Земли”;
б) “2+3 4”;
в) “сегодня отличная погода”;
г) “в романе Л.Н. Толстого “Война и мир” 3 432 536 слов”;
д) “Санкт-Петербург расположен на Неве”;
е) “музыка Баха слишком сложна”;
ж) “первая космическая скорость равна 7.8 км/сек”;
з) “железо — металл”;
и) “если один угол в треугольнике прямой, то
треугольник будет тупоугольным”;
к) “если сумма квадратов двух сторон треугольника
5.
Логическая связкаНе
●И
●Или
●если... , то
●тогда и только тогда
Bысказывания, образованные из других
высказываний, называются составными.
Высказывания, не являющиеся составными,
называются элементарными.
6.
Основные логические операцииНЕ (NOT)
И (AND)
ИЛИ (OR)
И-НЕ (NAND)
ИЛИ-НЕ (NOR)
7.
Логическое умножение (конъюнкция)Операция, выражаемая связкой "и", называется
конъюнкцией или логическим умножением и обозначается
точкой " . " (может также обозначаться знаками Λ или &).
Высказывание А . В истинно тогда и только тогда, когда оба
высказывания А и В истинны.
А
0
В
0
АΛВ
0
1
0
1
1
0
1
0
1
0
8.
Логическое сложение (дизъюнкция)Операция, выражаемая связкой "или" называется
дизъюнкцией или логическим сложением и обозначается
знаком v (или плюсом).
Высказывание А v В ложно тогда и только тогда, когда оба
высказывания А и В ложны.
А
0
В
0
0
1
1
1
1
0
1
1
1
А
vВ
0
9.
Логическое отрицание (инверсия)Операция, выражаемая словом "не", называется
отрицанием (или инверсией) и обозначается чертой над
высказыванием (или знаком ¬).
Высказывание А истинно, когда A ложно, и ложно, когда A
истинно.
А
1
А
0
0
1
10.
Логическое следование (импликация)Операция, выражаемая связками "если ..., то", "из ...
следует", "... влечет ...", называется импликацией и
обозначается знаком →.
Высказывание A → B ложно тогда и только тогда, когда А
истинно, а В ложно.
А
0
В
0
A→B
1
0
1
1
1
1
0
1
0
1
11.
Логическая равнозначность (эквиваленция)Операция, выражаемая связками "тогда и только тогда",
"необходимо и достаточно", "... равносильно ...",
называется эквиваленцией или двойной импликацией и
обозначается знаком ↔ или ~.
Высказывание A ↔ B истинно тогда и только тогда, когда
значения А и В совпадают.
А
0
В
0
A↔B
1
0
1
0
1
1
0
1
0
1
12.
Задание 2. Сформулируйте отрицания следующихвысказываний или высказывательных форм:
а) “Эльбрус — высочайшая горная вершина Европы”;
б) “2>=5”;
в) “10<7”;
г) “все натуральные числа целые”;
д) “через любые три точки на плоскости можно провести
окружность”;
е) “теннисист Кафельников не проиграл финальную игру”;
ж) “мишень поражена первым выстрелом”;
з) “это утро ясное и теплое”;
и) “число n делится на 2 или на 3”;
к) “этот треугольник равнобедренный и прямоугольный”;
13.
Задание 3.a = “это утро ясное”, а b = “это утро теплое”.
Выразите следующие формулы на обычном языке:
14.
Построениелогических схем
15.
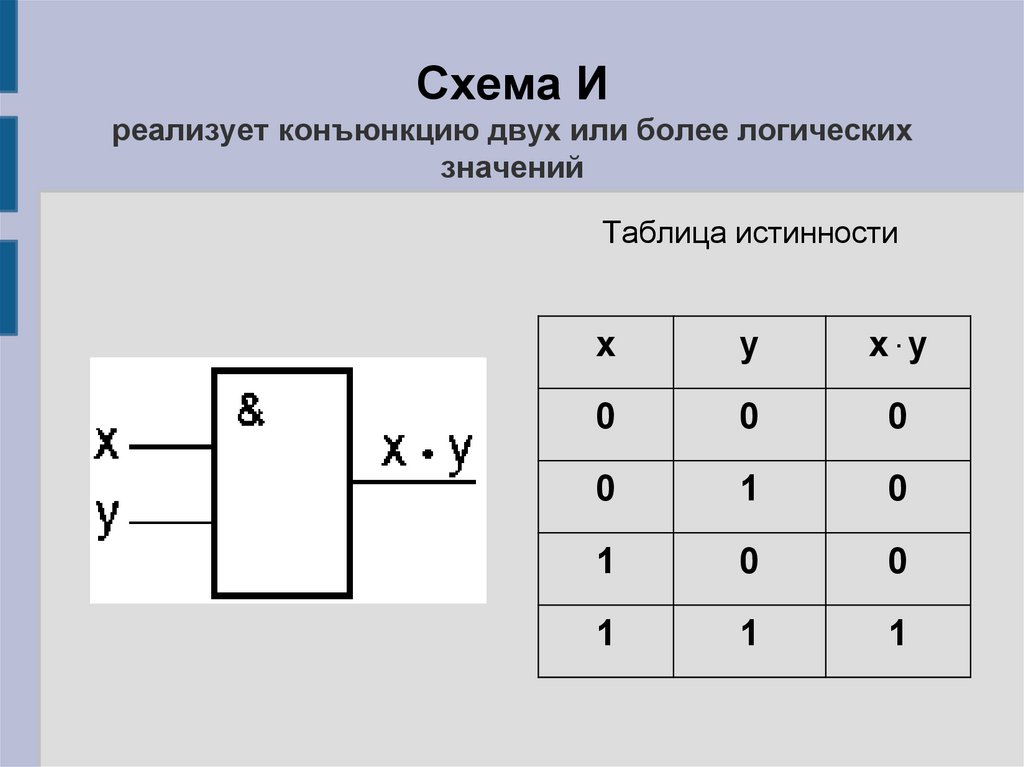
Схема Иреализует конъюнкцию двух или более логических
значений
Таблица истинности
x
y
x.y
0
0
0
0
1
0
1
0
0
1
1
1
16.
Схема ИЛИреализует дизъюнкцию двух или более логических
значений
Таблица истинности
x
y
xvy
0
0
0
0
1
1
1
0
1
1
1
1
17.
Схема НЕреализует операцию отрицания
Таблица истинности
x
X
1
0
0
1
18.
Схема И-НЕсостоит из элемента И и инвертора и осуществляет
отрицание результата схемы И
Таблица истинности
x
y
0
0
1
0
1
1
1
0
1
1
1
0
19.
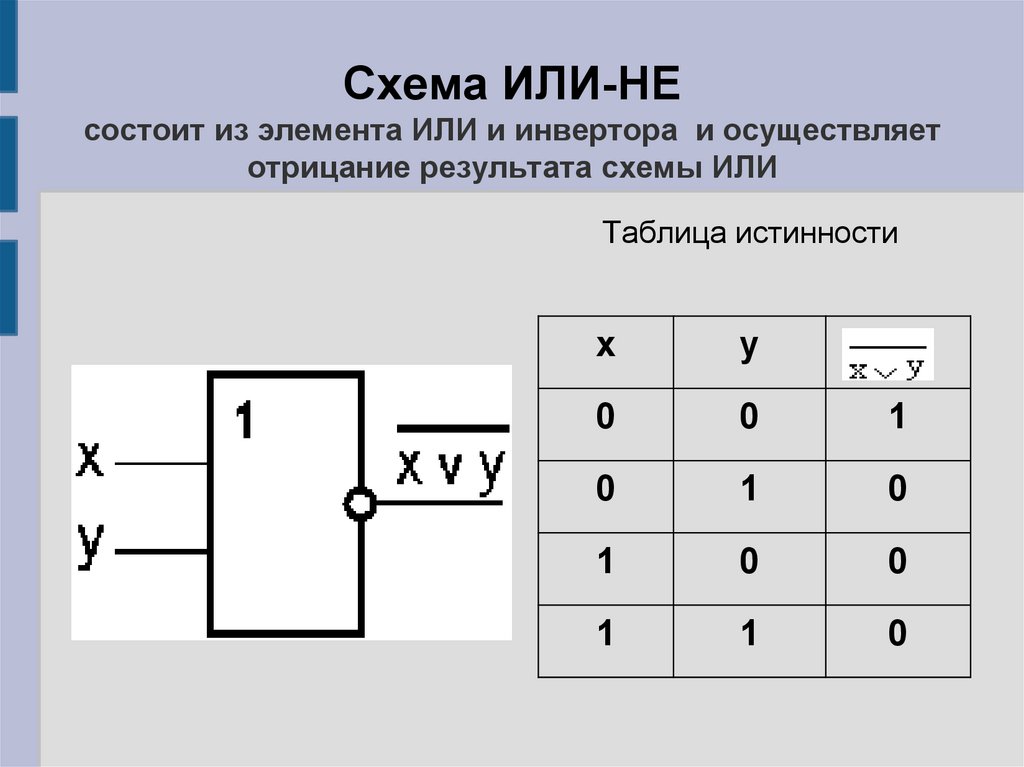
Схема ИЛИ-НЕсостоит из элемента ИЛИ и инвертора и осуществляет
отрицание результата схемы ИЛИ
Таблица истинности
x
y
0
0
1
0
1
0
1
0
0
1
1
0

















 Информатика
Информатика








