Похожие презентации:
Объединение-сортировка (Union-find)
1.
Объединение-сортировка(Union-find)
2.
Создание алгоритмаШаги:
Создание модели
Поиск алгоритма для решения
Работает быстро? Как использует память?
Если нет, то понять почему
Найти способ решения проблем
Повторять до выполнения условий
Научный подход
3.
Объединение-сортировка(Union-find)
Динамическая связность
4.
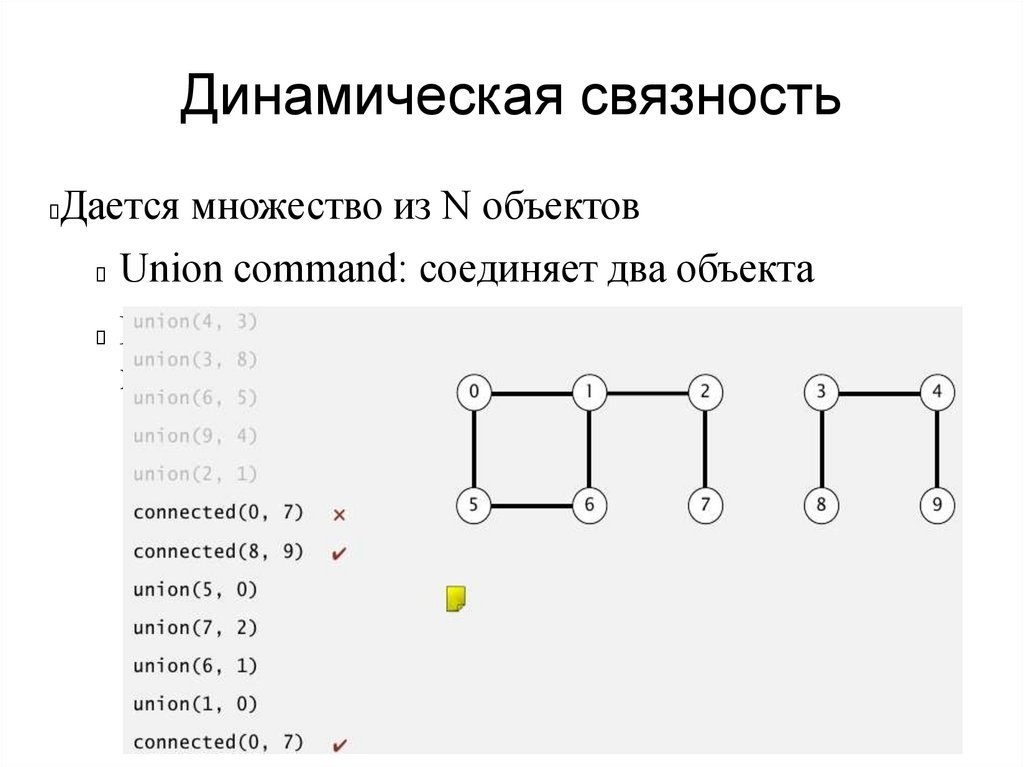
Динамическая связностьДается множество из N объектов
Union command: соединяет два объекта
Find/connected query: проверяет, есть ли путь
между двумя объектами
5.
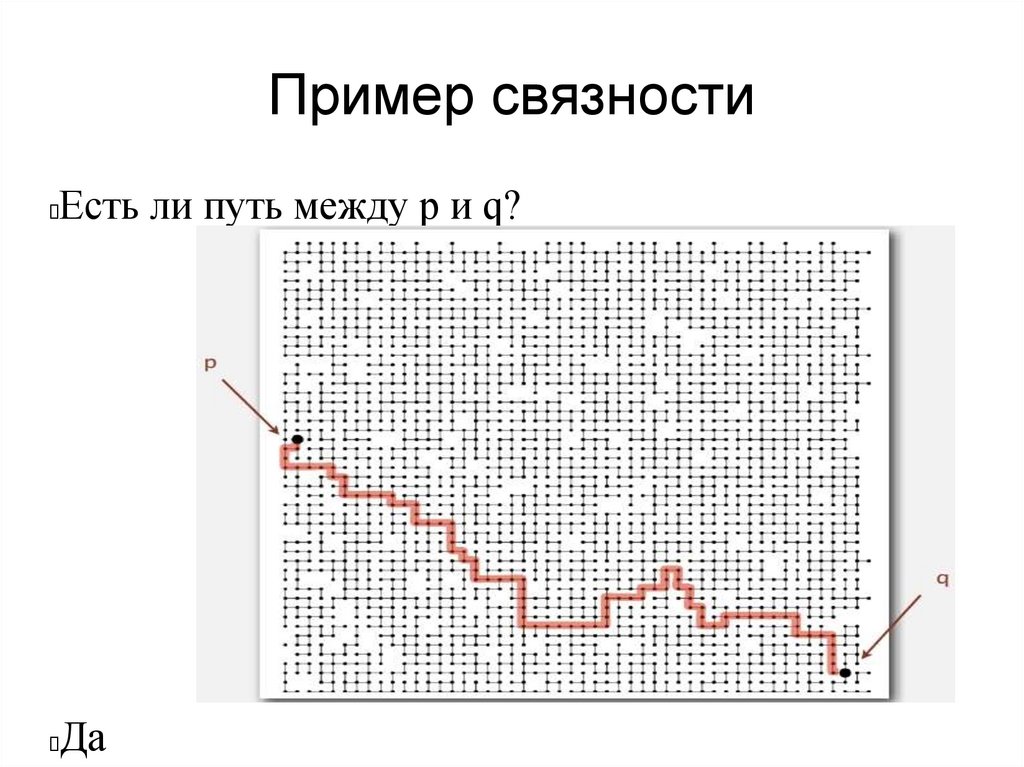
Пример связностиЕсть ли путь между p и q?
Да
6.
Моделирование объектовПриложения включают в себя работу с объектами
всех типов:
Пиксели на цифровых фотографиях
Компьютеры в сети
Люди в социальных сетях
Транзисторы в компьютерных чипах
Элементы в математических множествах
Имена переменных в программах
При программировании, назначай имена объектов
от 0 до N-1
7.
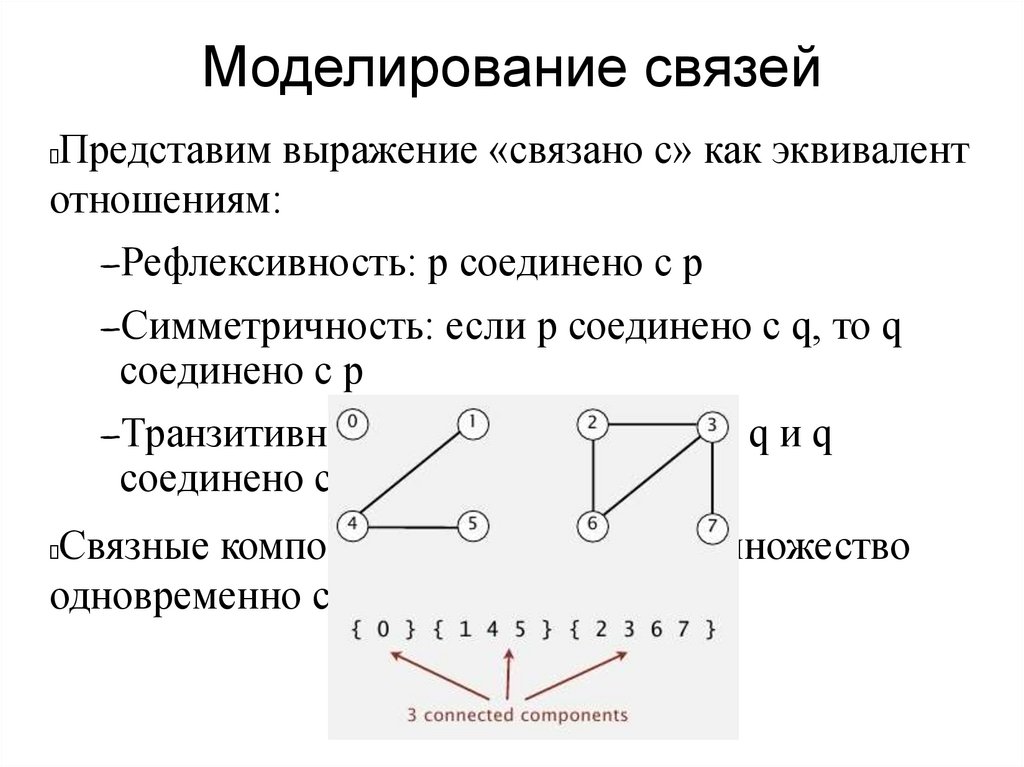
Моделирование связейПредставим выражение «связано с» как эквивалент
отношениям:
–Рефлексивность:
р соединено с р
–Симметричность:
соединено с p
если p соединено с q, то q
–Транзитивность:
Если p соединено q и q
соединено с r, то p соединено с r
Связные компоненты: максимальное множество
одновременно связанных объектов
8.
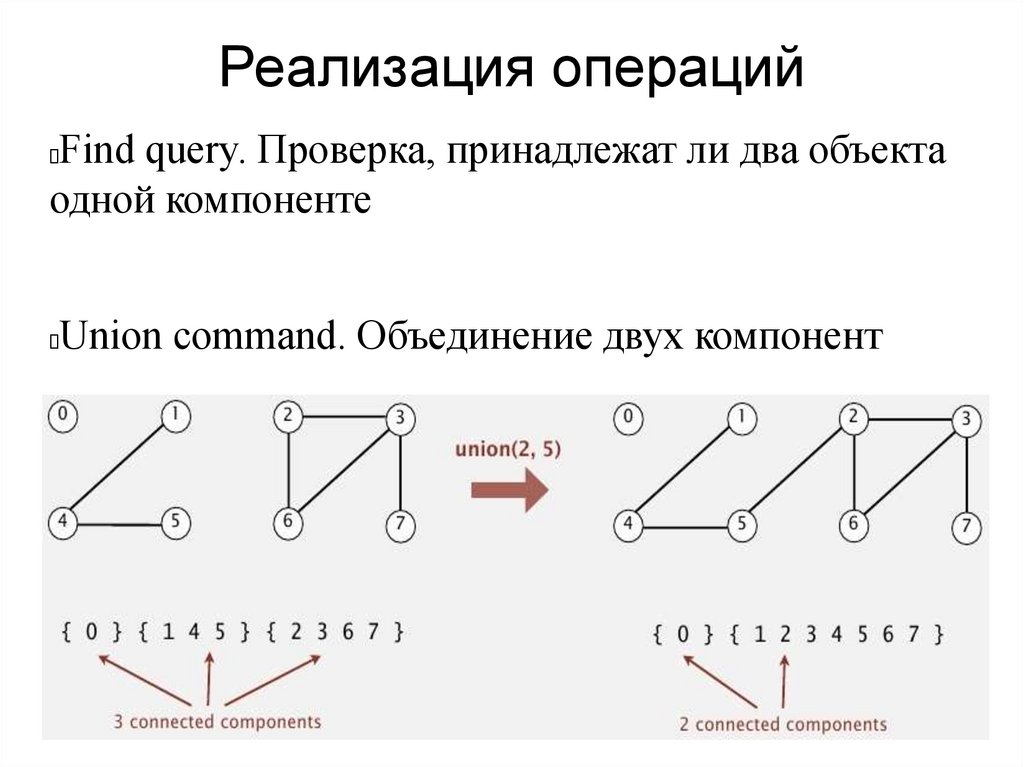
Реализация операцийFind query. Проверка, принадлежат ли два объекта
одной компоненте
Union command. Объединение двух компонент
9.
Типы данных для Union-find (API)Цель: создать эффективные структуры данных для
union-find
Количество объектов N может быть огромным
Количество операций М может быть огромным
Запросы на поиск и объединение могут быть
перемешаны
10.
ПриложениеЗагрузить N объектов из памяти
Повторять:
чтение пар объектов
если они не соединены, то соединить их и
вывести пару на экран
11.
Объединение-сортировка(Union-find)
Быстрый поиск
(Quick-find)
12.
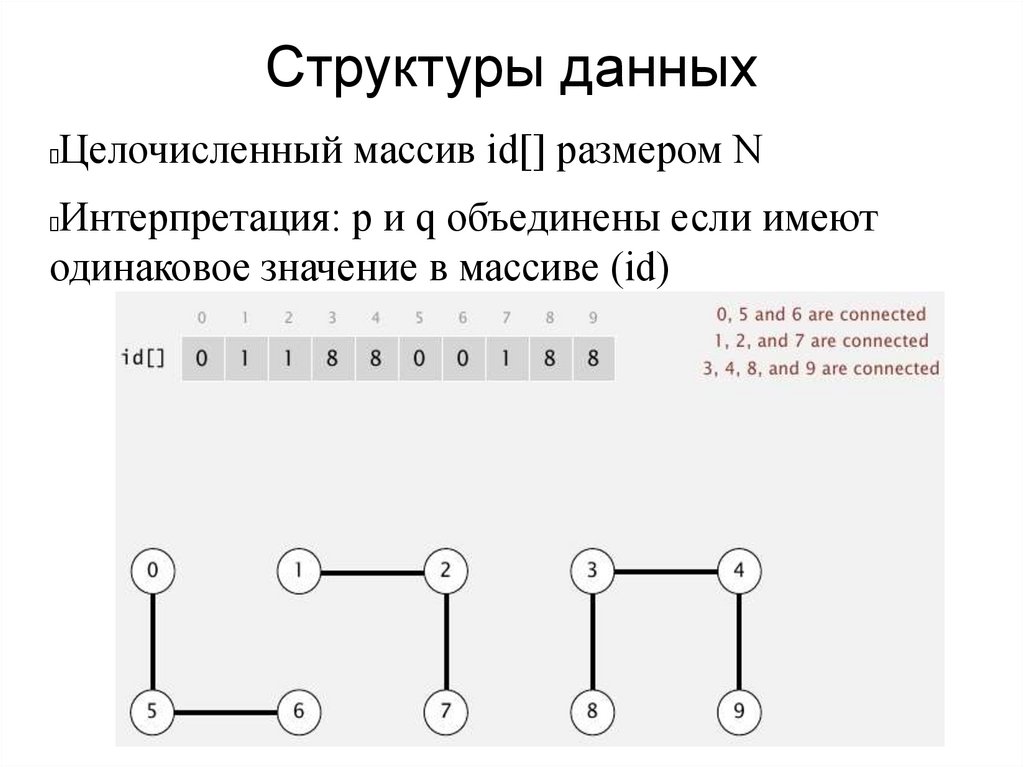
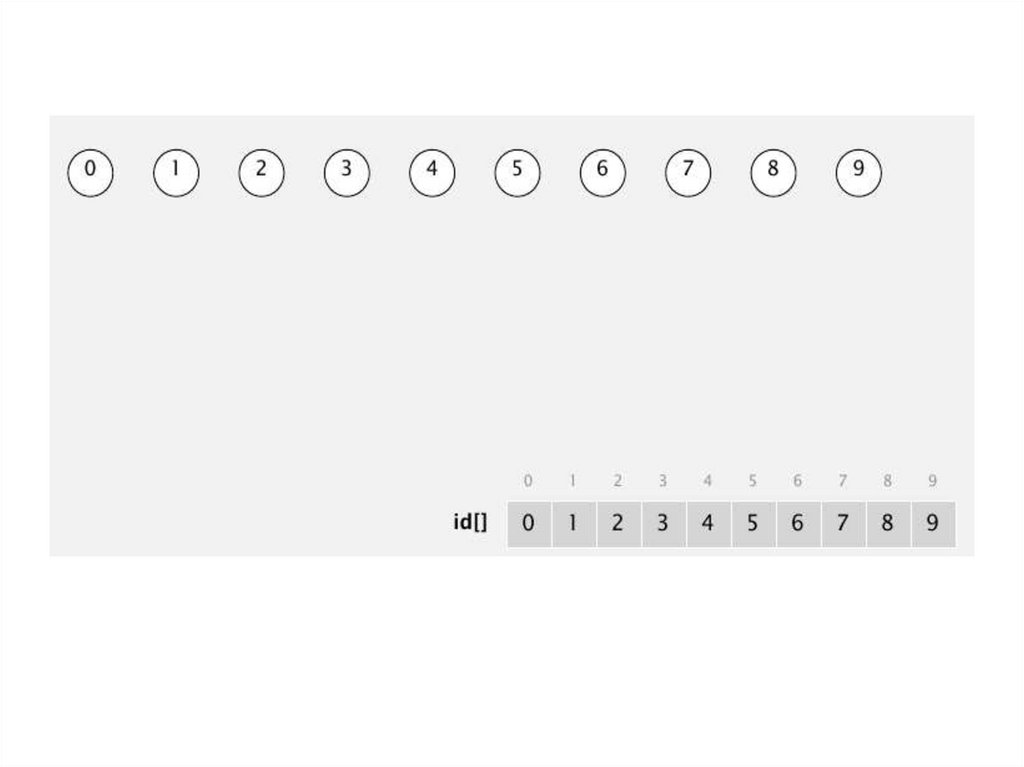
Структуры данныхЦелочисленный массив id[] размером N
Интерпретация: p и q объединены если имеют
одинаковое значение в массиве (id)
13.
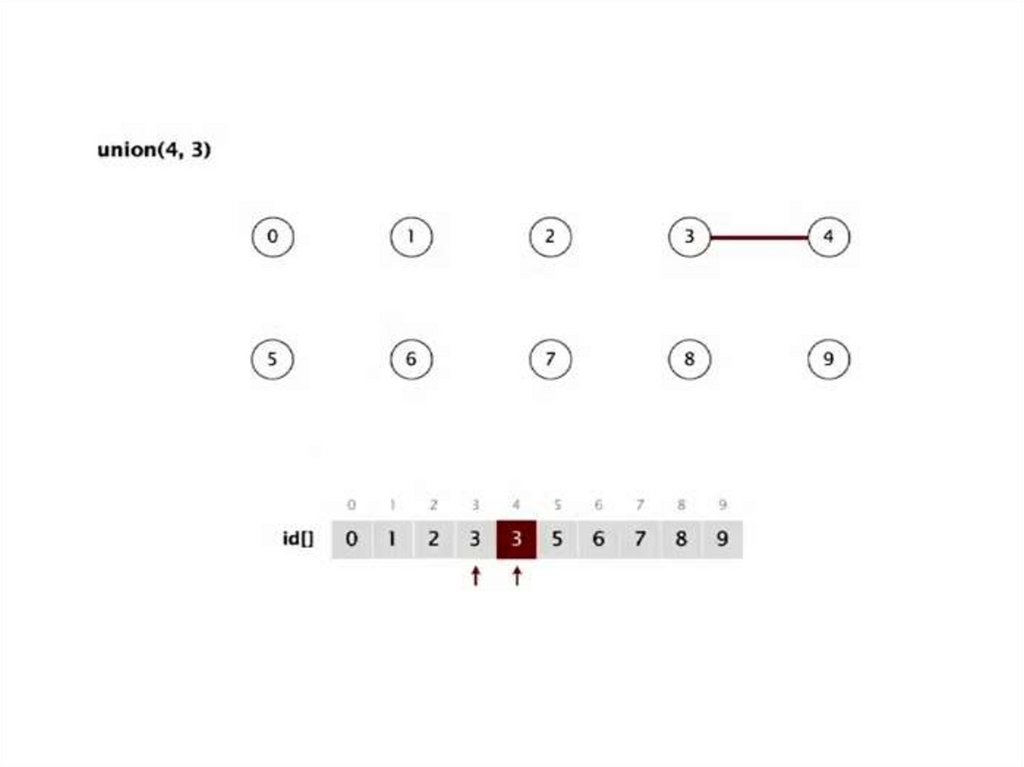
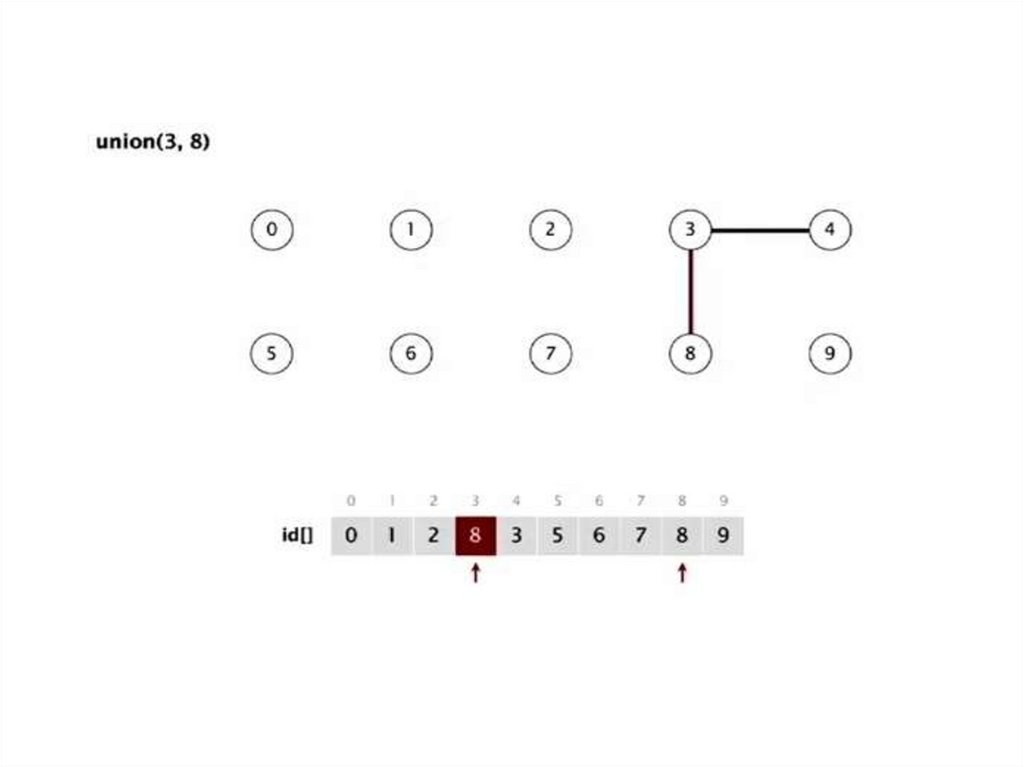
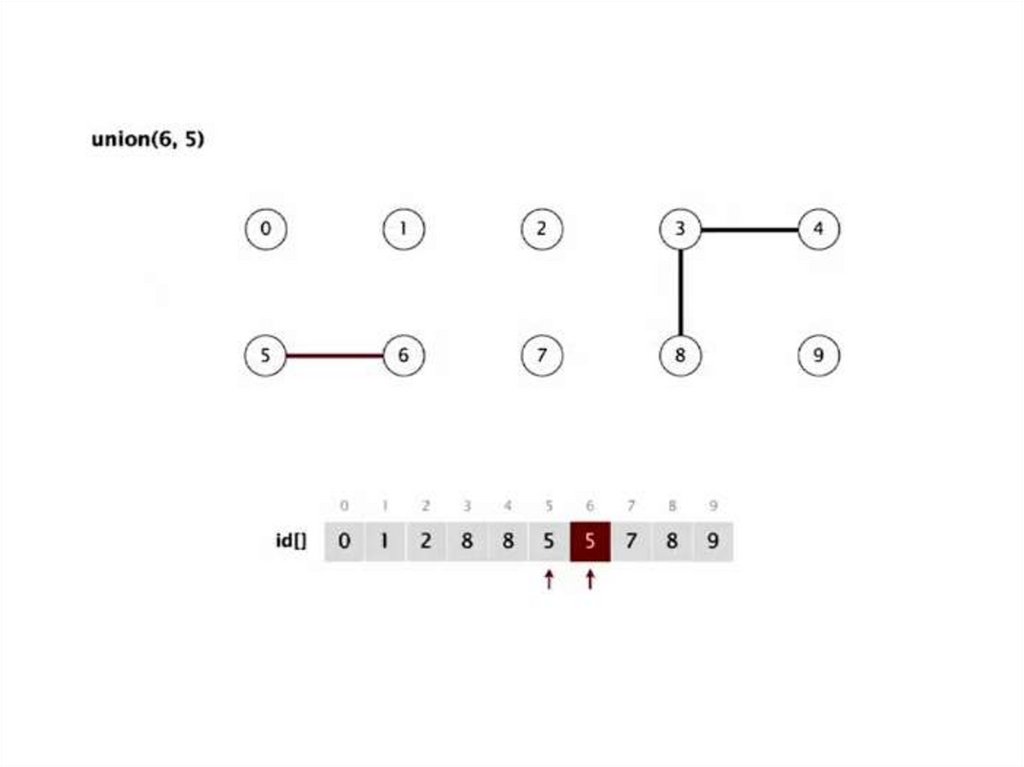
Структура данных:Целочисленный массив id[] размером N
Интерпретация: p и q объединены если имеют
одинаковое значение в массиве (id)
Find. Проверка, если p и q имеют одинаковый id
Объединение. Объединение компонент содержащих p и q. Замена всех значений id[p] н
14.
15.
16.
17.
18.
19.
20.
Быстрый поиск: реализация (жадныйподход)
21.
Свойства быстрого поискаСтоимость. Количество обращений к массиву
(чтение или запись)
Проблемы быстрого поиска. Трудоемкая операция
соединения
Квадратичная сложность. N2 обращений — N union
команд на N объектах
22.
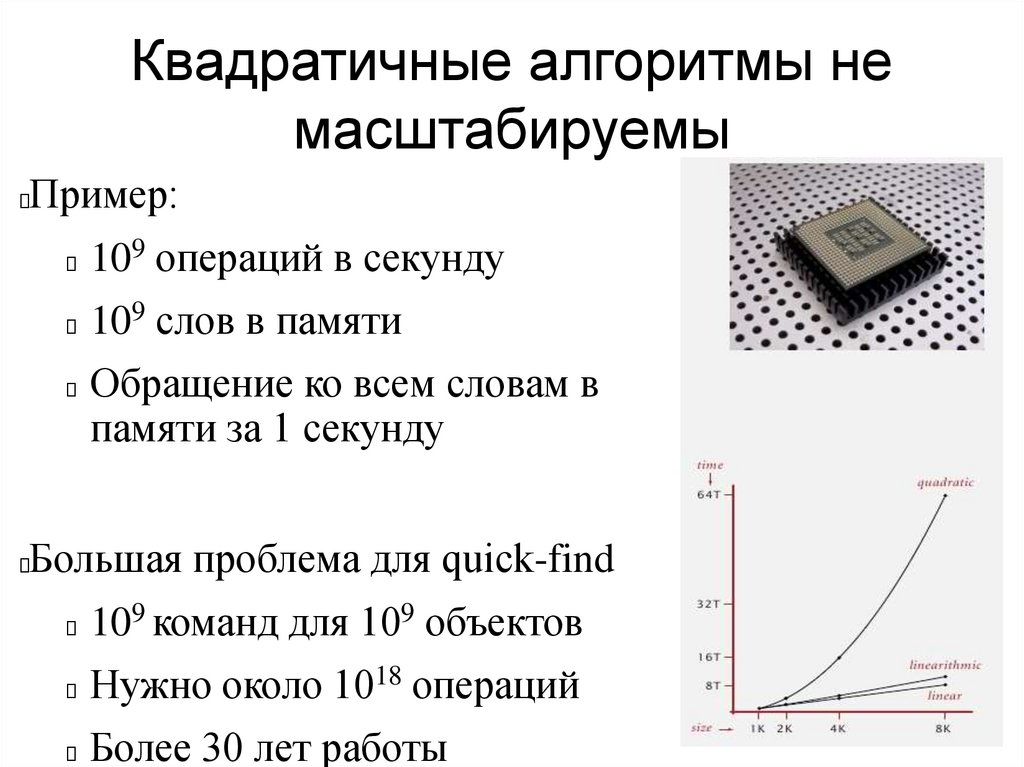
Квадратичные алгоритмы немасштабируемы
Пример:
109 операций в секунду
109 слов в памяти
Обращение ко всем словам в
памяти за 1 секунду
Большая проблема для quick-find
109 команд для 109 объектов
Нужно около 1018 операций
Более 30 лет работы
23.
Объединение-сортировка(Union-find)
Быстрое объединение
(Quick union)
24.
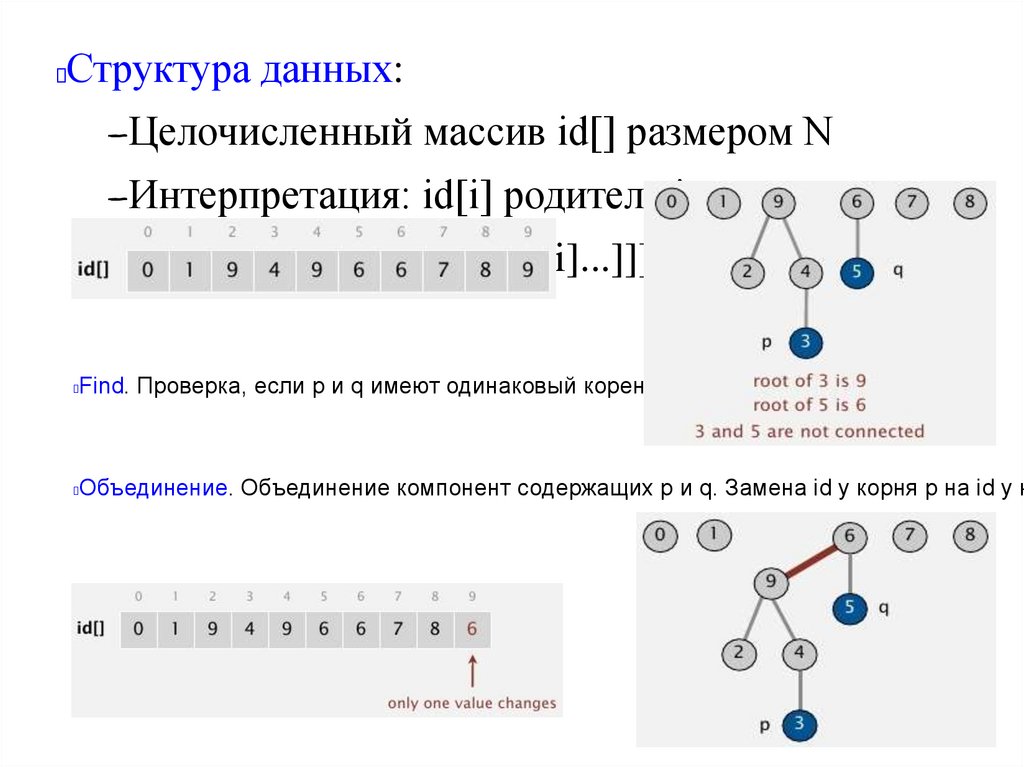
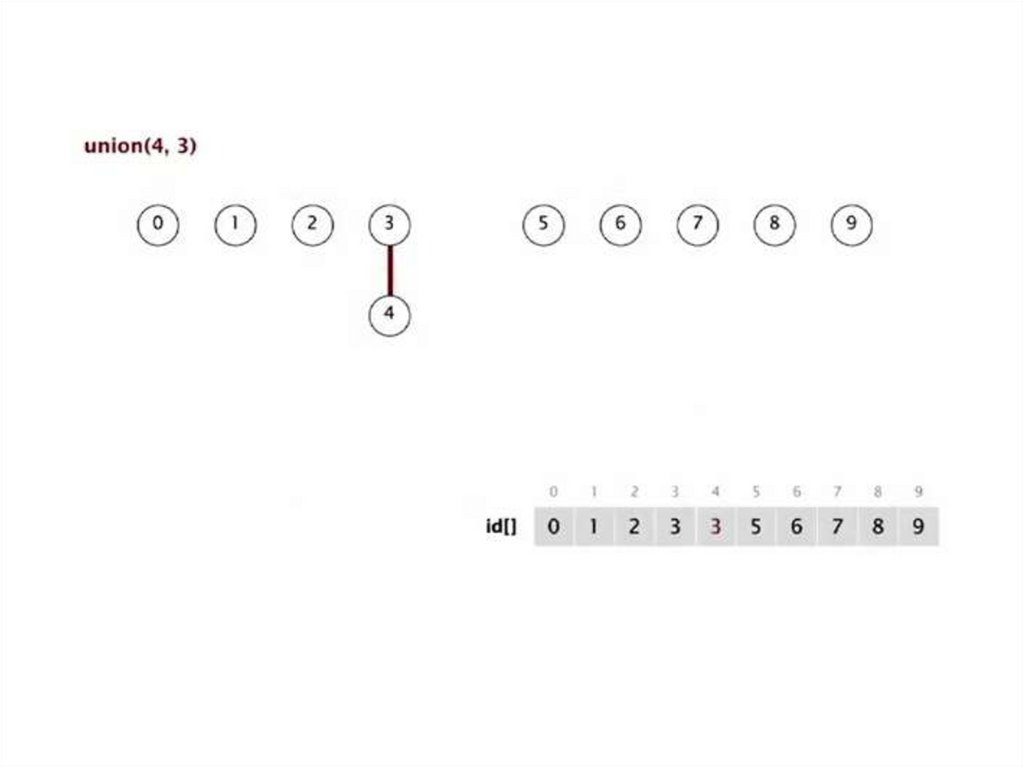
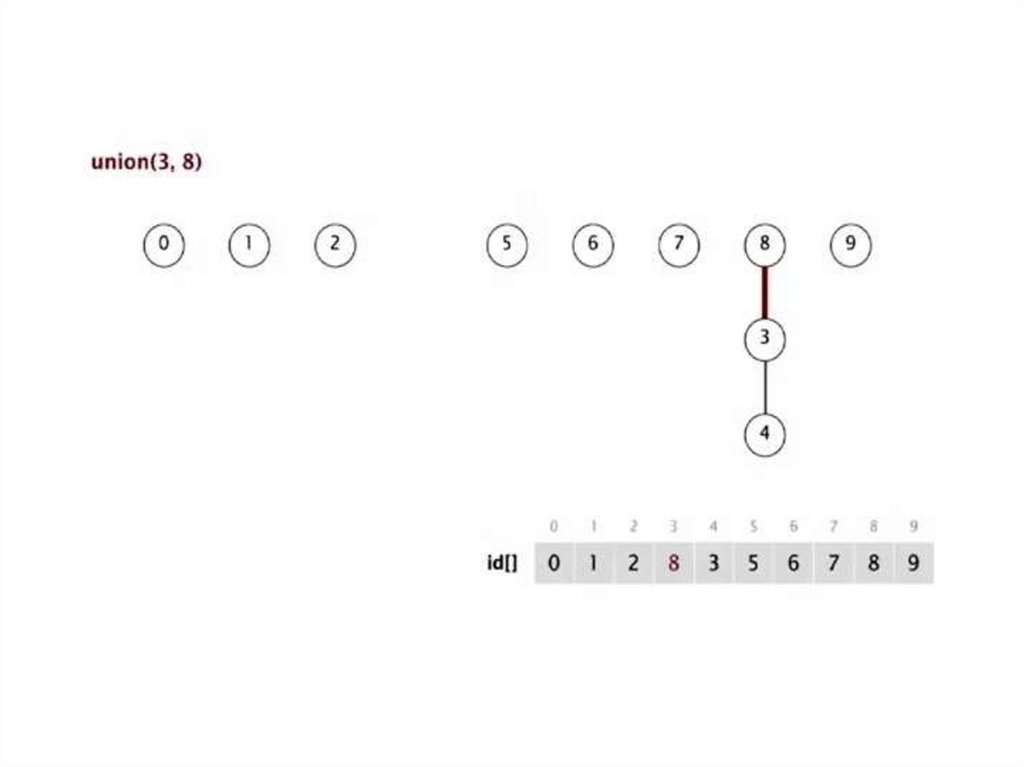
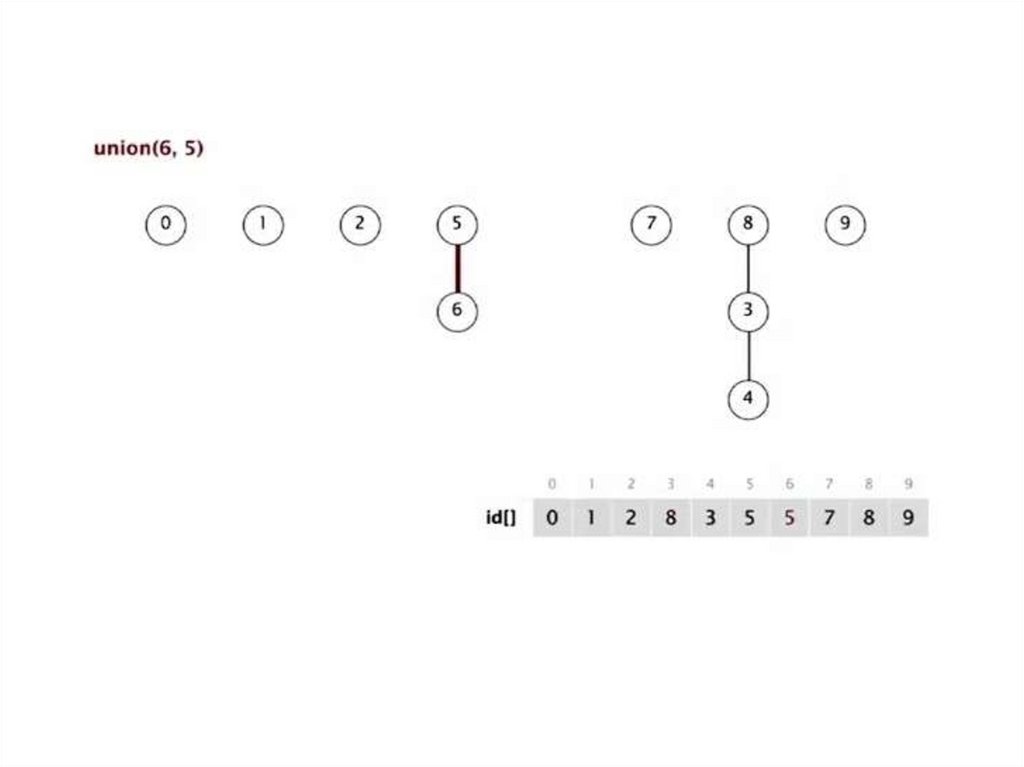
Быстрое объединение (ленивыйподход)
Структура данных
Целочисленный массив id[] размером N
Интерпретация: id[i] родитель i
Корень i — id[id[id[...id[i]...]]]
25.
Структура данных:–Целочисленный
массив id[] размером N
–Интерпретация:
id[i] родитель i
–Корень
i — id[id[id[...id[i]...]]]
Find. Проверка, если p и q имеют одинаковый корень
Объединение. Объединение компонент содержащих p и q. Замена id у корня p на id у к
26.
27.
28.
29.
30.
31.
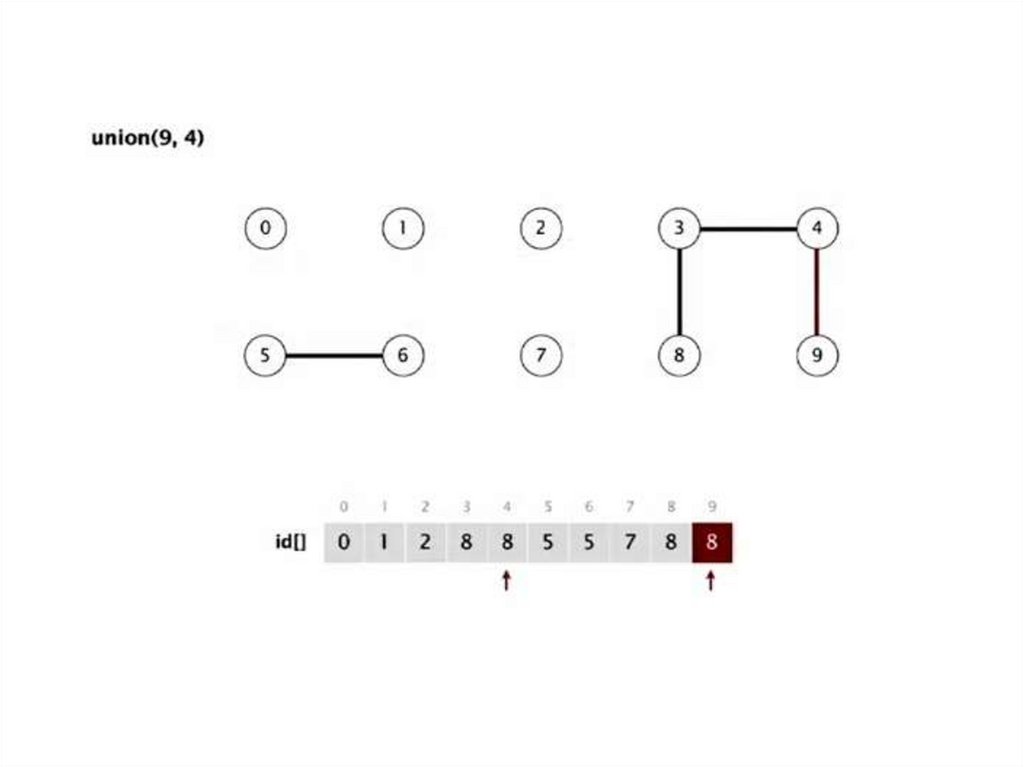
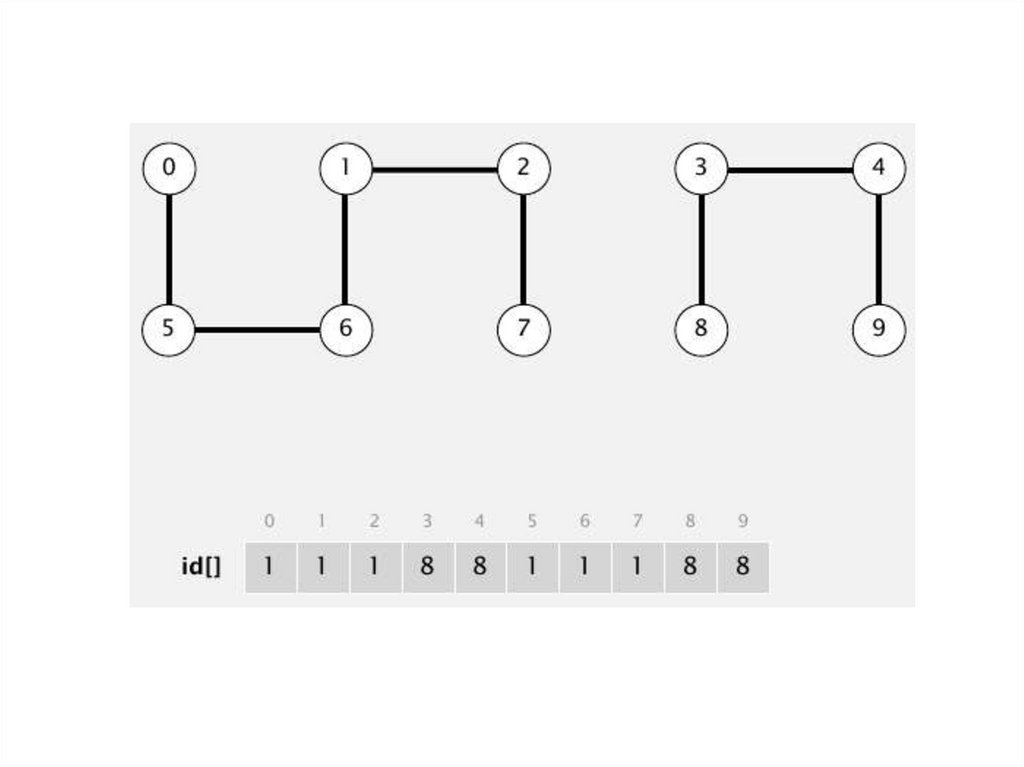
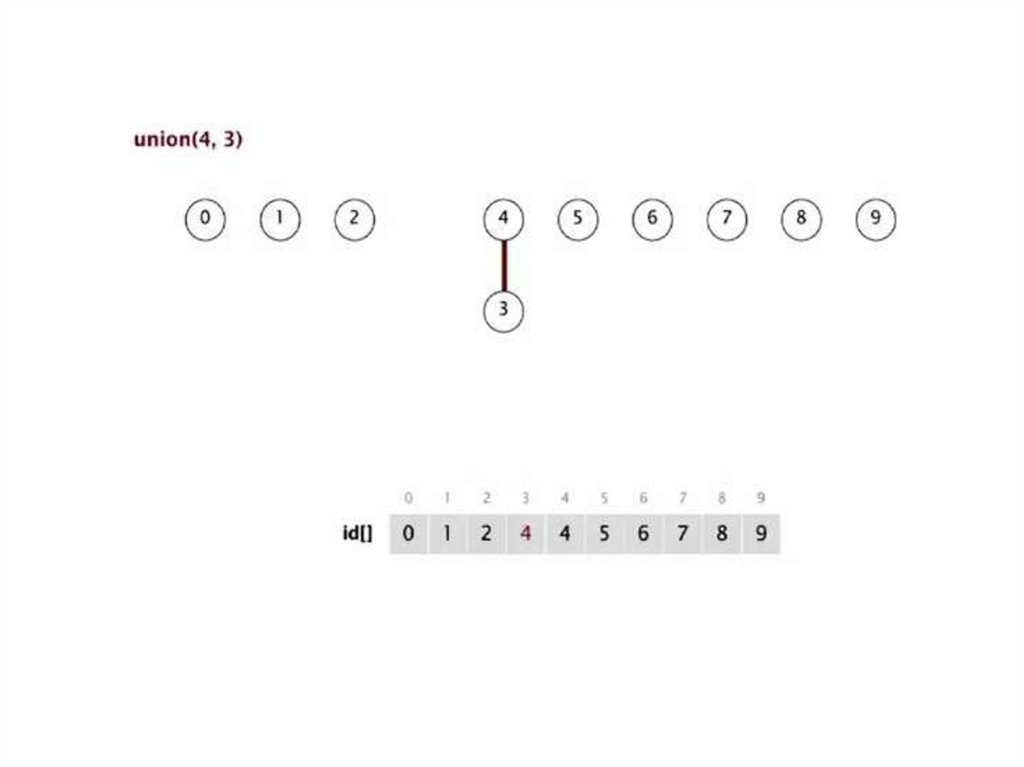
connected (8,9)connected (5,4)
union (5,0)
union (7,2)
union (6,1)
union (7,3)
32.
33.
Быстрое объединение: реализация34.
Свойства быстрого объединенияСтоимость. Количество обращений к массиву
(чтение или запись)
Проблемы быстрого поиска
Трудоемкая операция соединения
Дерево низкое, но дорого его поддерживать в
этом состоянии
Проблемы быстрого объединения
35.
Объединение-сортировка(Union-find)
Быстрое объединение
(Quick union)
Улучшения
36.
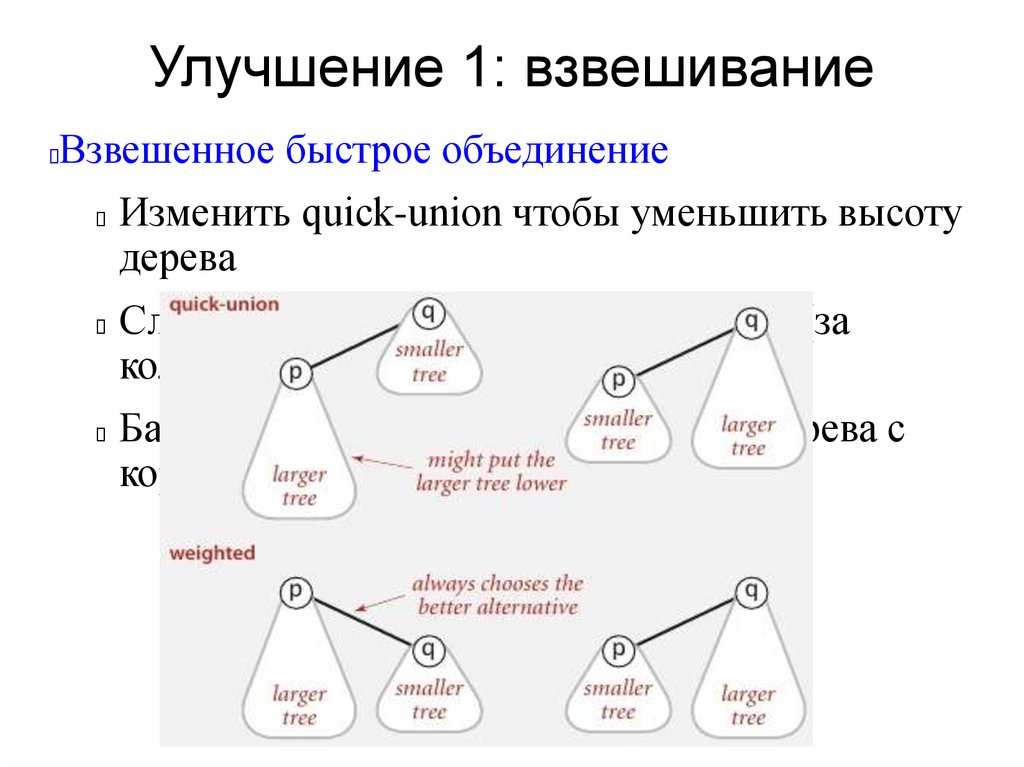
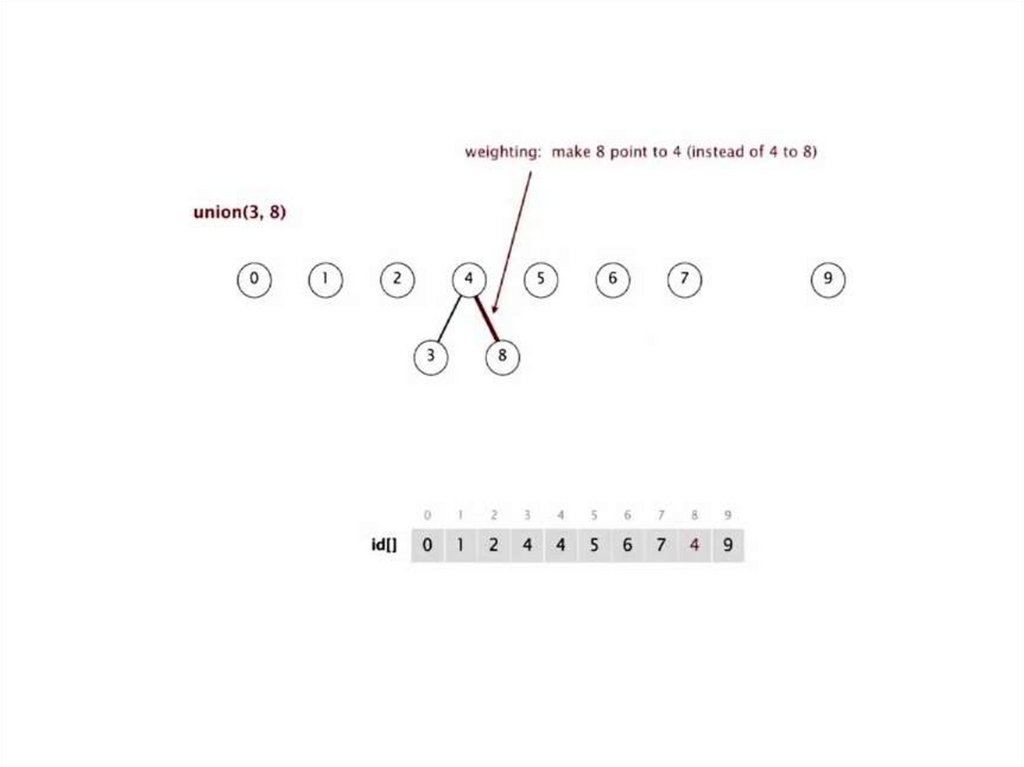
Улучшение 1: взвешиваниеВзвешенное быстрое объединение
Изменить quick-union чтобы уменьшить высоту
дерева
Следить за размерами каждого дерева (за
количество объектов)
Баланс: связывать корень меньшего дерева с
корнем большего дерева
37.
38.
39.
40.
41.
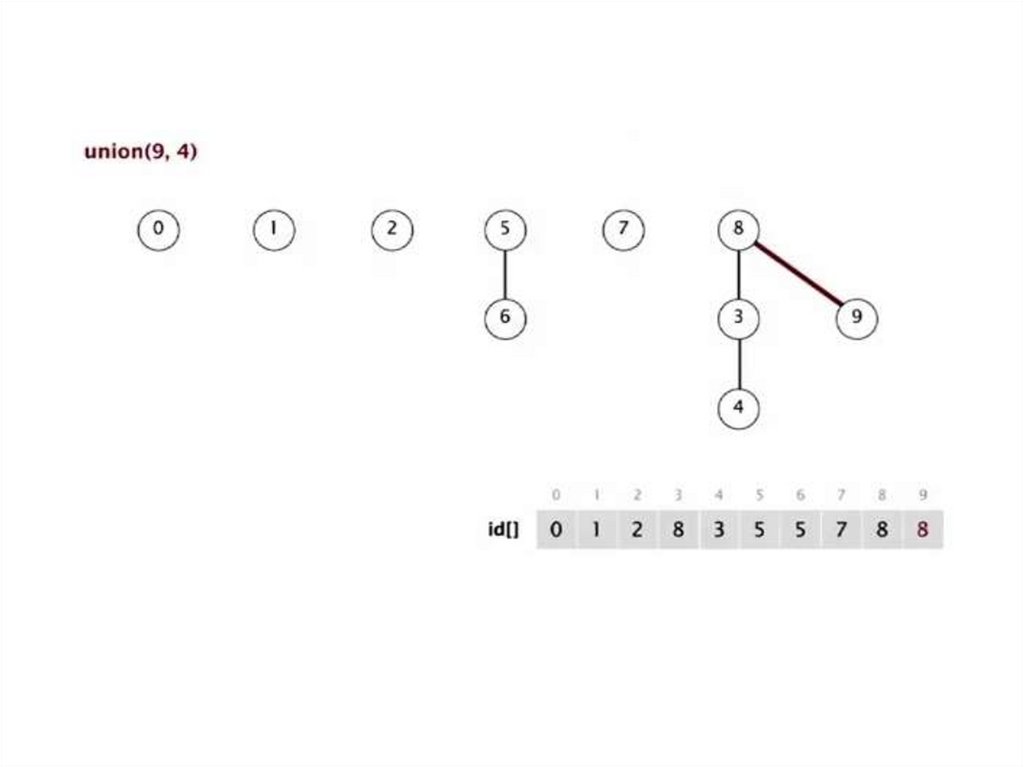
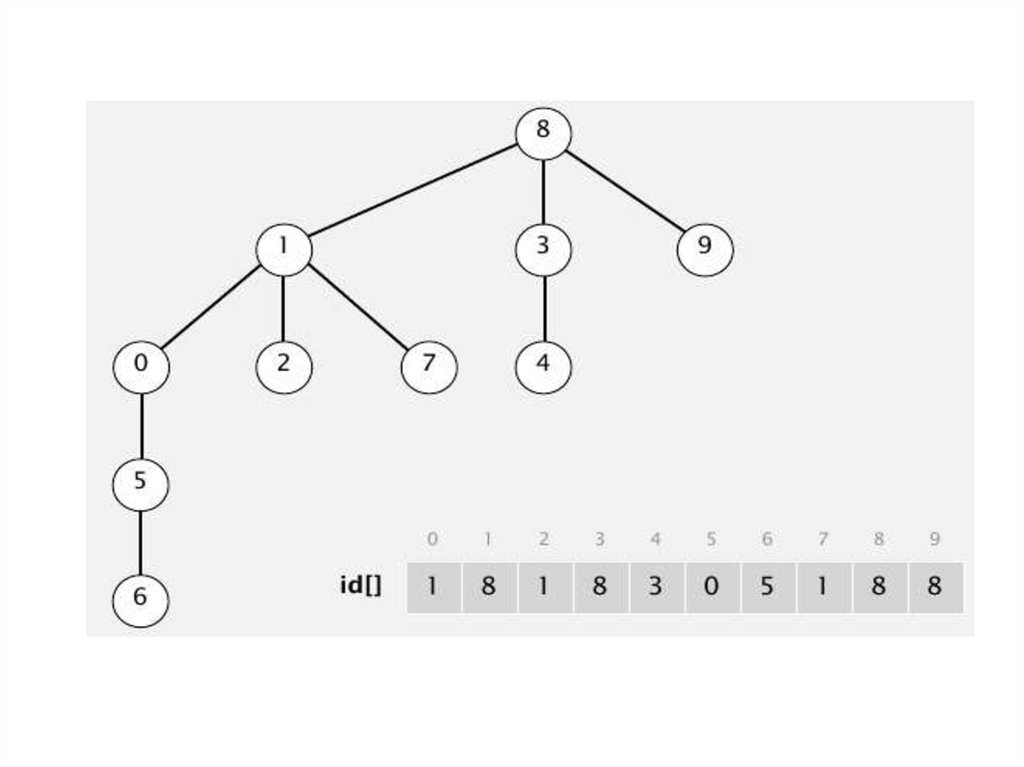
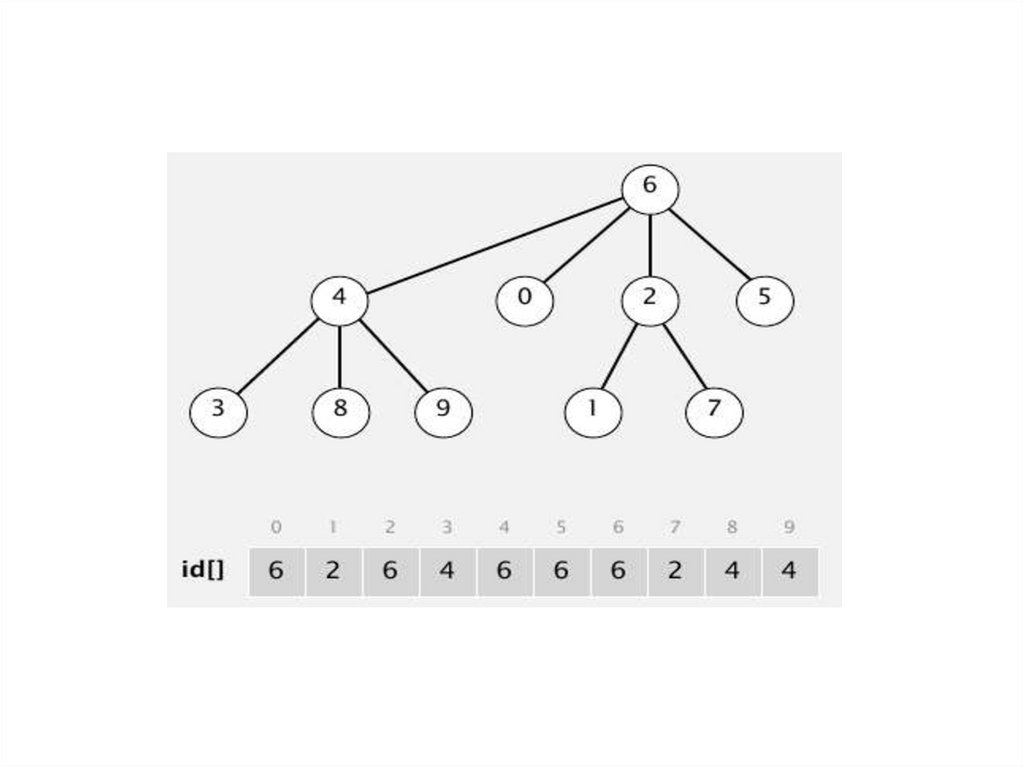
union (9,4)union (2,1)
union (5,0)
union (7,2)
union (6,1)
union (7,3)
42.
43.
44.
Структура данных:–
Такая же, как quick-union, плюс дополнительный массив, где sz[i] количество
объектов в дереве с корнем i
Find. Проверка, если p и q имеют одинаковый корень (так же, как quick-union)
Объединение:
–
Связывать корень меньшего дерева с корнем большего дерева
–
Обновить массив sz[]
45.
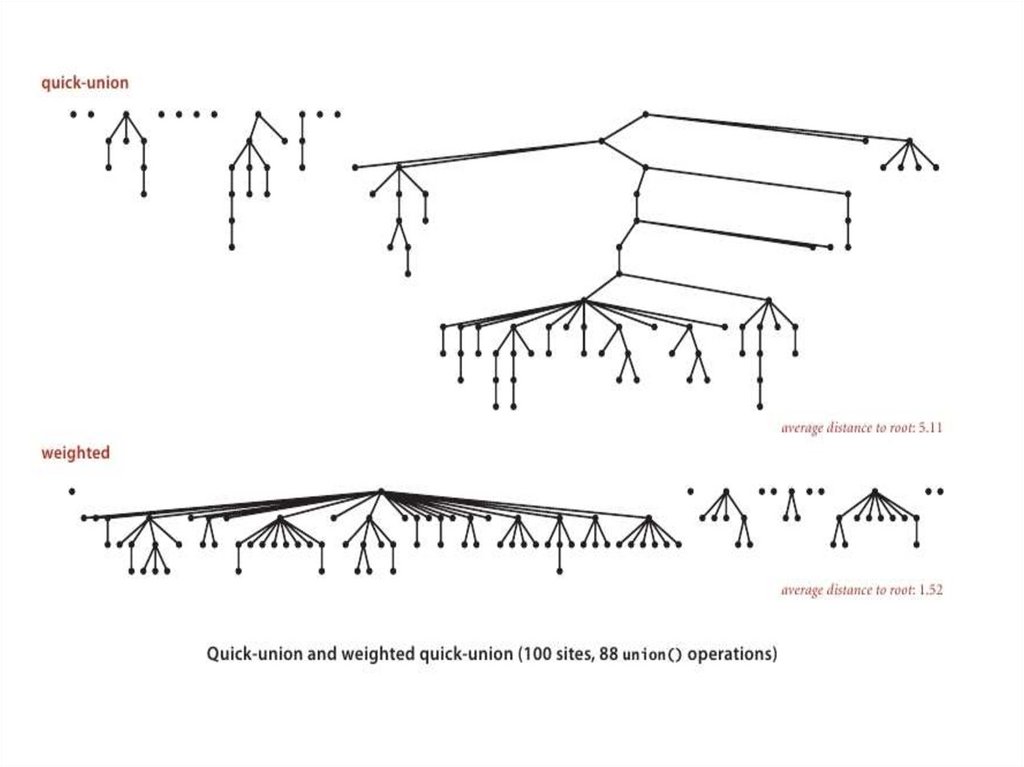
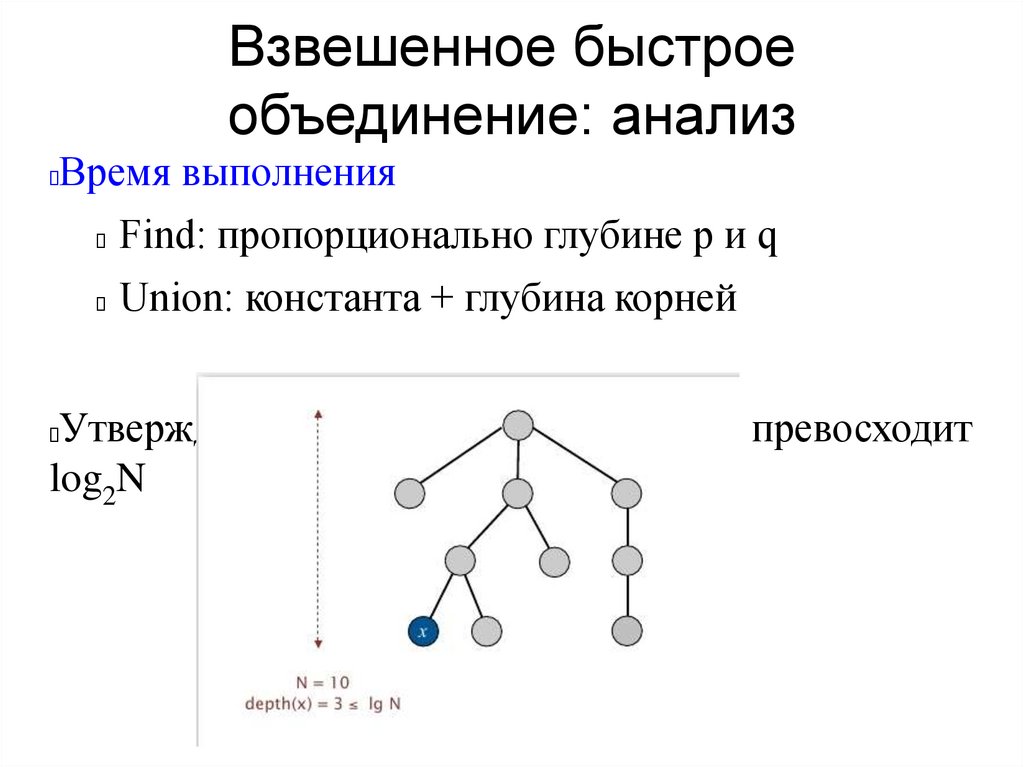
Взвешенное быстроеобъединение: анализ
Время выполнения
Find: пропорционально глубине p и q
Union: константа + глубина корней
Утверждение: Глубина любого узла не превосходит
log2N
46.
Взвешенное быстроеобъединение: анализ
Время выполнения
Find: пропорционально глубине p и q
Union: константа + глубина корней
Утверждение: Глубина любого узла не превосходит
log2N
Доказательство: Когда глубина х возрастает?
Возрастает на 1, когда дерево Т1, содержащее х,
объединяется с деревом Т2
Размер дерева Т1 как минимум в два раза
47.
Взвешенное быстроеобъединение: анализ
Время выполнения
Find: пропорционально глубине p и q
Union: константа + глубина корней
Утверждение: Глубина любого узла не превосходит
log2N
WQU гарантирует приемлемую
производительность?
Нет
48.
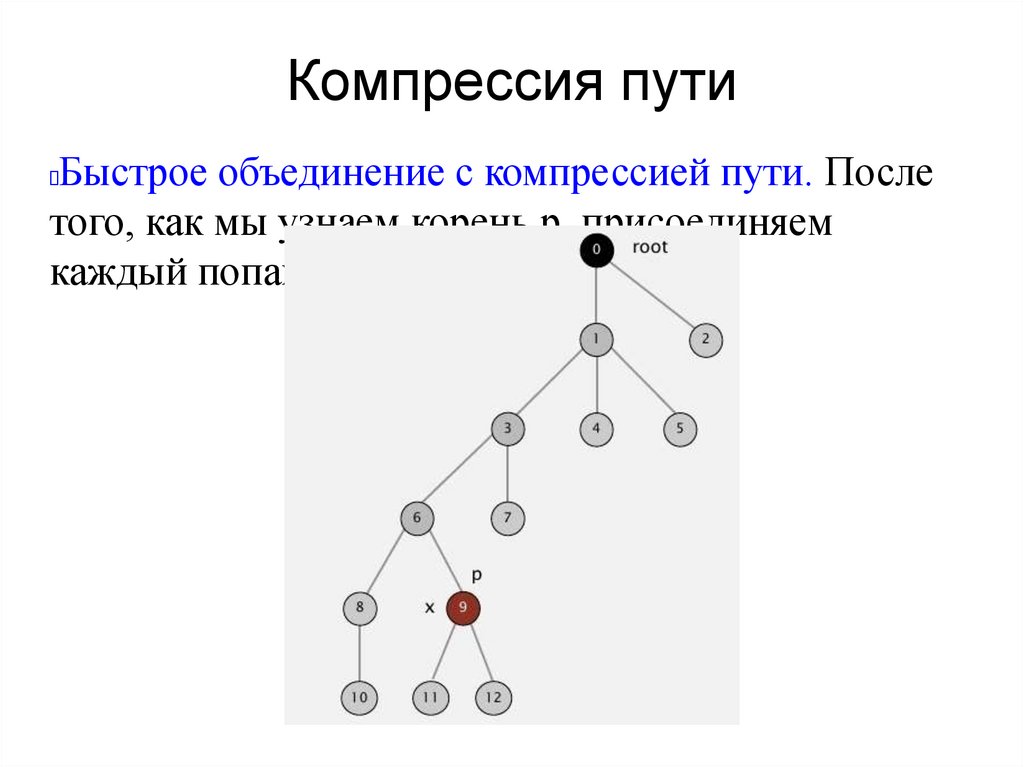
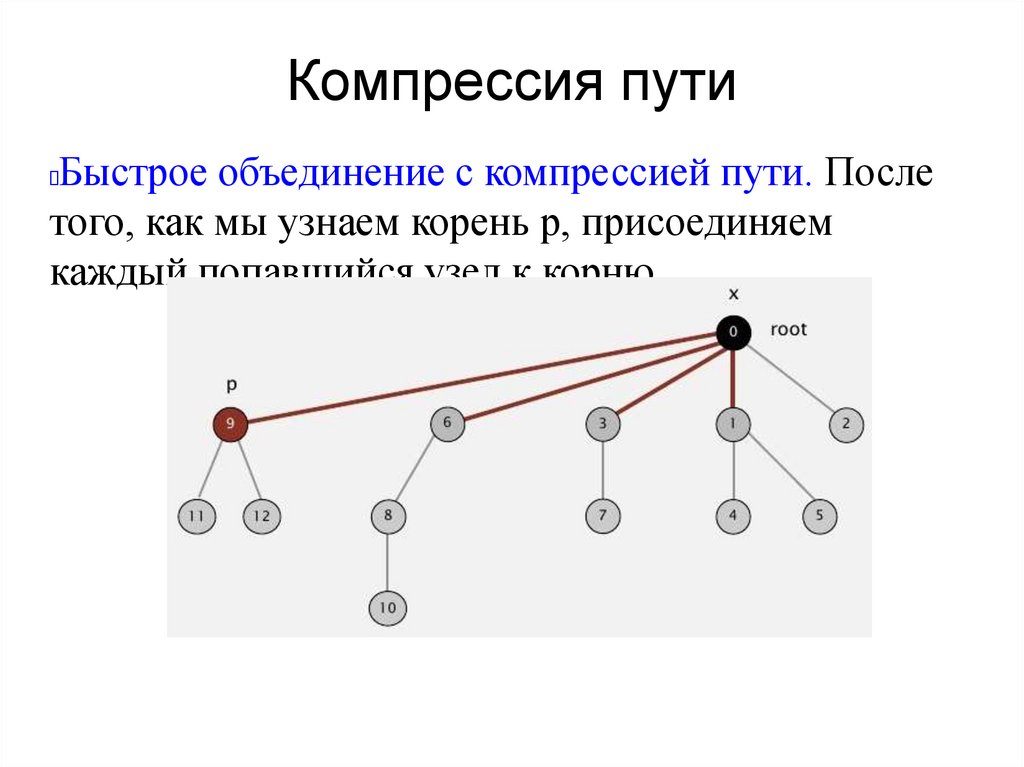
Компрессия путиБыстрое объединение с компрессией пути. После
того, как мы узнаем корень р, присоединяем
каждый попавшийся узел к корню.
49.
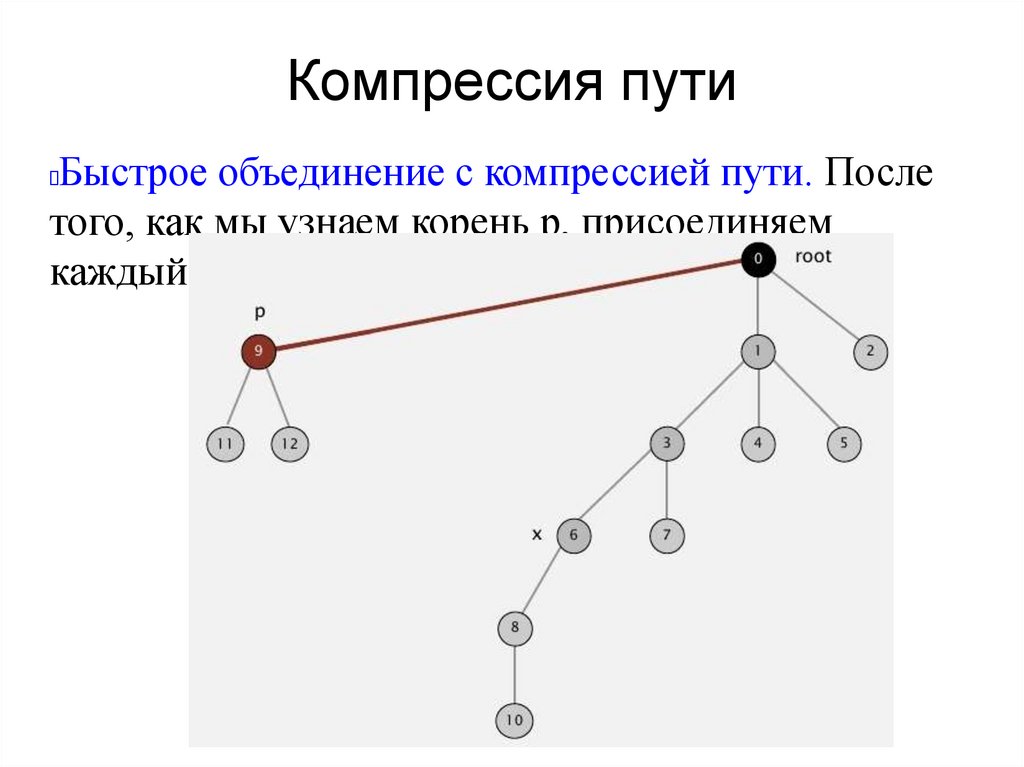
Компрессия путиБыстрое объединение с компрессией пути. После
того, как мы узнаем корень р, присоединяем
каждый попавшийся узел к корню.
50.
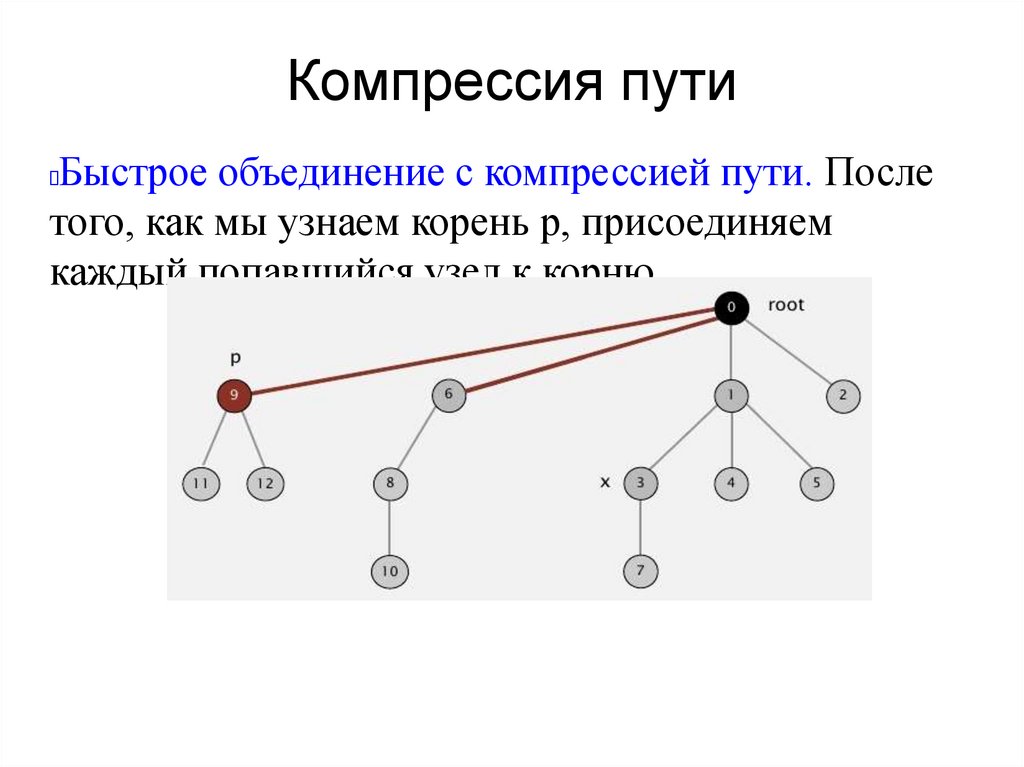
Компрессия путиБыстрое объединение с компрессией пути. После
того, как мы узнаем корень р, присоединяем
каждый попавшийся узел к корню.
51.
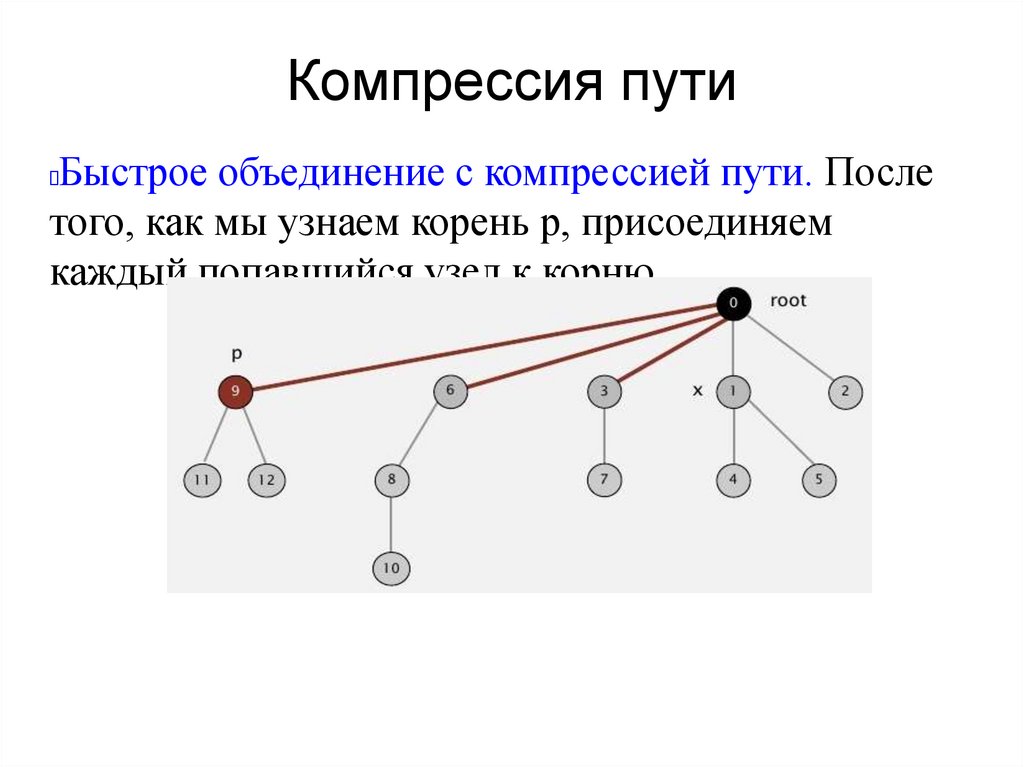
Компрессия путиБыстрое объединение с компрессией пути. После
того, как мы узнаем корень р, присоединяем
каждый попавшийся узел к корню.
52.
Компрессия путиБыстрое объединение с компрессией пути. После
того, как мы узнаем корень р, присоединяем
каждый попавшийся узел к корню.
53.
Компрессия пути: реализацияДобавляем одну строку в функцию root()
Нет причин чтобы этого не делать
54.
Взвешенное быстроеобъединение с компрессия пути
Утверждение. [Hopcroft-Ulman, Tarjan]
Начиная с пустой структуры данных,
последовательность из M union-find
операций на N объектах <= c(N + M
log2* N) доступов к массиву
Линейный алгоритм для М union-find
операций на N объектах
Постоянная стоимость обращения к
данным
Теоретически, WQUPC не линеен
55.
ВыводыWQUPC позволяет решать задачи, которые не
могут быть решены иначе
Пример [109 union-find операций над 109
объектами]
WQUPC сокращает время работы с 30 лет до 6
56.
Объединение-сортировка(Union-find)
Применение
57.
Применение Union-find58.
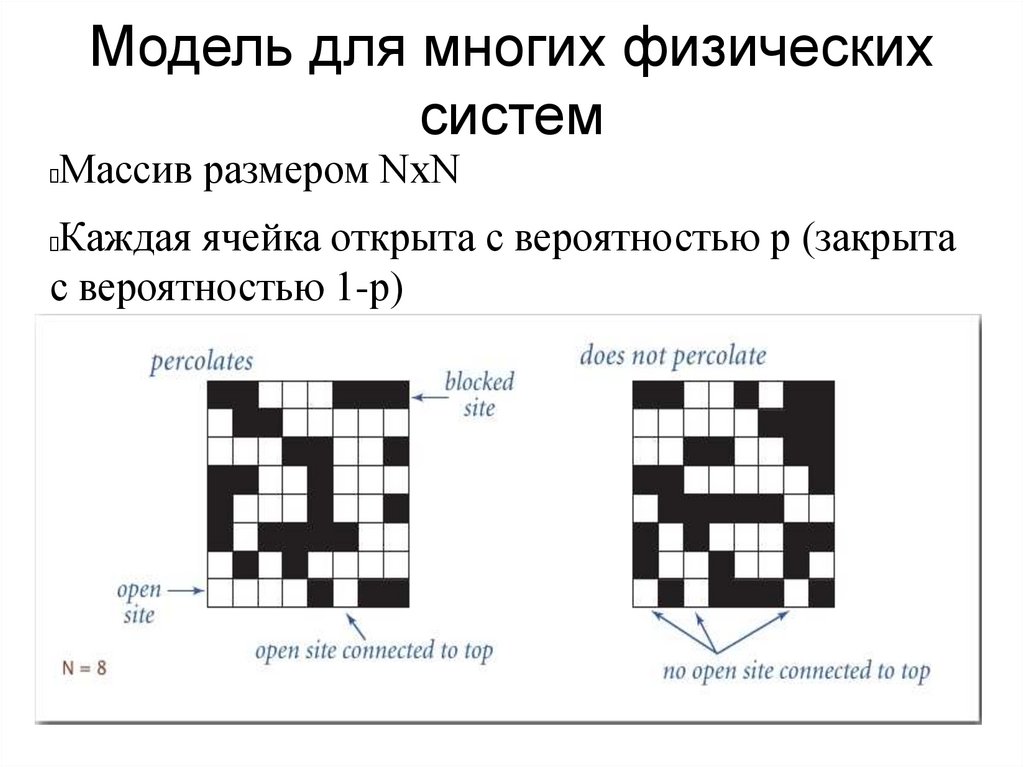
Модель для многих физическихсистем
Массив размером NxN
Каждая ячейка открыта с вероятностью р (закрыта
с вероятностью 1-р)
Просачивание: если есть путь через открытые
ячейки между противоположными сторонами
массива
59.
Модель для многих физическихсистем
Массив размером NxN
Каждая ячейка открыта с вероятностью р (закрыта
с вероятностью 1-р)
Просачивание: если есть путь через открытые
ячейки между противоположными сторонами
массива
60.
Вероятность просачивания61.
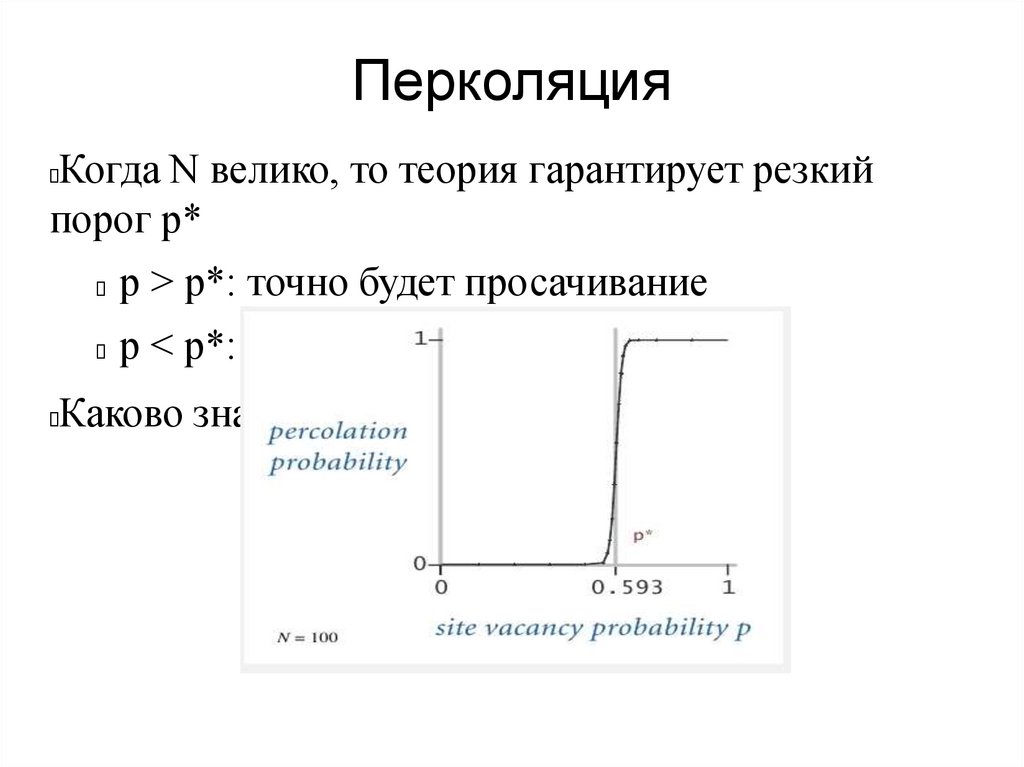
ПерколяцияКогда N велико, то теория гарантирует резкий
порог p*
р > p*: точно будет просачивание
p < p*: точно не будет
Каково значение р?
62.
Принцип Монте-КарлоИнициализируем весь массив NxN закрытым
В случайном порядке открываем ячейки, до тех
пор, пока не образуется путь от верха до низа
Оцениваем порог р*
63.
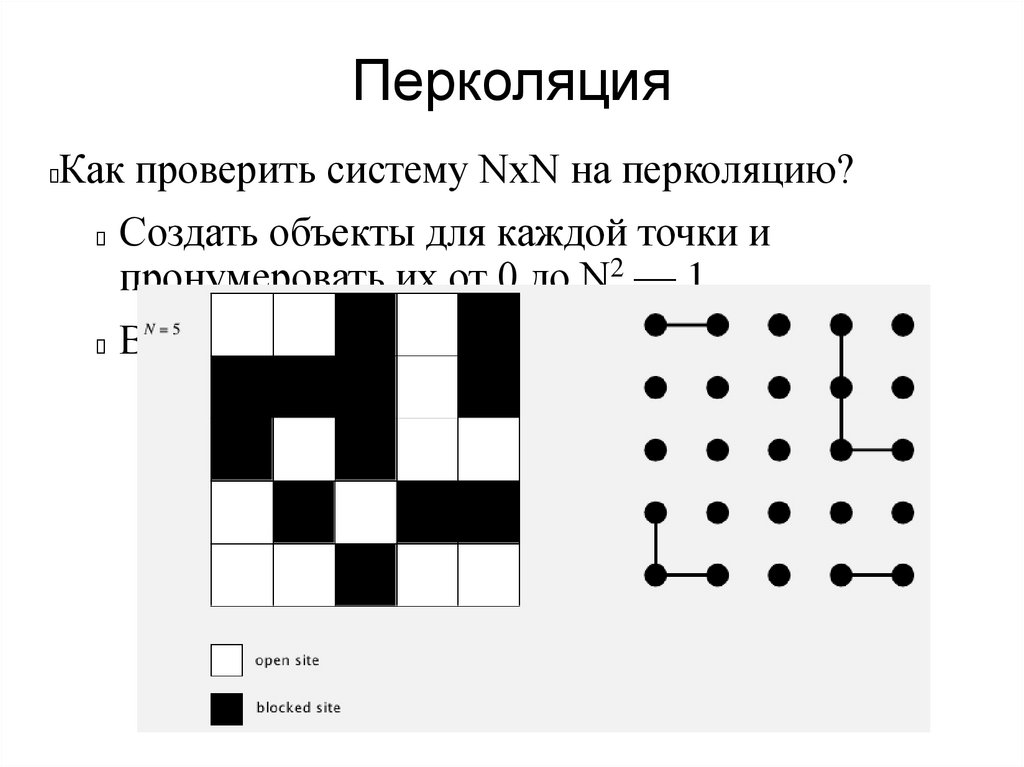
ПерколяцияКак проверить систему NxN на перколяцию?
Создать объекты для каждой точки и
пронумеровать их от 0 до N2 - 1
64.
ПерколяцияКак проверить систему NxN на перколяцию?
Создать объекты для каждой точки и
пронумеровать их от 0 до N2 — 1
Выделяем связные компоненты
65.
ПерколяцияКак проверить систему NxN на перколяцию?
Создать объекты для каждой точки и
пронумеровать их от 0 до N2 — 1
Выделяем связные компоненты
Проверяем относится ли, хотя бы одна точка из
верхней и нижней строчки к одной связной
компоненте (квадратичный алгоритм)
66.
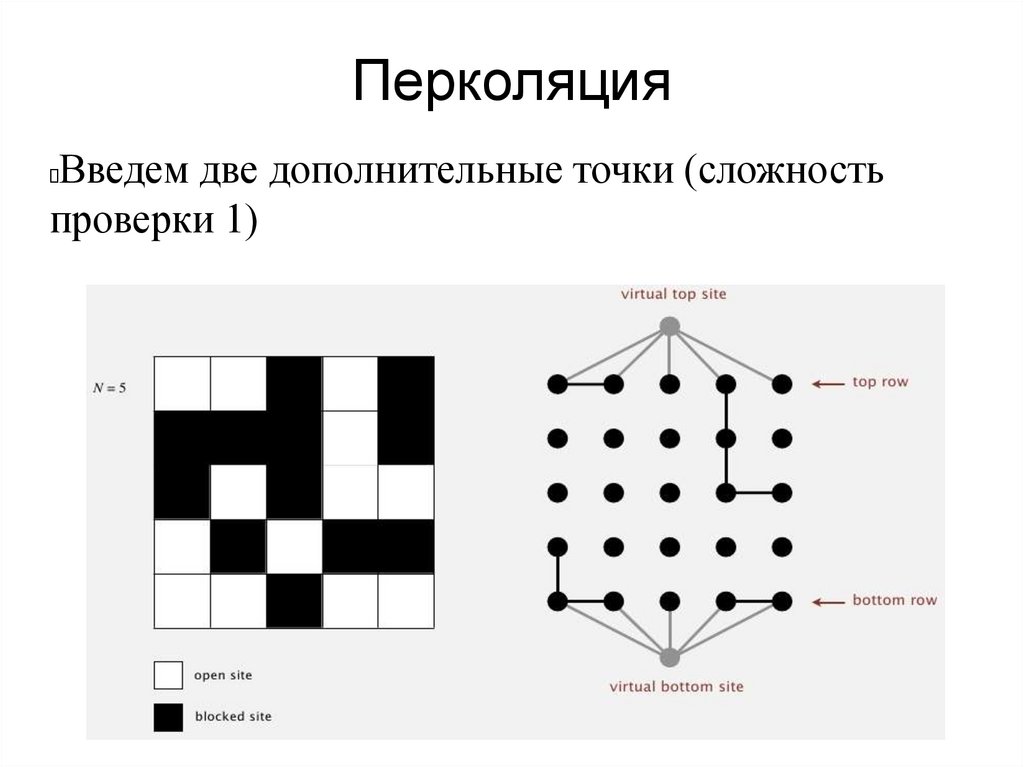
ПерколяцияВведем две дополнительные точки (сложность
проверки 1)
67.
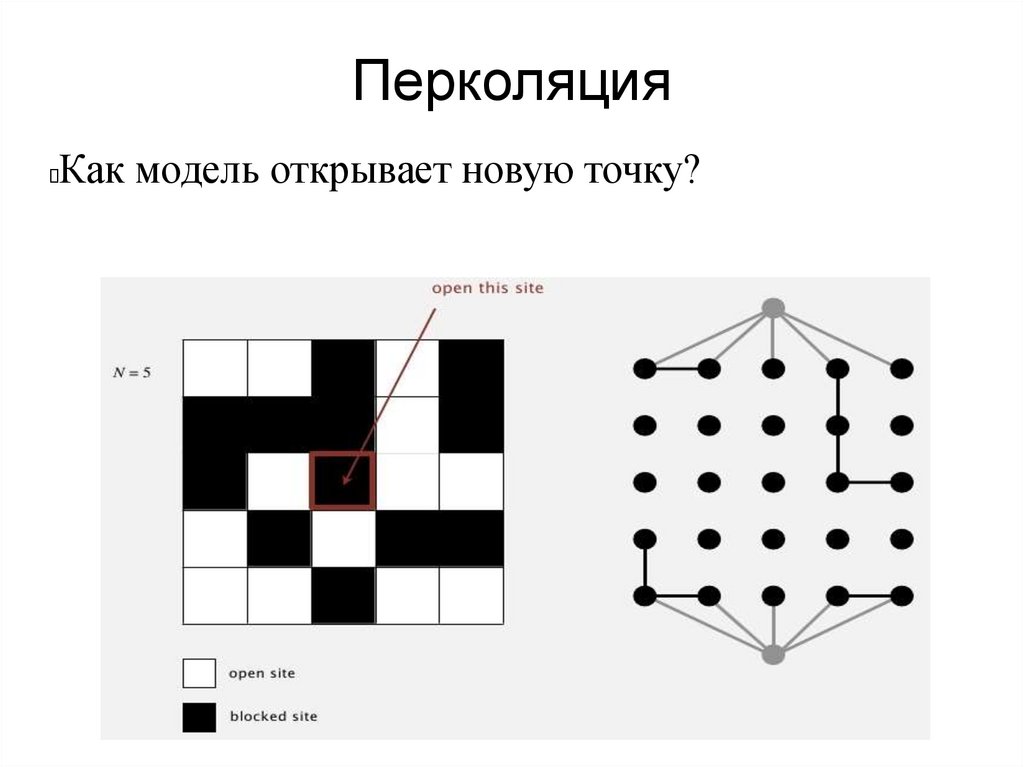
ПерколяцияКак модель открывает новую точку?
68.
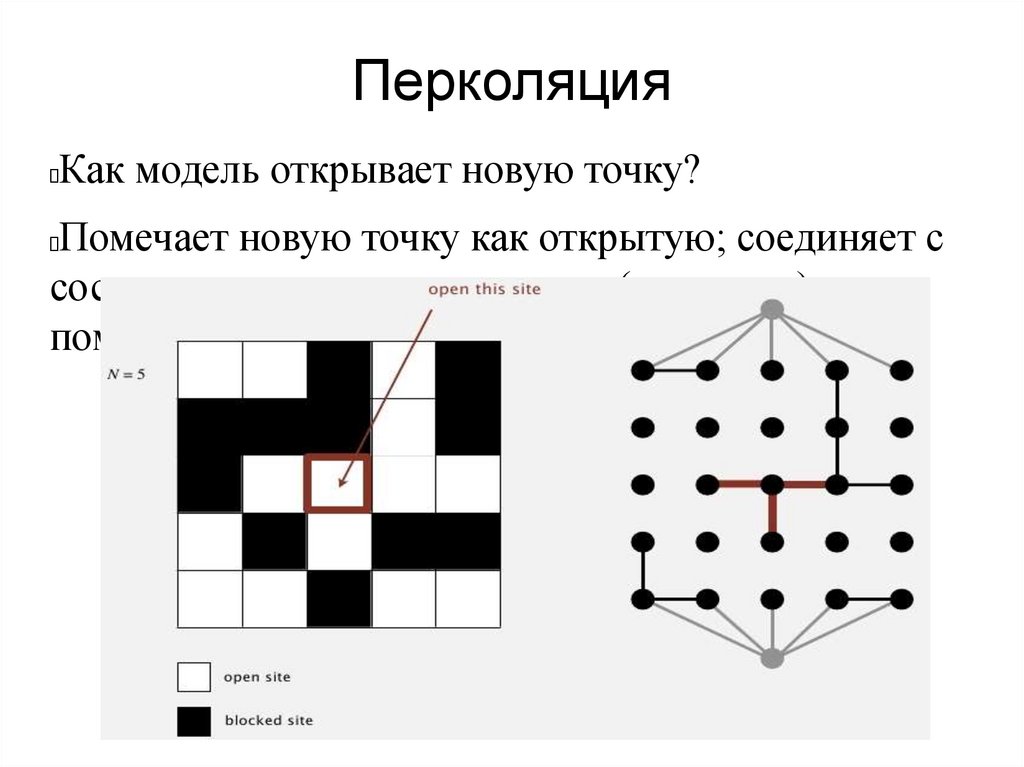
ПерколяцияКак модель открывает новую точку?
Помечает новую точку как открытую; соединяет с
соседними открытыми точками (если есть) при
помощи 4-х вызовов union()
69.
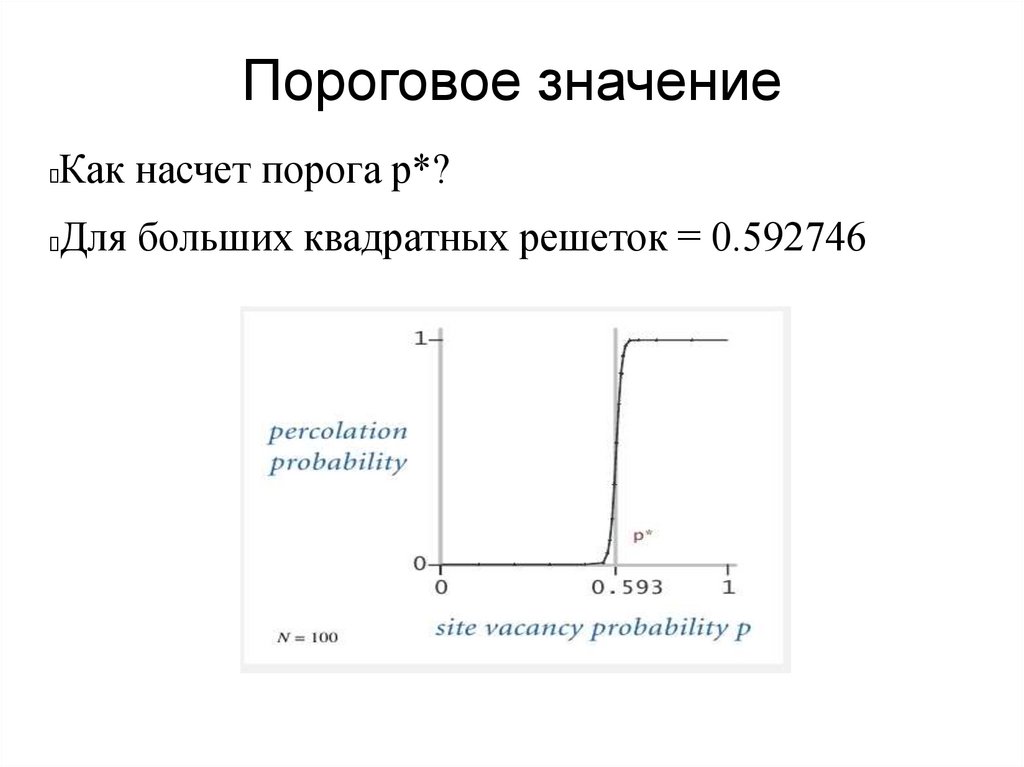
Пороговое значениеКак насчет порога р*?
Для больших квадратных решеток = 0.592746

































 Программирование
Программирование








