Побудова графа

1.

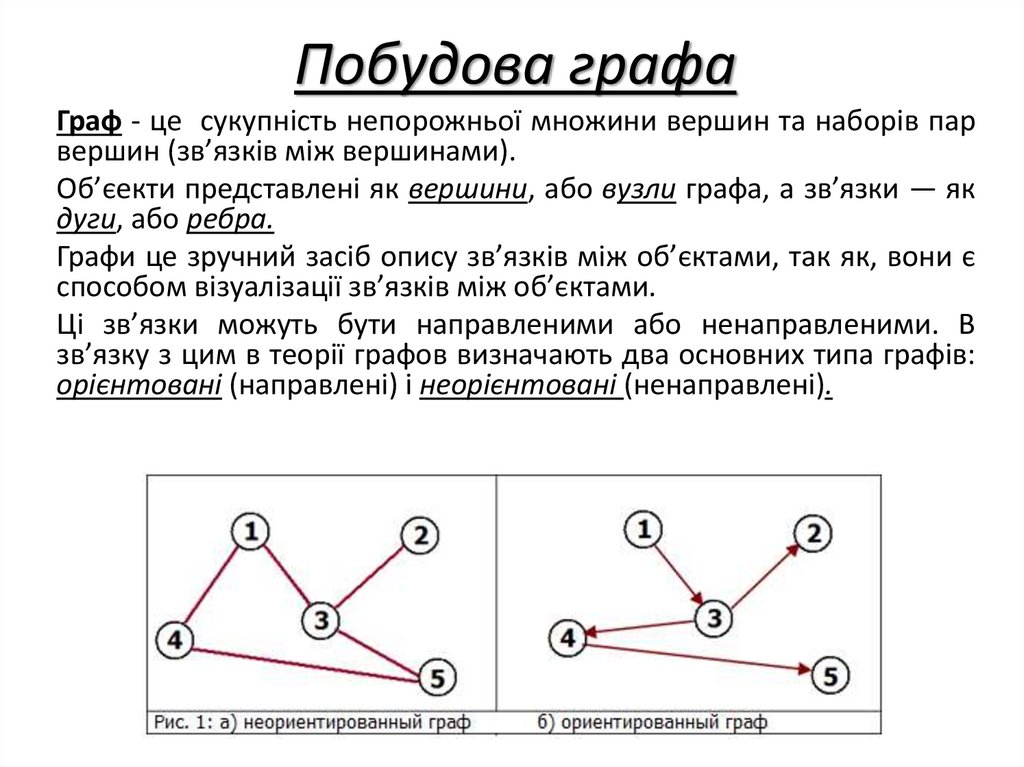
Побудова графа
Граф - це сукупність непорожньої множини вершин та наборів пар
вершин (зв’язків між вершинами).
Об’єекти представлені як вершини, або вузли графа, а зв’язки — як
дуги, або ребра.
Графи це зручний засіб опису зв’язків між об’єктами, так як, вони є
способом візуалізації зв’язків між об’єктами.
Ці зв’язки можуть бути направленими або ненаправленими. В
зв’язку з цим в теорії графов визначають два основних типа графів:
орієнтовані (направлені) і неорієнтовані (ненаправлені).

2.

Характеристика графа
Орієнтирований
граф
увпорядкована пара:
(скорочено
орграф)
–
це
G:=(V, A)
де V — непорожня множина вершин та вузлів,
A — множина (впорядкованих) пар різних ребер, які ще
мають назву дуг або орієнтованих ребер.

3.

Характеристика графа
• напівступень виходу вершини;
• напівступень заходу вершини;
• ступень вершини.
Ступень вершини = напівступень виходу + напівступень заходу
Сток - вершина орграфа, напівступень виходу якої дорівнює
нулю.
Джерело - вершина орграфа, напівступень заходу якої
дорівнює нулю.

4.

Побудова матриці суміжності
Матриця суміжності графа G з кінцевим числом вершин n
(пронумерованих числами від 1 до n) — це квадратна
матриця E розміру n*n, в який eij приймає одно з двох
значень:
1 – якщо від i-ой вершини графа можна дійти до j-ої
вершини,
0 – в протилежному випадку.
Матриця суміжності надає інформацію про всі шляхи
довжини 1 (тобто ребрах) в орграфе. Для пошука шляхів
довжини 2 можна знайти композицію відношення з с самим
собою.

5.

Побудова матриці досяжності
Матриця досяжності простого орієнтованого графа G –
бінарна матриця замикання по транзитивності відношення А
(задається матрицей суміжності графа).
Таким чином, в матриці досяжности зберігається інформация
про існування шляхів між вершинами орграфа.
Найьільш розповсюджений спосіб побудови матриці
досяжності є перемножіння матриць суміжностей можливих
композицій n:

6.

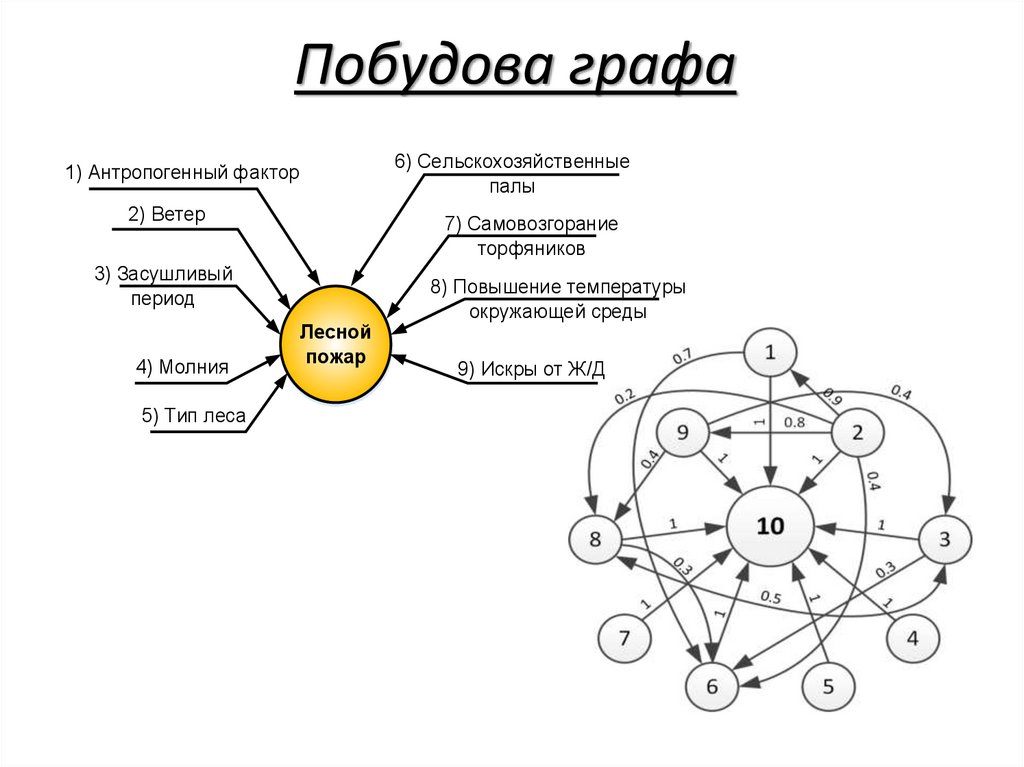
Побудова графа
6) Сельскохозяйственные
палы
1) Антропогенный фактор
2) Ветер
7) Самовозгорание
торфяников
3) Засушливый
период
4) Молния
5) Тип леса
Лесной
пожар
8) Повышение температуры
окружающей среды
9) Искры от Ж/Д

7.

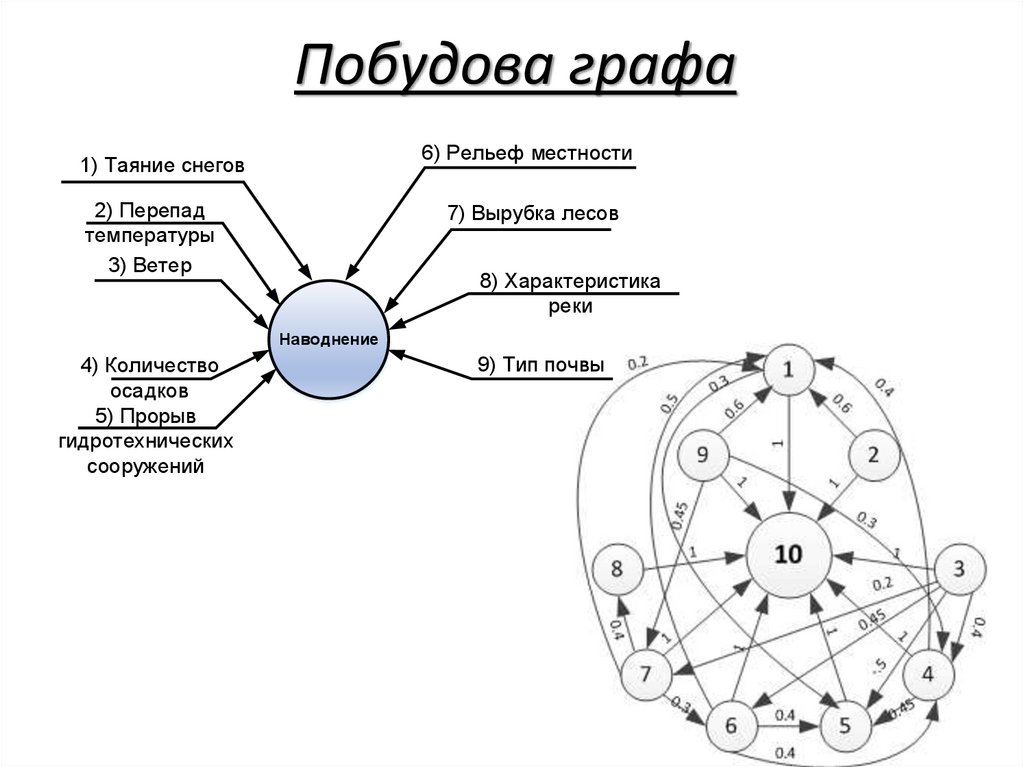
Побудова графа
6) Рельеф местности
1) Таяние снегов
2) Перепад
температуры
3) Ветер
7) Вырубка лесов
8) Характеристика
реки
Наводнение
4) Количество
осадков
5) Прорыв
гидротехнических
сооружений
9) Тип почвы

8.

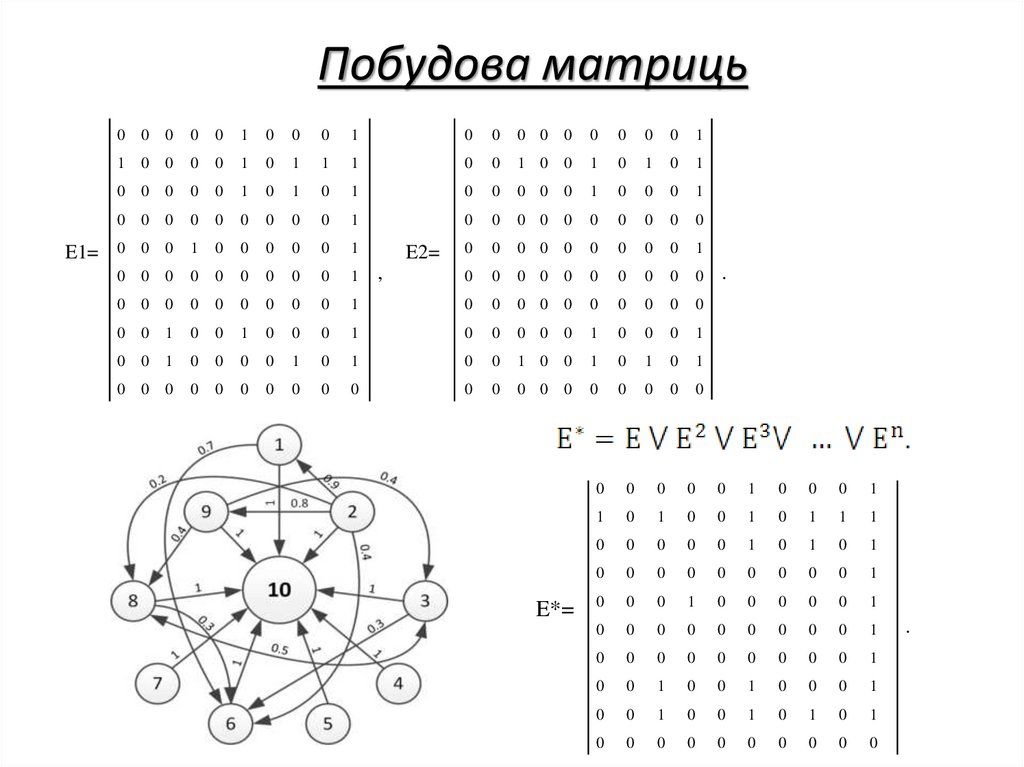
Побудова матриць
E1=
0 0
0
0
0
1
0
0
0
1
0
0
0 0
0
0
0
0
0
1
1 0
0
0
0
1
0
1
1
1
0
0
1 0
0
1
0
1
0
1
0 0
0
0
0
1
0
1
0
1
0
0
0 0
0
1
0
0
0
1
0 0
0
0
0
0
0
0
0
1
0
0
0 0
0
0
0
0
0
0
0 0
0
1
0
0
0
0
0
1
0
0
0 0
0
0
0
0
0
1
0 0
0
0
0
0
0
0
0
1
0
0
0 0
0
0
0
0
0
0
0 0
0
0
0
0
0
0
0
1
0
0
0 0
0
0
0
0
0
0
0 0
1
0
0
1
0
0
0
1
0
0
0 0
0
1
0
0
0
1
0 0
1
0
0
0
0
1
0
1
0
0
1 0
0
1
0
1
0
1
0 0
0
0
0
0
0
0
0
0
0
0
0 0
0
0
0
0
0
0
E2=
,
E*=
.
0
0
0
0
0
1
0
0
0
1
1
0
1
0
0
1
0
1
1
1
0
0
0
0
0
1
0
1
0
1
0
0
0
0
0
0
0
0
0
1
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
0
0
0
1
0
0
1
0
0
1
0
0
0
1
0
0
1
0
0
1
0
1
0
1
0
0
0
0
0
0
0
0
0
0
.

9.

Алгоритми пошука найкоротшого
шляху на графі
Пошук найкоротшого шляху з однієї вершини до всіх інших:
- алгоритм Дейкстри знаходить найкоротший шлях від однієї з вершин графа до
всіх інших. Алгоритм працює тільки для графоі без ребер негативної ваги;
- алгоритм Беллмана — Форда знаходить найкоротший шлях від однієї з вершин
графа до всіх інших у зваженому графі. Вага ребер може бути негативною;
-алгоритм пошука A* знаходить маршрут с найменшою вартістю від однієї
вершини (початкової) до другий (цельової, кінцевої), використовуя алгоритм
пошуку по першому найкращому співпадінню на графі.
Пошук найкоротшого шляху між всіма парами вершин:
- алгоритм Флойда — Уоршелла знаходить найкоротші шляхи між всіма
вершинами зваженого орієнтованого графа;
- алгоритм Джонсона також знаходить найкоротші шляхи між всіма парами
вершин зваженого орієнтованого графа;

10.

Алгоритм Флойда - Уоршелла
Алгоритм полягаєя в наступному:
1)на начальному етапі створюється матриця коефіцієнтів
впливу при взаємодії факторів і об’єкту.
2) матриця D0 визначається заданими величинами кожного її
елемента (u, v), що дорівнює довжині найкоротший дузі, яка
з’єднує вершину u з вершиною v. Якщо в графі вказані
вершини не з’єднуються дугами, то значення d0(u,v)=∞.
3)для всіх u визначити, що d0(u,v)=d0(v,u)=0 .
4) далі для цілого m, що послідовно приймає значення 1...N,
визначаються по елементам матриці Dm-1 елементи Dm :

11.

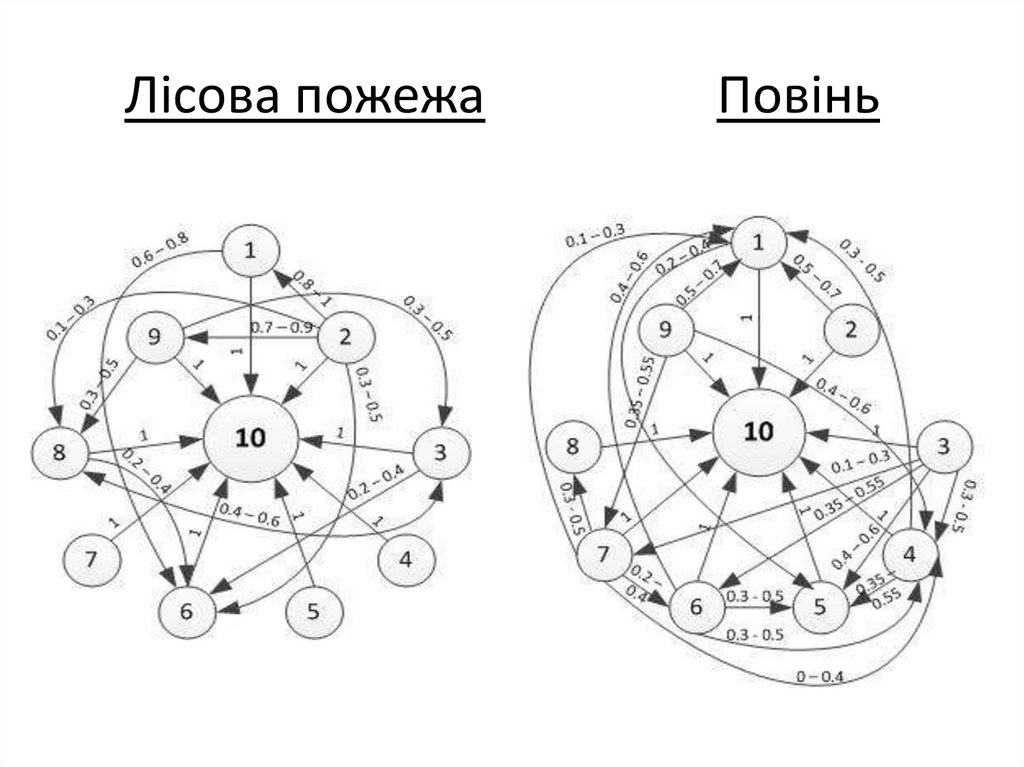
Лісова пожежа
Повінь

12.

D0 =
D1=
0
∞
∞
∞
∞
[0.8 – 1]
∞
∞
∞
1
[0.1 – 0.3]
0
∞
∞
∞
[0.3 – 0.5]
∞
[0.1 – 0.3]
[0.7 – 0.9]
1
∞
∞
0
∞
∞
[0.2 – 0.4]
∞
[0.4 – 0.6]
∞
1
∞
∞
∞
0
∞
∞
∞
∞
∞
1
∞
∞
∞
[0.7 – 0.9]
0
∞
∞
∞
∞
1
∞
∞
∞
∞
∞
0
∞
∞
∞
1
∞
∞
∞
∞
∞
∞
0
∞
∞
1
∞
∞
[0.4 – 0.6]
∞
∞
[0.2 – 0.4]
∞
0
∞
1
∞
∞
[0.3 – 0.5]
∞
∞
∞
∞
[0.3 – 0.5]
0
1
∞
∞
∞
∞
∞
∞
∞
∞
∞
0
0
∞
∞
∞
∞
[0.8 – 1]
∞
[0.1 – 0.3]
0
∞
∞
∞
[0.3 – 0.5]
∞
[0.1 – 0.3] [0.7 – 0.9]
1
∞
∞
0
∞
∞
[0.2 – 0.4]
∞
[0.4 – 0.6]
∞
1
∞
∞
∞
0
∞
∞
∞
∞
∞
1
∞
∞
∞
[0.7 – 0.9]
0
∞
∞
∞
∞
1
∞
∞
∞
∞
∞
0
∞
∞
∞
1
∞
∞
∞
∞
∞
∞
0
∞
∞
1
∞
∞
[0.4 – 0.6]
∞
∞
[0.2 – 0.4]
∞
0
∞
1
∞
∞
[0.3 – 0.5]
∞
∞
∞
∞
[0.3 – 0.5]
0
1
∞
∞
∞
∞
∞
∞
∞
∞
∞
0
∞
Матрица интервалов D2 соответствует матрице D1
∞
.
1
.

13.

D3=
0
∞
∞
∞
∞
[0.8 – 1]
∞
∞
∞
1
[0.1 – 0.3]
0
∞
∞
∞
[0.3 – 0.5]
∞
[0.1 – 0.3]
[0.7 – 0.9]
1
∞
∞
0
∞
∞
[0.2 – 0.4]
∞
[0.4 – 0.6]
∞
1
∞
∞
∞
0
∞
∞
∞
∞
∞
1
∞
∞
∞
[0.7 – 0.9]
0
∞
∞
∞
∞
1
∞
∞
∞
∞
∞
0
∞
∞
∞
1
∞
∞
∞
∞
∞
∞
0
∞
∞
1
∞
∞
[0.4 – 0.6]
∞
∞
[0.2 – 0.4]
∞
0
∞
1
∞
∞
[0.3 – 0.5]
∞
∞
[0.5 – 0.9]
∞
[0.3 – 0.5]
0
1
∞
∞
∞
∞
∞
∞
∞
∞
∞
0
.
Матриці інтервалів D4, D5, D6, D7 відповідають матриці D3
Алгоритм закінчується отриманням матриці інтервалів
всіх найкоротших шляхів Dn , N - число вершин графа:
Dn=
0
∞
∞
∞
∞
[0.8 – 1]
∞
∞
∞
1
[0.1 – 0.3]
0
[0.5 – 0.9]
∞
∞
[0.3 – 0.5]
∞
[0.1 – 0.3]
[0.7 – 0.9]
1
∞
∞
0
∞
∞
[0.2 – 0.4]
∞
[0.4 – 0.6]
∞
1
∞
∞
∞
0
∞
∞
∞
∞
∞
1
∞
∞
∞
[0.7 – 0.9]
0
∞
∞
∞
∞
1
∞
∞
∞
∞
∞
0
∞
∞
∞
1
∞
∞
∞
∞
∞
∞
0
∞
∞
1
∞
∞
[0.4 – 0.6]
∞
∞
[0.2 – 0.4]
∞
0
∞
1
∞
∞
[0.3 – 0.5]
∞
∞
[0.5 – 0.9]
∞
[0.3 – 0.5]
0
1
∞
∞
∞
∞
∞
∞
∞
∞
∞
0
.