Похожие презентации:
Логарифмическая функция, её свойства и график
1.
Логарифмическаяфункция, её
свойства и график
2.
На промежутке (0; +∞) определенафункция,
обратная
к
функции
у=ax (a > 0, a ≠ 1).
y = loga x
Эта функция называется
логарифмической
3.
4.
1)1)
;
2)
;
3) не является ни четной,
ни нечетной;
4) не ограничена;
5) не имеет ни
наибольшего, ни
наименьшего значений;
6) убывает на (0;+∞);
7) выпукла вниз;
8) непрерывна;
9) вертикальная
асимптота x=0.
5.
2)1)
;
2)
;
3) не является ни
четной, ни нечетной;
4) не ограничена;
5) не имеет ни
наибольшего, ни
наименьшего значения;
6) возрастает на (0;+∞);
7) выпукла вверх;
8) непрерывна;
9) вертикальная
асимптота x=0.
6.
а >10< а <1
если
если
то
то
7.
№1.у = log 3 х
х
у
1
9
-2
1
3
-1
у = log 1 х
3
1
3
9
х
0
1
2
у
1
9
2
1
3
1
1
3
9
0
-1
-2
8.
Т.к. 3>1 ито
6 5
> ,
5 6
>
Т.к.
то
1
0< <1
2
>
и е<π,
9.
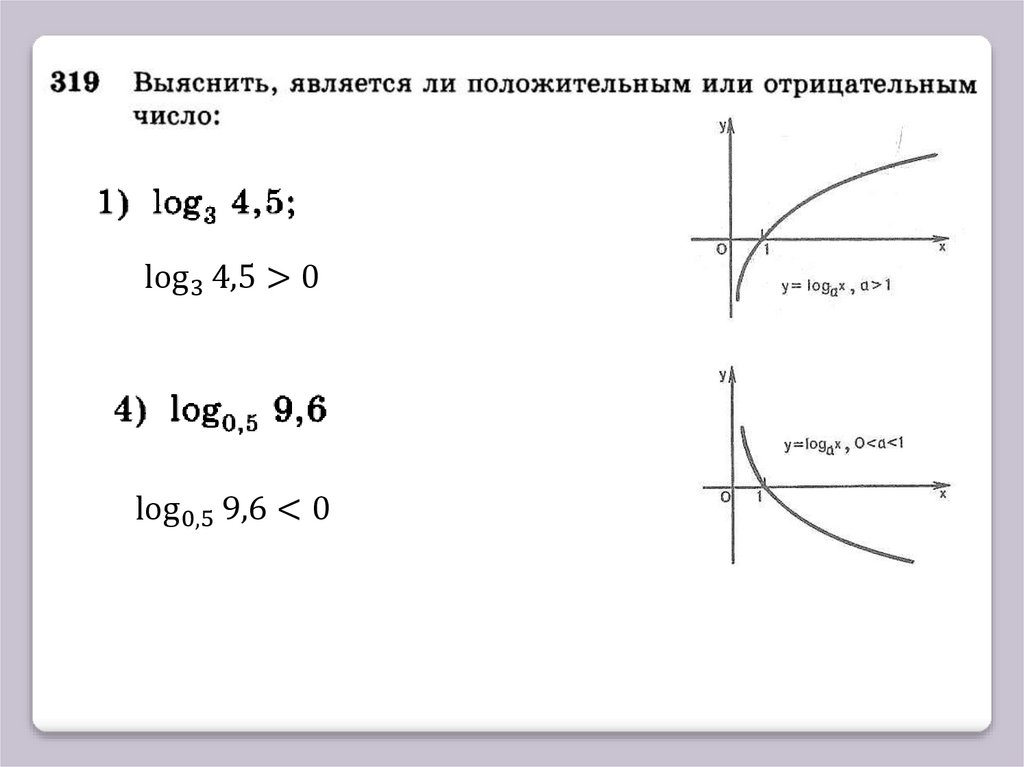
log 3 4,5 > 0log 0,5 9,6 < 0
10.
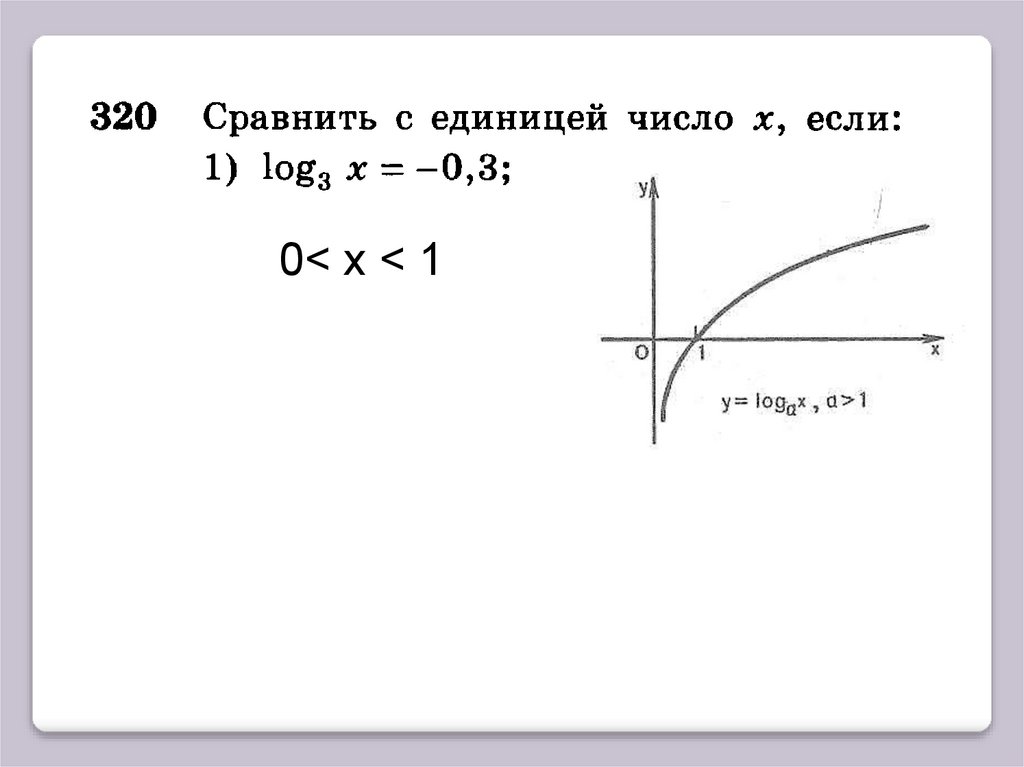
0< х < 111.
Т.к. 0 < 0,075 < 1, то функцияубывающая
Т.к. 10 > 1, то функция
возрастающая
12.
≈ 1,6≈ −1,7
≈ 2,3
≈ −0,5
13.
ОДЗ: 3х – 2 >02
х>
3
Ответ: 3
14.
ОДЗ: х > 0Т.к. 2 > 1, то
Ответ: (0; 8)
15.
ОДЗ: х > 01
Т.к. 0< <1, то
3
Ответ: [9; +∞)


















 Математика
Математика








