Похожие презентации:
Механика. Молекулярная физика
1.
КУРС ФИЗИКИII-й семестр
Механика. Молекулярная
физика
Тема 2
Динамика
2024 г.
1
2.
Содержание1. Законы Ньютона: область применимости
2. Первый закон Ньютона. Инерциальные и
неинерциальные системы отсчёта
3. Второй закон Ньютона. Импульс тела
4. Третий закон Ньютона. Закон сохранения импульса
5. Центр масс
6. Принцип относительности Галилея. Преобразования
Галилея. Закон сложения скоростей в классической
механике. Второй закон Ньютона для неинерциальных
систем отсчёта
7. Виды сил
8. Закон всемирного тяготения. Сила тяжести. Вес тела
9. Сила трения
10. Силы упругости
2
3.
Содержание11. Работа
12. Мощность
13. Энергия. Закон сохранения энергии
14. Кинетическая энергия
15. Потенциальная энергия в поле тяготения
16. Потенциальная энергия упругой
деформации
17. Графическое представление энергии
18. Признак потенциальности поля.
Консервативные силы. Диссипативные силы
19. Связь между консервативной силой и
потенциальной энергией
3
4.
Законы Ньютона – постулатыявляются обобщением большого
количества опытных данных
«Что такое время,
пространство, место
и движение, я не
объясняю, так как это
известно всем»
Сэр Исаа́к Нью́то́н (Sir Isaac Newton)
(1643 —1727)
английский физик, математик и астроном,
основатель классической механики.
Автор фундаментального труда
«Математические начала натуральной
философии»,
в котором он изложил закон
всемирного тяготения
и три закона механики, ставшие основой
классической механики.
4
5.
16891687
Сэр Исаа́к Нью́то́н (Sir Isaac Newton)
(1643 —1727)
английский физик, математик и астроном,
основатель классической механики.
Автор фундаментального труда
«Математические начала натуральной
философии»,
в котором он изложил закон
всемирного тяготения
и три закона механики, ставшие основой
классической механики.
5
6.
Законы Ньютона – постулатыявляются обобщением большого
количества опытных данных
Для случая малых скоростей (v << c) и макротел
Первый закон Ньютона
Всякому телу свойственно сохранять
состояние равномерного прямолинейного
движения или покоя, пока и поскольку
другие тела не вынудят его изменить это
состояние
6
7.
Первый закон НьютонаСкорость
любого
тела
остаётся
постоянной (в частности, равной нулю), пока
воздействие на это тело со стороны других
тел не вызовет её изменения.
Инерция — свойство тел оставаться в некоторых
системах отсчёта в состоянии покоя или равномерного
прямолинейного движения в отсутствии или при взаимной
компенсации внешних воздействий.
Поэтому первый закон Ньютона называют законом инерции.
Иногда инерцию называют инертностью, это не правильно, т.к.
инертностью называется способность тела воспринимать внешнее
7
воздействие.
8.
Первый закон НьютонаПервый закон Ньютона выполняется
инерциальных системах отсчёта.
в
Инерциальной системой отсчёта является
такая система отсчёта, относительно которой
материальная точка, свободная от внешних
воздействий, либо покоится, либо движется
прямолинейно и равномерно (т.е. с постоянной
скоростью).
Таким образом, первый закон Ньютона
утверждает существование инерциальных
систем отсчёта.
8
9.
Первый закон НьютонаСущность первого закона Ньютона
может быть сведена к трём
основным положениям:
• все тела обладают свойствами
инерции;
• существуют инерциальные системы
отсчёта, в которых выполняется
первый закон Ньютона;
• движение относительно.
9
10.
Второй закон НьютонаF
Сила – количественная мера воздействия
одного тела на другое
Если на тело действуют несколько сил, то их
совместное действие выражается векторной суммой
всех сил, которая называется равнодействующей
m
Масса - количественная мера инертности тела
Инертность - способность тела воспринимать
воздействие других тел
Масса – величина аддитивная (масса тела равна сумме
масс частей, составляющих это тело).
10
11.
Второй закон НьютонаFk
k
a
m
Ускорение тела прямо
пропорционально
равнодействующей всех
сил, приложенных к телу, и
обратно пропорционально
массе тела
Второй закон Ньютона можно сформулировать в иной форме,
которая называется импульсной
Произведение массы тела на
его
скорость
называется
импульсом (или количеством
движения) тела p
p m
11
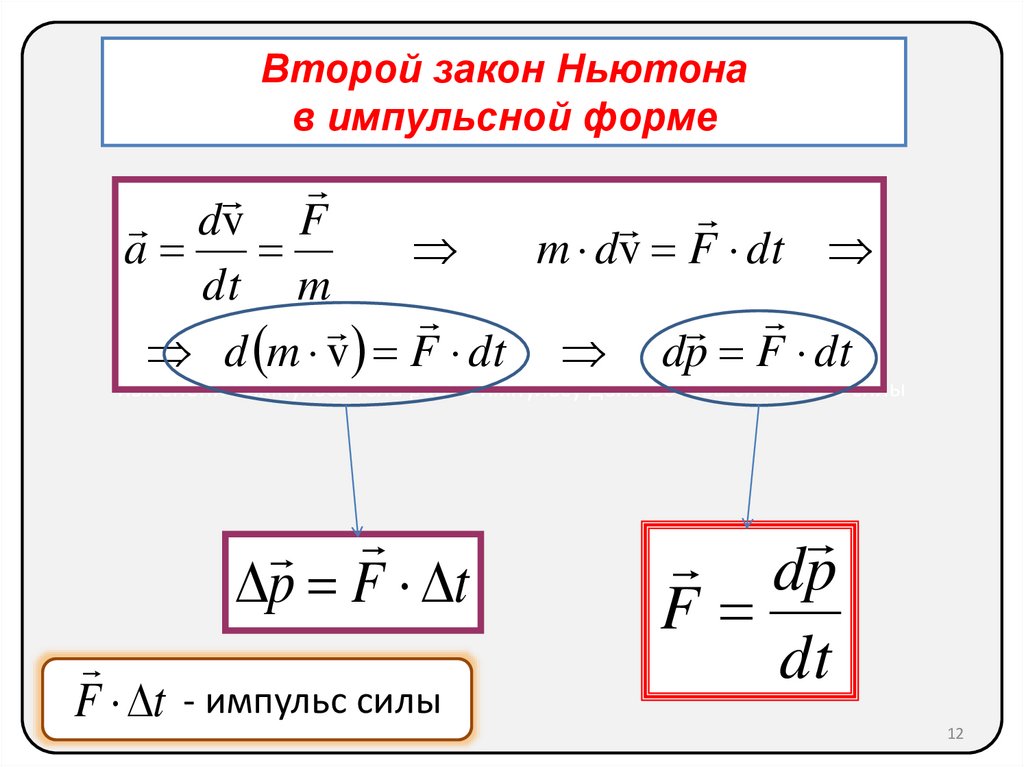
12.
Второй закон Ньютонав импульсной форме
dv F
a
m dv F dt
dt m
d m v F dt dp F dt
изменение импульса тела равно импульсу действовавшей на тело силы
p F t
F t - импульс силы
dp
F
dt
12
13.
Второй закон Ньютонав импульсной форме
p F t
Изменение импульса тела
равно импульсу
действовавшей на тело силы
изменение импульса тела равно импульсу действовавшей на тело силы
Изменение количества движения
dp пропорционально приложенной
движущей силе и происходит по
F
направлению той прямой, по
dt которой эта сила действует.
(И. Ньютон, 1687)
13
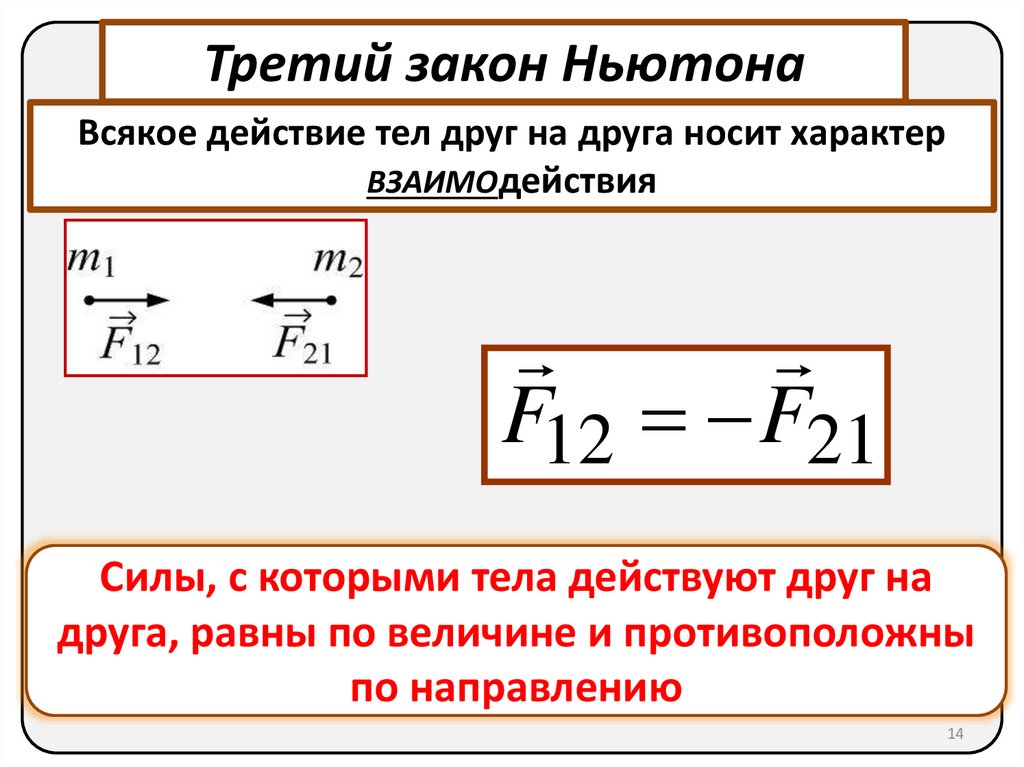
14.
Третий закон НьютонаВсякое действие тел друг на друга носит характер
ВЗАИМОдействия
F12 F21
Силы, с которыми тела действуют друг на
друга, равны по величине и противоположны
по направлению
14
15.
Третий закон Ньютона3-й Закон Ньютона в общем случае является
универсальным законом взаимодействий:
Всякое действие вызывает равное по величине
противодействие
Cилы, связанные по 3 закону Ньютона,
приложены
к
различным
телам
и,
следовательно, никогда не могут начинаться
в одной точке, но они всегда:
- направлены вдоль одной прямой;
- это силы одной природы.
15
16.
Замкнутая системаМеханическая
система
называется
замкнутой
(или
изолированной), когда на неё не действуют другие (внешние) тела, или
когда действие этих тел скомпенсировано.
Для замкнутой системы равнодействующая всех внешних сил
тождественно равна нулю
Строго говоря, каждая реальная система тел всегда не замкнута, т.к. подвержена, как
минимум воздействию гравитационных сил. Однако если внутренние силы гораздо больше
внешних, то такую систему можно считать замкнутой (например – Солнечная система).
Для замкнутой системы равнодействующая всех сил
действующих между телами внутри системы равна нулю (по III-му
закону Ньютона)
Рассмотрим замкнутую систему двух взаимодействующих тел 1 и 2
dp1 F12 dt
dp2 F21 dt
т.к., по III-му закону Ньютона:
d p1 p2 F12 F21 dt 0
F12 F21 p1 p2 const16
17.
Закон сохранения импульсаdp
В замкнутой системе
F 0,
полный импульс
d t
сохраняется
p const
Полный импульс системы сохраняется, даже если
есть внешние силы, но они скомпенсированы
внеш.
Fk 0
pi const
k
В проекциях:
i
внеш.
F
kx 0
k
p const
ix
i
17
18.
Галилео Галилей –первый физик, основатель
научного метода
Принцип относительности: «Дайте движение
кораблю, и притом с какой угодно скоростью;
тогда (если только движение его будет
равномерным, а не колеблющимся туда и сюда) вы
не заметите ни малейшей разницы»
Закон инерции: «…если бы все сопротивления были
уничтожены, то его (тела) движение было бы
вечно равномерным, если бы плоскость
простиралась в бесконечность» («неистребимо
запечатлённое движение»).
Законы свободного падения: скорость нарастает
пропорционально времени, а путь —
пропорционально квадрату времени.
Научный метод – наблюдение, размышление и опыт
ГАЛИЛЕЙ, ГАЛИЛЕО (Galilei, Galileo)
(1564–1642)
итальянский физик,
механик и астроном.
Основоположник экспериментальноматематического
метода исследования природы
В 1992 папа Иоанн Павел II объявил
решение суда инквизиции ошибочным
и реабилитировал Галилея.
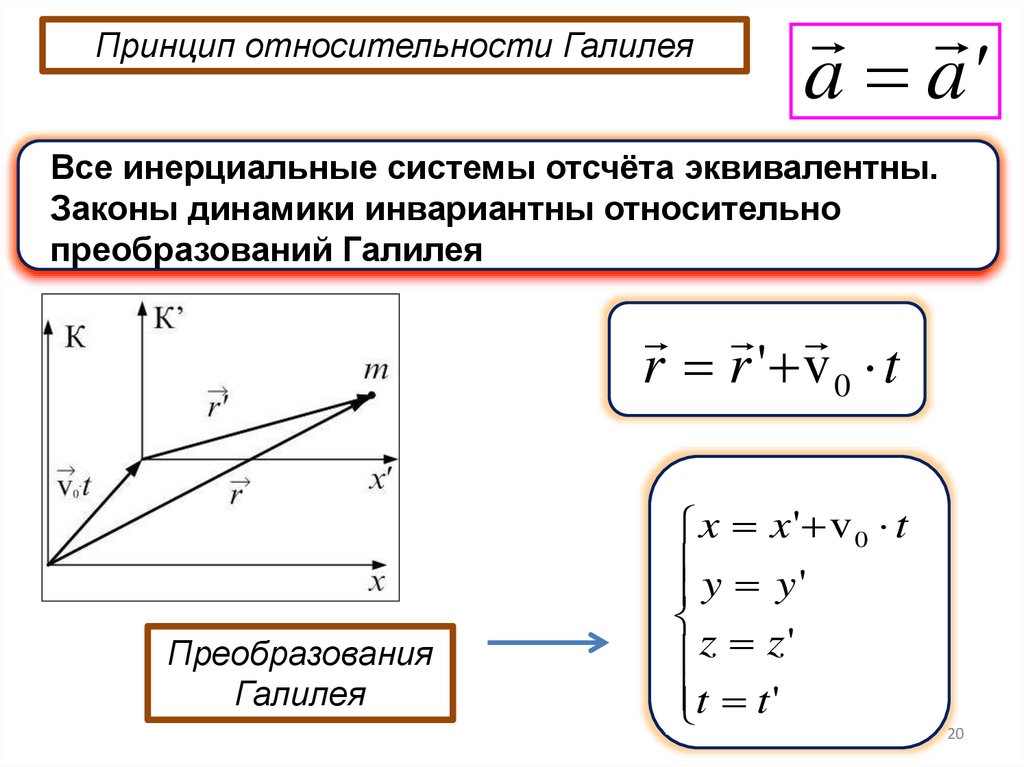
19.
Принцип относительности Галилеяr r ' v 0 t
dr dr ' dt
v0
dt dt
dt
v v' v
Теорема сложения скоростей
d v d v'
0
dt
dt
v
абс.
v
отн.
0
v
пер.
a a'
19
20.
Принцип относительности Галилеяa a'
Всеинерциальные
инерциальные
системы
эквивалентны.
все
системы
отсчётаотсчёта
эквивалентны.
Или: законы
Законы динамики
инвариантны
динамики
инвариантны
относительно относительно
преобразований Галилея
преобразований Галилея
r r ' v 0 t
Преобразования
Галилея
x x ' v 0 t
y y'
z z'
t t '
20
21.
Система тел. Центр массЦентром инерции или центром масс
системы материальных точек называют такую
точку С, радиус-вектор которой:
m r 1
r
m r,
m
m
n
i 1
i
c
n
где m i 1 mi
системы.
i 1
n
i
n
i 1
i
i
Это определение
центра масс
i
– общая масса системы, n – число точек
drc 1
dri 1
vc
mi mi v i
dt m i
dt m i
p m v с mi v i
i
– импульс системы тел равен произведению массы
системы на скорость её центра масс.
21
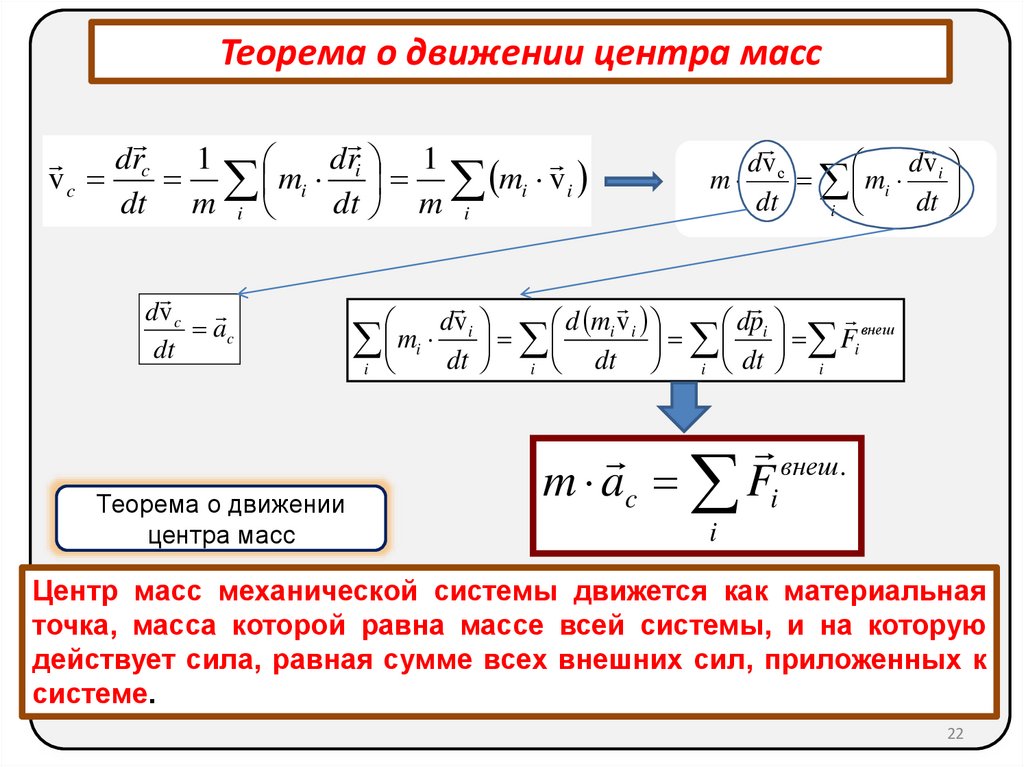
22.
Теорема о движении центра массdrc 1
d
r
1
i
vc
mi mi v i
dt m i
dt m i
dv c
ac
dt
Теорема о движении
центра масс
dv с
dv i
m
mi
dt
dt
i
внеш
dv i
d mi v i
dpi
i mi dt i dt i dt i Fi
внеш.
m ac Fi
i
Центр масс механической системы движется как материальная
точка, масса которой равна массе всей системы, и на которую
действует сила, равная сумме всех внешних сил, приложенных к
системе.
22
23.
Международная система единиц (СИ)В системе СИ семь основных единиц
м – метр,
кг – килограмм,
с – секунда,
А – ампер,
К – кельвин,
кд – кандела (единица силы света),
кмоль – единица количества вещества.
Остальные единицы производные,
они получаются из физических законов (формул) связывающих
их с основными единицами. Например из второго закона
Ньютона производная единица силы - Ньютон (Н)
1 кг·м/с2 = 1 Н.
23
24.
Виды силСила описывает действие
Действие носит характер взаимодействия
Возникновение силы –
проявление взаимодействия
В природе существует 4 вида фундаментальных взаимодействий:
Гравитационное
Электромагнитное
Сильное (ядерные силы)
Слабое (превращения элементарных частиц)
Все виды сил (трения, упругости, вязкости,
поверхностного натяжения и т.д.) – это проявления
фундаментальных взаимодействий
24
25.
Виды силВ природе существует 4 вида фундаментальных взаимодействий:
Гравитационное
Электромагнитное
Сильное (ядерные силы)
Слабое (превращения элементарных частиц)
Все виды сил (трения, упругости, вязкости,
поверхностного натяжения и т.д.) – это проявления
фундаментальных взаимодействий
25
26.
Виды и категории сил вприроде
фундаментальные взаимодействия
все виды сил – это
Гравитационное
проявления
Электромагнитное
фундаментальных
Сильное
взаимодействий
Слабое
Все виды сил (трения, упругости, вязкости, поверхностного натяжения и т.д.) – это
проявления фундаментальных взаимодействий
В классической механике проявляют себя
Гравитационные и электромагнитные силы
m1m2
F γ 2 ,
r
F k
,
r
1
0
2
2
26
27.
1. Сила тяжести и вес телаСилы тяжести – сила, с которой все тела
притягиваются к Земле.
Вблизи поверхности Земли все тела падают с
одинаковым ускорением – ускорением свободного падения g
Fтяж. mg
M m
R h 2
Если подвесить тело или положить его на опору, то сила тяжести уравновесится
силой – которую называют реакцией опоры или подвеса (силой натяжения) R.
Действуют на тело.
R это N или T
P
P
27
28.
PP
По третьему закону Ньютона тело действует
на подвес или опору с силой P
Вес тела – сила с которой
действует на опору или подвес
тело
Вес и сила тяжести приложены к разным точкам:
вес к подвесу или опоре, сила тяжести – к самому телу.
28
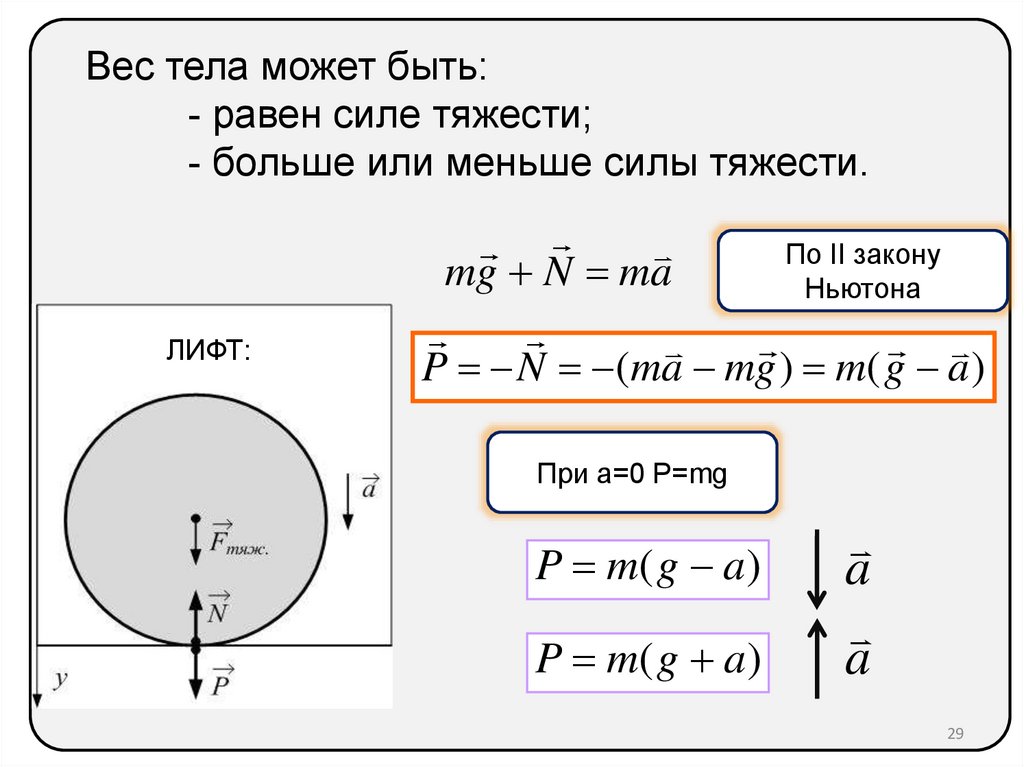
29.
Вес тела может быть:- равен силе тяжести;
- больше или меньше силы тяжести.
ЛИФТ:
По II закону
mg N ma
Ньютона
P N (ma mg ) m( g a )
При а=0 P=mg
P m( g a )
P m( g a )
a
a
29
30.
Закон всемирного тяготенияМежду любыми двумя материальными точками с массами
m1 и m2 действует сила взаимного притяжения (сила
гравитации), пропорциональная произведению масс и
обратно пропорциональная квадрату расстояния между
ними.
В векторном виде
m1 m 2
F12 = G 2 e12
r
Гравитационная сила - центральная сила, она направлена
вдоль линии, соединяющей две частицы.
Следовательно, формула
верна только
- Для материальных точек
- Для шарообразных тел
31.
Гравитационная постоянная (G)G = 6,67430(15)·10−11 м3·с−2·кг−1, или Н·м²·кг−2
Впервые измерил G Генри Кавендиш в 1797 г.. с
помощью крутильных весов
G – мировая постоянная
Ускорение свободного падения g различно на различных
планетах
M пл. m
Fтяг.пл. ma mg пл. G
2
Rпл.
M пл.
g пл. G
2
Rпл.
Тождественность инертной и гравитационной масс
Эйнштейн положил в основу общей теории
относительности.
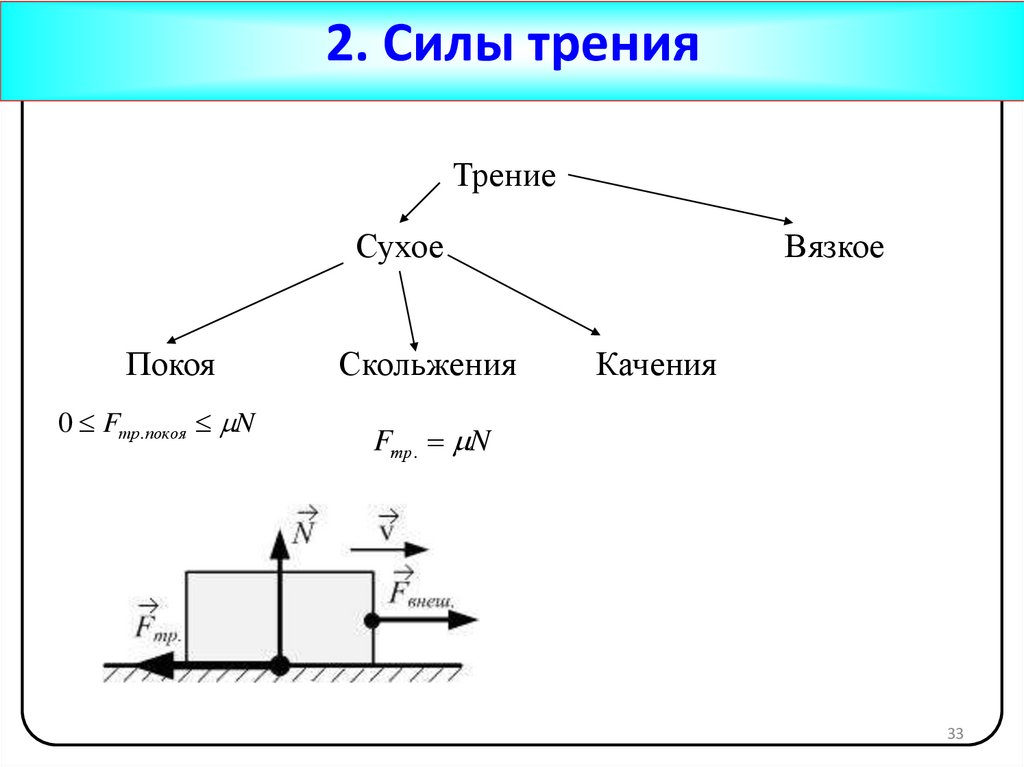
32.
2. Силы тренияТЕРМИНЛОГИЯ:
Трение подразделяется на внешнее и внутреннее.
Внешнее трение возникает при относительном перемещении
двух соприкасающихся твердых тел (трение скольжения или трение
покоя).
Внутреннее
трение
наблюдается
при
относительном
перемещении частей одного и того же сплошного тела (например,
жидкость или газ).
Различают сухое и жидкое (или вязкое) трение.
Трение
Вязкое
(жидкое)
Сухое
Покоя
Скольжения
Качения
32
33.
2. Силы тренияТрение
Сухое
Покоя
0 Fтр.покоя N
Скольжения
Вязкое
Качения
Fтр. N
33
34.
2. Силы тренияПричины возникновения трения скольжения и покоя
1. Шероховатости поверхностей.
Когда мы пытаемся двигать одно тело по
поверхности другого, или когда происходит
скольжение неровности цепляются друг за
друга и возникает сила препятствующая
движению. При шлифовке поверхности эта
сила уменьшается.
2. Взаимное притяжение молекул
соприкасающихся тел.
Играет заметную роль при хорошо
отшлифованных поверхностях.
Роль смазки – замена сухого трения
на вязкое
34
35.
Подействуемна
тело,
внешней силой F постепенно
увеличивая ее модуль. Вначале
брусок
будет
оставаться
неподвижным, значит внешняя
сила
уравновешивается
некоторой силой Fтр это и есть
сила трения покоя.
Когда
модуль
внешней
силы,
а
следовательно, и модуль
силы
трения
покоя
превысит значение F0, тело
начнет скользить по опоре
– трение покоя Fтр.пок.
сменится
трением
скольжения Fтр.ск
F0 – максимальная Fтр.пок. = Fтр.ск.
35
36.
Установлено, что максимальная сила тренияпокоя не зависит от площади соприкосновения тел и
приблизительно пропорциональна модулю силы
нормального давления N
F μ N,
0
0
μ0 – коэффициент трения – зависит от природы и
μ0– зависит от природы
и состоянияповерхностей.
трущихся поверхностей.
состояния
трущихся
0 Fтр. покоя N
Для силы трения скольжения:
F μN
тр.
36
37.
Трение каченияТрение качения – трение,
возникающее при качении одного
тела по поверхности другого.
Сила трения качения возникает
при качении тел цилиндрической
или шарообразной формы по
гладкой поверхности вследствие
деформации соприкасающихся
поверхностей.
Закон Кулона:
K
Fтр. кач. N
R
Здесь k – коэффициент трения качения, зависящий от
материала контактирующих тел, состояния их
поверхности и других факторов; N – сила нормального
давления, R радиус катящегося цилиндрического
(шарообразного тела).
37
38.
Вязкое трениеПомимо собственно силы трения, при движении вязкой среде
возникают и силы сопротивления среды.
При малых скоростях:
Fтр k1v
При больших скоростях:
2
Fтр k2 ev
Зависимость силы трения
от скорости скольжения
Коэффициент k1 зависит от формы и размеров тела, состояния его
поверхности и от вязкости среды.
Коэффициент k2 зависит от формы и размеров тела.
39.
3. Силы упругости. ДеформацииДеформациями называются изменения размеров и
формы тел под действием внешних сил.
Если после прекращения действия внешних сил
восстанавливаются прежние форма и размеры тела,
то
деформация
называется
упругой,
если
воостановления не происходит - пластической
В
деформированном
теле
возникают
упругие
силы,
уравновешивающие внешние
силы.
1
x Fвн. ,
k
F kx.
упр.
k – жесткость пружины.
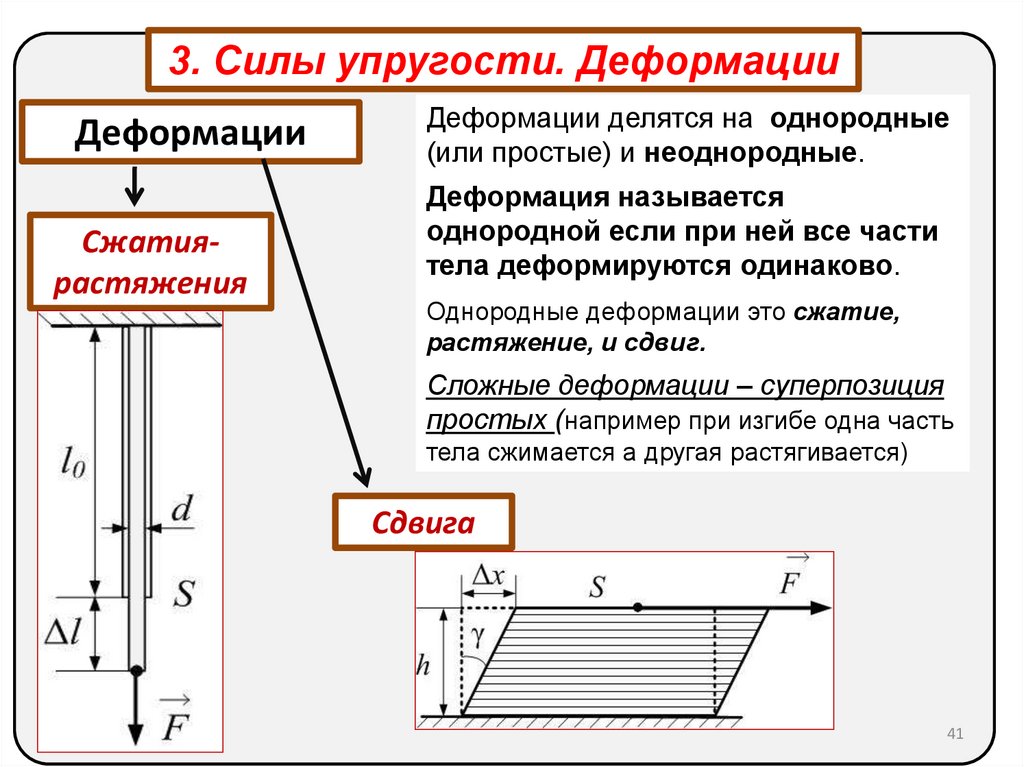
40.
3. Силы упругости. ДеформацииДеформации
Сжатиярастяжения
Деформации упругие и пластические
Упругие деформации исчезают, а
пластические (неупругие) остаются
после окончания действия
приложенных сил.
При пластической деформации происходит
разрыв некоторых межмолекулярных
связей, в результате этого изменённая
форма тела (остаточная деформация)
сохраняется и после снятия нагрузки
Сдвига
40
41.
3. Силы упругости. ДеформацииДеформации
Сжатиярастяжения
Деформации делятся на однородные
(или простые) и неоднородные.
Деформация называется
однородной если при ней все части
тела деформируются одинаково.
Однородные деформации это сжатие,
растяжение, и сдвиг.
Сложные деформации – суперпозиция
простых (например при изгибе одна часть
тела сжимается а другая растягивается)
Сдвига
41
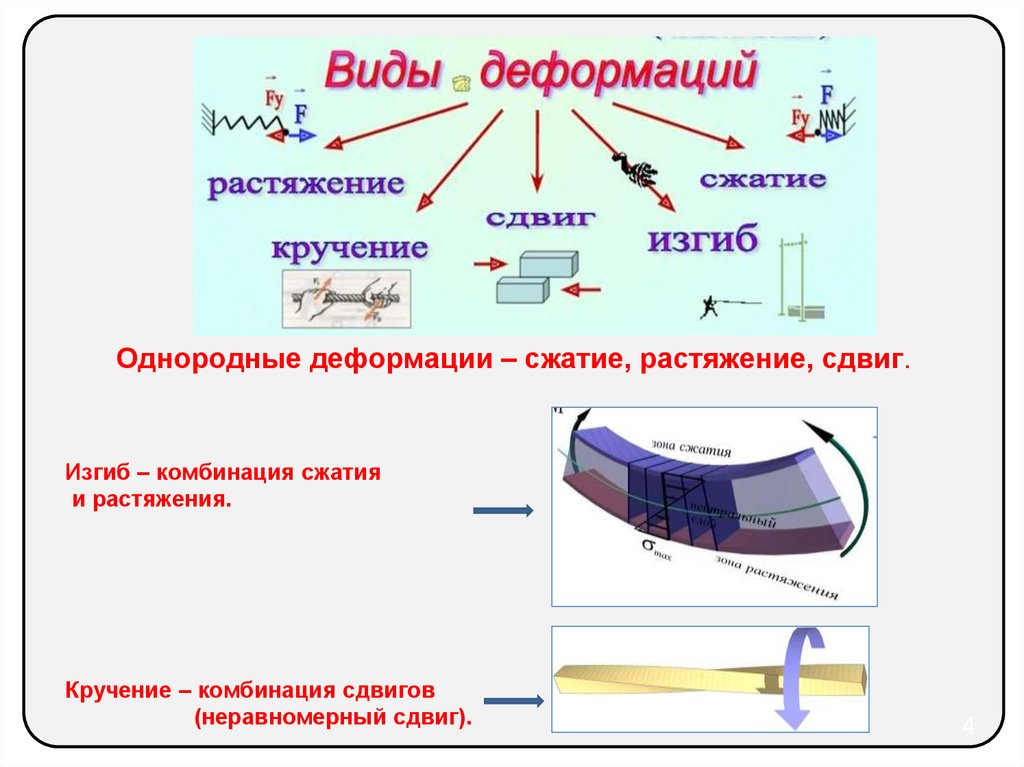
42.
Однородные деформации – сжатие, растяжение, сдвиг.Изгиб – комбинация сжатия
и растяжения.
Кручение – комбинация сдвигов
(неравномерный сдвиг).
4
43.
Деформация сжатия-растяженияF
S
dF
dS
||
l
l
Нормальное механическое
напряжение
Н Па
м2
Относительная продольная
деформация
1
Закон Гука в локальной форме
E ||
E - модуль Юнга
F S E || S E
l
ES
S
l k l
l
l
E Н2 Па
м
k
ES
l
43
44.
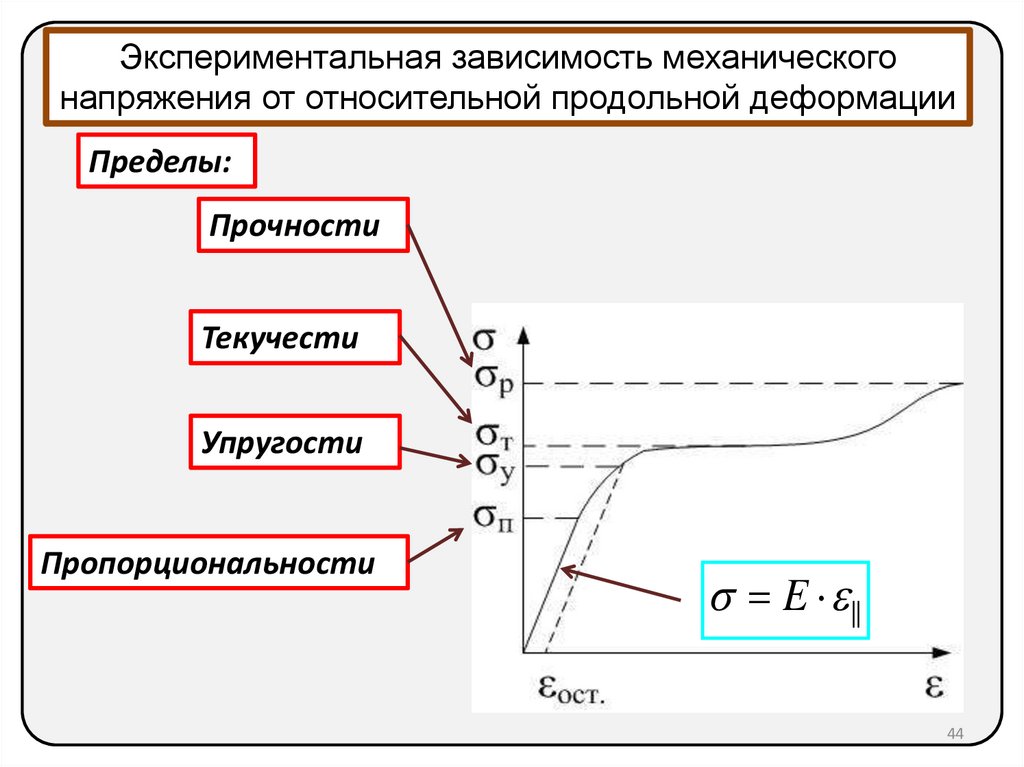
Экспериментальная зависимость механическогонапряжения от относительной продольной деформации
Пределы:
Прочности
Текучести
Упругости
Пропорциональности
E ||
44
45.
4. Силы инерции.Неинерциальные системы отсчета.
Силы
инерции
обусловлены
не
взаимодействием тел, а свойствами самих
неинерциальных систем отсчета.
На силы инерции законы Ньютона не
распространяются.
Но!
Можно
в
неинерциальной
системе
воспользоваться законами Ньютона, если ввести
силы инерции.
Силы
инерции
вводят
специально,
чтобы
воспользоваться
уравнениями
Ньютона
в
неинерциальной системе.
45
46.
Силы инерции при поступательномдвижении неинерциальной системы отсчета.
обозначения:
– Введем
a ' ускорение тела относительно неинерциальной системы;
–
ускорение
неинерциальной
системы
относительно
a
инерциальной (относительно Земли).
Тогда ускорение тела относительно инерциальной системы:
a a a '.
Ускорение в инерциальной системе можно
выразить через второй закон Ньютона
F
a a'
m
47.
Силы инерции при поступательномдвижении неинерциальной системы отсчета.
F
a a'
m
F
a a .
m
*
можно (формально) представить в соответствии с законом
aНьютона
F Fин
a
,
m
m
Fин – сила, направленная в сторону, противоположную
где
ускорению неинерциальной системы.
Fин ma
48.
Силы инерции при поступательномдвижении неинерциальной системы отсчета.
F Fин
a
,
m m
Fин ma
ma ' F Fин
это
уравнение
Ньютона
неинерциальной системы отсчета.
для
Здесь Fин – фиктивная сила, обусловленная
свойствами системы отсчета
49.
Силы инерции при вращательномдвижении неинерциальной системы отсчета.
Fцс maцс ,
Веревка
растягивается,
появляется
упругая
сила,
действующая
на
камень,
направленная вдоль веревки к
центру вращения.
Это есть
центростремительная сила
(при вращении Земли в качестве
центростремительной выступает
сила гравитации).
aцс an ,
υ
Fцс m .
R
Fцс man ,
2
Это сила, приложенная к телу.
50.
Силы инерции при вращательном движении неинерциальнойсистемы отсчета. Центробежная сила.
Fцб man ,
υ
an .
R
an ω R
2
2
Fцб mω R.
2
Центростремительная сила приложена к вращающему телу. Во
вращающейся системе отсчета тело покоится.
Центростремительную силу уравновешивает сила направленная
по радиусу от центра. Эта сила инерции называется
центробежной.
Центробежная сила действует всякие тела во вращающейся
системе отсчета – на неподвижные и на движущиеся.
51.
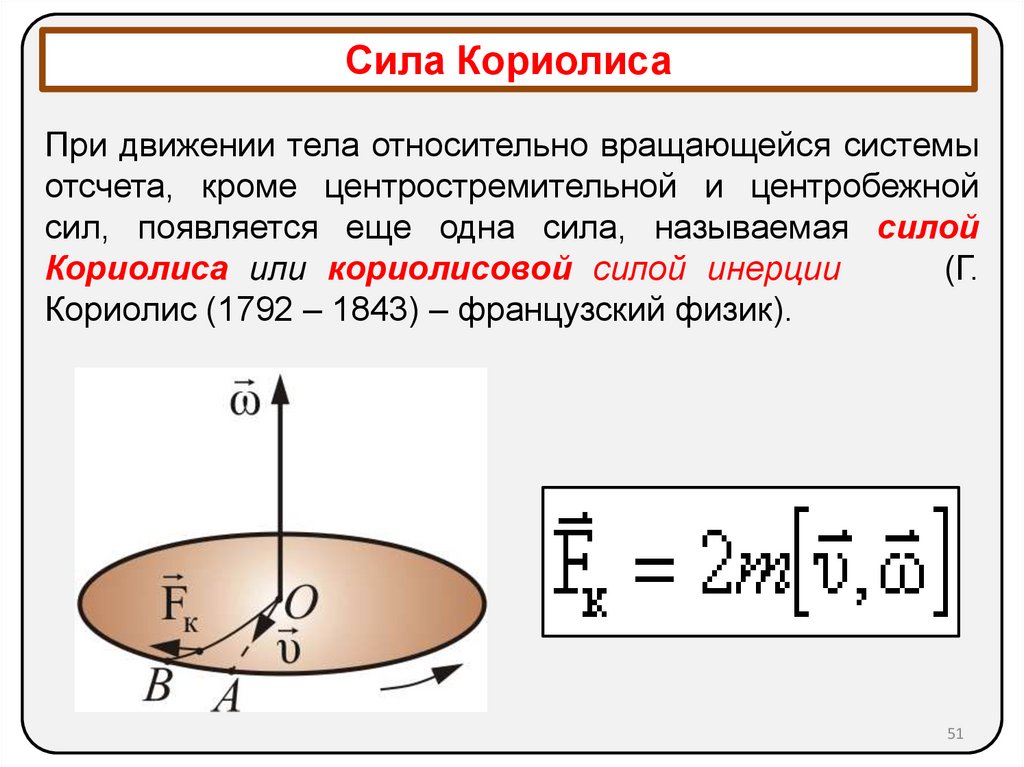
Сила КориолисаПри движении тела относительно вращающейся системы
отсчета, кроме центростремительной и центробежной
сил, появляется еще одна сила, называемая силой
Кориолиса или кориолисовой силой инерции
(Г.
Кориолис (1792 – 1843) – французский физик).
51
52.
Сила КориолисаСила Кориолиса
1. всегда лежит в плоскости,
перпендикулярной к оси
вращения;
2. направлена
перпендикулярно скорости и
поэтому не совершает
работы
53.
Сила КориолисаСила Кориолиса,
действует на тело,
движущееся вдоль
меридиана
в северном полушарии
вправо
и в южном – влево.
Это приводит к тому, что у
рек
подмывается
всегда
правый берег в севером
полушарии и левый – в
южном.
54.
Силы инерции. Неинерциальные системы отсчета.С учетом всех сил инерции, уравнение Ньютона для
неинерциальной системы отсчета примет вид:
ma ' F Fин Fцб Fк ,
Fин – сила инерции, обусловленная поступательным
движением неинерциальной системы отсчета;
Fцб Fк – две силы инерции, обусловленные
вращательным движением системы отсчета;
неинерциальной системы
a ' – ускорение тела относительно
отсчета.
Fин ma,
Fк 2m[ υ, ω],
2
Fцб mω R.












































 Физика
Физика








