Надстройка поиск решения Excel для решения задач оптимизации

1.

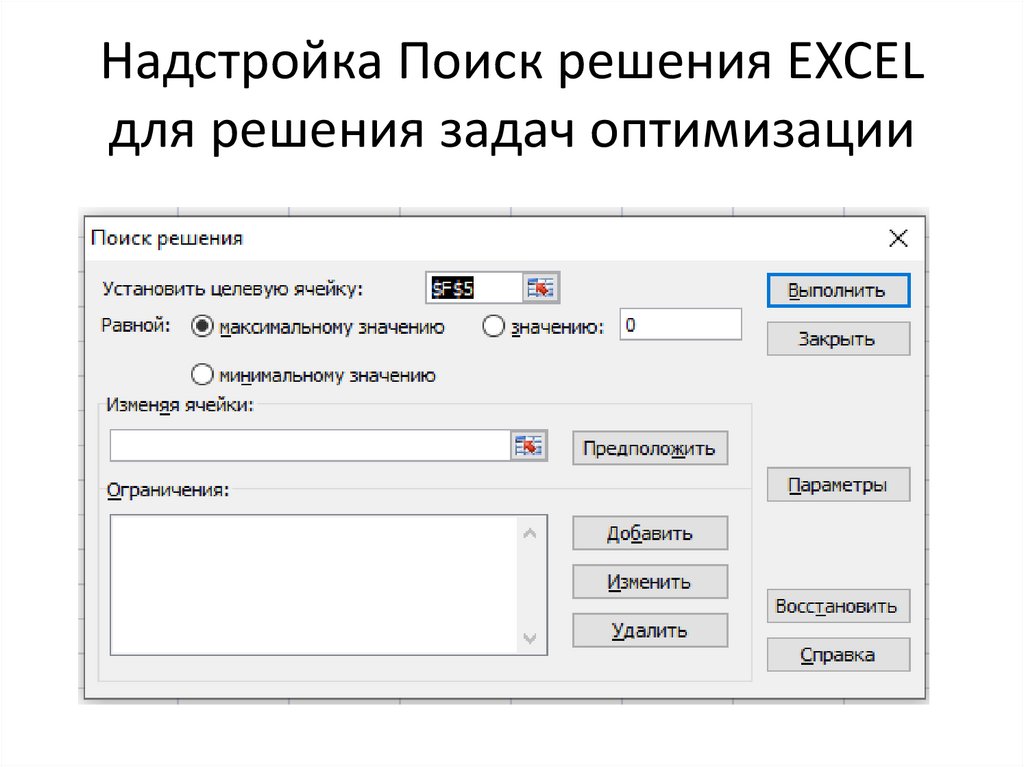
Надстройка Поиск решения EXCEL
для решения задач оптимизации

2.

Пример.
При проектировании строительной конструкции
с наименьшей стоимостью перед
проектировщиком была поставлена задача
использовать листовой металл, стекло и
пластмассу, стоимость которых составляет
соответственно 25, 20 и 40 р/м2. Массы 1 м2
листового металла, стекла и пластмассы
соответственно равны 10, 15 и 3 кг. Совместная
общая поверхность конструкции должна
составлять 14 м2. Из них не менее 4 м2 и не
более 5 м2 следует отвести под стекло. Масса
не должна превышать 150 кг. Какое
оптимальное количество листов металла,
стекла и пластмассы должно быть в проекте?

3.

Дано:
Стоимость материалов :
с1 25 руб / м
с2 20 руб / м
с3 40 руб / м
Массы материалов :
т1 10 кг
т2 15 кг
т3 3 кг
Ограничение на массу конструкции ( 150кг )
Ограничение на площадь поаерхности ( 14 м 2 )
Ограничение для стекла (4 м 2 стекло 5 м 2 )

4.

Переменные:
х1 расход металла ( м )
2
х2 расход стекла ( м )
2
х3 расход пластмассы ( м )
2
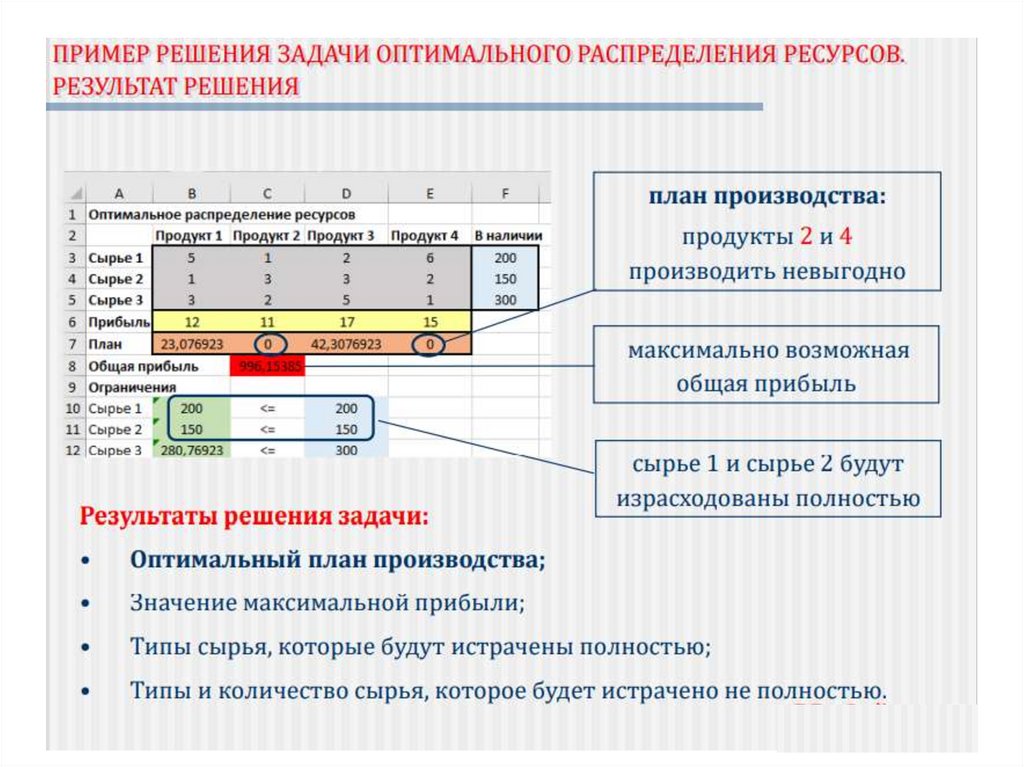
Найти: Оптимальный расход материалов для
проекта

5.

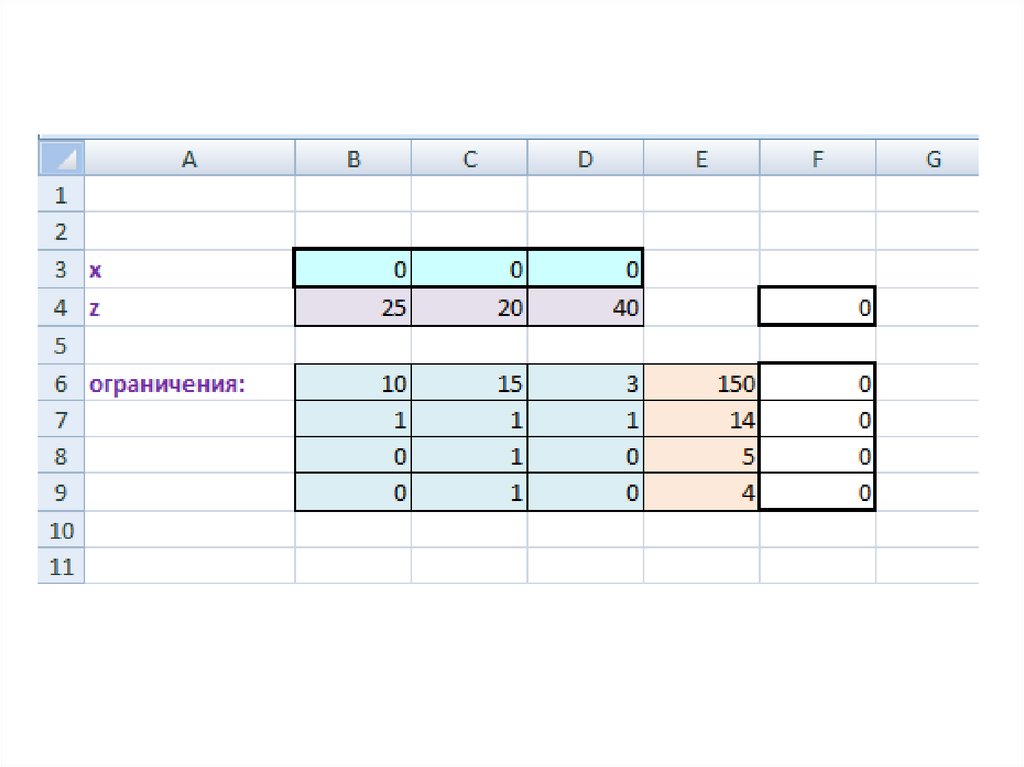
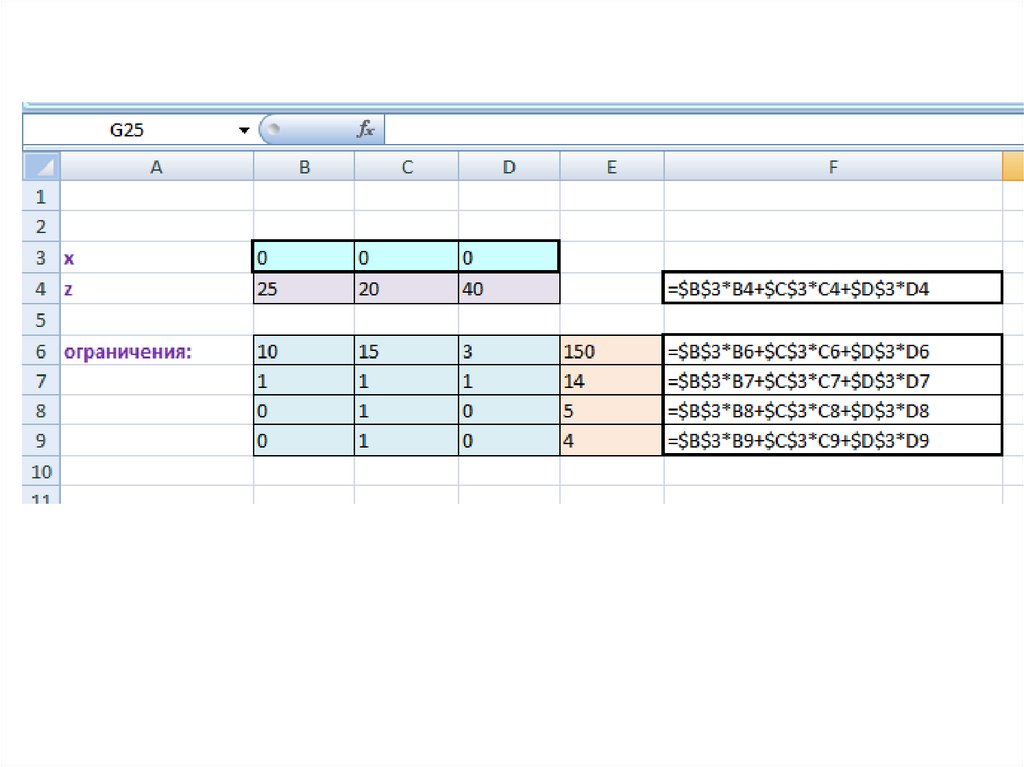
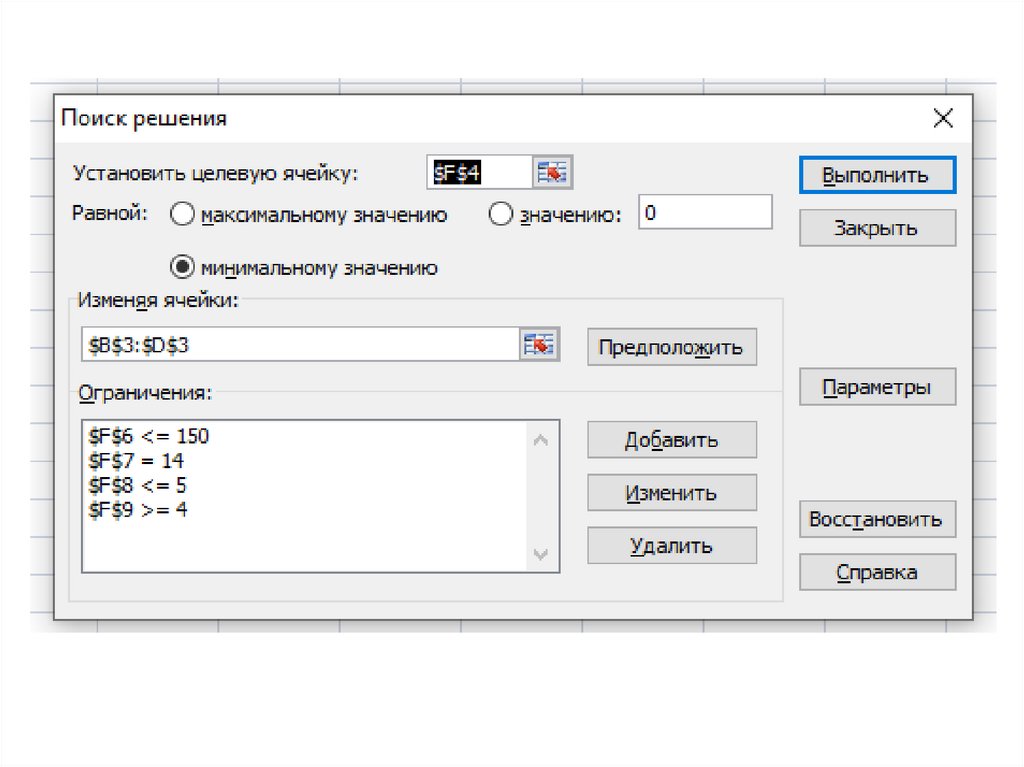
Математическая модель:
z 25 x1 20 x2 40 x3 min (целевая функция )
10 x1 15 x2 3x3 150 (ограничение на массу)
x1 x2 x3 14 (ограничение на площадь поверхности )
(ограничение для стекла)
x2 5
x 4
2
x j 0, j 1,2,3.

6.

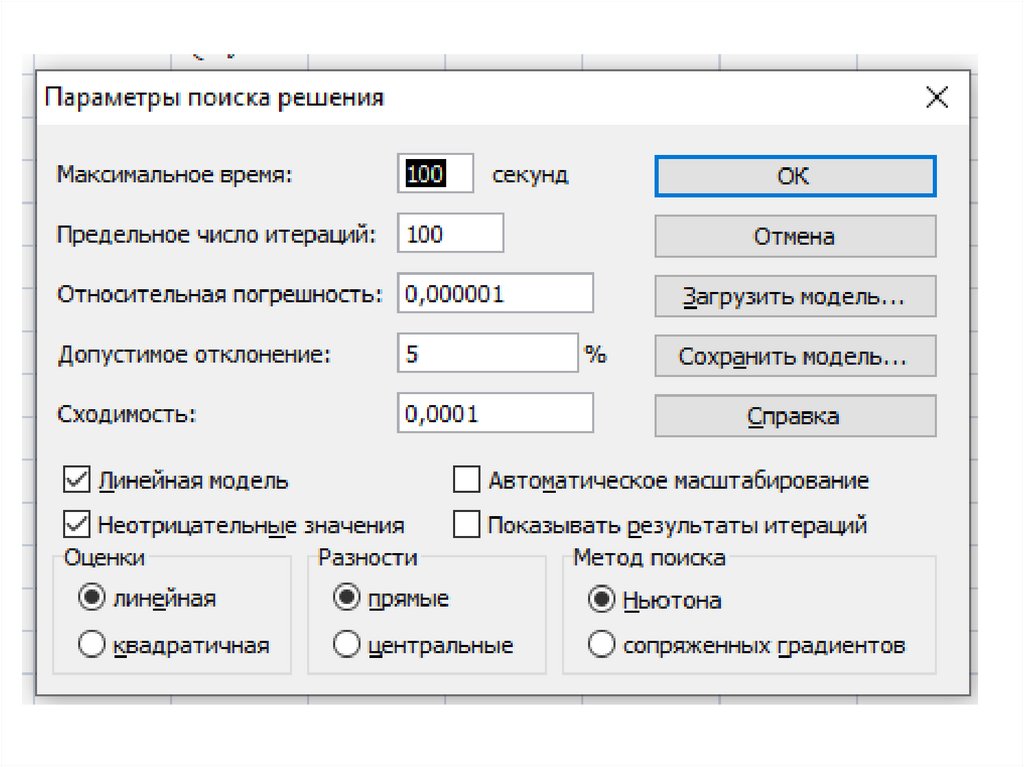
7.

8.

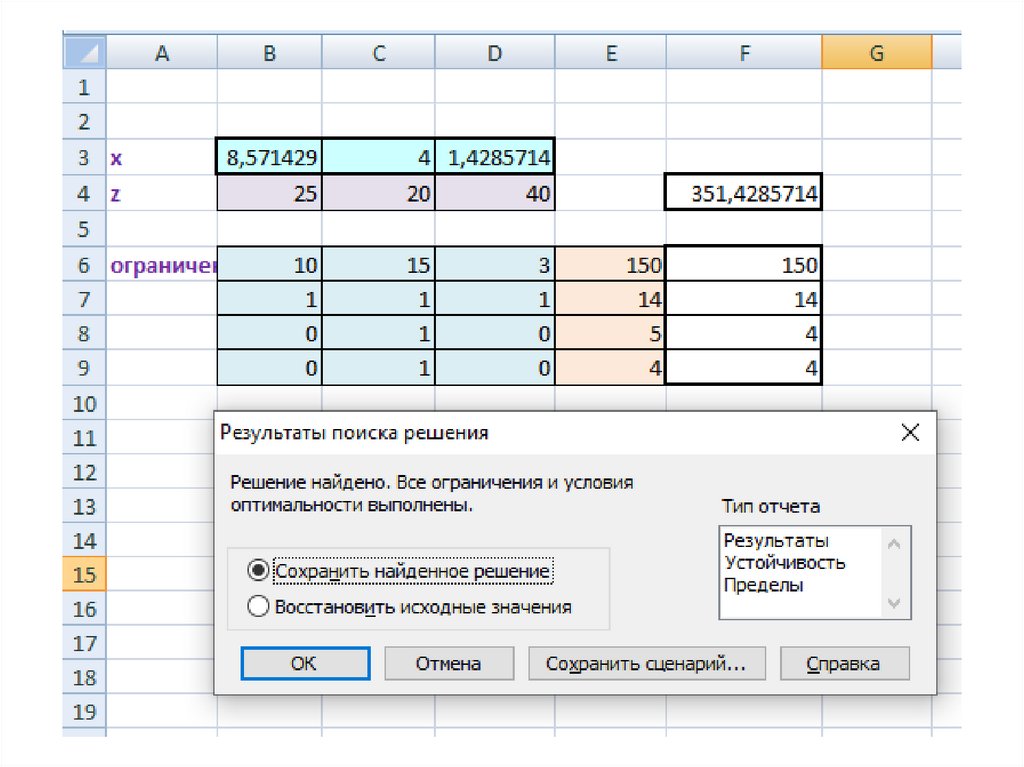
9.

10.

11.

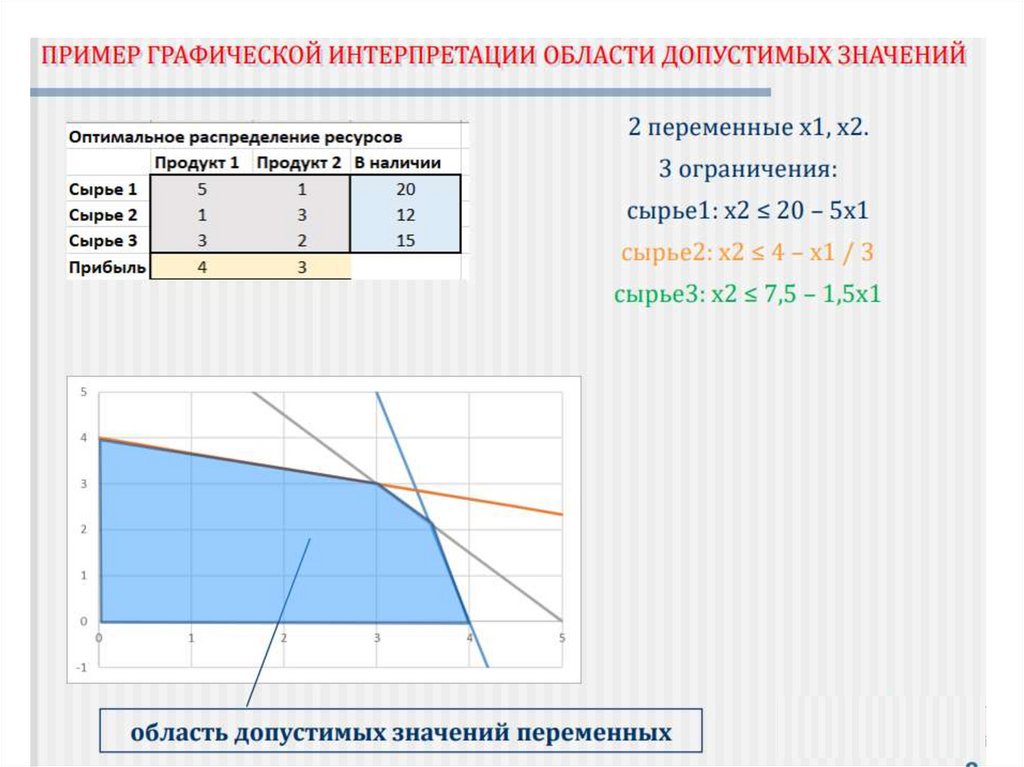
Задача об оптимальном распределении
ресурсов
Предприятие выпускает n типов продукции, на которое
затрачивается m видов сырья.
aij количество i го типа сырья или ресурсов,
затраченного на производство единицы
продукции j го типа;
bi количество i го вида сырья или ресурсов;
с j прибыль от реализации единицы
продукции j го типа;
i 1,..., m; j 1,..., n.

12.

x j количество единиц продукции j го ттипа
j 1,..., n.
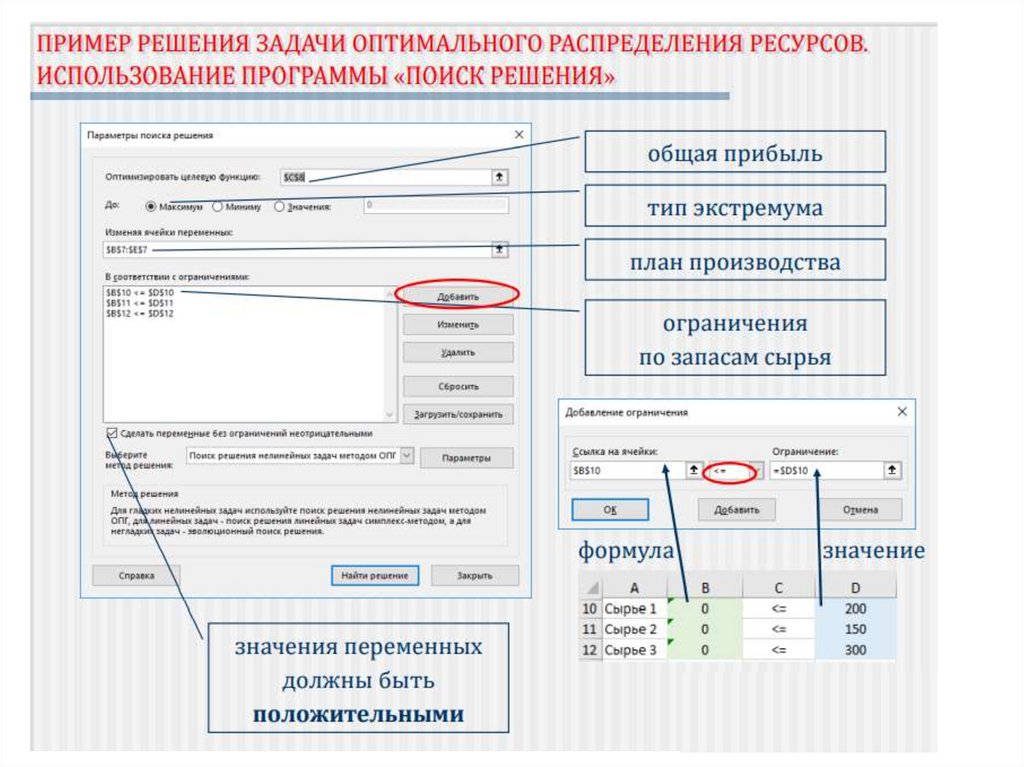
Требуется максимизировать прибыль от реализации
продукции.
Целевая функция задачи :
n
z c1 x1 c2 x2 ... cn xn c j x j max
j 1
(прибыль от реализации всей продукции
должна быть максимальной)

13.

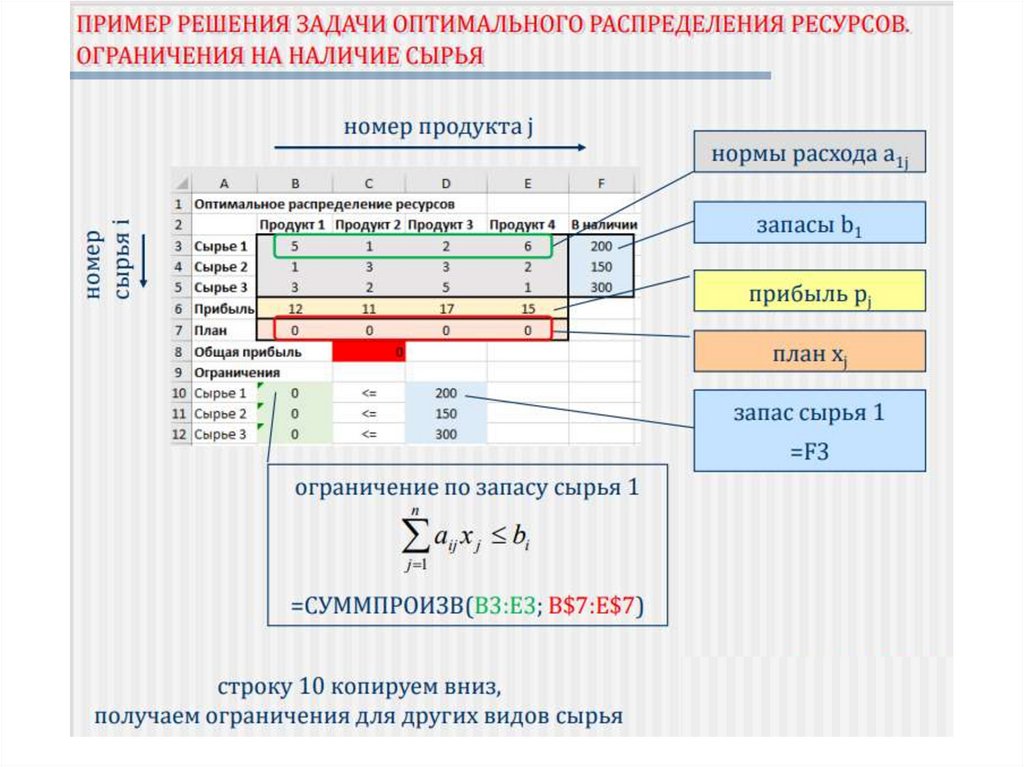
Ограничения (ммножество допустимых значений) :
a11 x1 a12 x2 ... a1n xn b1 ;
a21 x1 a22 x2 ... a2 n xn b2 ;
...
am1 x1 am 2 x2 ... amn xn bm ;
(расход каждого вида сырья не должен превышать
имеющегося запаса)
или
n
aij x j bi ; i 1,..., m.
j 1

14.

Условие неотрицательности :
x1 0; x2 0;...; xn 0.
или
х j 0, i 1,..., n.
Задача оптимизации имеет вид :
n
z c j x j max
j 1
n a x b ; i 1,..., m;
i
ij j
j 1
x j 0; j 1,..., n.

15.

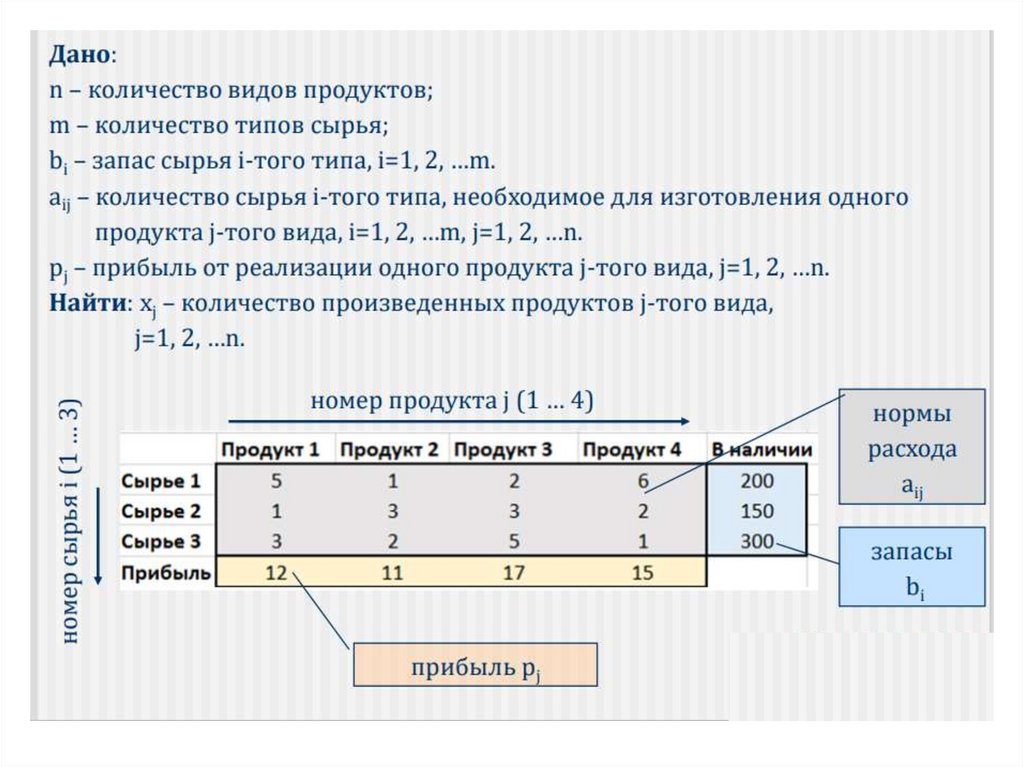
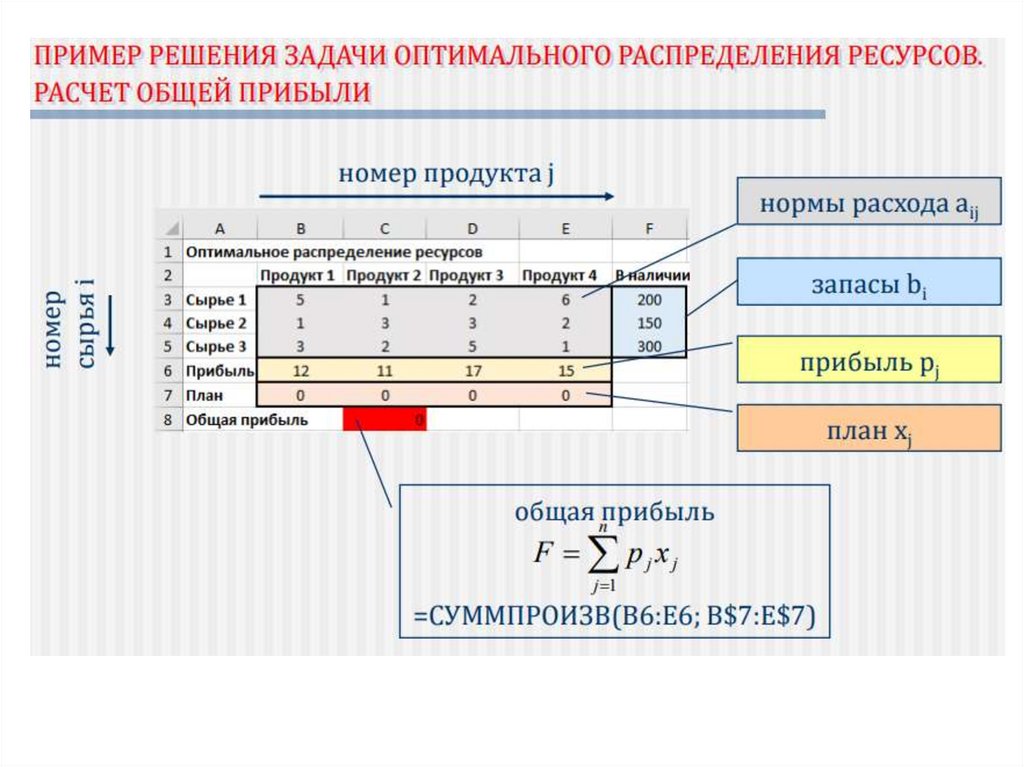
Пример.

16.

17.

Математическая модель
x1 , x2 , x3 , x4 переменные задачи
z 12 x1 11x2 17 x3 15 x4 max (целевая функция )
5 x1 x2 2 x3 6 x4 200
x 3x 3x 2 x 150
2
3
4
1
3x 2 x 5 x x 300
2
3
4
1
x j 0, j 1,4.