Похожие презентации:
Стеклообразное состояние полимеров. (Лекция 5)
1. Фазовое состояние полимеров
• Кристаллическое• Жидкокристаллическое
• Аморфное
• Изотропный расплав
(раствор)
2.
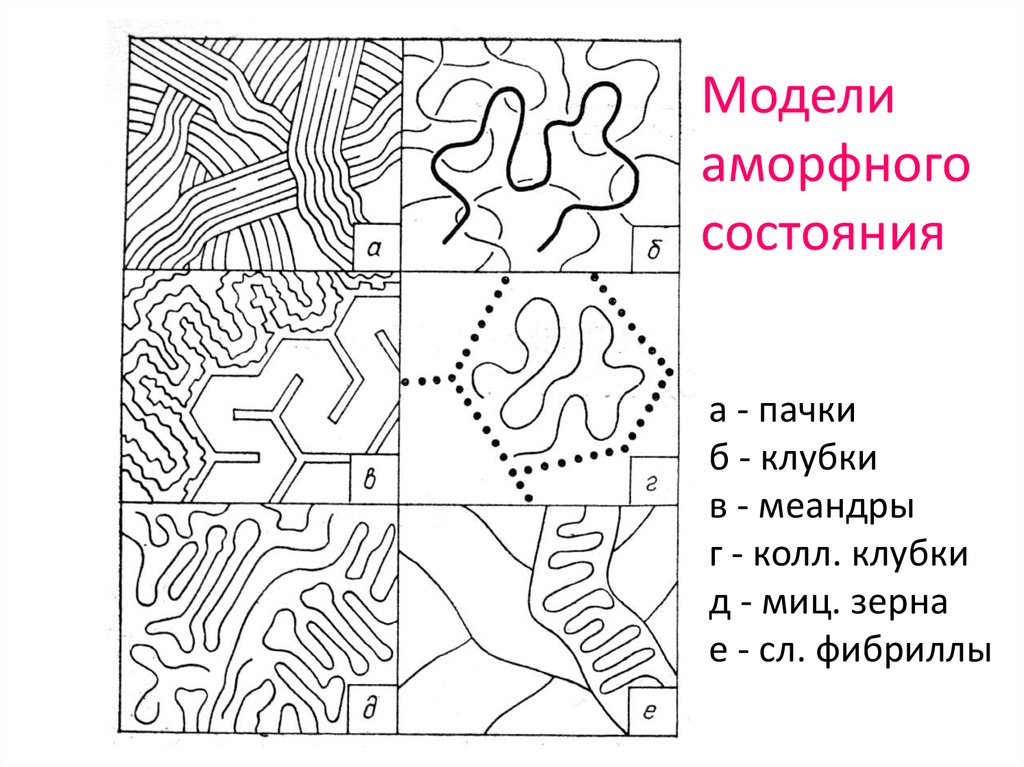
Моделиаморфного
состояния
а - пачки
б - клубки
в - меандры
г - колл. клубки
д - миц. зерна
е - сл. фибриллы
3.
Лекция №5Стеклообразное состояние полимеров.
Стеклообразное состояние достаточно распространено:
получены стеклообразные состояния для органических
веществ (глицерин и этиленгликоль), металлов (при очень
быстром охлаждении) и прочих материалов. Среди этого
класса полимерные стекла занимают ведущее место.
Определение:
с точки зрения агрегатного состояния:
- твердое агрегатное состояние;
с точки зрения фазового состояния:
- жидкость;
со структурной точки зрения:
- отсутствует дальний порядок (есть лишь ближний).
Таким образом, это метастабильное состояние с очень
высокой вязкостью, в которой тело может находиться
неограниченное количество времени.
4.
а)V
V - объем
T' Tc T"
Tкомн
Т
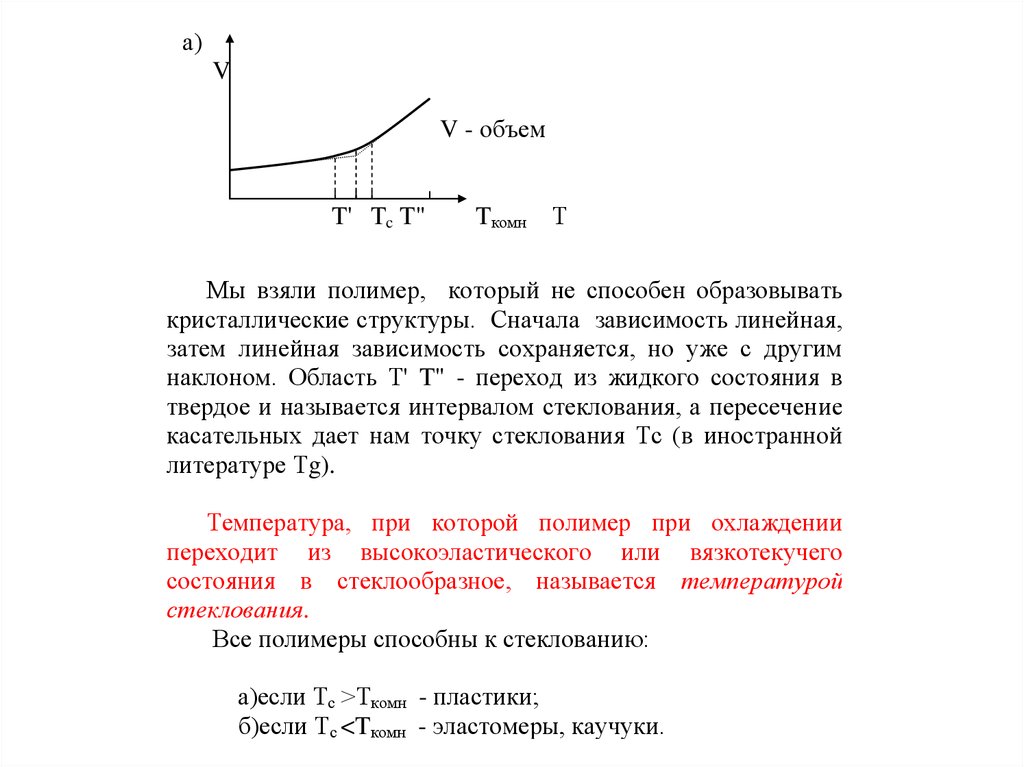
Мы взяли полимер, который не способен образовывать
кристаллические структуры. Сначала зависимость линейная,
затем линейная зависимость сохраняется, но уже с другим
наклоном. Область Т' T" - переход из жидкого состояния в
твердое и называется интервалом стеклования, а пересечение
касательных дает нам точку стеклования Тс (в иностранной
литературе Тg).
Температура, при которой полимер при охлаждении
переходит из высокоэластического или вязкотекучего
состояния в стеклообразное, называется температурой
стеклования.
Все полимеры способны к стеклованию:
а)если Тс >Ткомн - пластики;
б)если Тс <Tкомн - эластомеры, каучуки.
5.
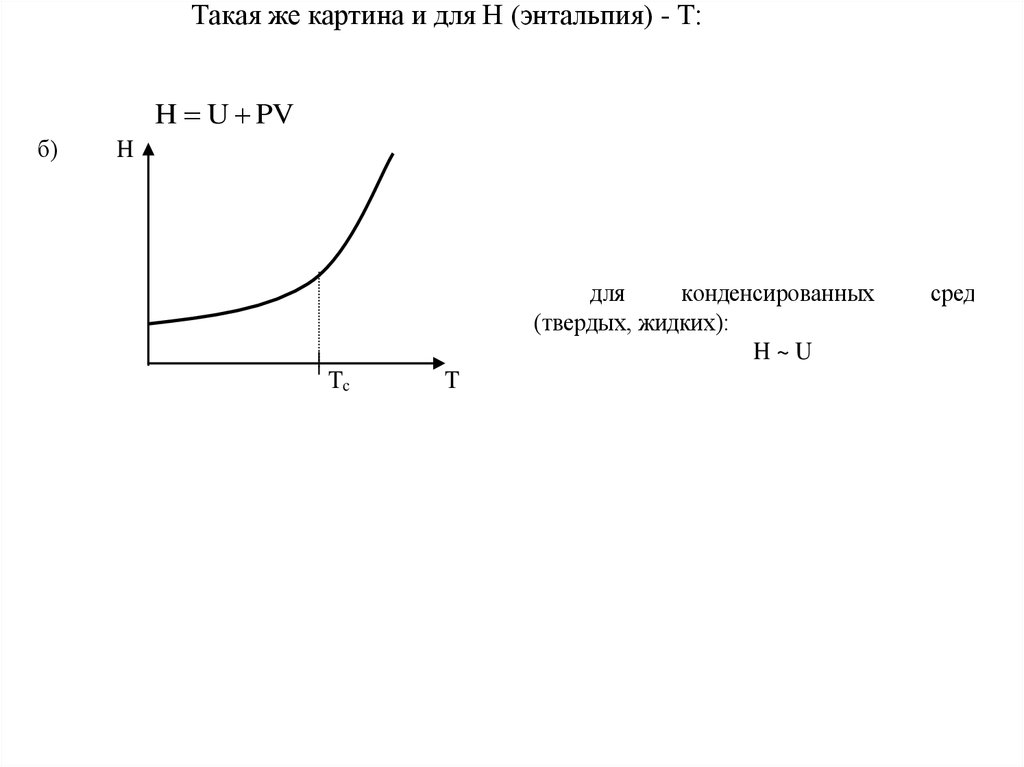
Такая же картина и для Н (энтальпия) - Т:H U PV
б)
H
для
конденсированных
(твердых, жидких):
H~U
Tc
T
сред
6.
в)1 dV
α
V dT p
в других координатах:
Tc
- коэффициент
расширения
T
dH
Cp
dT p
Ср - теплоемкость
Tc
T
объемного
7.
Переход в стеклообразное состояние не есть фазовый переход:а) обе формы - жидкие фазы.
Т.о., стеклование есть лишь кинетический переход (но не термодинамический). Однако по в)
и г) существует мнение, что стеклование - фазовый переход второго рода (это
неправильно, однако широко распространенная ошибка).
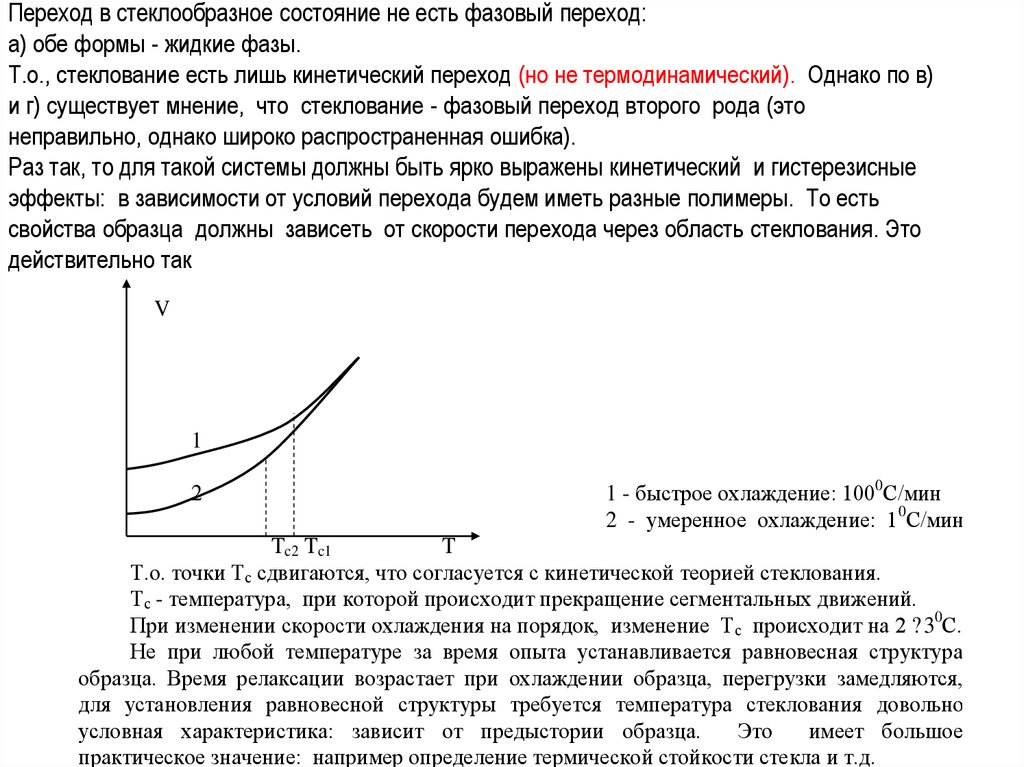
Раз так, то для такой системы должны быть ярко выражены кинетический и гистерезисные
эффекты: в зависимости от условий перехода будем иметь разные полимеры. То есть
свойства образца должны зависеть от скорости перехода через область стеклования. Это
действительно так
V
1
2
1 - быстрое охлаждение: 1000С/мин
2 - умеренное охлаждение: 10С/мин
Tc2 Tc1
T
Т.о. точки Тс сдвигаются, что согласуется с кинетической теорией стеклования.
Тс - температура, при которой происходит прекращение сегментальных движений.
При изменении скорости охлаждения на порядок, изменение Тс происходит на 2 ? 30С.
Не при любой температуре за время опыта устанавливается равновесная структура
образца. Время релаксации возрастает при охлаждении образца, перегрузки замедляются,
для установления равновесной структуры требуется температура стеклования довольно
условная характеристика: зависит от предыстории образца.
Это
имеет большое
практическое значение: например определение термической стойкости стекла и т.д.
8.
Другой тип явлений, который тоже характеризует кинетические эффекты при стекловании:а) сначала быстро охлаждаем (
) , а затем медленно нагреваем (
):
V
1 a)
2
б)
- быстрый процесс
- медленный процесс
2
1
Tc
T
Т. о. наблюдается гистерезисный эффект
для объема
б) другой случай: очень медленно охлаждаем ( ) и затем очень быстро нагреваем
(
) обратно: увеличение объема.
Появление гистерезисных эффектов обуславливается сильным различием скоростей нагрева и
охлаждения.
Существует количественное описание перехода в стеклообразное состояние:
9.
Т1< Т2< Т3<Т41
1-Tc=-10
2
2-Tc=-5
3
3-Tc=0
4
4-Tc=+2
Vt-V∞)
Чем
ниже
температура
стеклования,
тем
больше
скорость релаксации
Vt - в данный момент времени;
V∞ - равновесный
установленный объем при
релаксации.
Это опыты по изотермической релаксации объема: нагреваем до высокой
температуры, затем переносим в постоянную температуру, при которой происходит
переход в стеклообразное состояние, стандартная скорость охлаждения при
изменении Тс принято 1÷2 [0С/мин]
lg t
Простейшее предположение—это процесс первого порядка, скорость пропорциональна в каждый
момент времени самой величине.
tv - время релаксации
dV
1
(Vt V ),
dT
tv
(Vt V ) (Vucx V ) exp( t/t v )
Для образца полистирола:
T0C
tv, сек
100
10 -2
95
1
91
90
40
2 мин
0
Тс = 90 С
89
5 мин
79
60 час
10. Стеклование – фазовый переход?
• Удовлетворяет критерию Эренфеста: скачоктеплоемкости, следовательно, фазовый
переход второго рода:
Макрогалерея (университет Южного
Миссисипи), русский перевод ИНЭОС +
Физический факультет
http://pslc.ws/russian/index.htm
• Но: для аморфной фазы и стеклование, и
переход в вязкотекучее состояние – это
релаксационные переходы!
11.
• Делались неоднократные попытки создать физически простуюмодель процесса стеклования, которая бы позволила
количественно описать это явление. Существуют несколько
теорий стеклования: кинетическая, теория локальных
межмолекулярных связей, статистическая термодинамическая
теория Адама и Гиббса, теория свободного объёма.
Одновременное существование различных теорий стеклования
указывает на то, что ни одна из них не даёт всестороннего и
исчерпывающего описания закономерностей изменения
структуры и свойств при стекловании. Каждая теория вносит
свой вклад в понимание процесса стеклования в целом и
поэтому имеет право на самостоятельное существование.
Рассмотрим теорию свободного объёма.
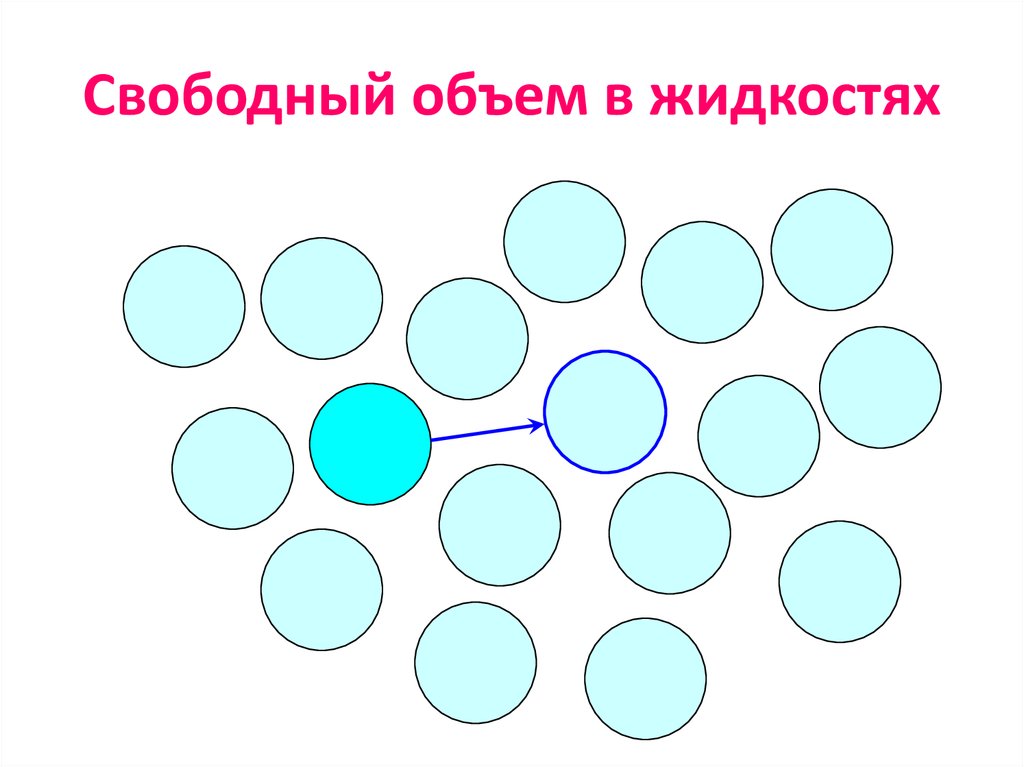
• Понятие о свободном объеме:
• Это разность между реальным объемом при данной То и
занятым объемом (при плотно упакованном слое - без
дефектов, с шахматным использованием пустот).
12. Свободный объем
13. Свободный объем в жидкостях
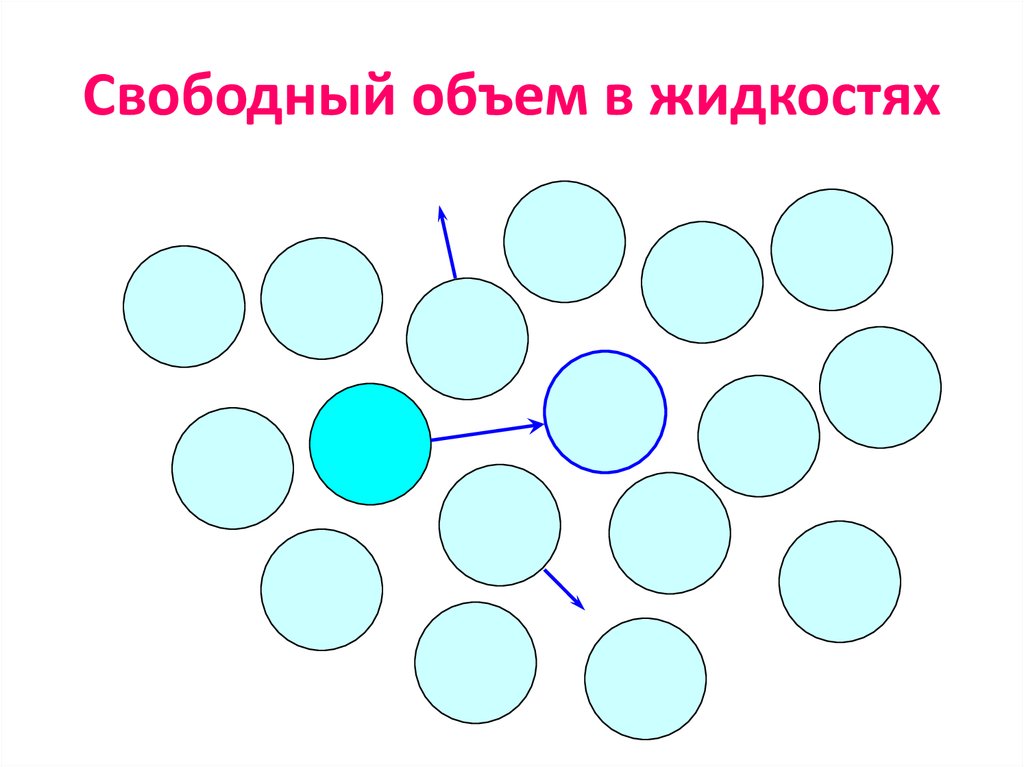
14. Свободный объем в жидкостях
15. Свободный объем в жидкостях
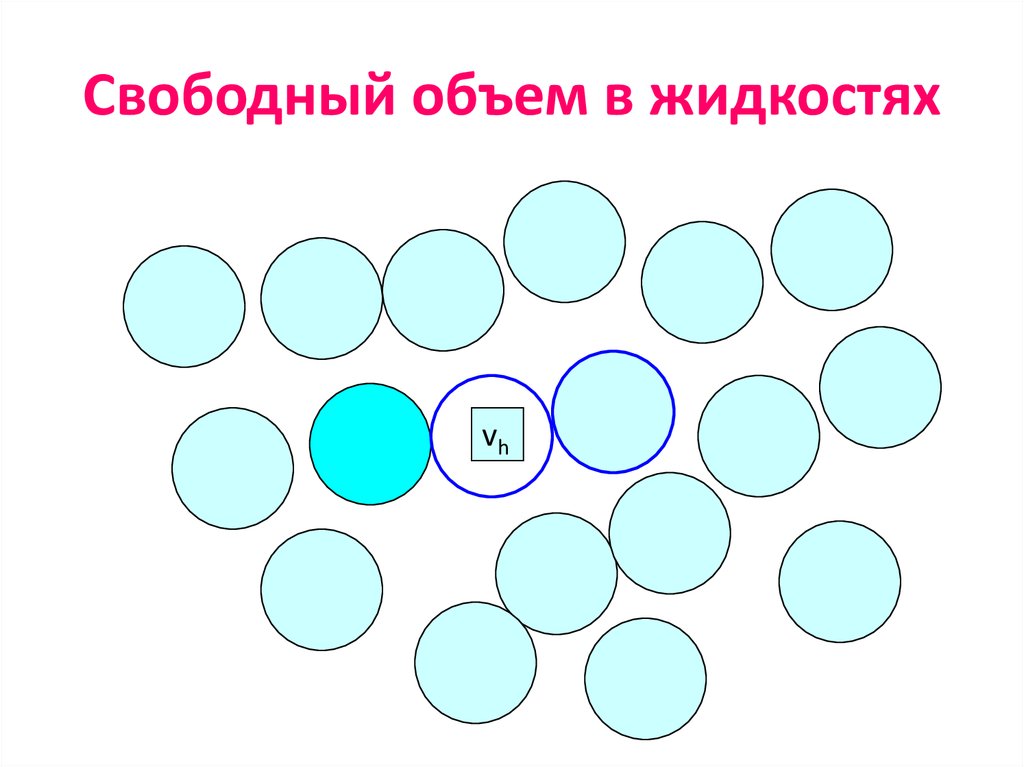
vh16. Свободный объем в жидкостях
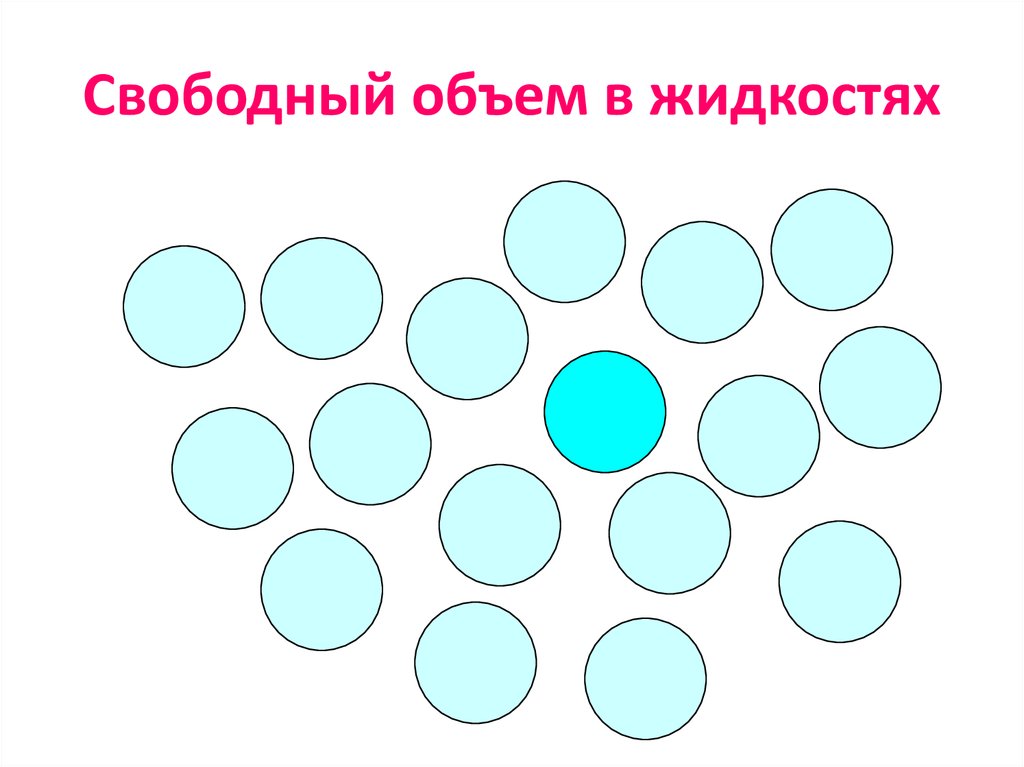
17. Свободный объем в жидкостях
Флуктуационный свободный объемопределяется как
суммарный объем дырок
vf=vh·exp{(Eh+p·vh)/RT}
vh - минимальный объем дырки
Eh - энергия образования дырки
Френкель Я.И., Кинетическая теория
жидкостей, 1959
1 d
k dt
1
1
18. Подвижность молекул жидкости
• Движение частицы осуществляется,когда по соседству с ней появляется
«дырка», размером не меньше
диффундирующей молекулы:
η=a·exp(γ·vh/vf)
Коэн – Тарнбалл – Дулитл, 1959
• С учетом энергетического барьера
скачка молекулы:
lnη=А+E0/RT+γ·vh/vf
19. Свободный объем в аморфных полимерах
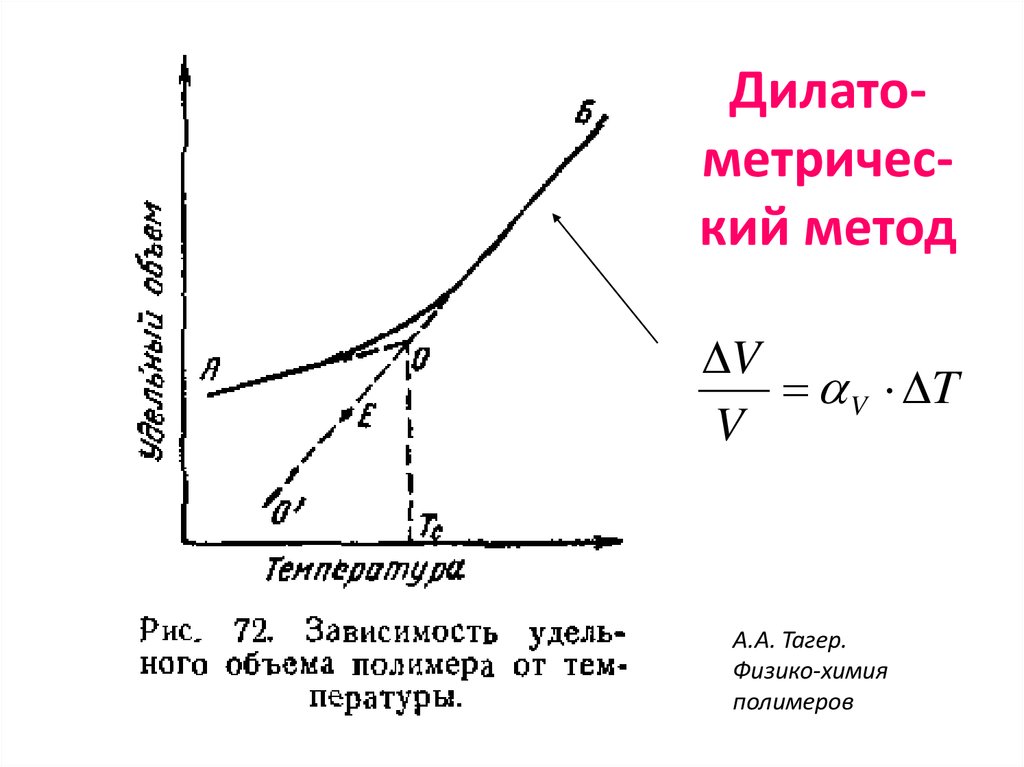
20. Дилато-метричес-кий метод
Дилатометрический методV
V T
V
А.А. Тагер.
Физико-химия
полимеров
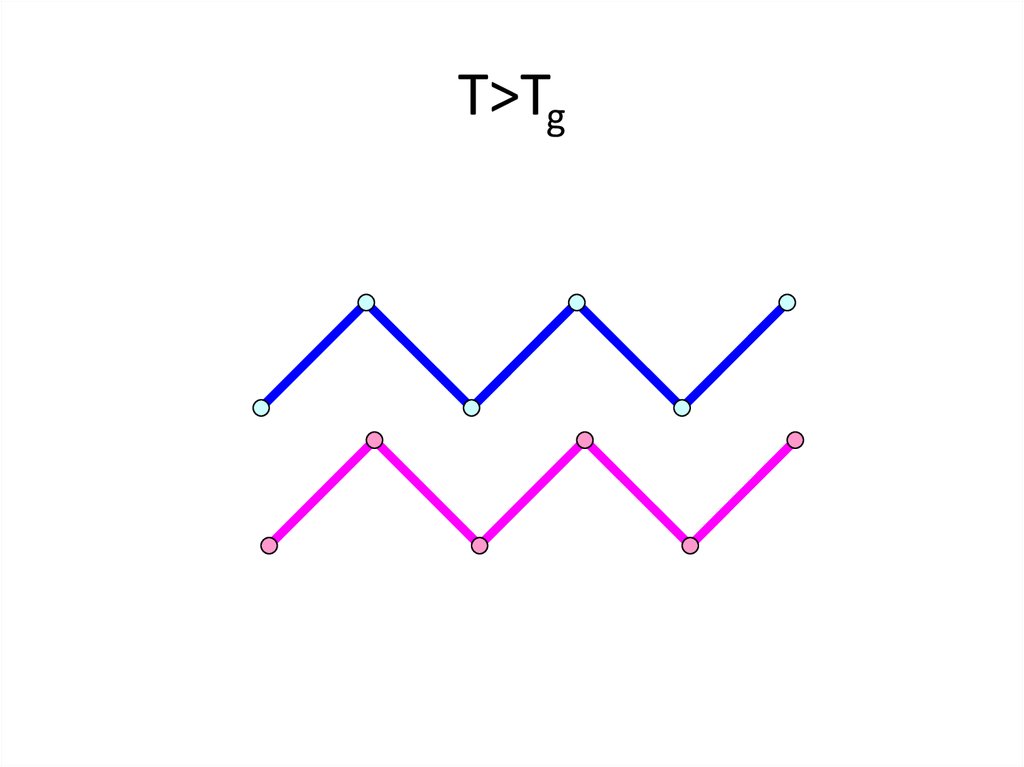
21. T>Tg
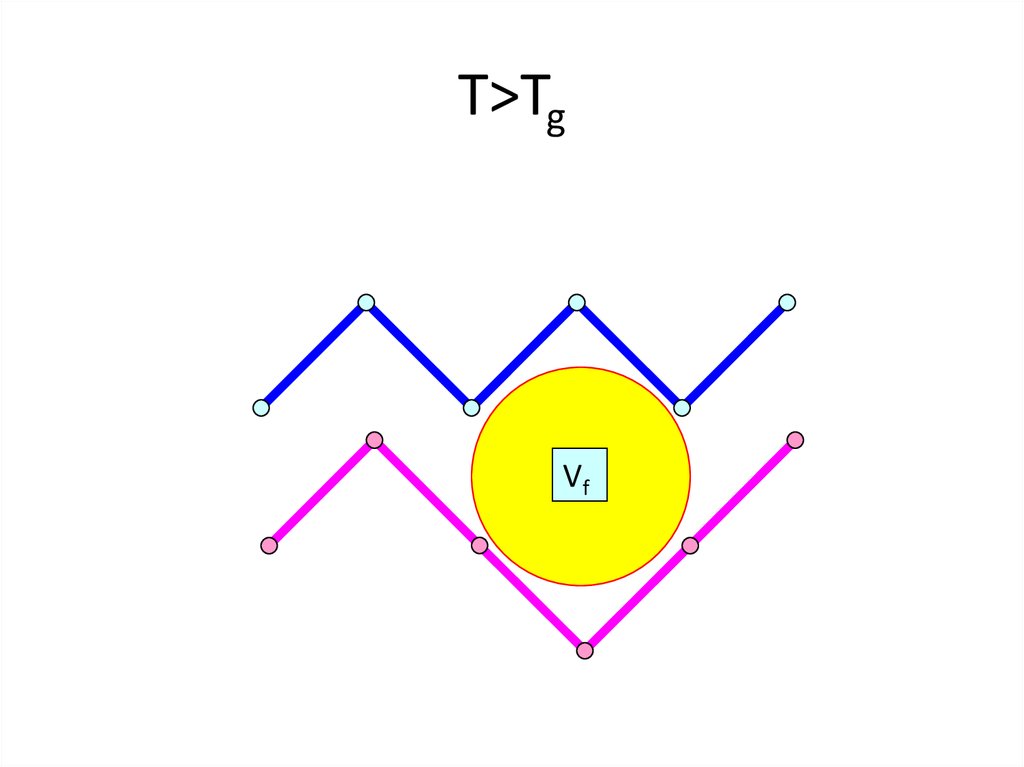
T>Tg22. T>Tg
T>TgVf
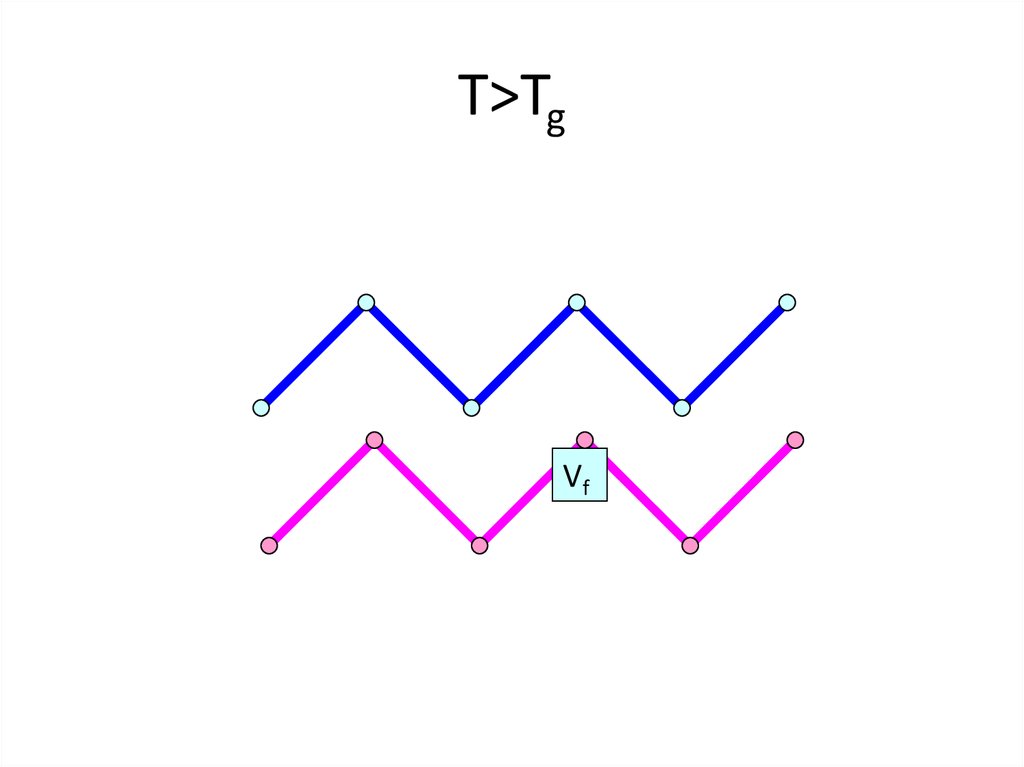
23. T>Tg
T>TgVf
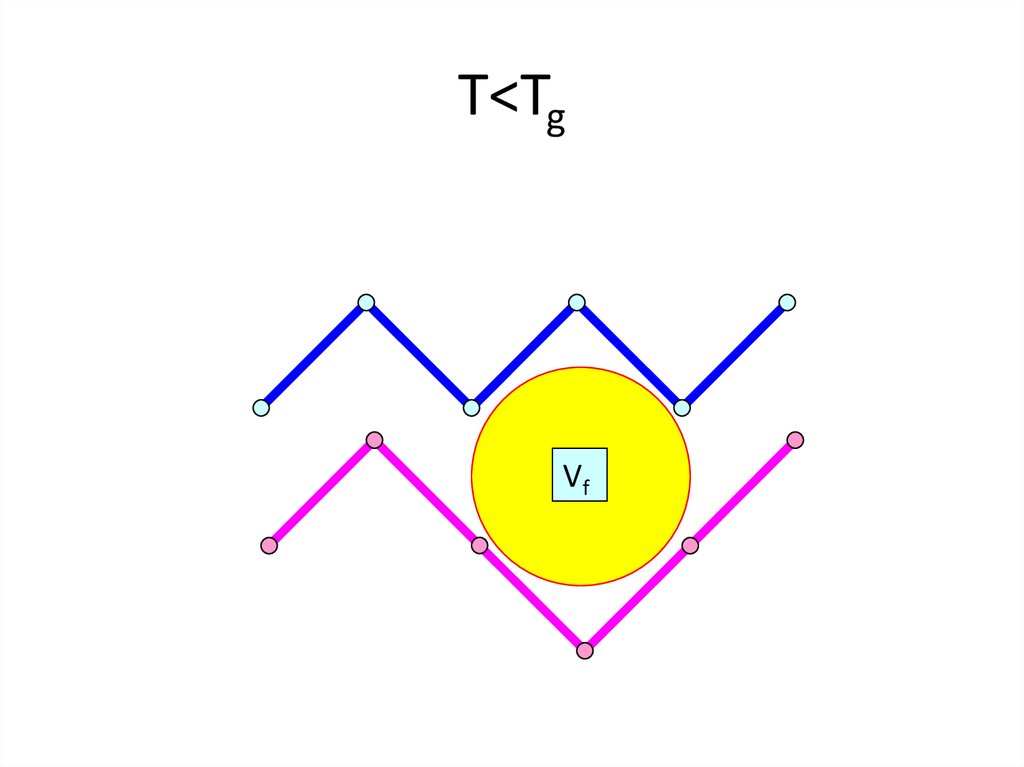
24. T<Tg
T<TgVf
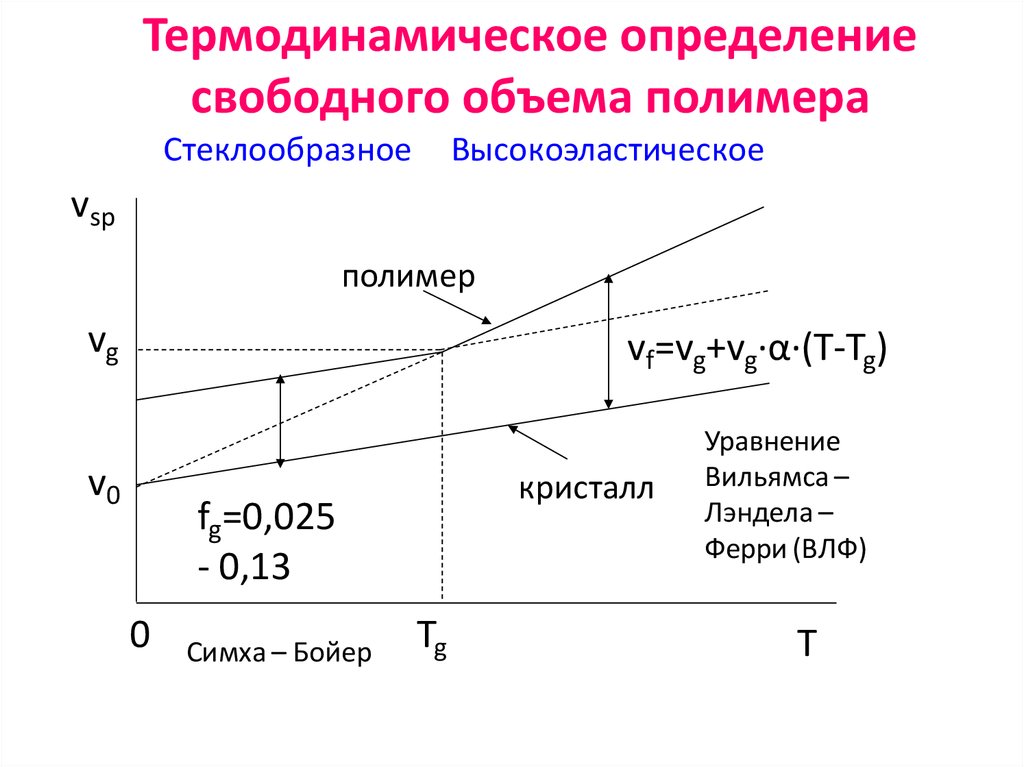
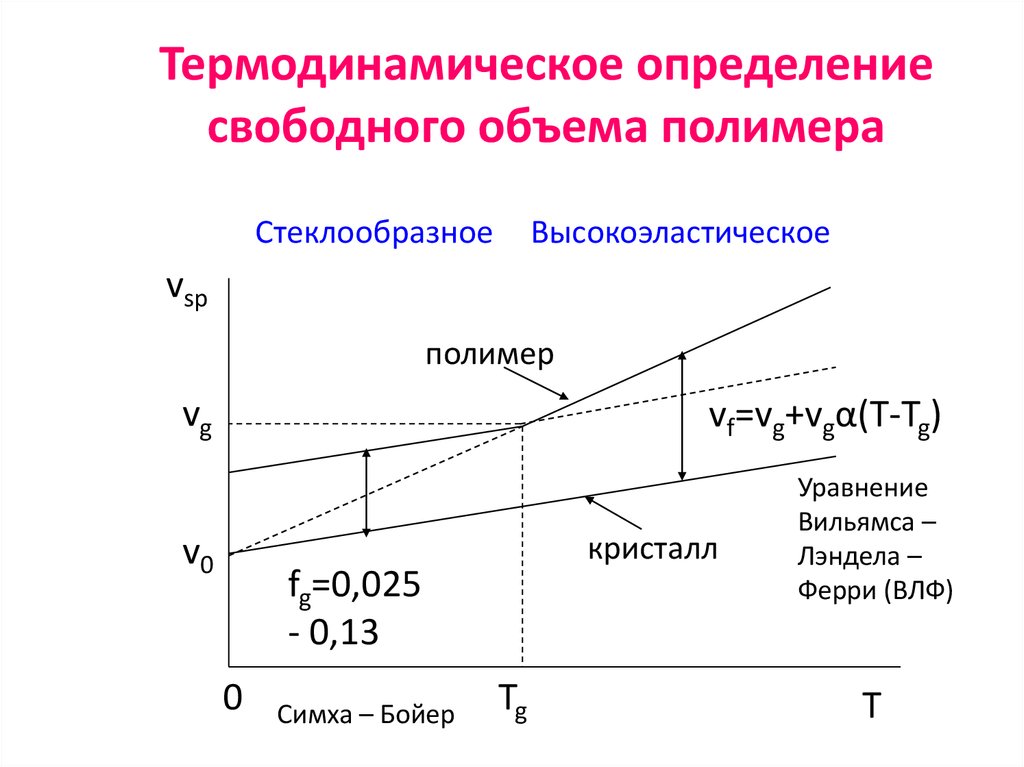
25. Термодинамическое определение свободного объема полимера
СтеклообразноеВысокоэластическое
vsp
полимер
vg
vf=vg+vg·α·(T-Tg)
v0
кристалл
fg=0,025
- 0,13
0
Симха – Бойер
Tg
Уравнение
Вильямса –
Лэндела –
Ферри (ВЛФ)
T
26. Геометрическое определение свободного объема
Vf=Vsp-Voc
(Vsp=1/ρ);
f=Vf/Vsp
(f=FFV=1-Voc/Vsp)
Пустой объем
Vempty=Vsp-Vw;
K=Vw/Vsp;
fempty=1-K
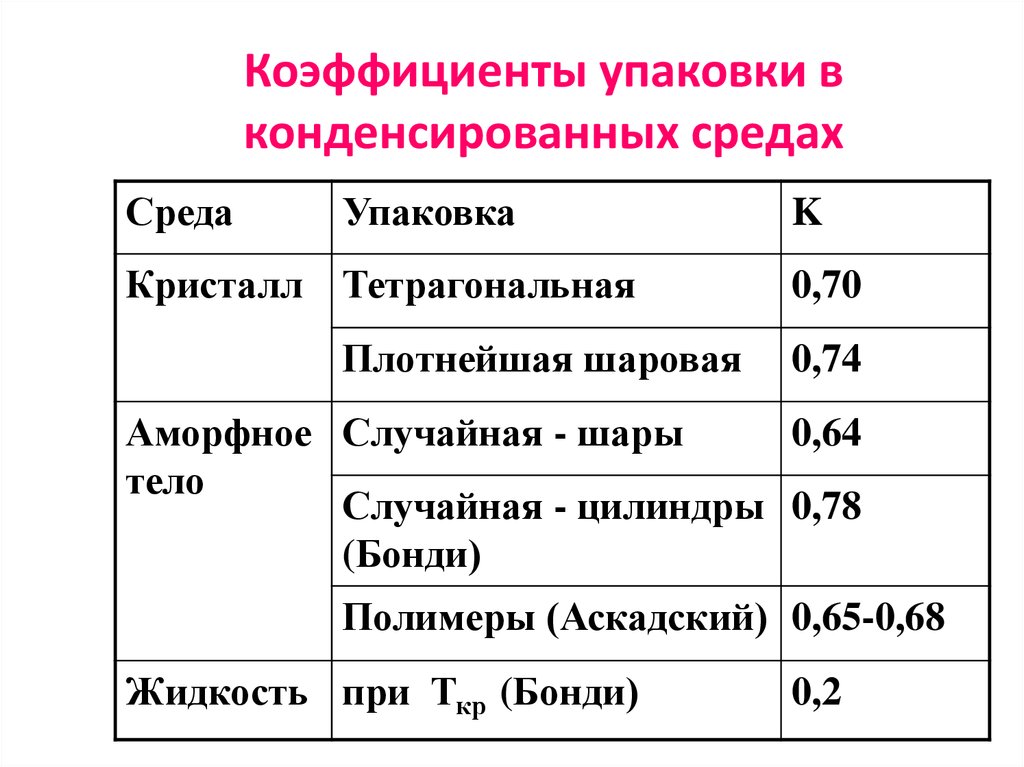
27. Коэффициенты упаковки в конденсированных средах
СредаУпаковка
Кристалл Тетрагональная
Плотнейшая шаровая
K
0,70
0,74
Аморфное Случайная - шары
0,64
тело
Случайная - цилиндры 0,78
(Бонди)
Полимеры (Аскадский) 0,65-0,68
Жидкость при Ткр (Бонди)
0,2
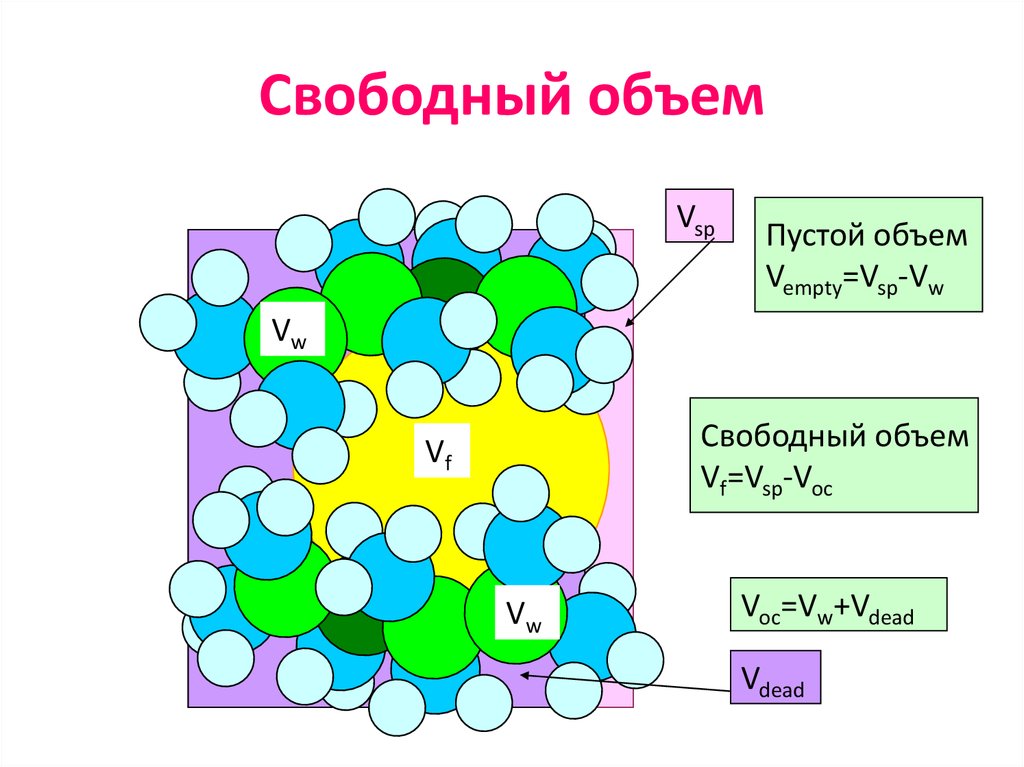
28. Свободный объем
VspПустой объем
Vempty=Vsp-Vw
Vw
Свободный объем
Vf=Vsp-Voc
Vf
Vw
Voc=Vw+Vdead
Vdead
29. Геометрическое определение свободного объема
Vf=Vsp-Voc; f=Vf/Vsp
Свободный объем (при диффузии)
Voc=Vw+Vdead;
Vdead=Vempty (плотноупакованной части
матрицы);
• Voc=Vw/K;
• Vf=Vsp-VW/K; f=1-Vw/(Vsp·K)
• Vf=Vsp-1,3·VW (Бонди)
30.
Теориясвободного объема
M.Cohen, T.Turnbull, 1959
D=A·exp(-B·vh/vf)
А, B, T=const
vf – свободный объем
vh – минимальный объем «дырки»,
достаточный для перемещения
диффундирующей молекулы
31.
Теориясвободного объема
M.Cohen, T.Turnbull, 1959
D=A·exp(-B/vf)
А, B, T=const
vf=vsp-voc
=1/ρ
vf – свободный объем
Занятый
объем
Расчетная величина
32. Термодинамическое определение свободного объема полимера
СтеклообразноеВысокоэластическое
vsp
полимер
vg
vf=vg+vgα(T-Tg)
v0
кристалл
fg=0,025
- 0,13
0
Симха – Бойер
Tg
Уравнение
Вильямса –
Лэндела –
Ферри (ВЛФ)
T
33.
Тепловое расширение выше Тс определяется изменением свободного объема: он болеечувствителен к Тс, и чем выше Т, тем больше Vf (до температуры стеклования). В области Т<Тс
свободный объем принимает постоянное значение и дальше не меняется. Это позволяет
объяснить состояние стеклования изменением свободного объема.
= (5·10-4 ÷1·10-3) – коэффициент объемного расширения для свободного объема выше Тс очень
большой.
При Тс стеклообразных состояниях в первом приближении замораживается один и тот же объем:
fc
Vf
const 0.025,
Vобщ
где fc - объемная доля свободного пространства.
Таким образом, при охлаждении жидкой системы, когда fc =2.5%, система переходит
в стеклообразное состояние (при fc >2.5% возможно перемещение сегмента под
действием теплового движения).
34.
Эмпирическое соотношение Дулиттла:η
η A exp(B V0 /Vf )
-- вязкость, А и В—константы
, где
f Vf /Vобщ Vf /(Vf V0 ) Vf /V0
(Vf V0 ),
тогда:
ln η lnA B/f
но происходит изменение доли свободного пространства зависимости от температуры:
f t f c α1 α 2 T Tc f c α f T Tc
,
fc – доля свободного объема при температуре стеклования
Тогда соответственно:
α1 α 2 α f
ln η T lnA B/f T
Для температуры стеклования (ниже ее не работает):
ln η T /η Tc
отсюда
ln a T B (1/f T - 1/f c ),
ln a T
ln η Tc lnA B/f Tc
T Tc
B
2,3 f c f c /α f T Tc
Из этого эксперимента можно получить:
f = 4.8·10-4 [К -1], - коэффициент сдвига или перемещения по шкале температур
В первом приближении эти константы характерны для всех стеклообразных
систем. При Тс вязкость для этих систем считается 1013 Пз (как только достигает такого значения, то значит
тело перешло в стеклообразное состояние
Получаем уравнение, названное уравнением Вильямса-Лендела-Ферри:
lg a T 17,4
T Tc
51,6 T Tc
Формула применима при температуре: Тc < T < Tc + 100˚С
35. Уравнение Вильямса – Лэндела – Ферри (ВЛФ)
v f v g v g T Tgb
E a exp
v
f
ln
C1 T Tg
C 2 T Tg
ln
A T Tg
B T Tg
36. Связь вязкости и скорости сдвига
сдconst
d
f
dt
d
k
dt
d
сд
dt
Ньютоновская жидкость
Неньютоновская жидкость
1 d
k dt
1
1
37. Наибольшая ньютоновская вязкость
0Вязкость, при которой жидкость ЕЩЕ ведет себя как
ньютоновская
vw
ln 0 a b Уравнение Дулитла
vf
vh Уравнение Коэна - Тарнбалла
ln 0 a
vf
NA
0
e
V
Gвязк
RT
NA
0
e
V
S вязк
R
e
H вязк
RT
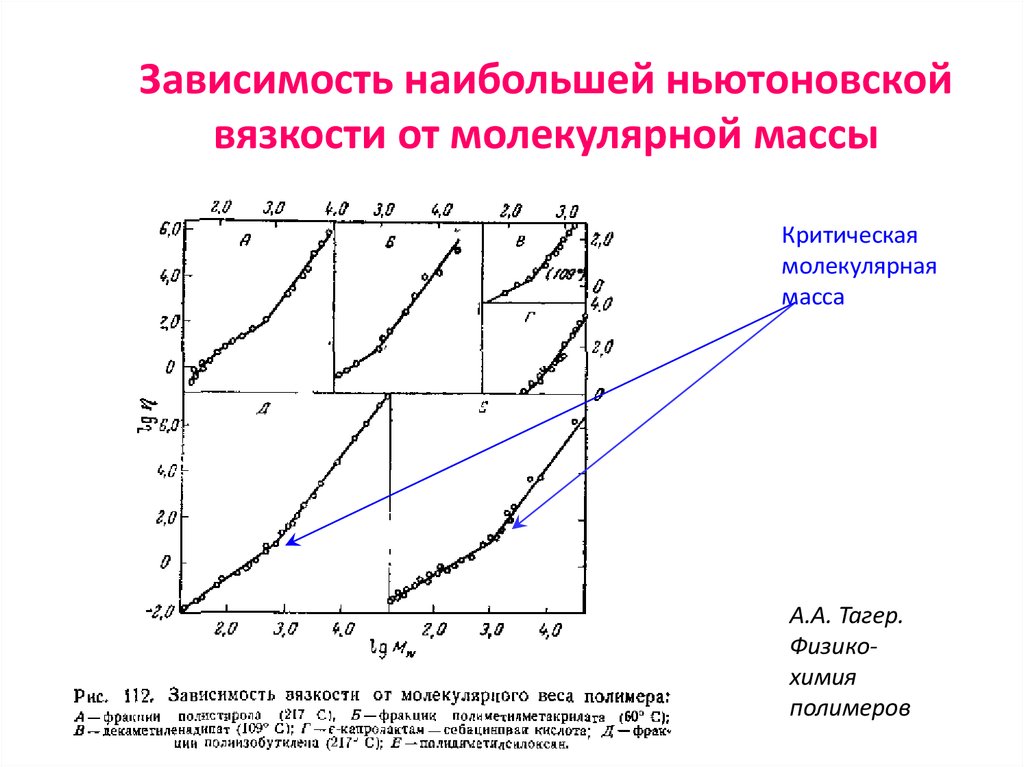
38. Зависимость наибольшей ньютоновской вязкости от молекулярной массы
Критическаямолекулярная
масса
А.А. Тагер.
Физикохимия
полимеров
39. Следствия уравнения Вильямса – Лэндела – Ферри (ВЛФ)
v f v g g v g T Tgln
C1 T Tg
C 2 T Tg
g b V
ln
vf
T Tg
T Tg
vf
v
g
g
A T T g
B T Tg
40. Для газов:
D=AD·exp(-BD/vf)
P=D·S
D – меняется на порядки
S – мало зависит от свойств полимера
P=AP·exp(-BP/vf)
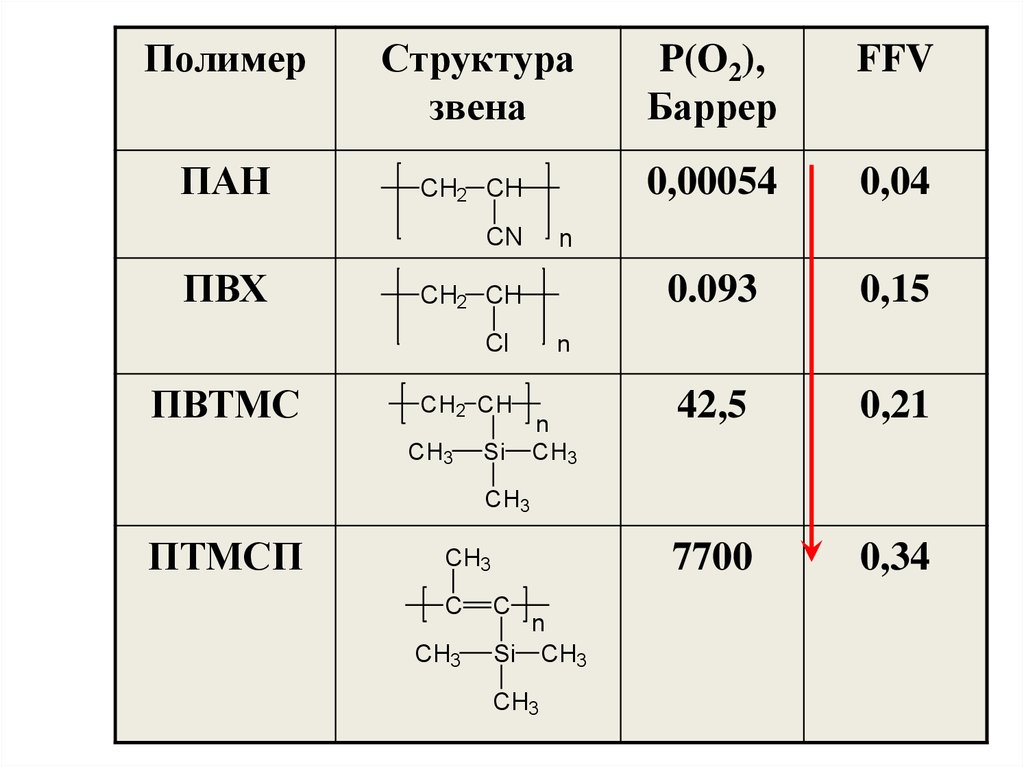
41.
ПолимерПАН
Структура
звена
P(O2),
Баррер
FFV
CH2 CH
0,00054
0,04
0.093
0,15
42,5
0,21
7700
0,34
CN
ПВХ
n
CH2 CH
Cl
ПВТМС
CH2 CH
CH3
Si
n
n
CH3
CH3
ПТМСП
CH3
C
CH3
C
n
Si CH3
CH3
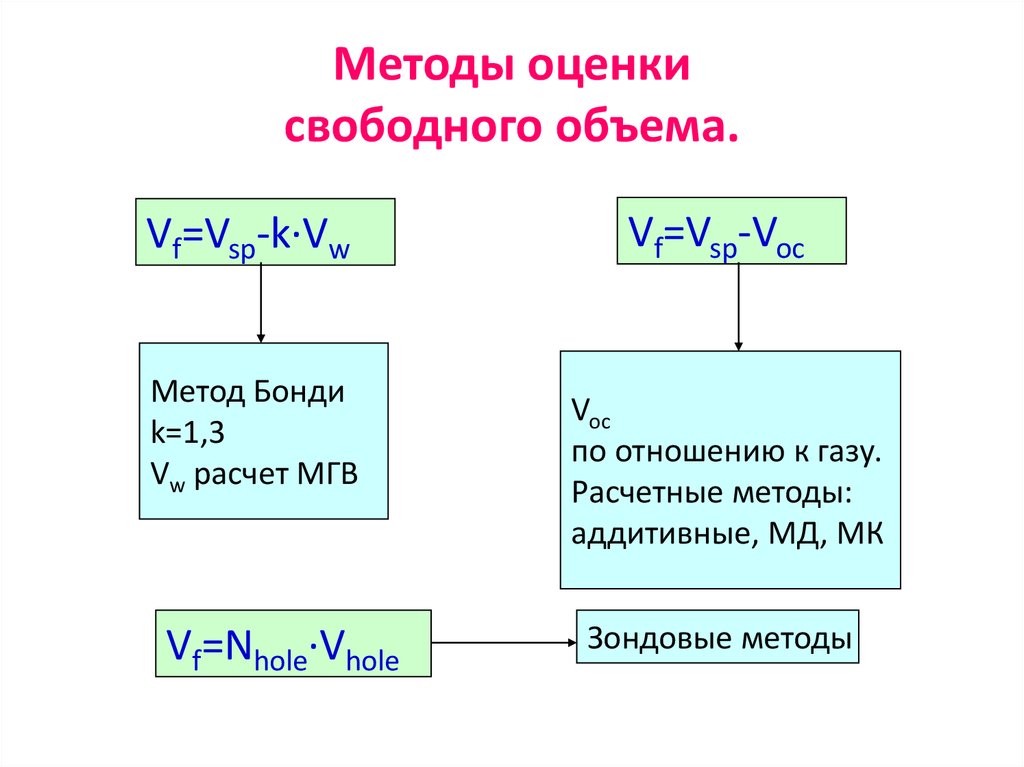
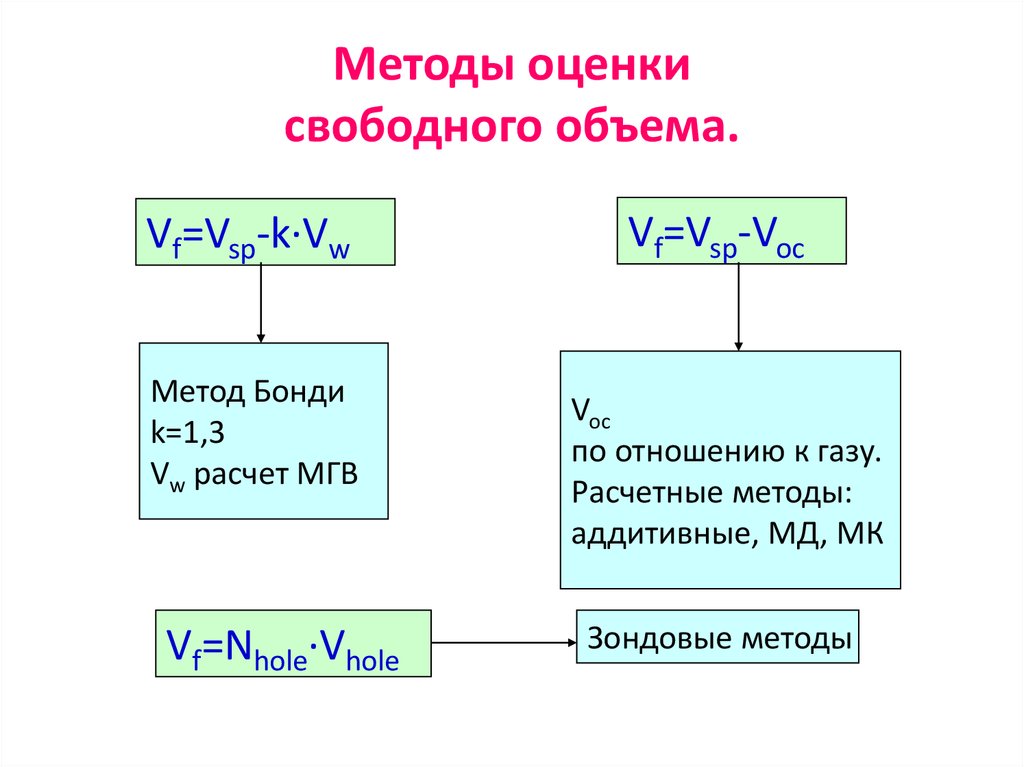
42. Методы оценки свободного объема.
Vf=Vsp-k·VwМетод Бонди
k=1,3
Vw расчет МГВ
Vf=Nhole·Vhole
Vf=Vsp-Voc
Voc
по отношению к газу.
Расчетные методы:
аддитивные, МД, МК
Зондовые методы
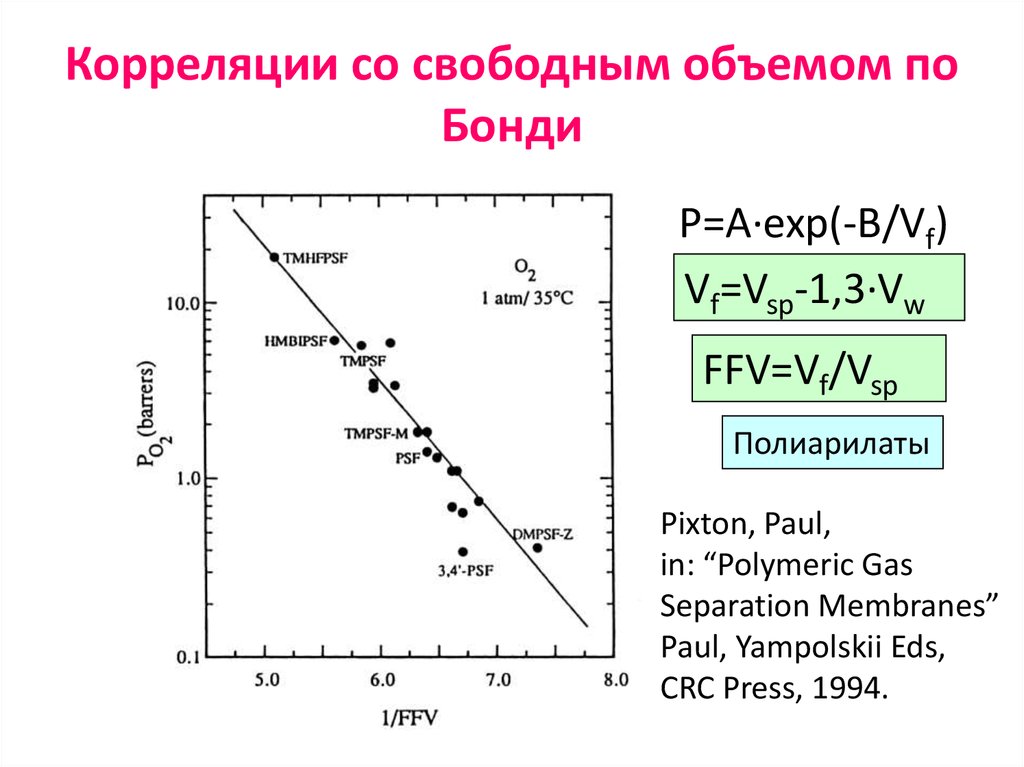
43. Корреляции со свободным объемом по Бонди
P=A·exp(-B/Vf)Vf=Vsp-1,3·Vw
FFV=Vf/Vsp
Полиарилаты
Pixton, Paul,
in: “Polymeric Gas
Separation Membranes”
Paul, Yampolskii Eds,
CRC Press, 1994.
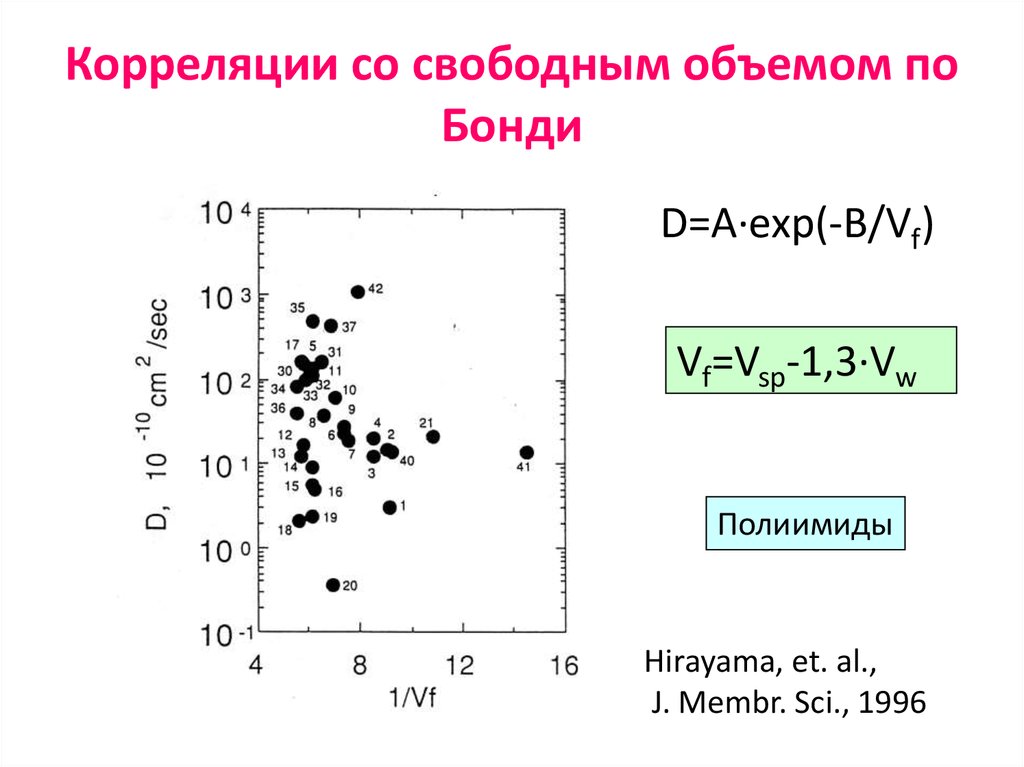
44. Корреляции со свободным объемом по Бонди
D=A·exp(-B/Vf)Vf=Vsp-1,3·Vw
Полиимиды
Hirayama, et. al.,
J. Membr. Sci., 1996
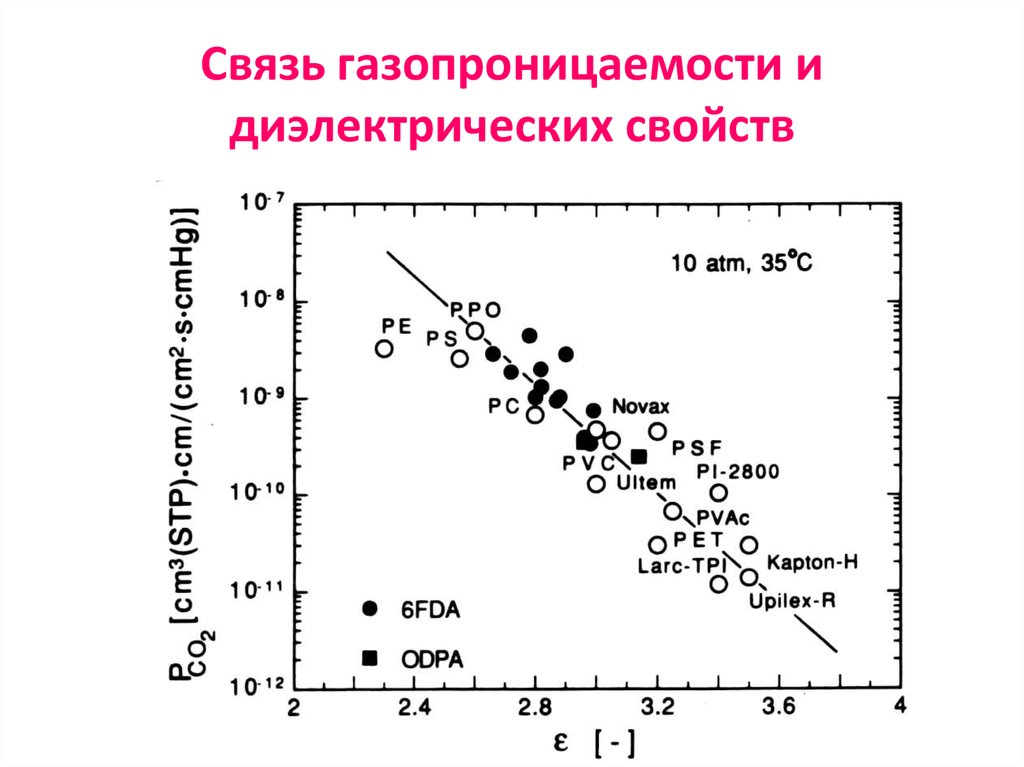
45. Связь газопроницаемости и диэлектрических свойств
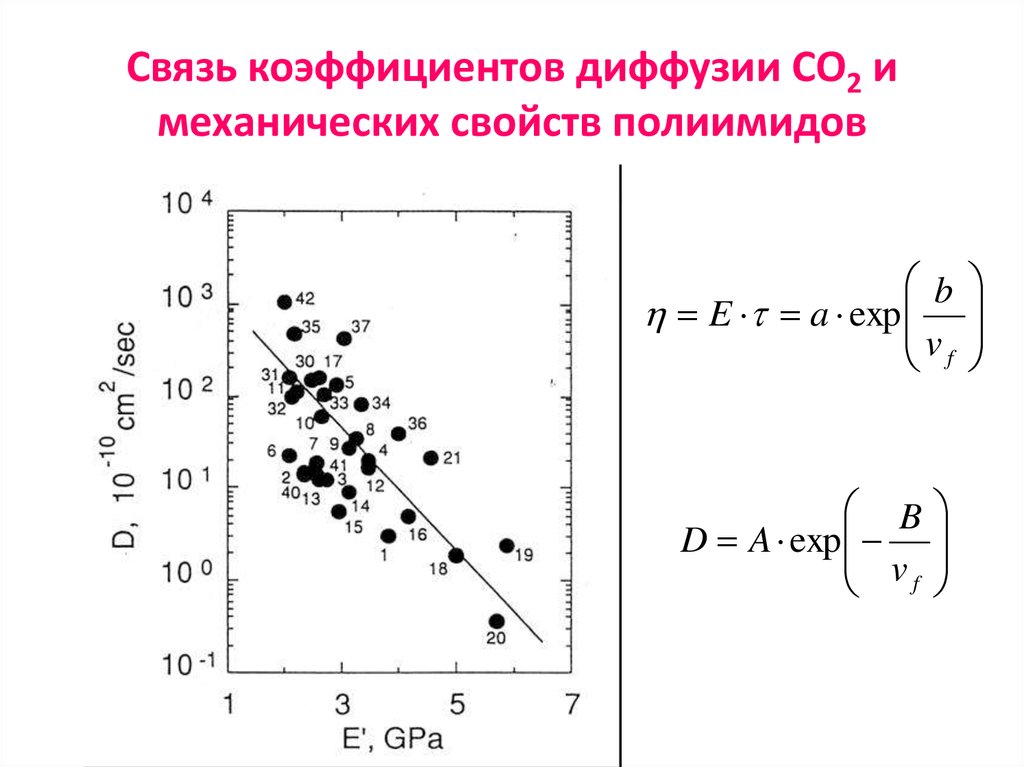
46. Связь коэффициентов диффузии CO2 и механических свойств полиимидов
bE a exp
vf
B
D A exp
v
f
47. Методы оценки свободного объема.
Vf=Vsp-k·VwМетод Бонди
k=1,3
Vw расчет МГВ
Vf=Nhole·Vhole
Vf=Vsp-Voc
Voc
по отношению к газу.
Расчетные методы:
аддитивные, МД, МК
Зондовые методы
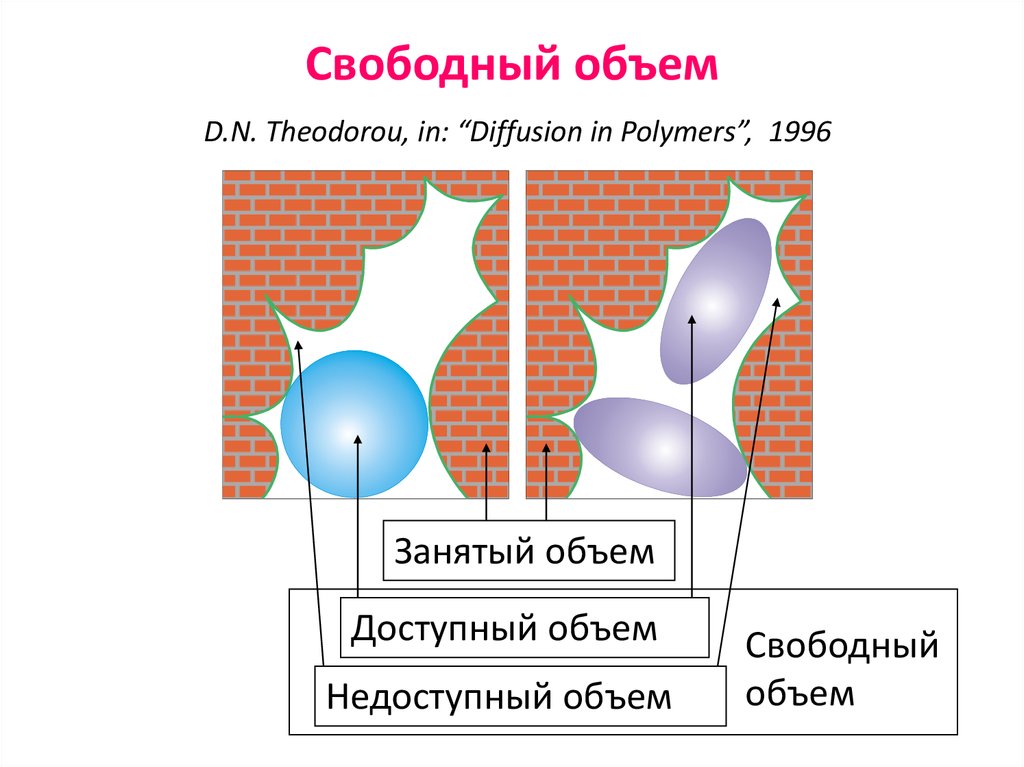
48. Свободный объем D.N. Theodorou, in: “Diffusion in Polymers”, 1996
Занятый объемДоступный объем
Недоступный объем
Свободный
объем
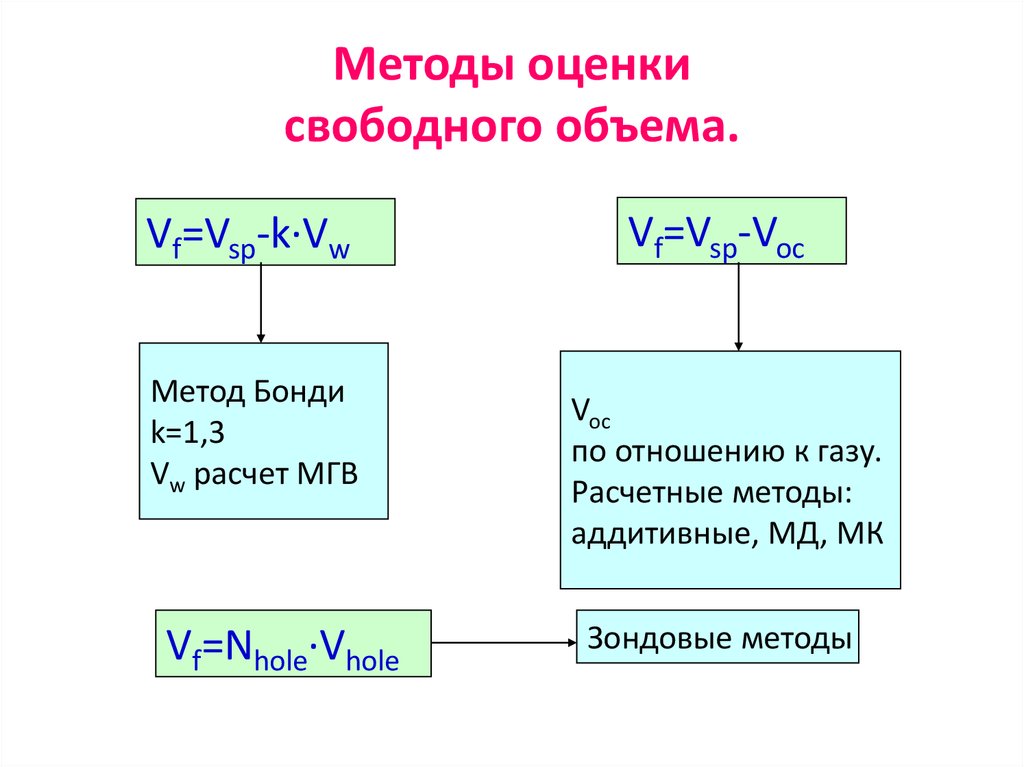
49. Методы оценки свободного объема.
Vf=Vsp-k·VwМетод Бонди
k=1,3
Vw расчет МГВ
Vf=Nhole·Vhole
Vf=Vsp-Voc
Voc
по отношению к газу.
Расчетные методы:
аддитивные, МД, МК
Зондовые методы
50. Зондовые методы
1. Методы с переменным размером зонда:Сорбция газов и паров (CH’)
Обращенная газовая хроматография
Спиновые зонды
Фотохромные зонды
Электрохромные зонды
Конформационные зонды (ИК)
Проницаемость и диффузия газов
2. Методы с постоянным размером зонда
Аннигиляция позитронов
129Xe-ЯМР
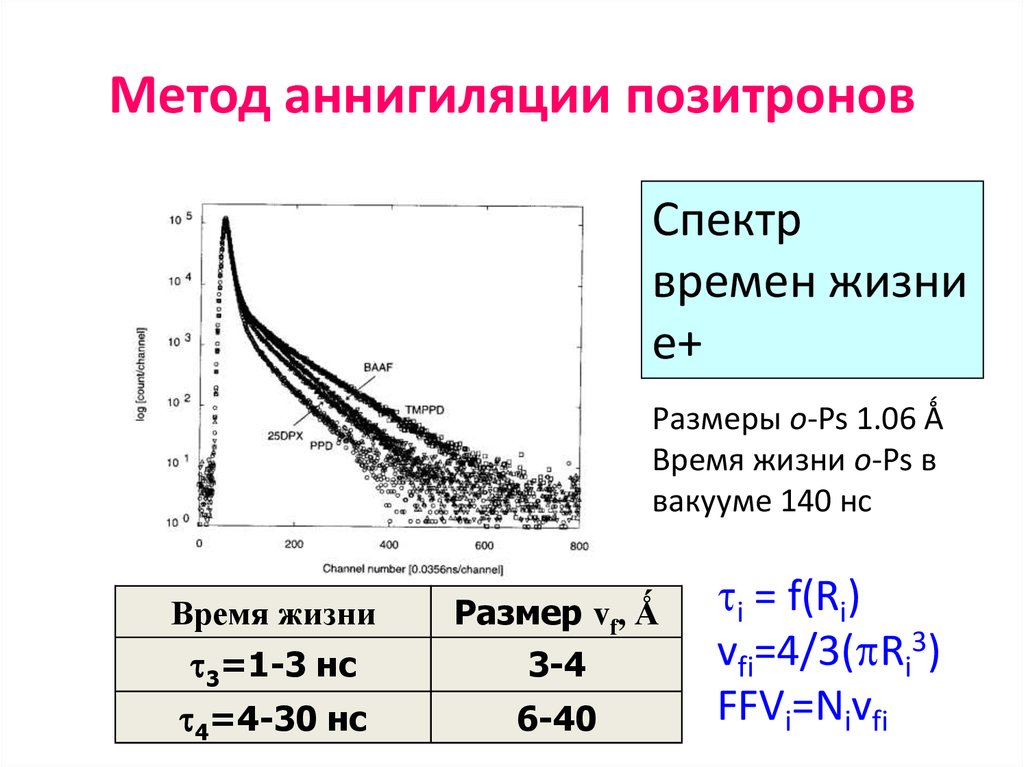
51. Метод аннигиляции позитронов
Спектрвремен жизни
e+
Размеры o-Ps 1.06 Ǻ
Время жизни o-Ps в
вакууме 140 нс
Время жизни
Размер vf, Ǻ
3=1-3 нс
3-4
4=4-30 нс
6-40
i = f(Ri)
vfi=4/3( Ri3)
FFVi=Nivfi
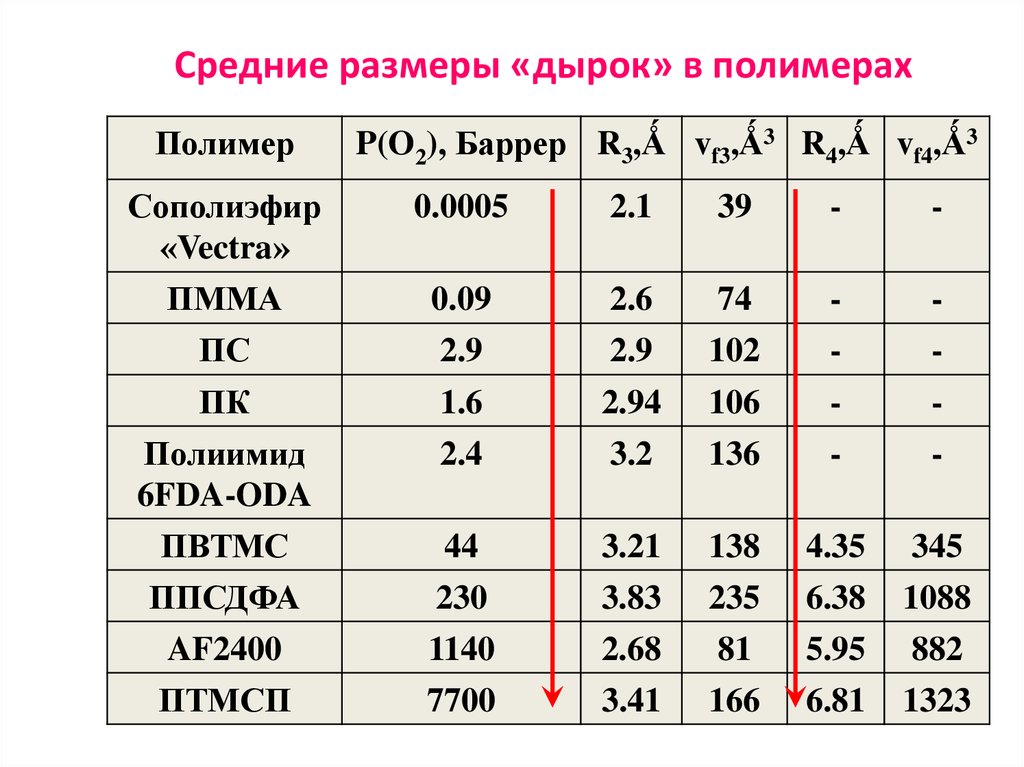
52. Средние размеры «дырок» в полимерах
ПолимерP(O2), Баррер R3,Ǻ vf3,Ǻ3 R4,Ǻ vf4,Ǻ3
Сополиэфир
«Vectra»
ПММА
ПС
0.0005
2.1
39
-
-
0.09
2.9
2.6
2.9
74
102
-
-
ПК
Полиимид
6FDA-ODA
ПВТМС
1.6
2.4
2.94
3.2
106
136
-
-
44
3.21
138
4.35
345
ППСДФА
AF2400
ПТМСП
230
1140
7700
3.83
2.68
3.41
235
81
166
6.38
5.95
6.81
1088
882
1323
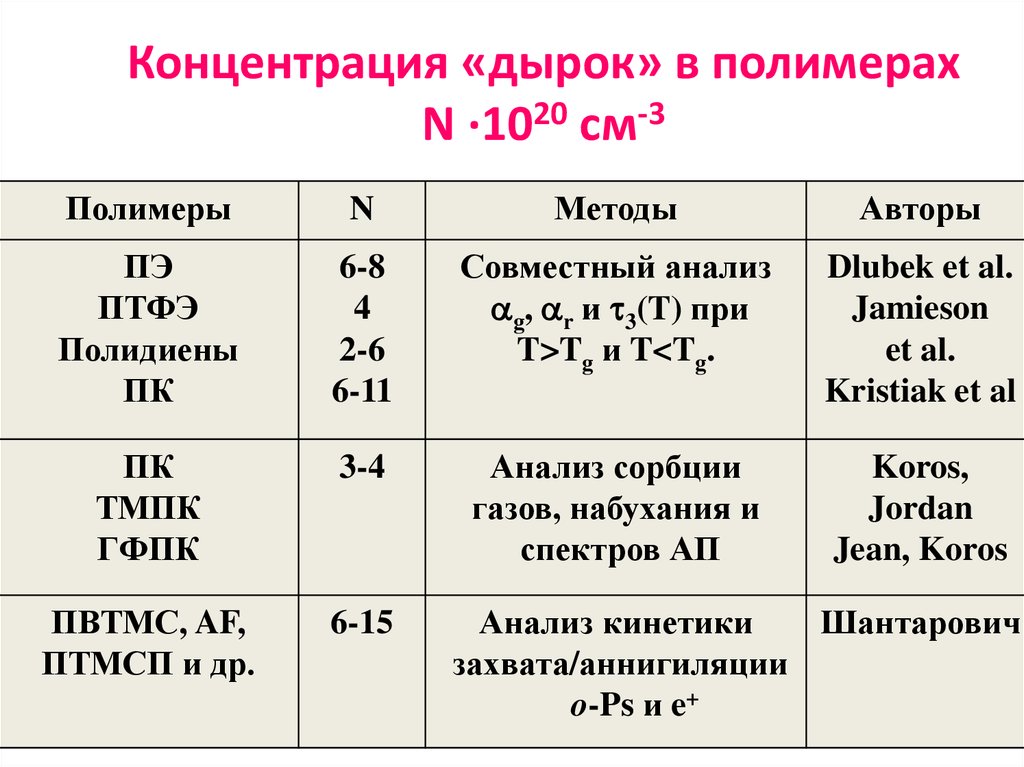
53. Концентрация «дырок» в полимерах N ·1020 см-3
ПолимерыN
Методы
Авторы
ПЭ
ПТФЭ
Полидиены
ПК
6-8
4
2-6
6-11
Совместный анализ
g, r и 3(T) при
T>Tg и T<Tg.
Dlubek et al.
Jamieson
et al.
Kristiak et al
ПК
ТМПК
ГФПК
3-4
Анализ сорбции
газов, набухания и
спектров АП
Koros,
Jordan
Jean, Koros
ПВТМС, AF,
ПТМСП и др.
6-15
Анализ кинетики
Шантарович
захвата/аннигиляции
o-Ps и e+
54. Подвижность «дырок»
Масштабный эффектИзменение характеристик
пленки с изменением ее
толщины
Следствие релаксационных
процессов в полимерах
(процессов старения)
55.
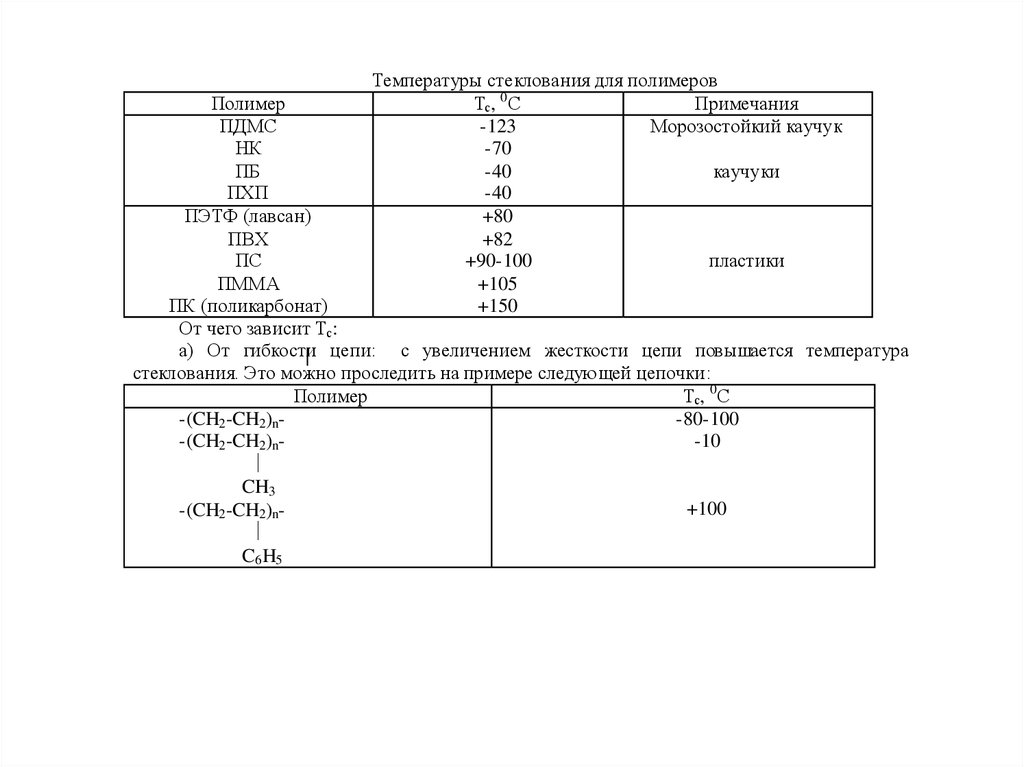
Температуры стеклования для полимеровТс, 0 С
Примечания
-123
Морозостойкий каучук
-70
-40
каучуки
-40
+80
+82
+90-100
пластики
+105
+150
Полимер
ПДМС
НК
ПБ
ПХП
ПЭТФ (лавсан)
ПВХ
ПС
ПММА
ПК (поликарбонат)
От чего зависит Тс:
а) От гибкости цепи: с увеличением жесткости цепи повышается температура
стеклования. Это можно проследить на примере следующей цепочки:
Полимер
Тс, 0 С
-(CH2 -CH2 )n-80-100
-(CH2 -CH2 )n-10
CH3
+100
-(CH2 -CH2 )n
C6 H5
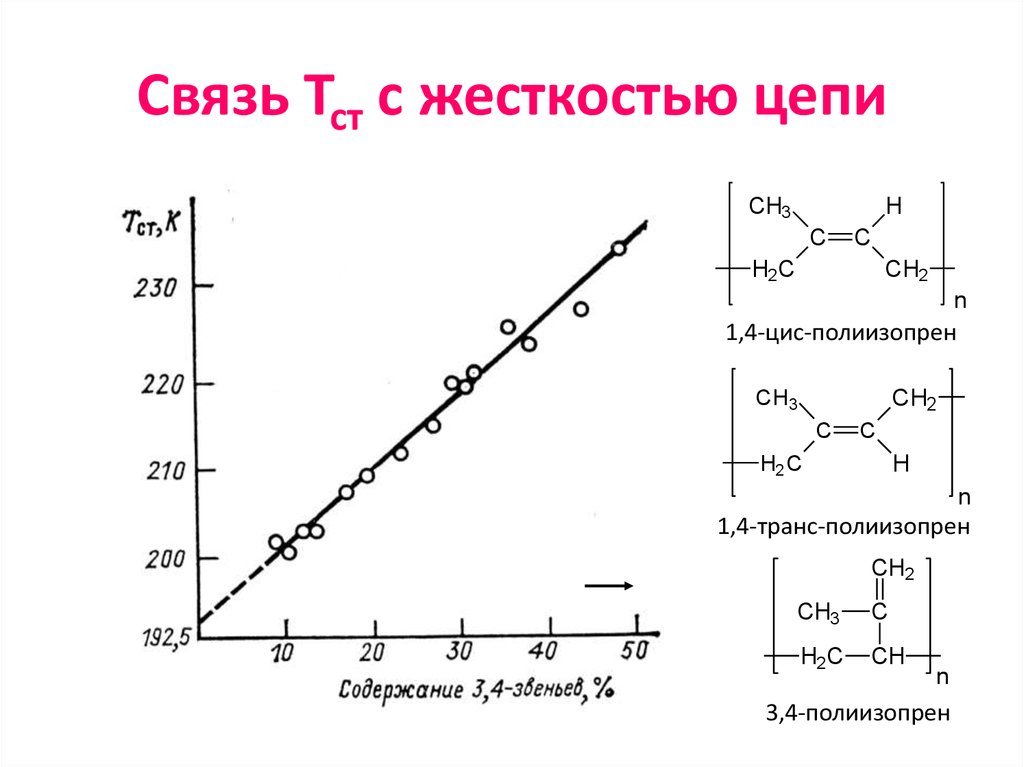
56. Связь Тст с жесткостью цепи
CH3H
C
C
H2C
CH2
n
1,4-цис-полиизопрен
CH2
CH3
C
C
H
H2 C
n
1,4-транс-полиизопрен
CH2
CH3
C
H2C
CH
n
3,4-полиизопрен
57. Связь Тст с жесткостью цепи
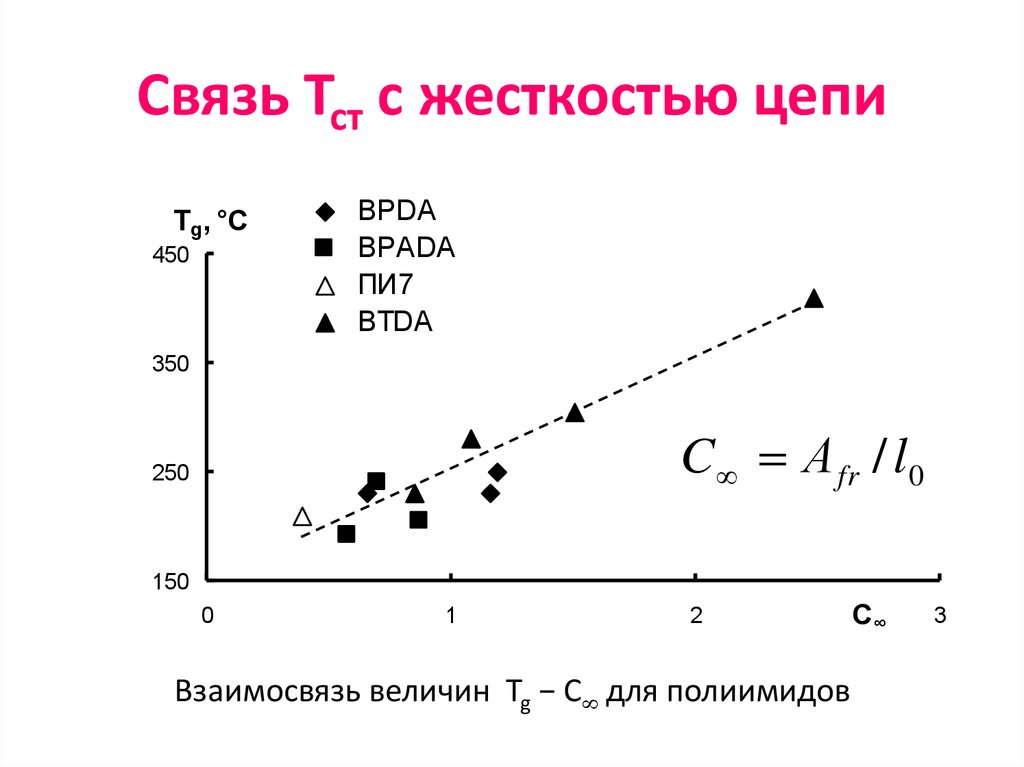
Tg, °С450
BPDA
BPADA
ПИ7
BTDA
350
C А fr / l0
250
150
0
1
2
Взаимосвязь величин Tg − C для полиимидов
С∞
3
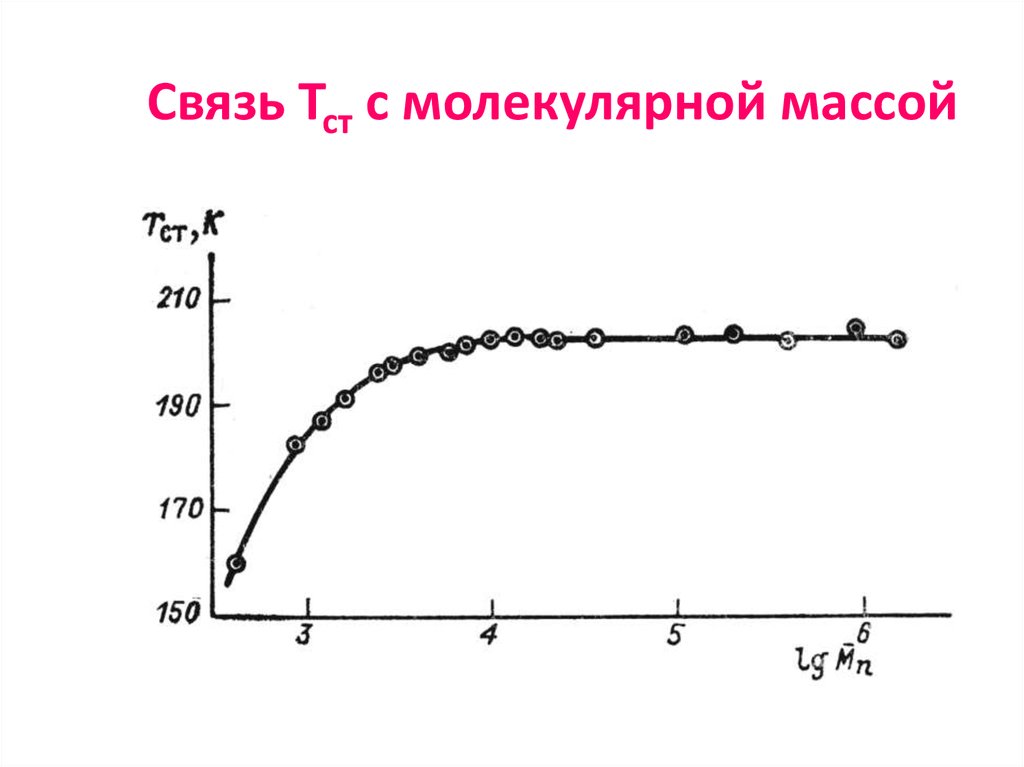
58. Связь Тст с молекулярной массой
59. Пластификация
• Термодинамическая совместимость с полимером(истинный раствор)
• Следовательно, «разбавление» раствора,
увеличение подвижности цепей и снижение Тс
• Отсутствие «сильных» взаимодействий с
функциональными группами полимера
• Следовательно, ВСЕГДА снижение Тс и увеличение
пластичности материала
• Для пластификаторов пластмасс важно: нелетучесть
(в условиях эксплуатации), отсутствие
«выпотевания», нетоксичность, химическая
стойкость, температура разложения ниже
температуры переработки полимера
60.
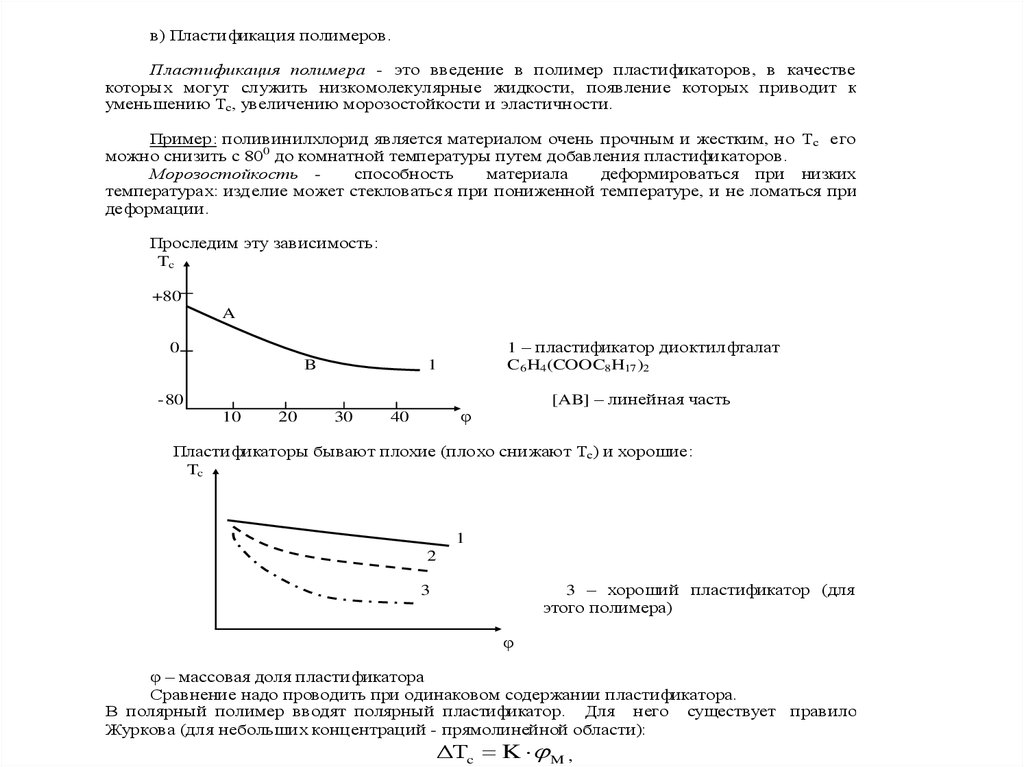
в) Пласти фикация полимеров.Пластификация полимера - это введение в полимер пластификаторов, в качестве
которы х могут служить низкомолекулярные жидкости, появление которых приводит к
уменьшению Тс, увеличению морозостойкости и эластичности.
Пример: поливинилхлорид является материалом очень прочным и жестким, но Тс его
можно снизить с 800 до комнатной температуры путем добавления пластифи каторов.
Морозостойкость способность
материала
деформироваться при низких
температурах: изделие может стекловаться при пониженной температуре, и не ломаться при
деформации.
Проследим эту зависимость:
Tc
+80
A
1 – пластификатор диоктилфталат
C6 H4 (COOC8 H17 )2
0
B
1
[AB] – линейная часть
-80
10
20
30
φ
40
Пласти фикаторы бывают плохие (плохо снижают Тс) и хорошие:
Tc
1
2
3 – хороший пластификатор (для
этого полимера)
3
φ
φ – массовая доля пласти фикатора
Сравнение надо проводить при одинаковом содержании пластификатора.
В полярный полимер вводят полярный пластификатор. Для него существует правило
Журкова (для небольши х концентраций - прямолинейной области):
ΔTc K M ,
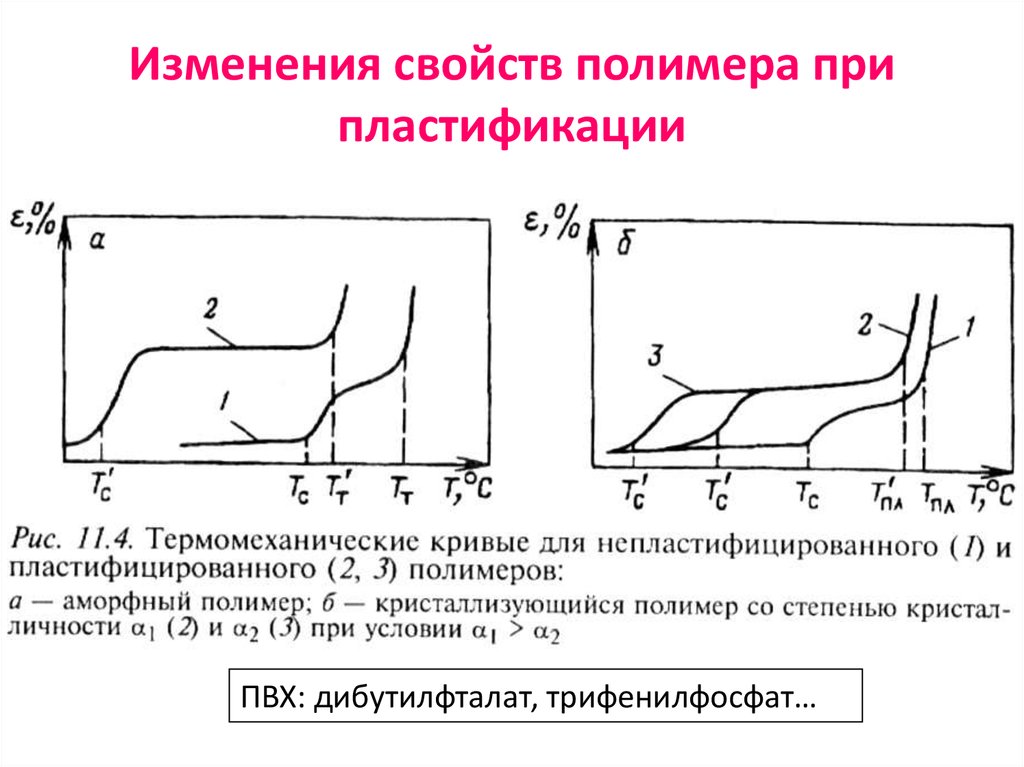
61. Изменения свойств полимера при пластификации
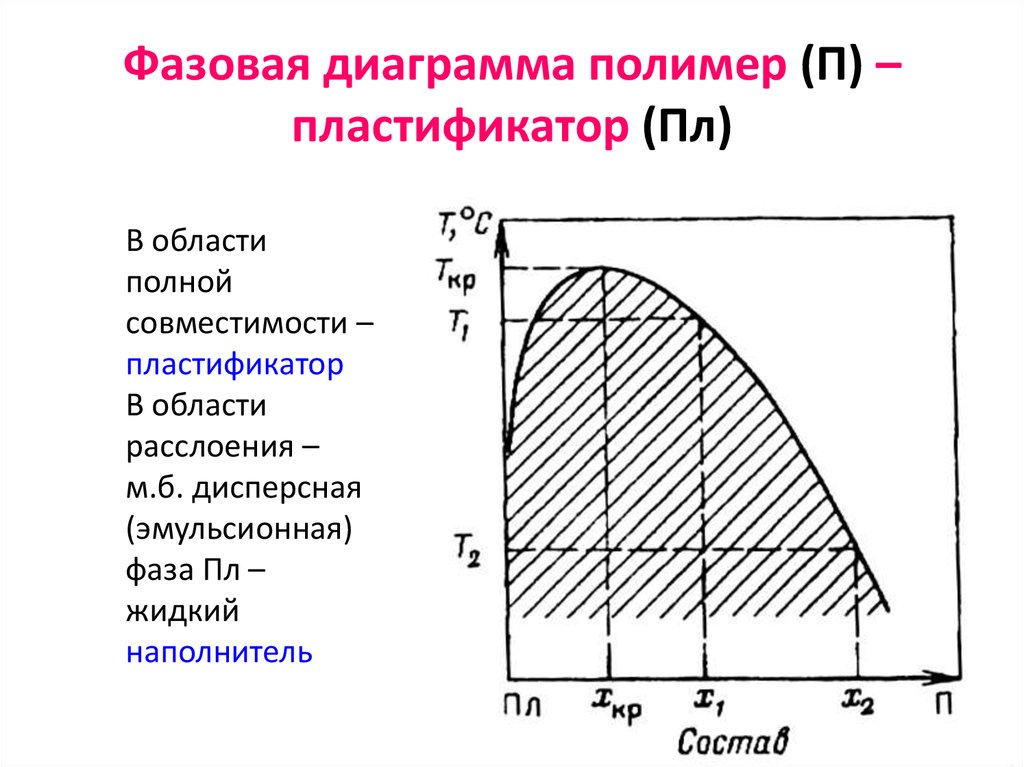
ПВХ: дибутилфталат, трифенилфосфат…62. Фазовая диаграмма полимер (П) – пластификатор (Пл)
В областиполной
совместимости –
пластификатор
В области
расслоения –
м.б. дисперсная
(эмульсионная)
фаза Пл –
жидкий
наполнитель
63. Антипластификация
• Термодинамическая совместимость с полимером(истинный раствор)
• Следовательно, «разбавление» раствора, увеличение
подвижности цепей и снижение Тс
• Наличие «сильных» взаимодействий с
функциональными группами полимера
• Следовательно, увеличение Тс и увеличение
жесткости материала
• Поэтому, антипластификация может приводить как к
снижению, так и к увеличению Тс, а, следовательно, к
возможности управления свойствами пластмасс.
• Вопрос изучен мало
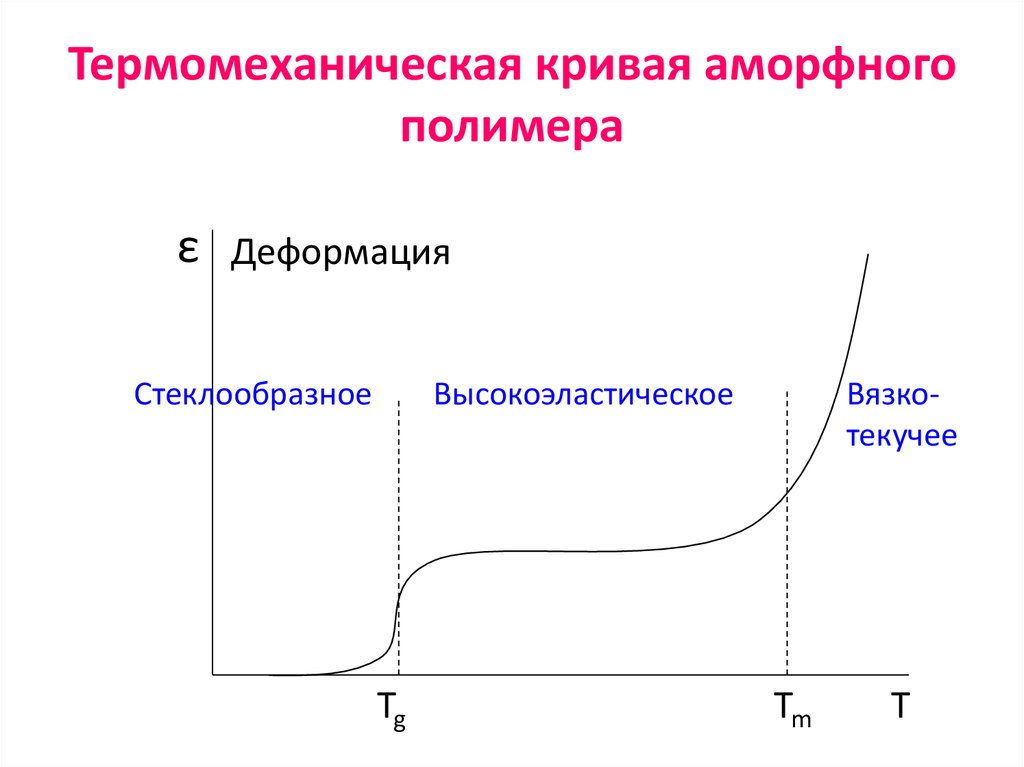
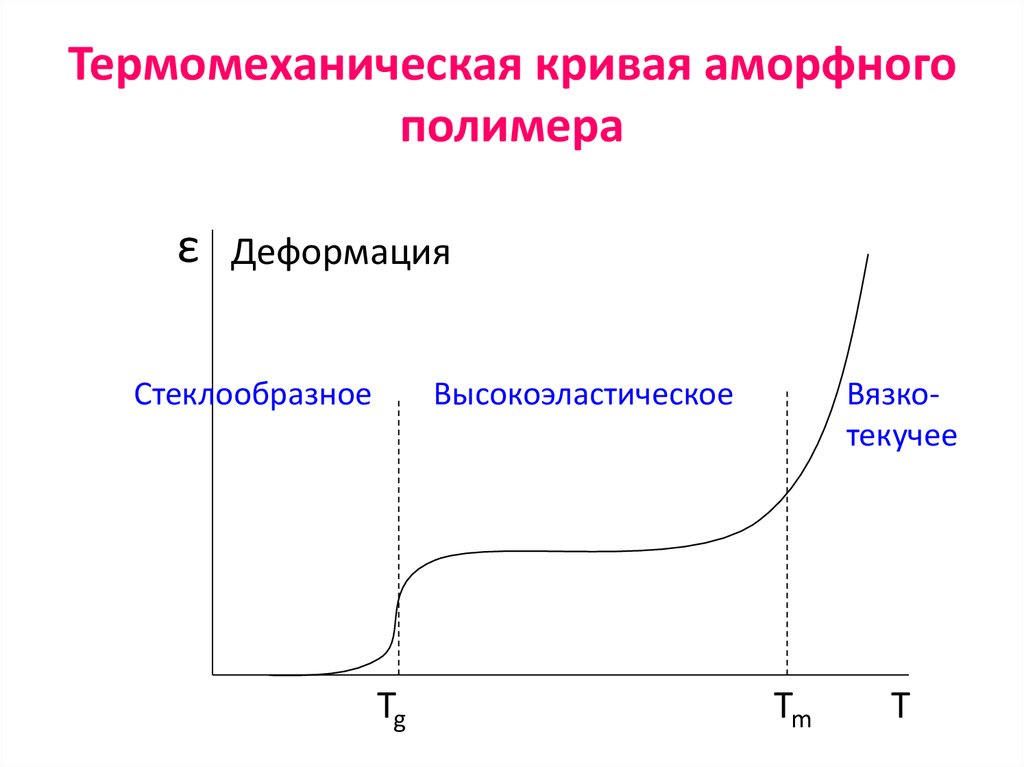
64. Термомеханическая кривая аморфного полимера
εДеформация
Стеклообразное
Высокоэластическое
Tg
Вязкотекучее
Tm
T
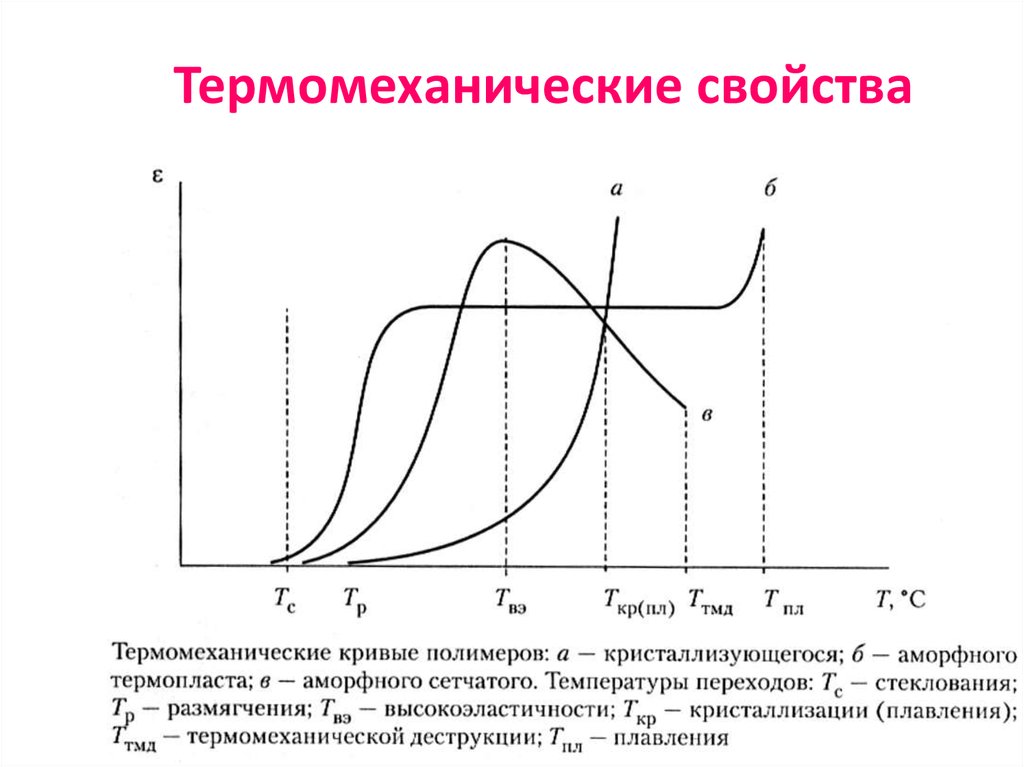
65. Термомеханические свойства
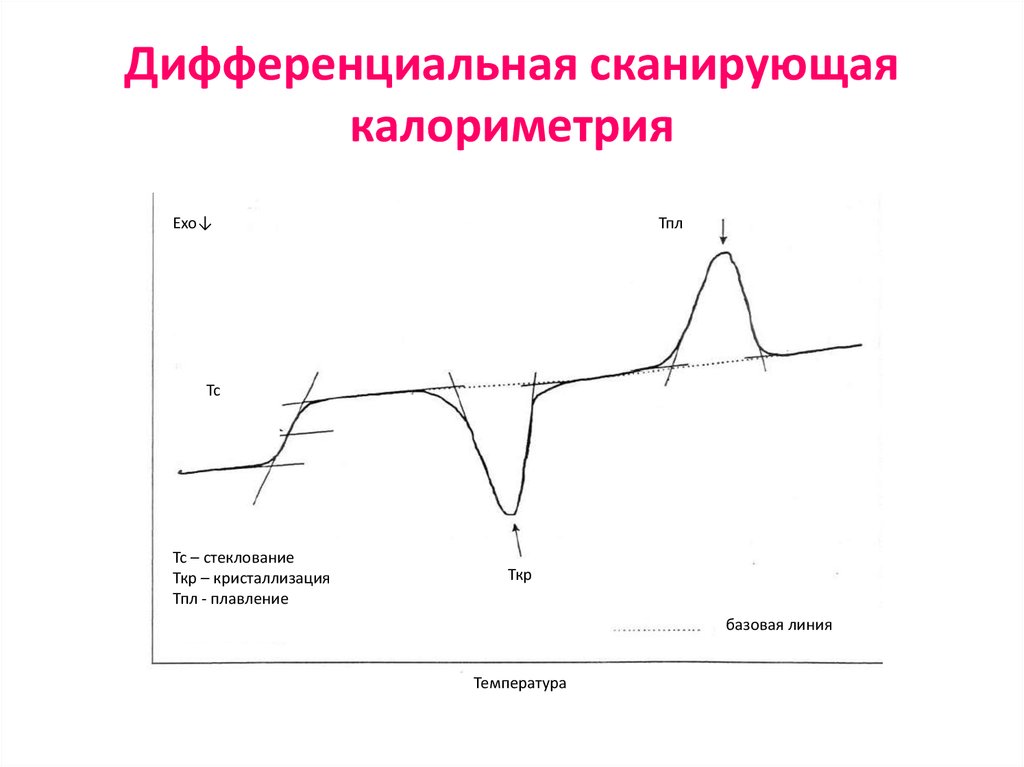
66. Дифференциальная сканирующая калориметрия
Exo↓Тпл
Тс
Тс – стеклование
Ткр – кристаллизация
Тпл - плавление
Ткр
базовая линия
Температура
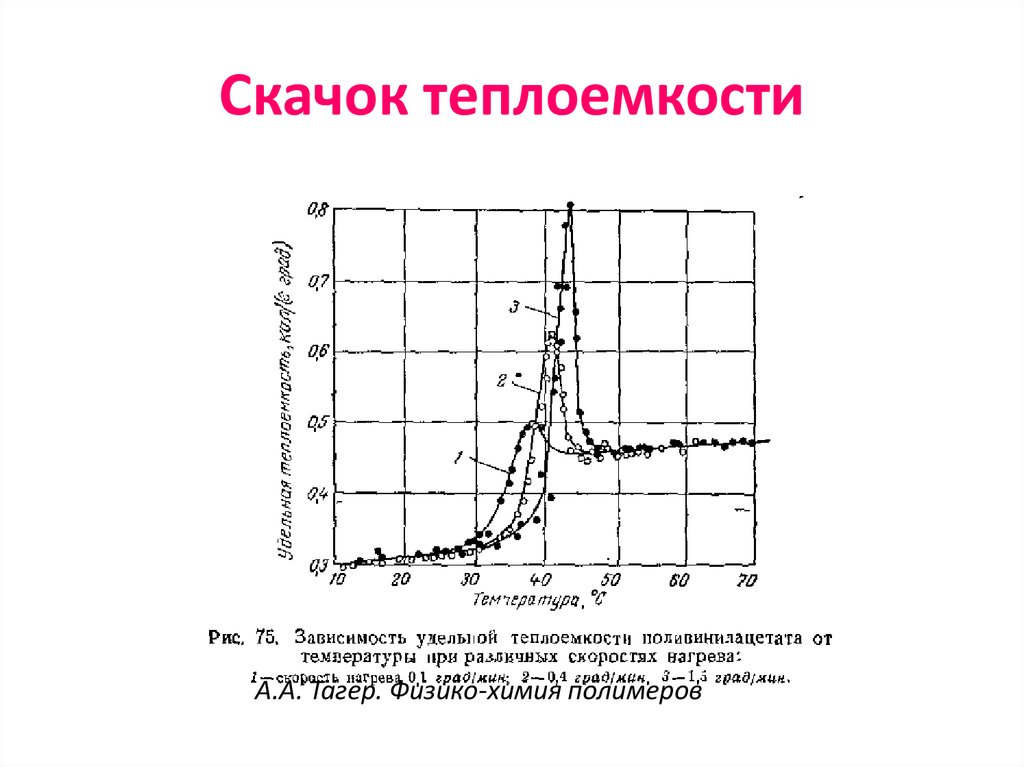
67. Скачок теплоемкости
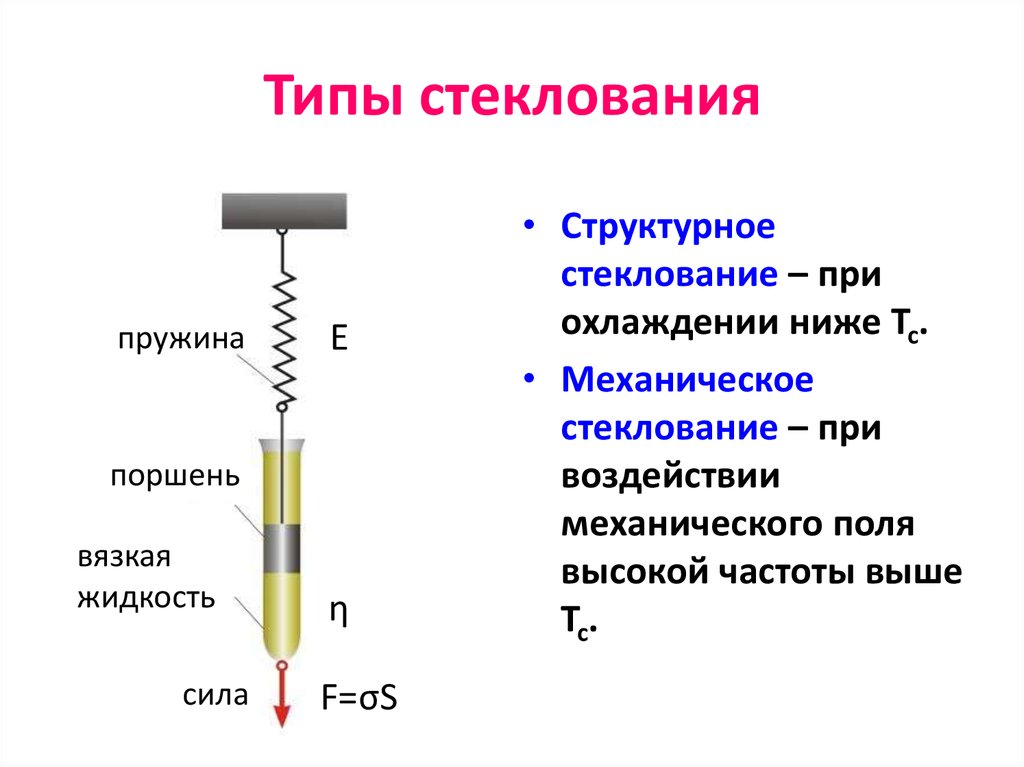
А.А. Тагер. Физико-химия полимеров68. Типы стеклования
пружинаE
поршень
вязкая
жидкость
сила
η
F=σS
• Структурное
стеклование – при
охлаждении ниже Тс.
• Механическое
стеклование – при
воздействии
механического поля
высокой частоты выше
Тс.
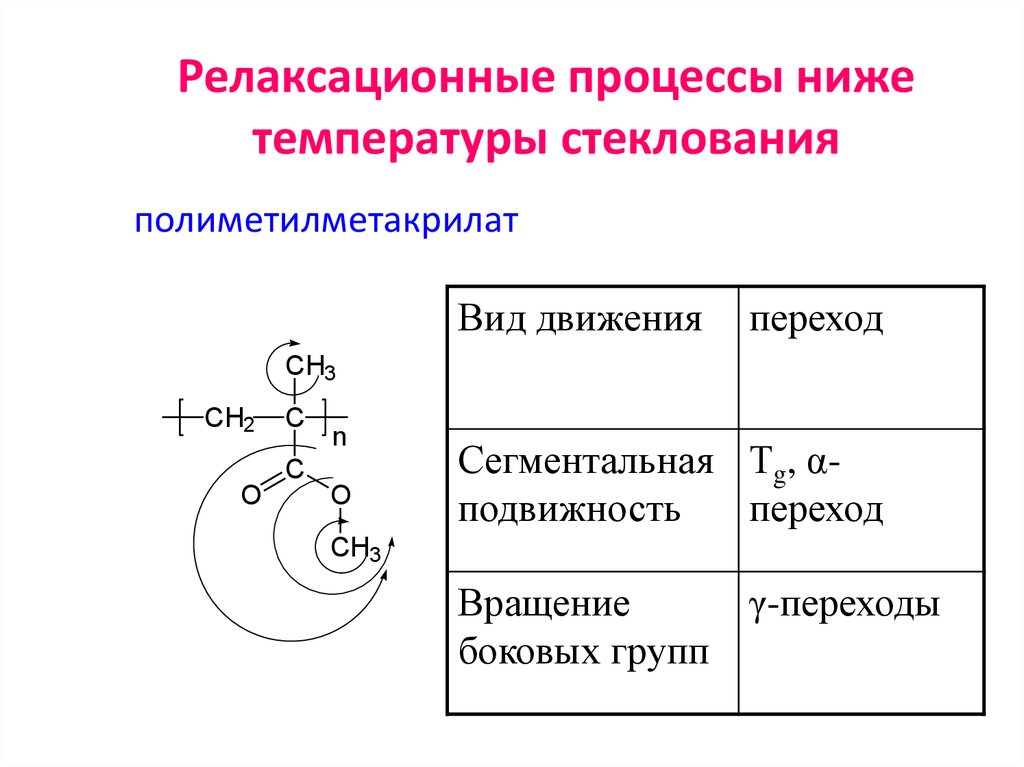
69. Релаксационные процессы ниже температуры стеклования
полиметилметакрилатВид движения
переход
CH3
CH2
O
C
C
n
O
Сегментальная Тg, αподвижность
переход
CH3
Вращение
γ-переходы
боковых групп
70. Итак:
• «Дырки» в стеклообразном полимере– физические объекты, характерный
размер и подвижность которых
определяется физическими методами
• Средний размер «дырок» в
стеклообразном полимере определяет
его газопроницаемость
• Средняя концентрация «дырок» в
стеклообразном полимере – величина
постоянная
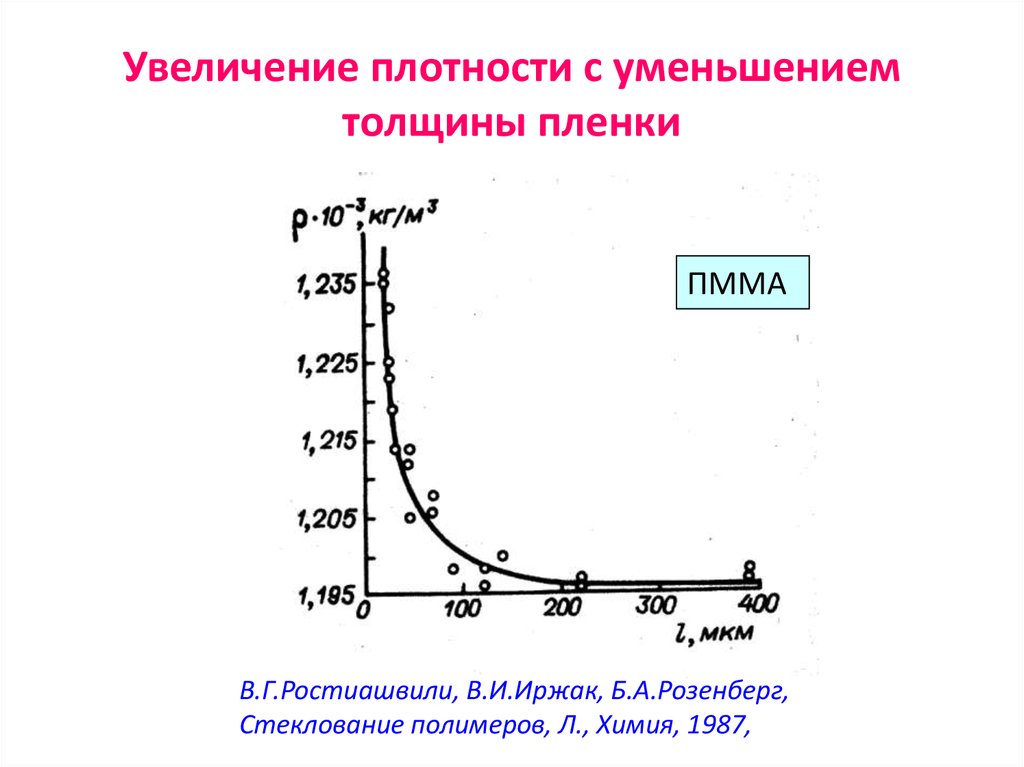
71. Увеличение плотности с уменьшением толщины пленки
ПММАВ.Г.Ростиашвили, В.И.Иржак, Б.А.Розенберг,
Стеклование полимеров, Л., Химия, 1987,
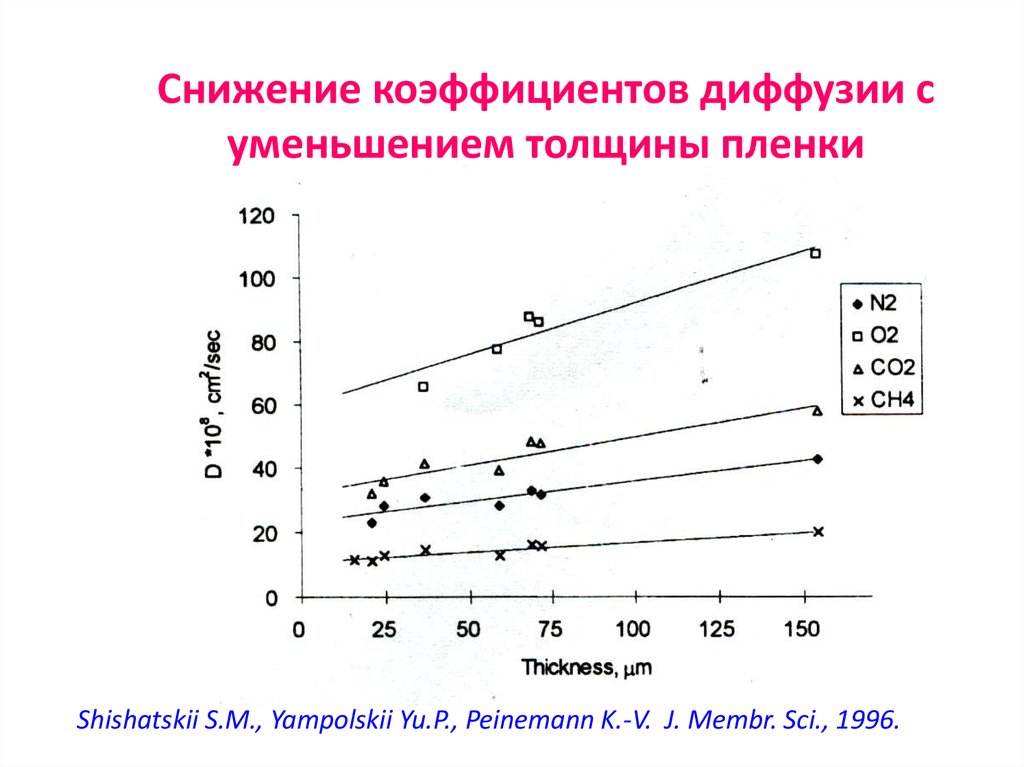
72. Снижение коэффициентов диффузии с уменьшением толщины пленки
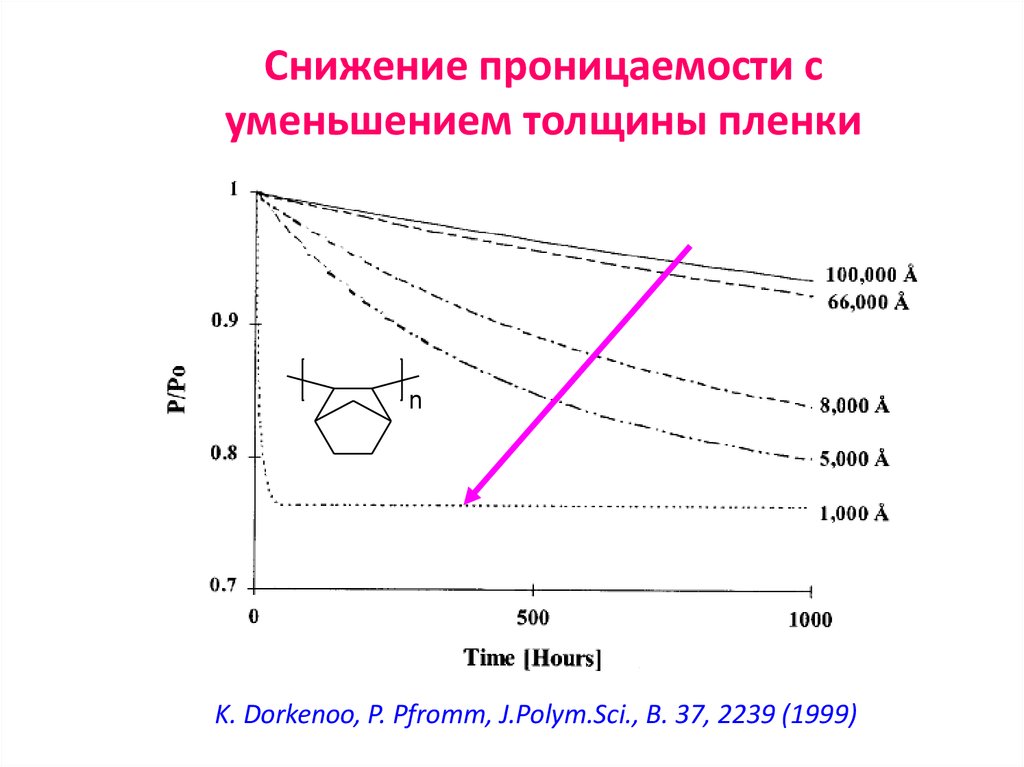
Shishatskii S.M., Yampolskii Yu.P., Peinemann K.-V. J. Membr. Sci., 1996.73. Снижение проницаемости с уменьшением толщины пленки
nK. Dorkenoo, P. Pfromm, J.Polym.Sci., B. 37, 2239 (1999)
74. Причины масштабного эффекта
Диффузия «дырок» (элементов свободного объема) кповерхности образца (пленка, мембрана)
В.Г.Ростиашвили, В.И.Иржак, Б.А.Розенберг,
Стеклование полимеров, Л., Химия, 1987,
M.McCaig, D.Paul, Polymer, 41(2), 629 (2000)
По скорости старения и профилю плотности
определяется коэффициент диффузии «дырок» в
стеклообразных полимерах
D = 10-14 – 10-16 см2/с
75. Термомеханическая кривая аморфного полимера
εДеформация
Стеклообразное
Высокоэластическое
Tg
Вязкотекучее
Tm
T
76. Свободный объем и реология полимеров
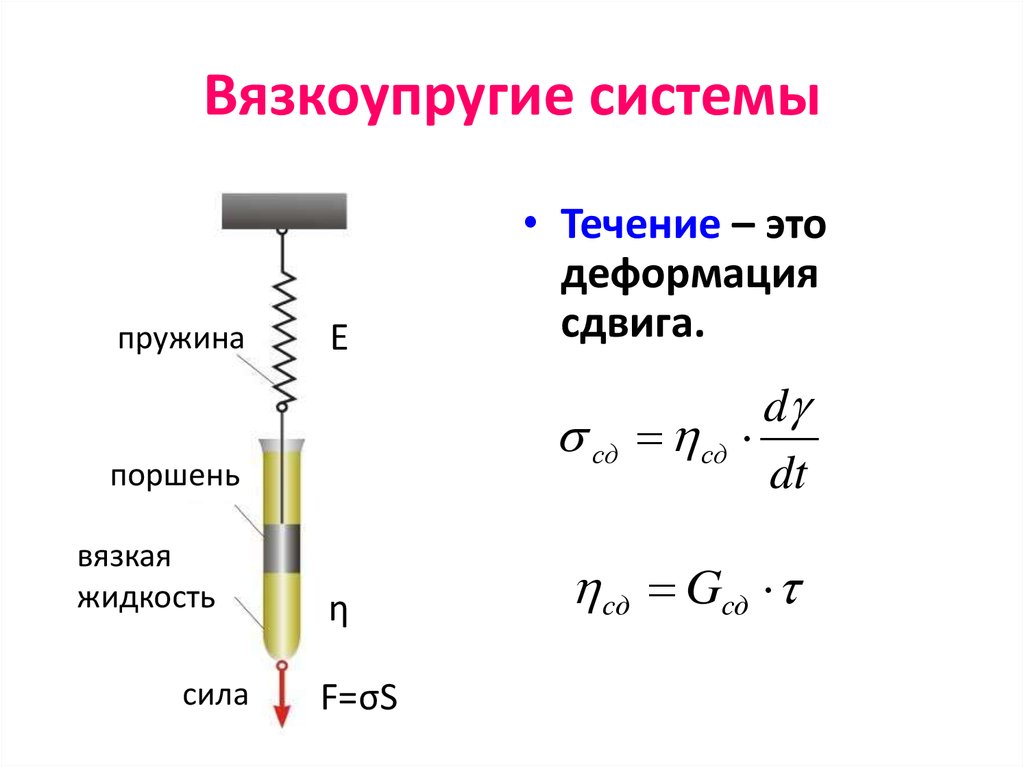
77. Вязкоупругие системы
пружинаE
сд
поршень
вязкая
жидкость
сила
• Течение – это
деформация
сдвига.
η
F=σS
d
сд
dt
сд Gсд
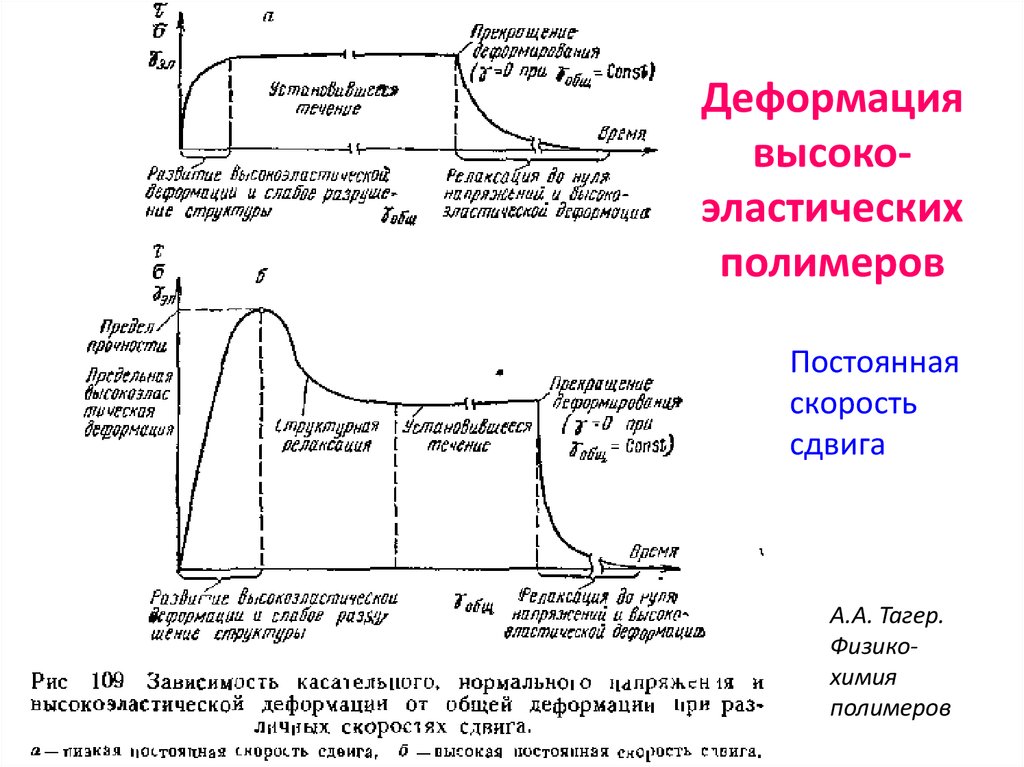
78. Деформация высоко-эластических полимеров
Деформациявысокоэластических
полимеров
Постоянная
скорость
сдвига
А.А. Тагер.
Физикохимия
полимеров
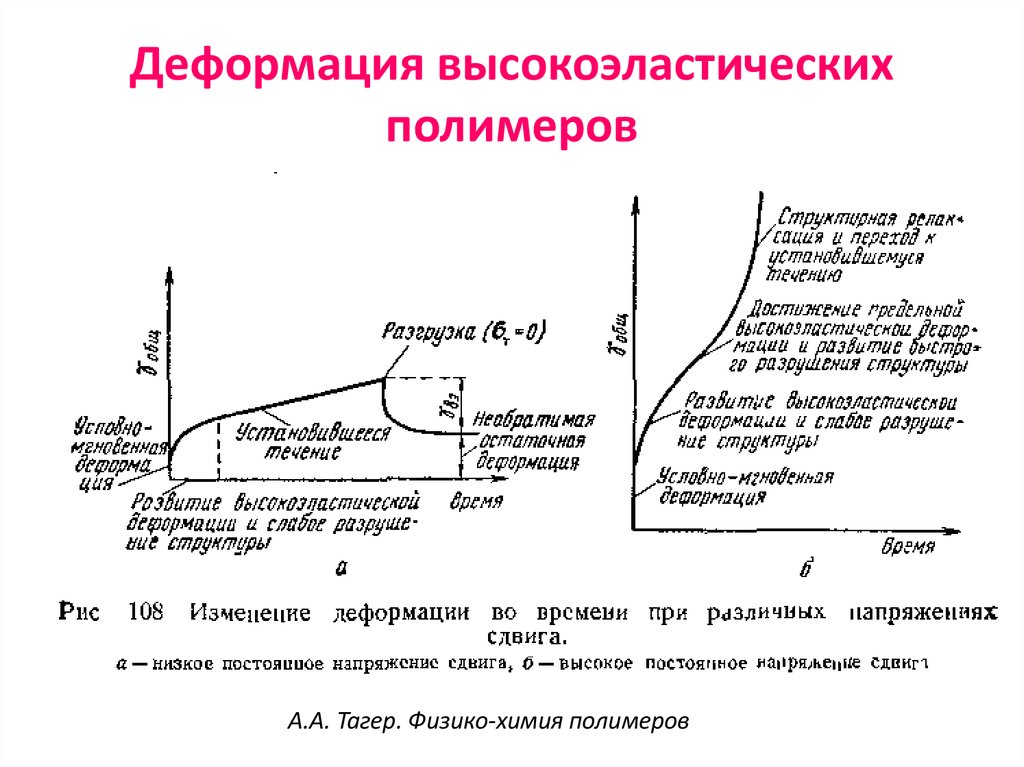
79. Деформация высокоэластических полимеров
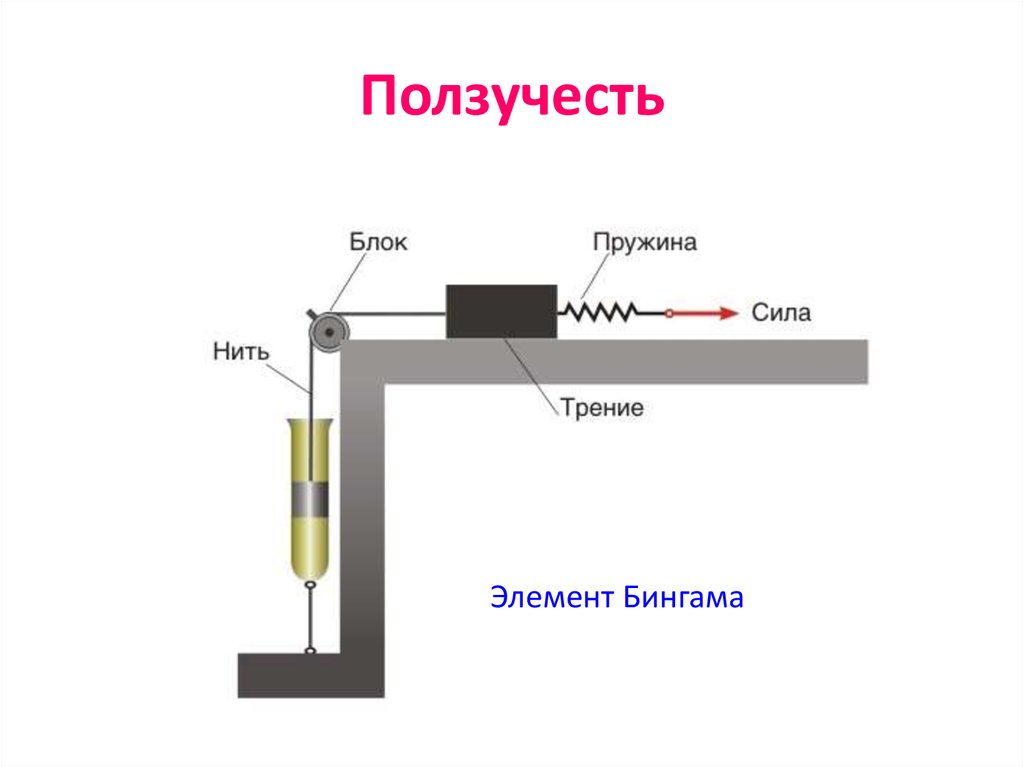
А.А. Тагер. Физико-химия полимеров80. Ползучесть
Элемент Бингама81. Высокоэластичность вязкотекучего состояния
При определенных значениях напряжения сдвига вязкая жидкостьпроявляет высокоэластические свойства
82. Высокоэластичность вязкотекучего состояния
Эффект ВейсенбергаПри больших скоростях
деформирования
вязкоупругие жидкости
способны к большим
обратимым
высокоэластическим
деформациям
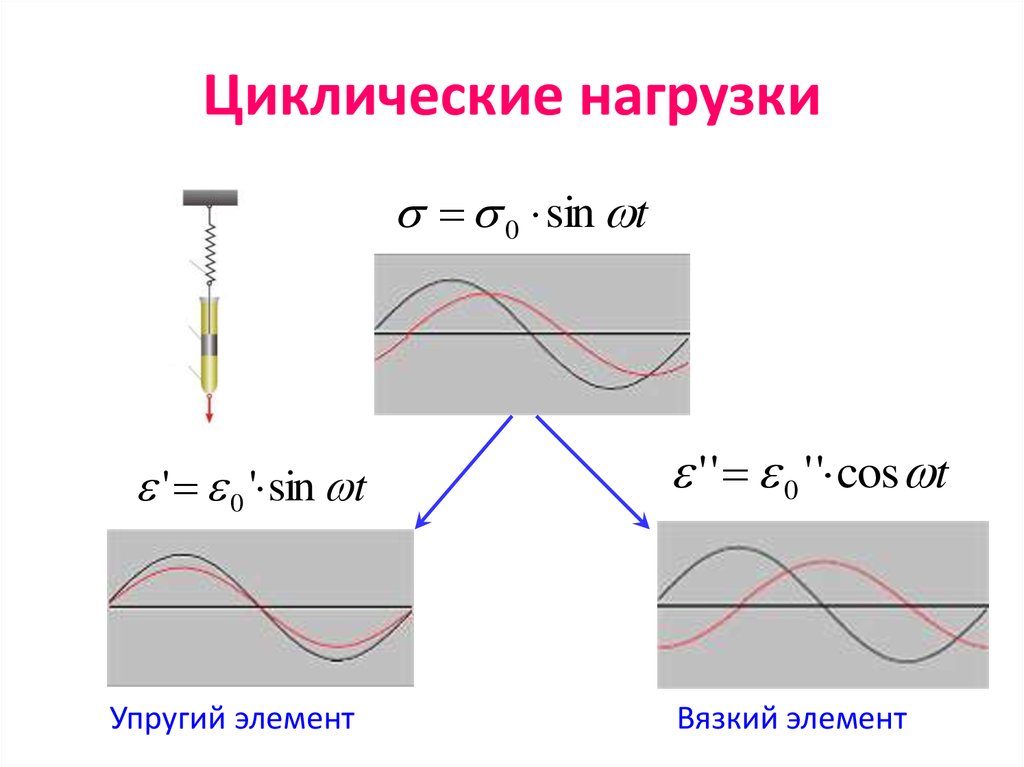
83. Циклические нагрузки
0 sin t' 0 ' sin t
Упругий элемент
' ' 0 ' ' cos t
Вязкий элемент
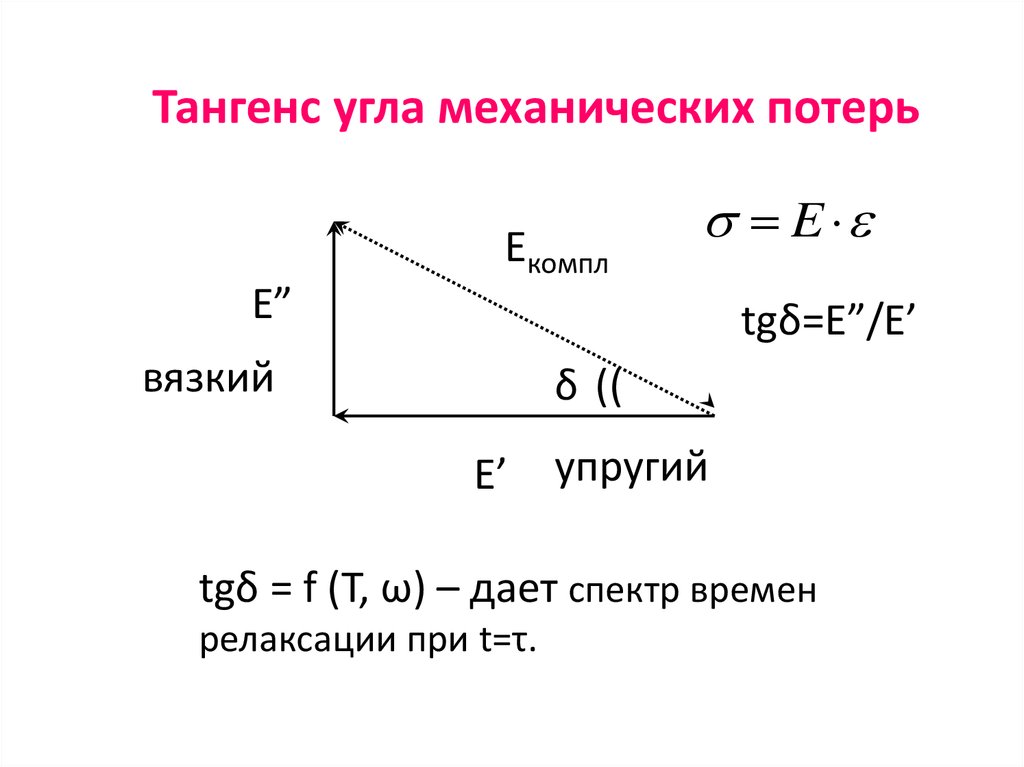
84. Тангенс угла механических потерь
EкомплE
E”
tgδ=E”/E’
вязкий
δ ((
E’
упругий
tgδ = f (T, ω) – дает спектр времен
релаксации при t=τ.
85. Итак:
• Аморфные полимеры – это жидкости сбольшой вязкостью и большим
временем релаксации
• Понимание физических свойств
полимеров немыслимо без изучения
их деформационных и реологических
характеристик
86. Релаксационные состояния аморфных полимеров
• Стеклообразное (механически-твердое,но структурно-жидкое)
• Высокоэластическое (структурно-жидкое
с огромными обратимыми деформациями)
• Вязкотекучее (механически и структурножидкое с необратимыми деформациями)
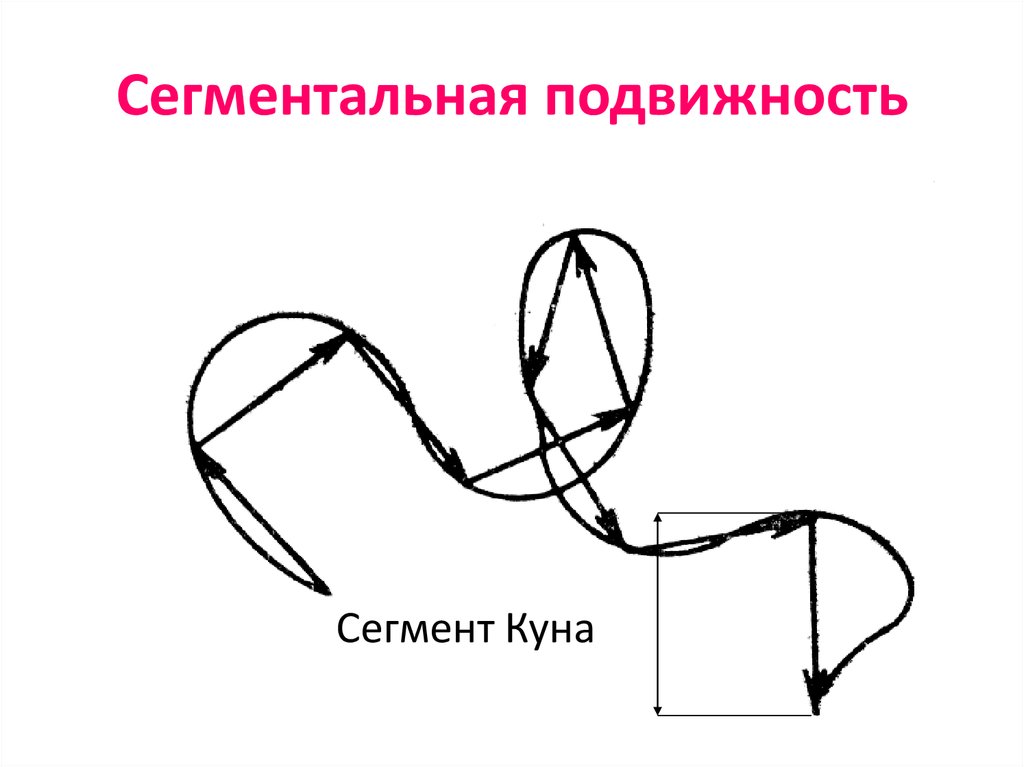
87. Сегментальная подвижность
Сегмент Куна88. Энергия активации сегментальной подвижности
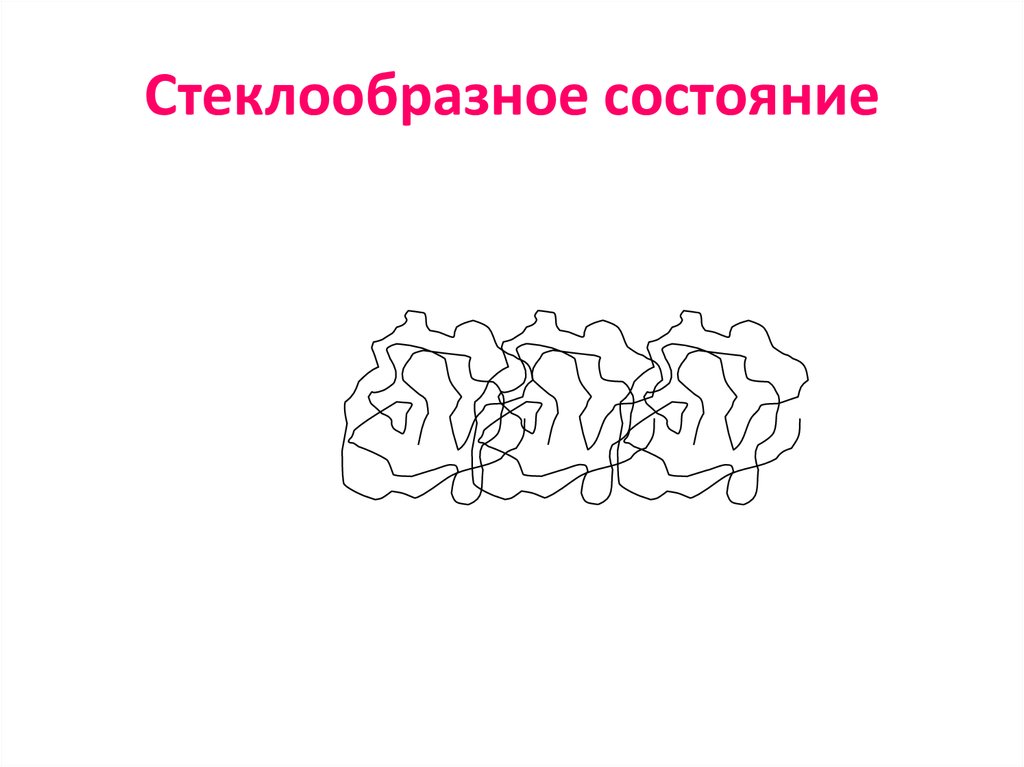
89. Стеклообразное состояние
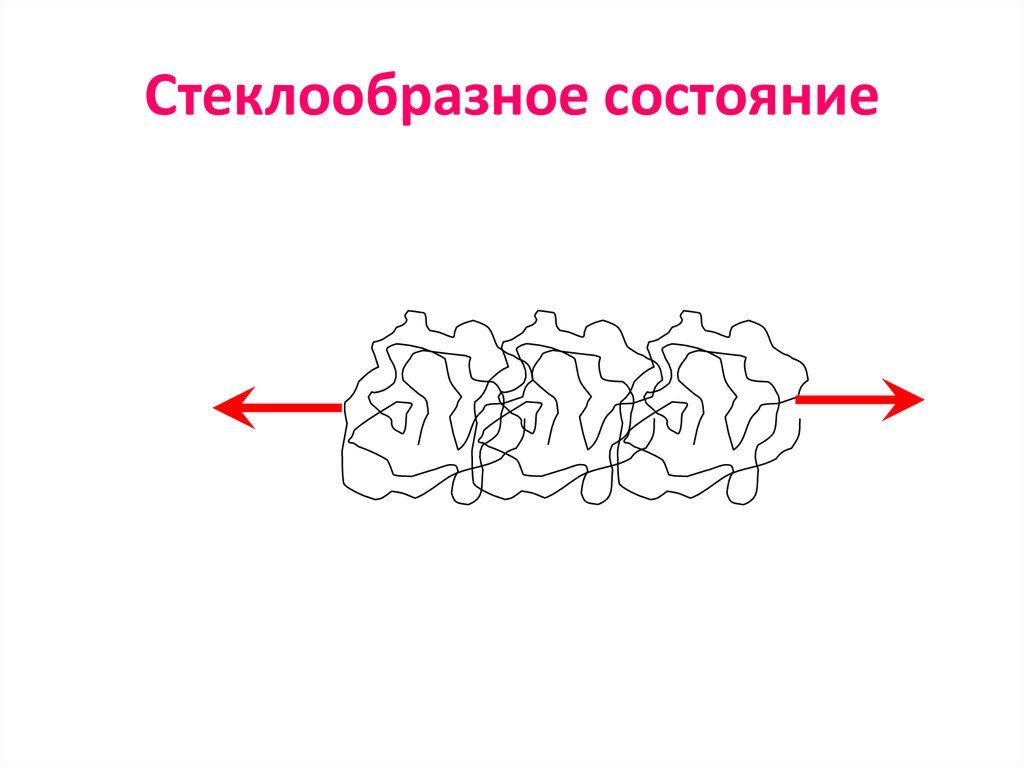
90. Стеклообразное состояние
91. Стеклообразное состояние
92. Фазовое состояние полимеров
• Кристаллическое• Жидкокристаллическое
• Аморфное
• Изотропный расплав
(раствор)
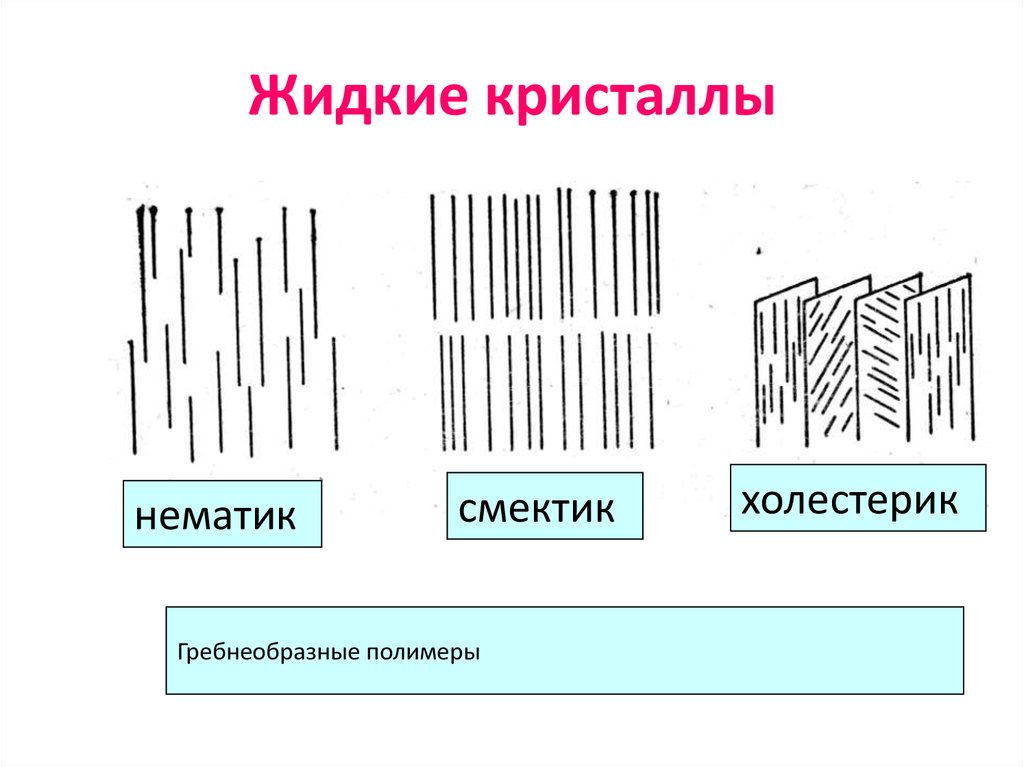
93. Жидкие кристаллы
нематиксмектик
Гребнеобразные полимеры
холестерик
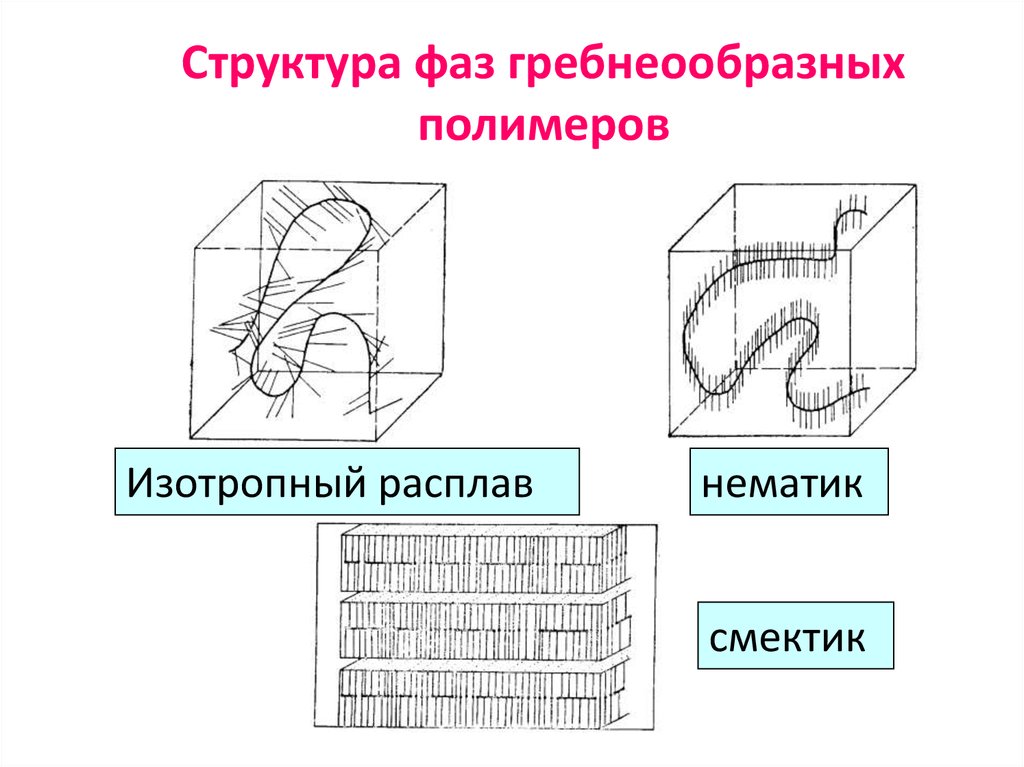
94. Структура фаз гребнеообразных полимеров
Изотропный расплавнематик
смектик
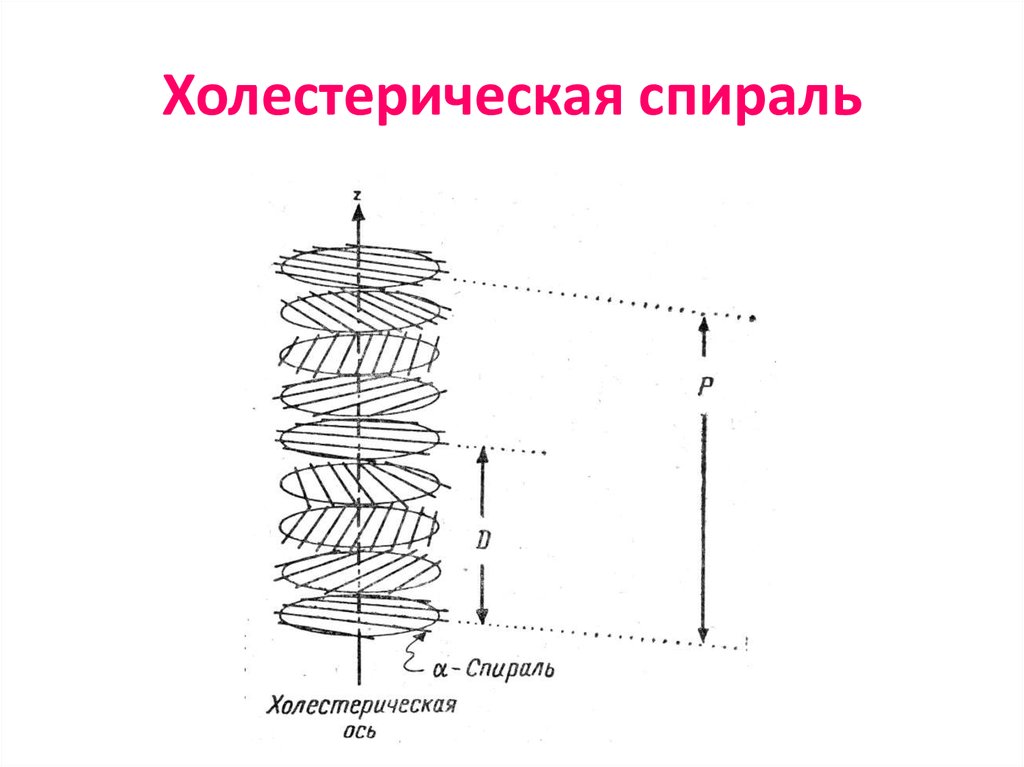
95. Холестерическая спираль
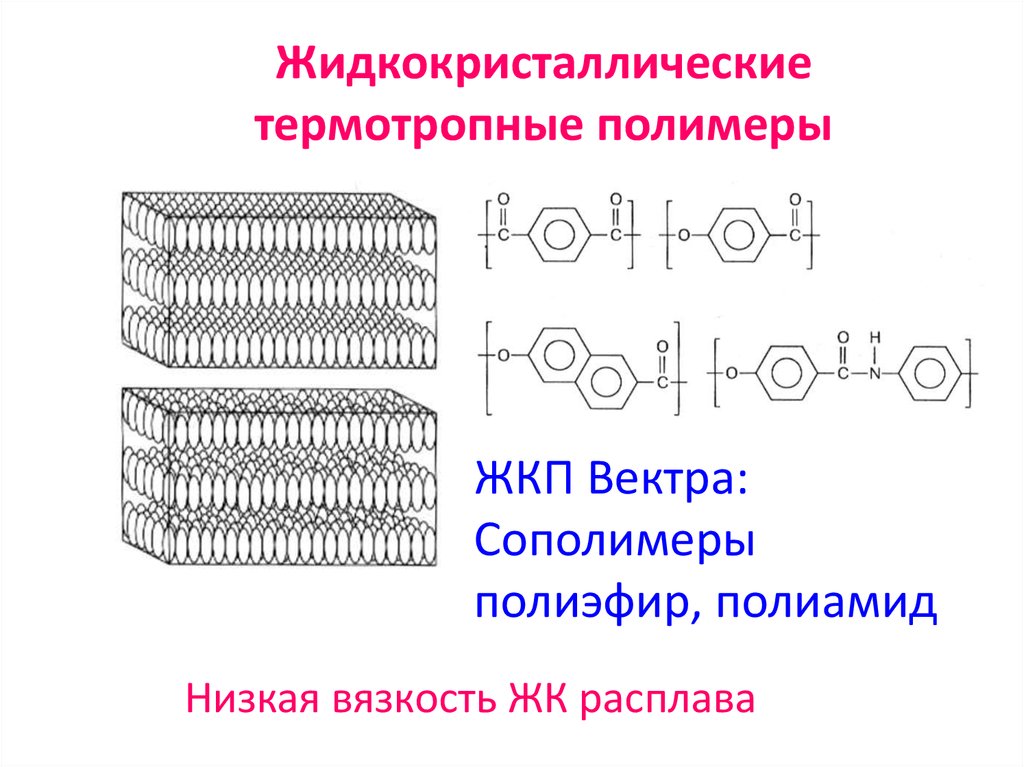
96. Жидкокристаллические термотропные полимеры
ЖКП Вектра:Сополимеры
полиэфир, полиамид
Низкая вязкость ЖК расплава



































 Физика
Физика Химия
Химия








