Похожие презентации:
Численное решение двумерного уравнения Пуассона (работа 6)
1.
Введение в технологии суперкомпьютерныхвычислений
Работа 6. Численное решение двумерного уравнения Пуассона
Цель работы - разработать программу, параллелизующую средствами
OpenMP алгоритм численного решения дифференциальных уравнений в
частных производных.
Задание к работе:
Разработать программу, параллелизующую средствами OpenMP алгоритм
численного решения двумерного уравнения Пуассона. Исследовать
эффективность параллелизации.
2.
Уравнение ПуассонаРассмотрим OpenMP-параллелизацию численного решения дифференциальных
уравнений в частных производных на примере двумерного уравнения Пуассона
следующего вида:
Применим упрощенную постановку задачи Дирихле: вычисления будем
выполнять для области в форме прямоугольника с нулевыми граничными
условиями (ξ - координата по оси x, η - координата по оси y, χ - отношение
ширины прямоугольного сечения к высоте).
Используем ортогональную равномерную расчетную сетку, включающую NxN
узлов.
3.
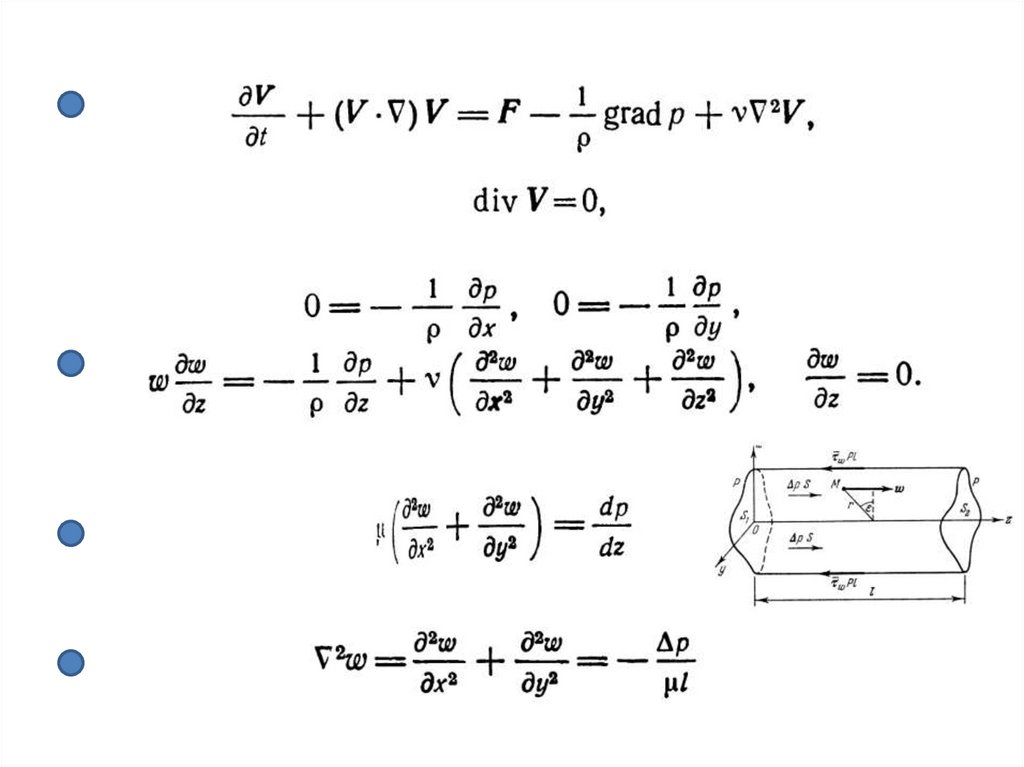
Задача об установившемся теченииФормулировка линейной задачи в такой постановке дает, в частности, решение
задачи об установившемся ламинарном движении вязкой несжимаемой
жидкости сквозь трубу квадратного сечения.
Искомая функция w представляет собой распределение продольной скорости по
сечению трубы.
Данная задача имеет аналитическое решение в виде разложения в бесконечные
ряды, которое можно использовать для верификации программы (в
безразмерной форме):
4.
5.
6.
7.
8.
Численная дискретизацияПространственную дискретизацию уравнения Пуассона проведем по методу
конечных разностей со вторым порядком точности
В результате дискретизации может быть явным образом записана СЛАУ с
ленточной (пятидиагональной) матрицей размерности, после чего вызвана
процедура решения СЛАУ тем или иным из известных методов.
В данном случае для наглядности и экономии памяти не станем переходить к
матричной формулировке задачи.
9.
Метод ЯкобиМетод Зейделя
10.
Ход выполнения работы1. Выбрать индивидуальное значение параметра χ (отношение ширины
прямоугольного сечения к высоте).
2. Найти решение рассматриваемого уравнения Пуассона в виде ряда в
фиксированном наборе точек (написав программу или используя возможности
математических пакетов), изучив влияние на результаты точности вычисления ряда и
выбрав подходящее значение.
3. Разработать и отладить последовательную версию программы, выполняющую
численное решение уравнения Пуассона по методу Зейделя. Сопоставить решение с
результатами вычисления ряда в нескольких точках сечения.
4. Выполнить параллелизацию программы с использованием OpenMP.
5. Проверить правильность выполнения параллелизации, сопоставив результаты с
полученными в последовательной версии программы.
6. Визуализировать результаты, построив на основании значений скорости в
заданном числе точек прямоугольного сечения 3D-поверхность.
7. Провести исследование эффективности распараллеливания программы (задавая
при запуске разное число нитей, в диапазоне от 1 до 8). Результаты представить в
графическом виде, в форме зависимости ускорения программы от числа нитей.
8. Модифицировать код программы, реализуя проверку условия сходимости после
выполнения заданного количества шагов (подобрать оптимальное значение шага для
фиксированного числа нитей например двух).
11.
Структура отчета по лабораторной работеПо результатам выполнения лабораторной работы необходимо подготовить
развернутый отчет, который должен включать следующие разделы:
1. название лабораторной работы и текст задания к ней
2. информация о количестве ядер, объеме оперативной памяти
использованного в работе компьютера и использованном для разработки и
компиляции кодов программном обеспечении
3. формулировка параллельного алгоритма
4. исходный код разработанной программы с содержательными
комментариями к реализующим параллельные алгоритмы фрагментам
программ и использованным OpenMP-инструкциям
5. результаты верификации программы
6. показатели эффективности распараллеливания программы при задании
разного числа нитей
7. общие выводы по лабораторной работе
12.
ПОСЛЕДОВАТЕЛЬНЫЙАЛГОРИТМ
int main() {
ofstream out20("output_temp1.plt");
ofstream out21("output_temp2.plt");
ofstream out22("output_temp3.plt");
int NUM_THREADS = 1;
omp_set_num_threads(NUM_THREADS);
double ta = omp_get_wtime();
double umax, temp, h, p, eps;
int N = 100;
h = 2. / N;
eps = 1e-8;
double** a = new double* [N];
double** f = new double* [N];
for (int i = 0; i < N; i++)
a[i] = new double[N];
for (int i = 0; i < N; i++)
for (int j = 0; j < N; j++)
a[i][j] = 0.;
int i, j;
int m = 0;
do {
umax = 0;
for (i = 1; i < N-1 ; i++) {
for (j = 1; j < N-1 ; j++) {
temp = a[i][j];
a[i][j] = 0.25 * (a[i - 1][j] + a[i + 1][j] + a[i][j - 1] + a[i][j + 1] + 1*1*h * h);
p = fabs(temp - a[i][j]);
if (umax < p) umax = p;
}
}
m++;
} while (umax > eps);
ta = omp_get_wtime() - ta;
printf("\n\t Time for serial execution: %0.30f\n\n", ta);
13.
ПОСЛЕДОВАТЕЛЬНЫЙАЛГОРИТМ
cout << "umax =" << umax << endl;
cout << "a[0][0] =" << a[N/2][N/2] << endl;
cout << "a[0][0]_exact =" << func(0,0,h) << endl;
cout <<"m =" << m << endl;
out20 << "Variables=x, y, T" << std::endl;
out20 << "zone T= ""Color"", I= " << N << " J= " << N << endl;
for (int i = 0; i < N ; i++) {
for (int j = 0; j < N; j++) {
out20 << i << " " << j << " " << a[i][j] << std::endl;
}
}
out21 << "Variables=x, y, T" << std::endl;
out21 << "zone T= ""Color"", I= " << N << " J= " << N << endl;
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
out21 << i << " " << j << " " << func(i-N*0.5, j-N*0.5, h) << std::endl;
}
}
out22 << "Variables=x, y, dT" << std::endl;
out22 << "zone T= ""Color"", I= " << N << " J= " << N << endl;
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) {
out22 << i << " " << j << " " << fabs(a[i][j]-func(i - N * 0.5, j - N * 0.5, h))/ func(i - N * 0.5, j - N * 0.5, h) << std::endl;
}
}
system("pause");
return 0;
}
14.
ПОСЛЕДОВАТЕЛЬНЫЙАЛГОРИТМ
double func(int i, int j, double h)
{
double x, y, c, summ,pi;
x = (i+0.00001) * 1.*h;
y = (j + 0.00001) * 1.*h;
c = 1.;
pi = 3.1415;
int k;
summ = 0;
for (k = 0; k <= 100; k++) {
summ += pow(-1, k) * (1.-cosh(0.5 * (2. * k + 1.) * pi * y / c)/ cosh(0.5 * (2. * k + 1.) * pi
/c))*cos(0.5*(2.*k+1.)*pi*x/c) / pow((2. * k + 1.), 3.);
}
return summ* 16. * c * c / (pi * pi * pi);
}
15.
Параллельный алгоритмint i, j;
int m = 0;
do {
umax = 0;
#pragma omp parallel for private(i,j, temp, p) shared(a, N, umax)
for (i = 1; i < N-1 ; i++) {
for (j = 1; j < N-1 ; j++) {
temp = a[i][j];
a[i][j] = 0.25 * (a[i - 1][j] + a[i + 1][j] + a[i][j - 1] + a[i][j + 1] + 1*1*h * h);
p = fabs(temp - a[i][j]);
if (umax < p) umax = p;
}
}
m++;
} while (umax > eps);
ta = omp_get_wtime() - ta;
printf("\n\t Time for parallel execution: %0.30f\n\n", ta);
16.
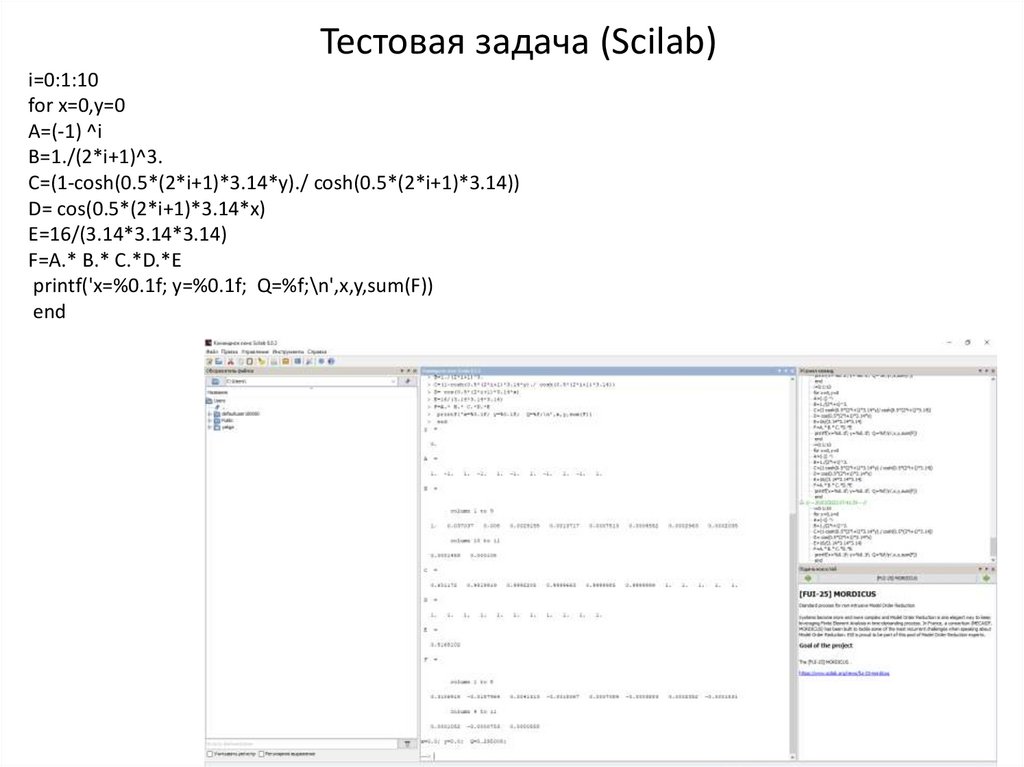
Тестовая задача (Scilab)i=0:1:10
for x=0,y=0
A=(-1) ^i
B=1./(2*i+1)^3.
C=(1-cosh(0.5*(2*i+1)*3.14*y)./ cosh(0.5*(2*i+1)*3.14))
D= cos(0.5*(2*i+1)*3.14*x)
E=16/(3.14*3.14*3.14)
F=A.* B.* C.*D.*E
printf('x=%0.1f; y=%0.1f; Q=%f;\n',x,y,sum(F))
end
17.
y =Тестовая задача (Scilab)
0.
A =
1. -1. 1. -1. 1. -1. 1. -1. 1. -1. 1.
B =
column 1 to 9
1. 0.037037 0.008 0.0029155 0.0013717 0.0007513 0.0004552 0.0002963 0.0002035
Для n = 10
column 10 to 11
0.0001458 0.000108
x=0.0; y=0.0; Q=0.295008;
C =
0.601172 0.9819919 0.9992205 0.9999663 0.9999985 0.9999999 1. 1. 1. 1. 1.
D =
Для n = 50
x=0.0; y=0.0; Q=0.294985;
1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.
Для n = 100
E =
0.5168102
x=0.0; y=0.0; Q=0.294984;
F =
column 1 to 8
0.3106918 -0.0187964 0.0041313 -0.0015067 0.0007089 -0.0003883 0.0002352 -0.0001531
column 9 to 11
0.0001052 -0.0000753 0.0000558
x=0.0; y=0.0; Q=0.295008;
18.
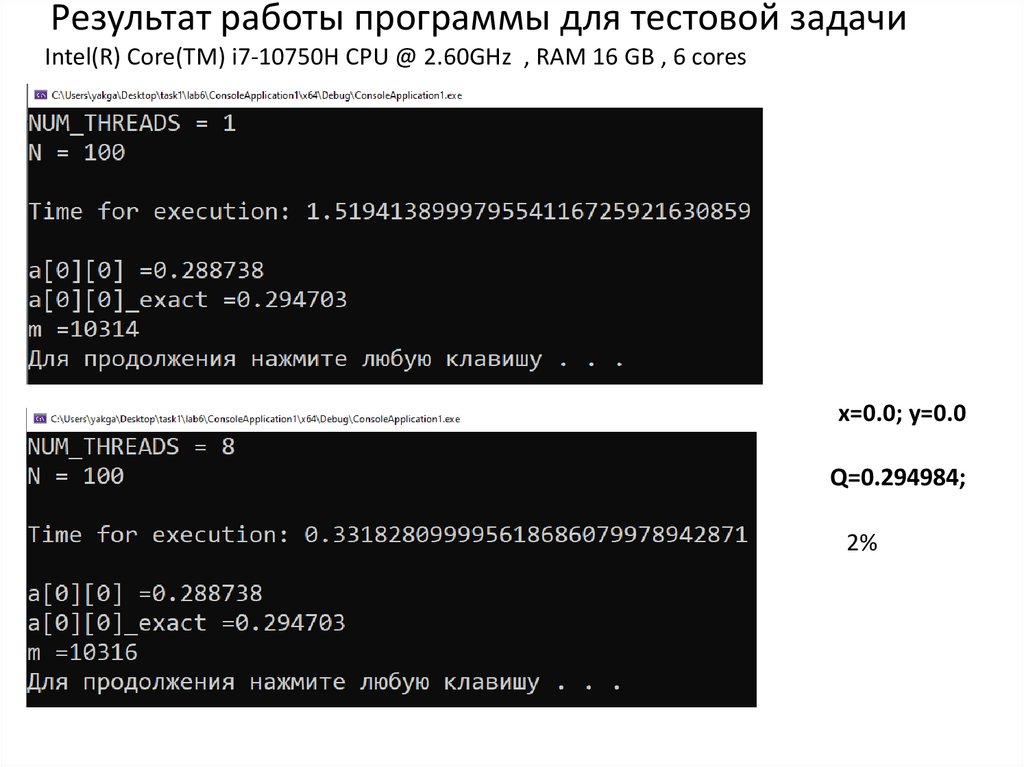
Результат работы программы для тестовой задачиIntel(R) Core(TM) i7-10750H CPU @ 2.60GHz , RAM 16 GB , 6 cores
x=0.0; y=0.0
Q=0.294984;
2%
19.
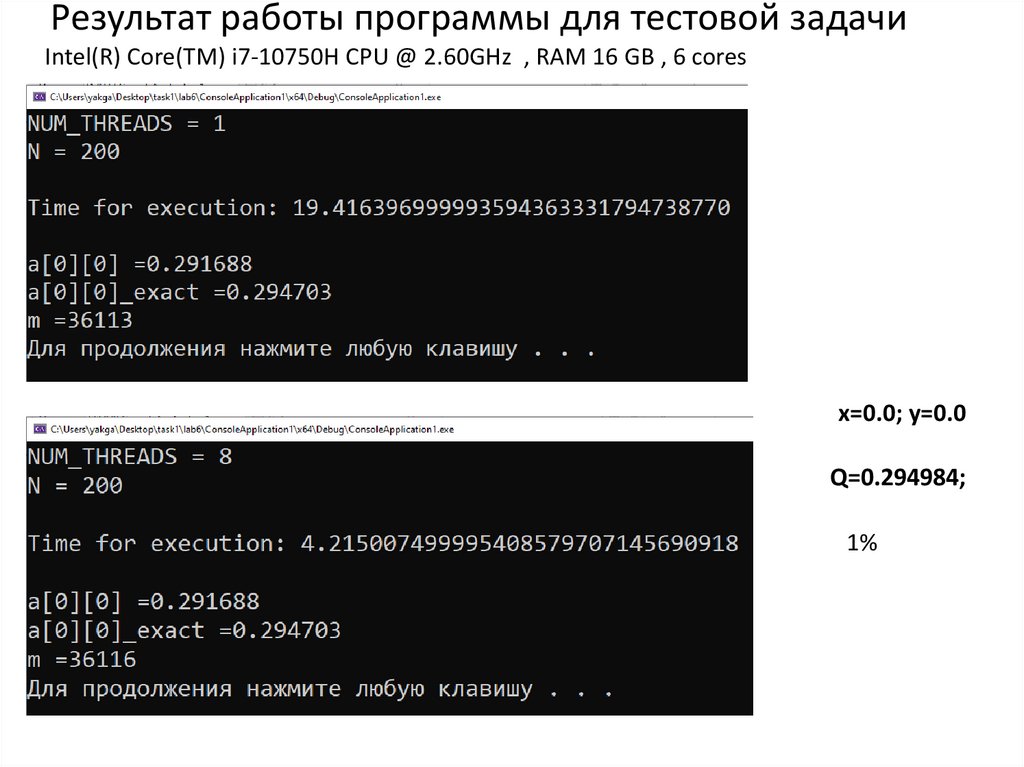
Результат работы программы для тестовой задачиIntel(R) Core(TM) i7-10750H CPU @ 2.60GHz , RAM 16 GB , 6 cores
x=0.0; y=0.0
Q=0.294984;
1%
20.
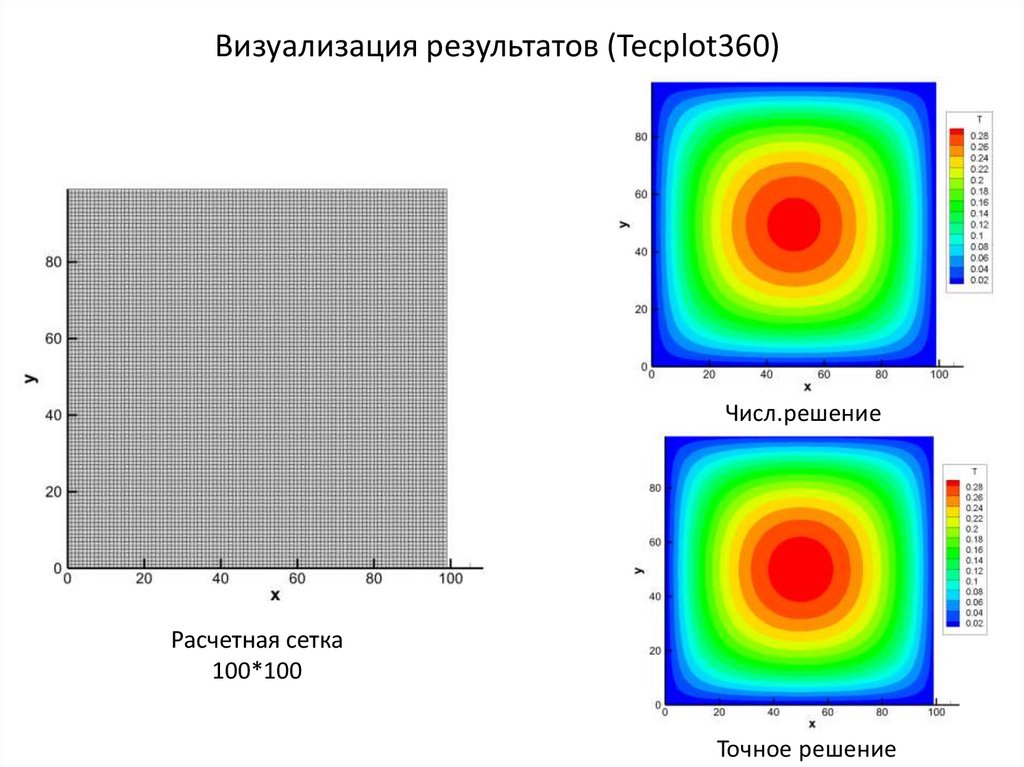
Визуализация результатов (Tecplot360)Числ.решение
Расчетная сетка
100*100
Точное решение
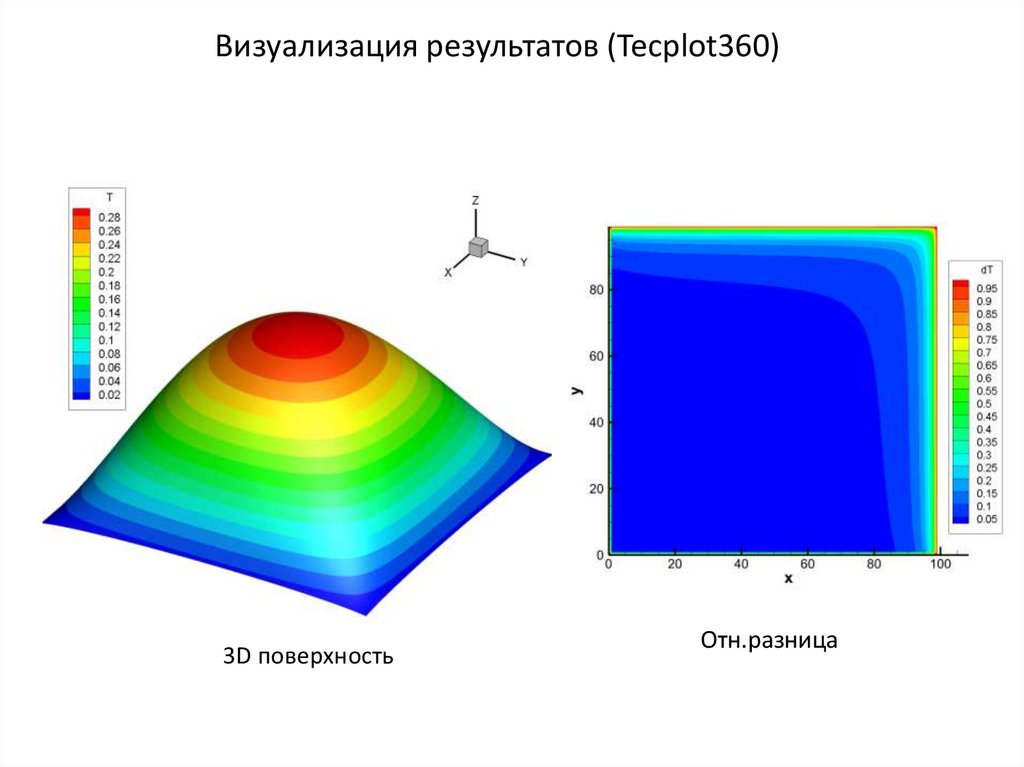
21.
Визуализация результатов (Tecplot360)3D поверхность
Отн.разница
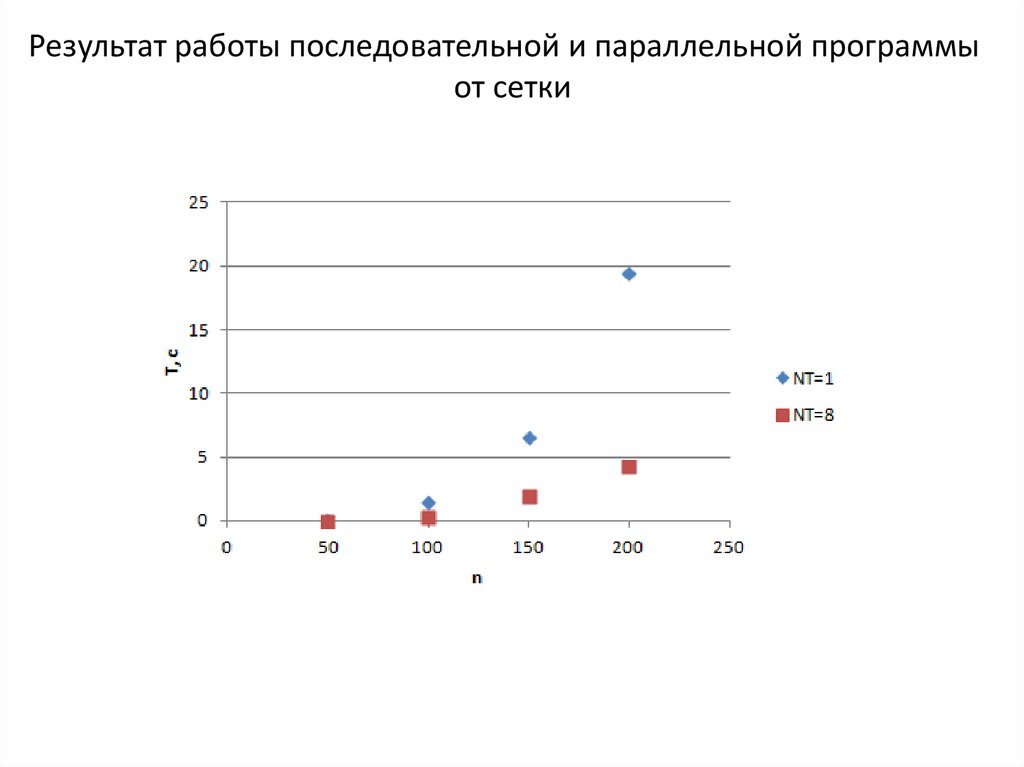
22.
Результат работы последовательной и параллельной программыот сетки
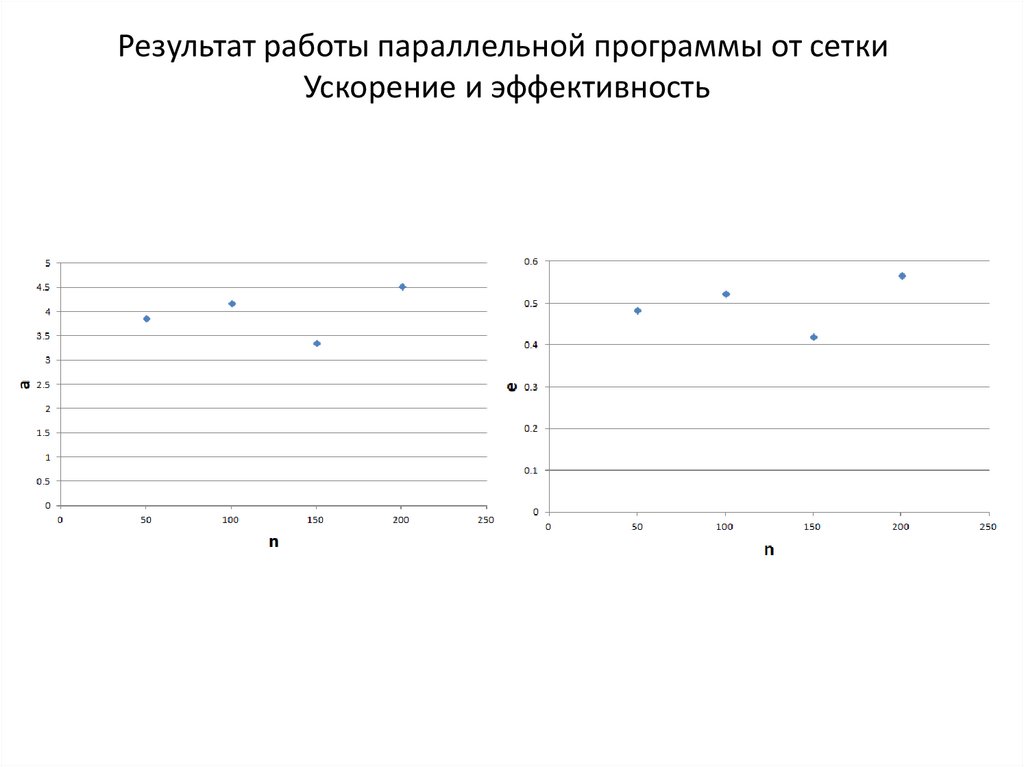
23.
Результат работы параллельной программы от сеткиУскорение и эффективность
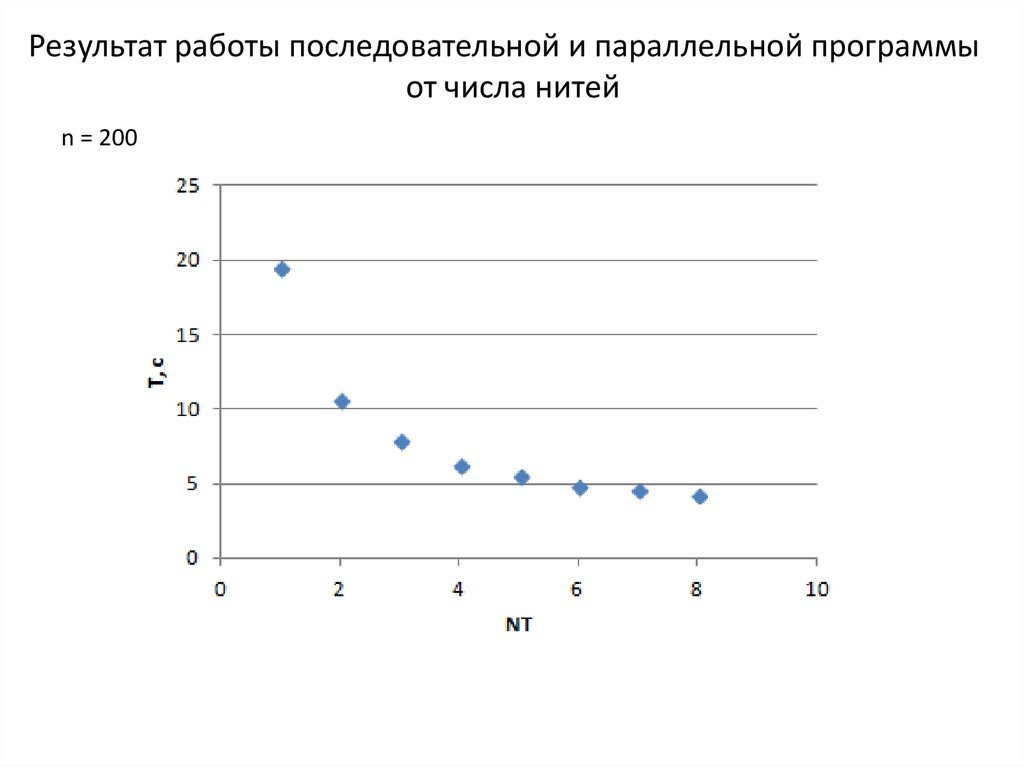
24.
Результат работы последовательной и параллельной программыот числа нитей
n = 200
25.
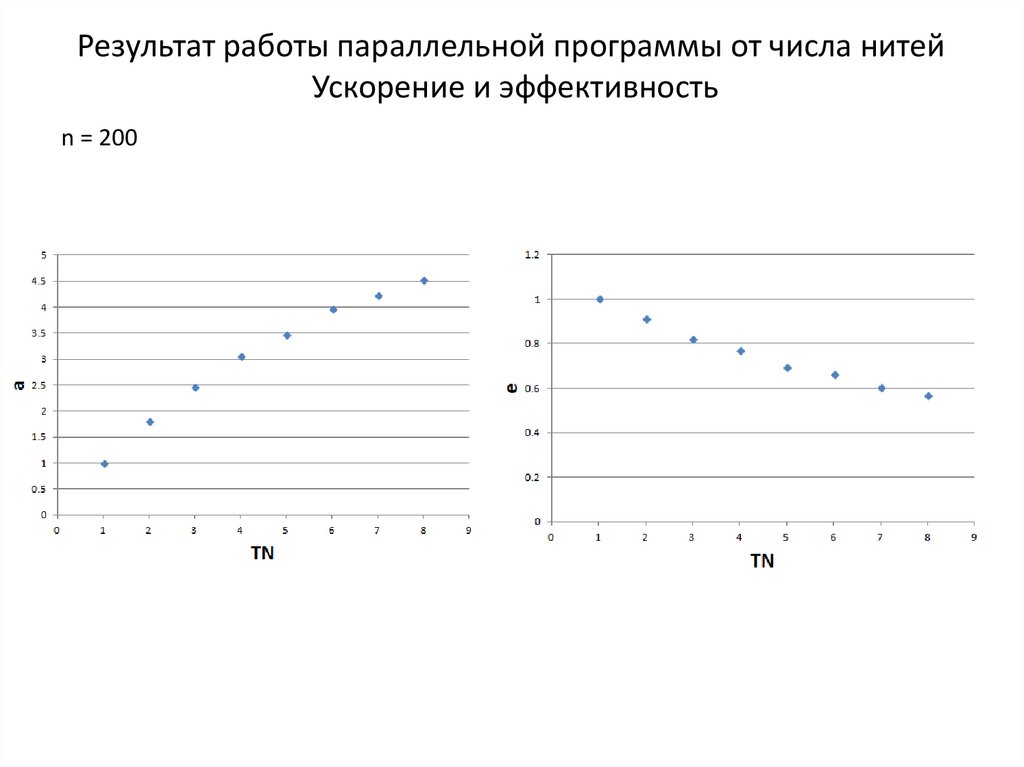
Результат работы параллельной программы от числа нитейУскорение и эффективность
n = 200
26.
Ускорение за счет оптимизацииNT=1
T, c
(NT=1) + O(1) (NT=1) + O(2)
19.462
7.281
7.0617
1
2.67
2.76
a(T1/T)
NT=8
(NT=8) + O(1) (NT=8) + O(2)
T, c
4.304
2.125
1.5456
a(T1/T)
4.52
9.2
12.6



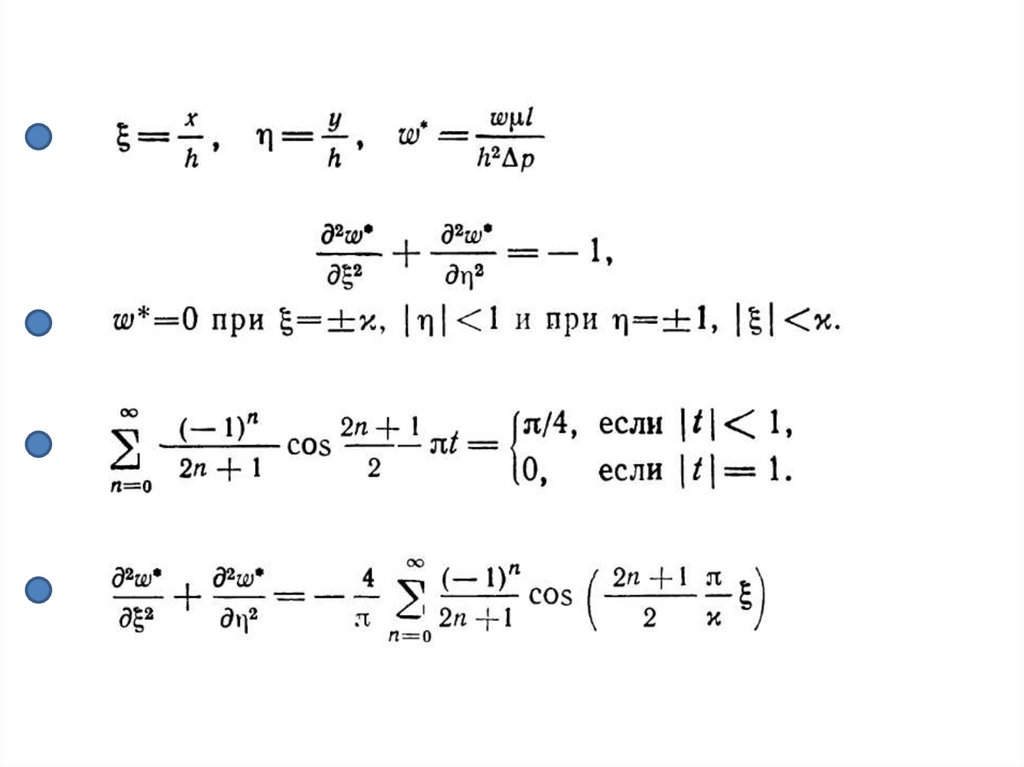
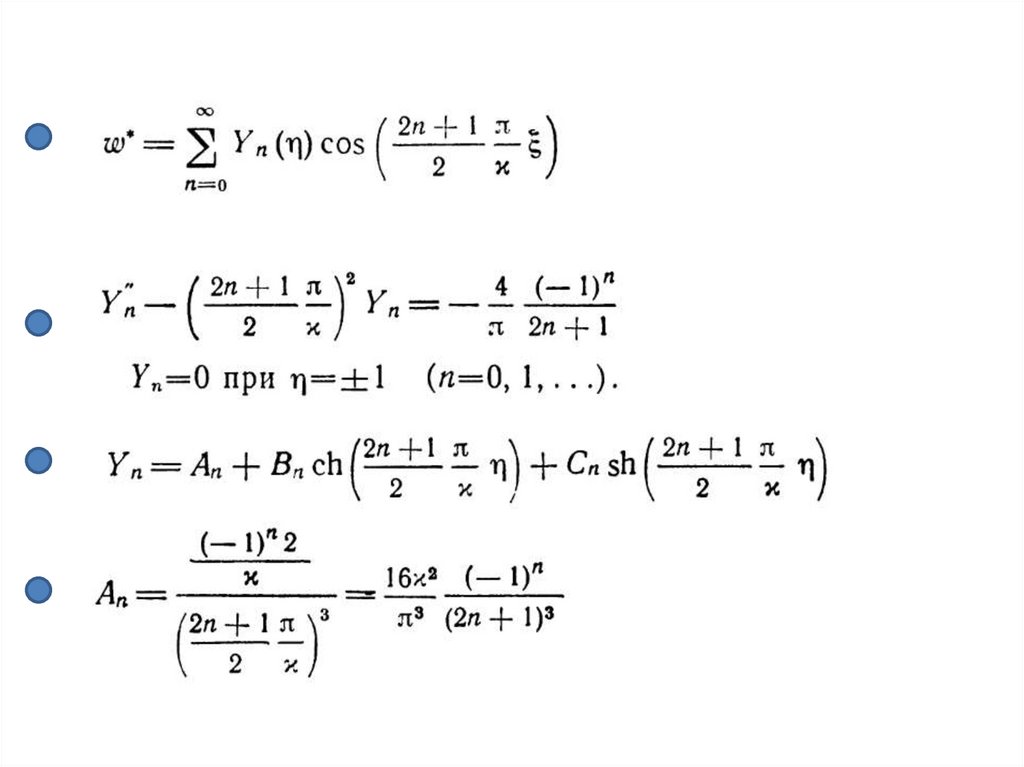











 Программирование
Программирование