Похожие презентации:
Дискретная и непрерывная математика (лекция 1)
1.
Лекция-118.01.2024
2.
IО множествах и отношениях
3.
ВведениеДискретная математика изучает математические модели
объектов, процессов и зависимостей, с которыми имеют дело
в технике, биологии, социологии и других областях
деятельности человека.
Их особенность – дискретный, как правило, конечный
характер.
Это ограничивает возможность использования моделей и
методов классической непрерывной математики.
Поэтому дискретная математика – самостоятельное
направление современной математики.
4.
Дискретная и непрерывная математика взаимно дополняютдруг друга.
Понятия и методы одной часто используются в другой.
Например, системы линейных уравнений как модели
непрерывной математики характеризуются конечным
множеством линейно независимых уравнений и при
определенных условиях конечным множеством решений.
Один и тот же объект может рассматриваться с двух точек
зрения и в зависимости от этого выбирается непрерывная или
дискретная модель.
5.
ПримерЭлектрическая схема
I
граф – модель ее структуры
II
непрерывный объект – вектор значений параметров
III
получаем систему линейных или нелинейных
уравнений для расчетов токов и напряжений в схеме.
6.
Классическая непрерывная математика развивалась вусловиях, когда возникли и требовали решения задачи
механики и физики.
Дискретная математика сложилась и интенсивно развивается
в связи с необходимостью решения задач управления и
создания сложных технических систем.
Многие задачи, возникшие в прошлом как головоломки,
сегодня нашли интерпретацию как задачи управления.
7.
Особенность большинства задач дискретной математики –возможность их решения полным перебором допустимых
решений в силу конечного множества их вариантов.
НО:
с ростом размерности задачи простой перебор быстро
становится бессильным.
8.
Для многих важных прикладных задач до настоящего временине найдено эффективных алгоритмов решения.
Выход:
Ищем «хитрые» алгоритмы для упрощения перебора и
определения пусть не точного,
а хотя бы приближенного, но хорошего решения.
9.
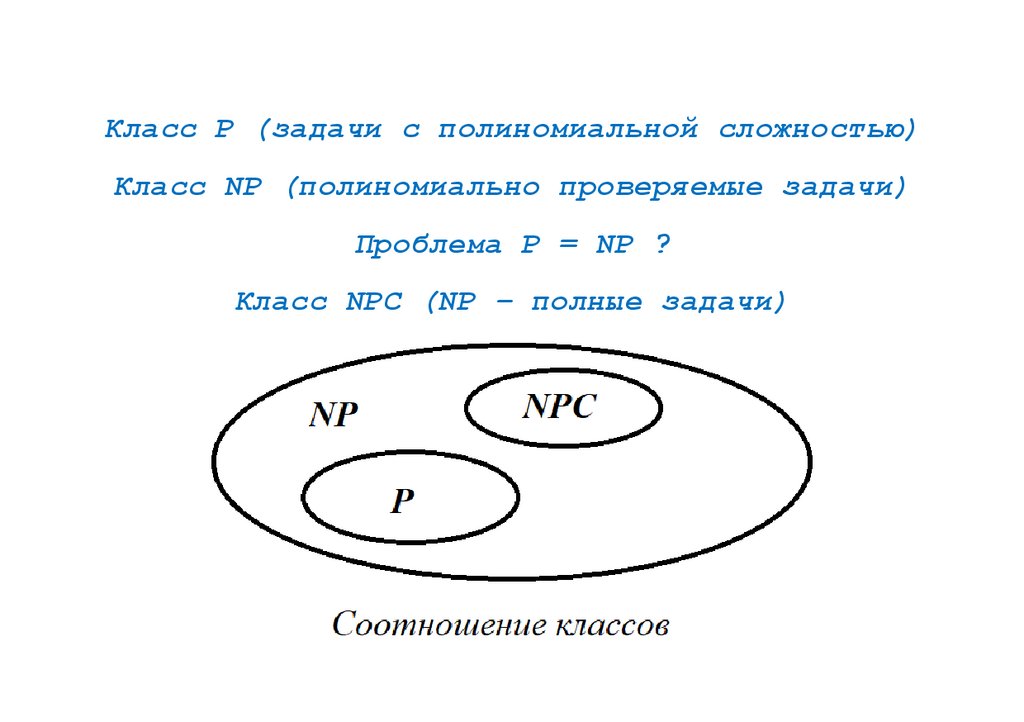
Класс P (задачи с полиномиальной сложностью)Класс NP (полиномиально проверяемые задачи)
Проблема P = NP ?
Класс NPC (NP – полные задачи)
10.
ПримерПри исследовании логических схем на риски сбоя необходимо
проверить переходы от любого входного набора к любому
другому, а входных наборов 2n,
где n – число входов схемы.
Таким образом, от каждого из 2n наборов надо перейти к 2n – 1
наборам, т.е. всего надо осуществить 2n(2n-1) 22n переходов.
Если n = 64, а исследовать один переход можно за 1 нс, то
время анализа будет 10 9 2128 1022 лет!
11.
В Дискретную математику сегодня входят такие разделы:– Теория множеств
(счетных и конечных),
– Алгебраические системы,
– Комбинаторика,
– Математическая логика,
– Теория кодирования,
– Теория графов,
– Теория рекурсивных функций,
– Булева алгебра,
– Машинная арифметика,
– Теория алгоритмов,
– Теория конечных
автоматов,
– Теория формальных
грамматик,
– Числовые системы.
12.
О множествах и отношениях{a, b, c}
{a, b} = {b, a}
{a, a} = {a}
и { } – это совсем разные множества.
Но
(a, b) (b, a)
(a, a) и (a) – совсем разные конструкции.
13.
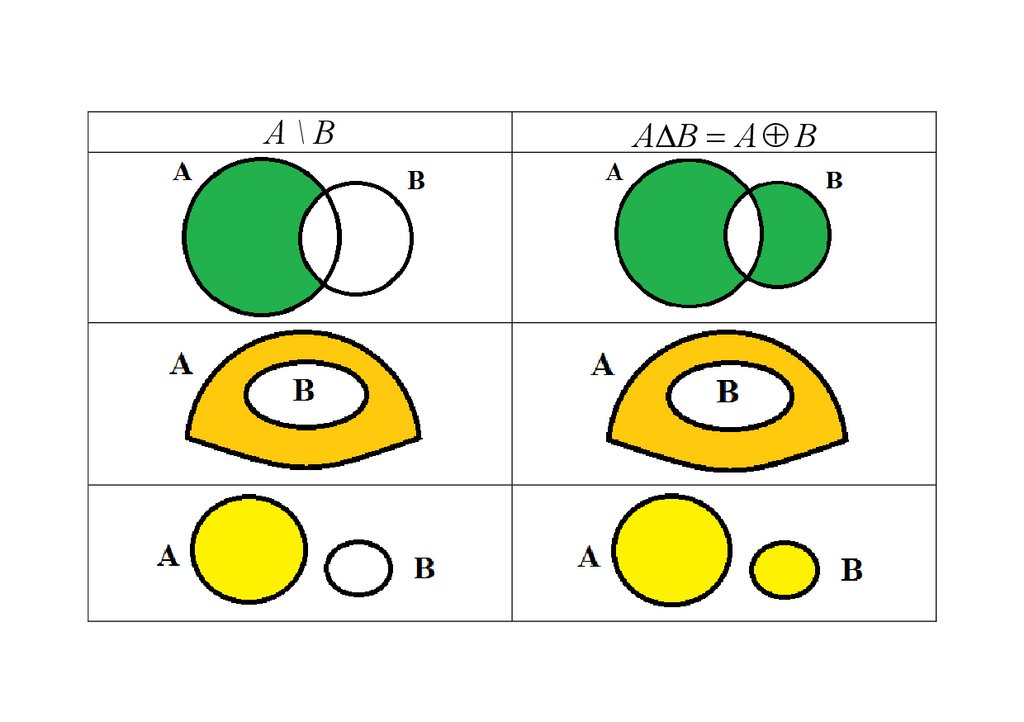
Некоторые операцииСимметрической разностью двух множеств А и В,
обозначаемой
A B (или A B),
называют множество (A \ B) (B \ A) или, по-другому,
(A B) \ (B A) или, по-другому,
A B = {x : (x A x B) (x B x A)}.
Оно состоит из всех тех и только тех элементов,
которые либо принадлежат А и не принадлежат B,
либо наоборот, принадлежат В, но не А.
14.
А\ВA B А B
15.
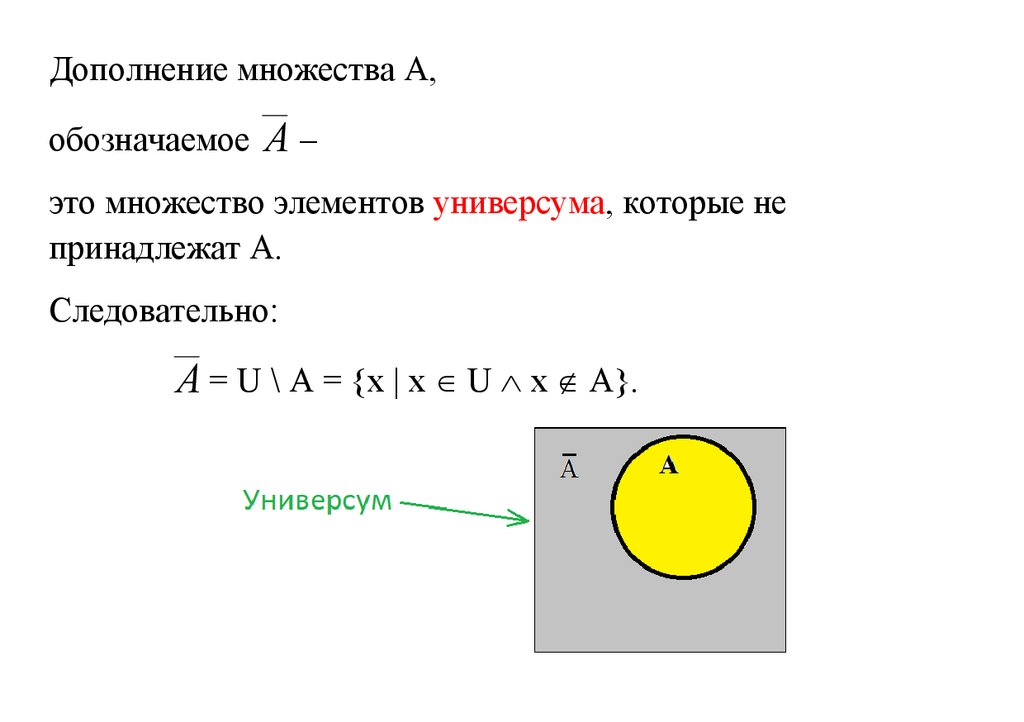
Дополнение множества A,обозначаемое A –
это множество элементов универсума, которые не
принадлежат А.
Следовательно:
A = U \ A = {x | x U x A}.
16.
А что такое универсум?17.
Количество элементов конечных множествМощностью конечного множества M называется количество
его элементов и обозначается символом
|M|
18.
Например,| | = 0 (мощность пустого множества равна 0),
|{a, b, c}| = 3,
|{ }| = 1 (мощность множества, состоящего из одного пустого
множества, равна 1).
Если
|A| = |B|,
то множества A и B называются равномощными.
19.
А что означает выражение:2M
где M – множество?
20.
Это множество всех подмножеств M.А чему равно
|2M|
21.
Ответ|2M| = 2|M|
0) M =
2M = { }
|2M| = 1
1) M = {a}
2M = { , M}
|2M| = 2
2) M = {a, b}
2M = { , {a}, {b}, M}
|2M| = 4
3) M = {a, b, c}
2M = { , {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, M}
|2M| = 8
А дальше?
22.
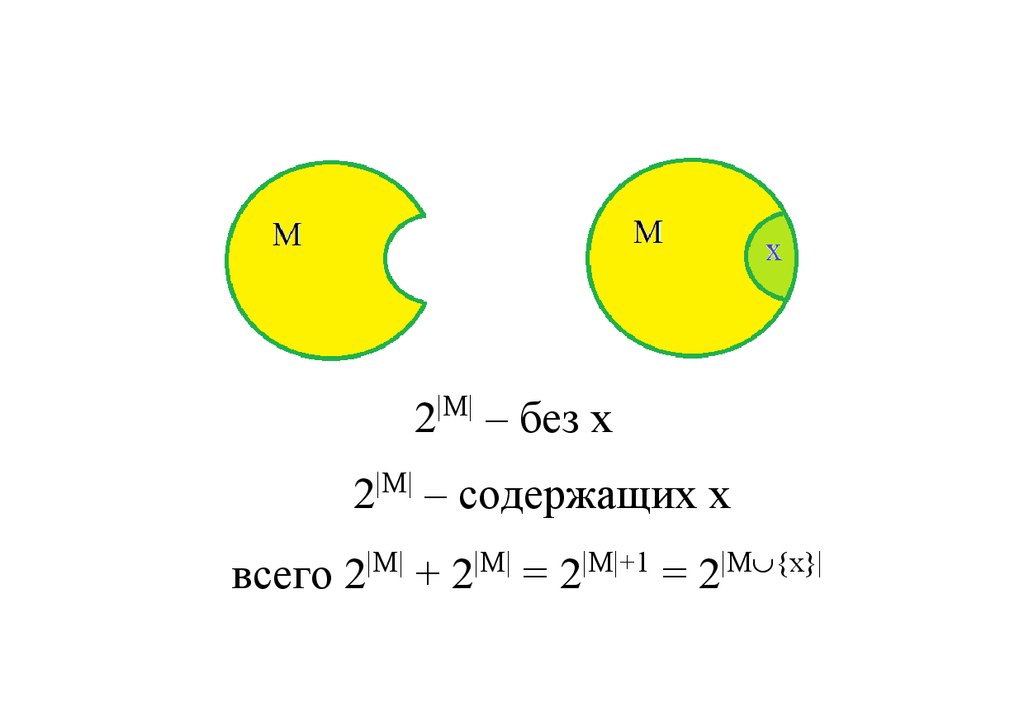
2|M| – без x2|M| – содержащих x
всего 2|M| + 2|M| = 2|M|+1 = 2|M {x}|
23.
Теорема|2M| > |M|
Для конечных множеств это следует из неравенства:
2n > n
(докажем самостоятельно)
24.
Правило суммыЕсли A и B непересекающиеся конечные множества,
содержащие m и n элементов соответственно, то объединение
A B содержит m + n элементов.
Т.е., если A B = ,
то |A B| = |A| + |B|.
25.
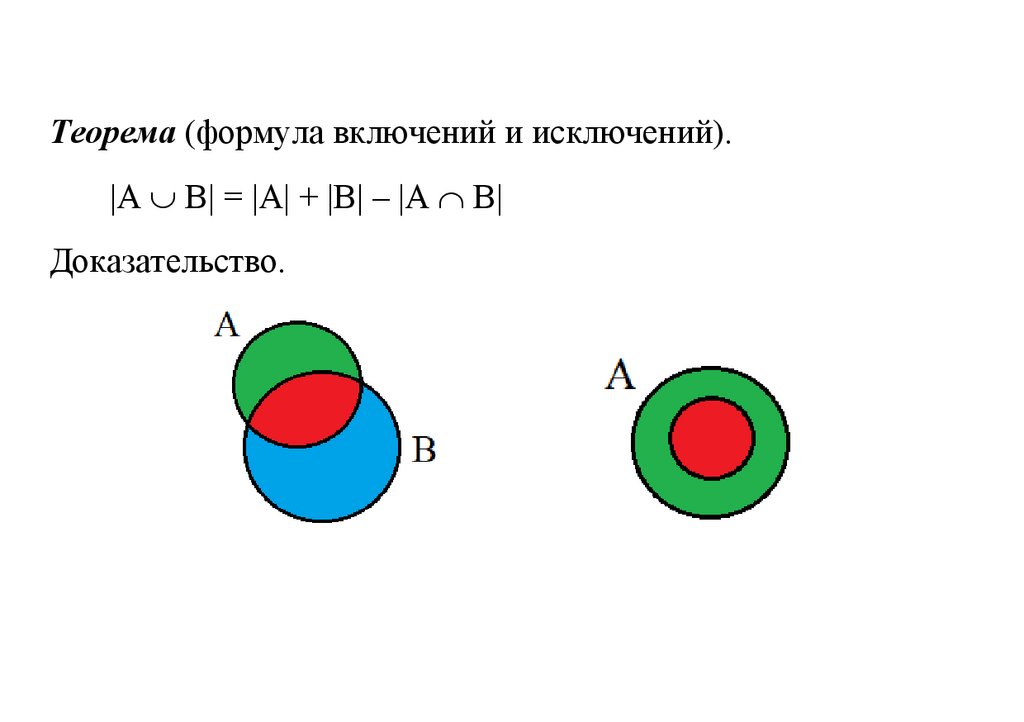
Теорема (формула включений и исключений).|A B| = |A| + |B| – |A B|
Доказательство.
26.
Формула для подсчета мощности объединения может бытьобобщена на произвольное количество множеств.
Для трех множеств она может быть получена из диаграммы
Эйлера и имеет вид
|A B C| =
|A| + |B| + |C| – |A B| – |B C| – |C A| + |A B C|
27.
Теорема|A B| = |A| |B|
Доказательство
Первый компонент упорядоченной пары можно выбрать
|A| способами,
второй – |B| способами.
На каждый способ выбора первого компонента второй можно
выбрать |B| способами.
Таким образом, всего имеется |A| |B| различных
упорядоченных пар.
28.
Следствие|An| = |A|n
29.
Основные законы и тождества алгебрымножеств
Основные законы алгебры множеств
(булевой алгебры множеств)
представляются в виде тождеств,
в которых участвуют символы обозначений множеств,
включая символы универсального и пустого множеств,
и символы операций:
объединения, пересечения разности и дополнения.
30.
Ассоциативный закон1) (X Y) Z = X (Y Z) = X Y Z
2) (X Y) Z = X (Y Z) = X Y Z
Коммутативный закон
3) X Y = Y X
4) X Y = Y X
Закон идемпотентности (повторения)
5) X X = X
6) X X = X
Дистрибутивный закон
7) (X Y) Z = (X Z) ( Y Z)
8) (X Y) Z = (X Z) (Y Z) (нет в обычной алгебре).
31.
Законы универсального U и пустого множеств(законы нуля и единицы 0, U 1)
9) X = X
10) X =
11) X U = U
12) X U = X
13) = U
14) U =
Законы исключенного третьего и противоречия
15) X X = U
16) X X = .
Законы де Моргана
17) X Y X Y ;
18) X Y X Y
32.
Закон двойного отрицания19) X = X
Если имеет место включение A B , то
А В А и А В В
А В и А В U
33.
Законы 5) и 6) можно записать и такX X X X … = X
X X X X … = X
что позволяет при выполнении операций объединения и
пересечения обходиться без коэффициентов и показателей
степеней.
При работе с множествами могут оказаться полезными
тождества, приведенные ниже.
Однако они требуют доказательства.
Доказать их можно, используя основные законы
(свойства операций пересечения, объединения и дополнения).
34.
Дистрибутивный закон пересечения относительно разностиX (Y \ Z ) ( X Y ) \ ( X Z )
Дистрибутивный закон пересечения относительно
симметрической разности
X (Y Z ) ( X Y ) ( X Z )
Дистрибутивный закон разности относительно пересечения
( X Y ) \ Z ( X \ Z ) (Y \ Z )
Дистрибутивный закон разности относительно объединения
( X Y ) \ Z ( X \ Z ) (Y \ Z )
35.
Дистрибутивные законы объединения и пересеченияотносительно разности
X\(Y Z) = (X\Y) (X\Z)
X\(Y Z) = (X\Y) (X\Z)
Представление пересечения и объединения через разность
X Z = X\(X\Z)
X Y= (X\Y) (Y\X) (X Y) = (X\Y) (Y\X) X\(X\Y)
Законы нуля и единицы для разности
(X\Y) (X Y) =
\X = X
U\X = X
X\ = X\U =
X\X =
36.
Законы поглощенияX (X Y) X
Закон склеивания
(X Y) (X Y ) X
X (X Y) X
37.
Свойства симметрической разностиА А ,
А А А
A B A B A B
если C A B,
то можно записать A B C или B A C ,
A B A B ( A B)
A B A B ( A B)
A B ( A B) \ ( A B)
или A B ( A \ B) ( B \ A)
A B ( A B ) ( A B)
или
A B ( A B) ( A B )
38.
Доказательства тождественности формулНаиболее часто в теории множеств возникает необходимость
доказательства равенства соотношений типа Х = Y.
Доказательство можно проводить путем рассуждений с
применением законов и тождеств алгебры множеств,
построением диаграмм Эйлера–Венна
(или на примерах конкретных множеств, составленных,
например, из алфавитно–цифровых символов ???).
39.
Ниже, в примерах, доказательство соотношений типа X = Y,где Х и Y – множества,
основано на использовании определений I и II равенства двух
множеств.
В соответствии с определением I
для равенства двух множеств требуется совпадение их
элементов.
В соответствии с определением II
Х = Y, если X Y и Y X
40.
ПримерДоказать справедливость соотношения
A B A B
Возьмем произвольный элемент x A B
Это значит,
что x A и x B ,
значит x A и x B
Следовательно, x A B
41.
Пусть теперь некоторый элемент y A B ,т.е. y A и y B .
Это значит, что y A и y B , т.е.
y A B.
Следовательно, y A B .
Таким образом, доказано, что
A B A B.
42.
ПримерПроиллюстрируем справедливость соотношения
A B A B
Пусть имеем
U = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9},
A = {0, 1, 3, 7},
B = {2, 3, 4, 6, 7}.
43.
Определим левую часть:A B = {0, 1, 3, 7} {2, 3, 4, 6, 7} = {0, 1, 2, 3, 4, 6, 7},
A B = U \ ( A B) =
= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} \ {0, 1, 2, 3, 4, 6, 7} = {5, 8, 9}.
Определим правую часть:
A = U \ A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} \ {0, 1, 3, 7} =
{2, 4, 5, 6, 8, 9},
B = U \ B = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} \ {2, 3, 4, 6, 7} =
{0, 1, 5, 8, 9},
A B = {2, 4, 5, 6, 8, 9} {0, 1, 5, 8, 9} = {5, 8, 9}.
44.
Как видим, левая часть равна правой, следовательно, что?45.
ПримерДоказать справедливость соотношения
(A\B)\C = A\(B C).
Используем соотношение
A\ B A B .
Левая часть
(A\B)\C = ( A B ) \С = ( A B ) C A B C .
Правая часть
A\(B C) = A ( B C ) A ( B C ) A B C .
Как видим, левая часть равна правой, следовательно,
соотношение справедливо.
46.
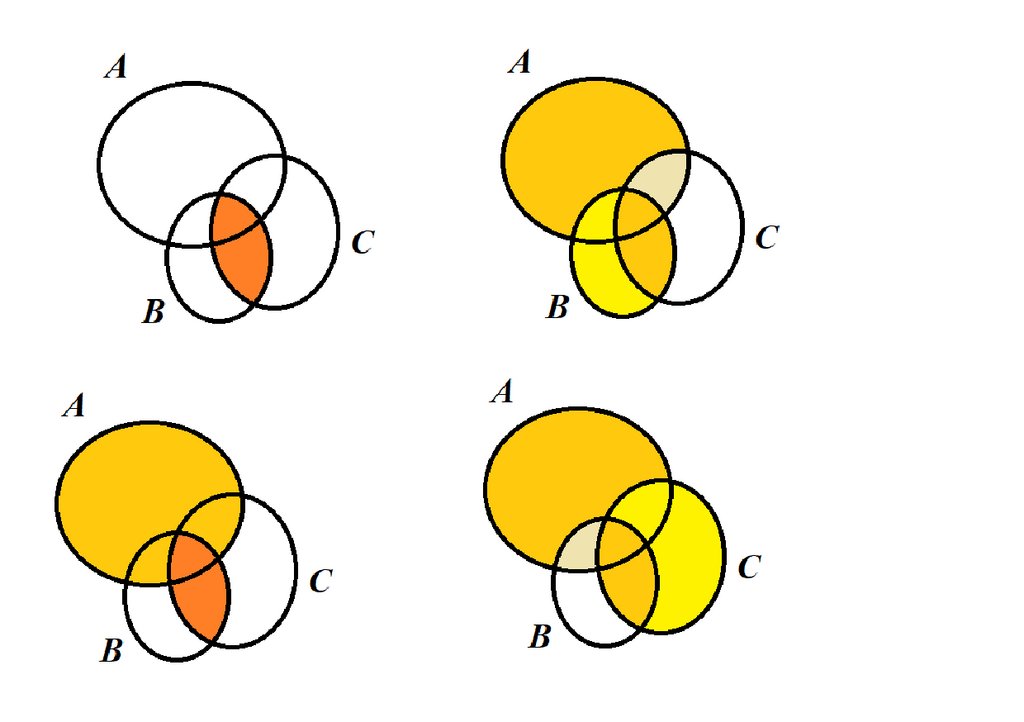
Пример. Доказать справедливость соотношенияA ( B C ) ( A B) ( A C )
Это свойство дистрибутивности слева объединения
относительно пересечения .
Такое доказательство может быть выполнено с помощью
диаграмм Эйлера–Венна.
47.
48.
Здесь для этих целей используем один из приемовдоказательства равенства двух множеств.
В соответствии с первым определением равенства множеств
множества равны, если их элементы совпадают.
Это означает,
что Х = Y,
если из того,
что a X , следует a Y ,
и из того, что a X , следует a Y .
49.
1. Покажем сначала, что еслипроизвольный элемент а принадлежит
левой части соотношения, т.е.
a A ( B C ) , то он принадлежит и
правой части данного соотношения, т.е.
a ( A B) ( A C ) .
Пусть a A ( B C ) .
Из определения операции объединения следует, что элемент а
принадлежит объединению множеств А и ( B C ) , если он
принадлежит хотя бы одному из них (или, что очевидно, тому
и другому).
50.
Таким образом, a A или a ( B C ) , приэтом возможны следующие случаи:
1.1. а принадлежит множеству А и а не
принадлежит пересечению множеств B C :
a A и a (B C) .
Последнее условие выполняется, если а не принадлежит В,
или С, или им обоим (это является лишним);
1.2. a A и a ( B C ) , т.е. a A, a B, a C ;
1.3. a A и a ( B C ) , т.е. a A, a B, a C .
51.
Рассмотрим каждый из этих случаев.1.1. Так как a A, то а принадлежит объединению
множества А с любым множеством, в том числе a ( A B ) и
a ( A C ) . Следовательно, а принадлежит и их пересечению:
a ( A B) ( A C ) .
1.2. Так как a B , a C , то a ( A B ) и a ( A C ) ,
следовательно, a ( A B ) ( A C ) .
1.3. Так как a A, то этого достаточно, чтобы a ( A B )
и a ( A C ) , следовательно, a ( A B ) ( A C ) .
Таким образом, в любом из рассмотренных случаев из того,
что a A ( B C ) , следует, что a ( A B ) ( A C ) .
52.
2. Покажем теперь справедливость второго условияопределения I равенства множеств:
если произвольный элемент а не принадлежит левой части
соотношения a A ( B C ) ,
то он не принадлежит и правой части данного соотношения
a ( A B) ( A C )
Пусть теперь:
a A (B C)
Элемент а не принадлежит объединению двух множеств, если
он не принадлежит ни одному их них.
53.
Тогда а А и a ( B C ) , т.е. возможны следующие случаи:2.1. a A, a B, a C ;
2.2. a A, a B, a C ;
2.3. a A, a B, a C .
54.
Рассмотрим каждый из этих случаев:2.1. Так как a A,
a B , то a ( A B ) , следовательно,
a ( A B) ( A C ) .
2.2. Так как a A,
a С , то a ( A С ) , следовательно,
a ( A B) ( A C ) .
2.3. Так как a A, a B , то этого достаточно, чтобы
a ( A B ) , следовательно, a ( A B ) ( A C ) .
55.
Как видим, в любом из этих случаев из того, чтоa A ( B C ) , следует, что a ( A B ) ( A C ) .
Таким образом, множества A ( B C ) и ( A B ) ( A C )
совпадают т.е.
A ( B C ) ( A B) ( A C ) .
56.
Рассуждения с использованием исчисления высказыванийОбозначим:
Тогда:
Событие
a:
x A
Событие
b:
x B
Событие
c:
x C
x A B a b
x A B a b
x A \ B a ( b)
x A a
57.
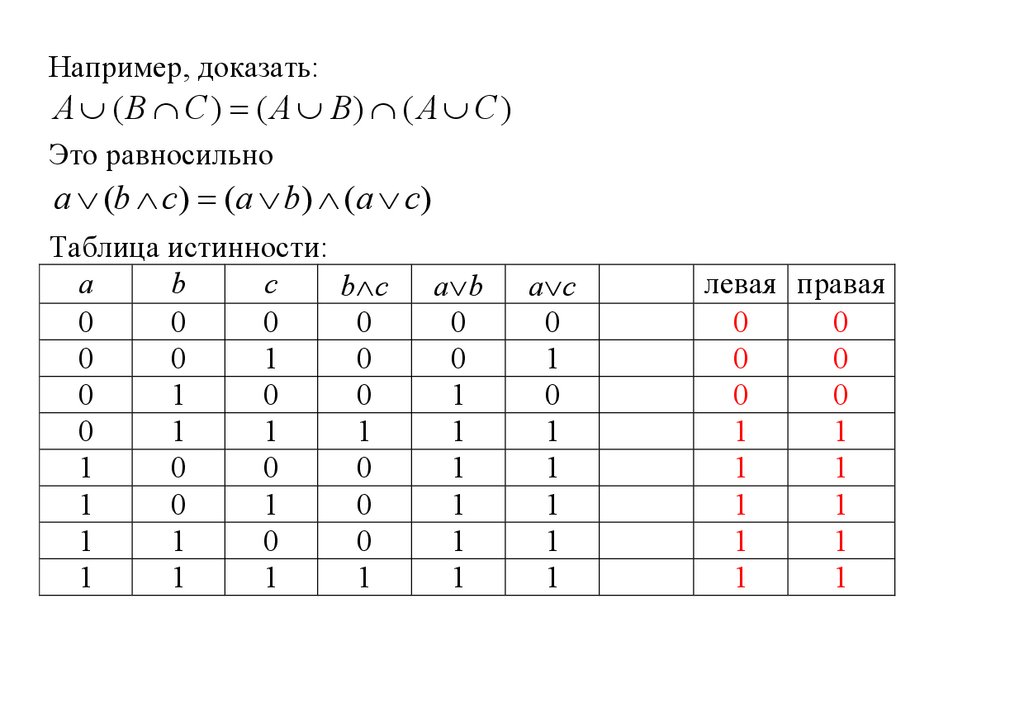
Например, доказать:A ( B C ) ( A B) ( A C )
Это равносильно
a (b c) (a b) (a c)
Таблица истинности:
a
b
c
b c
0
0
0
0
0
0
1
0
0
1
0
0
0
1
1
1
1
0
0
0
1
0
1
0
1
1
0
0
1
1
1
1
a b
0
0
1
1
1
1
1
1
a c
0
1
0
1
1
1
1
1
левая правая
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
58.
Семейства множествПусть дано множество U (конечное или бесконечное) и из
элементов этого множества образована некоторая
совокупность множеств Xa, называемая семейством множеств.
Обозначим:
X a C,
X a D.
a
a
Если C = U, то имеем полное семейство.
Если C = U и D ,
то совокупность множеств Xa образует систему
классов эквивалентности.
Над множествами, принадлежащими семействам, можно
выполнять операции объединения и пересечения по обычным
правилам.
59.
Символическая записьn
i 1
i 1
n
i 1
i 1
A; Ai ; Ai ; Ai ,
A U
i I
A; Ai ; Ai ; Ai .
A U
i I
В первом варианте объединяются или пересекаются множества,
принадлежащие универсальному множеству U.
Во втором варианте объединяются или пересекаютcя множества
A1, A2, A3, …, An.
В третьем варианте объединяется или пересекаетcя бесконечное
число множеств A1, A2, A3, …
В четвертом варианте объединяются или пересекаютcя
множества, индекс которых принадлежит счетному множеству I
(I = {1, 2, 3, …, n}).
60.
Для операций пересечения и объединения справедливоX Y ( X ) Y ;
a
a
a
a
X Y ( X ) Y .
a
a
a
a
Здесь Y – некоторое подмножество множества U.
Пусть множества семейства формируются последовательным
добавлением элементов. Если с некоторого k Хk+1 = Хk, то
n
Xi Xk .
i 1
61.
Операция разности – бинарная, поэтому для семействмножеств она выполняется по следующим правилам
( X a ) \ Y X a \ Y ;
a
a
( X a ) \ Y X a \ Y ;
a
a
Y \ X a Y \ X a ;
a
a
Y \ X a Y \ X a .
a
a
62.
Прямое произведение семейства множествX1, X2, …, Xn –
это множество элементов вида ( x1 , x2 ,..., xn ),
где x1 X1 , x2 X 2 ,..., xn X n .
Обозначается оно так
X 1 X 2 ... X n X i
i I
или так
X1 X 2 ... X n
{( x1 , x2 ,..., xn )| x1 X1, x2 X 2 ,..., xn X n }.
63.
Произведение множеств – операция некоммутативная –переставлять множества в произведении нельзя.
(почему?)
Мощность множества X1 X 2 ... X n равна произведению
мощностей множеств сомножителей
n
| X1 X 2 ... X n | = | X i | .
i 1
Для степени множества X получаем
|X n| = |X|n
64.
Для произведения множеств справедливы следующиесвойства
В Аi ( B Ai ) ,
i I
i I
В Ai ( B Ai ) .
i I
i I
65.
Пусть дано семейство множеств А1, А2, …, Аn и пустьтребуется определить мощность их объединения
А1 А2 … Аn
В первом приближении (если не пересекаются!!!)
n
n
Ai
Ai
i 1
i 1
Однако, если есть пересечение,
Аi Аj ,
то это не так.
66.
Исключение “лишних” элементов производится на основепринципа включений и исключений по формуле
n
n
A A A A A A A
i
i 1
i 1
... 1
n 1
i
1 i j n
i
j
i
1 i j k n
j
A1 ... An .
(Как доказать?)
k
67.
ОтношенияЕсли в декартовом произведении множества А на себя
выделить некоторые упорядоченные пары
(например, отличающиеся особым свойством),
то получим новое множество R.
Это множество R будет подмножеством A2, т. е.
R A 2.
Множество R называют бинарным отношением, заданным на
множестве А.
68.
Если бинарное отношение состоит из упорядоченных пар, вкоторых первая компонента совпадает со второй, то оно
называется тождественным на всем множестве А и
обозначается IA.
Таким образом:
IA = {(a, a) | a A}.
Заметим, что каждый элемент множества А образует пару с
одинаковыми компонентами, попадающую в тождественное
отношение.
Например, если C = {1, *}, то тождественное отношение,
заданное на всем C, есть множество
IC = {(1, 1), (*, *)}.
69.
Если дано бинарное отношение R A2,то обратным к нему называют отношение
R-1 = {(b, a) | b A, a A, (a, b) R}.
Например, если на множестве C = {1, *} задано бинарное
отношение
R = {(1, *}, (*, *)},
то обратным к нему будет отношение
R-1 = {(*, 1), (*, *)}.
Заметим, что в обратном отношении R-1 все упорядоченные
пары записываются в обратном порядке, нежели пары в
исходном R.
70.
Если даны два бинарных отношенияR A2 и S A2,
то композицией R и S называют новое отношение
T = {(a, c) | a A, c A, b A, (a, b) R, (b, c) S}.
Отношение T обозначают R S.
Замечание.
Композиция R S будет отличаться от S R.
71.
Некоторые виды отношений1. Отношение R на M рефлексивно, если:
a M (a, a) R.
2. Отношение R на M симметрично, если:
(a, b) R (b, a) R.
3. Отношение R на M транзитивно, если:
(a, b) R (b, с) R (a, c) R.
4. Рефлексивноe симметричное транзитивное отношение
называется отношением эквивалентности.
72.
5. Отношение R на M антирефлексивно, если:a M (a, a) R.
6. Отношение R на M антисимметрично, если:
∀ a, b ∈ X, (a R b) ∧ a≠b ⇒ ¬(b R a)
Антисимметричность отношения не исключает симметричности.
Существуют бинарные отношения:
одновременно симметричные и антисимметричные (отношение
равенства)
ни симметричные, ни антисимметричные
симметричные, но не антисимметричные
антисимметричные, но не симметричные ("меньше или равно",
"больше или равно")
73.
ТеоремаОтношение эквивалентности делит множество на
непересекающиеся классы (классы эквивалентности).
Как доказать?
- Предъявить алгоритм построения
74.
Теорема (обратная)Любое деление множества на непересекающиеся классы
задает отношение эквивалентности.
Как доказать?
- Построить соответствующее отношение
75.
Матрица бинарного отношенияЕсли множество A конечно, то его элементы можно
пронумеровать.
Если на конечном множестве A задано бинарное отношение
R A 2,
то можно построить матрицу этого отношения.
Номера строк и столбцов матрицы будут совпадать с
номерами элементов множества А.
Таким образом, матрица отношения будет квадратной, n-го
порядка, где n – количество элементов, содержащихся в А.
Матрицу заданного отношения R обозначим MR.
76.
Каждый элемент mij матрицы MR равен нулю или единице.mij = 1, если упорядоченная пара (ai , aj) R.
Но если пара (ai , aj) не принадлежит R, то mij = 0.
Например, если на множестве C = {1, *}
задано бинарное отношение R = {(1, *), (*, *)},
то матрица отношения примет вид:
0 1
MR
0 1
77.
Но заметим, что если поменять нумерацию элементов вомножестве C, то матрица того же самого отношения R примет
другой вид:
1 0
MR
1 0
Эту матрицу перестановкой столбцов можно свести к
исходной.
78.
Нетрудно доказать следующие свойства матриц отношений.1. Если отношение R рефлексивно, то его матрица имеет
на главной диагонали только единицы.
2. Если отношение R антирефлексивно, то его матрица
имеет на главной диагонали только нули.
3. Если отношение R симметрично, то и его матрица
симметрическая.
4. Если отношение R антисимметрично, то для каждого
элемента его матрицы такого, что mij = 1 симметричный ему
элемент mji = 0.
79.
5. Если отношение R транзитивно, то элементы егоматрицы должны удовлетворять следующему условию:
Если mij = 1 и в то же самое время mjk = 1,
то обязательно должно выполняться mik = 1.
80.
0 1Рассмотрим, например, матрицу отношения M R
0 1
1) Поскольку на главной диагонали стоят ноль и единица, то R
не является ни рефлексивным, ни антирефлексивным
отношением.
2) В силу того, что элементу m12 = 1 соответствует
симметричный ему элемент m21 = 0, делаем вывод, что
отношение R антисимметрично.
3) Для элемента m12 = 1 только один соответствующий ему
элемент m22 = 1. Проверяем, что выполняется условие
транзитивности m12 = 1, следовательно, отношение R
транзитивно.
81.
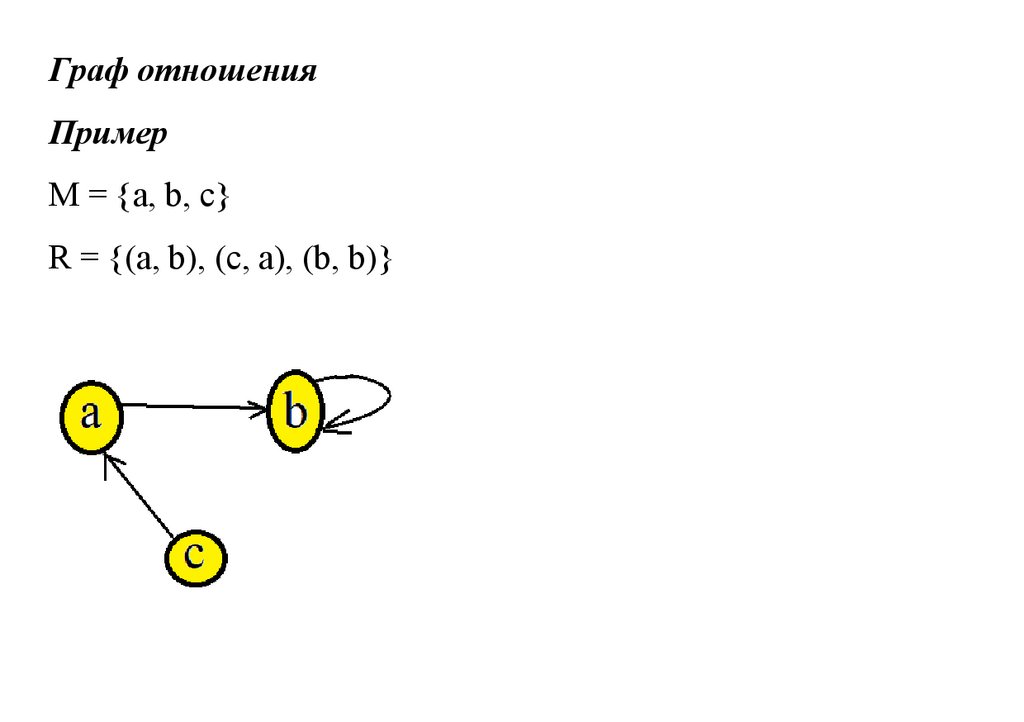
Граф отношенияПример
M = {a, b, c}
R = {(a, b), (c, a), (b, b)}
82.
Отношения порядкаОпределение
Отношение R на множестве A называется отношением
порядка, если оно обладает следующими свойствами:
1) (x, x) R для всех x (рефлексивность)
2) Если (x, y) R и (y, x) R, то x = y (антисимметричность)
3) Если (x, y) R и (y, z) R, то (x, z) R (транзитивность)
Обычно отношение порядка обозначают знаком .
Если для двух элементов x и y выполняется x y, то говорят,
что x "предшествует" y.
83.
Как и для отношения эквивалентности, условия 1-3 в такихобозначениях выглядят более естественно:
x x для всех x (рефлексивность)
Если x y и y x, то x = y (антисимметричность)
Если x y и y z, то x z (транзитивность)
84.
ПримерПростым примером отношения порядка является отношение,
задаваемое обычным неравенством на множестве
вещественных чисел.
Заметим, что любые два числа сравнимы между собой.
Такие отношения называются отношениями полного порядка.
85.
ПримерРассмотрим на множестве A всех сотрудников некоторого
предприятия отношение, задаваемое следующим образом:
сотрудник x предшествует сотруднику y тогда и только тогда,
когда выполняется одно из условий:
x=y
x является начальником (не обязательно непосредственным) y.
Назовем такое отношение "быть начальником".
Легко проверить, что отношение "быть начальником" является
отношением порядка.
Заметим, что в отличие от предыдущего примера, существуют
такие пары сотрудников x и y, которые не сравнимы.
Такие отношения, в которых есть несравнимые между собой
элементы, называют отношениями частичного порядка.
86.
Функциональное отношениеОпределение
Отношение R на паре множеств A и B, т.е. R A B
называется функциональным отношением, если оно обладает
следующим свойством:
Если (x, y) R и (x, z) R, то y = z (однозначность функции).
87.
Обычно, функциональное отношение обозначают в видефункциональной зависимости y = f(x).
Функциональные отношения (подмножества декартового
произведения!) называют иначе графиком функции или
графиком функциональной зависимости.
88.
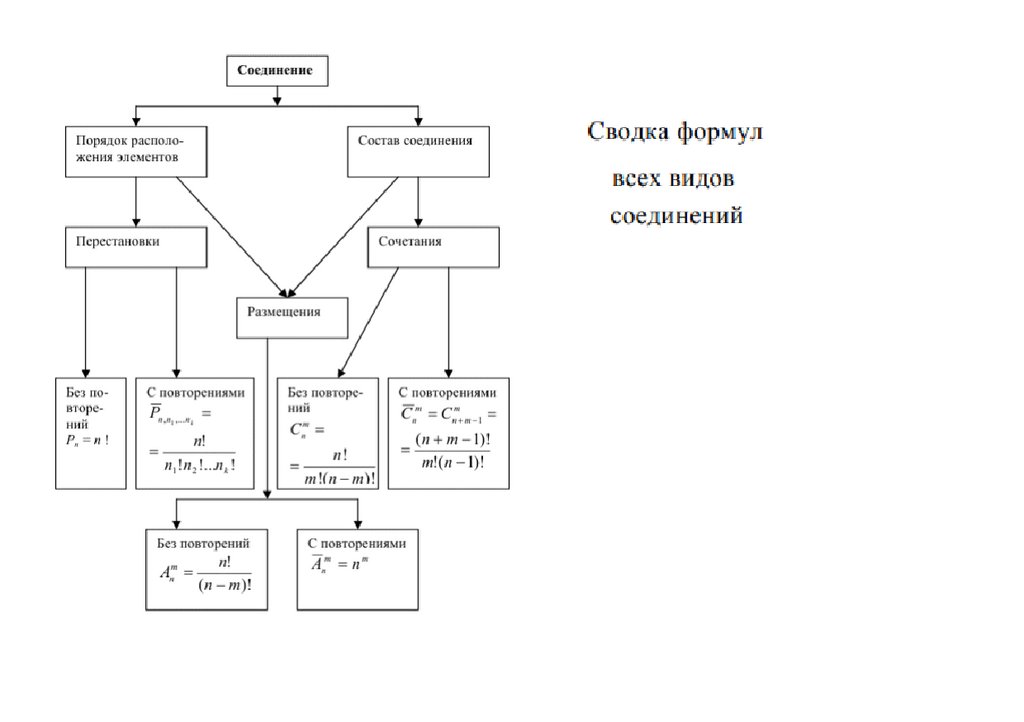
IIКомбинаторный анализ
89.
ОпределениеКомбинаторный анализ – раздел математики, имеющий дело
с конечными множествами.
Определение
Особые подмножества конечных множеств называются
комбинаторными конфигурациями.
Количество комбинаторных конфигураций определённого
вида называется комбинаторным числом.
Определение
Перечислительные задачи – раздел комбинаторики,
занимающийся нахождением комбинаторных чисел.
90.
Введём универсальное множество из n элементов(n-множество) U и рассмотрим его подмножества из k
элементов (k-подмножества).
Они могут быть упорядочены или не упорядочены (линейно).
U e1 , e2 ...en
91.
ОпределениеНеупорядоченное подмножество ei1 , ei2 ...eik называется
k-сочетанием n-множества U (из n по k).
Упорядоченное подмножество (ei , ei ...ei ) называется
1
2
k
k-размещением n-множества U (из n по k).
Обозначение
обозн. n
k
Cn – число сочетаний из n элементов по k.
k
Ank – число размещений из n элементов по k.
92.
ОпределениеПусть e1 , e2 ...en – названия типов элементов, тогда сочетанием
(размещением) с повторениями называется сочетание
(размещение), в котором элементы одного типа могут
повторяться.
Обозначение
Ĉnk – число сочетаний
из n элементов по k с повторениями.
Ânk – число размещений
из n элементов по k с повторениями.
93.
УтверждениеAnk n n 1 ... n k 1
Ank Ank
n!
C k
k! k! n k !
Ak
Aˆ nk n k
k
n
n!
n k !
94.
Теорема(правило произведения)
Если объект O1 может быть выбран m1 способами,
объект O2 может быть выбран m2 способами
и они выбираются независимо друг от друга,
то
пара O1 и O2 может быть выбрана m1 m2 способами.
95.
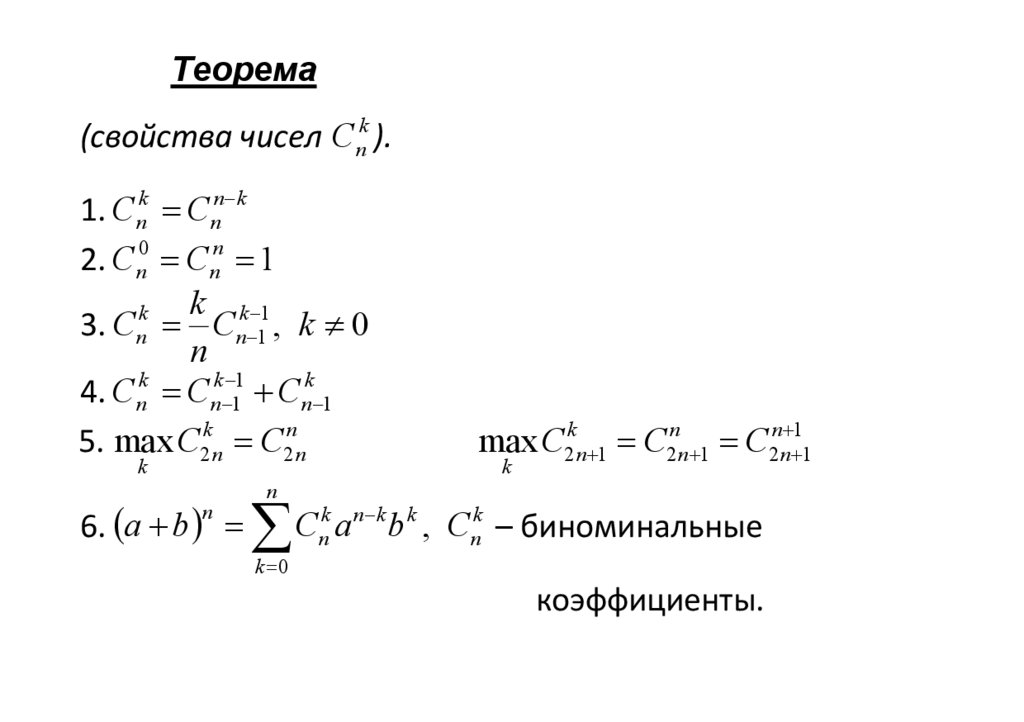
96.
Теорема(свойства чисел Cnk ).
1. Cnk Cnn k
2. Cn0 Cnn 1
k
3. Cnk Cnk 11 , k 0
n
4. Cnk Cnk 11 Cnk 1
5. max C2kn C2nn
k
6. a b
n
n
max C2kn 1 C2nn 1 C2nn 11
k
Cnk a n k b k , Cnk – биноминальные
k 0
коэффициенты.
97.
n7.
Cnk 2 n
k 0
n
8.
k
k
1
C
n 0
k 0
n
9.
n
C
Cnk 2 n 1
k 0
k 0
k
n
k чётно
10.
k нечётно
Cn0 Cn1 1 Cn2 2 ... Cnm m
m
C
k
n k
Cnm m 1
k 0
11. C0k C1k C2k ... Cnk Cnk 11
(сумма усечённого k-ого столбца треугольника Паскаля).
98.
k12.
m 0
Cnm1 Cnk2 m Cnk1 n2
Числа Cnk образуют треугольник Паскаля:
0 1 2 3 ... k
13.
0
1
1
1
1
2
1
2
1
3
1
3
3
n
1
99.
11
1
1
1
1
2
3
4
5
1
1
3
6
10
1
4
10
…
1
5
1
100.
6. a b a b a b ... a bn
n
Преобразуем в сумму произведений.
Каждое произведение содержит n множителей a или b.
Нужно выбрать k скобок, из которых возьмём множитель b.
Они же однозначно определяют n – k скобок, откуда берём
a. Число таких скобок Cnk , k 0,1,2...n .
101.
7.I способ.
Воспользуемся формулой 7 при a = b = 1
1 1
n
n
Cnk 2 n .
k 0
II способ.
2 n – число всех подмножеств n-множества.
Cnk – число k-подмножеств n-множества.
n
k 0
Cnk 2 n .
102.
8.В формуле Бинома положим a = 1, b = –1
1 1
n
n
k 0
Cnk 1 0 .
k
103.
9.S0
n
n
C , S C
k
n
1
k
n
k 0
k 0
k чётно
k нечётно
Cn0 Cn1 Cn2 ... Cnn 2 n
C C C ... 1 C 0
0
n
1
n
2
n
n
n
n
2Cn0 2Cn2 2Cn4 ... 2Cn2 k 2 n S 0 2 n 1
104.
10.Cnm m 1 по свойству 4 Cnm m Cnm m1
Cnm m Cnm m1 1 Cnm m2 1 ...
Cn0 Cn1 1 Cn2 2 ... Cnm m
105.
11.Cnk 11 Cnk 1 Cnk Cnk Cnk 11 Cnk 1
Cnk Cnk 1 Cnk 2 Cnk 21 ...
C0k C1k C2k ... Cnk
106.
ТеоремаCˆ nk Cnk k 1 Cnn k1 1
Универсальное множество U e1 , e2 ...en .
Рассмотрим выборку G объёма k:
G e j1 , e j2 ,...e jk , где j1 , j2 ... jk 1,2,3...n .
Поставим G в соответствие вектор
G X x1 , x2 ...xn , где 0 xi k , xi число вхождений
ei в выборку G.
n
x k
i
i 1
107.
yi xi 1,Положим
т.
е.
установим
соответствие
G X Y y1 , y2 ... yn .
Число Ĉnk выборок G равно числу таких векторов y, что
yi 1,
n
n
n
y x 1 x n n k
i
i 1
i
i 1
i
i 1
Число таких векторов y равно количеству разбиений числа
n+k в сумму n натуральными слагаемых y1 , y2 ... yn .
108.
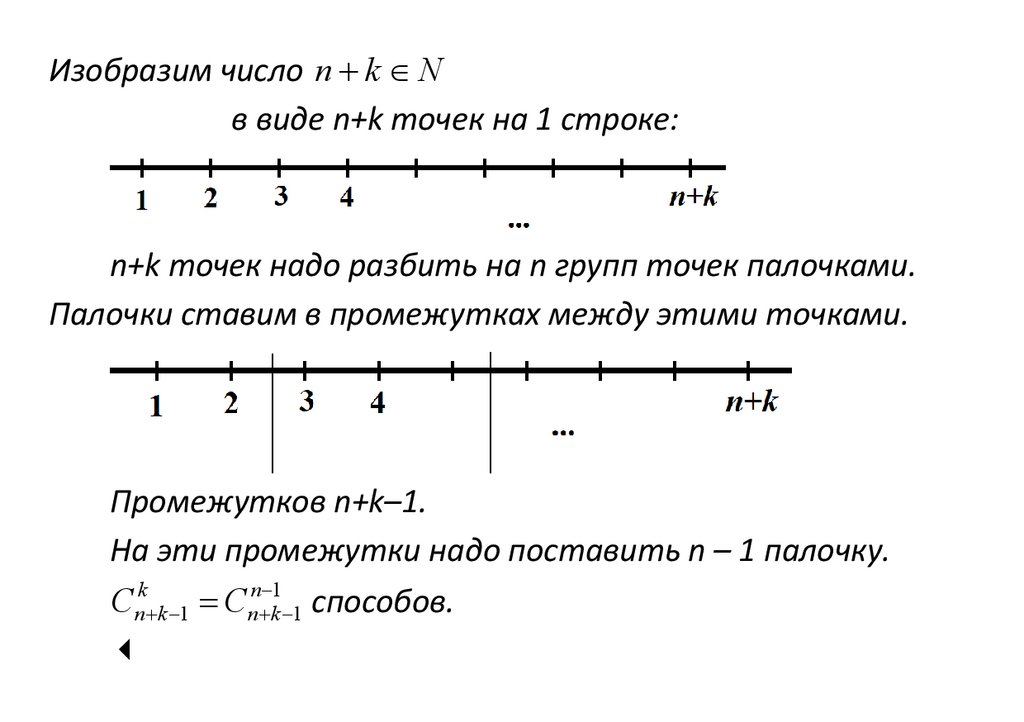
Изобразим число n k Nв виде n+k точек на 1 строке:
n+k точек надо разбить на n групп точек палочками.
Палочки ставим в промежутках между этими точками.
Промежутков n+k–1.
На эти промежутки надо поставить n – 1 палочку.
Cnk k 1 Cnn k1 1 способов.
109.
ПримерAˆ 23 2 3 8
Cˆ 23 C43 4
U 0,1
Все Aˆ 23 :
000, 001, 010, 011, 100, 101, 110, 111
Все Cˆ 23 :
000, 001, 011, 111
110.
Производящие функцииОпределение
Рассмотрим последовательность a a0 , a1 , a2 ...an ...
комбинаторных чисел и рассмотрим формальный степенной
ряд:
Fa t
an t n
n 0
Этот ряд называется производящей функцией
последовательности а.
Пример
Последовательность Cn0 , Cn1 , Cn2 ,...Cnn , 0, 0...
F t
n
k 0
Cnk t k 1 t
n
для
111.
Свойства производящих функций:1. Линейность.
Если Cn an bn , то FC t Fa t Fb t
2. Сдвиг влево на m элементов.
b am , am 1 , am 2 ...
Fa t a0 a1
am 1
Fb t
m 1 ...
m
t
t
t
3. Сдвиг последовательности вправо на m элементов.
b 0
,
0
, ...,
0
,
a
,
a
,
a
...
0 1 2
m нулей
Fb t t m Fa t
112.
4. Дифференцирование и интегрирование производящихфункций.
1
Если bn n an , cn
an ,
1 n
d
F
t
t
Fa t
b
dt
то
t
1
Fс t Fa x dx
t0
113.
Рассмотрим производящие функции для часто встречающихсяпоследовательностей:
1. an a n , a 0
Fa t
n 0
at
n n
1
n
at
n 0
1 at
114.
2. an nFa t
nt t
n
n 0
S t
nt n 1 t S t
n 1
nt n 1
t
n 1
t
S x dx
t
1
t
S t dt
S t
2
1 t
1 t 1 t
n 1 0
0
Fa t
n 1
nx dx
t n t t 2 t 3 ...
n 1
/
t
1 t 2
t
1 t
115.
3. cn n n 12t 2
Интегрируем предыдущий пример Fc t
1 t 3
4. d n n 2 cn bn по свойству 1.
2t 2
t
t2 t
Fd t Fc t Fb t
3
2
1 t 1 t 1 t 3
116.
Линейные рекуррентные уравненияЧасто комбинаторные числа выражаются через предыдущие
члены той же последовательности.
Пример
(задача о разрезании пиццы).
На сколько частей делят плоскость n прямых,
из которых любые 2 пересекаются
и никакие 3 не пересекаются в 1 точке?
117.
x n – искомое число. Очевидно:x0 1
x1 2
x2 4
x3 7
Пусть есть n 1 прямых l1 , l2 ...ln 1 .
Проведём ещё одну l n , она пересекает l1 , l2 ...ln 1 в точках
A1 , A2 , ... An 1 .
Эти точки разбивают ln на n частей, увеличивающих число
частей на n xn xn 1 n .
118.
Это и есть рекуррентное уравнение для последовательностиx0 , x1 , x2 ....
С учётом начального условия x0 1 можем вычислить
xn n xn 1 n (n 1) xn 2 ...
n n 1 n 2 ... 1 x0
n n 1 .
1 1 2 ... n 1
2
n n 1
Таким образом x n 1
является решением уравнения
2
xn xn 1 n .
119.
ПримерИзвестно рекуррентное соотношение для Cnk :
Cnk Cnk 11 Cnk 1
120.
Пример(«Задача Фибоначчи о кроликах», монах Леонардо Пизанский,
XI в).
Есть пара (самец и самка) новорожденных кроликов. Через 2
месяца они могут размножаться. Размножаются они каждый
месяц и пара рождает всегда тоже одну пару (самца и самку),
которые через 2 месяца тоже будут размножаться каждый
месяц и т. д.
121.
Fn – количество пар кроликов спустя n месяцев.F0 F1 1 (через месяц исходные кролики ещё не
размножаются).
Fn 2 Fn 1 Fn – рекуррентное уравнение для чисел
Фибоначчи и начальные условия.
Можем построить таблицу чисел Фибоначчи:
n
0
1
2
3
4
5 ...
Fn 1
1
2
3
5
8 ...
122.
Выведем замкнутую формулу для чисел Фибоначчи, т. е.выразим Fn только через n.
Пусть Fn t Fn t n –
n 0
производящая функция для последовательности чисел
Фибоначчи.
Тогда сдвинув последовательность влево на 1, получим
F t F0
Fn 1 t n
,
t
а при сдвиге последовательности влево на 2 получим
F t F F
Fn 2 t n 2 0 1 .
t
t
123.
Т. к. образом, переходя от рекуррентного уравнения куравнению для ПФ, получим
Fn t 1 1 Fn t 1
Fn t
2
t
t
t
t 2 t 1 Fn t 1 Fn t 2 1
t t 1
Корни знаменателя обозначим так
1 5
1 5
,
, тогда
2
2
124.
11/ 5 1/ 5
1 1 1
1 1
Fn t
t t t t 5 1 t 1 t
1
разложение
1 x x 2 ... геометрической прогрессии
1 x
n
n
1 1 t 1 t 1 1
1 n
n 1 n 1 t Fnt n
5 n 0 n 0 n 0 5
n 0
Fn равно коэффициенту при t n :
n 1
n 1
1 5
1 1 5
.
Fn
5 2
2
Несмотря на эти иррациональности, все Fn целые.
125.
Матричный подходFn
n
, n 0
Fn 1
1
1
1
n M n 1 , n 1
Fn a b Fn 1 aFn 1 bFn 2
Fn 1 c d Fn 2 cFn 1 dFn 2
a 1, b 1, c 1, d 0
1 1
M
1
0
n M n 1 M 2 n 2 ... M n 1 1 , n 1
126.
ОпределениеУравнение
x n k ak 1 xn k 1 ak 2 xn k 2 ... a1 xn 1 a0 xn b
называется рекуррентным уравнением
последовательности x0 , x1 , x2 , ...
порядка
k
для
В данном случае члены последовательности могут быть
любыми числами (т.е. рациональные, действительные,
комплексные) коэффициенты ak 1 , ak 2 ,..., a1 , a0 , b тоже.
Если b 0 , то уравнение называется однородным.
127.
УтверждениеЕсли a0 a`1 ... ak 1 1,
то неоднородное уравнение
сводится к однородному заменой xn yn для некоторой
const .
x n k yn k , ..., xn yn подставляем в уравнение:
yn k ak 1 yn k 1 ... a1 yn 1 yn 1 ak 1 ... a1 a0 b .
Уравнение станет однородным, если
1 ak 1 ... a1 a0 b
b
1 ak 1 ... a1 a0
128.
Метод решенияоднородных линейных уравнений порядка k
аналогичен
методу решения однородных линейных дифференциальных
уравнений порядка k.
129.
ОпределениеАлгебраическое уравнение относительно
k ak 1 k 1 ... a1 a0 0
степени k называется характеристическим уравнением для
x n k ak 1xn k 1 ak 2 xn k 2 ... a0 xn 0 .
130.
УтверждениеЕсли 0 – корень характеристического уравнения,
то xn 0 является решением уравнения
n
x n k ak 1xn k 1 ak 2 xn k 2 ... a0 xn 0 .
Утверждение
Если последовательности xn и
yn являются решением
уравнения
x n k ak 1xn k 1 ak 2 xn k 2 ... a0 xn 0 .
то любая их линейная комбинация zn Axn Byn A, B C
также является решением этого уравнения.
131.
Теорема(Общее решение однородного уравнения)
Пусть 1 , 2 , ..., S – все корни характеристического
уравнения, имеющие кратности
k1 , k2 , ..., k S k1 k2 ... k S k .
Тогда общее решение однородного уравнения имеет вид
xn
C C n C n ... C
S
2
0j
j 1
1j
2j
k 1
j
k j 1n
n
j
При фиксированных значениях Cl j получим частное решение.
132.
Для нахождения частного решения используют начальныеусловия:
x0 A0
x A
1
1
...
xk 1 Ak 1
Этих условий – k штук
133.
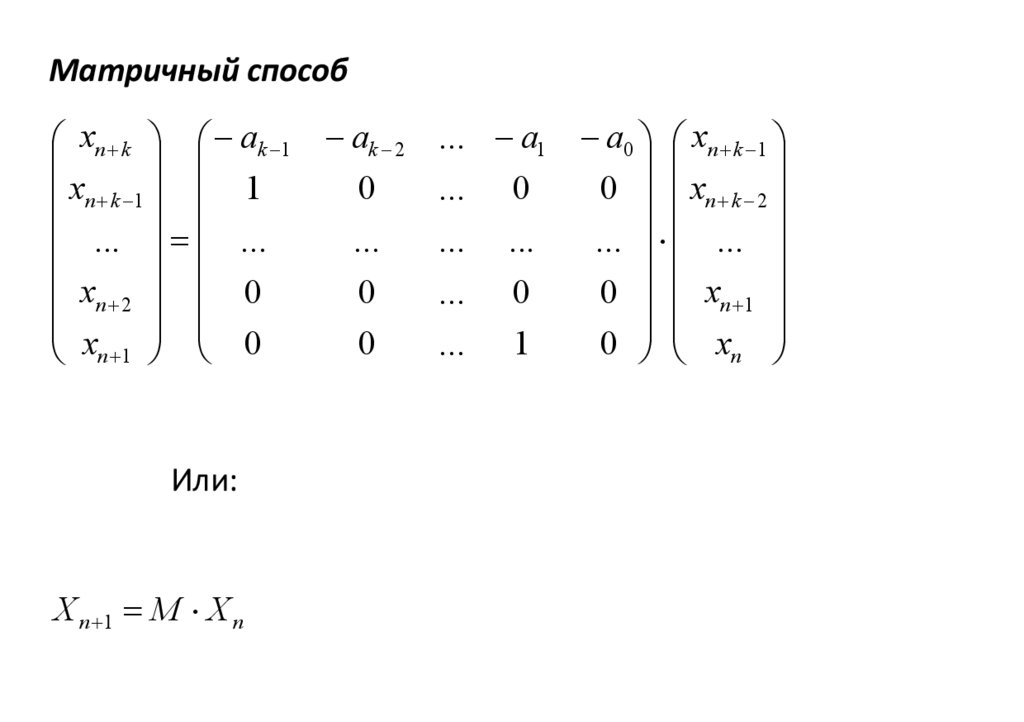
Матричный способxn k ak 1 ak 2
x
0
n k 1 1
... ...
...
0
xn 2 0
x 0
0
n 1
Или:
X n 1 M X n
... a1 a0 xn k 1
x
... 0
0 n k 2
... ...
... ...
... 0
0 xn 1
... 1
0 xn
134.
Получаем:X n 1 M X n M 2 X n 1 ... M n 1 X 0
135.
ПримерРешить неоднородное уравнение.
x m 1 12 xm 10
x0 9
x m 1 12 xm 10
1) Сведём уравнение к однородному заменой y m xm
y m 1 12 ym 1 12 10
11 10
xm ym
10
11
10
11
136.
2) Решим однородное уравнение :y m 1 12 ym 0
3) Характеристическое уравнение :
12 0 1 12 k1 1
4) Общее решение :
y m C112m
5) Общее решение исходного уравнения :
10
xm C112m
11
137.
6) Найдём коэффициент С1 из начального условия :10
109
9 С1
11
11
109 т 10
xm
12
11
11
x0 C1
Ответ : x m
109 т 10
12
11
11
138.
ПриложениеМетод построения производящей функции для числа
сочетаний с заданной спецификацией Cˆ nk k1 , k 2 , ... kn .
ki – число вхождений элементов li типа i в сочетание.
i 1,2,3..n
n
k k
i
i 1
1. Если li входит в сочетание ровно m1 , m2 , ... mki раз, то
ему соответствует множитель Fi t t m1 t m2 ... t ki
m
2. F t
n
F t
i
i 1
3. Cˆ nk k1 , k 2 ...ki – коэффициент при t k в разложении F t .
139.
Метод построения производящей функции для самихсочетаний с заданной спецификацией Cˆ nk k1 , k2 , ... km .
ki – число вхождений элементов l типа i в сочетание.
i
n
k k
i 1,2,3..n
i
i 1
1. Если li входит в сочетание ровно m1 , m2 , ... mki раз, то
ему соответствует множитель Fi t lim1 t m1 lim2 t m2 ...
2. F t
n
F t
i
i 1
3. Сочетания будут коэффициенты при t k в разложении F t .
140.
ПриложениеПример
Числа Стирлинга II рода S n , k – число разбиений
n-множества на k непустых блоков, 1 k n .
Формально положим S0,0 1
S n ,n 1
Sn,k S n 1,k 1 kSn 1,k
S n ,1 1
S 0 при n 1
n,0
Пусть n-множество U e1 , e2 , ..., en 1 , en .
Все его разбиения можно разделить на 2 группы:
141.
1. Те, которые содержат блок en .Их число равно числу разбиений (n – 1)-подмножества
e1, e2 , ..., en 1 на (k–1) блоков, т. е. Sn 1,k 1 .
2. Те, которые не содержат блок en .
Они соответствуют разбиениям подмножества
e1, e2 , ..., en 1 на k блоков, и в любой из этих k блоков
поместим en . Таких разбиений ровно kSn-1,k .
По правилу суммы Sn,k S n 1,k 1 kSn 1,k .
142.
СледствиеИз начальных условий
S n,n 1
S n,1 1
S0,0 1
S n,0 0 при n 1
и рекуррентного уравнения
Sn,k S n 1,k 1 kSn 1,k
можно построить таблицу для чисел Sn,k ,
аналогичную треугольнику Паскаля для чисел Cnk .
143.
Справа в столбце указаны суммы строк таблицы Bnn
S .
n ,k
k 0
0
1
2
3
4
0
1
0
0
0
0
1 2 3 4 ... k Bn
1
1
1
1 1
2
1 3 1
5
1 7 6 1
15
n
Числа Стирлинга II рода применяются во многих задачах, в
частности:
144.
Пример(«Задача о пирогах и тарелках», один из вариантов).
Сколькими способами можно n различных пирогов разложить
по k различным тарелкам так,
чтобы не было пустых тарелок?
Ответ: k! S n,k
Пример
(задача эквивалентна предыдущей).
Найти число сюръекций n-множества А на k-множество B.
S : A B, A n, B k , 1 k n
Ответ: k! S n,k
145.
ПримерЧисла Белла Bn – число всех разбиений n-множества,
оно же равно числу отношений эквивалентности
на n-множестве.
B0 B1 1
n
S n ,k
Bn
k 0
Утверждение
Bn 1
n
C B
k
n
k 0
k
146.
Пусть (n+1)-множество U e1 , e2 , ..., en 1 .Все его разбиения можно получить так:
взять разбиение k-подмножества A i ei1 , ei2 , ..., eik
множества e1 , e2 , ..., en
и в каждый его блок поместить элемент en 1 .
Если k изменять от 0 до n, то получим все разбиения U.
Можем построить таблицу чисел Белла:
n 0 1 2 3 4 5 ...
Bn 1 1 2 5 15 52 ...


























































































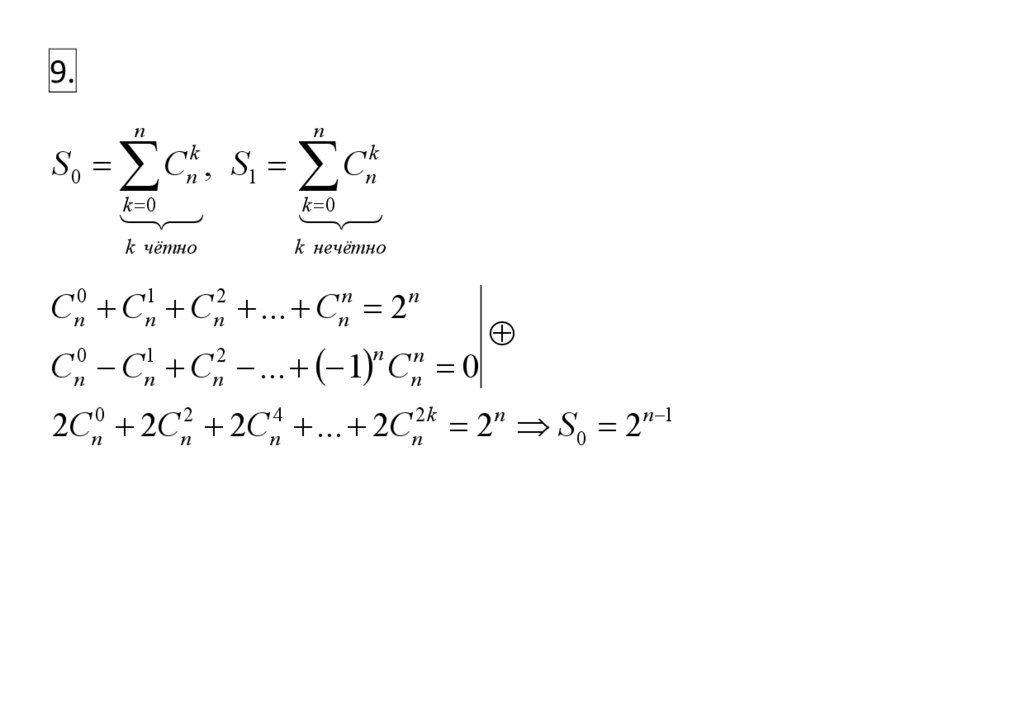
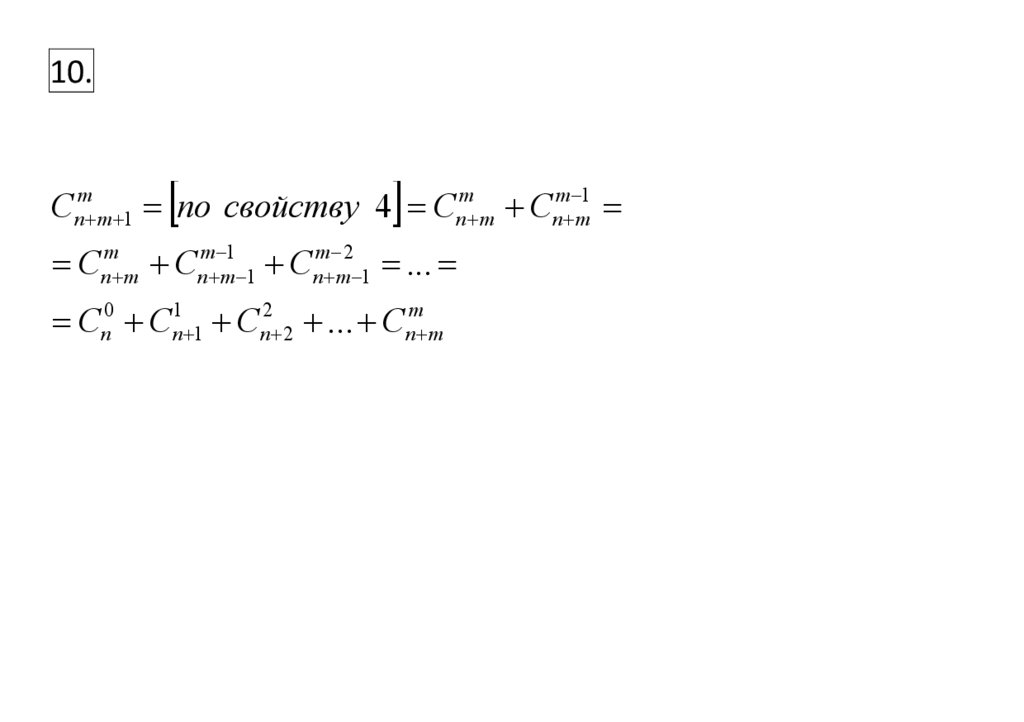
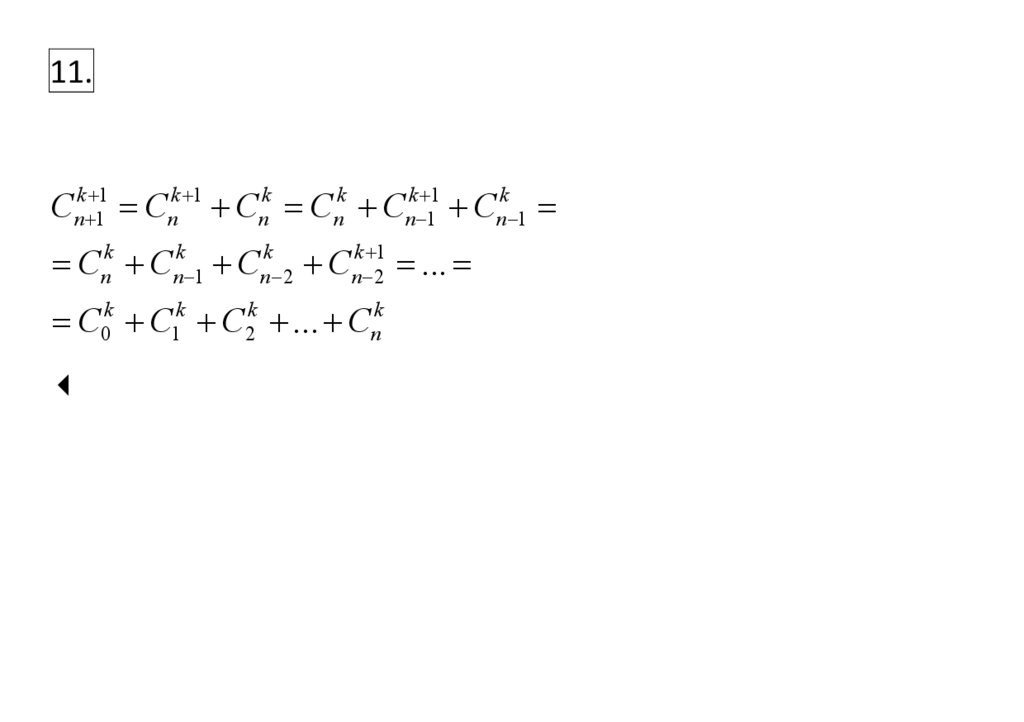







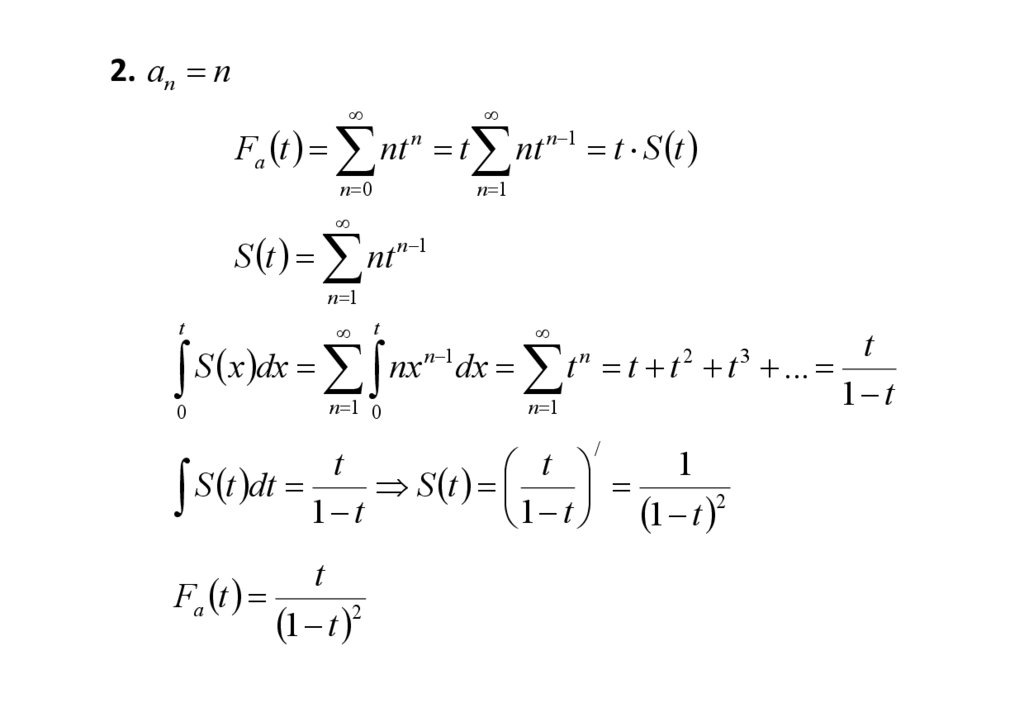










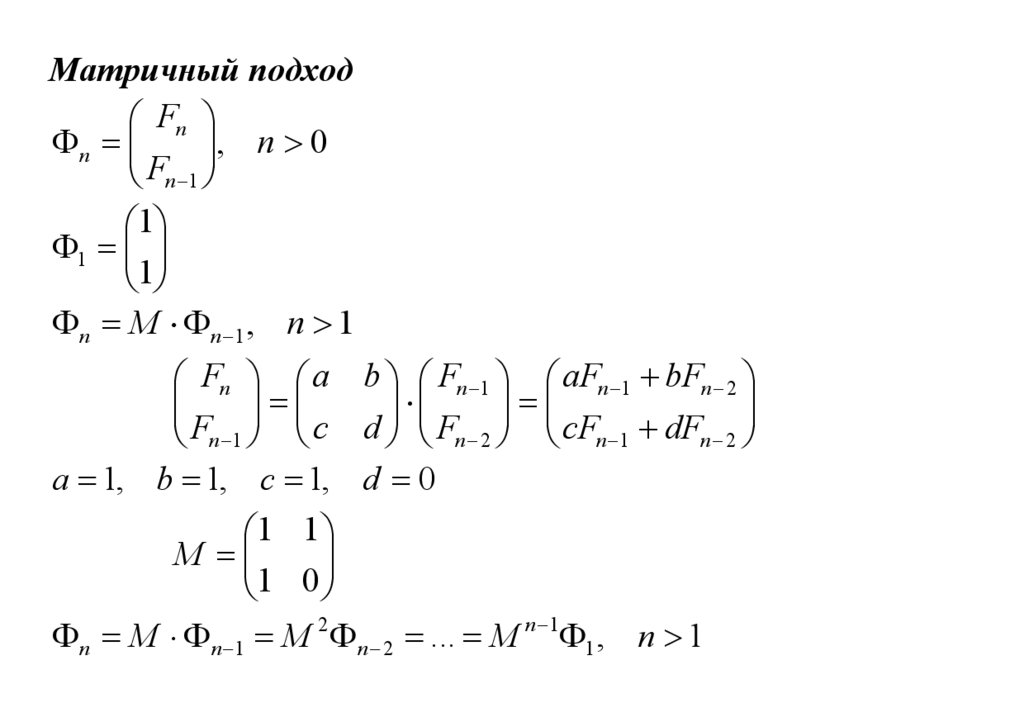




















 Математика
Математика








