Схема гибели и размножения

1.

Схема гибели и размножения.

2.

Схема гибели и размножения
• В теории массового обслуживания широкое
распространение имеет специальный класс
случайных процессов – так
называемый процесс гибели и
размножения. Название этого процесса
связано с рядом биологических задач, где
он является математической моделью
изменения численности биологических
популяций.

3.

Схема гибели и размножения
• Марковский процесс с дискретными
состояниями называется процессом гибели
и размножения, если все состояния можно
вытянуть в цепочку, в которой каждое из
промежуточных состояний может
переходить только в соседние состояния, а
крайние состояния переходят лишь в
состояния и соответственно.

4.

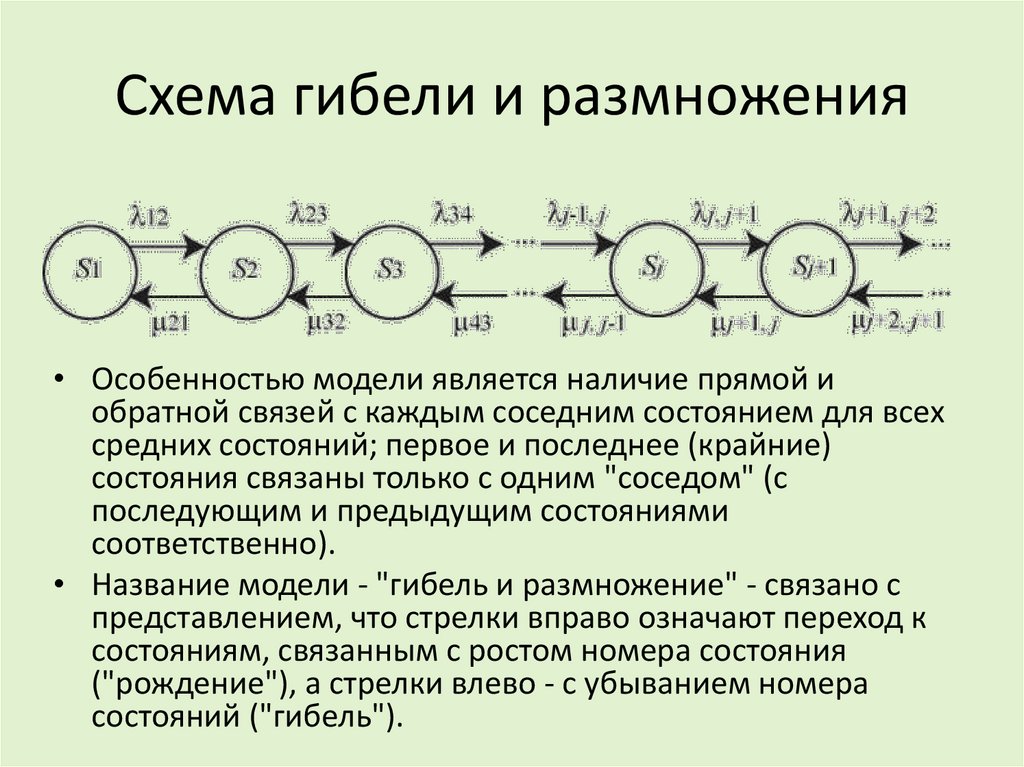
Схема гибели и размножения
• Особенностью модели является наличие прямой и
обратной связей с каждым соседним состоянием для всех
средних состояний; первое и последнее (крайние)
состояния связаны только с одним "соседом" (с
последующим и предыдущим состояниями
соответственно).
• Название модели - "гибель и размножение" - связано с
представлением, что стрелки вправо означают переход к
состояниям, связанным с ростом номера состояния
("рождение"), а стрелки влево - с убыванием номера
состояний ("гибель").

5.

Схема гибели и размножения
• Марковским процессом гибели и
размножения с непрерывным временем
называется такой случайный процесс,
исследуемый параметр которого может
принимать только целые неотрицательные
значения. Изменения рассматриваемого
параметра могут происходить в любой
момент времени, т.е. в любой момент
времени он может либо увеличиться, либо
уменьшиться на единицу.

6.

Схема гибели и размножения
Процессом чистого размножения называется такой процесс, у
которого интенсивности всех потоков гибели равны нулю;
аналогично процессом чистой «гибели» называется процесс, у
которого равны нулю интенсивности всех потоков размножения.
Предельные (финальные) вероятности состояний для
простейшего эргодического процесса гибели и размножения,
находящегося в стационарном режиме, определяются по
следующим формулам:

7.

Пример
• В качестве примера решения системы уравнений схемы гибели и
размножения рассмотрим эксплуатацию автомобилей в крупной
транспортной фирме.
• Интенсивность поступления автомобилей на предприятие равна .
Каждый поступивший на предприятие автомобиль списывается через
случайное время . Срок службы автомобиля распределен по
показательному закону с параметром . Процесс эксплуатации
автомобилей является случайным процессом. - число автомобилей
данной марки, находящихся в эксплуатации в момент времени .
• Рассмотрим два случая: 1) нет ограничений на число эксплуатируемых
автомобилей, 2) на предприятии может эксплуатироваться не более
автомобилей.
• Если в начальный момент на предприятии не было ни одного
автомобиля, то решать систему уравнений нужно при начальных
условиях

8.

Пример
• Решение системы дифференциальных
уравнений Колмогорова
при произвольном виде функции не может
быть найдено в аналитическом виде. Однако
при постоянных интенсивностях потоков
гибели и размножения и конечном числе
состояний будет существовать стационарный
режим. Система в этом случае является
простейшей эргодической системой(Система, в
которой фазовые средние совпадают с
временными).

9.

Вывод формул
• Составим и решим СЛАУ для предельных
вероятностей состояний (а их
существование вытекает из возможности
перехода из каждого состояния в каждое
другое за конечное число шагов)

10.

• Аналогично, записывая уравнения для
предельных вероятностей других состояний,
можно получить следующую систему
уравнений:

11.

Вывод формул
• Решим эту систему:
• Обратим внимание на
формулы для Pi :
числители представляют
собой произведения всех
интенсивностей, стоящих у
стрелок, ведущих слева
направо (от начала до
данного состояния Si);
знаменатели –
произведения всех
интенсивностей, стоящих у
стрелок, ведущих справа
налево (из состояния Si до
начала).

12.

Вывод формул
• Таким образом, все вероятности состояний Pi
выражены через одну из них (через вероятноять
P0). Подставим эти выражения в нормировочное
условие и получим:

13.

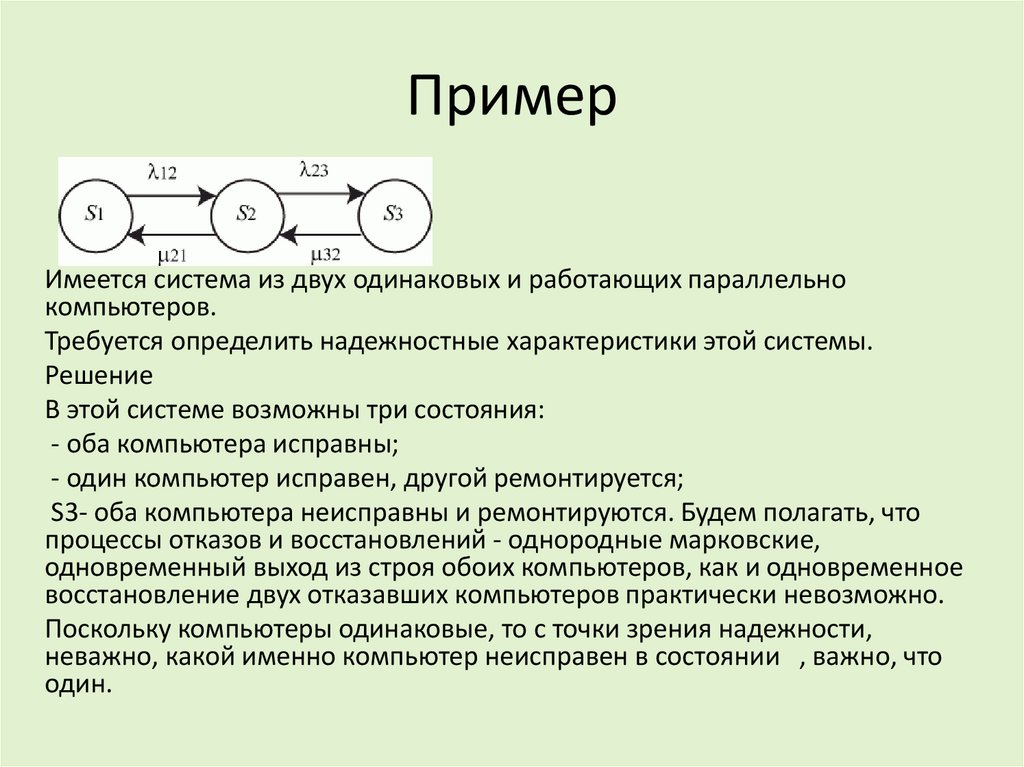
Пример
Имеется система из двух одинаковых и работающих параллельно
компьютеров.
Требуется определить надежностные характеристики этой системы.
Решение
В этой системе возможны три состояния:
- оба компьютера исправны;
- один компьютер исправен, другой ремонтируется;
S3- оба компьютера неисправны и ремонтируются. Будем полагать, что
процессы отказов и восстановлений - однородные марковские,
одновременный выход из строя обоих компьютеров, как и одновременное
восстановление двух отказавших компьютеров практически невозможно.
Поскольку компьютеры одинаковые, то с точки зрения надежности,
неважно, какой именно компьютер неисправен в состоянии , важно, что
один.

14.

15.

16.

Тест
https://joyteka.com/100168196

17.

Процессы размножения
и гибели Непрерывное
время
https://www.youtube.com
/watch?v=h_wkGGJYHP0
Процессы размножения
и гибели Дискретное
время
https://www.youtube.com
/watch?v=Menpuz8f0Gs