Многокритериальное оценивание: метод Topsis. Теория систем и системный анализ

1.

Южный федеральный университет
Кафедра синергетики и процессов управления
Презентация к практическим занятиям
по дисциплине
«Теория систем и системный анализ»
тема:
«Многокритериальное оценивание:
метод TOPSIS»

2.

ОПИСАНИЕ МЕТОДА
TOPSIS (Technique for Order Preference by Similarity to an Ideal Solution) метод
наименьшего удаления от идеального решения и наибольшего от неприемлемого
решения. Предложен Хвонгом (Hwang) и Юном (Yoon) в 1981 г. («Hwang C.L., Yoon
K. Multiple Attribute Decision Making. Berlin: Springer-Verlag, 1981.»).
Идеальное решение представляет собой вектор, содержащий наилучшие значения
по каждому критерию для всех альтернатив, а неприемлемое решение есть вектор,
содержащий наихудшие значения по каждому критерию.
Основная идея метода TOPSIS заключается в том, что наиболее предпочтительная
(компромиссная/эффективная) альтернатива должна иметь не только наибольшую
близость к идеальному решению, но и быть дальше всех остальных альтернатив от
неприемлемого решения.
2

3.

Достоинства метода TOPSIS:
- отражает логику человеческого выбора;
- в одном скалярном значении агрегирует наилучшее и наихудшее значение альтернатив;
- простые вычисления, которые легко реализуются в программных продуктах и электронных таблицах.
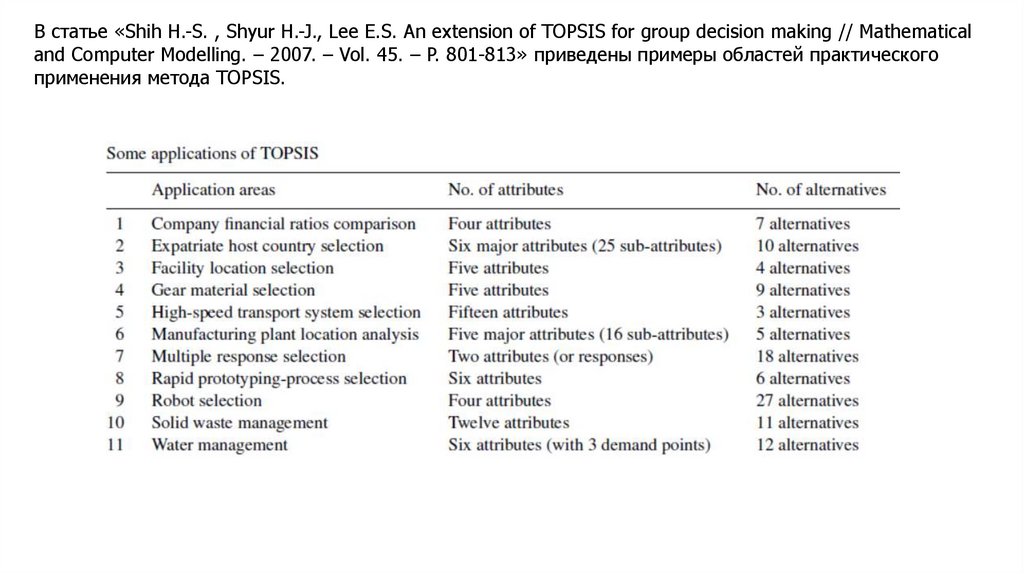
В статье «Shih H.-S. , Shyur H.-J., Lee E.S. An extension of TOPSIS for group decision making // Mathematical
and Computer Modelling. – 2007. – Vol. 45. – P. 801-813» выполнено сравнение методов МАИ и TOPSIS.
Характеристика
МАИ
TOPSIS
Основной процесс
Парные сравнения объектов
задачи (относительные
измерения)
Вычисление расстояния каждой
альтернативы до идеального и
неприемлемого решения (абсолютные
измерения)
Выявление весов важности
критериев
Обеспечивается вычисление
самим методом
Исходные данные
Проверка согласованности
оценок
Присутствует
Отсутствует
Рекомендуемое количество
критериев
7±2 на основном уровне
Любое
Рекомендуемое количество
альтернатив
7±2
Любое

4.

В статье «Shih H.-S. , Shyur H.-J., Lee E.S. An extension of TOPSIS for group decision making // Mathematical
and Computer Modelling. – 2007. – Vol. 45. – P. 801-813» приведены примеры областей практического
применения метода TOPSIS.

5.

ПОСТАНОВКА ЗАДАЧИ
Пусть имеется n альтернатив (Xi) и m критериев (Kj). Тогда uij оценка (полезность)
i-той альтернативы по j-тому критерию. В результате имеем матрицу полезностей
(решений):
n m
U uij
K1
K2
…
Km
X1
u11
u12
…
u1m
X2
u21
u22
…
u2m
…
…
…
…
…
Xn
un1
un2
…
unm
5

6.

ПОСТАНОВКА ЗАДАЧИ
Пусть J множество критериев, которые необходимо максимизировать.
Пусть J' множество критериев, которые необходимо минимизировать.
Для метода TOPSIS характерно, что веса важности критериев w j являются
входными данными, т.е. должны быть предварительно определены, при этом
m
обязательно должно выполняться условие нормировки wj 1 .
j 1
6

7.

АЛГОРИТМ TOPSIS
Шаг 1. Построение нормированной матрицы решений
n m преобразовываем в матрицу
Исходную матрицу решений U uij
n m в соответствии с выражением:
R rij
rij
uij
n
.
2
u
ij
i 1
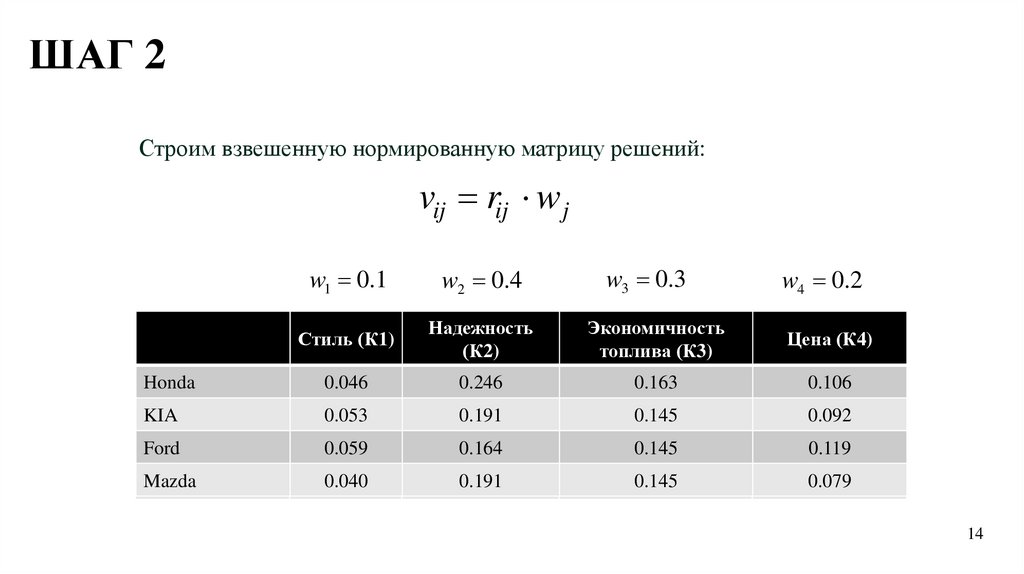
Шаг 2. Построение взвешенной нормированной матрицы решений
vij rij w j ,
где w j весовой коэффициент важности соответствующего j-го критерия.
7

8.

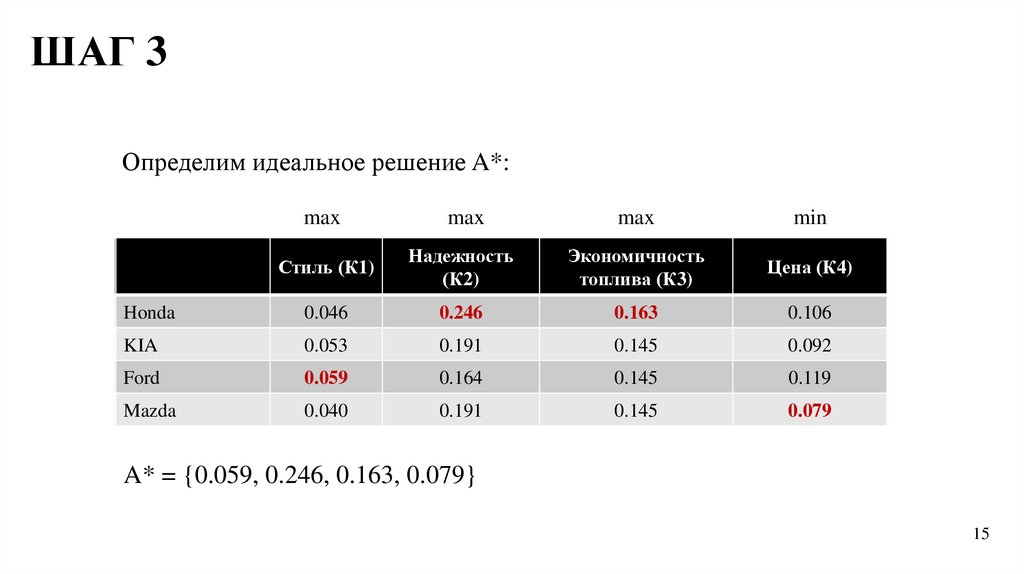
Шаг 3. Построение идеального и неприемлемого решения
где
i
i
v*j max vij , j J ;min vij , j J ' .
Неприемлемое решение:
где
A* v1* , v*2 ,....., v*m ,
Идеальное решение:
'
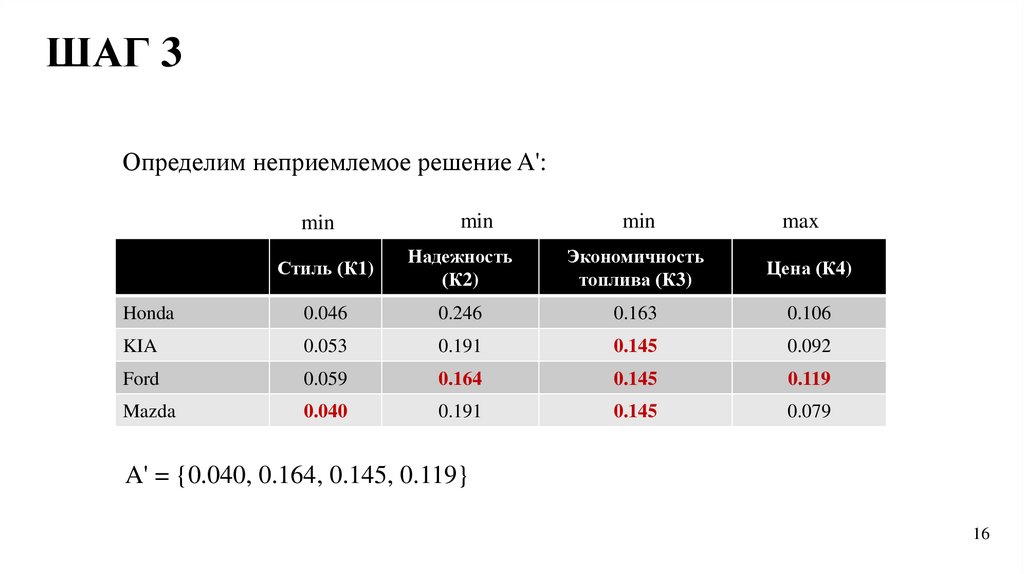
vj
'
'
'
'
A v1, v2 ,....., vm ,
min v , j J ;max v , j J ' .
i
ij
i
ij
8

9.

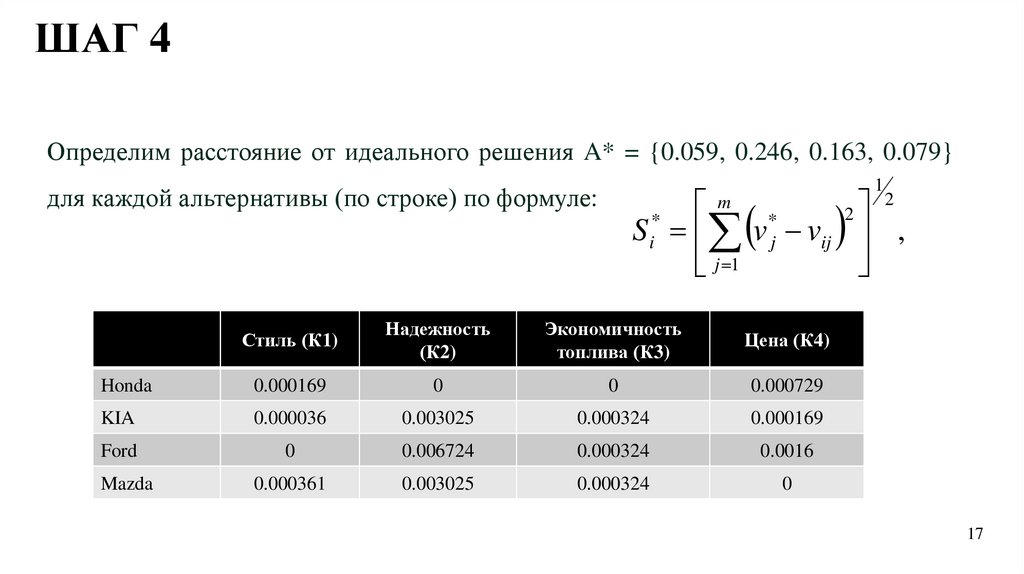
Шаг 4. Вычисление расстояния до идеального и неприемлемого решения
Расстояние до идеального решения для i-й альтернативы:
1
2
m
2
Si* v*j vij
j 1
1
2
m
2
'
Расстояние до неприемлемого решения для i-й альтернативы : S '
v j vij
i
j 1
* '
v j , v j элементы векторов идеального и неприемлемого решения, соответственно.
9

10.

Шаг 5. Вычисление относительной приближенности к идеальному решению
'
S
Сi* * i ' ,
Si Si
0 Сi* 1.
Шаг 6. Ранжирование альтернатив в соответствии со значениями, полученными на
Шаге 5
Наилучшей (компромиссной/эффективной) считается альтернатива со значением Сi* ,
ближайшим к единице.
10

11.

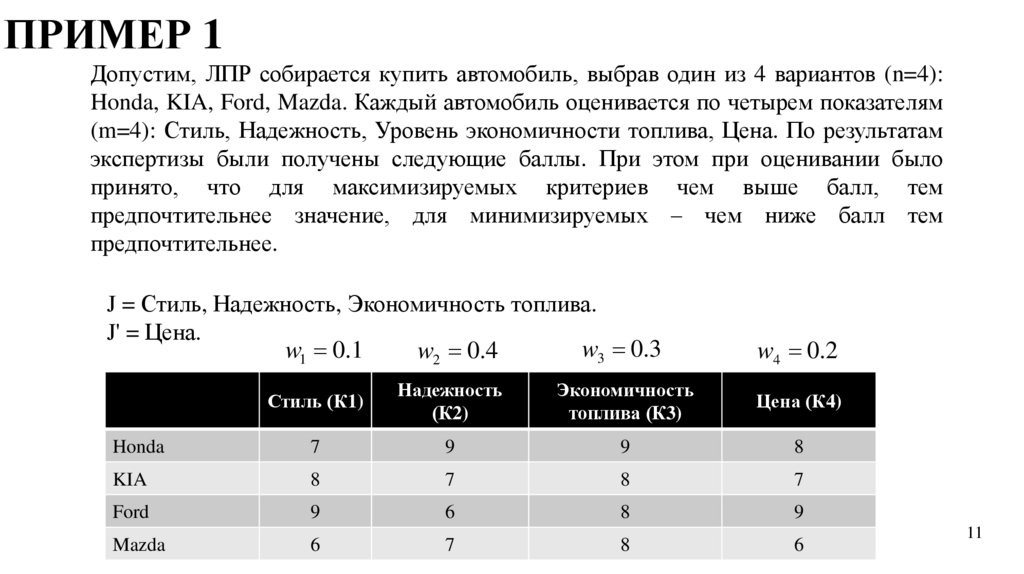
ПРИМЕР 1
Допустим, ЛПР собирается купить автомобиль, выбрав один из 4 вариантов (n=4):
Honda, KIA, Ford, Mazda. Каждый автомобиль оценивается по четырем показателям
(m=4): Стиль, Надежность, Уровень экономичности топлива, Цена. По результатам
экспертизы были получены следующие баллы. При этом при оценивании было
принято, что для максимизируемых критериев чем выше балл, тем
предпочтительнее значение, для минимизируемых – чем ниже балл тем
предпочтительнее.
J = Стиль, Надежность, Экономичность топлива.
J' = Цена.
w1 0.1
w2 0.4
w3 0.3
w4 0.2
Стиль (К1)
Надежность
(К2)
Экономичность
топлива (К3)
Цена (К4)
Honda
7
9
9
8
KIA
8
7
8
7
Ford
9
6
8
9
Mazda
6
7
8
6
11

12.

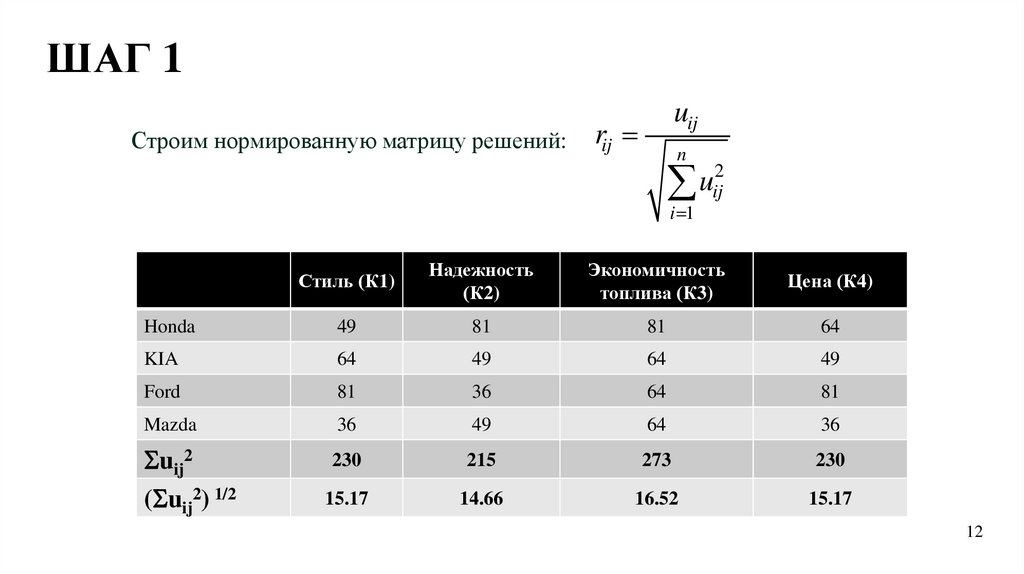
ШАГ 1
Строим нормированную матрицу решений:
uij
rij
n
2
u
ij
i 1
Стиль (К1)
Надежность
(К2)
Экономичность
топлива (К3)
Цена (К4)
Honda
49
7
81
9
81
9
64
8
KIA
64
8
49
7
64
8
49
7
Ford
81
9
36
6
64
8
81
9
Mazda
36
6
49
7
64
8
36
6
230
215
273
230
15.17
14.66
16.52
15.17
uij2
( uij2) 1/2
12

13.

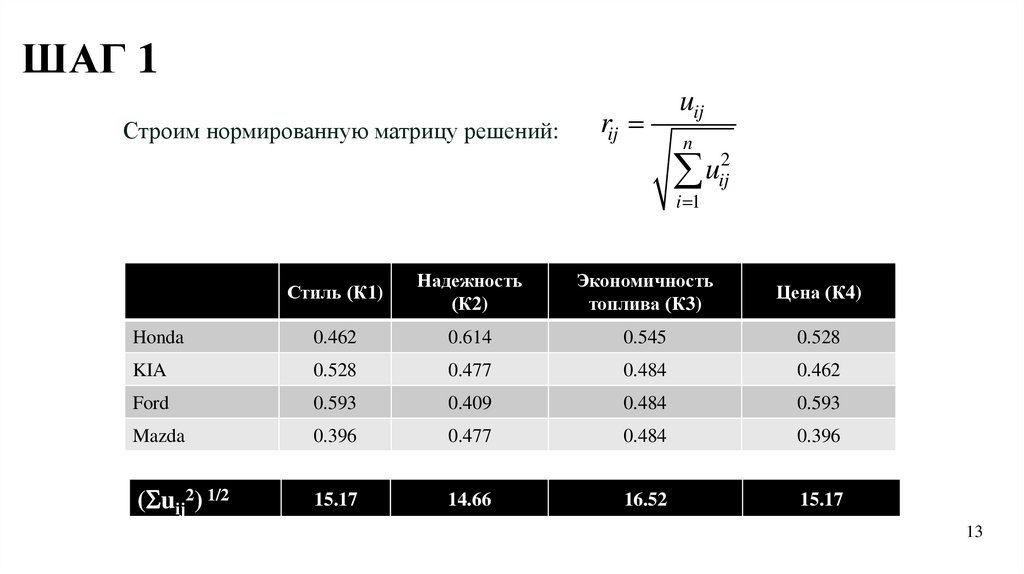
ШАГ 1
Строим нормированную матрицу решений:
rij
uij
n
2
u
ij
i 1
Стиль (К1)
Надежность
(К2)
Экономичность
топлива (К3)
Цена (К4)
Honda
7/15.17
0.462
7
9/14.66
0.614
9
9/16.52
0.545
9
8/15.17
0.528
8
KIA
8/15.17
0.528
8
7/14.66
0.477
7
8/16.52
0.484
8
7/15.17
0.462
7
Ford
9/15.17
0.593
9
6/14.66
0.409
6
8/16.52
0.484
8
9/15.17
0.593
9
Mazda
6/15.17
0.396
6
7/14.66
0.477
7
8/16.52
0.484
8
6/15.17
0.396
6
( uij2) 1/21/2
15.17
14.66
16.52
15.17
13

14.

ШАГ 2
Строим взвешенную нормированную матрицу решений:
vij rij w j
w1 0.1
w2 0.4
w3 0.3
w4 0.2
Стиль (К1)
Надежность
(К2)
Экономичность
топлива (К3)
Цена (К4)
Honda
0.046
0.462
0.246
0.614
0.163
0.545
0.106
0.528
KIA
0.053
0.528
0.191
0.477
0.145
0.484
0.092
0.462
Ford
0.059
0.593
0.164
0.409
0.145
0.484
0.119
0.593
Mazda
0.040
0.396
0.191
0.477
0.145
0.484
0.079
0.396
14

15.

ШАГ 3
Определим идеальное решение A*:
max
max
max
min
Стиль (К1)
Надежность
(К2)
Экономичность
топлива (К3)
Цена (К4)
Honda
0.046
0.246
0.163
0.106
KIA
0.053
0.191
0.145
0.092
Ford
0.059
0.164
0.145
0.119
Mazda
0.040
0.191
0.145
0.079
A* = {0.059, 0.246, 0.163, 0.079}
15

16.

ШАГ 3
Определим неприемлемое решение A':
min
min
min
max
Стиль (К1)
Надежность
(К2)
Экономичность
топлива (К3)
Цена (К4)
Honda
0.046
0.246
0.163
0.106
KIA
0.053
0.191
0.145
0.092
Ford
0.059
0.164
0.145
0.119
Mazda
0.040
0.191
0.145
0.079
A' = {0.040, 0.164, 0.145, 0.119}
16

17.

ШАГ 4
Определим расстояние от идеального решения A* = {0.059, 0.246, 0.163, 0.079}
для каждой альтернативы (по строке) по формуле:
2
m
2
Si* v*j vij ,
j 1
Стиль (К1)
Надежность
(К2)
Экономичность
топлива (К3)
Цена (К4)
KIA
0.046 2 2
(0.013)
(0.059-0.046)
0.000169
0.053 2 2
(0.006)
(0.059-0.053)
0.000036
2
0.246
(0)
(0.246-0.246)
02
0.191 2 2
(0.055)
(0.246-0.191)
0.003025
2
0.163
(0)
(0.163-0.163)
02
0.145 2 2
(0.018)
(0.163-0.145)
0.000324
0.106 2 2
(-0.027)
(0.079-0.106)
0.000729
0.092 2 2
(-0.013)
(0.079-0.092)
0.000169
Ford
Mazda
Mazda
2
0.059
(0)
(0.059-0.059)
02
0.040 2 2
(0.019)
(0.059-0.040)
0.000361
0.164 2 2
(0.082)
(0.246-0.164)
0.006724
0.191 2 2
(0.055)
(0.246-0.191)
0.003025
0.145 2 2
(0.018)
(0.163-0.145)
0.000324
0.145 2 2
(0.018)
(0.163-0.145)
0.000324
0.119 2 2
(-0.04)
(0.079-0.119)
0.0016
2
0.079
(0)
(0.079-0.079)
02
Honda
Honda
1
17

18.

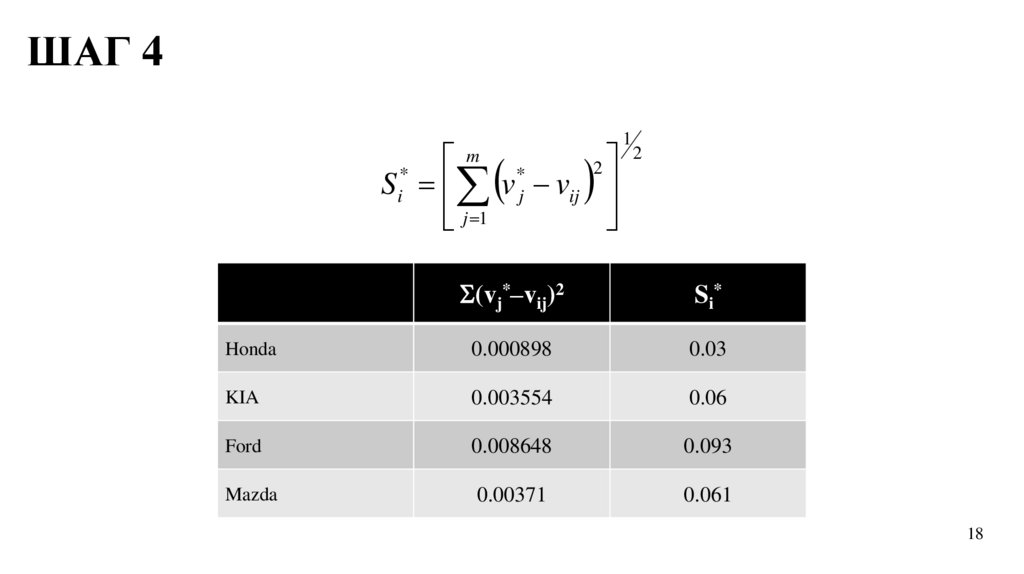
ШАГ 4
1
2
m
2
Si* v*j vij
j 1
(vj*–vij)2
Si*
Honda
0.000898
0.03
KIA
0.003554
0.06
Ford
0.008648
0.093
Mazda
0.00371
0.061
18

19.

ШАГ 4
Определим расстояние от неприемлемого решения
A' = {0.040, 0.164, 0.145, 0.119} для каждой альтернативы (по строке) по формуле:
1
2
m
2
'
'
Si v j vij
j 1
Стиль (К1)
Надежность
Надежность
(К2)
(К2)
Экономичность
Экономичность
топлива
топлива (К3)
(К3)
Цена (К4)
Honda
Honda
(0.040-0.046)
0.046 2 2
0.000036
(-0.006)
(0.164-0.246)
0.246 2 2
0.006724
(-0.082)
(0.145-0.163)
0.163 2 2
0.000324
(-0.018)
(0.119-0.106)
0.106 2 2
0.000169
(0.013)
KIA
KIA
(0.040-0.053)
0.053 2 2
0.000169
(-0.013)
(0.164-0.191)
0.191 2 2
0.000729
(-0.027)
2
(0.145-0.145)
0.145
02
(0)
(0.119-0.092)
0.092 2 2
0.000729
(0.027)
Ford
Ford
(0.040-0.059)
0.059 2 2
0.000361
(-0.019)
2
(0.164-0.164)
0.164
02
(0)
2
(0.145-0.145)
0.145
02
(0)
2
(0.119-0.119)
0.119
02
(0)
Mazda
Mazda
2
(0.040-0.040)
0.040
02
(0)
(0.164-0.191)
0.191 2 2
0.000729
(-0.027)
2
(0.145-0.145)
0.145
02
(0)
(0.119-0.079)
0.0792 2
0.0016
(0.04)
19

20.

ШАГ 4
1
2
m
2
Si' v 'j vij
j 1
(vj' –vij)2
Si'
Honda
0.007253
0.085
KIA
0.001627
0.040
Ford
0.000361
0.019
Mazda
0.002329
0.048
20

21.

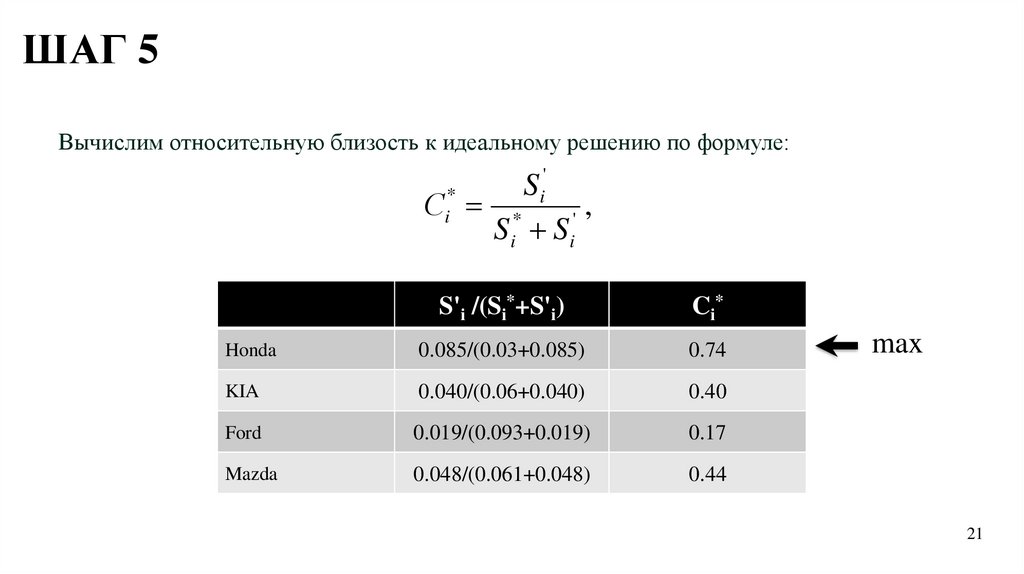
ШАГ 5
Вычислим относительную близость к идеальному решению по формуле:
'
S
Сi* * i ' ,
Si Si
S'i /(Si*+S'i)
Ci*
Honda
0.085/(0.03+0.085)
0.74
KIA
0.040/(0.06+0.040)
0.40
Ford
0.019/(0.093+0.019)
0.17
Mazda
0.048/(0.061+0.048)
0.44
max
21

22.

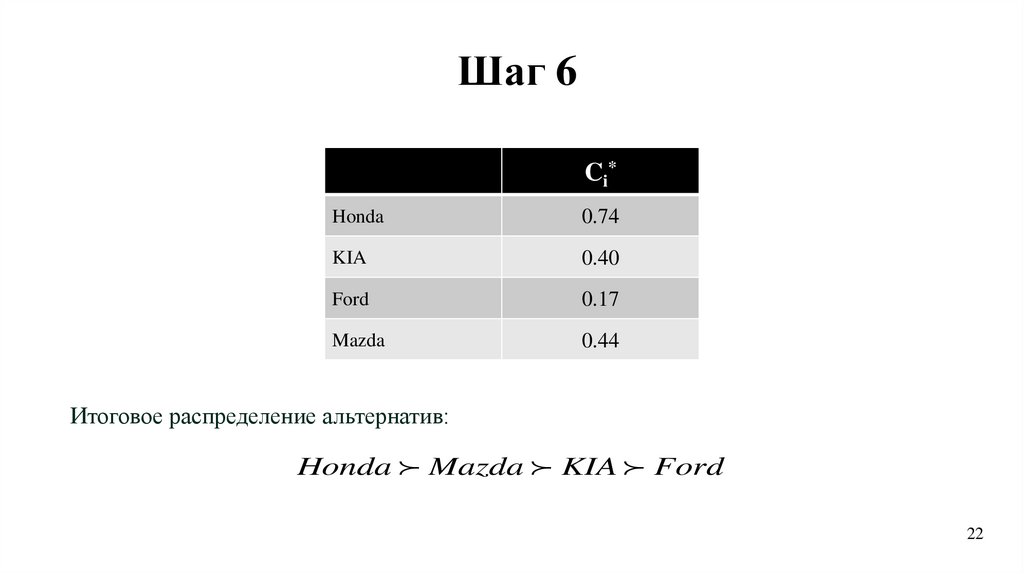
Шаг 6
Ci*
Honda
0.74
KIA
0.40
Ford
0.17
Mazda
0.44
Итоговое распределение альтернатив:
Honda Mazda KIA Ford
22

23.

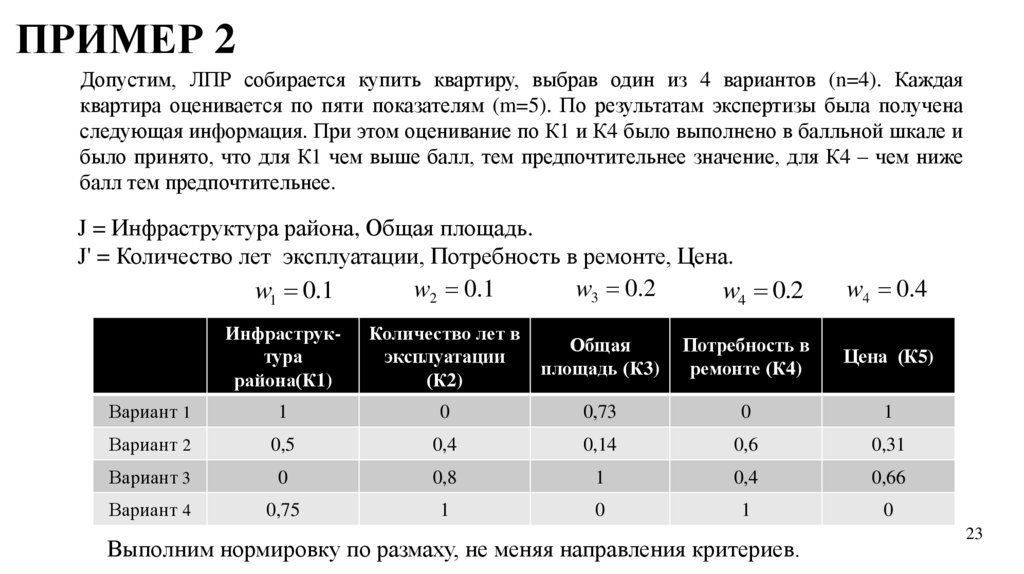
ПРИМЕР 2
Допустим, ЛПР собирается купить квартиру, выбрав один из 4 вариантов (n=4). Каждая
квартира оценивается по пяти показателям (m=5). По результатам экспертизы была получена
следующая информация. При этом оценивание по К1 и К4 было выполнено в балльной шкале и
было принято, что для К1 чем выше балл, тем предпочтительнее значение, для К4 – чем ниже
балл тем предпочтительнее.
J = Инфраструктура района, Общая площадь.
J' = Количество лет эксплуатации, Потребность в ремонте, Цена.
w3 0.2
w4 0.2
w4 0.4
Количество лет в
эксплуатации
(К2)
Общая
площадь (К3)
Потребность в
ремонте (К4)
Цена (К5)
91
20
0,73
56
10
2 2001 000
Вариант 2
0,5
7
0,4
4
0,14
43
0,6
4
0,31000
1 770
Вариант 3
50
0,8
6
1
62
0,4
3
0,66000
1 990
Вариант 4
0,75
8
71
0
40
61
1 5800 000
w1 0.1
w2 0.1
Инфраструктура
района(К1)
Вариант 1
Выполним нормировку по размаху, не меняя направления критериев.
23

24.

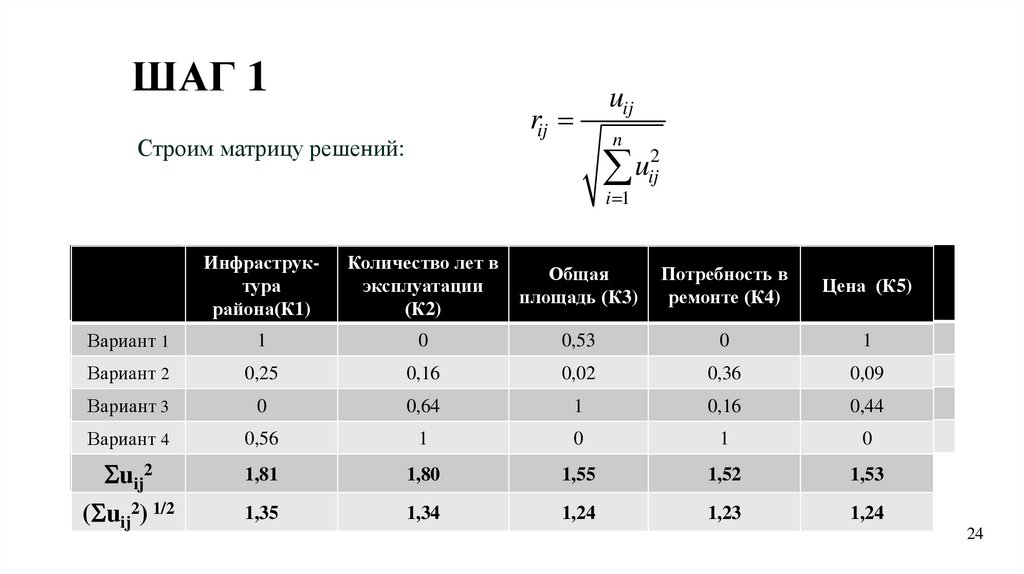
ШАГ 1
rij
Строим матрицу решений:
uij
n
2
u
ij
i 1
ИнфраструкИнфраструк- Количество
Количество
лет
вв в
ИнфраструкКоличество
летлет
Общая
Общая Потребность
Потребность
вв в
Общая
Потребность
тура
тура
эксплуатации
эксплуатации
Цена
Цена
(К5)
(К5)
тура
эксплуатации
Цена
(К5)
площадь
площадь
(К3)
(К3) ремонте
ремонте
(К4)
(К4)
площадь
(К3)
ремонте
(К4)
района(К1)
района(К1)
(К2)
(К2)
района(К1)
(К2)
Вариант
Вариант
11 1
Вариант
11 1
00 0
0,53
0,73
0,53
0,53
00 0
11 1
Вариант
Вариант
22 2
Вариант
0,25
0,25
0,5
0,25
0,16
0,16
0,4
0,16
0,02
0,14
0,02
0,02
0,36
0,36
0,6
0,36
0,09
0,31
0,09
0,09
Вариант
Вариант
33 31
Вариант
00 0
0,64
0,64
0,8
0,64
11 1
0,16
0,16
0,4
0,16
0,44
0,66
0,44
0,44
Вариант
Вариант
44 4
Вариант
0,56
0,75
0,56
0,56
11 1
00 0
11 1
00 0
uijij22
1,81
1,81
1,80
1,80
1,55
1,55
1,52
1,52
1,53
1,53
( uij2) 1/2
1,35
1,34
1,24
1,23
1,24
24

25.

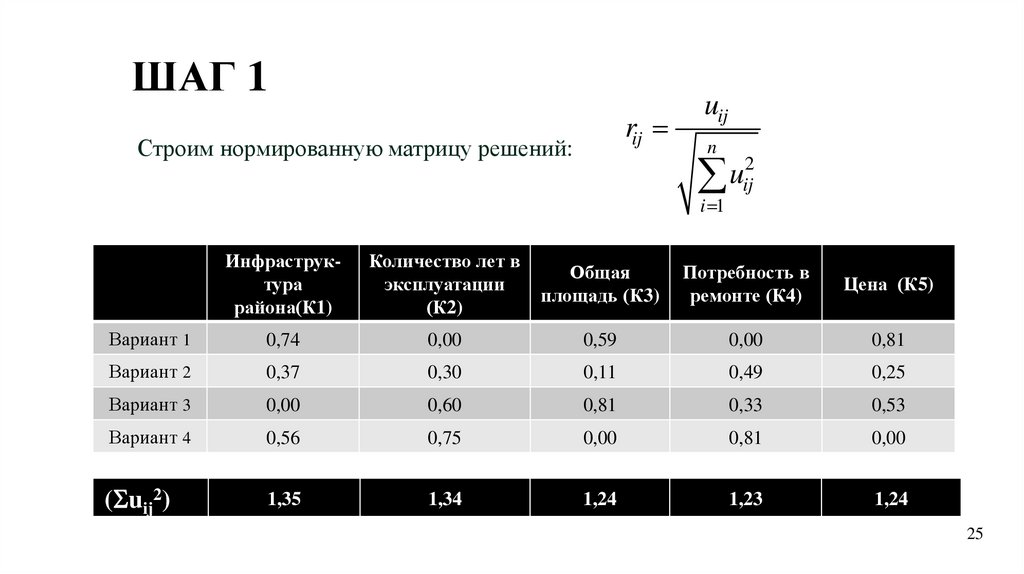
ШАГ 1
rij
Строим нормированную матрицу решений:
uij
n
2
u
ij
i 1
Инфраструктура
района(К1)
Количество лет в
эксплуатации
(К2)
Общая
площадь (К3)
Потребность в
ремонте (К4)
Цена (К5)
Вариант 1
1/1,35
1
0,74
0/1,34
0
0,00
0,73/1,24
0,73
0,59
0/1,23
0
0,00
1/1,24
1
0,81
Вариант 2
0,5/1,35
0,5
0,37
0,4/1,34
0,4
0,30
0,14/1,24
0,14
0,11
0,6/1,23
0,6
0,49
0,31/1,24
0,31
0,25
Вариант 3
0/1,35
0
0,00
0,8/1,34
0,8
0,60
1/1,24
1
0,81
0,4/1,23
0,4
0,33
0,66/1,24
0,66
0,53
Вариант 4
0,75/1,35
0,75
0,56
1/1,34
1
0,75
0/1,24
0
0,00
1/1,23
1
0,81
0/1,24
0
0,00
( uij2) 1/2
1,35
1,34
1,24
1,23
1,24
25

26.

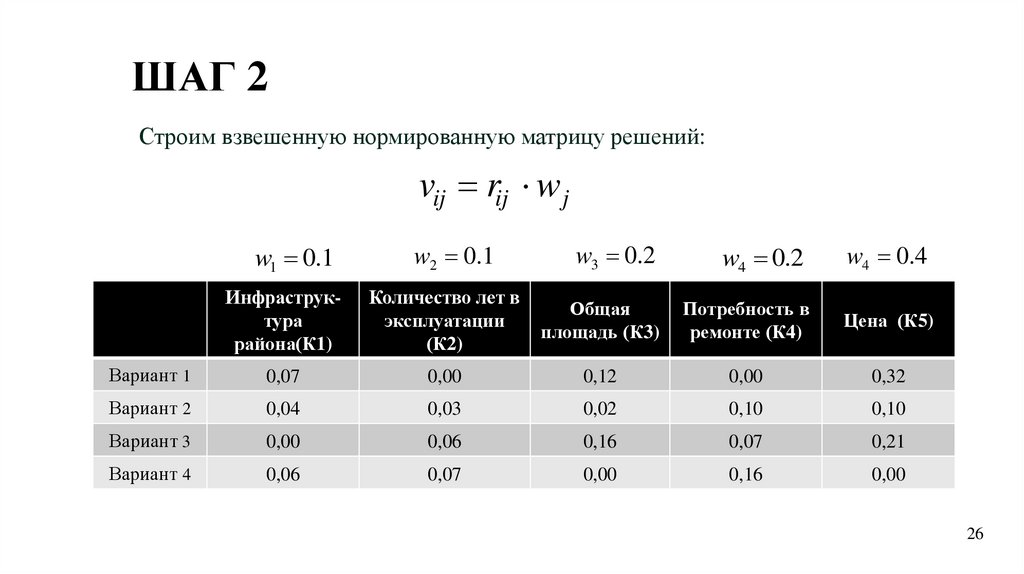
ШАГ 2
Строим взвешенную нормированную матрицу решений:
vij rij w j
w3 0.2
w4 0.2
w4 0.4
Количество лет в
эксплуатации
(К2)
Общая
площадь (К3)
Потребность в
ремонте (К4)
Цена (К5)
0,07
0,74
0,00
0,12
0,59
0,00
0,32
0,81
Вариант 2
0,04
0,37
0,03
0,30
0,02
0,11
0,10
0,49
0,10
0,25
Вариант 3
0,00
0,06
0,60
0,16
0,81
0,07
0,33
0,21
0,53
Вариант 4
0,06
0,56
0,07
0,75
0,00
0,16
0,81
0,00
w1 0.1
w2 0.1
Инфраструктура
района(К1)
Вариант 1
26

27.

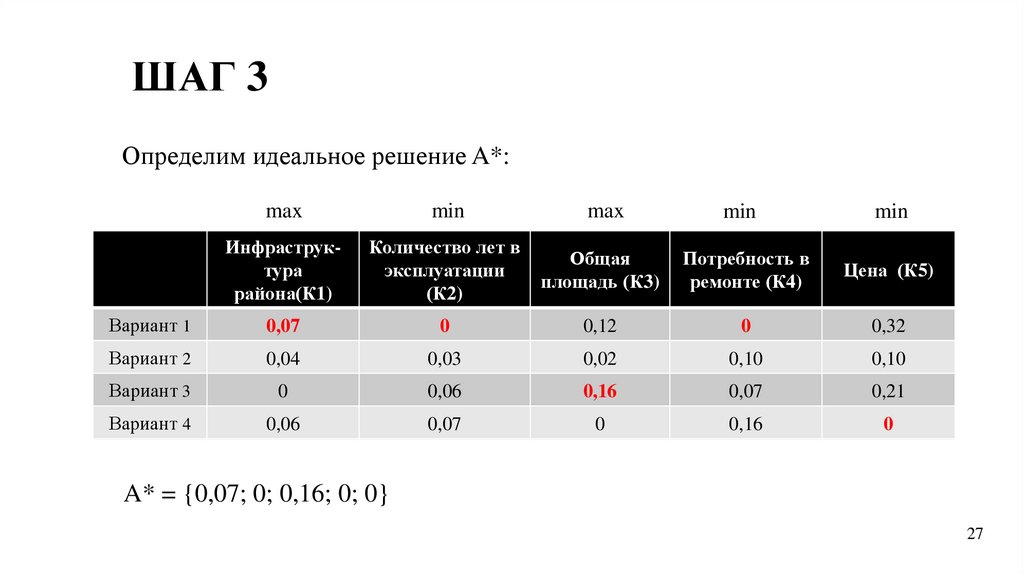
ШАГ 3
Определим идеальное решение A*:
max
min
max
min
min
Инфраструктура
района(К1)
Количество лет в
эксплуатации
(К2)
Общая
площадь (К3)
Потребность в
ремонте (К4)
Цена (К5)
Вариант 1
0,07
0
0,00
0,12
0
0,00
0,32
Вариант 2
0,04
0,03
0,02
0,10
0,10
Вариант 3
0
0,00
0,06
0,16
0,07
0,21
Вариант 4
0,06
0,07
0
0,00
0,16
0
0,00
A* = {0,07; 0; 0,16; 0; 0}
27

28.

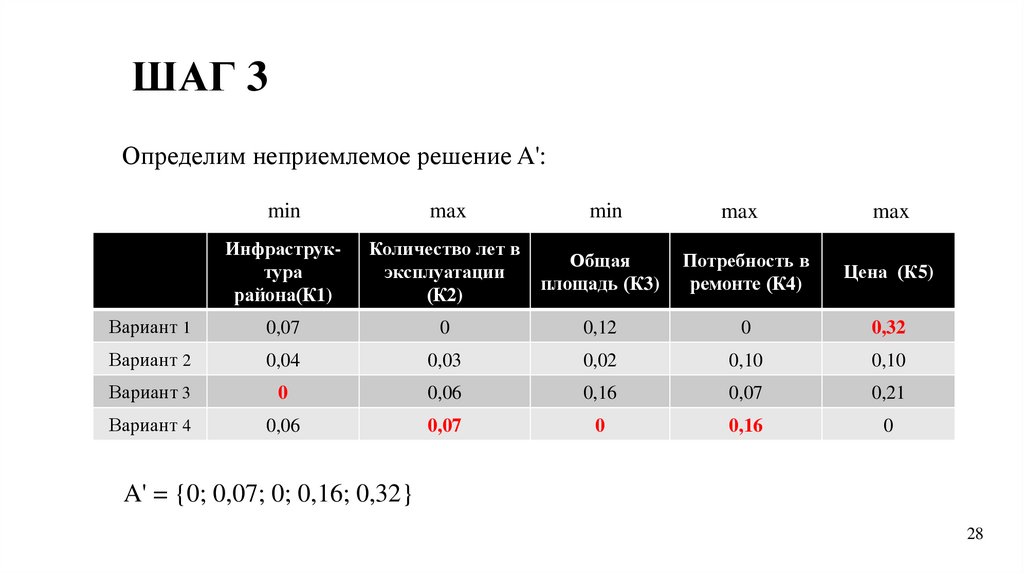
ШАГ 3
Определим неприемлемое решение A':
min
max
min
max
max
Инфраструктура
района(К1)
Количество лет в
эксплуатации
(К2)
Общая
площадь (К3)
Потребность в
ремонте (К4)
Цена (К5)
Вариант 1
0,07
0
0,12
0
0,32
Вариант 2
0,04
0,03
0,02
0,10
0,10
Вариант 3
0
0,06
0,16
0,07
0,21
Вариант 4
0,06
0,07
0
0,16
0
A' = {0; 0,07; 0; 0,16; 0,32}
28

29.

ШАГ 4
Определим расстояние от идеального решения A* = {0,07; 0; 0,16; 0; 0} для
каждой альтернативы (по строке) по формуле:
1
2
m
2
S i* v*j vij ,
j 1
Инфраструктура
района(К1)
Количество лет в
эксплуатации
(К2)
Общая
площадь (К3)
Потребность в
ремонте (К4)
Цена (К5)
Вариант 1
2
(0,07-0,07)
0,07
0
(0-0)
0 2
(0,16-0,12)
0,0016
0,12 2
(0-0)
0 2
(0-0,32)
0,1024
0,32 2
Вариант 2
(0,07-0,04)
0,0016
0,04 2
(0-0,03)
0,0009
0,03 2
(0,16-0,02)
0,0196
0,02 2
(0-0,10)
0,10 2
0,01
(0-0,10)
0,10 2
0,01
Вариант 3
(0,07-0)
0,0049
0 2
(0-0,06)
0,0036
0,06 2
2
(0,16-0,16)
0,16
0
(0-0,07)
0,0049
0,07 2
(0-0,21)
0,0441
0,21 2
Вариант 4
(0,07-0,06)
0,0001
0,06 2
(0-0,07)
0,0049
0,07 2
(0,16-0)
0,0256
0 2
(0-0,16)
0,0256
0,16 2
(0-0)
0 2
29

30.

ШАГ 4
1
2
m
2
S i* v*j vij
j 1
(vj*–vij)2
Si*
Вариант 1
0,1040
0,32
Вариант 2
0,0421
0,21
Вариант 3
0,0575
0,24
Вариант 4
0,0562
0,24
30

31.

ШАГ 4
Определим расстояние от неприемлемого решения A' = {0; 0,07; 0; 0,16; 0,32}
1
для каждой строки по формуле:
2
m
2
'
S v j vij
j 1
'
i
Инфраструктура
района(К1)
Количество лет в
эксплуатации
(К2)
Общая
площадь (К3)
Потребность в
ремонте (К4)
Цена (К5)
Вариант 1
(0-0,07)
0,0049
0,07 2
(0,07-0)
0,0049
0 2
(0-0,12)
0,0144
0,12 2
(0,16-0)
0,0256
0 2
2
(0,32-0,32)
0
0,32
Вариант 2
(0-0,04)
0,0016
0,04 2
(0,07-0,03)
0,0016
0,03 2
(0-0,02)
0,0004
0,02 2
(0,16-0,10)
0,0036
0,10 2
(0,32-0,10)
0,0484
0,10 2
Вариант 3
(0-0)
0 2
(0,07-0,06)
0,0001
0,06 2
(0-0,16)
0,0256
0,16 2
(0,16-0,07)
0,0081
0,07 2
(0,32-0,21)
0,0121
0,21 2
Вариант 4
(0-0,06)
0,0036
0,06 2
2
(0,07-0,07)
0
0,07
(0-0)
0 2
2
(0,16-0,16)
0
0,16
(0,32-0)
0,1024
0 2
31

32.

ШАГ 4
1
2
m
2
Si' v 'j vij
j 1
(vj' –vij)2
Si'
Вариант 1
0,0498
0,22
Вариант 2
0,0556
0,24
Вариант 3
0,0459
0,21
Вариант 4
0,1060
0,33
32

33.

ШАГ 5
Вычислим относительную близость к идеальному решению по формуле:
'
S
*
Сi * i ' ,
Si Si
S'i /(Si*+S'i)
Ci*
Вариант 1
0.22/(0.32+0.22)
0.41
Вариант 2
0.24/(0,21+0.24)
0,53
Вариант 3
0.21/(0.24+0.21)
0,47
Вариант 4
0.33/(0.24+0.33)
0.58
max
33

34.

Шаг 6
Ci*
Вариант 1
0.41
Вариант 2
0,53
Вариант 3
0,47
Вариант 4
0.58
Итоговое распределение альтернатив:
Вариант 4 Вариант 2 Вариант 3 Вариант1
34

35.

Задание для самостоятельного решения
Определить эффективное
гидроэлектростанций.
решение
методом
TOPSIS
в
задаче
выбора
места
строительства
Имеется четыре альтернативы, оцениваемых по трем критериям:
F1 (max) – мощность гидроэлектростанции, МВт;
F2 (min) – площадь затапливаемой территории, км2;
F3 (min) – стоимость строительства гидроэлектростанции, млрд. у.е.
Критерии
Альтерна
тивы
F1
F2
F3
А1
А2
А3
А4
10
20
40
75
70
85
120
200
1,6
1,2
3
5,4
Веса важности : w1= 0,2, w2= 0,5, w3=0,3.
35

36.

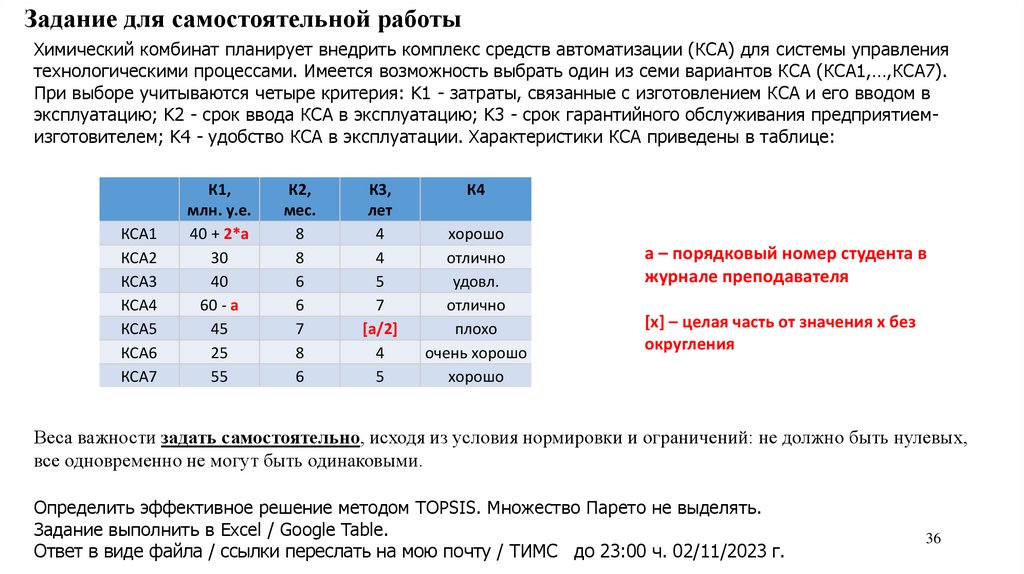
Задание для самостоятельной работы
Химический комбинат планирует внедрить комплекс средств автоматизации (КСА) для системы управления
технологическими процессами. Имеется возможность выбрать один из семи вариантов КСА (КСА1,…,КСА7).
При выборе учитываются четыре критерия: K1 - затраты, связанные с изготовлением КСА и его вводом в
эксплуатацию; K2 - срок ввода КСА в эксплуатацию; K3 - срок гарантийного обслуживания предприятиемизготовителем; K4 - удобство КСА в эксплуатации. Характеристики КСА приведены в таблице:
КСА1
КСА2
КСА3
КСА4
КСА5
КСА6
КСА7
К1,
млн. у.е.
40 + 2*a
30
40
60 - a
45
25
55
К2,
мес.
8
8
6
6
7
8
6
К3,
лет
4
4
5
7
[a/2]
4
5
К4
хорошо
отлично
удовл.
отлично
плохо
очень хорошо
хорошо
a – порядковый номер студента в
журнале преподавателя
[x] – целая часть от значения х без
округления
Веса важности задать самостоятельно, исходя из условия нормировки и ограничений: не должно быть нулевых,
все одновременно не могут быть одинаковыми.
Определить эффективное решение методом TOPSIS. Множество Парето не выделять.
Задание выполнить в Excel / Google Table.
Ответ в виде файла / ссылки переслать на мою почту / ТИМС до 23:00 ч. 02/11/2023 г.
36