Методы численного решения нелинейных уравнений

1.

МЕТОДЫ ЧИСЛЕННОГО РЕШЕНИЯ НЕЛИНЕЙНЫХ УРАВНЕНИЙ
1. Метод дихотомии (половинного деления)
f ( x, p1 , p2 ,..., pn ) 0
Считаем, что отделение корней уравнения
проведено и на отрезке [а,b] расположен один корень, который необходимо
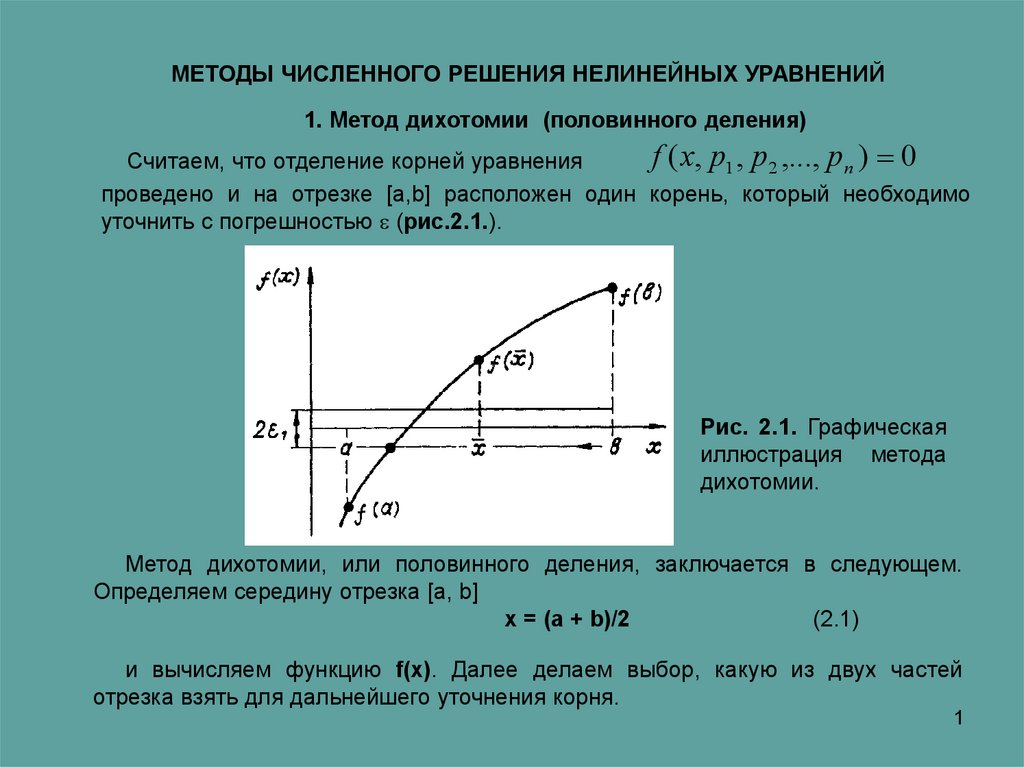
уточнить с погрешностью (рис.2.1.).
Рис. 2.1. Графическая
иллюстрация метода
дихотомии.
Метод дихотомии, или половинного деления, заключается в следующем.
Определяем середину отрезка [а, b]
x = (a + b)/2
(2.1)
и вычисляем функцию f(x). Далее делаем выбор, какую из двух частей
отрезка взять для дальнейшего уточнения корня.
1

2.

Если левая часть уравнения f(x) есть непрерывная функция аргумента х, то
корень будет находиться в той половине отрезка, на концах которой f(x) имеет
разные знаки (f(a) f(b) < 0). На рис. 2.1. это будет отрезок [а, х], т.е. для
очередного шага уточнения точку b перемещаем в середину отрезка х и
продолжаем процесс деления как с первоначальным отрезком [а, b].
Итерационный (повторяющийся) процесс будем продолжать до тех пор, пока
интервал [а, b] не станет меньше заданной погрешности .
Так как за каждую итерацию интервал, где расположен корень, уменьшается
в два раза, то через n итераций интервал будет равен (b - а)/2n. За 10 итераций
интервал уменьшится в 210 = 1024 103 раз, за 20 итераций - в 220 106 раз.
2. Метод Ньютона (метод касательных)
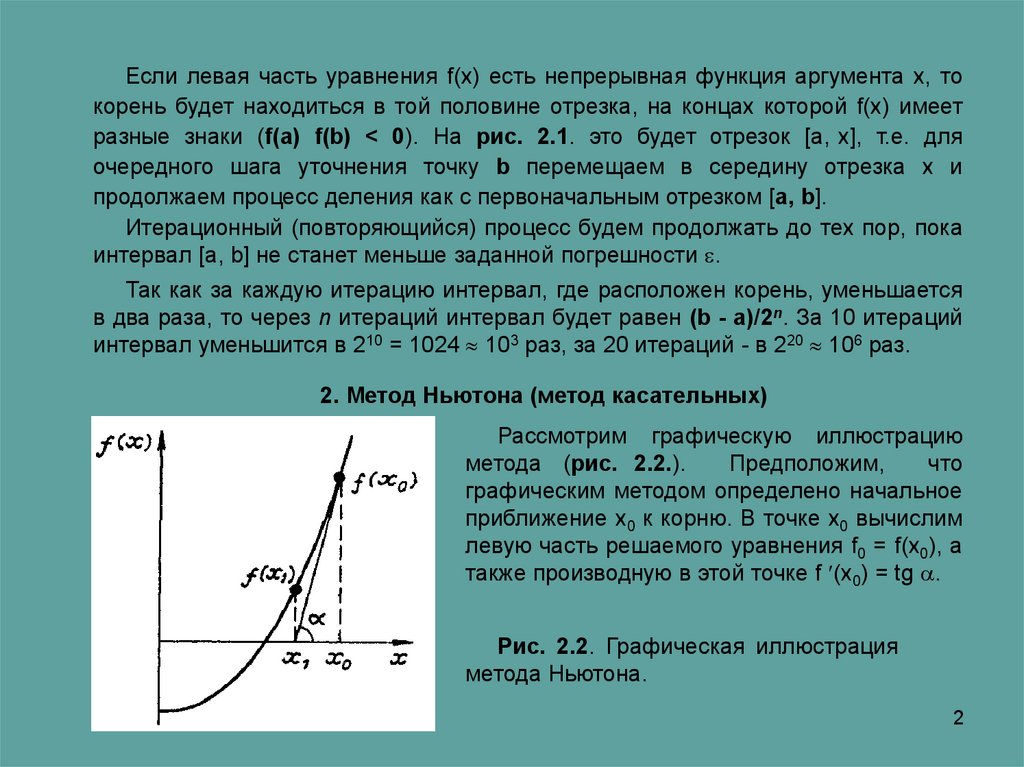
Рассмотрим графическую иллюстрацию
метода (рис. 2.2.).
Предположим,
что
графическим методом определено начальное
приближение х0 к корню. В точке х0 вычислим
левую часть решаемого уравнения f0 = f(x0), а
также производную в этой точке f (x0) = tg .
Рис. 2.2. Графическая иллюстрация
метода Ньютона.
2

3.

Следующее приближение к корню найдем в точке х1, где касательная к функции
f(x), проведенная из точки (х0, f0), пересекает ось абсцисс. Затем считаем точку
х1 в качестве начальной и продолжаем итерационный процесс.
Из рис. 2.2 видно, что таким способом можно приближаться к корню х*. При
этом с каждой итерацией расстояние между очередным хк+1 и предыдущим хк
приближениями к корню будет уменьшаться.
Процесс уточнения корня закончим, когда выполнится условие
,
где - допустимая погреш-
ность определения корня.
Из геометрических соотношений (рис. 2.2) получим основную формулу
метода Ньютона
(2.3)
Метод Ньютона обладает высокой скоростью сходимости. Обычно
абсолютная точность решения 10-5 – 10-6 достигается через 5-6 итераций.
Недостатком метода является необходимость вычисления на каждой итерации
не только левой части уравнения, но и ее производной.
3. Метод простых итераций
От исходного уравнения (2.1) перейдем к эквивалентному уравнению
(2.4)
3

4.

Пусть известно начальное приближение к корню х = х0, тогда подставим его в
первую часть уравнения (2.4) и получим новое приближение х1 = (х0), затем
аналогичным образом получим x2 = (х1) и так далее,
(2.5)
Необходимо установить, при каких условиях итерационный процесс (2.5)
будет сходиться к корню уравнения х*.
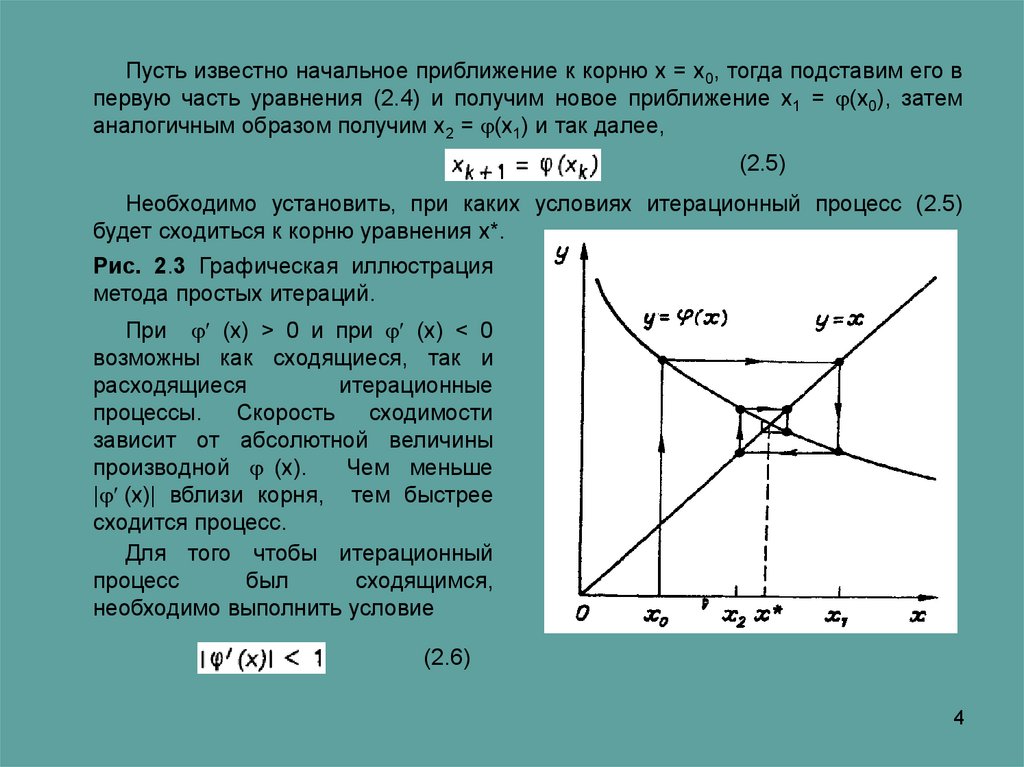
Рис. 2.3 Графическая иллюстрация
метода простых итераций.
При (х) > 0 и при (х) < 0
возможны как сходящиеся, так и
расходящиеся
итерационные
процессы.
Скорость
сходимости
зависит от абсолютной величины
производной (х).
Чем меньше
| (х)| вблизи корня, тем быстрее
сходится процесс.
Для того чтобы итерационный
процесс
был
сходящимся,
необходимо выполнить условие
(2.6)
4

5.

4. Метод секущих
Если итерации хk и xk+1 расположены достаточно близко друг к другу, то
производную f (хk) в алгоритме Ньютона (2.3) можно заменить ее
приближенным значением в виде отношения приращения функции f = f(xk) –
f(xk-1) к приращению аргумента х = хk – хk – 1. Таким образом, запишем формулу
метода секущих
(2.7)
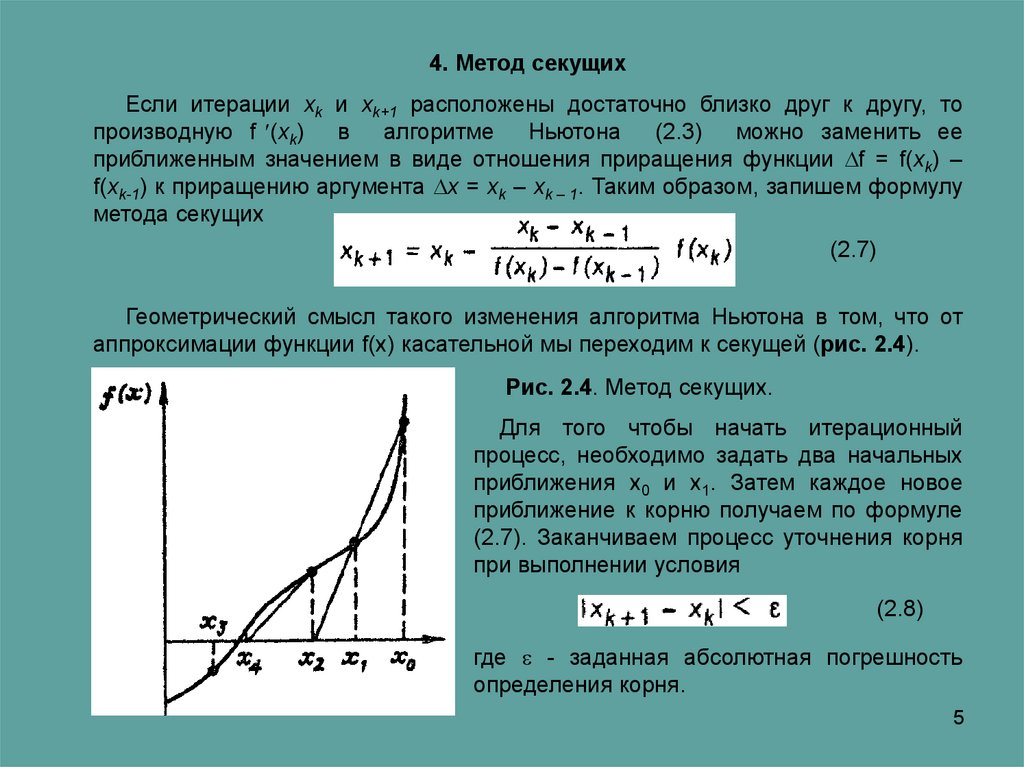
Геометрический смысл такого изменения алгоритма Ньютона в том, что от
аппроксимации функции f(x) касательной мы переходим к секущей (рис. 2.4).
Рис. 2.4. Метод секущих.
Для того чтобы начать итерационный
процесс, необходимо задать два начальных
приближения х0 и х1. Затем каждое новое
приближение к корню получаем по формуле
(2.7). Заканчиваем процесс уточнения корня
при выполнении условия
(2.8)
где - заданная абсолютная погрешность
определения корня.
5

6.

Алгоритмы функций MathCad, используемых для
решения нелинейных уравнений
Итерационный алгоритм, реализованный в функции root, который называется
методам секущих, состоит в следующем (рис. 2.4):
1. Начальное приближение принимают за нулевое приближение к корню: х0 = х.
2. Выбирают шаг h = TOL.х и определяют первое приближение к корню
x1 = x0 + h. Если х = 0, то принимают h = TOL.
3. Через эти две точки проводят секущую — прямую линию, которая пересекает
ось х в некоторой точке х2. Эту точку принимают за второе приближение.
4. Новую секущую проводят через первую и вторую точки, тем самым определяя
третье приближение, и т. д.
5. Если на каком-либо шаге оказывается, что уравнение выполнено, т. е.
|f (х)| < TOL, то итерационный процесс прерывается и х выдается в качестве
решения.
Во встроенной функции Find реализовано несколько градиентных численных
алгоритмов, один из которых может выбрать либо программа Mathcad, либо сам
пользователь. Приведем наиболее простую форму алгоритма, называемого
методом Ньютона:
1. За нулевую итерацию принимается введенное пользователем начальное
значение х0 = х.
2. В точке х0 методом конечных разностей вычисляется производная f (х0).
6

7.

3. Пользуясь разложением Тейлора, можно заменить f(х) в окрестности х0
касательной — прямой линией f(x) f (х0) + f (х0) .(х – х0).
4. Определяется точка x1, в которой прямая пересекает ось х (рис. 2.4).
5. Если f(x1) < TOL, то итерации прерываются, и значение x1 выдается в
качестве решения. В противном случае x1 принимается за новую итерацию, и
цикл повторяется: строится касательная к f(x) в точке x1, определяется х2 —
точка ее пересечения с осью х и т. д.
Выбор градиентного алгоритма
Mathcad предлагает три различных варианта градиентных методов. Чтобы
поменять численный метод:
1. Щелкните правой кнопкой мыши на названии функции Find.
2. Наведите указатель мыши на пункт Nonlinear (Нелинейный) в контекстном
меню.
3. В появившемся подменю выберите один из трех методов: Conjugate Gradient
(Сопряженных
градиентов).
Quasi-Newton
(Квази-ньютоновский)
или
Levenberg-Marquardt (Левенберга—Маркарда).
Параметры градиентных алгоритмов
Помимо выбора самих методов имеется возможность устанавливать их
некоторые параметры. Для этого нужно вызвать с помощью контекстного меню
диалоговое окно Advanced Options (Дополнительные параметры), выбрав в
контекстном меню пункты Nonlinear/Advanced options (Нелинейный
/Дополнительные параметры).
7

8.

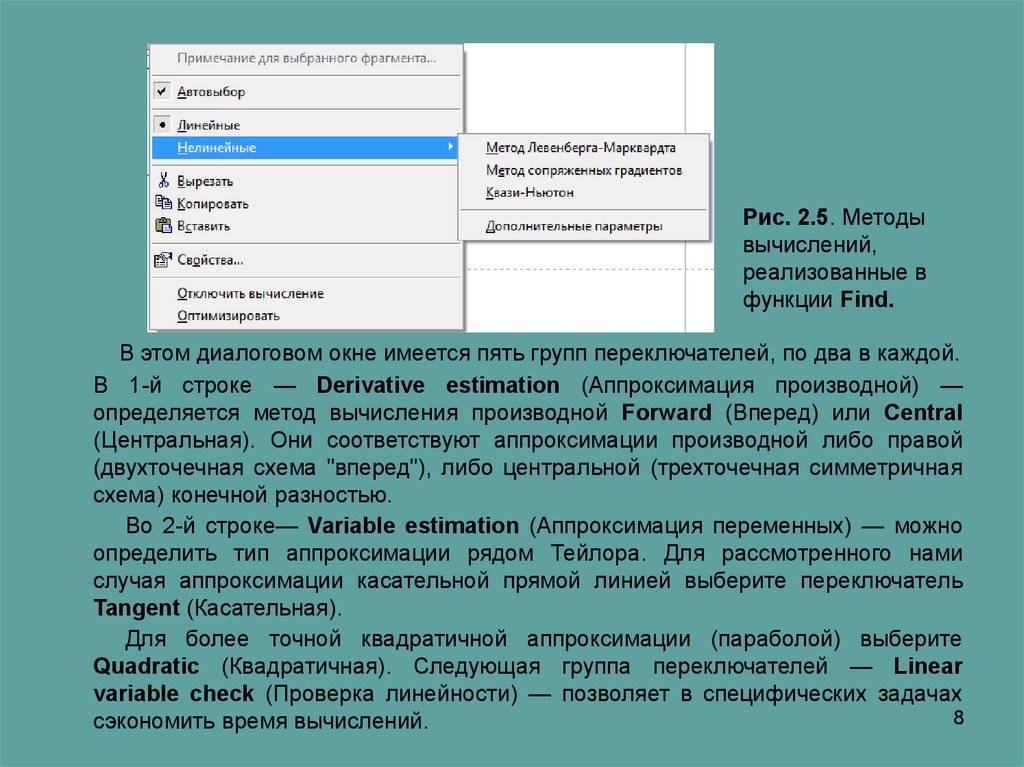
Рис. 2.5. Методы
вычислений,
реализованные в
функции Find.
В этом диалоговом окне имеется пять групп переключателей, по два в каждой.
В 1-й строке — Derivative estimation (Аппроксимация производной) —
определяется метод вычисления производной Forward (Вперед) или Central
(Центральная). Они соответствуют аппроксимации производной либо правой
(двухточечная схема "вперед"), либо центральной (трехточечная симметричная
схема) конечной разностью.
Во 2-й строке— Variable estimation (Аппроксимация переменных) — можно
определить тип аппроксимации рядом Тейлора. Для рассмотренного нами
случая аппроксимации касательной прямой линией выберите переключатель
Tangent (Касательная).
Для более точной квадратичной аппроксимации (параболой) выберите
Quadratic (Квадратичная). Следующая группа переключателей — Linear
variable check (Проверка линейности) — позволяет в специфических задачах
8
сэкономить время вычислений.