§31. ДУ

1.

§31. Дифференциальные
уравнения
п.1. Основные понятия.
Дифференциальным называется уравнение,
связывающее между собой независимую
переменную x, неизвестную функцию
и
ее производные.
Если искомая функция зависит от одной
переменной, то ДУ называют обыкновенным.
Если искомая функция зависит от нескольких
переменных, то ДУ называют ДУ в частных
производных.

2.

Порядком ДУ называется порядок старшей
производной, входящей в уравнение.
Пример.
y '' 2 y ' 5 y sin x
— обыкновенное ДУ 2-го порядка.
xy ' 2 y ln x 0
— обыкновенное ДУ 1-го порядка.
z
z
xy
cos y sin x ze
x
y
— ДУ в частных производных 1-го порядка.

3.

Решением ДУ называется такая
дифференцируемая функция, определенная
на некотором интервале, которая при
подстановке в уравнение обращает его в
тождество.
Процесс нахождения всех решений ДУ
называется интегрированием.
График решения ДУ называется интегральной
кривой.
Пример. Является ли функция y e
решением уравнения
Да.
y '' 2 y ' y 0?
x

4.

п.2. ДУ первого порядка.
ДУ вида
F ( x, y , y ') 0
называется ДУ 1-го порядка.
В частности,
y ' f ( x, y )
(1)
— ДУ 1-го порядка, разрешенное
относительно производной,
P ( x, y )dx Q ( x, y )dy 0
— ДУ 1-го порядка в дифференциальной
форме.
(2)

5.

Замечание 1.
Переход между уравнениями (1) и (2)
осуществляется с учетом того, что
dy
y' .
dx
Пример.
( x y )dx xydy 0,
2
2
( x y ) xyy ' 0,
2
2
x y
y'
.
xy
2
2
|: dx

6.

Пример. Решить уравнение
y ' 2 x.
Решение.
y 2 xdx x C.
2
Получили бесконечное количество решений
y x C, C .
2
Условие вида
y ( x0 ) y0
называется начальным.
Задачей Коши или начальной задачей
называют задачу нахождения решения ДУ по
начальному условию.

7.

Пример. Решить задачу Коши
y ' 2 x,
y (1) 3.
Решение. Так как
y x C,
2
то
3 1 C,
C 2.
Получаем решение
y x 2.
2

8.

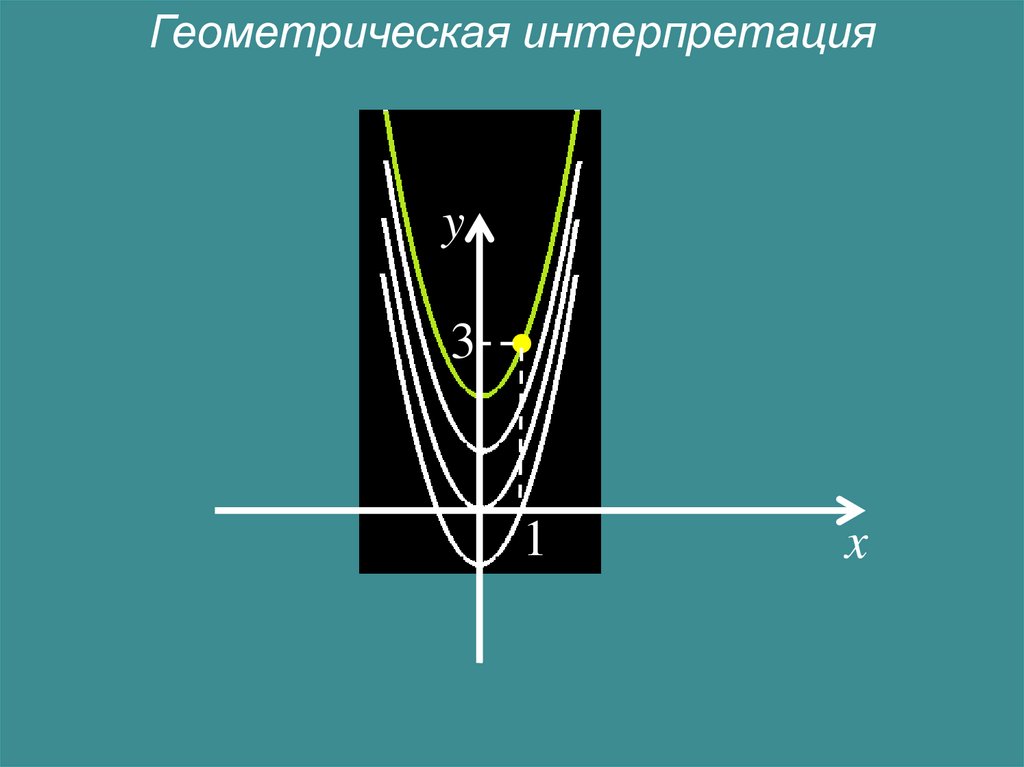
Геометрическая интерпретация
y
3
1
x

9.

Общим решением ДУ 1-го порядка называется
такая функция
y ( x, C ),
где С —произвольная константа, что:
1) функция y ( x, C ) является решением
ДУ при каждом фиксированном C;
2) для любого допустимого начального
условия y ( x0 ) y0 можно найти такое
значение C C0 , что функция y ( x, C0 )
удовлетворяет этому начальному условию, т.е.
( x0 , C0 ) y0 .

10.

Частным решением ДУ 1-го порядка
называется любая функция y ( x, C0 ),
получаемая из общего решения при
конкретном значении произвольной
постоянной C C0 .
Геометрическая интерпретация
Общее решение — это множество
интегральных кривых.
Частное решение — это одна интегральная
кривая из этого множества.

11.

Теорема (о существовании и единственности
решения задачи Коши).
Рассмотрим ДУ
y ' f ( x, y ).
Пусть функции f ( x, y ) и f y ( x, y ) непрерывны
в некоторой области D плоскости Oxy.
Тогда для любой точки ( x0 , y0 ) D существует
единственное решение этого уравнения,
удовлетворяющее начальному условию
y ( x0 ) y0 .

12.

Геометрическая интерпретация
Через каждую точку ( x0 , y0 ) D проходит
одна и только одна интегральная кривая
дифференциального уравнения
y ' f ( x, y ).
Решение, в каждой точке которого нарушаются
условия теоремы существования и
единственности решения задачи Коши
называется особым.
Особое решение не может быть получено из
общего ни при каких числовых значениях
константы С, включая C .

13.

Пример. Рассмотрим уравнение
y' 3 y .
2
3
Общее решение имеет вид:
y (x C) .
3
Проверка:
y ' 3( x C ) ,
2
3 y 3( x C ) .
3
2
Также решением является функция
y 0.
Это решение нельзя получить из общего
решения ни при каком числовом значении
константы:
0 (x C) ,
3
C x.
2

14.

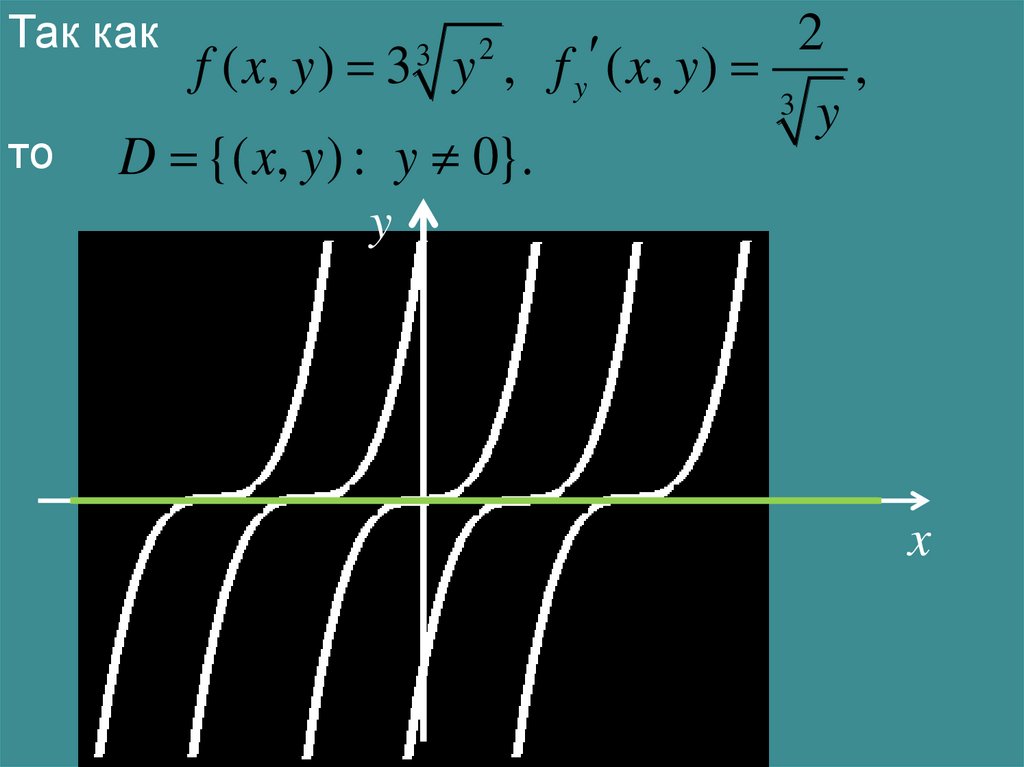
Так как
то
2
,
f ( x , y ) 3 y , f y ( x, y )
3 y
D {( x, y ) : y 0}.
y
3
2
x

15.

Геометрическая интерпретация ДУ 1-го
порядка
Уравнение
y ' f ( x, y )
устанавливает связь между координатами
точки
( x, y )
и угловым коэффициентом касательной
y'
к интегральной кривой, проходящей через эту
точку.

16.

Линия, в каждой точке которой y ' постоянен,
называется изоклиной.
Уравнение изоклины
f ( x, y ) c.

17.

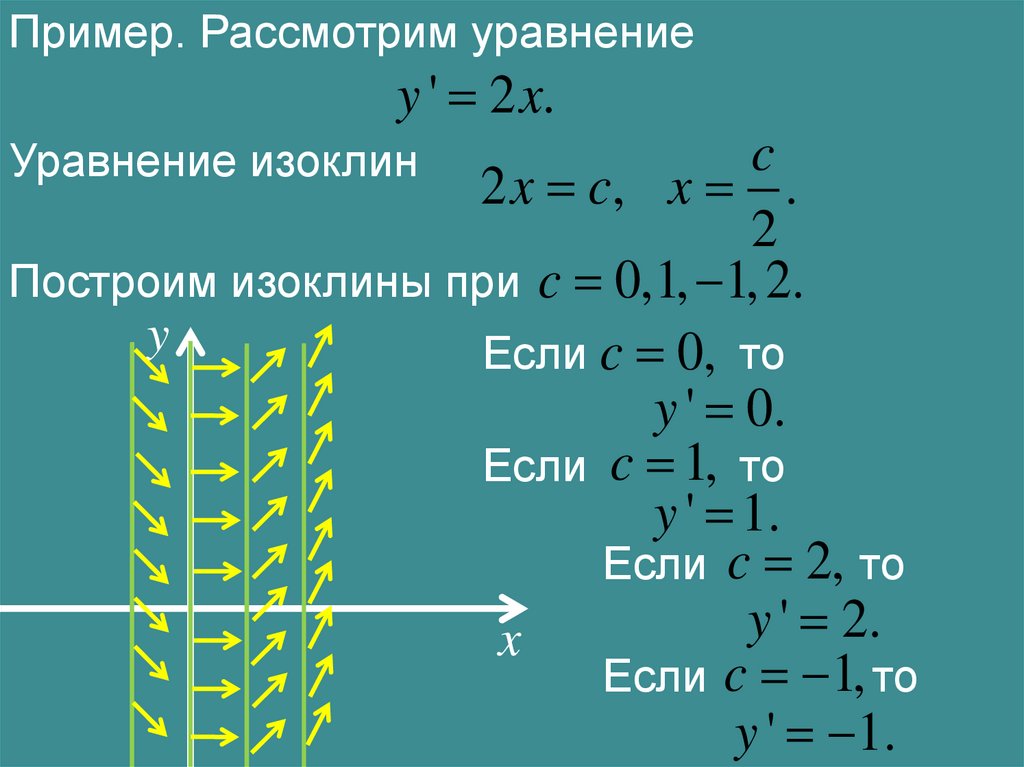
Пример. Рассмотрим уравнение
y ' 2 x.
c
2 x c, x .
2
Построим изоклины при c 0,1, 1, 2.
y
Если c 0, то
y ' 0.
Если c 1, то
y ' 1.
Если c 2, то
y
'
2.
x
Если c 1, то
y ' 1.
Уравнение изоклин