Элементы комбинаторики - размещения

1. Элементы комбинаторики -

РАЗМЕЩЕНИЯ

2. Задача 1. Имеется 4 шара и 4 пустых ячейки в коробке. Сколько вариантов расположения шаров можно получить?

СРАВНИТЕ 2 ЗАДАЧИ:
Задача 1. Имеется 4 шара и 4 пустых
ячейки в коробке.
Сколько вариантов расположения шаров
можно получить?
Задача 2. Имеется 4 шара и 3 пустых
ячейки в коробке.
Какие варианты расположения можно
получить?

3. Решение 1 задачи:

Порядок расположения шаров задаётся
условием 1,2,3,4. Это элементы
множества, тогда число перестановок
P4 = n! = 4! = 24. – (искомое количество
способов)

4. Отличие от предыдущей задачи: количество шаров превосходит количество ячеек. Т.е. невозможно применить теорему о количестве

перестановок.
Размещением из n элементов по k (k ≤ n)
называется любое множество, состоящее
из любых k элементов, взятых в определённом
порядке из данных n элементов.
Обозначение
k
n
A
читают: «A из n по k»

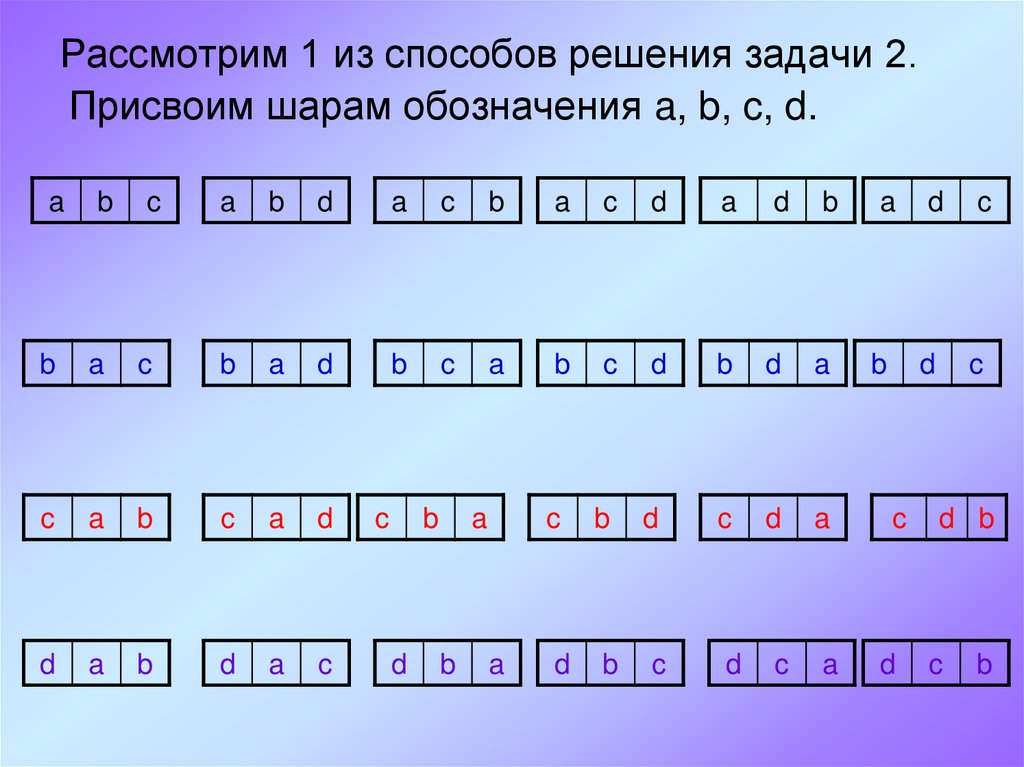
5. Рассмотрим 1 из способов решения задачи 2.

Присвоим шарам обозначения a, b, c, d.
a
b
c
a
b
d
a
c
b
a
c
d
a
d
b
a
d
c
b
a
c
b
a
d
b
c
a
b
c
d
b
d
a
b
d
c
c
a
b
c
a
d
c
b
d
c
d
a
c
d b
d
a
b
d
a
c
d
b
c
d
c
a
d
c
c
b
d
a
b
a
b

6.

*
a
b
c
b
d
a
c
c
d
a
b
d
d
a
b
c
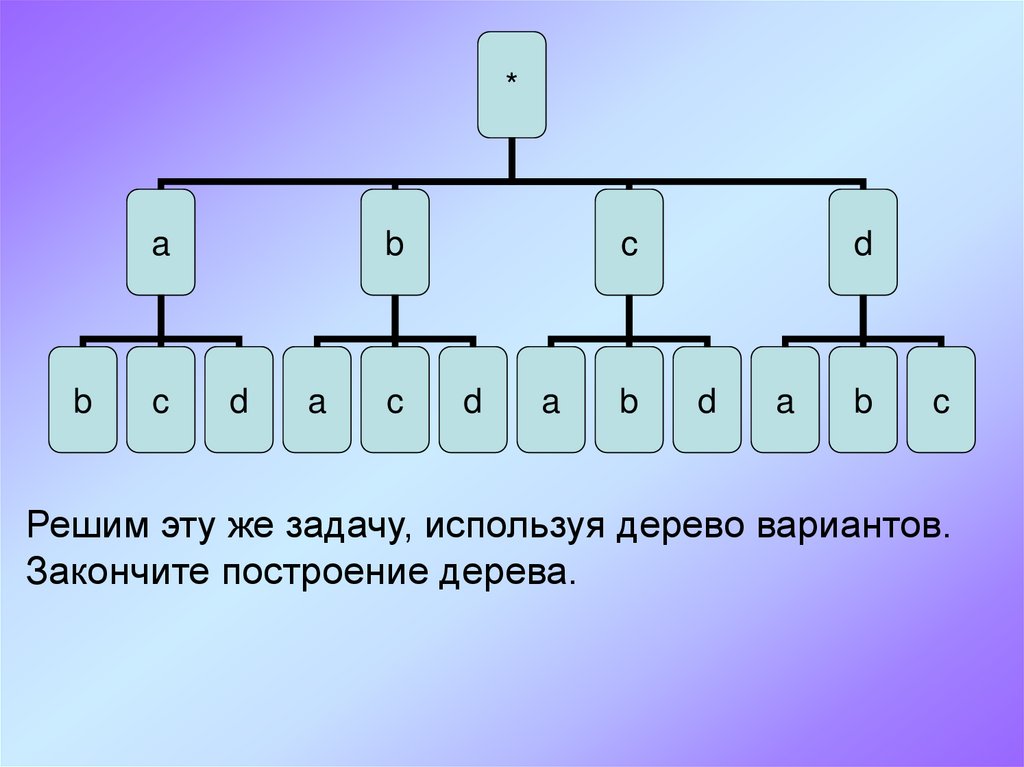
Решим эту же задачу, используя дерево вариантов.
Закончите построение дерева.

7. Заметим, что для каждого выбранного первого элемента можно тремя способами выбрать из трёх оставшихся элементов второй элемент.

Далее, для каждых первых двух
элементов можно двумя способами выбрать из
оставшихся элементов третий элемент.

8. Решение 2 задачи:

Размещение 4 элементов по 3.
Количество множителей равно 3
A 4 3 2 24
3
4

9.

Аналогично рассуждая, подсчитаем
сколько можно составить размещений из n
элементов по k , где k≤n.
1 элемент
n способов
из n элементов множества
2 элемент
n-1 способов
из n-1 элементов множества
3 элемент
n-2 способов
из n-2 элементов множества
4 элемент
n-3 способов
из n-3 элементов множества
K-ый элемент
n – (k-1) способов
из n-(k-1) элементов множества

10. Правило вычисления размещений из n элементов по k элементов

A n (n 1) (n 2) ... (n (k 1))
k
n

11. Пример 1:

В классе 27 учеников. К доске нужно
вызвать двоих. Сколькими способами это можно
сделать, если первый ученик должен решить
задачу по геометрии, другой – по алгебре?
Порядок выбора двух элементов множества из
27 элементов важен, поэтому:
В данном случае k=2, потому количество множителей
в формуле равно 2,значит:
A272 n(n 1) 27 26 702

12. Пример 2:

В классе 27 учеников, из которых нужно
выбрать троих. Первый ученик должен решить
задачу, второй – сходить за мелом, третий –
дежурить в столовую. Сколькими способами это
можно сделать?
Порядок во множестве из 27 элементов важен,
поэтому:
В данном случае k=3, потому количество множителей
в формуле равно 3,значит:
A273 n(n 1)(n 2) 27 26 25 17550

13. Пример 3:

Из 30 учащихся класса требуется выбрать
старосту класса и заместителя старосты
класса. Сколькими способами это можно
сделать?
В данном случае k=2, потому количество множителей
в формуле равно 2,значит:
A n(n 1) 30 29 870
2
30

14.

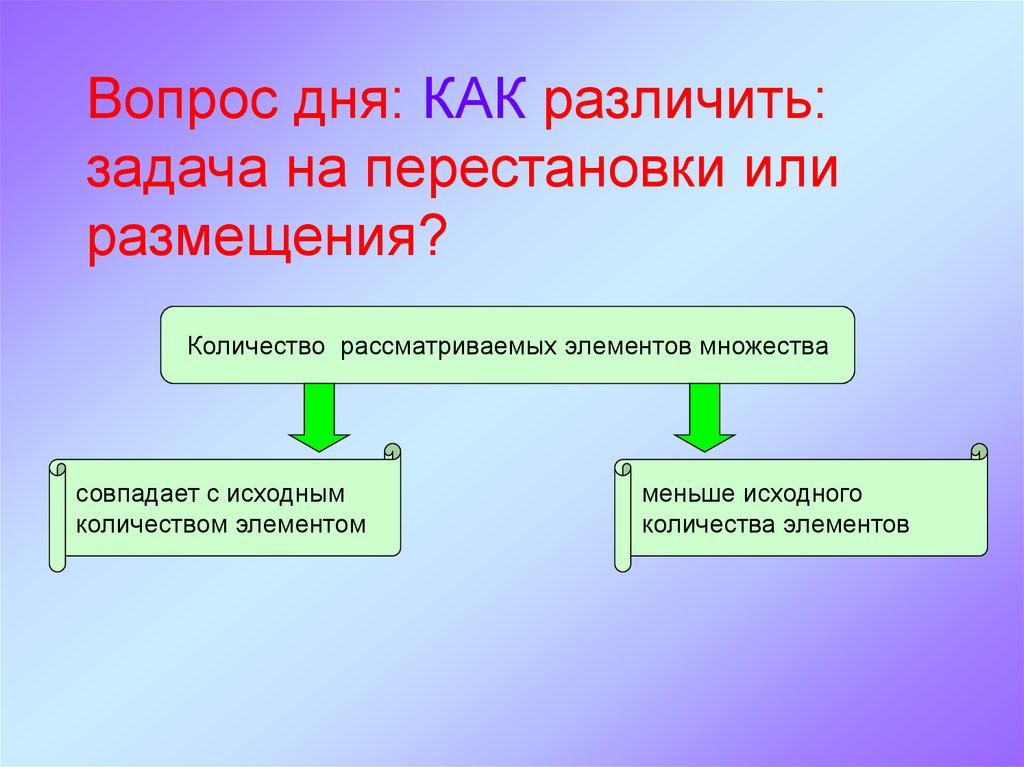
Вопрос дня: КАК различить:
задача на перестановки или
размещения?
Количество рассматриваемых элементов множества
совпадает с исходным
количеством элементом
меньше исходного
количества элементов