Похожие презентации:
Элементы комбинаторики - сочетания
1. Элементы комбинаторики -
Сочетания2.
Вопрос дня:КАК РАЗЛИЧАТЬ
ПРИМЕНЕНИЕ ТЕОРЕМ?
3.
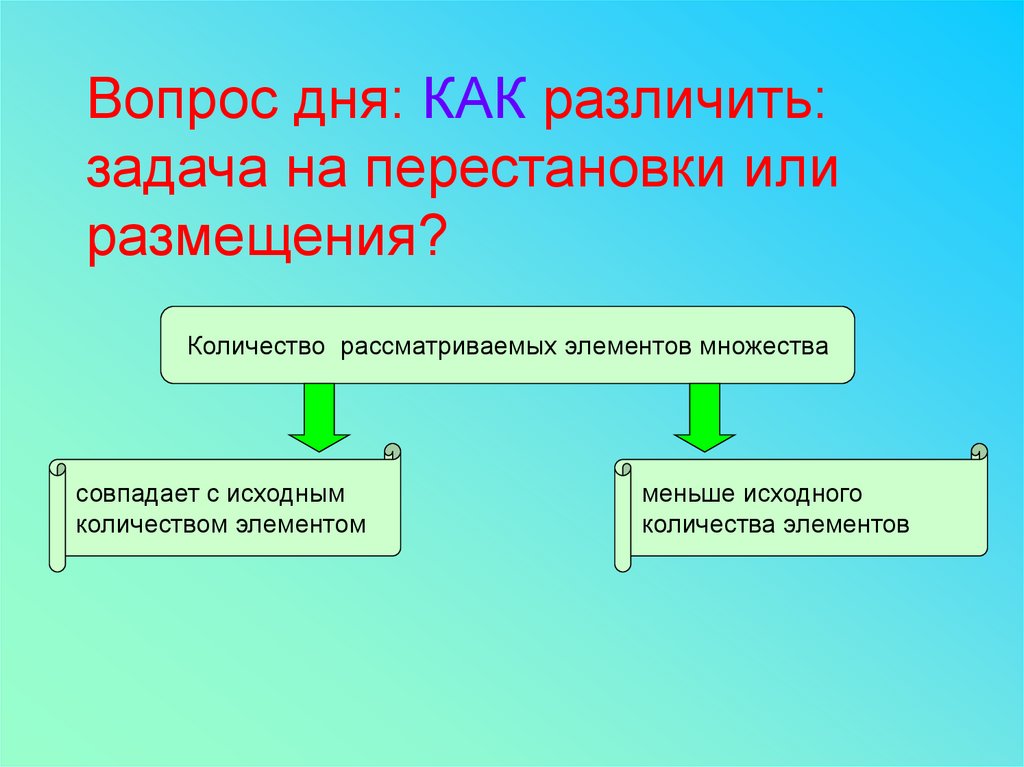
Вопрос дня: КАК различить:задача на перестановки или
размещения?
Количество рассматриваемых элементов множества
совпадает с исходным
количеством элементом
меньше исходного
количества элементов
4.
Перестановкой из n элементовмножества называется
расположение этих элементов
в определённом порядке
Размещением из n элементов
по k элементов называется любое
множество, состоящее из k элементов,
взятых в определённом порядке из данных
n элементов.
Сочетанием из n элементов по k называется
любое множество, составленное из k
элементов, выбранных из данных n элементов
5.
Пусть имеются пять гвоздик разного цвета:a, b, c, d, e.
Требуется составить букет из трёх гвоздик.
Если в букет входит гвоздика a, то можно
составить такие букеты:
abc, abd, abe, acd, ace, ade
Если в букет не входит гвоздика a, но входит
гвоздика b, то можно составить такие букеты:
bcd, bce, bde
Если в букет не входят ни гвоздика a, ни
гвоздика b, возможен один вариант
составления букета c, d, e
6.
Указали все возможные способысоставления букетов, в которых поразному сочетаются три гвоздики из
данных пяти
Составили все возможные СОЧЕТАНИЯ
из 5 элементов по 3 элемента.
Обозначение:
С
k
n
В рассмотренном примере
С53 10
«combinations»
7.
Рассмотрим множество, содержащее n элементов, ииз его элементов составлены все возможные
сочетания по k элементов.
Число таких сочетаний равно Сnk
В каждом сочетании можно выполнить
перестановок
Рk
В результате получим все размещения ,
которые можно составить из n элементов по k
Их число равно
значит
Отсюда
Ank Cnk Pk
k
A
Сnk n
Pk
Аnk
8.
Другими словами:n(n 1)(n 2) .... (n (k 1))
C
1 2 3 4 .... (k 1) k
k
n
Несложные преобразования
приводят полученную формулу к виду:
n!
С
k! (n k )!
k
n
Запомним 0!=1
9. Пример 1:
Из 15 членов туристической группы надовыбрать 3 дежурных. Сколькими способами это
можно сделать?
Речь идёт о сочетаниях из 15 элементов по 3.
Сnk C153
n!
15! 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 13 14 15
455
k! (n k )! 3! 12! 1 2 3 1 2 3 4 5 6 7 8 9 10 11 12 13
1 2 3
10. Пример 2:
Из вазы с фруктами, в которой лежит 9 яблок и6 груш, надо выбрать 3 яблока и 2 груши.
Сколькими способами можно сделать такой
выбор?
3
С
Выбрать 3 яблока из 9 можно
9 способами,
А выбрать 2 груши из 6 можно С 2 способами.
6
Таким образом, учитывая правило умножения, выбор,
соответствующий условию задачи, можно сделать
9 8 7 6 5
С С
1260
1 2 3 1 2
3
9
2
6










 Математика
Математика








