Похожие презентации:
Кодирование информации при передаче по дискретному каналу с помехами
1.
12. КОДИРОВАНИЕ ИНФОРМАЦИИ ПРИ ПЕРЕДАЧЕ ПО ДИСКРЕТНОМУКАНАЛУ С ПОМЕХАМИ
12.1. Постановка задачи
12.2. Классификация корректирующих кодов
12.3. Основные характеристики корректирующих кодов
12.4. Способы введения избыточности в сигнал
12.5. Систематические коды
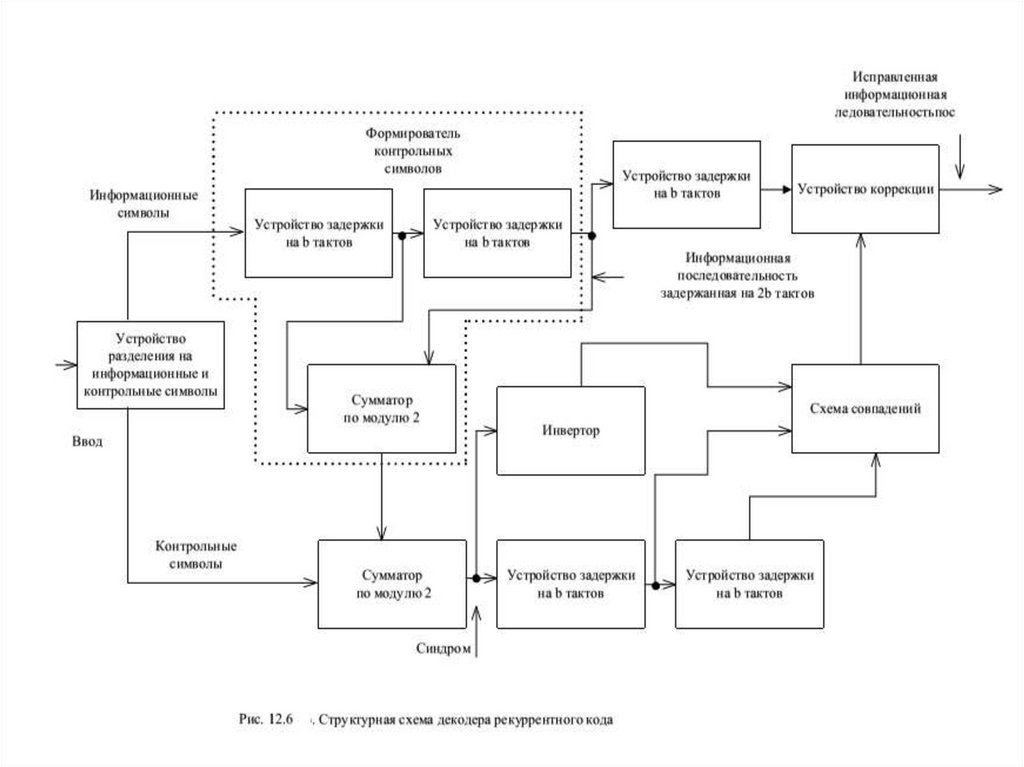
12.6. Рекуррентные коды
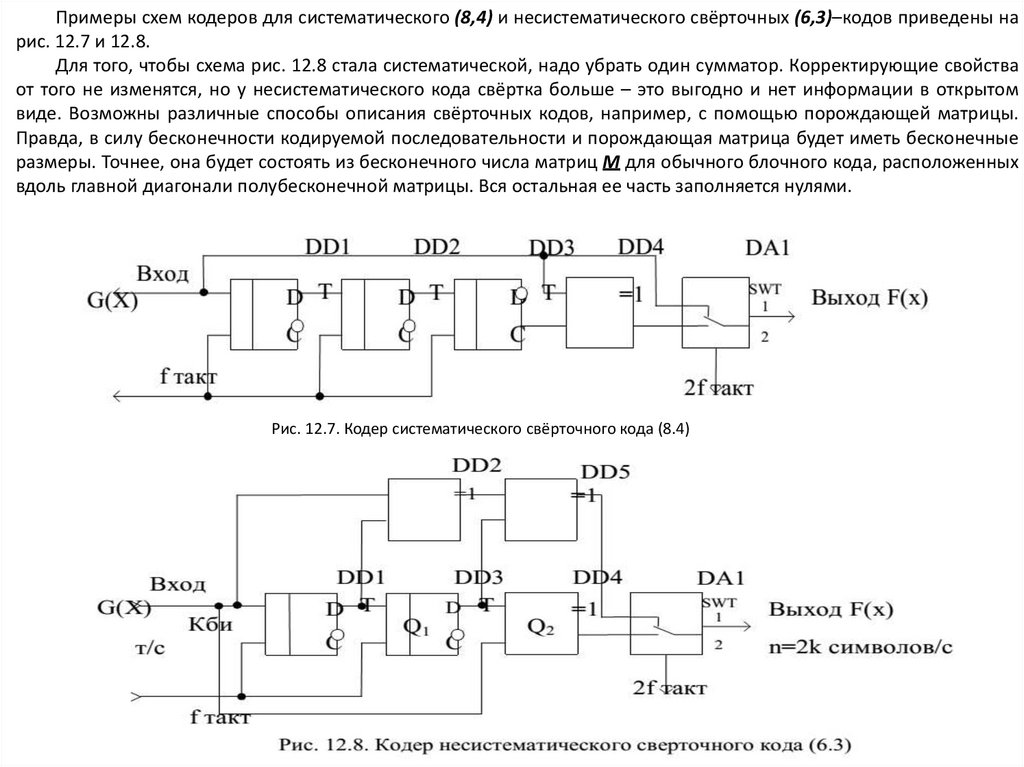
12.7. Свёрточные коды
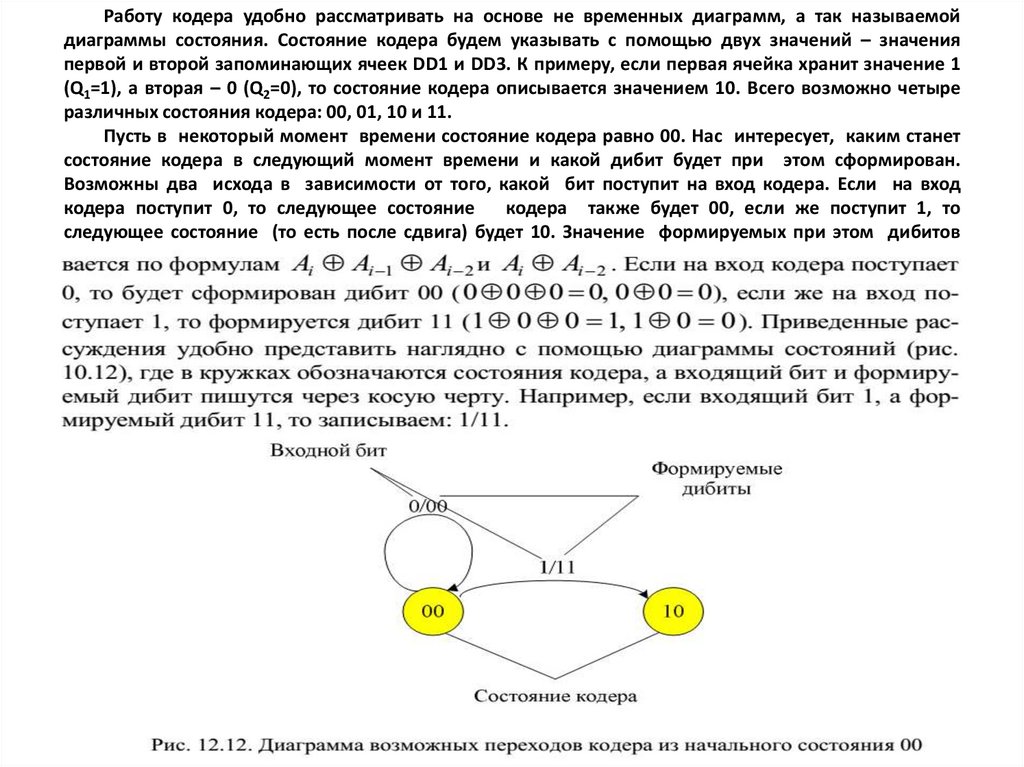
12.7.1. Кодовое дерево и решетчатая диаграмма
12.7.2. Треллис-кодирование
12.7.3. Декодер Витерби
2.
Постановка задачиДействие помехи на дискретный сигнал с конечным числом элементов приводит к количественным и
качественным изменениям его структуры (к ошибкам в числе и состоянии элементов). Чтобы обеспечить в таких
условиях передачу информации с заданной достоверностью, возможные ошибки должны быть обнаружены, а
если требуется, то и исправлены.
Теория помехоустойчивого кодирования базируется на результатах исследований, проведенных Шенноном и
сформулированных им в виде теоремы:
1. При любой производительности источника сообщений, меньшей, чем пропускная способность канала,
существует такой способ кодирования, который позволяет обеспечить передачу всей информации, создаваемой
источником сообщений, со сколь угодно малой вероятностью ошибки.
2. Не существует способа кодирования, позволяющего вести передачу информации со сколь угодно малой
вероятностью ошибки, если производительность источника сообщений больше пропускной способности канала.
Теорема устанавливает теоретический предел возможной эффективности системы при достоверной передаче
информации. Ею опровергнуто представление о том, что достижение сколь угодно малой вероятности ошибки в
случае передачи информации по каналу с помехами возможно лишь при введении бесконечно большой
избыточности, то есть при уменьшении скорости передачи до нуля. Из теоремы следует, что помехи в канале не
накладывают ограничений на точность передачи. Ограничение накладывается только на скорость передачи, при
которой может быть достигнута сколь угодна высокая достоверность передачи.
В теореме затрагивается вопрос о путях построения кодов, обеспечивающих указанную идеальную передачу
(при любой конечной скорости передачи информации вплоть до пропускной способности сколь угодно малая
вероятность ошибки достигается лишь при безграничном увеличении длительности кодируемых
последовательностей знаков, безошибочная передача при наличии помех возможна лишь теоретически. На
практике степень достоверности и эффективности ограничивается двумя факторами: размерами и стоимостью
аппаратуры
кодирования
и
временем
задержки
передаваемого
сообщения).
Помехоустойчивое кодирование представляет собой обширную область теоретических и прикладных
исследований. Основные задачи: отыскание кодов, эффективно исправляющих ошибки требуемого вида,
нахождение методов кодирования и декодирования, способов их реализации. Все коды разделяются на коды с
обнаружением ошибок и коды с исправлением ошибок (корректирующие коды).
Задачи корректирующего кодирования обычно решают при следующих предположениях: избыточность
эффективного кода равна нулю, кодирование выполняется двоичными сигналами, характеристики дискретного
двоичного канала известны, канал является симметричным, то есть вероятности перехода нуля в единицу и
единицы в нуль одинаковы.
3.
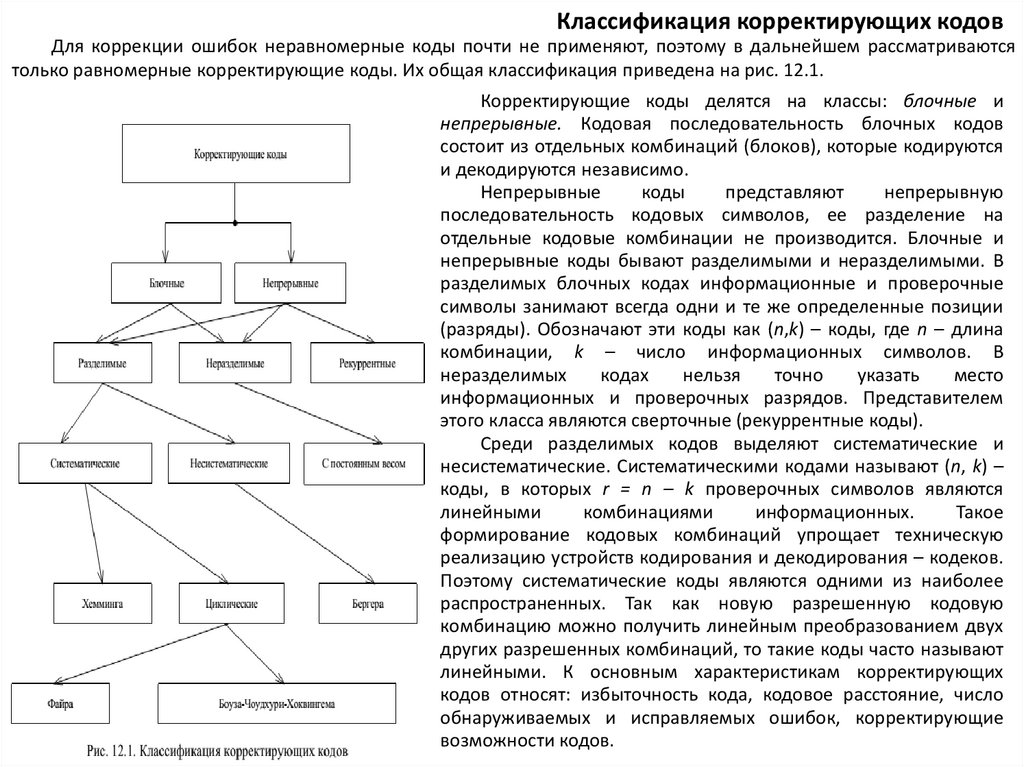
Классификация корректирующих кодовДля коррекции ошибок неравномерные коды почти не применяют, поэтому в дальнейшем рассматриваются
только равномерные корректирующие коды. Их общая классификация приведена на рис. 12.1.
Корректирующие коды делятся на классы: блочные и
непрерывные. Кодовая последовательность блочных кодов
состоит из отдельных комбинаций (блоков), которые кодируются
и декодируются независимо.
Непрерывные
коды
представляют
непрерывную
последовательность кодовых символов, ее разделение на
отдельные кодовые комбинации не производится. Блочные и
непрерывные коды бывают разделимыми и неразделимыми. В
разделимых блочных кодах информационные и проверочные
символы занимают всегда одни и те же определенные позиции
(разряды). Обозначают эти коды как (n,k) – коды, где n – длина
комбинации, k – число информационных символов. В
неразделимых
кодах
нельзя
точно
указать
место
информационных и проверочных разрядов. Представителем
этого класса являются сверточные (рекуррентные коды).
Среди разделимых кодов выделяют систематические и
несистематические. Систематическими кодами называют (n, k) –
коды, в которых r = n – k проверочных символов являются
линейными
комбинациями
информационных.
Такое
формирование кодовых комбинаций упрощает техническую
реализацию устройств кодирования и декодирования – кодеков.
Поэтому систематические коды являются одними из наиболее
распространенных. Так как новую разрешенную кодовую
комбинацию можно получить линейным преобразованием двух
других разрешенных комбинаций, то такие коды часто называют
линейными. К основным характеристикам корректирующих
кодов относят: избыточность кода, кодовое расстояние, число
обнаруживаемых и исправляемых ошибок, корректирующие
возможности кодов.
4.
Принцип обнаружения и исправления ошибок кодами хорошо иллюстрируется с помощью геометрических моделей. Любой n –элементный двоичный код можно представить n–мерным кубом (рис.12.2), в котором каждая вершина отображает кодовую
комбинацию, а длина ребра куба соответствует одной единице. В таком кубе расстояние между вершинами (кодовыми комбинациями) измеряется минимальным количеством ребер, находящимся между ними, обозначается d и называется кодовым расстоянием
Хемминга.
Таким образом, кодовое расстояние – это минимальное число элементов, в которых любая кодовая комбинация отличается от
другой (по всем парам кодовых слов). Например, код состоит из комбинаций 1011, 1101, 1000 и 1100. Сравнивая первые две
комбинации, путем сложения их по модулю два находим, что d = 2. Сравнение первой и третьей комбинаций показывает, что и в этом
случае d = 2. Наибольшее значение d = 3 обнаруживается при сравнении первой и четвертой комбинаций, а наименьшее d = 1 – второй
и четвертой, третьей и четвертой комбинаций. Таким образом, для данного кода минимум рас- стояния dmin = 1.
В общем случае кодовое расстояние между двумя комбинациями
двоичного кода равно числу единиц, полученных при сложении этих
комбинаций по модулю два. Такое определение кодового расстояния
удобно при большой разрядности кодов. Так, складывая комбинации
определим, что кодовое расстояние между ними d = 5.
Если использовать все восемь кодовых комбинаций, записанных в
вершинах куба, то образуется двоичный код на все сочетания. Такой код
является не помехоустойчивым, так как любое искажение приводит к
кодовой комбинации, принадлежащей данному сомножеству, а
следовательно, искажение не будет обнаружено. Если же уменьшить
число используемых комбинаций с восьми до четырех, то появится
возможность обнаружения одиночных ошибок. Для этого выберем
только такие комбинации, которые отстоят друг от друга на расстоянии d
= 2, например, 000, 110, 011, 101. Остальные кодовые комбинации не
используются. Если передавалась комбинация 101, а принята
комбинация 100, то очевидно, что при приеме произошла ошибка.
Таким образом, для обнаружения искажений необходимо все кодовые
комбинации разделить на две группы: разрешенные и запрещенные.
Из приведенного примера можно сделать вывод, что способность кода обнаруживать и исправлять ошибки обусловлена
наличием избыточности, кото- рая обеспечивает минимальное расстояние между любыми двумя разрешенными комбинациями dmin >=
2 , т.е. к исходной k – элементной комбинации необходимо добавить r контрольных символов, сформированных по определенным
правилам.
5.
Пусть на вход кодирующего устройства поступает последовательность из k информационных двоичныхсимволов. На выходе ей соответствует последовательность из n = k + r двоичных символов. Всего может быть 2 k
разрешенных кодовых комбинаций и 2 n различных выходных последовательностей, а следовательно,
2n - 2k возможных выходных последовательностей для передачи не используются и являются запрещенными
комбинациями. Искажение информации в процессе передачи сводится к тому, что некоторые из переданных
символов заменяются другими. Так как каждая из 2k раз- решенных комбинаций в результате действия помех
может трансформироваться в любую другую, то всего имеется 2k×2n возможных случаев передачи (рис. 12.3). В это
число входят:
2k случаев безошибочной передачи (на рис. 12.3 обозначены жирными линиями);
2k (2k- 1) случаев перехода в другие разрешенные комбинации, что соответствует необнаруженным ошибкам
(на рис. 12.3 обозначены пунктирными линиями);
2k (2n- 2k )случаев перехода в запрещенные комбинации, которые могут быть обнаружены (на рис. 12.3
обозначены штрихпунктирными линиями).
Следовательно, число обнаруживаемых ошибочных кодовых комбинаций от общего числа возможных
случаев передачи составляет:
Отношение числа исправляемых кодом ошибочных кодовых комбинаций к числу
обнаруживаемых ошибочных комбинаций равно:
Из приведенных выше рассуждений можно сделать вывод, что коррекция ошибок
возможна благодаря введению избыточности, которая определяется выражением:
Рис. 12.3. Возможные варианты
трансформаций кодовых комбинаций
Xi в Bj
6.
Эта величина показывает, какую часть от общего числа символов кодовой комбинации составляютконтрольные символы. В теории кодирования величину k/n принято называть скоростью передачи. Необходимо
отметить, что величина k/n характеризует относительную скорость передачи информации. Если
ഥ
производительность источника информации равна




























 Информатика
Информатика








