Теорфизика без формул. Квантовая информатика

1.

ТЕОРФИЗИКА без ФОРМУЛ
лекция 5: КВАНТОВАЯ
ИНФОРМАТИКА
Парфенов К.В., физический
факультет МГУ им. М.В.Ломоносова

2.

Господа, в гильбертовом
пространстве
остается
еще много места.
Саундерс Маклейн

3.

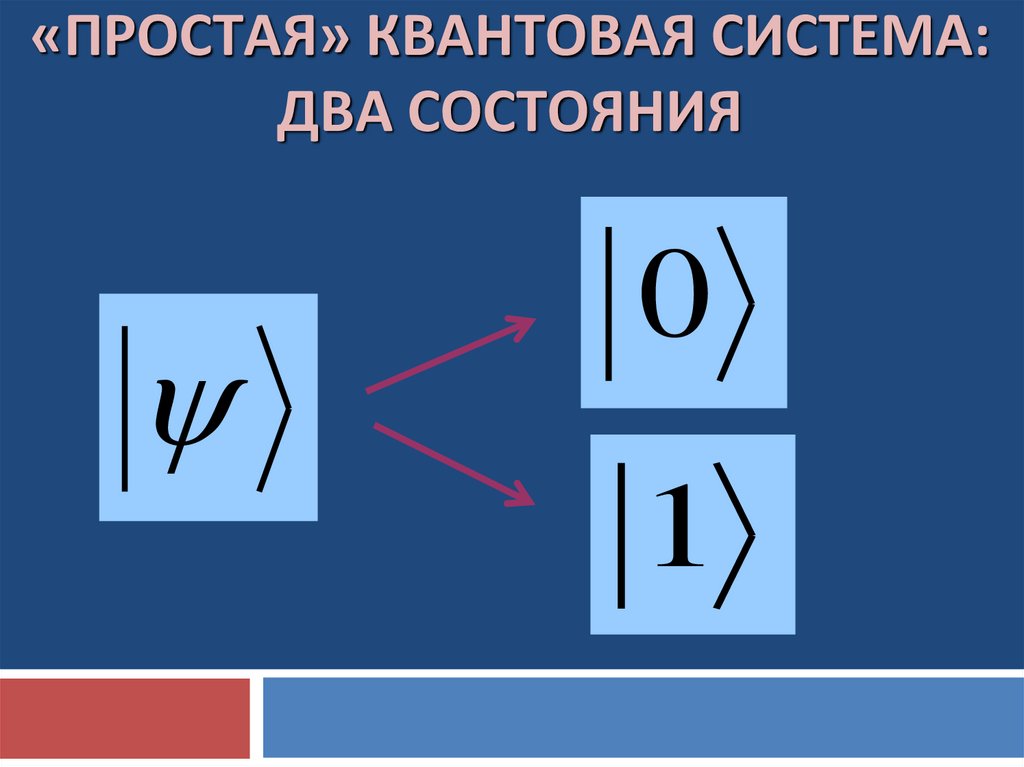
«ПРОСТАЯ» КВАНТОВАЯ СИСТЕМА:
ДВА СОСТОЯНИЯ
0
1

4.

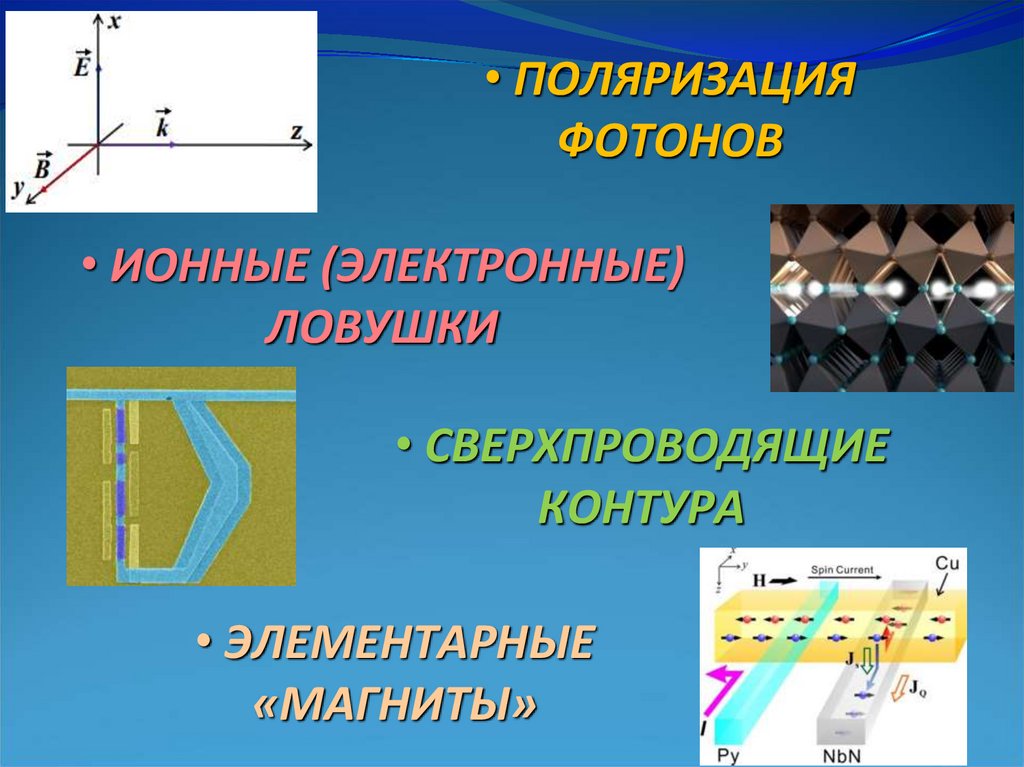
• ПОЛЯРИЗАЦИЯ
ФОТОНОВ
• ИОННЫЕ (ЭЛЕКТРОННЫЕ)
ЛОВУШКИ
• СВЕРХПРОВОДЯЩИЕ
КОНТУРА
• ЭЛЕМЕНТАРНЫЕ
«МАГНИТЫ»

5.

КВАНТОВАЯ СУПЕРПОЗИЦИЯ
0 1
w0
2
w1
w0 w1 1
2

6.

ГЕОМЕТРИЧЕСКАЯ АНАЛОГИЯ
r x ex y e y
x y 1
2
2

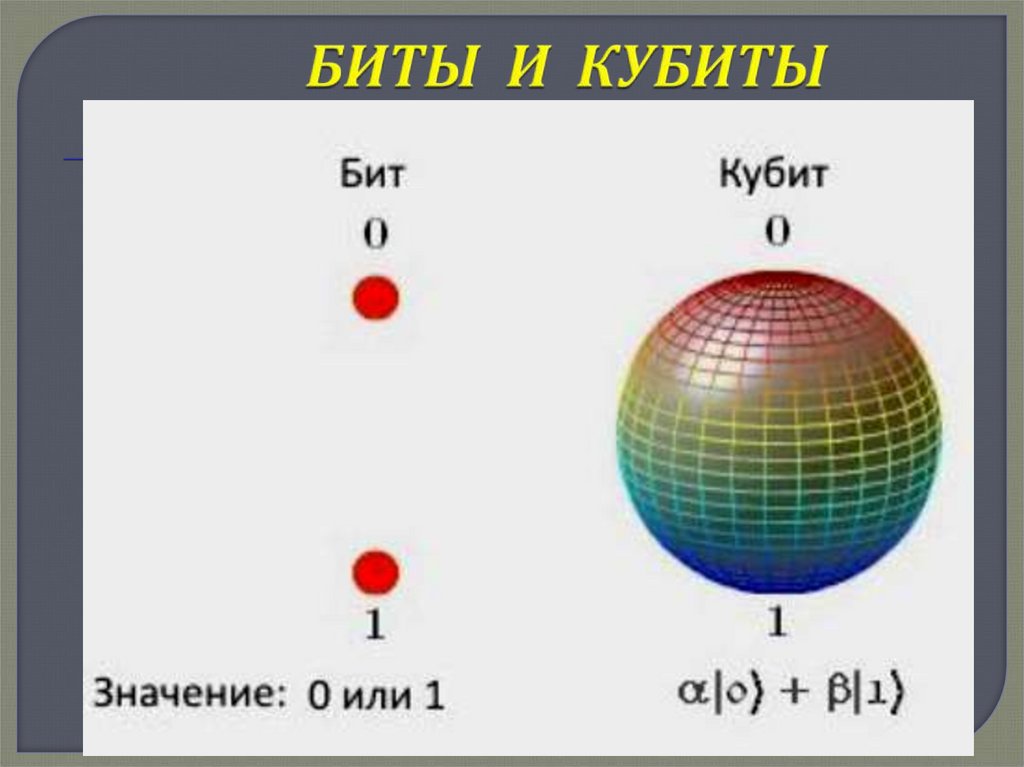
7. БИТЫ И КУБИТЫ

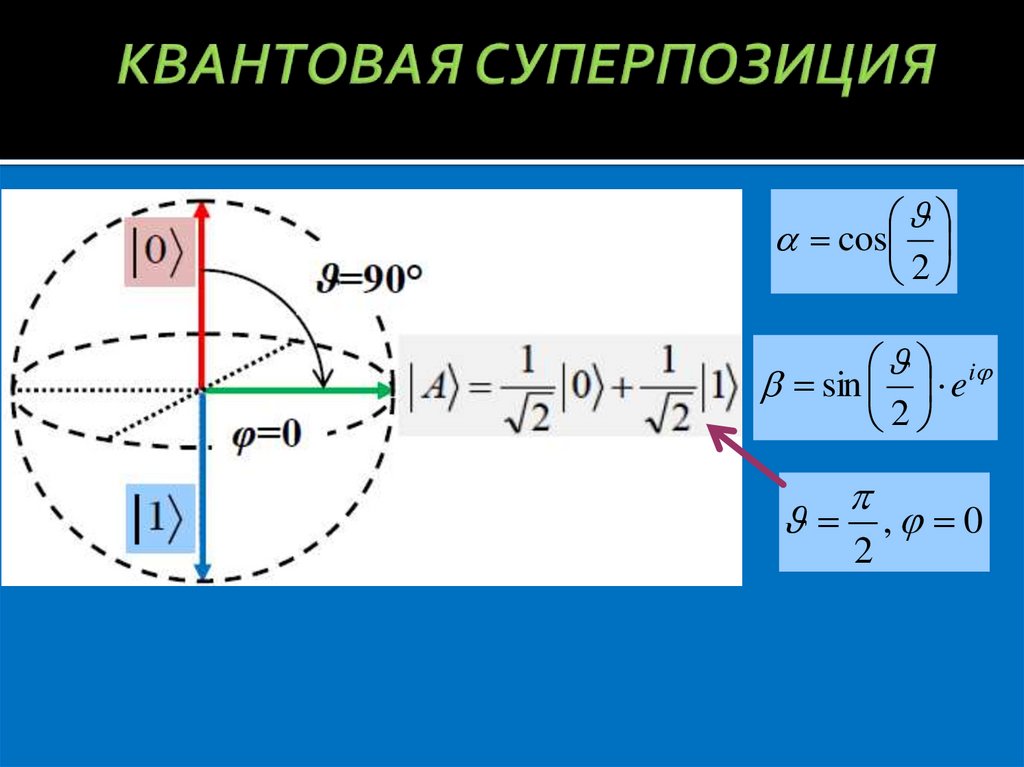
8. КВАНТОВАЯ СУПЕРПОЗИЦИЯ

cos
2
i
sin e
2
2
, 0

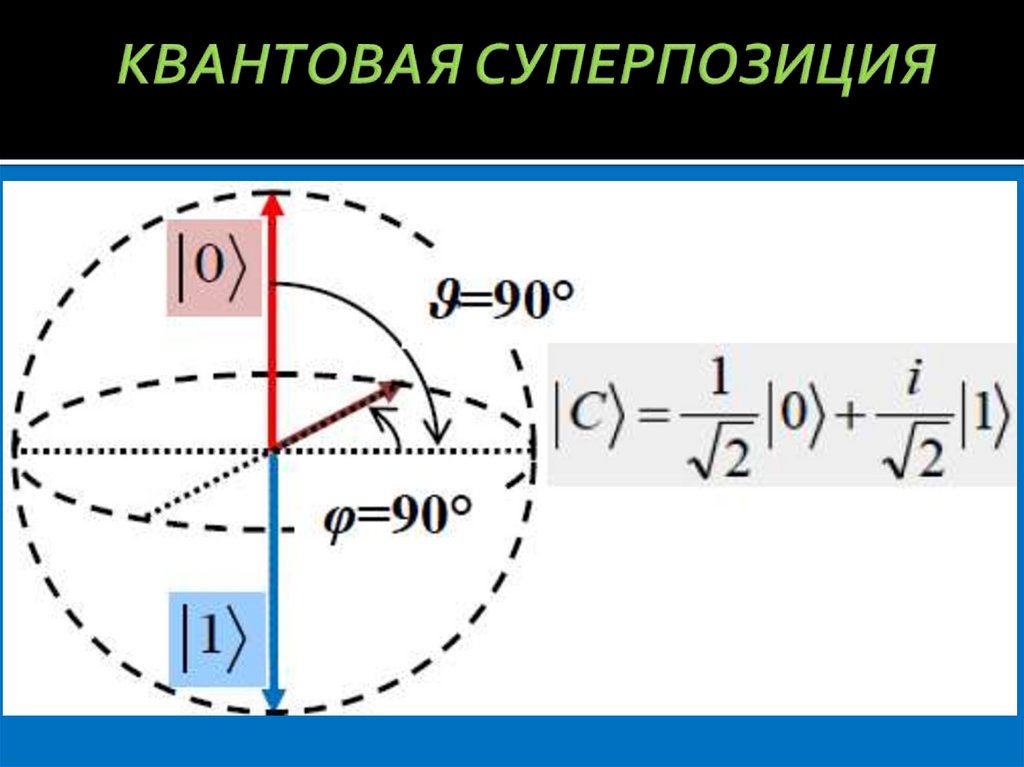
9. КВАНТОВАЯ СУПЕРПОЗИЦИЯ

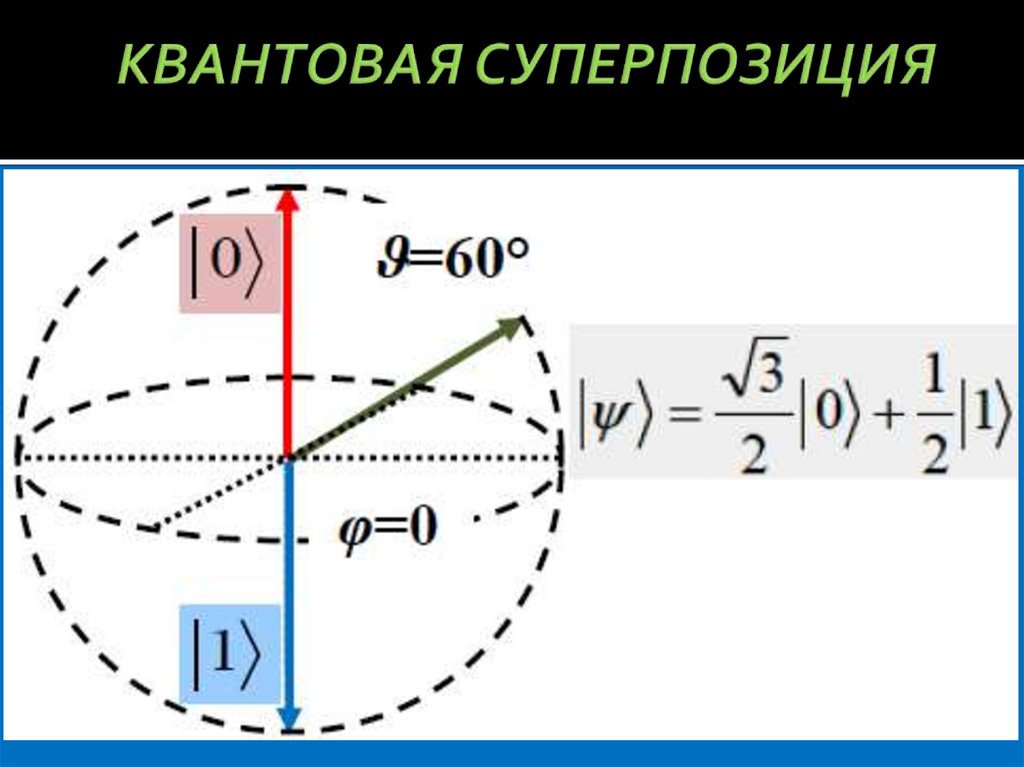
10. КВАНТОВАЯ СУПЕРПОЗИЦИЯ

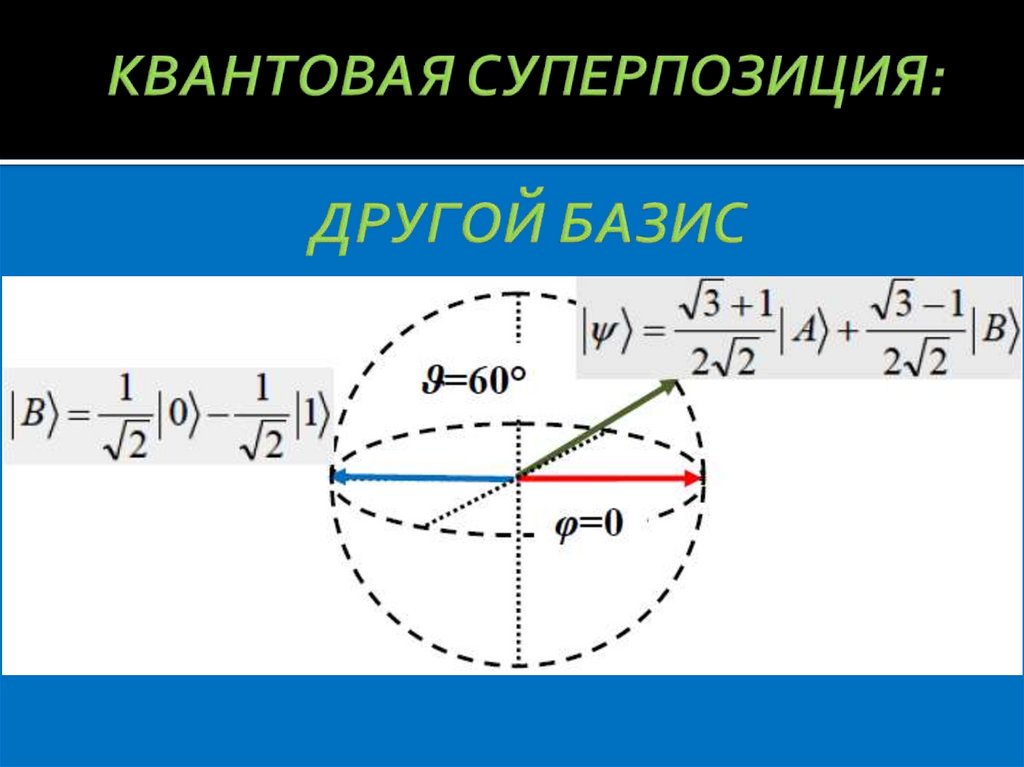
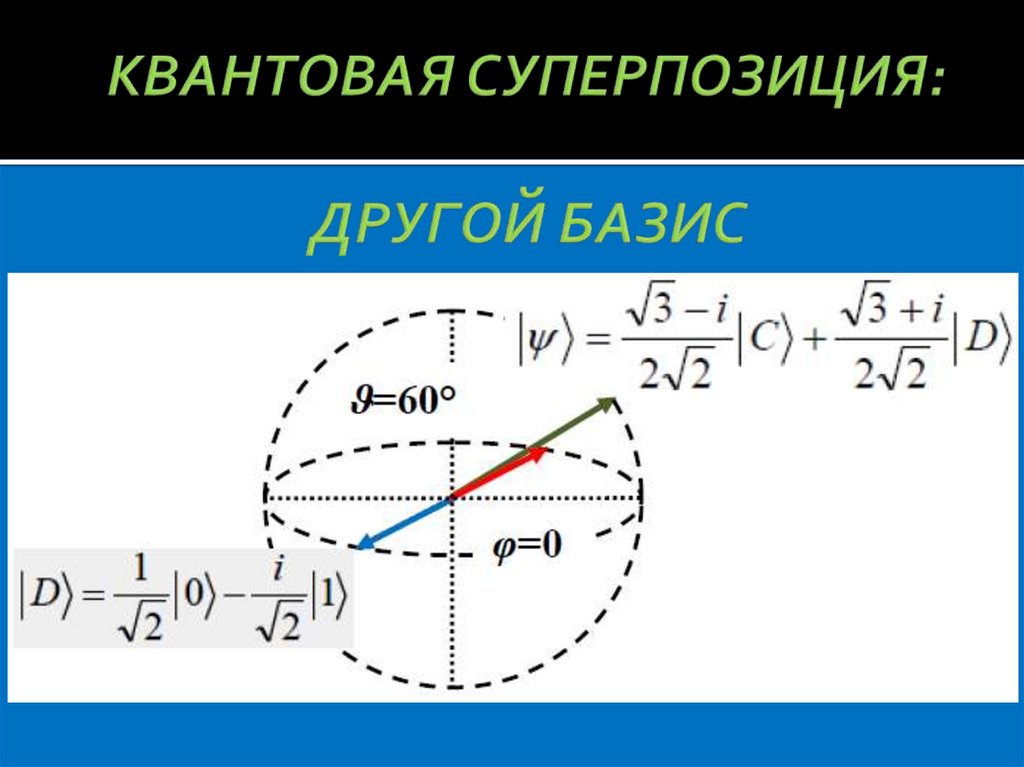
11. КВАНТОВАЯ СУПЕРПОЗИЦИЯ: ДРУГОЙ БАЗИС

12. КВАНТОВАЯ СУПЕРПОЗИЦИЯ: ДРУГОЙ БАЗИС

2
3 1
1
3
wA
0,933
2
4
2 2
2
3 1
1
3
wB
0,067
2
4
2 2

13. КВАНТОВАЯ СУПЕРПОЗИЦИЯ: ДРУГОЙ БАЗИС

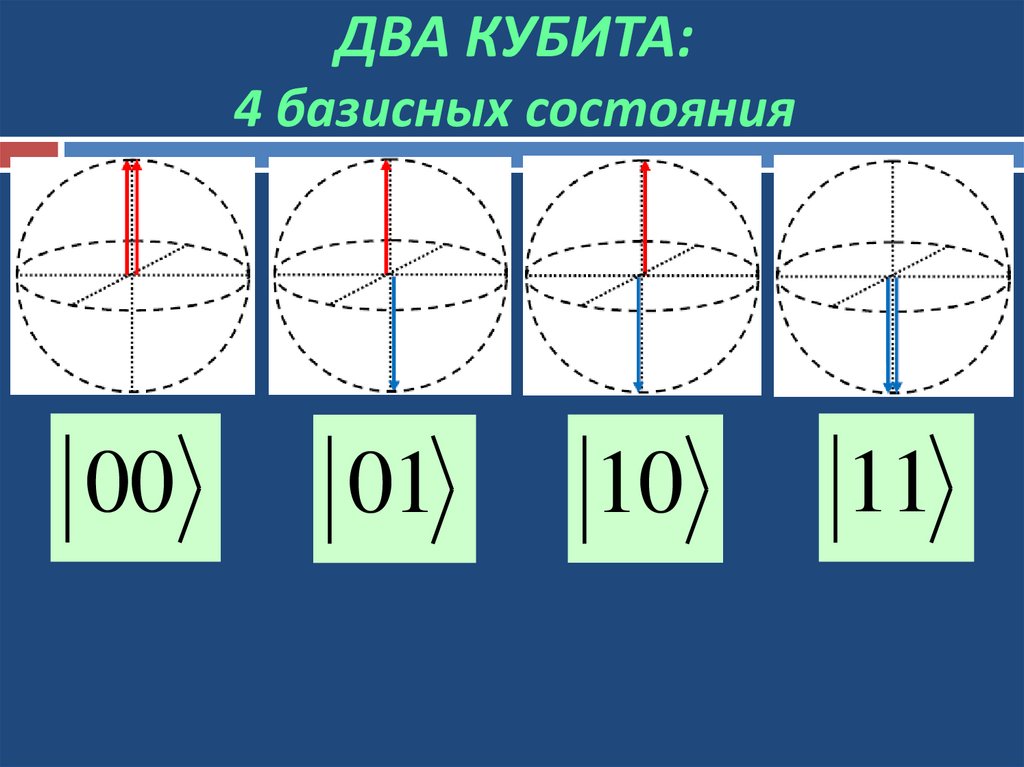
14. ДВА КУБИТА: 4 базисных состояния

00
01
10
11

15. ДВА КУБИТА: ПРОИЗВОЛЬНОЕ СОСТОЯНИЕ

00 10 01 11
N КУБИТ:
2N БАЗИСНЫХ СОСТОЯНИЙ

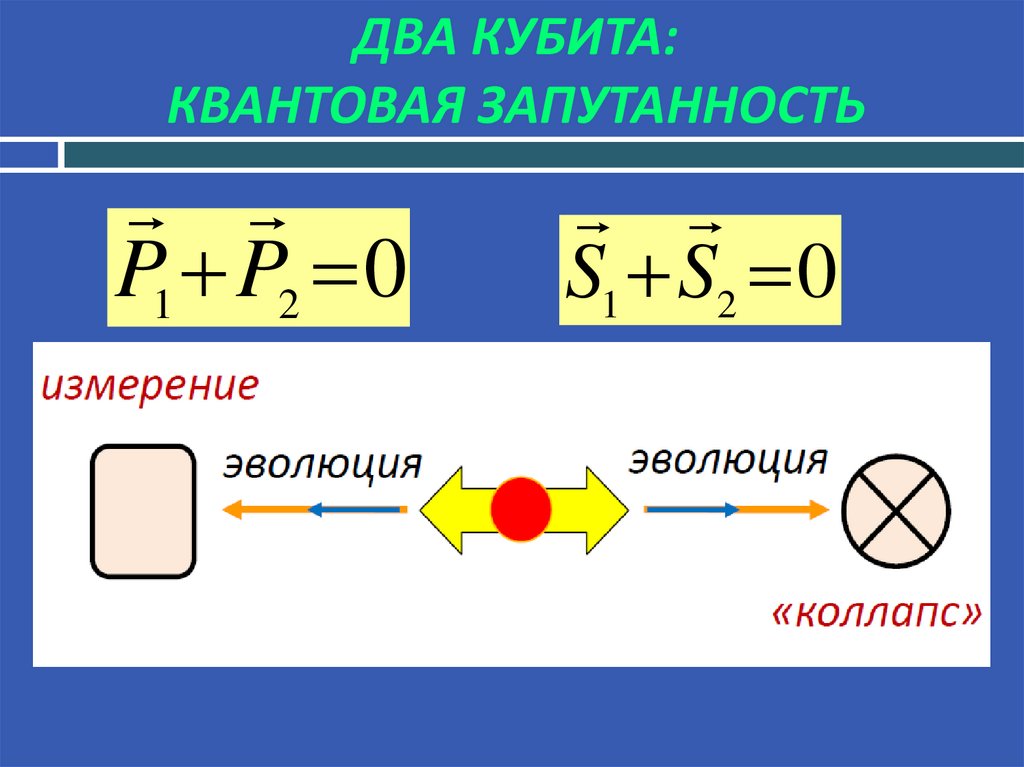
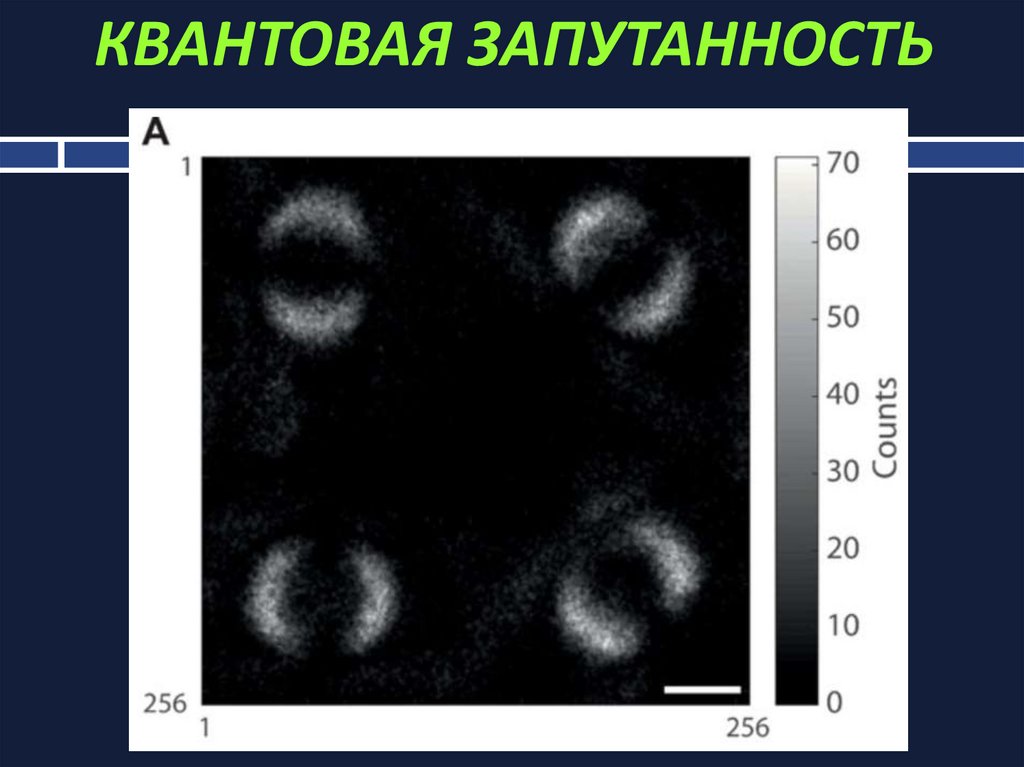
16. ДВА КУБИТА: КВАНТОВАЯ ЗАПУТАННОСТЬ

P1 P2 0
S1 S2 0

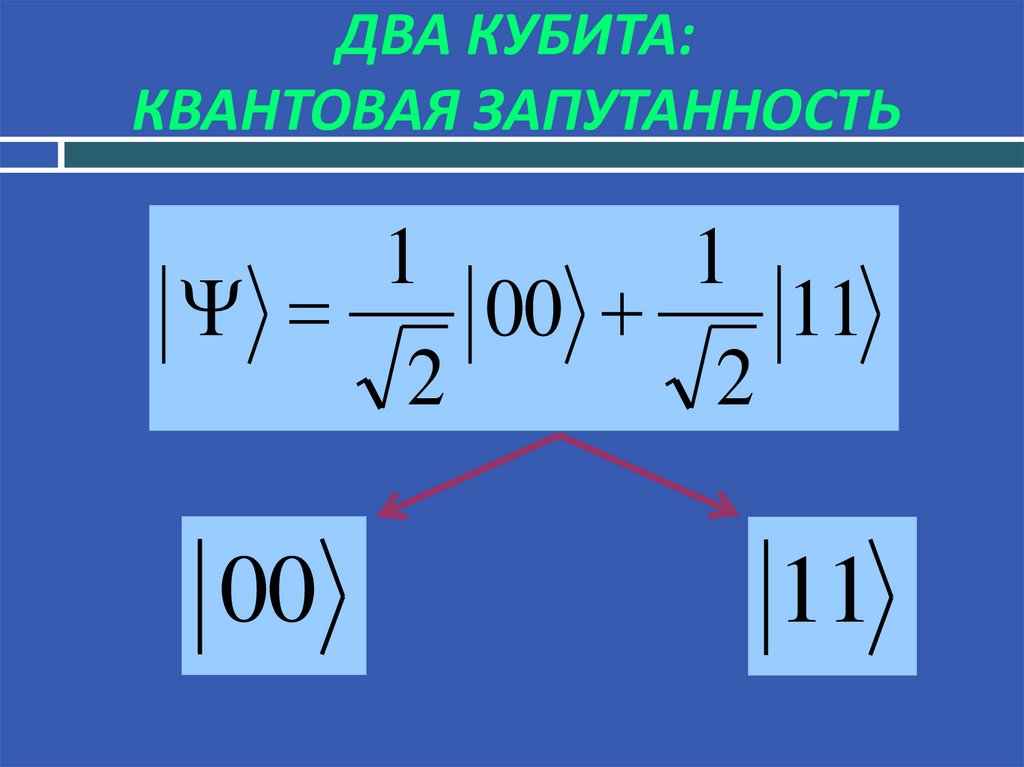
17. ДВА КУБИТА: КВАНТОВАЯ ЗАПУТАННОСТЬ

1
1
00
11
2
2
00
11

18. КВАНТОВАЯ ЗАПУТАННОСТЬ

19. ПЛОТНОЕ КОДИРОВАНИЕ: ДВА БИТА ОДНИМ КУБИТОМ

А и В приготовили пару
запутанных кубит и поделили ее
1
1
I
00
11
2
2

20.

А ВОЗДЕЙСТВУЕТ на свой
кубит и ПЕРЕСЫЛАЕТ его В:
1
1
I
00
11
2
2
1
1
II
10
01
2
2
1
1
III
10
01
2
2
1
1
IV
00
11
2
2

21.

В ИЗМЕРЯЕТ пару кубит
в базисе
I IV
И ПОЛУЧАЕТ два бита
информации!

22. КВАНТОВАЯ ТЕЛЕПОРТАЦИЯ

23. КВАНТОВАЯ ТЕЛЕПОРТАЦИЯ

0 1
I
2
000
2
1
1
I
00
11
2
2
011
2
100
2
111
1
1
I I ( 0 1 ) II ( 0 1 )
2
2
1
1
III ( 0 1 ) IV ( 0 1 )
2
2

24.

А ИЗМЕРЯЕТ пару кубит
в базисе I-IV
I
B 0 1
II
B 0 1
III
B 0 1
IV
B 0 1

25. КВАНТОВАЯ ТЕЛЕПОРТАЦИЯ

Получив сообщение А, В
ЗНАЕТ , что делать, чтобы
получить
0 1

26. СПАСИБО ЗА ВНИМАНИЕ!