Похожие презентации:
Неопределенность измерений
1. Неопределенность измерений Вернидуб Ольга Дмитриевна Руководитель Экспертной организации по аккредитации испытательных
лабораторийФГУП ЦНИИчермет им. И.П.Бардина,
(тел./факс (495) 777-93-83, 777-93-86
e-mail: metaltest@chermet.net
2. ГОСТ ИСО /МЭК17025-2009 п.5.4.6 - Оценка неопределенности измерений
Лаборатории, аккредитованные поГОСТ ИСО/МЭК 17025-2009, обязаны
оценивать неопределенность
измерений в выполняемых ими
измерениях и испытаниях, и при
необходимости указывать ее.
3. ГОСТ ИСО/МЭК 17025-2009 ГОСТ Р ИСО 5725-(1-6)-2002
п.5.4.5 - Оценка пригодностиметодов
------------------------------------------- п.5.4.6 - Оценка неопреде-
ленности измерений
5.6 - Прослеживаемость
измерений
5.9 - Обеспечение качества
результатов испытаний
----------------------------------------- 5.9 b) Участие в межлабораторных испытаниях
Оценка качества применения
лабораторией методов измерений, соблюдение стандартизованных процедур
выполнения измерений
5725-1, р7 5725-4, р.5
5725-6, р.7, п.7.1, 7.2
------------------------------------------ Соответствие применения
процедур контроля
показателей точности
результатов измерений
5725-6, р.6, р.7 п.7.3
------------------------------------------ Межлабораторные
сравнительные испытания
5725-1, п.п.4.2.1, 5725-6, р.7,
п.п.7.1, 7.2.4, 7.3.4
4. 5. Технические требования методы испытаний и оценка метода (5.4)
5.4.6 Оценка неопределенности измеренийЛаборатории должны иметь и применять
процедуры оценки неопределенности
измерений, идентификации ее
составляющих в лаборатории
Степень необходимой тщательности при
оценке неопределенности измерений
(результатов) зависит от:
-требования метода испытаний,
-требования заказчика,
-наличия узких пределов, на которых
основывается решение о соответствии НД
5. Зачем следует уметь оценивать неопределенность результатов?
Без количественной оценкинеопределенности невозможно решить
-превышает ли наблюдаемое расхождение
между результатами изменчивость,
обусловленную экспериментом;
-соответствуют ли объекты
испытаний требованиям
технических условий;
- не нарушены ли законы, связанные с
предельными нормами
6. К чему может привести неправильная интерпретация результатов?
- к ненужным затратам впроизводстве;
- неправильным судебным
преследованиям;
- отразиться на здоровье населения
и вызвать неблагоприятные
социальные последствия
7.
-Руководство по выражениюнеопределенности измерения
Guide to the Expression of Uncertainty in
Measurement, 1993
РМГ 43-2001
-Государственная система обеспечения
единства измерений Применение
«Руководства по выражению
неопределенности измерений»
-EUROCHEM/CITAC Guide “Quantifying
Uncertainty in Analytical Measurements”,Second
Ed., 2000
Перевод. Руководство ЕВРАХИМ/СИТАК
«Количественное описание
неопределенности в аналитических
измерениях» Второе изд.Санкт-Петерб. 2002
8.
ISO/TS 21748-2004 (Rus) Руководство поприменению оценок повторяемости,
воспроизводимости и правильноти при
оценивании неопределенности измерения
Р 50.1.060-2006 Статистические методы.
Руководство по использованию оценок
повторяемости, воспроизводимости и
правильности при оценке
неопределенности измерений (отменен!!!)
9.
ГОСТ Р 54500.1-2011/Руководство ИСО/МЭК 98-1:2009Неопределенность измерения
Часть 1
Введение в руководства по неопределенности измерения
ISO/IEC Guide 98-1:2009
Uncertainty of measurement – Part 1: Introduction to the expression of uncertainty in
measurement
(IDT)
ГОСТ Р 54500.3-2011/Руководство ИСО/МЭК 98-3:2009
Неопределенность измерения
Часть 3
Руководство выражению неопределенности измерения
ISO/IEC Guide 98-3:2008
Uncertainty of measurement – Part 3: Guide to the expression of uncertainty in
measurement
(IDT)
10. ГОСТ Р 54500.1-2011/Руководство ИСО/МЭК 98-1:2009
Настоящий документ служит введением в концепциюнеопределенности измерения.
Цель разработки ГОСТа – продвижение идей оценивания
неопределенности измерений, изложенных в «Руководстве
по выражению неопределенности измерения» ( GUM).
ГОСТ распространяется на следующие сферы
деятельности:
наука;
промышленность;
деятельность калибровочных и испытательных
лабораторий ( в т.ч. в сферах здравоохранения,
безопасности, охраны окружающей среды);
деятельность органов по аккредитации, а также
органов контроля, надзора и оценки соответствия
11. ГОСТ Р 54500.1-2011/Руководство ИСО/МЭК 98-1:2009
Настоящий стандарт может быть использован--при проектировании изделий и материалов,
поскольку установление характеристик с учетом
требований к контролю и связанными с ними
измерениями позволит избежать завышенных
технологических требований при их
производстве;
-- в сфере высшего образования, т.к. позволит
включать в программы по различным
дисциплинам разделы по неопределенности
измерений, что позволит подготовить
специалистов к восприятию концепции
неопределенности измерения и применению ее в
различных измерительных задачах
12. ГОСТ Р 54500.3-2011/Руководство ИСО/МЭК 98-3:2008
Руководство ИСО/МЭК 98-3:2008 устанавливаетобщие правила и представления
неопределенности применительно к широкому
спектру измерений
Цель данного руководства
-обеспечение представления полной информации
о том, как получены утверждения о
неопределенности измерений;
-создание основы для международного
сопоставления результатов измерений.
13. ГОСТ Р 54500.3-2011/Руководство ИСО/МЭК 98-3:2008
14. ГОСТ Р 54500.3-2011/Руководство ИСО/МЭК 98-3:2008
В стандарте приведены:- Термины и определения;
- Основные понятия;
- Оценивание стандартной неопределенности;
- Определение суммарной стандартной
неопределенности;
- Определение расширенной неопределенночти;
- Представление результатов оценивания
неопределенности;
- Краткое описание процедуры оценивания и
представления неопределенности
В Приложениях даны
основные метрологические термины и понятия
математической сьаьтсьткт, практические рекомендации
по оцениванию составляющих неопределенности, примеры
и т.д.
15. 5. Технические требования методы испытаний и оценка метода (5.4) 5.4.6 Оценка неопределенности измерений
При оценке неопределенностиизмерений все составляющие
неопределенности, являющиеся
существенными в данной ситуации,
должны быть приняты во внимание:
-исходные эталоны и СО
-применяемые методы и СИ
-окружающая среда;
-свойства и состояние объекта
испытаний;
-оператор и пр.
16. В каких случаях лаборатория должна приводить сведения о неопределенности в протоколах испытаний?
-По требованию заказчика-При возможности неправильной
интерпретации результата из-за
отсутствия сведений о
неопределенности,
-При увелечении неопределенности по
сравнению с рассчитанной по данным,
приведенным в методике
17. Неопределенность и погрешность результатов. В чем различие?
18.
РМГ 91-2009Рекомендации по межгосударственной
стандартизации
Государственная система обеспечения единства
измерений
Совместное использование понятий
«погрешность измерения» и «неопределенность
измерения». Общие принципы
Настоящие рекомендации содержат основные принципы
совместного применения понятий «погрешность измерения» и
«неопределенность измерения»…., рекомендуемые при разработке
нормативных документов по различным метрологическим задачам.
Положения , содержащиеся в данном документе,
рекомендуется применять в документах всех видов, научнотехнической, учебной и справочной литературе по метрологии,
входящих в сферу работ по стандартизации или использующих
результаты этих работ
19. Погрешность
«Классическое» определениепогрешности:
Погрешность (d)– отклонение
результата измерения (X) от
истинного значения измеряемой
величины (m)
d =X-m
Погрешность возникает из-за несовершенства процесса
измерения. Хотя погрешность не может быть точна
известна , это понятие удобно использовать для
статистического описания процесса измерения.
20. РМГ 91-2009 Совместное использование понятий «погрешность измерения» и «неопределенность измерения»
Относительная погрешностьотношение погрешности
измерения к опорному значению
измеряемой величины:
d/m
21. РМГ 91-2009 Совместное использование понятий «погрешность измерения» и «неопределенность измерения»
Случайная погрешность измерения:Составляющая погрешности измерения, которая в
повторных измерениях изменяется непредсказуемым
образом
Примечание 1
Опорным значением величины для случайной погрешности измерения
является среднее значение, получаемое в результате бесконечного
числа повторных измерений одной и той же измеряемой величины
Примечание 2.
Случайная погрешность измерения ряда повторных измерений образует
распределение, которое может быть подытожено его математическим
ожиданием, обычно предполагаемым равным нулю, и его дисперсией
Примечание 3
Случайная погрешность измерения – погрешность измерения минус
систематическая погрешность измерения
22. РМГ 91-2009 Совместное использование понятий «погрешность измерения» и «неопределенность измерения»
Систематическая погрешностьизмерения:
Составляющая погрешности измерения, которая в
повторных измерениях остается постоянной или
изменяется предсказуемым образом
Примечание 1
Опорным значением величины для систематической погрешности измерения
является истинное значение величины или измеренное значение величины
эталона с незначительной неопределенностью измерения, или
приписанное(стандартизованное) значение величины
Примечание 2.
Систематическая погрешность измерения и ее причины могут быть известны
или неизвестны. Поправка может быть применена для компенсации известной
систематической погрешности измерения
Примечание 3
Систематическая погрешность измерения равна погрешности измерения минус
случайная погрешность измерения
23. Неопределенность ( uncertainty)
Неопределенность измерений – параметр,связанный с результатом измерений и
характеризующий рассеяние значений,
которые могли бы быть обоснованно
приписаны измеряемой величине
(Предполагается нормальное распределение результатов
измерений. При этом рассматриваются симметричные
распределения результатов измерений и стандартные
отклонения, характеризующие случайные и невыявленные
погрешности измерений, оцененные разными способами)
24. РМГ 91-2009 Совместное использование понятий «погрешность измерения» и «неопределенность измерения»
Неопределенность измерения :Неотрицательный параметр,
характеризующий разброс значений
величины, приписываемых
измеряемой величине на основе
имеющейся информации
25. Неопределённость -
Неопределённость Параметр, связанный с результатом измерений ихарактеризующий рассеяние значений, которые можно
приписать измеряемой величине (дисперсия, СКО или
стандартная неопределенность, ½ интервала, имеющего
указанный уровень доверия).
Результат измерений может быть близок к
истинному значению (т.е. минимальную
погрешность после введения поправки), но
иметь большую неопределенность.
26. «Неопределенность измерения» и «погрешность измерения» - в каких случаях корректно применение этих понятий
«Неопределенность измерения» и «погрешностьизмерения» в каких случаях корректно применение этих понятий
В аттестованных методиках измерений (МВИ) устанавливают
совокупность операций и правил, выполнение которых
обеспечивает получение результата измерения с
погрешностью, не превышающей допускаемых пределов (норм
погрешности измерений). В таких МВИ рекомендуется
использовать понятие «погрешность» в виде нормативных
пределов погрешностей. Результаты измерения по этим МВИ
не требуется сопровождать конкретной характеристикой
точности.
Результаты измерения по МВИ, характеристики точности
которых определяют в процессе или после их
применения, рекомендуется сопровождать оценками
неопределенности измерения. Оснований для
оперирования погрешностью в таких случаях нет.
27. «Неопределенность измерения» и «погрешность измерения» - в каких случаях корректно применение этих понятий
«Неопределенность измерения» и «погрешностьизмерения» в каких случаях корректно применение этих понятий
Общее правило применения этих
понятий:
Результаты измерений в
большинстве метрологических
ситуаций характеризуются
неопределенностью,
а нормативы точности средств
измерений, измерительных и
контрольных процедур
характеризуются погрешностью
28. Смысловое различие между показателями точности по ИСО 5725 и неопределенностью измерений
Неопределенность измерения характеризуетиндивидуальные результаты.
Повторяемость, воспроизводимость и
систематическая погрешность, напротив,
характеризуют процесс измерений или испытаний
(Под процессом измерения или испытания, изучаемым в
соответствии с ИСО 5725, понимается единый метод
измерения, используемый всеми лабораториями,
принимающими участие в исследовании).
29. Неопределенность ( uncertainty)
Неопределенность измерений – параметр,связанный с результатом измерений и
характеризующий рассеяние значений, которые
могли бы быть обоснованно приписаны измеряемой
величине
(Предполагается нормальное распределение результатов
измерений. При этом рассматриваются симметричные
распределения результатов измерений и стандартные
отклонения, характеризующие случайные и невыявленные
погрешности измерений, оцененные разными способами)
30. Эффекты, которые порождают неопределенность измерений, могут быть следующие:
• случайные – там где повторение измеренийслучайно дает различный результат.
( Если можно получить больше результатов и затем
вычислить среднее, то можно ожидать лучшую оценку )
• систематические – там, где при повторение
измерений на результат измерения оказывает
влияние один и тот же эффект (но это
невозможно подсчитать).
(В этом случае вы ничего не узнаете дополнительно
повторением измерений. Необходимо применить другой
метод для оценки неопределенности, связанной с
систематическим эффектом (влиянием) или другое
измерение или вычисление.
31. Неопределенность результата измерения
Неопределенность результатаизмерения отражает отсутствие
точного знания значения измеряемой
величины. Результат измерения
после внесения поправки на
известные систематические
эффекты все еще является только
оценкой значения измеряемой
величины вследствие
неопределенности, возникающей изза случайных эффектов и неточной
поправки результата на
систематические эффекты
32. На практике существует много возможных источников неопределенности при измерениях:
a) неполное определение измеряемой величины;b) несовершенная реализация определения измеряемой величины;
c) нерепрезентативная выборка – измеренный образец может не
представлять определяемую измеряемую величину;
d) неадекватное знание эффектов от условий окружающей среды,
влияющих на измерение, или несовершенное измерение условий
окружающей среды;
e) субъективная систематическая погрешность оператора при
снятии показаний аналоговых приборов;
f) конечное разрешающая способность прибора или порог
чувствительности;
g) неточные значения, приписанные эталона, используемым для
измерения, и стандартным образцам веществ и материалов;
h) неточные значения констант и других параметров, полученных
из внешних источников и с используемых в алгоритме обработки
данных;
i) аппроксимация и предположения, используемые в методе
измерения и измерительной аппаратуре;
j) изменения в повторных наблюдениях измеряемой величины при
явно одинаковых условиях
(Эти источники не обязательно являются независимыми и
некоторые из них от a до i могут вносить вклад в источник j.)
33. Бюджет неопределенности
Список источниковнеопределенности и их
стандартные неопределенности,
представленные в удобном для
оценивания суммарной
стандартной неопределенности
результата измерений.
34. Неопределенность ( uncertainty)
Обычный путьколичественной оценки
диапазона (разброса) –
стандартное отклонение.
Стандартное
отклонение выборки
измерений –
число (цифра), которое
говорит нам насколько
индивидуальный
(отдельный) замер
отличается от
среднего значения
выборки измерений
S
N
2
Xi X
i 1
N 1
)
35. Неопределенность ( uncertainty)
Истинное значениестандартного отклонения
может быть найдено (оценено)
только из очень большого числа
результатов. Из умеренного
(среднего) числа значений может
быть проведена только оценка
его значения. Символ S обычно
используется только для оценки
стандартного отклонения .
36. Неопределенность ( uncertainty)
Что бы количественно выразитьнеопределенность необходимо иметь
два числа:
Одно из них – ширина диапазона или
интервал.
Другое - уровень доверия, который
показывает, насколько мы уверены в
том, что "реальное значение"
находится в этом пределе
37. Стандартная неопределенность
Для получения стандартнойнеопределенности все входящие в нее
неопределенности должны быть выражены
для одного и того же уровня вероятности
(доверия) .
Стандартная неопределенность
представляет собой диапазон, размеры
которого могут быть определены как ‘плюс
или минус одно стандартное отклонение ’.
Стандартная неопределенность говорит нам
о неопределенности среднего (не только о
размахе значений).
Стандартная неопределенность обычно
обозначается символом u
(маленькое u),
или u(y) (стандартная неопределенность y).
38. Стандартная неопределенность
Стандартная неопределенность (u) дляединичного результата измерений Хi
выражается в виде квадратического
отклонения S = U(Xi)
u ( Xi )
N
2
Xi X
i 1
N 1
)
39. Суммарная стандартная неопределенность (применительно к КХА)
Суммарная стандартная неопределенность (Uc):Стандартная неопределенность результата измерений,
полученного через значения других величин, равна
положительному квадратному корню суммы
Uc(X) = √u2 + u2(δ) + ∑ c2u2(zi)2
u2(δ) – величина, учитывающая неточность аттестации
стандартных образцов, равна
- где ∆ - полуширина интервала, в котором
лежит принятое опорное
3
значение
∑ c2u2(zi)2 – вклад матричных эффектов ( мал, в отечественной литературе
не рассматривается)
40. Расширенная неопределенность
Расширенная неопределенность (U)– Величина, определяющая интервал
вокруг результата измерений, в пределах
которого, как можно ожидать, находится
большая часть распределения значений,
которые с достаточным основанием
могли бы быть приписаны измеряемой
величине.
U = kuc
k-коэффициент охвата, равный значению коэффициента
Стъюдента для νэфф степеней свободы, которое определяется
как
n
эфф . u (Y ) / ci4 u 4 ( x i ) / i
4
c
i
где , vi – число степеней свободы для каждой измеряемой
величины Хi ,определяется как ni-1
41. Два пути (способа) оценки неопределенности
Не зависимо от источника неопределенности измерения, естьдва подхода к оценке: "Тип А" и "Тип B". В большинстве
случаев необходимо использовать оба типа.
Тип А - неопределенность оценивают, используя статистику
(обычно из многократных измерений)
(Стандартная неопределенность по типу А является
фактически статистической оценкой дисперсии S2, т.е. u = S)
Тип B - неопределенность оценивается из любых других
источников (информации, сведений). Это может быть
информация из информация (сведения) из прошлого опыта
измерений, из сертификатов калибровки, спецификаций
производителей, из вычислений и расчетов, из
опубликованных сведений (информации), и из здравого
смысла.
Существует соблазн считать, что ‘Тип A’ определяют
случайные причины, а ‘Тип B’ – систематические, но это не
всегда верно.
42. Неопределенность ( uncertainty) Стандартная неопределенность
Тип А-Определяется статистическидисперсия закона распределения
многократных результатов
измерения
Тип В –
Определяется с использованием
других способов
43. Два способа оценки неопределенности
Целью классификации на Тип А и Тип В являетсядемонстрация двух различных способов оценки
составляющих неопределенности,
-используется только для удобства обсуждения;
-она не предназначена для показа того факта, что
существует какое-либо различие в природе
этих составляющих, являющихся результатом
этих двух типов вычисления.
-Оба типа оценивания основаны на
распределениях вероятностей и составляющие
неопределенности, являющиеся результатом
использования каждого типа, определяются
количественно дисперсией или стандартным
отклонением.
44. Восемь основных шагов оценки неопределенности
1. Решить, что вы хотите получить от ваших измерений икакие действительно необходимы измерения и вычисления для
получения окончательного результата.
2. Провести необходимые измерения.
3. Оценить неопределенность каждого количественного
результата, входящего в окончательный результат.
Выразить все неопределенности в общих терминах.
4. Решить, зависят ли погрешности входящих измерений друг
от друга. Если нет, то определите, какие дополнительные
вычисления или информация (сведения) необходимы.
5. Рассчитайте результаты измерений (включая все, что
известно о поправках, например, из калибровки).
6. Найдите суммарные стандартные неопределенности для
всех отдельных аспектов.
7. Выразите неопределенность, используя коэффициент
охвата для установления интервала неопределенности при
определенном (установленном) уровне вероятности
8. Запишите результаты измерений и неопределенность,
указав е точно, как вы их получили
45. Стандартная неопределенность Тип А
Стандартная неопределенность (u)- длясреднего значения результатов
измерений, полученного из N измерений,
выражается в виде среднего
квадратического отклонения, деленного
на число измерений U(Xср) /√N =
u(
X)
N
2
Xi X
i 1
N ( N 1)
)
46. Расширенная неопределенность
Расширенная неопределенность (U)– Величина, определяющая интервал
вокруг результата измерений, в
пределах которого, как можно
ожидать, находится большая часть
распределения значений, которые с
достаточным основанием могли бы
быть приписаны измеряемой
величине.
U = kuc
K – коэффициент охвата
47. Стандартная неопределенность Тип B
Исходные данные :-данные предшествовавших измерений;
-данные основанные на опыте
исследователя или общих знаний о
поведении и свойствах приборов и
материалов;
-неопределенность констант или
справочных данных;
-данные поверки, калибровки, сведения
изготовителя о приборе и пр.
48. Вычисление стандартной неопределенности
В большинстве случаев измеряемаявеличина Y не является прямо
измеряемой, а зависит от N других
измеряемых величин Х1, Х2, Х3……ХN через
функциональную зависимость:
У = f(Х1, Х2, Х3……ХN )
В этом случае стандартная суммарная
неопределенность равна квадратному
корню из выражения
f 2 2
uc (Y ) ( ) u ( xi )
i 1 xi
2
N
49.
Если соотношение между измеряемойвеличиной Y, и A, B и C для общего случая
выражено как Y = f(A,B,C), то
f
f
f
uc y ) u(a ) u(b) u(c)
a
b
c
2
2
2
где u(a), u(b) and u(c) – стандартные
неопределенности для величин a, b и c
соответственно, полученные по Типу A или Типу B
коэффициенты чувствительности,
f
f
f
a
b
c
показывающие как выходная оценка Y меняется с
изменением значений выходных оценок A, B, C
50. Вычисление стандартной неопределенности
При определении физикомеханических характеристик, такихкак , предел прочности при
испытании на растяжение -σв ,
определяется как
σв = F/T*W, где
- F - сила разрыва,
-T, W - толщина и ширина поперечного
сечения образца, каждые из которых
определяются с соответствующей
неопределенностью, иными словами
Y = f ( F, T, W)= F/T*W
51.
Y = f ( F, T, W)= F/T*WДля приведенного выше примера коэффициенты чувствительности
сi=∂f/∂Xi будут равны
Если , например, среднеквадратичные отклонения для величин T, W и F,
являются известными стандартными неопределенностями, то
суммарная стандартная неопределенность uc ,будет равна:
При измеренном значении σв , например, равным 13600 (psi),
конечный результат будет иметь следующий вид с учетом
расширенной неопределенности ( k=2) и округления :
13600±1600 (psi). .
52.
Пример оценки неопределенностиДано:
масса, m, проволоки 2.255 g со стандартной
неопределенностью 0.032 g.
Длина, l, проволоки 0.2365 m со стандартной
неопределенностью 0.0035 m.
m
Отношение массы к единице длины , m, составляет
m
l
Оценить стандартную неопределенность m
m
2.255
m
9.535 g/m
l
0.2365
53.
mm
l
Продолжение примера
m
m
u m )
u( m ) u(l )
m
l
m 1
1
-1
2
2
2
c
4.2283 m
m l 0.2365
m
m
2.255
2
2
40
.
317
g/m
l
l
0.2365 2
u m ) 4.2283 0.032) 40.317 0.0035)
2
c
2
uc m ) 0.1955 g/m
2
54. Как оценивать неопределенность?
В Руководстве (EUROCHEM/CITAC Guide “QuantifyingUncertainty in Analytical Measurements”,Second Ed., 2000
Пер. Руководство ЕВРАХИМ/СИТАК «Количественное описание
неопределенности в аналитических измерениях» Второе изд.СанктПетерб. 2002) подробно разъяснены способы оценки
неопределенности.
Но.....согласно ему необходимо теоретически или
экспериментально оценить все составляющие
неопределенности и просуммировать их по определенным
правилам, т.е. неопределенность рассчитывается как
сумма неопределенности всех этапов
выполнения измерений
55. На практике существует много возможных источников неопределенности при измерениях:
a) неполное определение измеряемой величины;b) несовершенная реализация определения измеряемой величины;
c) нерепрезентативная выборка – измеренный образец может не
представлять определяемую измеряемую величину;
d) неадекватное знание эффектов от условий окружающей среды,
влияющих на измерение, или несовершенное измерение условий
окружающей среды;
e) субъективная систематическая погрешность оператора при
снятии показаний аналоговых приборов;
f) конечное разрешающая способность прибора или порог
чувствительности;
g) неточные значения, приписанные эталона, используемым для
измерения, и стандартным образцам веществ и материалов;
h) неточные значения констант и других параметров, полученных
из внешних источников и с используемых в алгоритме обработки
данных;
i) аппроксимация и предположения, используемые в методе
измерения и измерительной аппаратуре;
j) изменения в повторных наблюдениях измеряемой величины при
явно одинаковых условиях
(Эти источники не обязательно являются независимыми и
некоторые из них от a до i могут вносить вклад в источник j.)
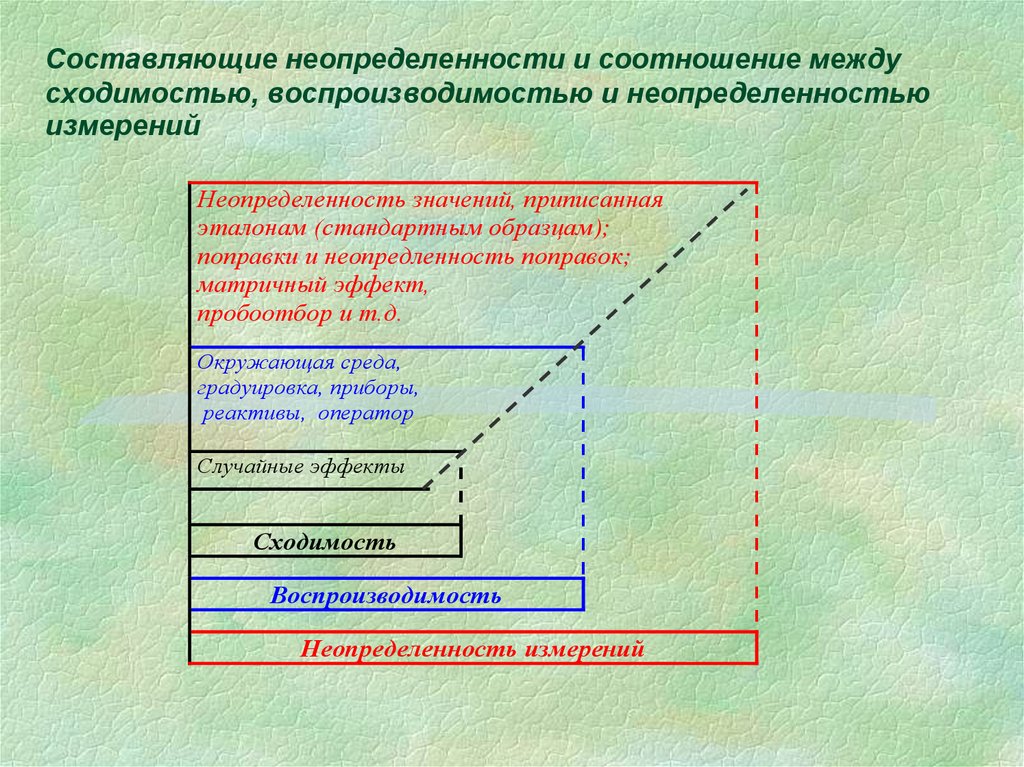
56. Составляющие неопределенности и соотношение между сходимостью, воспроизводимостью и неопределенностью измерений
Неопределенность значений, приписаннаяэталонам (стандартным образцам);
поправки и неопредленность поправок;
матричный эффект,
пробоотбор и т.д.
Окружающая среда,
градуировка, приборы,
реактивы, оператор
Случайные эффекты
Сходимость
Воспроизводимость
Неопределенность измерений
57. Как оценивать неопределенность?
Для рутинных измерений способоценки неопределенности,
предложенный в Руководстве,
малопригоден из-за отсутствия
полной модели процесса
измерений. Кроме того, обычно в
ходе аттестации методик или их
стандартизации проведена
оценка метрологических
характеристик
58. ISO/TC 21748-2004 Р 50.1.060-2006 (ОТМЕНЕН!!!)
Все характеристики процесса , полученные врезультате изучения методики,
приписываются всем индивидуальным
результатам измерений
Различия между индивидуальными объектами
испытаний следует учитывать, но для
хорошо описанного и стабильного
измерительного процесса нет
необходимости проводить детальное
исследование неопределенности для каждого
объекта испытаний
59. ISO/TC 21748-2004 Р 50.1.060-2006 (ОТМЕНЕН!!!)
Основой для оцениваниянеопределенности измерений
является стандартное отклонение
воспроизводимости
Эффекты, не изучаемые в процессе
совместных исследований должны
либо признаваться незначительными,
либо наоборот, учитываться в явном
виде.
60. Как оценивать неопределенность?
1. Получить (или использоватьустановленные ранее при
аттестации или
стандартизации МВИ) оценки
повторяемости,
воспроизводимости и
правильности
( ГОСТ Р ИСО 5725)
61. Как оценивать неопределенность?
2. Установить, не выходит лилабораторная составляющая
систематической погрешности за
ожидаемые пределы, основанные на
оценке правильности
3. Установить, не выходит ли
прецизионность, полученная в
результате текущих измерений (или
по результатам ВЛК), в ожидаемых
пределах, базирующих на оценках
повторяемости и воспроизводимости
62. Как оценивать неопределенность?
4. Идентифицировать всевозможные влияния, которые не
были адекватно учтены на
стадии аттестации методики и
количественно оценить степень
разброса , связанного с этими
эффектами, принимая в расчет
их неопределенности и
кэффициенты
63. Как оценивать неопределенность?
5. Получить оценку суммарнойнеопределенности путем
совмещения оценки
воспроизводимости с оценками
неопределенностей, связанных с
правильностью и с эффектами
от дополнительных влияний
64. Как оценивать неопределенность?
65. Примеры нахождения неопределенности
ГОСТ 26781-85 «Молоко. Метод измерения рН»В стандарте указано
«предел возможных значений погрешности
измерений =±0,04 рН для принятой
вероятности Р=0,95»
Эту величину можно считать
неопределенностью!
66. Примеры нахождения неопределенности
ГОСТ Р 51258-99 (DIN 10326-86) Молоко и молочные продукты.Метод определения сахарозы и глюкозы. (Приведены
фотометрические методы)
Для методики определения глюкозы
для диапазона от 0,1 до 0,5 (%) и вероятности Р=0,95
показатели сходимости (r) и воспроизводимости (R)
составляют 0,06%.
Для расчета неопределенности определяют σR, R=2.77* σR,
σR = 0.06/2.77= 0.02 (%)
- Стандартная неопределенность u = σR = 0,02%
- Для коэффициента охвата K=3
расширенная неопределенность U = 0.02*3=0.06%
Например, для найденного результата измерения 0,48%
0,48±0,06
67. (введен в 01.06.2007)
ГОСТ Р ИСО 10576-1Статистические методы
Руководство по оценке соответствия
установленным требованиям
Часть 1
Общие принципы
ISO 10576-1:2003
Statistical methods
Guidelines for the evaluation of conformity with specified
requirements
Part 1 General principles
68. ГОСТ Р ИСО 10576-1
Стандарт является руководством- при разработке требований к объекту
оценки, которые могут быть
сформулированы в виде предельных
значений для количественных
параметров объекта;
- при оценке соответствия упомянутым
требованиям, когда результаты
измерений или испытаний включают
неопределенность
69. ГОСТ Р ИСО 10576-1-2006
4.1 Требования к установлению предельныхзначений
4.1.1 Объект должен быть четко и однозначно
определен.
4.1.2 Количественный параметр объекта
должен быть четко и однозначно определен.
Значение параметра должно определяться
посредством процедур измерений или
испытаний, которые позволяют получить
оценку неопределенности измерений.
4.1.3 Процедура измерений или испытаний
должна быть стандартизованной процедурой.
70. ГОСТ Р ИСО 10576-1-2006
При сравнении результата измерений илииспытаний с предельными значениями
необходимо учитывать неопределенность
результатов измерений
Результаты измерений параметра и
неопределенность измерений должны быть
зарегистрированы. Неопределенность измерений
следует представлять в виде интервала
неопределенности. Если этот интервал
является доверительным интервалом,
необходимо указывать доверительную
вероятность (1 - ), соответствующую
интервалу. В противном случае следует
фиксировать коэффициент охвата интервала
неопределенности
71. ГОСТ Р ИСО 10576-1-2006 Оценка соответствия с двумя этапами
Этап 1Выполняют процедуру измерений и подсчитывают
неопределенность результатов измерений.
Решение о соответствии требованиям может
быть принято тогда и только тогда, если,
интервал неопределенности результатов
измерений находится внутри области допустимых
значений.
Второй этап должен быть выполнен тогда и
только тогда, когда границы интервала
неопределенности, подсчитанные после первого
этапа, выходят за пределы поля допуска.
72. ГОСТ Р ИСО 10576-1-2006 Оценка соответствия с двумя этапами
Этап 2.Выполняют процедуру измерений еще
раз и определяют соответствующую
комбинацию результатов измерений
двух этапов, чтобы сформировать
окончательный результат измерений и
неопределенность этого результата.
Решение о соответствии требованиям
может быть принято только в том
случае, если интервал неопределенности
окончательного результата измерений
находится внутри области
допустимых значений
73. ГОСТ Р ИСО 10576-1-2006
Если после первого или послевторого этапа принимают
решение о соответствии, его
формулируют в виде
утверждения:
оценка соответствия
продемонстрировала, что
значение контролируемого
параметра соответствует
требованиям
74. ГОСТ Р ИСО 10576-1-2006
Если интервал неопределенности,рассчитанный после этапа 2,
включает границу поля допуска,
результат оценки соответствия
является неокончательным. Решение
формулируют в виде утверждения:
оценка соответствия не способна
продемонстрировать, что значение
параметра соответствует или не
соответствует требованиям.
75. ГОСТ Р ИСО 10576-1-2006
Если интервал неопределенностинаходится в области
недопустимых значений и одна из
границ интервала
неопределенности совпадает с
границей поля допуска, считают,
что интервал неопределенности
находится в области
недопустимых значений.
76. ГОСТ Р ИСО 10576-1-2006 Оценка содержания асбеста в доломите ( L<0.1%)
ГОСТ Р ИСО 10576-1-2006Оценка содержания асбеста в доломите
( L<0.1%)
Из партии доломита было отобрано
пять первичных образцов для первого
этапа оценки и четыре – для второго
этапа.
Из каждого образца было сформировано
по 10 лабораторных проб, по которым
после проведения анализа подсчитывали
среднее значение массовой доли асбеста.
77. Пример оценки неопределенности по типу А ГОСТ Р ИСО 10576-1-2006 Оценка содержания асбеста в доломите L<0.1%)
Пример оценки неопределенности по типу АГОСТ Р ИСО 10576-1-2006
Оценка содержания асбеста в доломите L<0.1%)
При достаточном количестве лабораторных проб
распределение выборочных средних хорошо
описывается нормальным распределением - 2,
которая содержит вклады отклонений между
первичными образцами, отклонений в пределах
первичных образцов и неопределенность измерений,
связанную с анализом лабораторных проб
n
s
2
2
(
X
X
)
i
i 1
n 1
X
t1- / 2( n 1) s
n
где t1- /2(n–1) - квантиль распределения Стъюдента
уровня (1- /2) с (n–1) степенями свободы
78. ГОСТ Р ИСО 10576-1-2006 Оценка содержания асбеста в доломите ( L<0.1%)
ГОСТ Р ИСО 10576-1-2006Оценка содержания асбеста в доломите ( L<0.1%)
На первом этапе были получены следующие результаты
(в долях массы асбеста):
0,152 %; 0,0704 %; 0,0772 %; 0,0731 %; 0,0551 %
На основе наблюдений первого этапа для
= 0,05
был получен следующий доверительный
интервал для Х ср.
0,0856 % (2,776 0,0381/√5 )% = (0,038 %; 0,133 %).
Так как граница поля допуска 0,1 % лежит в этом
интервале, т.е. установленное требование не
выполняется, было принято решение о переходе ко
второму этапу оценки.
79. ГОСТ Р ИСО 10576-1-2006 Оценка содержания асбеста в доломите ( L<0.1%)
ГОСТ Р ИСО 10576-1-2006Оценка содержания асбеста в доломите ( L<0.1%)
Во втором этапе были получены
следующие результаты:
0,0828 %; 0,0671 %; 0,0743 %; 0,0561 %.
Используя приведенные выше процедуры,
определен доверительный интервал
0,0787 % (2,306 0,0290/√9) % =
(0,056 %; 0,101 %).
Так как этот интервал также содержит
границу поля допуска, принимается
решение о несоответствии
установленным требованиям
















































































 Математика
Математика








