Похожие презентации:
Основы алгебры логики
1. Основы алгебры логики
Кривко-Красько Сергей ВасильевичМОУ «Лицей № 26», г. Подольск
2014
2. Логические переменные
Логика – наука о «высказываниях».Высказывание– это форма мышления, в которой чтолибо утверждается или отрицается об объектах, их
свойствах или отношениях объектов. Высказывание
может быть либо истинно, либо ложно.
Алгебра логики отвлекается от смысловой
содержательности высказываний.
Ее интересует только: истинно или ложно высказывание.
Логическая переменная
– символическое
обозначение высказывания.
Истинность высказывания обозначается значением
Ложность высказывания обозначается значением
1
0
3.
Булева алгебраДвоичное кодирование – все виды
информации кодируются с помощью 0 и 1.
Задача – разработать оптимальные правила
обработки таких данных.
Джордж Буль разработал основы алгебры,
в которой используются только 0 и 1
(алгебра логики, булева алгебра).
Почему «логика»?
Результат выполнения операции можно
представить как истинность (1) или ложность
(0) некоторого высказывания.
3
4.
Логические высказыванияЛогическое высказывание – это
повествовательное предложение,
относительно которого можно однозначно
сказать, истинно оно или ложно.
Высказывание или нет?
Сейчас идет дождь.
Жирафы летят на север.
История – интересный предмет.
У квадрата – 10 сторон и все разные.
Красиво!
В городе N живут 2 миллиона человек.
Который час?
4
5.
Обозначение высказыванийA – Сейчас идет дождь.
B – Температура выше нуля.
!
простые
высказывания
(элементарные)
Любое высказывание может быть
ложно (0) или истинно (1).
Составные высказывания строятся из простых с помощью
логических связок (операций) «и», «или», «не»,
«если … то», «тогда и только тогда» и др.
AиB
Сейчас идет дождь и температура выше нуля.
A или B
Сейчас идет дождь или температура выше нуля.
если A, то B
Если сейчас идет дождь, то температура выше нуля.
не A и B
Сейчас нет дождя и температура выше нуля.
5
6. Логические функции
Логическая функция (операция) –функция F(x1, x2,…xn),
значение которой и значения
аргументов являются логическими.
Логическая функция может быть задана
или с помощью элементарных
логических функций (операций), или
путем перечисления ее значений для
всех возможных наборов (сочетаний)
аргументов.
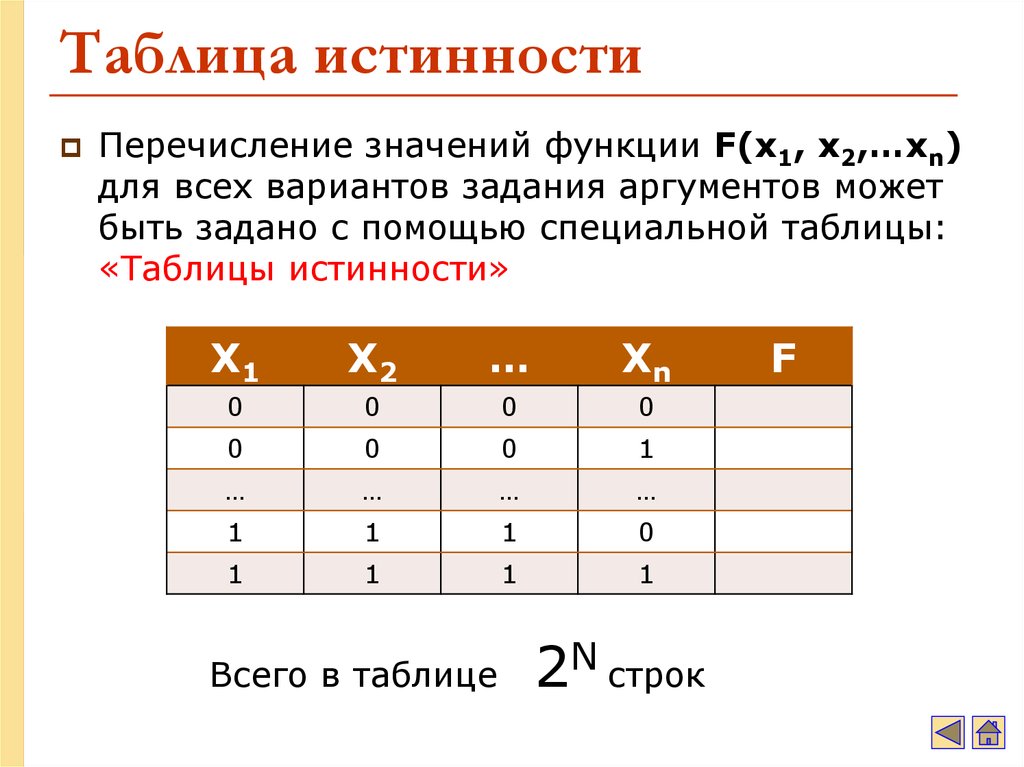
7. Таблица истинности
Перечисление значений функции F(x1, x2,…xn)для всех вариантов задания аргументов может
быть задано с помощью специальной таблицы:
«Таблицы истинности»
X1
X2
…
Xn
0
0
0
0
0
0
0
1
…
…
…
…
1
1
1
0
1
1
1
1
Всего в таблице
2N строк
F
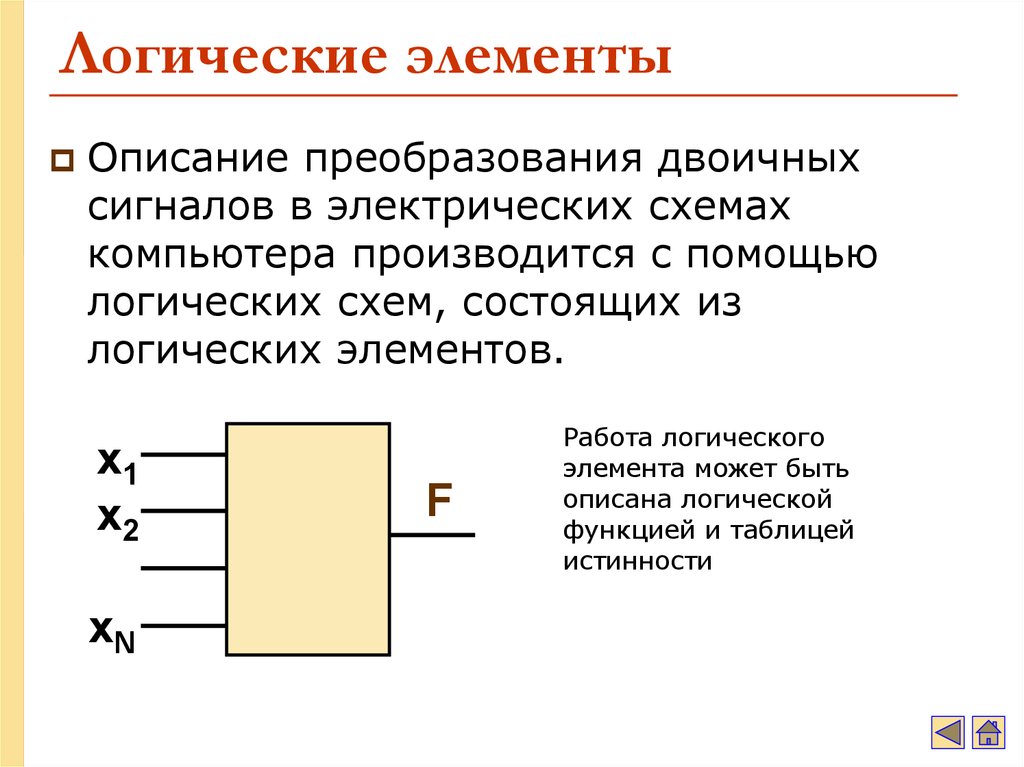
8. Логические элементы
Описание преобразования двоичныхсигналов в электрических схемах
компьютера производится с помощью
логических схем, состоящих из
логических элементов.
x1
x2
xN
F
Работа логического
элемента может быть
описана логической
функцией и таблицей
истинности
9. ЭЛЕМЕНТАРНЫЕ ЛОГИЧЕСКИЕ ФУНКЦИИ (ОПЕРАЦИИ)
10. Логическое отрицание (инверсия)
НЕНЕВЕРНО, ЧТО
Обозначение:
X, ¬X, not X.
Таблица истинности
X
0
1
X
1
0
Пример:
X – Идет снег
X - Неверно, что
идет снег
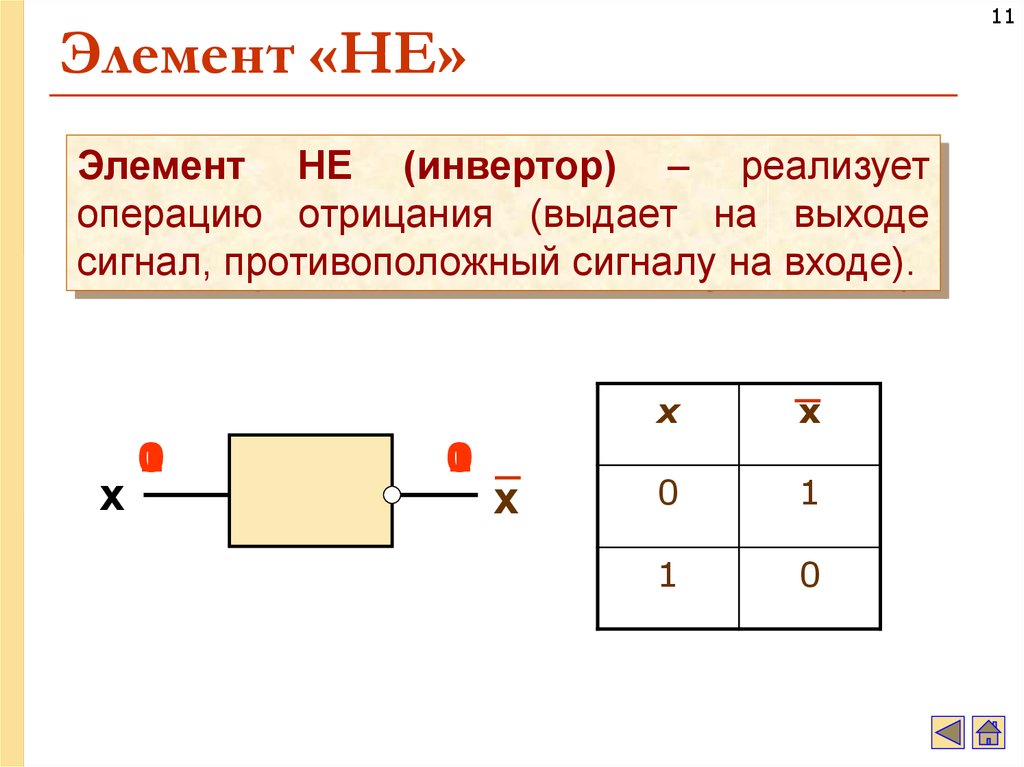
11. Элемент «НЕ»
11Элемент «НЕ»
Элемент НЕ (инвертор) – реализует
операцию отрицания (выдает на выходе
сигнал, противоположный сигналу на входе).
x
0
1
1
0
x
x
x
0
1
1
0
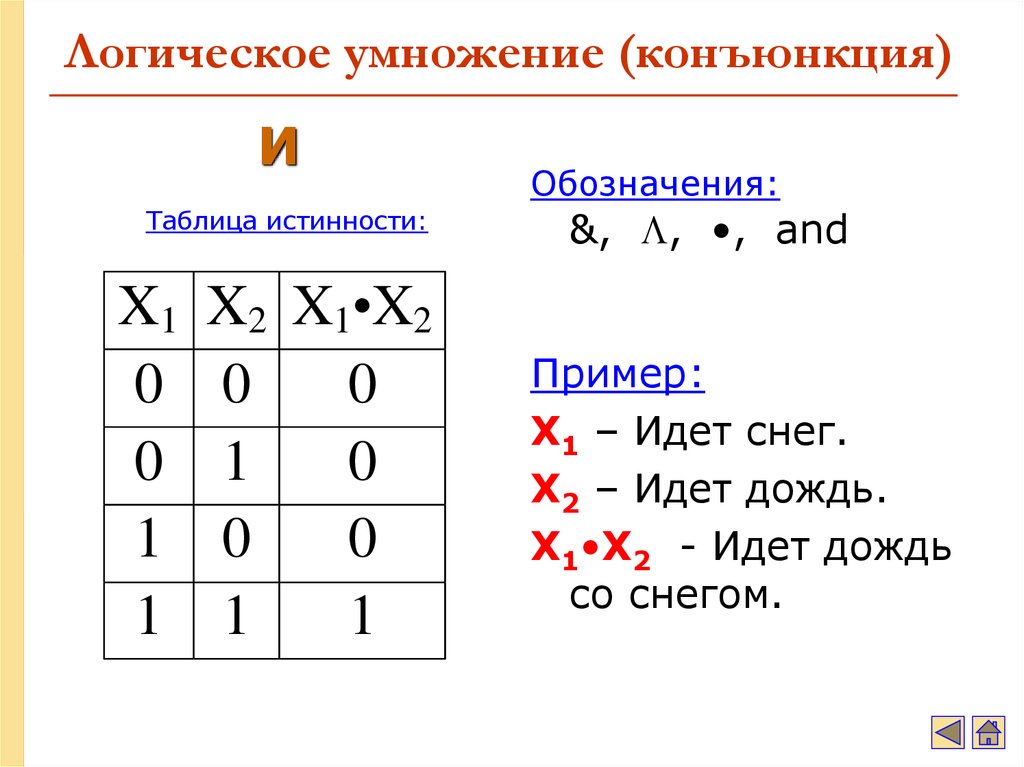
12. Логическое умножение (конъюнкция)
ИТаблица истинности:
X1
0
0
1
1
X2 X1•X2
0
0
0
1
0
0
1
1
Обозначения:
&, , •, and
Пример:
X1 – Идет снег.
X2 – Идет дождь.
X1•X2 - Идет дождь
со снегом.
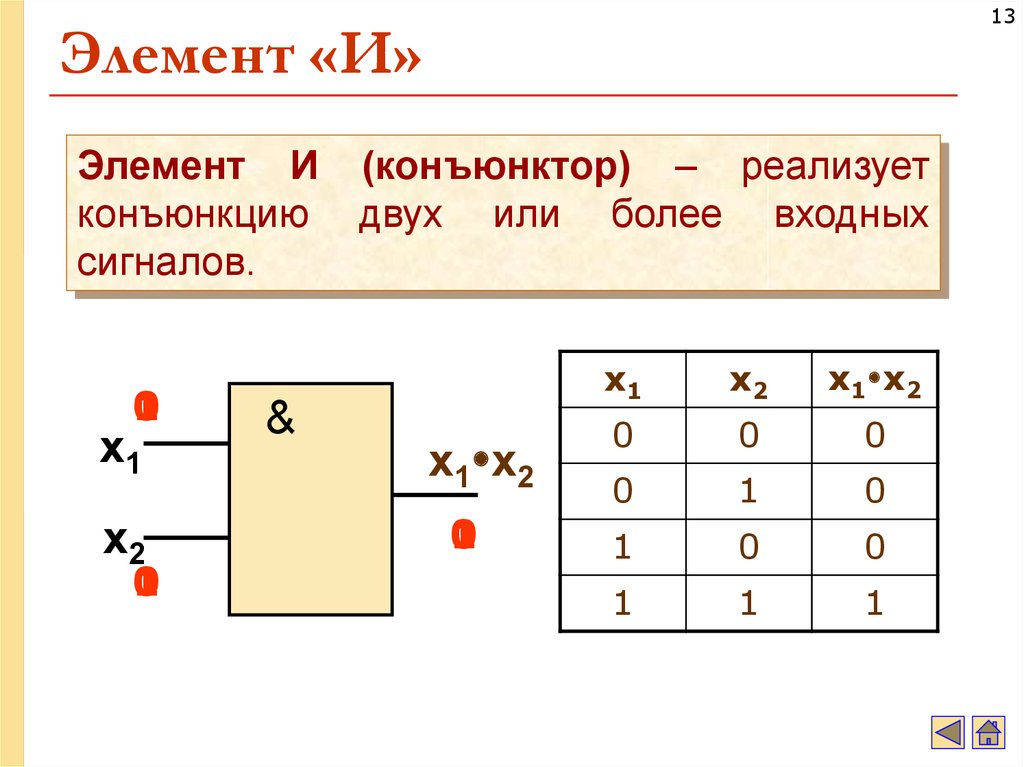
13. Элемент «И»
13Элемент «И»
Элемент И
конъюнкцию
сигналов.
0
1
x1
x2
0
1
&
(конъюнктор) – реализует
двух или более входных
x1 x2
0
1
x1
x2
x1 x2
0
0
0
0
1
0
1
0
0
1
1
1
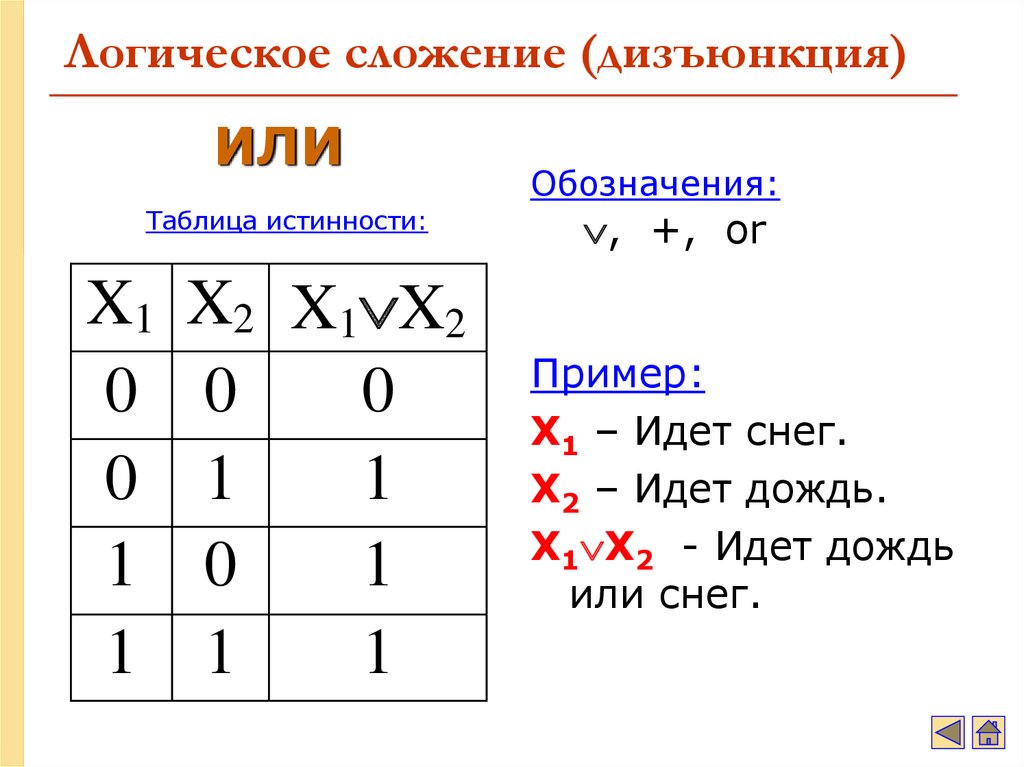
14. Логическое сложение (дизъюнкция)
ИЛИТаблица истинности:
X1
0
0
1
1
X2 X1 X2
0
0
1
1
0
1
1
1
Обозначения:
, +, or
Пример:
X1 – Идет снег.
X2 – Идет дождь.
X1 X2 - Идет дождь
или снег.
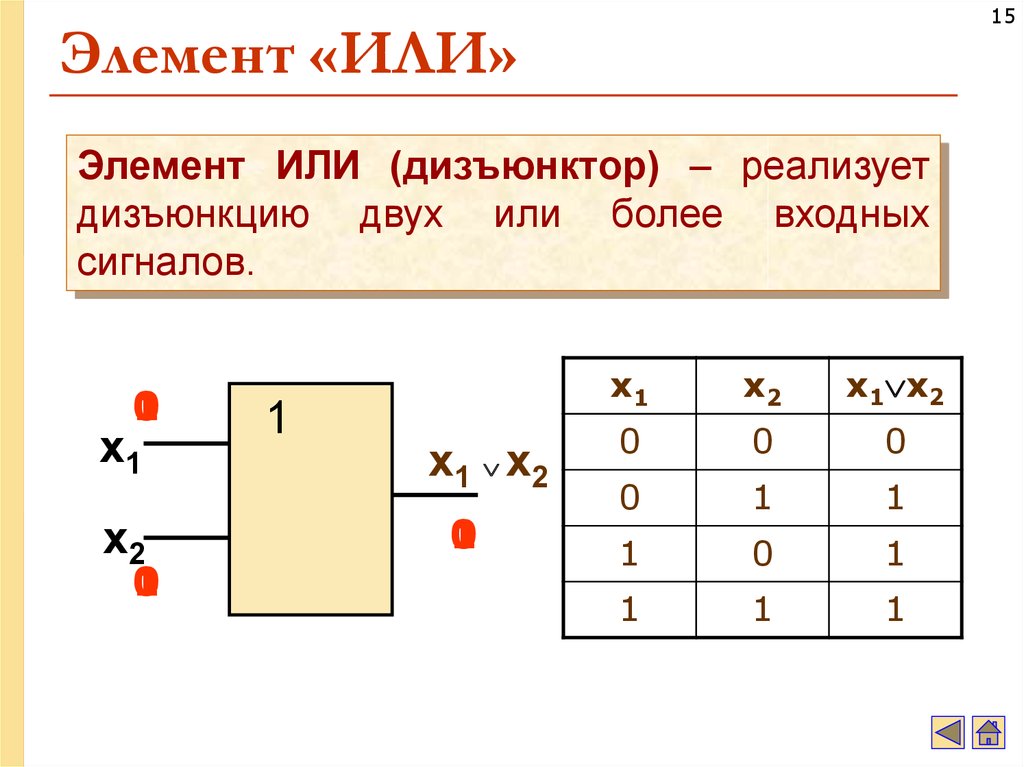
15. Элемент «ИЛИ»
15Элемент «ИЛИ»
Элемент ИЛИ (дизъюнктор) – реализует
дизъюнкцию двух или более входных
сигналов.
0
1
x1
x2
0
1
1
x1 x2
0
1
x1
x2
x1 x2
0
0
0
0
1
1
1
0
1
1
1
1
16. Строгая дизъюнкция
ЛИБО, ЛИБОТаблица истинности:
X1
0
0
1
1
X2 X1 X2
0
0
1
1
0
1
1
0
Обозначения:
,
XOR
Пример:
X1 – Первый урок
физика.
X2 – Первый урок
химия.
X1 X2- Первый урок
либо физика, либо
химия.
17. Следование (импликация)
Условная связьЕСЛИ, ТО
Обозначения:
Таблица истинности:
X1
0
0
1
1
X2 X1 X2
0
1
1
1
0
0
1
1
Пример:
X1 – Идет дождь.
X2 – Асфальт мокрый.
X1 X2 Если идет дождь,
то асфальт мокрый.
18. Равнозначность (эквиваленция)
Если и только еслиТогда и только тогда,
Обозначения:
Таблица истинности:
X1
0
0
1
1
X2 X1 X2
0
1
1
0
0
0
1
1
=
Пример:
X1 – Небо голубое.
X2 –Светит солнце.
X1 X2 – Небо голубое
тогда и только тогда,
когда светит солнце.
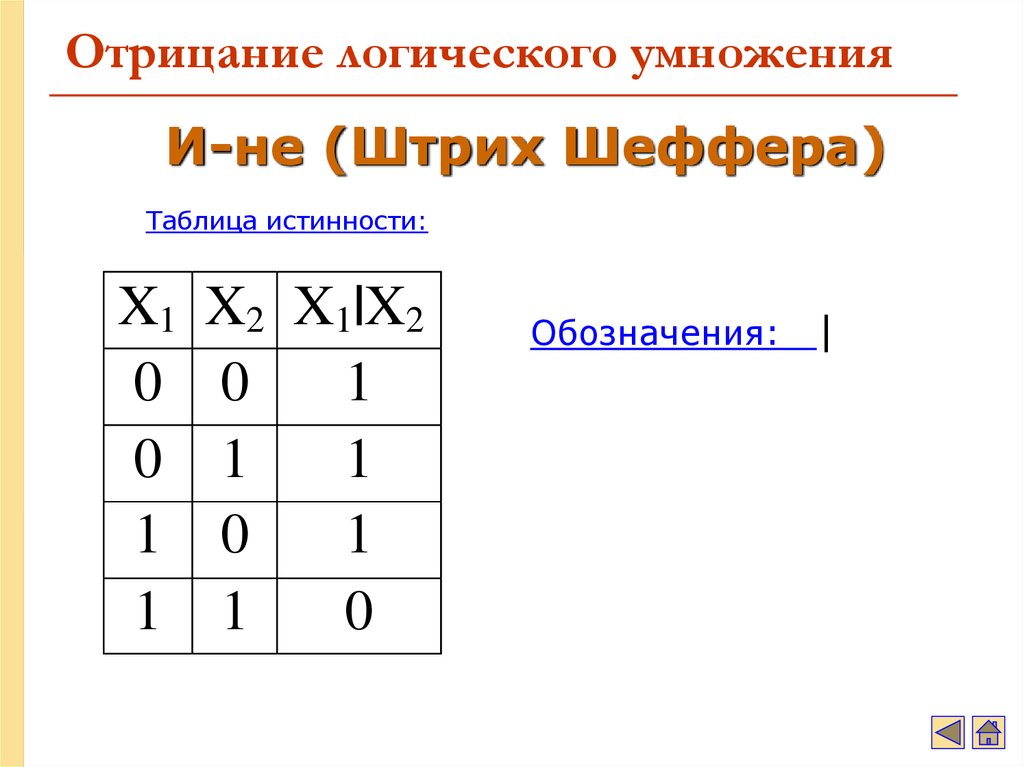
19. Отрицание логического умножения
И-не (Штрих Шеффера)Таблица истинности:
X1
0
0
1
1
X2 X1|X2
1
0
1
1
1
0
0
1
Обозначения:
|
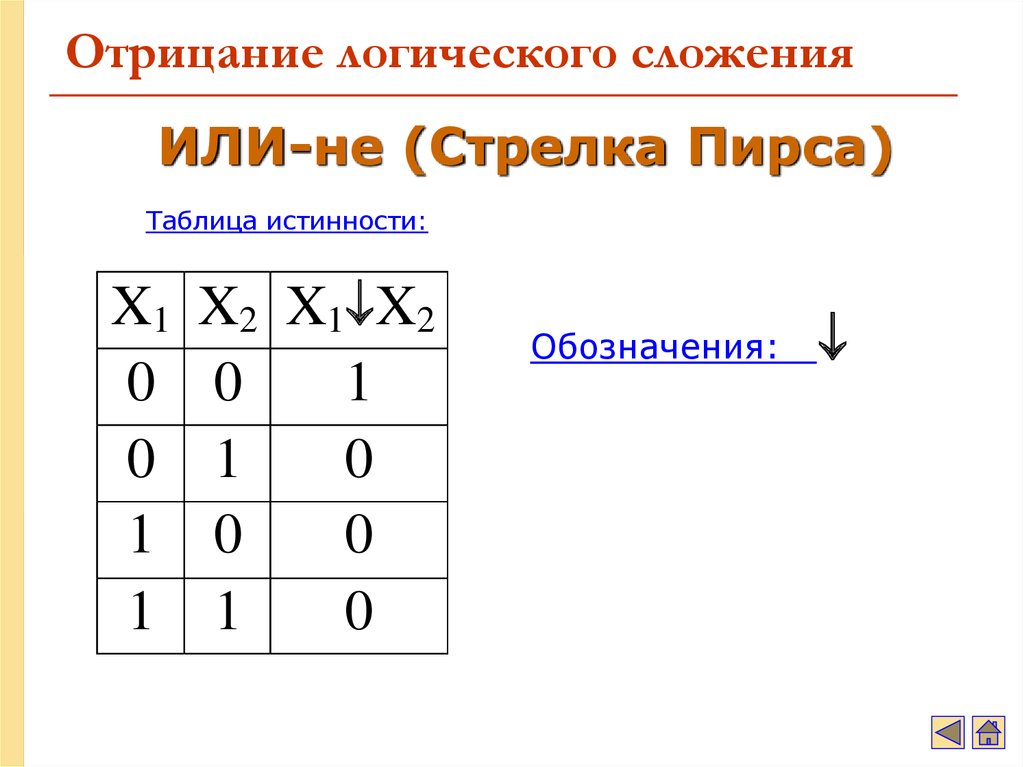
20. Отрицание логического сложения
ИЛИ-не (Стрелка Пирса)Таблица истинности:
X1
0
0
1
1
X2 X1 X2
1
0
0
1
0
0
0
1
Обозначения:
21. Приоритет логических операций
1.2.
3.
4.
Инверсия
Конъюнкция
Дизъюнкция и
строгая дизъюнкция
Импликация и
эквиваленция
¬
^
22. Законы логики
ЗАКОНЫ ЛОГИКИ23. Переместительный (коммутативный)закон
X·Y = Y·XX Y = Y X
Сочетательный (ассоциативный)закон
(X·Y)·Z = Y·(X·Z)
(X Y) Z = Y (X Z)
24. Распределительный (дистрибутивный)закон
X·(Y Z) = X·Y X·ZX Y·Z = (X Y)·(X Z)
Закон отрицания (де Моргана)
X·Y = X Y
X Y = X·Y
25. Основные тождества
X·1 = ХX 1 = 1
X·0 = 0
X 0 = Х
Правила
исключения
констант
26. Основные тождества
X·Х = ХX Х = Х
X·Х = 0
X Х = 1
X=X
Правила
равносильности
Закон
непротиворечия
Закон исключенного
третьего
Закон двойного
отрицания
27. Правила упрощения выражений
Правилопоглощения
X Х·Y = Х
X Х·Y=X·1 Х·Y=X·(1 Y)=X·1=X
Правило
свертки
Правило
склеивания
X Х·Y = Х Y
X Х·Y=(X Х)·(X Y)=1·(X Y)=X Y
X·Y Х·Y = Y
X·Y Х·Y=(X Х) ·Y=1·Y=Y
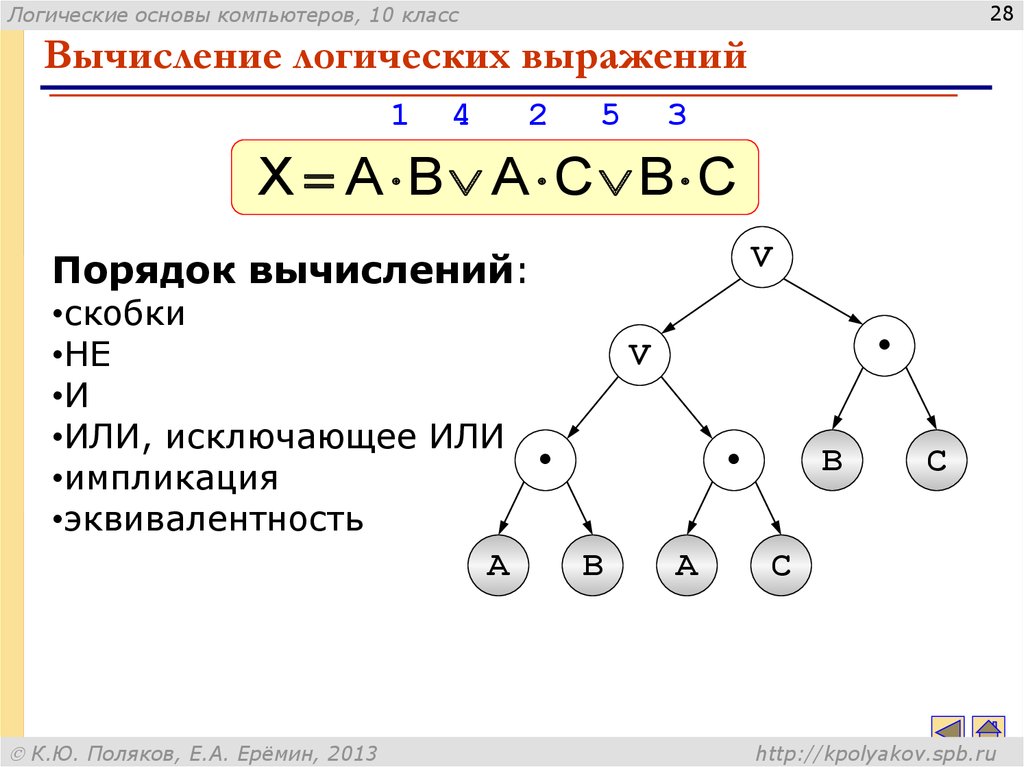
28. Вычисление логических выражений
28Логические основы компьютеров, 10 класс
Вычисление логических выражений
1
4
2
5
3
X A B A C B C
Порядок вычислений:
V
•скобки
V
•НЕ
•И
•ИЛИ, исключающее ИЛИ
B
•импликация
•эквивалентность
A
B
A
С
К.Ю. Поляков, Е.А. Ерёмин, 2013
C
http://kpolyakov.spb.ru
29. Вычислите значение функции
F1 x1 x2 x1 x3При x1=0, x2=0, x3=1
1
При x1=1, x2=1, x3=1
0
30. Вычислите значение функции
F2 ( x1 x2 x3 ) ( x2 x3 )При x1=1, x2=0, x3=0
1
При x1=0, x2=1, x3=0
0
31. Вычислите значение функции
F3 ( x1 x 2 x 3 )При x1=1, x2=0, x3=0
1
При x1=0, x2=1, x3=0
1
32. Определите значение логического выражения
Учебник, стр. 178, № 10( X 2) ( X 3)
При X =1
1
При X =2
1
При X =3
0
При X =4
1
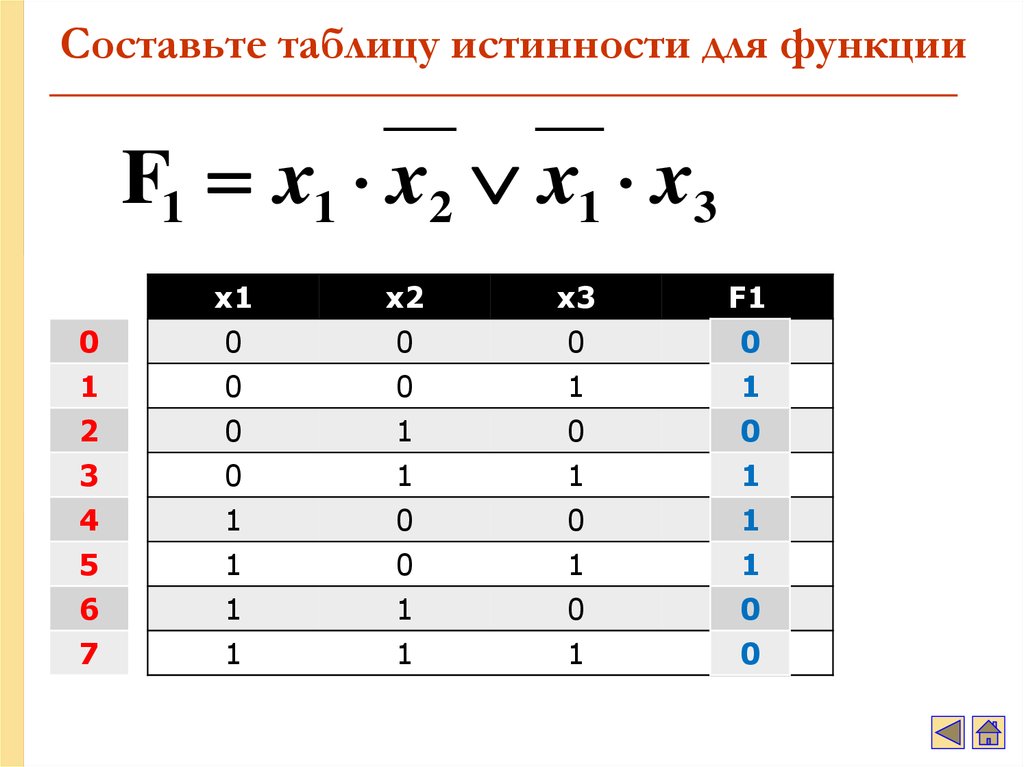
33. Составьте таблицу истинности для функции
F1 x1 x2 x1 x3x1
x2
x3
F1
0
0
0
0
0
1
0
0
1
1
2
0
1
0
0
3
0
1
1
1
4
1
0
0
1
5
1
0
1
1
6
1
1
0
0
7
1
1
1
0
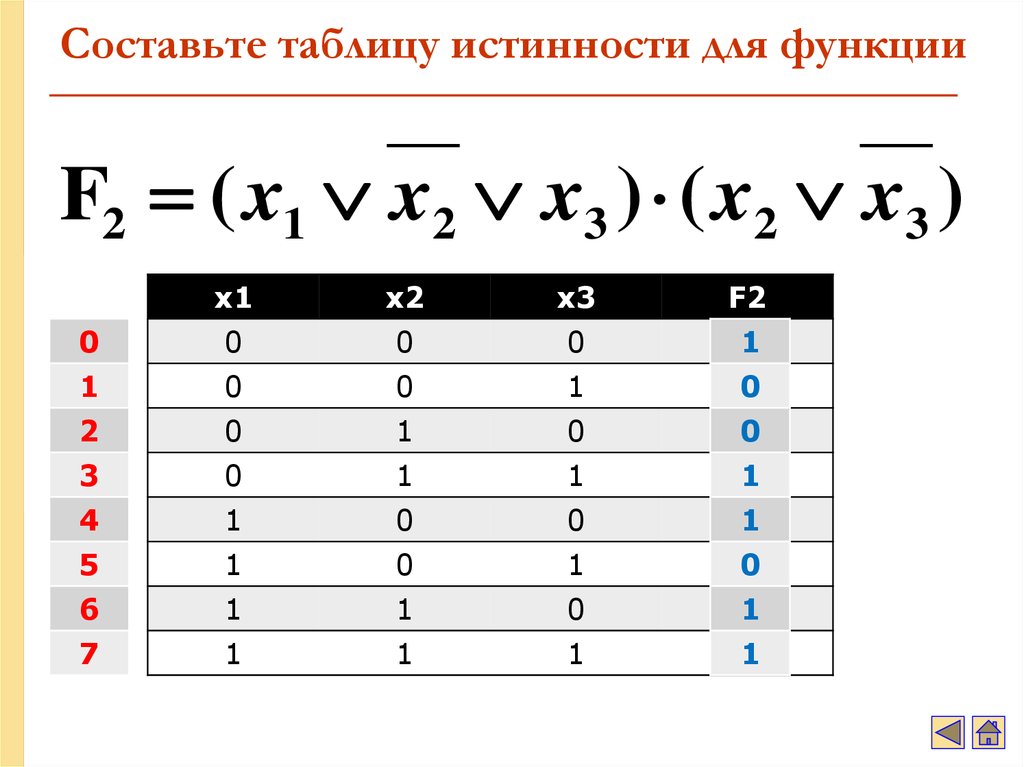
34. Составьте таблицу истинности для функции
F2 ( x1 x2 x3 ) ( x2 x3 )x1
x2
x3
F2
0
0
0
0
1
1
0
0
1
0
2
0
1
0
0
3
0
1
1
1
4
1
0
0
1
5
1
0
1
0
6
1
1
0
1
7
1
1
1
1
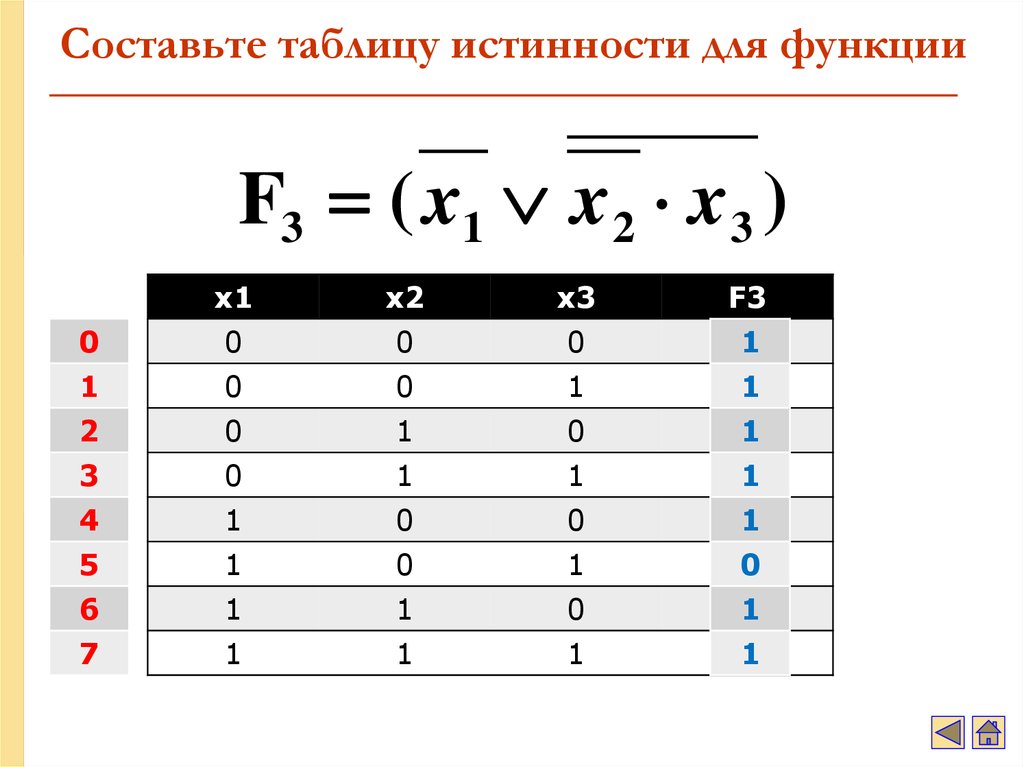
35. Составьте таблицу истинности для функции
F3 ( x1 x 2 x 3 )x1
x2
x3
F3
0
0
0
0
1
1
0
0
1
1
2
0
1
0
1
3
0
1
1
1
4
1
0
0
1
5
1
0
1
0
6
1
1
0
1
7
1
1
1
1
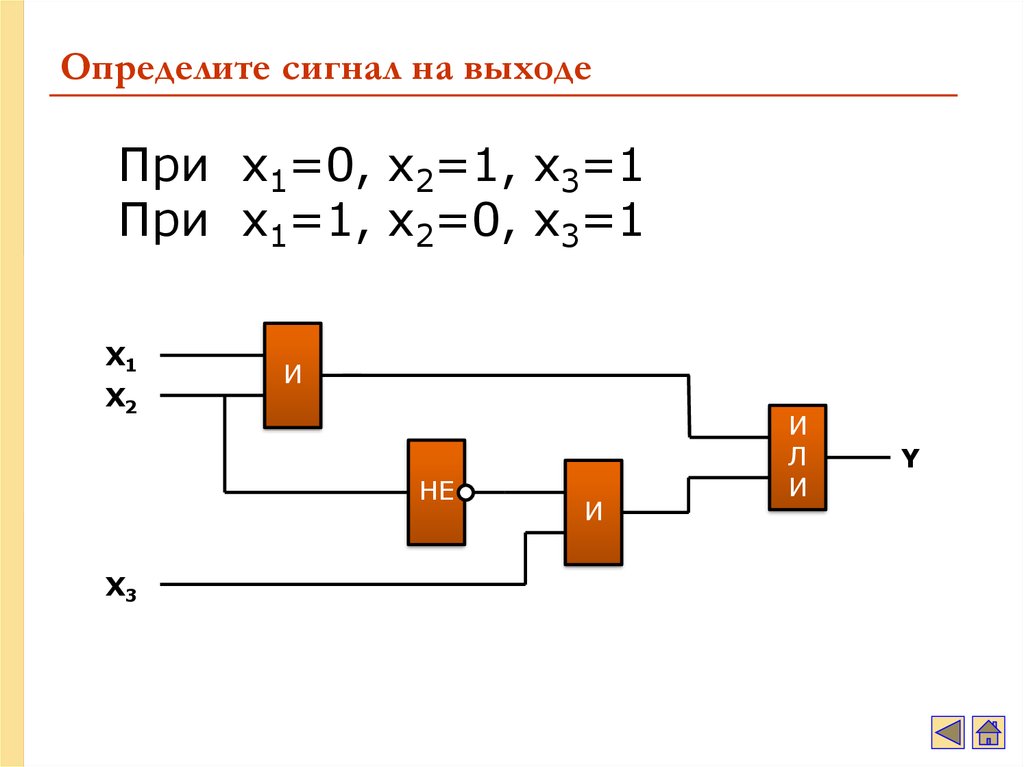
36. Определите сигнал на выходе
При x1=0, x2=1, x3=1При x1=1, x2=0, x3=1
X1
X2
И
НЕ
X3
И
И
Л
И
Y
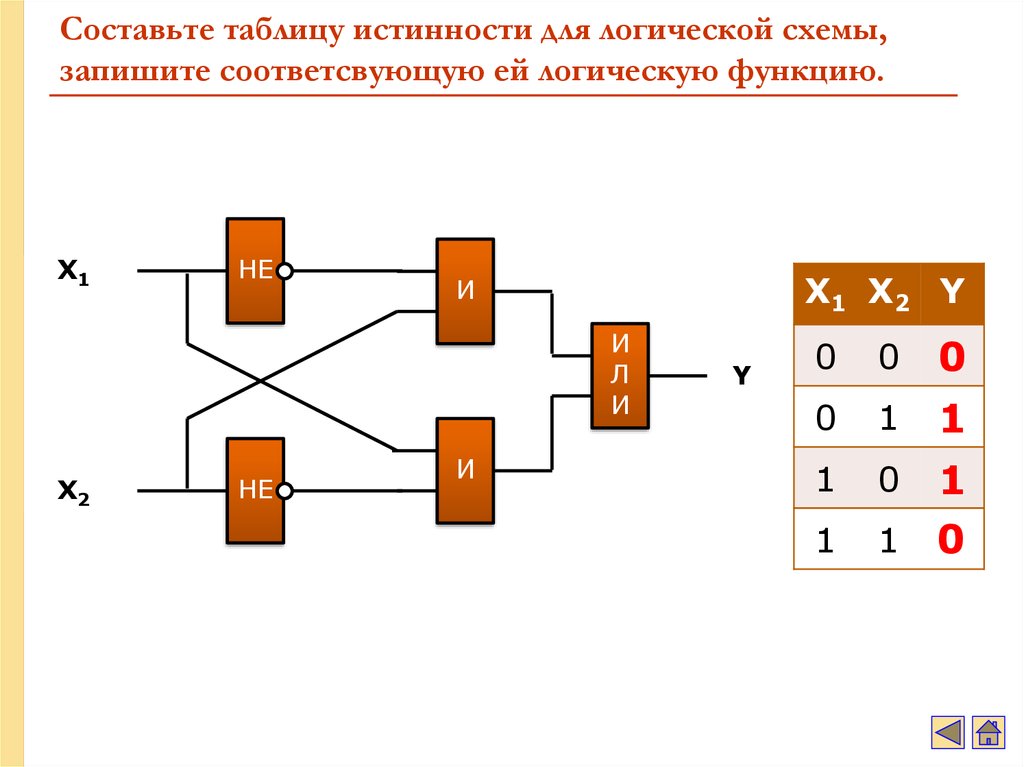
37. Составьте таблицу истинности для логической схемы, запишите соответсвующую ей логическую функцию.
X1НЕ
X1 X2 Y
И
И
Л
И
X2
НЕ
И
Y
0
0
0
0
1
1
1
0
1
1
1 0
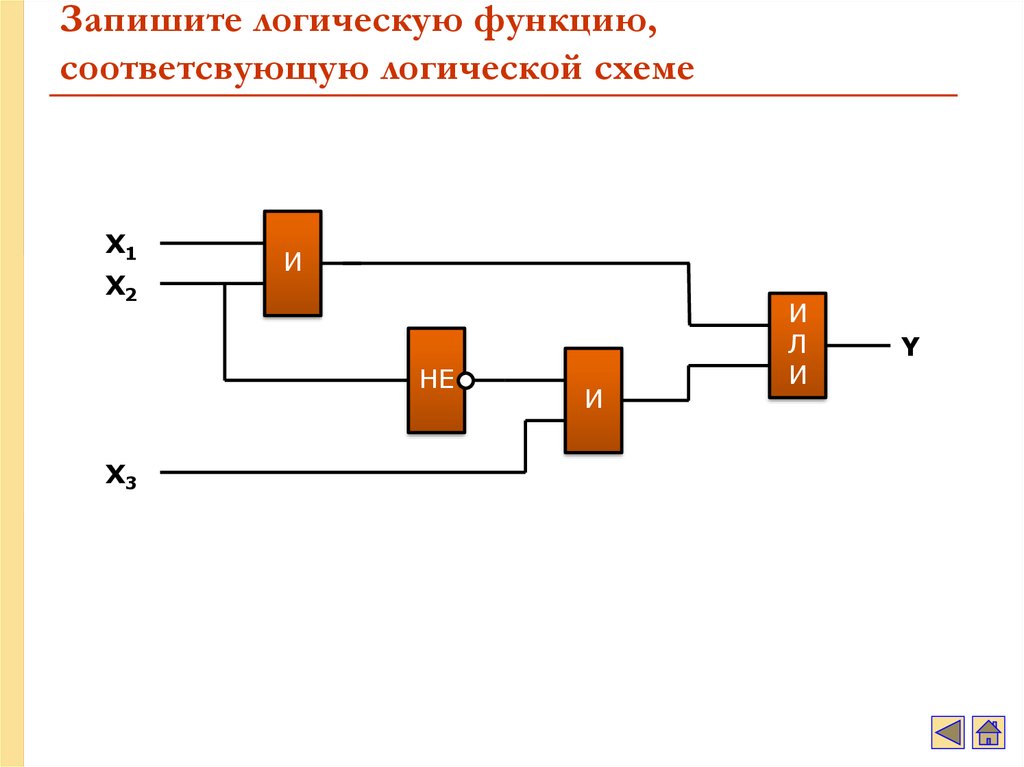
38. Запишите логическую функцию, соответсвующую логической схеме
X1X2
И
НЕ
X3
И
И
Л
И
Y
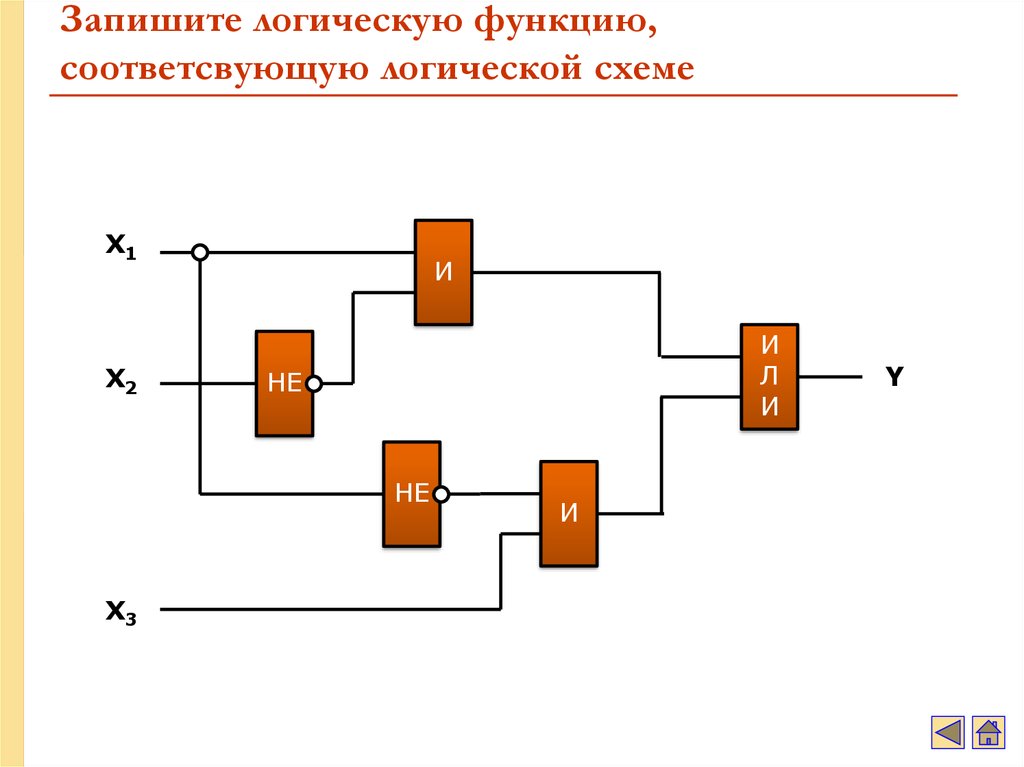
39. Запишите логическую функцию, соответсвующую логической схеме
X1X2
И
И
Л
И
НЕ
НЕ
X3
И
Y
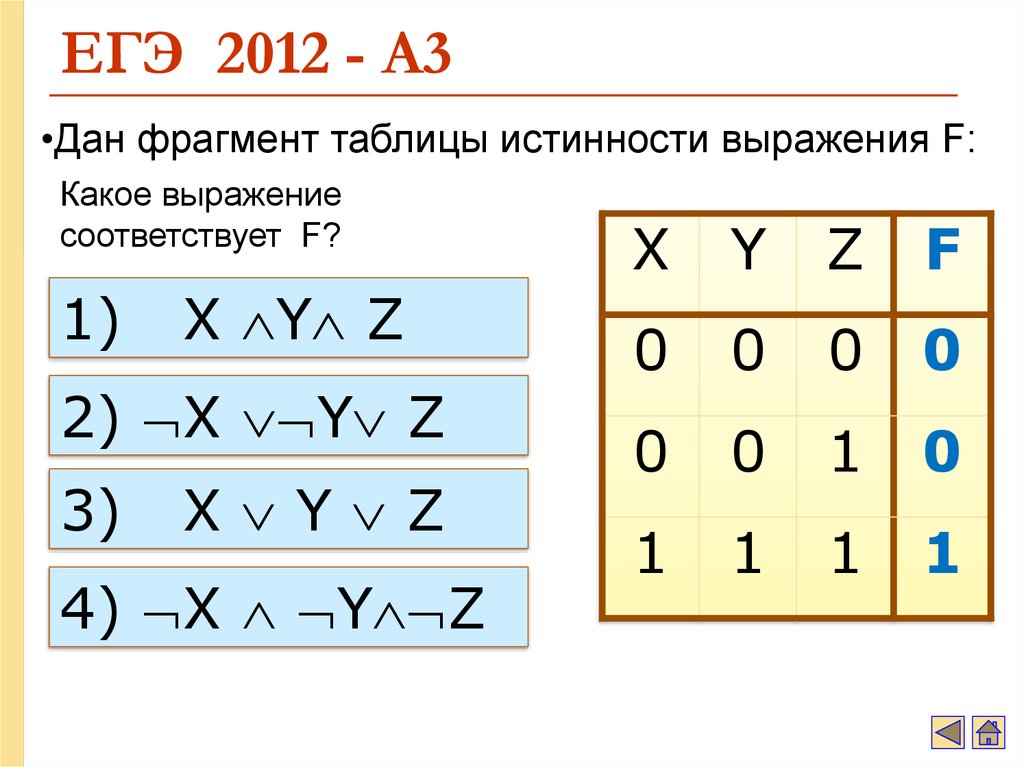
40. ЕГЭ 2012 - А3
•Дан фрагмент таблицы истинности выражения F:Какое выражение
соответствует F?
1)
X Y Z
2) X Y Z
3)
X Y Z
4) X Y Z
X
Y
Z
F
0
0
0
0
0
0
1
0
1
1
1
1
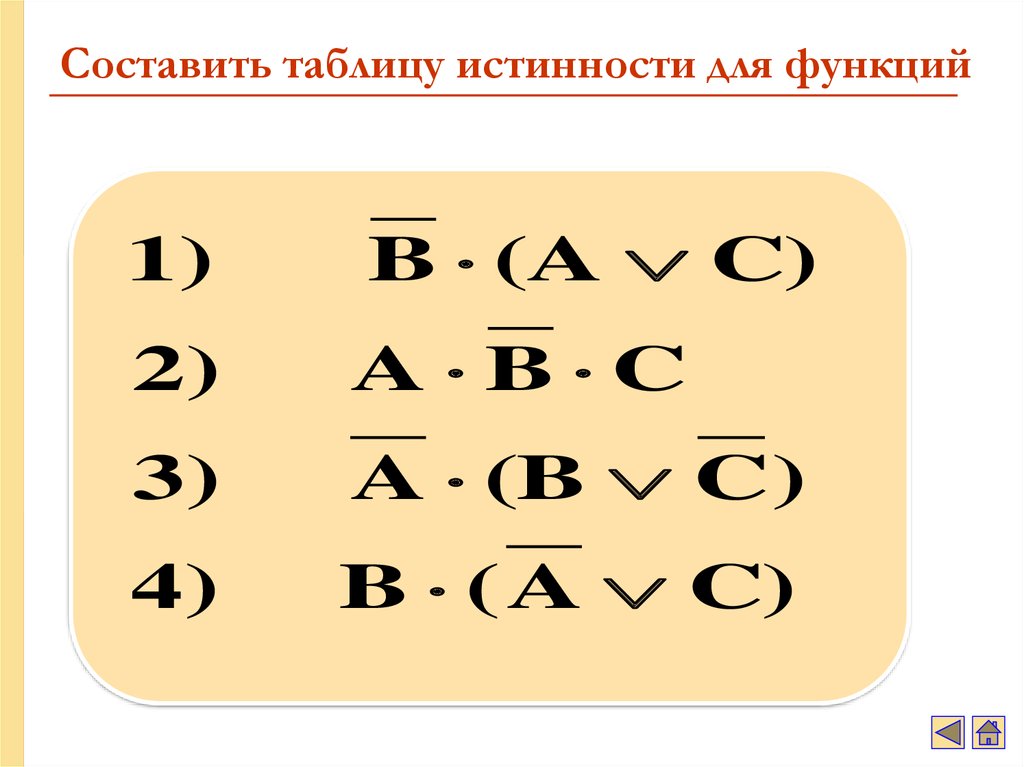
41. Составить таблицу истинности для функций
1)B (A C)
2)
A B C
3)
A (B C )
4)
B ( A C)
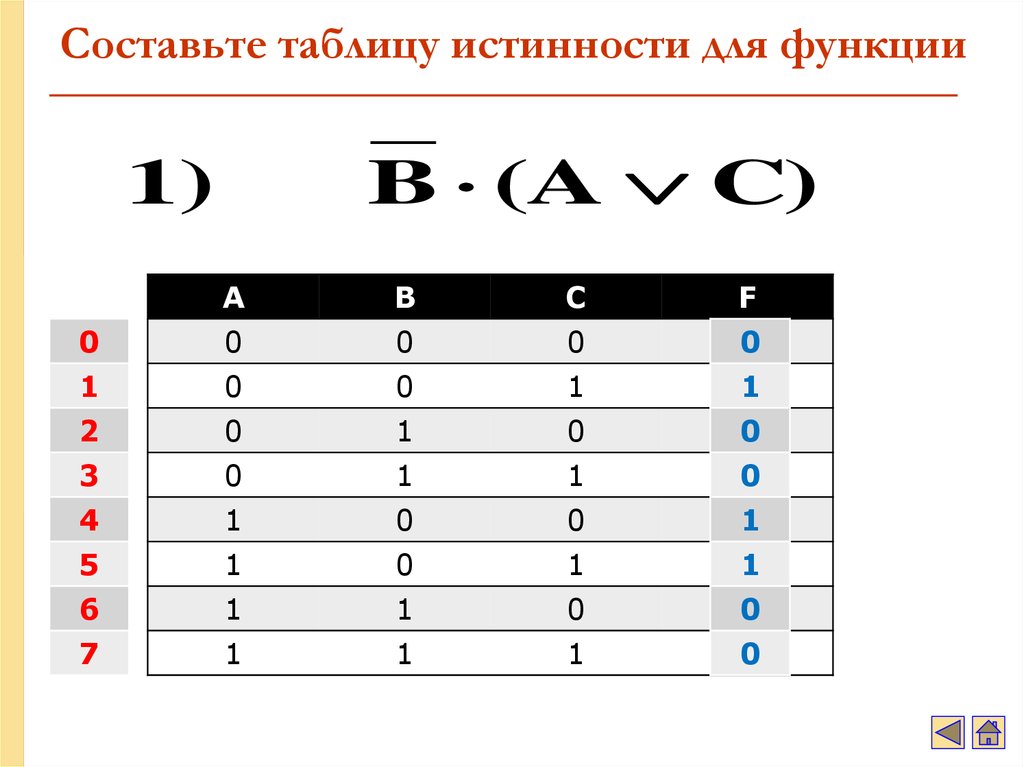
42. Составьте таблицу истинности для функции
B (A C)1)
A
B
C
F
0
0
0
0
0
1
0
0
1
1
2
0
1
0
0
3
0
1
1
0
4
1
0
0
1
5
1
0
1
1
6
1
1
0
0
7
1
1
1
0
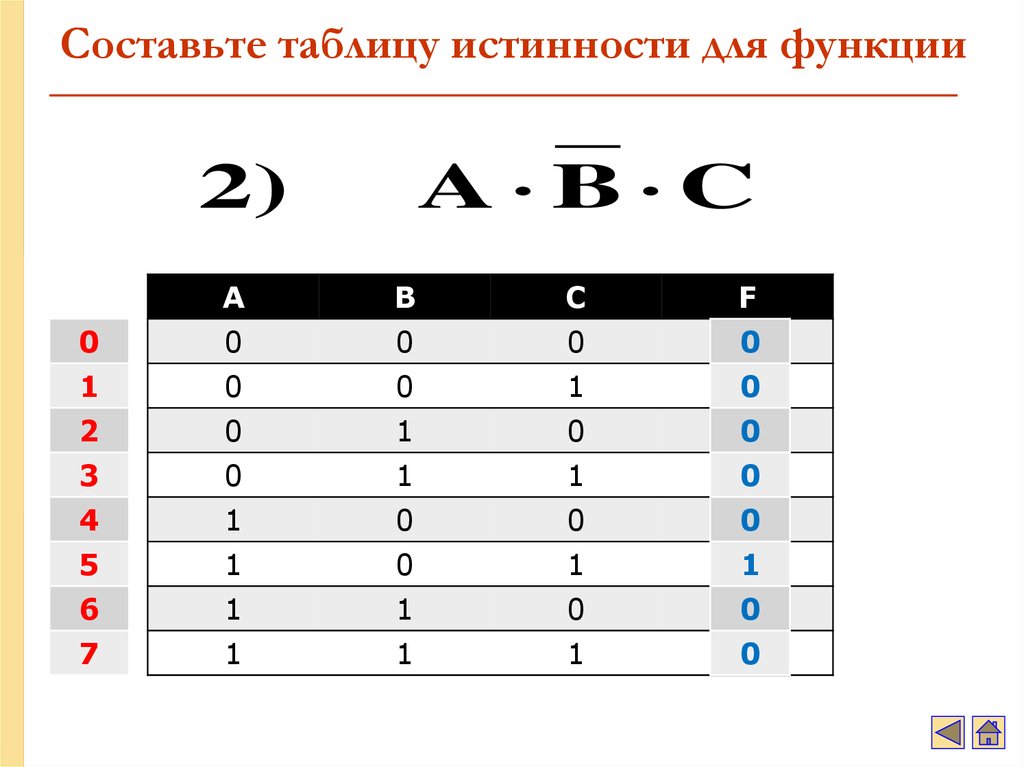
43. Составьте таблицу истинности для функции
A B C2)
A
B
C
F
0
0
0
0
0
1
0
0
1
0
2
0
1
0
0
3
0
1
1
0
4
1
0
0
0
5
1
0
1
1
6
1
1
0
0
7
1
1
1
0
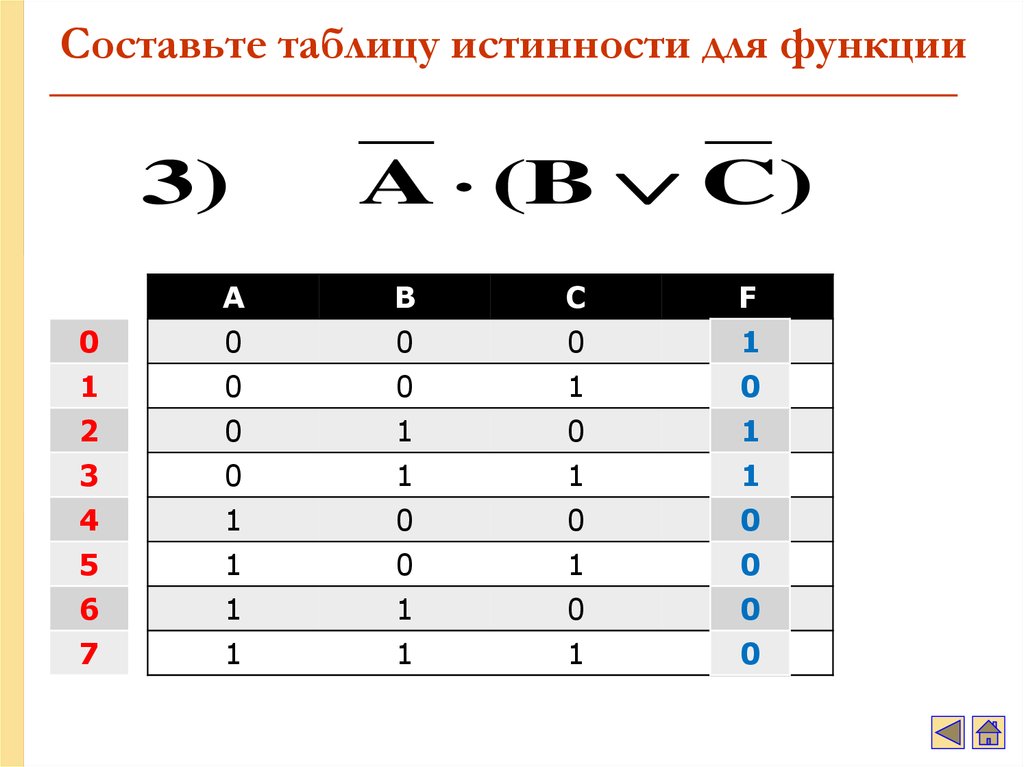
44. Составьте таблицу истинности для функции
3)A (B C)
A
B
C
F
0
0
0
0
1
1
0
0
1
0
2
0
1
0
1
3
0
1
1
1
4
1
0
0
0
5
1
0
1
0
6
1
1
0
0
7
1
1
1
0
45. Составьте таблицу истинности для функции
4)B ( A C)
A
B
C
F
0
0
0
0
0
1
0
0
1
0
2
0
1
0
0
3
0
1
1
0
4
1
0
0
1
5
1
0
1
1
6
1
1
0
0
7
1
1
1
1
46. Упрощение выражений
1a b b a c
2
a b b c a
3
a c c b a
47. Упрощение выражений
1(( A B ) B ) ( A B )
2
( A B) ( A B C )
3
( A B С ) ( A B)
4
( A B) ( B C ) A B
48. ЕГЭ-2012 А10 Знание основных понятий и законов математической логики
Укажите, какое логическое выражениеравносильно выражению ¬A \/ ¬ (¬B \/ ¬C)
1
¬A \/ B \/ ¬C
2
¬ A \/ (B /\ C)
3
A \/ B \/ C
4
A \/ ¬B \/ ¬C
49. Задачи (упрощение)
49Логические основы компьютеров, 10 класс
Задачи (упрощение)
Какое логическое выражение равносильно
выражению
A ¬(¬B C)?
1)A B C
1) ¬A ¬B ¬C
2) A B C
2) A ¬B ¬C
3) A B C
3) A B ¬C
4) A B C
4) A ¬B C
A ( B C) A B C A B C
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
50. Запишите логическую функцию, соответствующую логической схеме и упростите
X1X2
И
И
Л
И
НЕ
НЕ
X3
И
Л
И
НЕ
Y
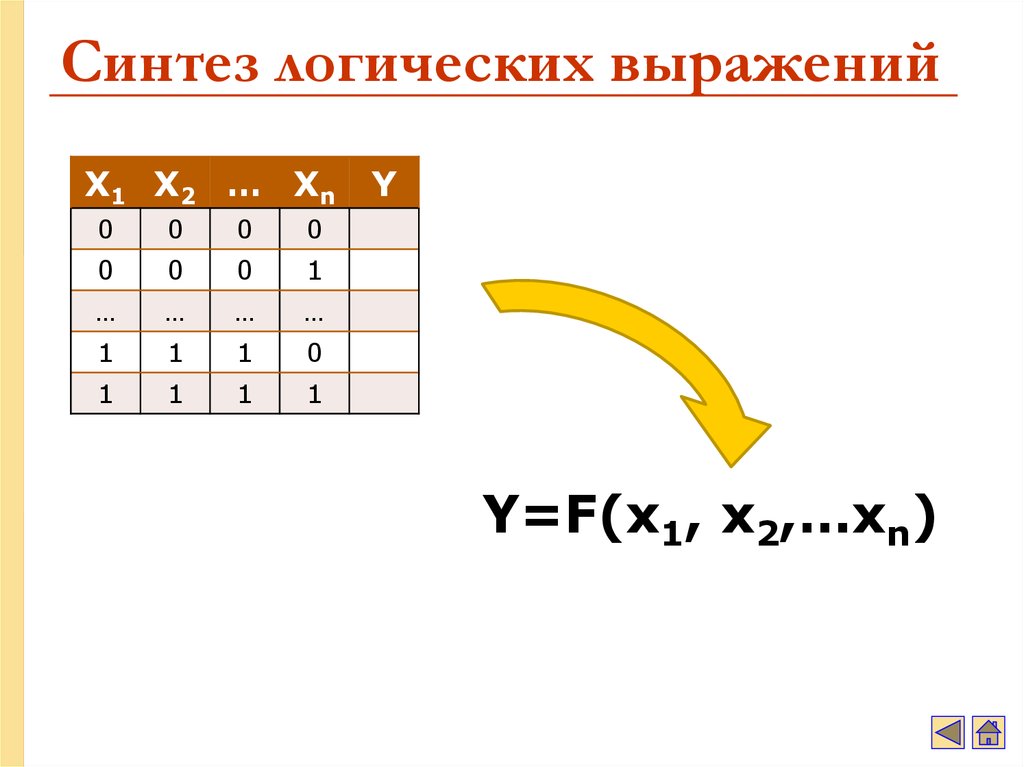
51. Синтез логических выражений
X1 X2 … X n0
0
0
0
0
0
0
1
…
…
…
…
1
1
1
0
1
1
1
1
Y
Y=F(x1, x2,…xn)
52. Совершенная дизъюнктивная нормальная форма
Задана F(x1,x2,..xn)СДНФ – форма, в которой функция представлена в виде
логической суммы, каждое слагаемое является
произведением всех переменных или их отрицаний.
F( x1 , x 2 ) x1 x 2 x1 x 2
F( x1 , x2 , x3 ) x1 x2 x3 x1 x2 x3 x1 x2 x3
F(A, B, C) A B C A B C A B C
F(A, B, C) A B C A B C A C
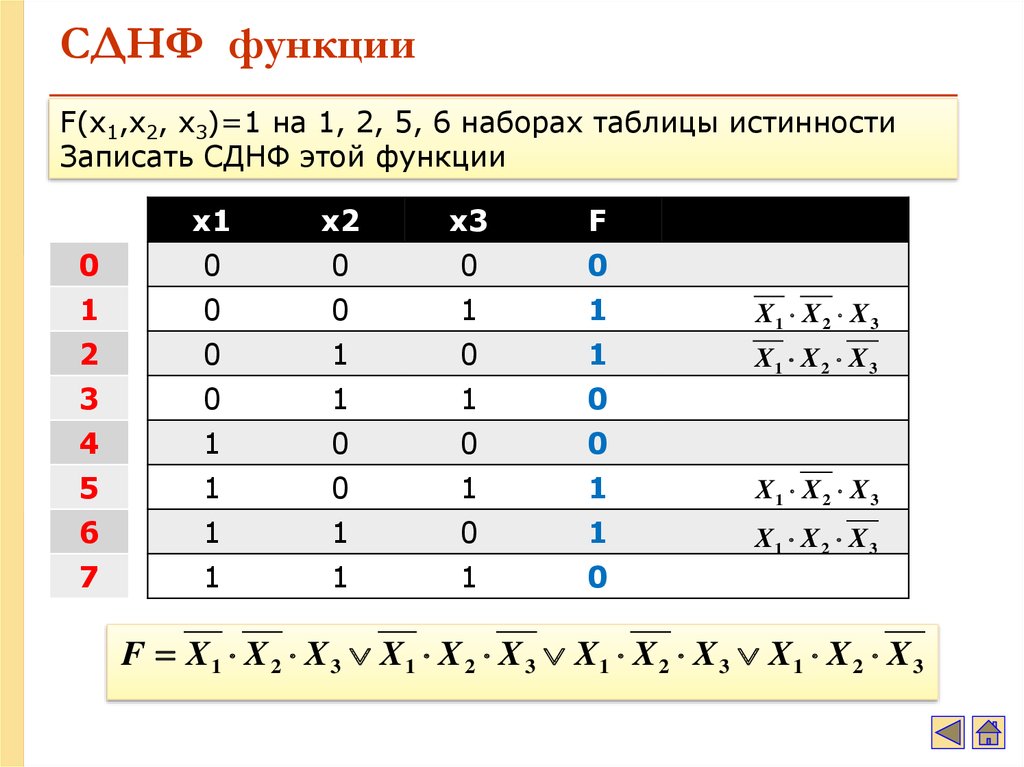
53. СДНФ функции
F(x1,x2, x3)=1 на 1, 2, 5, 6 наборах таблицы истинностиЗаписать СДНФ этой функции
x1
x2
x3
F
0
0
0
0
0
1
0
0
1
1
X1 X 2 X 3
2
0
1
0
1
X1 X 2 X 3
3
0
1
1
0
4
1
0
0
0
5
1
0
1
1
X1 X 2 X 3
6
1
1
0
1
X1 X 2 X 3
7
1
1
1
0
F X1 X 2 X 3 X1 X 2 X 3 X1 X 2 X 3 X1 X 2 X 3
54. СДНФ функции
F(x1,x2, x3)=1 на 1, 2, 5, 6 наборах таблицы истинностиЗаписать СДНФ этой функции
F X1 X 2 X 3 X1 X 2 X 3 X1 X 2 X 3 X1 X 2 X 3
Упростим функцию
F = X 2 X 3 ∨X 2 X 3
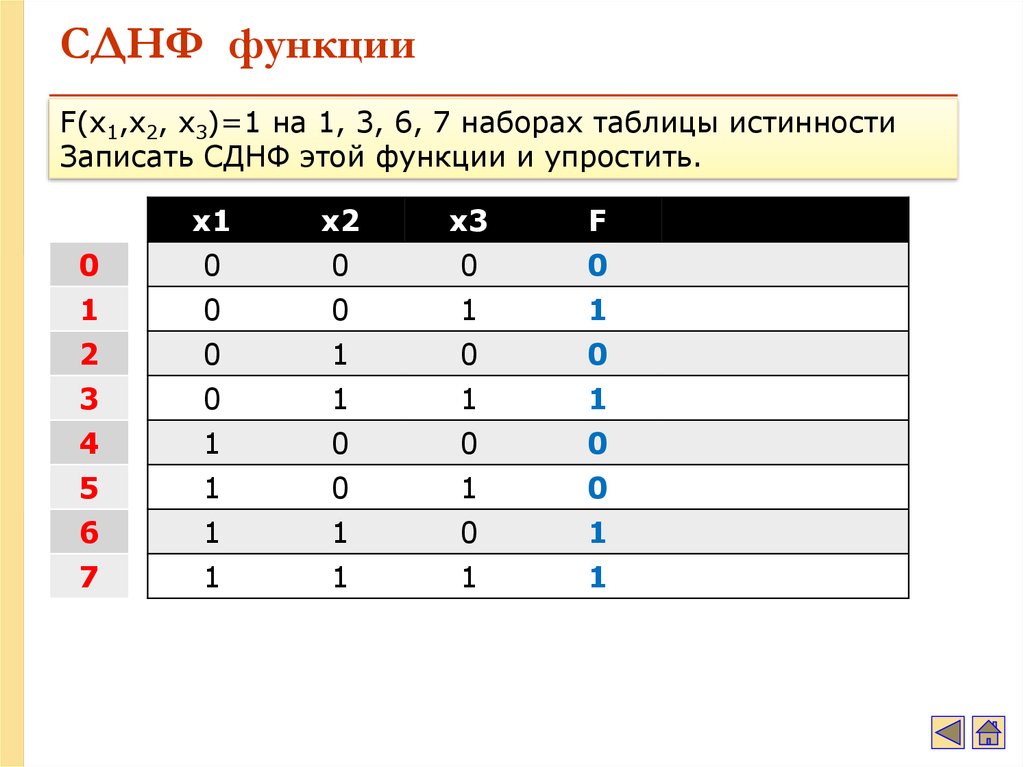
55. СДНФ функции
F(x1,x2, x3)=1 на 1, 3, 6, 7 наборах таблицы истинностиЗаписать СДНФ этой функции и упростить.
x1
x2
x3
F
0
0
0
0
0
1
0
0
1
1
2
0
1
0
0
3
0
1
1
1
4
1
0
0
0
5
1
0
1
0
6
1
1
0
1
7
1
1
1
1
56. СДНФ функции
F(x1,x2, x3)=1 на 3, 5, 6, 7 наборах таблицы истинностиЗаписать СДНФ этой функции и упростить.
x1
x2
x3
F
0
0
0
0
0
1
0
0
1
0
2
0
1
0
0
3
0
1
1
1
4
1
0
0
0
5
1
0
1
1
6
1
1
0
1
7
1
1
1
1
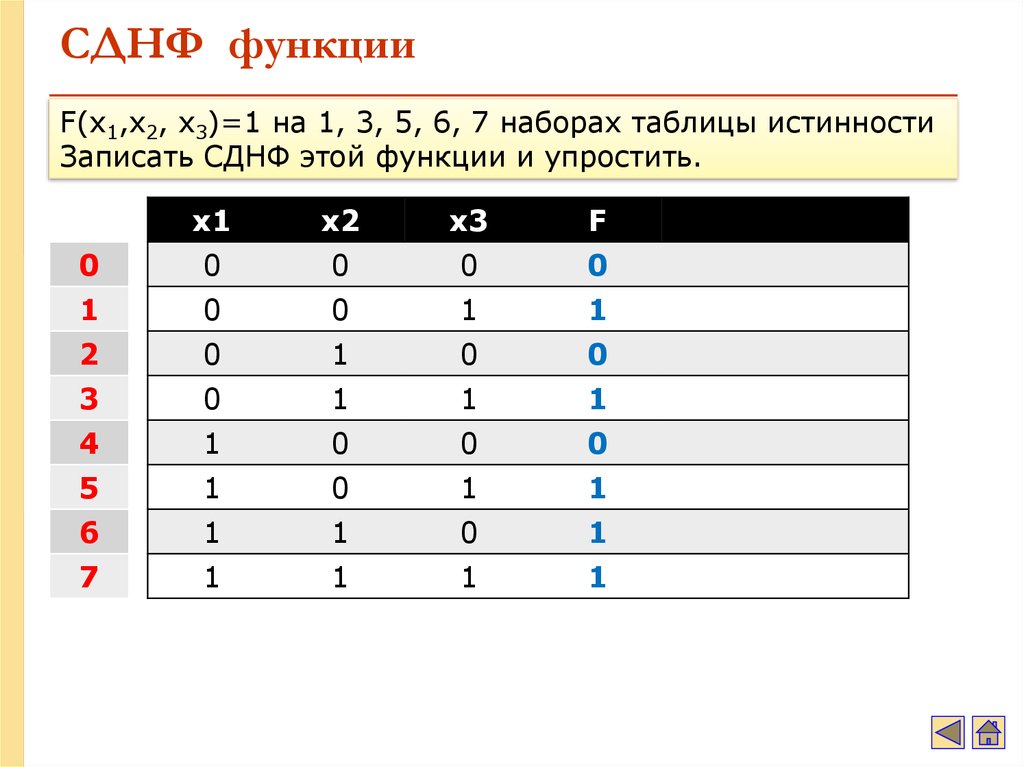
57. СДНФ функции
F(x1,x2, x3)=1 на 1, 3, 5, 6, 7 наборах таблицы истинностиЗаписать СДНФ этой функции и упростить.
x1
x2
x3
F
0
0
0
0
0
1
0
0
1
1
2
0
1
0
0
3
0
1
1
1
4
1
0
0
0
5
1
0
1
1
6
1
1
0
1
7
1
1
1
1
58. СДНФ функции ДЗ
1) F(x1,x2, x3)=1 на 0, 2, 6, 7 наборах таблицы истинности2) F(x1,x2, x3)=1 на 0, 1, 2, 3, 4 наборах таблицы истинности
Записать СДНФ этих функций и упростить.
59. СДНФ функции AB
СДНФ функции A BА
В
F
0
0
0
1
1
0
1
1
2
1
0
0
3
1
1
1
A B
A B
A B
A B A B A B A B
A A B
A B A B
A B
60. СДНФ функции AB
СДНФ функции A BА
В
F
0
0
0
1
1
0
1
0
2
1
0
0
3
1
1
1
A B
A B
A B A B A B
61. СДНФ функции AB
СДНФ функции A BА
В
F
0
0
0
0
1
0
1
1
2
1
0
1
3
1
1
0
A B
A B
A ⊕B = AB ∨AB
62. ЕГЭ-2012 А10 Знание основных понятий и законов математической логики
Для какого имени ложно высказывание:Первая буква имени согласная Последняя
буква имени гласная ?
1
Егор
2
Максим
3
Саша
4
Юля
63. ЕГЭ-2012 А10 Знание основных понятий и законов математической логики
(2012-демо) Какое из приведенных имен удовлетворяетлогическому условию:
вторая буква согласная)
(предпоследняя буква гласная последняя буква
(первая буква согласная
гласная)?
1
Кристина
2
Степан
3
Максим
4
Мария
64. Логические уравнения
1.Каково наибольшее целое число X, прикотором истинно высказывание
(90<X·X) (X < (X -1))
65. Логические уравнения
3. Укажите значения логическихпеременных K, L, M, N, при которых
логическое выражение
(K M) (M ¬L N) ложно.
К=
L=
M=
N=
66. Логические уравнения
Сколько различных решений имеетуравнение
(¬K ¬ L ¬ M) (L ¬ M ¬ N)) = 0
К=
L=
M=
N=
67. Логические уравнения
Найти все решения уравнения((B \/ C)⋅ A)→(A ⋅ C \/ D)= 0
A=
B=
C=
D=
68. Логические уравнения
Найти все решения уравненияA \/ B \/ (B→(C \/ D)= 0
A=0
B=
1
C=0
D=0
69. Использование алгебры логики
Следующие два высказывания истинны:1. Неверно, что если корабль A вышел в море, то
корабль C – нет.
2. В море вышел корабль B или корабль C, но не
оба вместе.
Определить, какие корабли вышли в море.
A C 0 или
A C 1
B C 1
( A C ) (B C ) 1
70. Использование алгебры логики
По обвинению в ограблении перед судомпредстали три человека - Иванов, Петров и
Сидоров. Установлено следующее:
1) если Иванов невиновен, или Петров виновен,
то Сидоров виновен;
2) если Иванов невиновен, то Сидоров
невиновен.
Установить, виновен ли Иванов.
71. Использование алгебры логики
Четверо друзей Андрей, Борис, Сергей и Дмитрийрешили пойти на рыбалку. Но Дмитрий в
последний момент отказался и высказал
следующие предположения:
1) Если Андрей не пойдет на рыбалку, то
Борис обязательно пойдет;
2) Не верно, что пойдут Андрей и Сергей;
3) Борис пойдет на рыбалку или пойдет
Сергей;
4) Если пойдет Борис, то пойдет на рыбалку
и Сергей.
Все предположения Дмитрия оказались
истинными. Кто пошел на рыбалку?
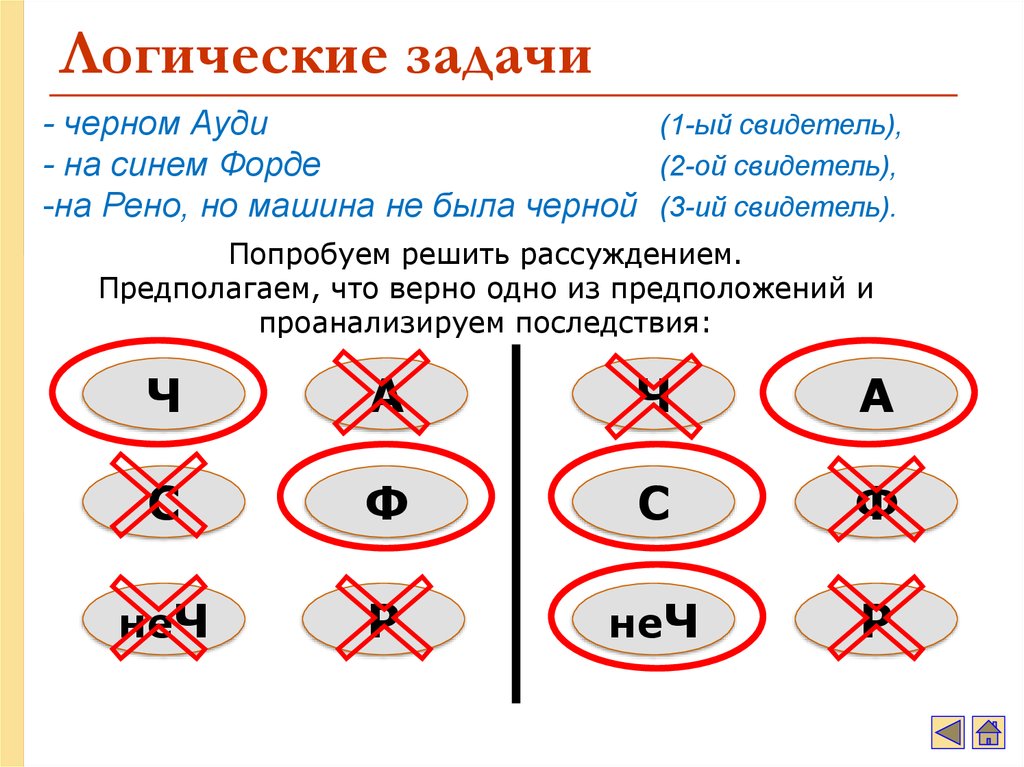
72. Логические задачи
•Три свидетеля дали показания о том, что преступники скрылись сместа преступления на:
- черном Ауди
(1-ый свидетель),
- на синем Форде
(2-ой свидетель),
-на Рено, но машина не была черной (3-ий свидетель).
Оказалось, что каждый свидетель в одном своем утверждении был
прав, а в одном ошибся. На какой машине скрылись преступники?
Ч А 1
Ч А Ч А 1
С Ф 1
С Ф С Ф 1
Ч Р 1
Ч Р Ч Р 1
73. Логические задачи
- черном Ауди(1-ый свидетель),
- на синем Форде
(2-ой свидетель),
-на Рено, но машина не была черной (3-ий свидетель).
Ч А Ч А 1
С Ф С Ф 1
Ч Р Ч Р 1
(Ч А Ч А) (С Ф С Ф) (Ч Р Ч Р ) 1
Учтем условия:
Ч С 0
А Ф 0
Ф Р 0
А Р 0
Упростим выражение и получим:
Ч С А Ф Р 1
74. Логические задачи
- черном Ауди(1-ый свидетель),
- на синем Форде
(2-ой свидетель),
-на Рено, но машина не была черной (3-ий свидетель).
Попробуем решить рассуждением.
Предполагаем, что верно одно из предположений и
проанализируем последствия:
Ч
А
Ч
А
C
Ф
C
Ф
неЧ
Р
неЧ
Р
75. Логические задачи
Алеша, Боря и Володя нашли в море сосуд.•Алеша сказал: «Это сосуд греческий,
изготовлен в 5-ом веке до н.э.»
•Боря сказал: «Это сосуд
финикийский, 3-го века до н.э.».
•Володя предположил: «Сосуд
негреческий, изготовлен в 4-ом веке
до н.э.».
Учитель осмотрел сосуд и сделал вывод, что каждый из
ребят был прав только в чем-то одном. Определите, чей это
сосуд, и в каком веке изготовлен.
76. Логические задачи
Перед началом Турнира Четырех болельщики высказалиследующие предположения по поводу своих кумиров:
А) Макс победит, Билл – второй;
В) Билл – третий, Ник – первый;
С) Макс – последний, а первый – Джон.
Когда соревнования закончились, оказалось, что каждый
из болельщиков был прав только в одном из своих
прогнозов.
Какое место на турнире заняли Джон, Ник, Билл, Макс?
77. Логические задачи
Д, Даша и Маша остались дома одни. Кто-то из нихел варенье. На вопрос мамы, кто это сделал, они
сказали:
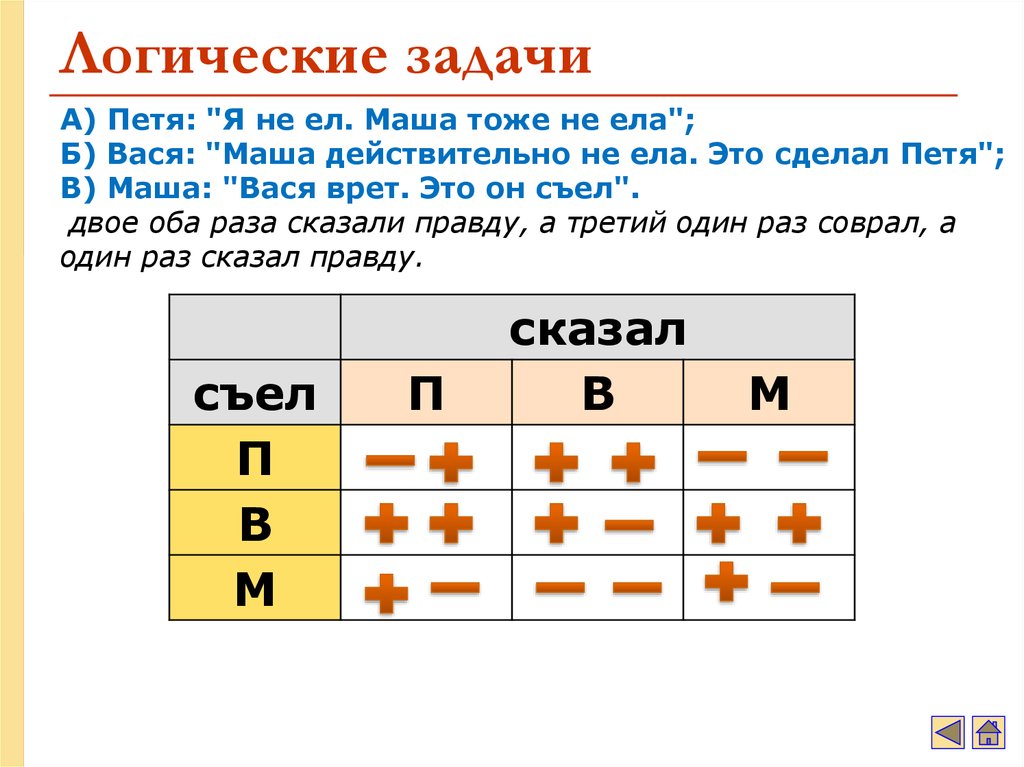
А) Петя: "Я не ел. Маша тоже не ела";
Б) Вася: "Маша действительно не ела. Это
сделал Петя";
В) Маша: "Вася врет. Это он съел".
Выясните, кто ел варенье, если известно,
что двое оба раза сказали правду, а
третий один раз соврал, а один раз сказал правду.
78. Логические задачи
А) Петя: "Я не ел. Маша тоже не ела";Б) Вася: "Маша действительно не ела. Это сделал Петя";
В) Маша: "Вася врет. Это он съел".
двое оба раза сказали правду, а третий один раз соврал, а
один раз сказал правду.
съел
П
В
М
П
сказал
В
М
79. Логические задачи
Девять школьников, остававшихся в классе на перемене,были вызваны к директору. Один из них разбил окно в
кабинете. На вопрос директора, кто это сделал, были
получены следующие ответы:
Володя: «Это сделал Саша».
Аня: «Володя лжет!»
Егор: «Маша разбила».
Саша: «Аня говорит неправду!»
Рома: «Разбила либо Маша, либо Нина…»
Маша: «Это я разбила!»
Нина: «Маша не разбивала!»
Коля: «Ни Маша, ни Нина этого не делали».
Олег: «Нина не разбивала!»
Кто разбил окно, если известно, что из этих девяти
высказываний истинны только три?
80. Логические задачи
(На одной улице стоят в ряд 4 дома, в которых живут4 человека: Алексей, Егор, Виктор и Михаил.
Известно, что каждый из них владеет ровно одной из
следующих профессий:
Токарь, Столяр, Хирург и Окулист, но неизвестно, кто
какой и неизвестно, кто в каком доме живет.
Однако, известно, что:
1) Токарь живет левее Столяра
2) Хирург живет правее Окулиста
3) Окулист живет рядом со Столяром
4) Токарь живет не рядом со Столяром
5) Виктор живет правее Окулиста
6) Михаил не Токарь
7) Егор живет рядом со Столяром
8) Виктор живет левее Егора
Выясните, кто какой профессии, и кто где живет.
81. Логические задачи
Аня, Вика и Сергей решили пойти в кино.Учитель хорошо знавший этих ребят, высказал следующие
предположения:
Аня пойдет в кино только тогда, когда пойдут Вика и Сергей;
Аня и Сергей пойдут в кино вместе или же оба останутся
дома;
чтобы Сергей пошел в кино, необходимо, чтобы пошла Вика.
Когда ребята пошли в кино, оказалось, что учитель немного
ошибался, из трех его утверждений истинными оказались
только два.
Кто из названных ребят пошел в кино?
82.
82Диаграммы Вена (круги Эйлера)
A
A
A
B
B
A·B
A
A+B
A
A
A
B
A B
B
A B
B
A B
83.
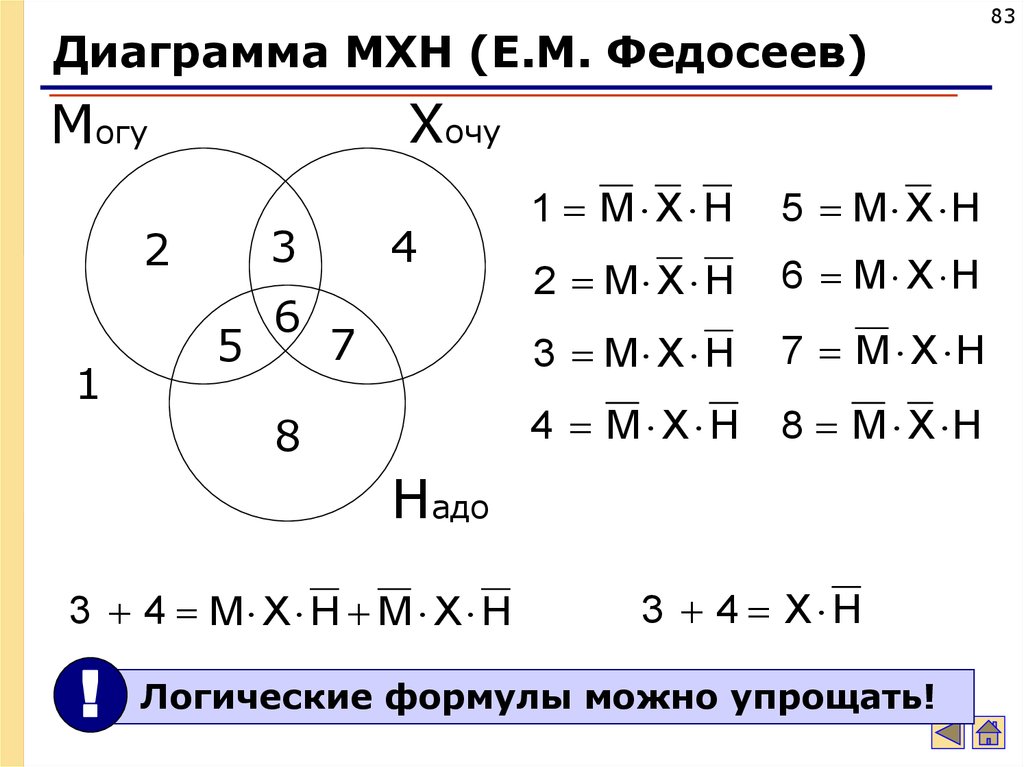
Диаграмма МХН (Е.М. Федосеев)Хочу
Могу
3
2
1
5
6
4
7
8
1 M X H
5 M X H
2 M X H
6 M X H
3 M X H
7 M X H
4 M X H
8 M X H
Надо
3 4 M X H M X H
!
3 4 X H
Логические формулы можно упрощать!
83
84. Задачи
84Логические основы компьютеров, 10 класс
Задачи
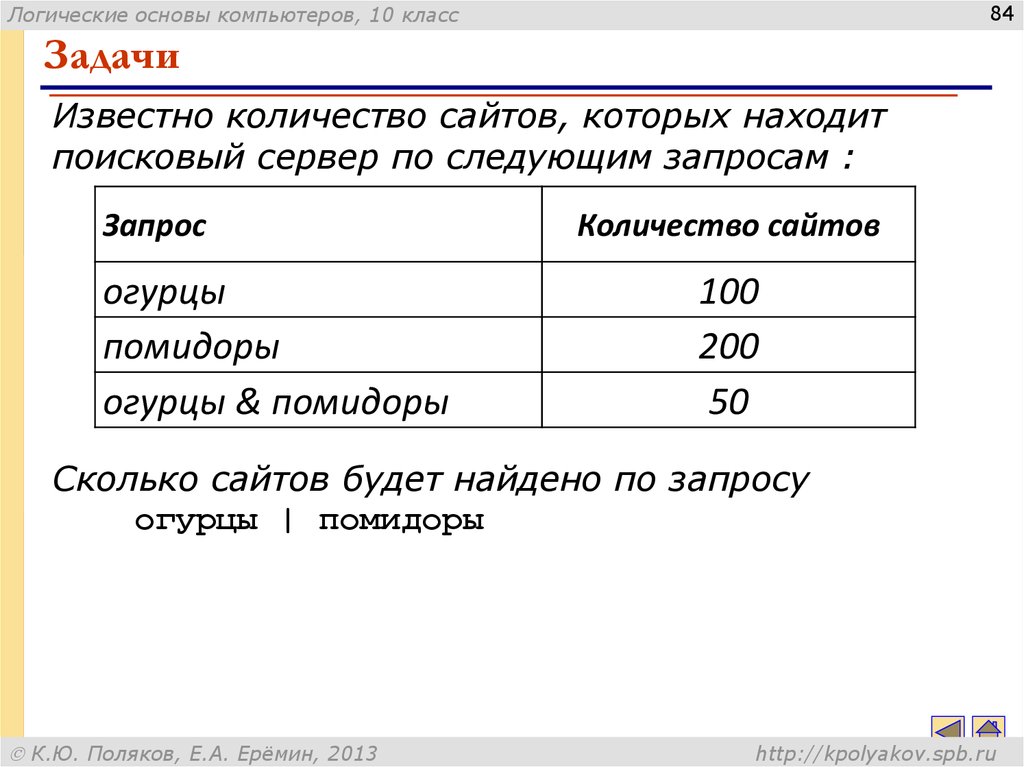
Известно количество сайтов, которых находит
поисковый сервер по следующим запросам :
Запрос
огурцы
помидоры
огурцы & помидоры
Количество сайтов
100
200
50
Сколько сайтов будет найдено по запросу
огурцы | помидоры
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
85. Задачи
85Логические основы компьютеров, 10 класс
Задачи
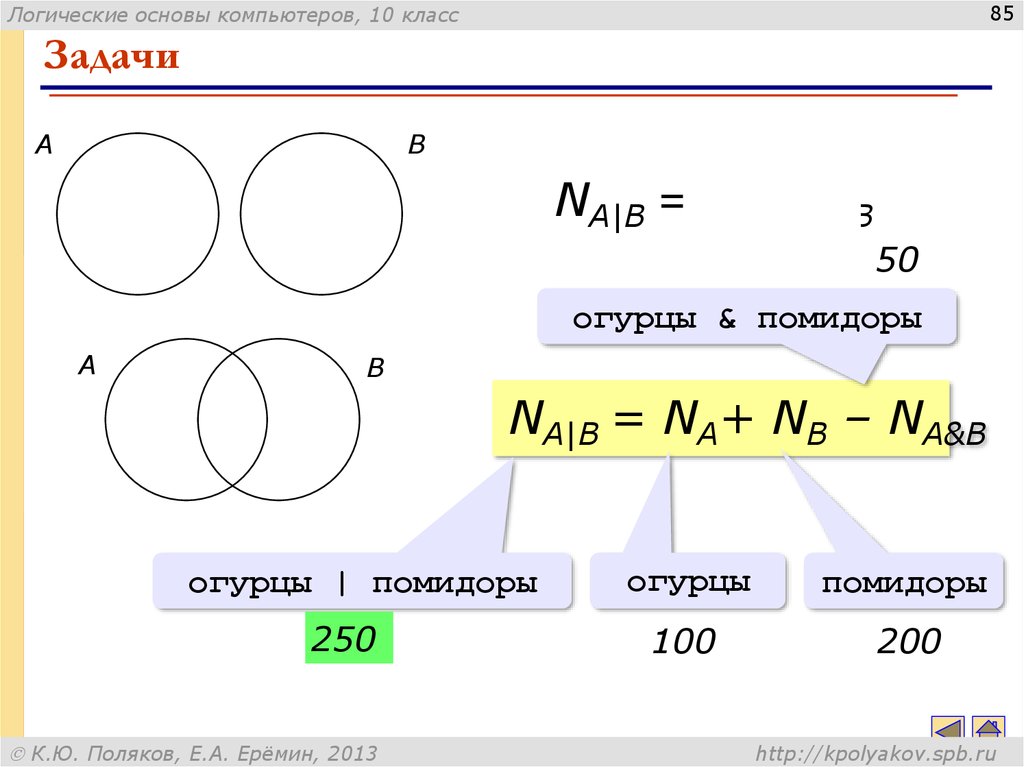
A
B
NA|B = NA+ NB
50
огурцы & помидоры
A
B
NA|B = NA+ NB – NA&B
огурцы | помидоры
250
К.Ю. Поляков, Е.А. Ерёмин, 2013
огурцы
помидоры
100
200
http://kpolyakov.spb.ru
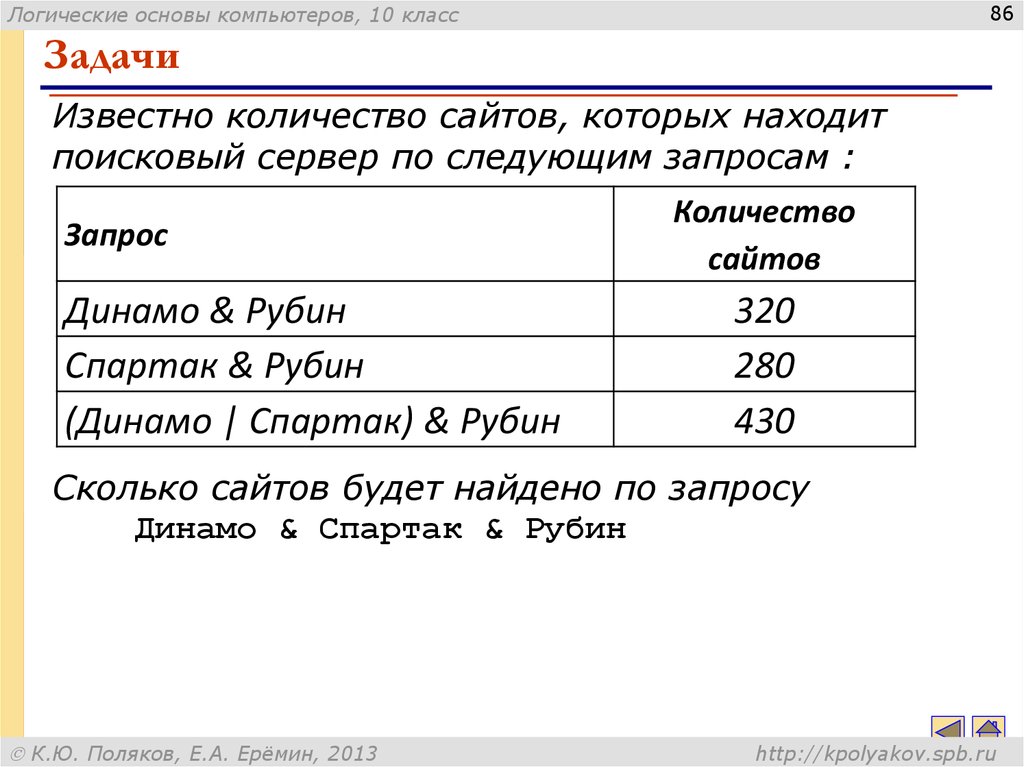
86. Задачи
86Логические основы компьютеров, 10 класс
Задачи
Известно количество сайтов, которых находит
поисковый сервер по следующим запросам :
Запрос
Динамо & Рубин
Спартак & Рубин
(Динамо | Спартак) & Рубин
Количество
сайтов
320
280
430
Сколько сайтов будет найдено по запросу
Динамо & Спартак & Рубин
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
87. Задачи
87Логические основы компьютеров, 10 класс
Задачи
Спартак
Динамо
Динамо & Рубин
= 1 + 2 = 320
1
Спартак & Рубин
= 2 + 3 = 280
2
3
Рубин
(Динамо | Спартак) & Рубин
= 1 + 2 + 3 = 430
Динамо & Спартак & Рубин
= 2
= (320 + 280) – 430 = 17
0
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
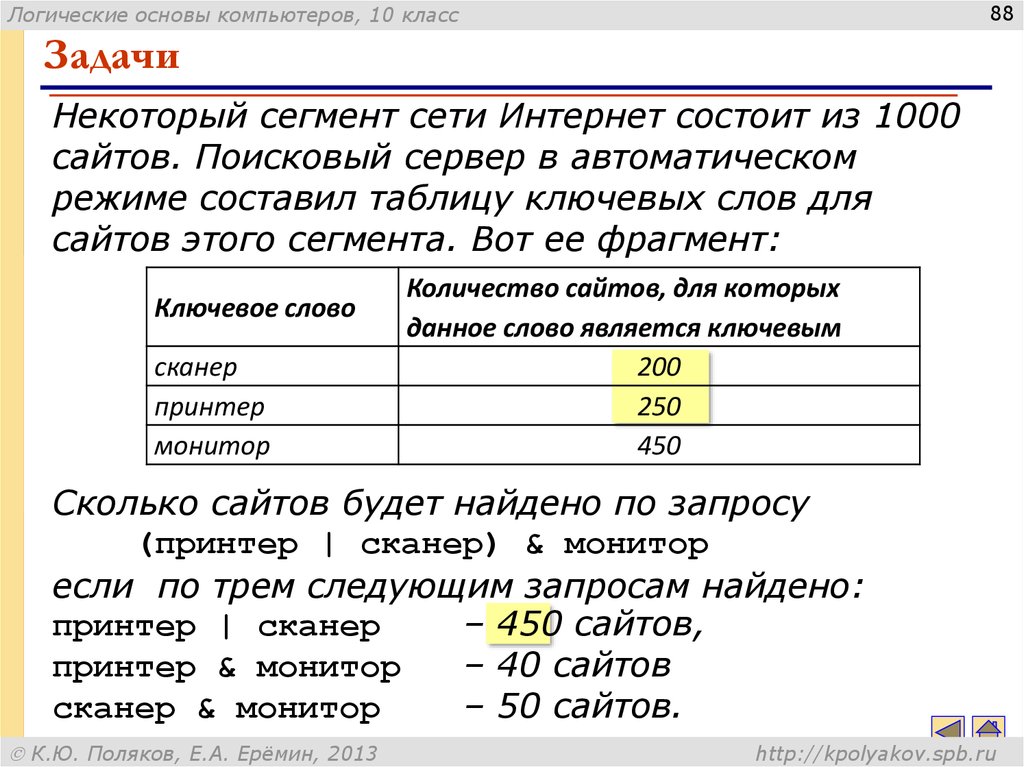
88. Задачи
88Логические основы компьютеров, 10 класс
Задачи
Некоторый сегмент сети Интернет состоит из 1000
сайтов. Поисковый сервер в автоматическом
режиме составил таблицу ключевых слов для
сайтов этого сегмента. Вот ее фрагмент:
Ключевое слово
сканер
принтер
монитор
Количество сайтов, для которых
данное слово является ключевым
200
250
450
Сколько сайтов будет найдено по запросу
(принтер | сканер) & монитор
если по трем следующим запросам найдено:
принтер | сканер
– 450 сайтов,
принтер & монитор
– 40 сайтов
сканер & монитор
– 50 сайтов.
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
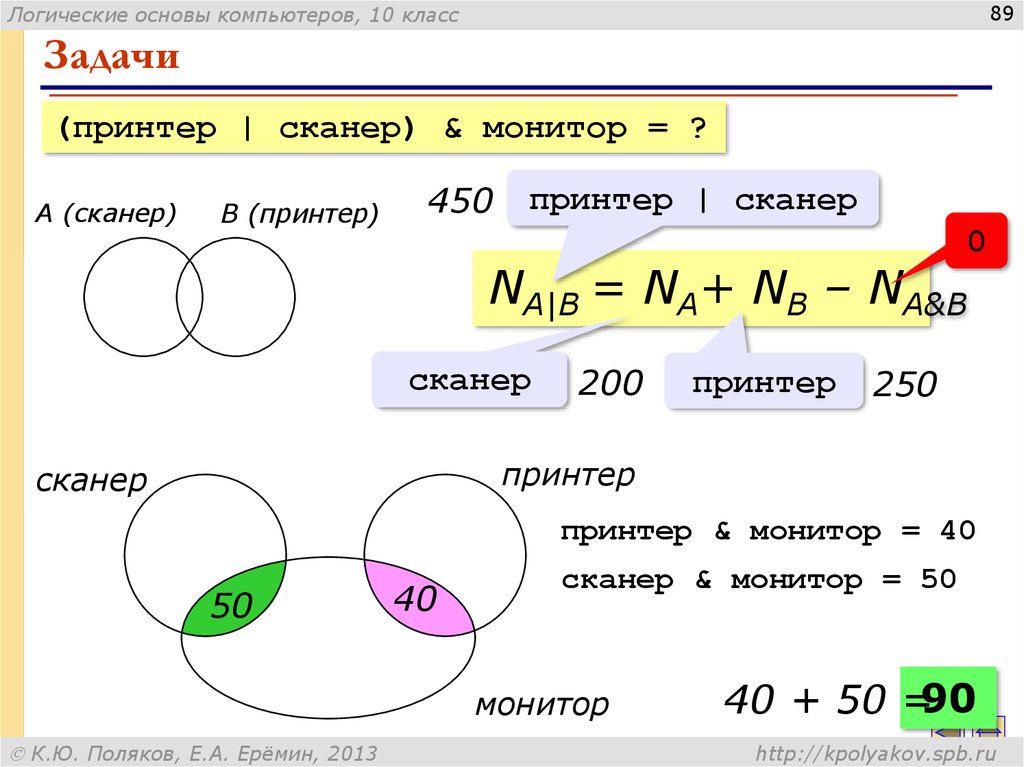
89. Задачи
89Логические основы компьютеров, 10 класс
Задачи
(принтер | сканер) & монитор = ?
А (сканер)
B (принтер)
450
принтер | сканер
0
NA|B = NA+ NB – NA&B
сканер
200
принтер
250
принтер
сканер
принтер & монитор = 40
50
40
сканер & монитор = 50
монитор
К.Ю. Поляков, Е.А. Ерёмин, 2013
40 + 50 =90
http://kpolyakov.spb.ru
90. Сложная задача
90Логические основы компьютеров, 10 класс
Сложная задача
Ниже приведены запросы и количество страниц, которые
нашел поисковый сервер по этим запросам в некотором
сегменте Интернета:
мезозой
500
кроманьонец
600
неандерталец
700
мезозой | кроманьонец
800
мезозой | неандерталец
1000
неандерталец & (мезозой | кроманьонец) 200
Сколько страниц будет найдено по запросу
кроманьонец & (мезозой | неандерталец)
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
91.
91§ 23. Предикаты и
кванторы
92. Предикаты
Логические основы компьютеров, 10 класс92
Предикаты
Предикат (логическая функция) – это
утверждение, содержащее переменные.
Предикат-свойство – от одной переменной:
P(N) = «В городе N живут более 2 млн
человек»
P(Москва) = 1
P(Якутск) = 0
Простое(x) = «x – простое число»
Спит(x) = «x всегда спит на уроке»
Предикат-отношение – от нескольких
переменных:
Больше(x, y) = «x > y»
Живет(x, y) = «x живет в городе y» http://kpolyakov.spb.ru
К.Ю. Поляков, Е.А. Ерёмин, 2013
93. Предикаты и кванторы
93Логические основы компьютеров, 10 класс
Предикаты и кванторы
Предикаты задают множества:
P( x ) ( x 0)
P( x, y ) ( x y 1)
Предикаты, которые всегда истинны:
P( x) ( x 2 0) для всех вещественных чисел
«Для любого допустимого x утверждение P(x)
истинно»:
высказыван
квантор
x P(x )
ие
Квантор – знак, обозначающий количество.
А
(all – все)
К.Ю. Поляков, Е.А. Ерёмин, 2013
E
(exists – существует)
http://kpolyakov.spb.ru
94. Кванторы
94Логические основы компьютеров, 10 класс
Кванторы
Какой квантор использовать?
«
… моря соленые».
«
… кошки серые».
«
… числа чётные».
«
… окуни – рыбы».
«
… прямоугольники – квадраты».
«
… квадраты – прямоугольники».
Истинно ли высказывание?
x P(x ) при P( x ) ( x 0)
x P(x ) при P( x ) ( x 0)
x P(x ) при P( x) ( x 2 0)
x P(x ) при P( x) ( x 2 0)
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
95. Кванторы
95Логические основы компьютеров, 10 класс
Кванторы
Дано:
A = «Все люди смертны» = 1.
B = «Сократ – человек» = 1.
Доказать:
C = «Сократ смертен» = 1.
Доказательство:
A
0
0
B
0
1
А B
1
1
1
1
0
1
0
1
P(x) = «x – человек»
Q(x) = «x –
x (P( x ) Q( x))
смертен»
A = 1:
P( Сократ) Q( Сократ) 1
при
x =Сократ»
P(«Сократ
) 1
B = 1:
Q( Сократ) 1
по свойствам импликации
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
96. Несколько кванторов
96Логические основы компьютеров, 10 класс
Несколько кванторов
Квантор связывает одну переменную:
x P( x, y ) – предикат от переменной y
y P( x, y ) – предикат от переменной x
Два квантора связывают две переменных:
x y P( x, y ) – высказывание «для любого x
существует y, при котором
x,y)=1»
x y P( x, y ) – P(
высказывание
«существует
x,
такой что при любом y верно
P(x,y)=1» высказывания при:
Сравните два последних
P( x, y ) ( x y 0)
К.Ю. Поляков, Е.А. Ерёмин, 2013
P( x, y ) ( x y 0)
http://kpolyakov.spb.ru
97. Отрицание
97Логические основы компьютеров, 10 класс
Отрицание
НЕ «для любого
x выполняется P(x)»
«существует x, при котором не выполняется P(x)»
x P(x) x P(x)
НЕ «существует x, при котором выполняется
P(x)»
«для любого x не выполняется P(x)»
x P(x) x P(x)
К.Ю. Поляков, Е.А. Ерёмин, 2013
http://kpolyakov.spb.ru
98.
ЕГЭ -2016 -2F = (¬z) x x y.
Задана лог. функция
Определите, какому столбцу таблицы истинности функции F
соответствует каждая из переменных x, y, z.
Перем.1
Перем 2. Перем 3. Функция
???
???
???
F
0
0
0
0
0
1
0
0
1
0
0
0
1
1
0
0
0
0
1
1
0
1
1
1
1
0
1
0
1
1
1
1
99. ЕГЭ -2016 -2
ЕГЭ -2015 -2Александра заполняла таблицу истинности для выражения F. Она
успела заполнить лишь небольшой фрагмент таблицы:
x1
1
x2
0
x3
x4
x5
0
1
x6
x7
x8
1
1
F
0
1
1
Каким выражением может быть F?
1) x1 /\ ¬x2 /\ x3 /\ ¬x4 /\ x5 /\ x6 /\ ¬x7 /\ ¬x8
2) x1 \/ x2 \/ x3 \/ ¬x4 \/ ¬x5 \/ ¬x6 \/ ¬x7 \/ ¬x8
3) ¬x1 /\ x2 /\ ¬x3 /\ x4 /\ x5 /\ ¬x6 /\ x7 /\ x8
4) x1 \/ ¬x2 \/ x3 \/ ¬x4 \/ ¬x5 \/ ¬x6 \/ ¬x7 \/ ¬x8
100. ЕГЭ -2015 -2
ЕГЭ -2016 -23Сколько существует различных наборов значений
логических переменных
x1, x2, ... x9, y1, y2, ... y9, которые удовлетворяют
всем перечисленным ниже условиям?
(¬ (x1 ≡ y1)) ≡ (x2 ≡ y2)
(¬ (x2 ≡ y2)) ≡ (x3 ≡ y3)
…
(¬ (x8 ≡ y8)) ≡ (x9 ≡ y9)













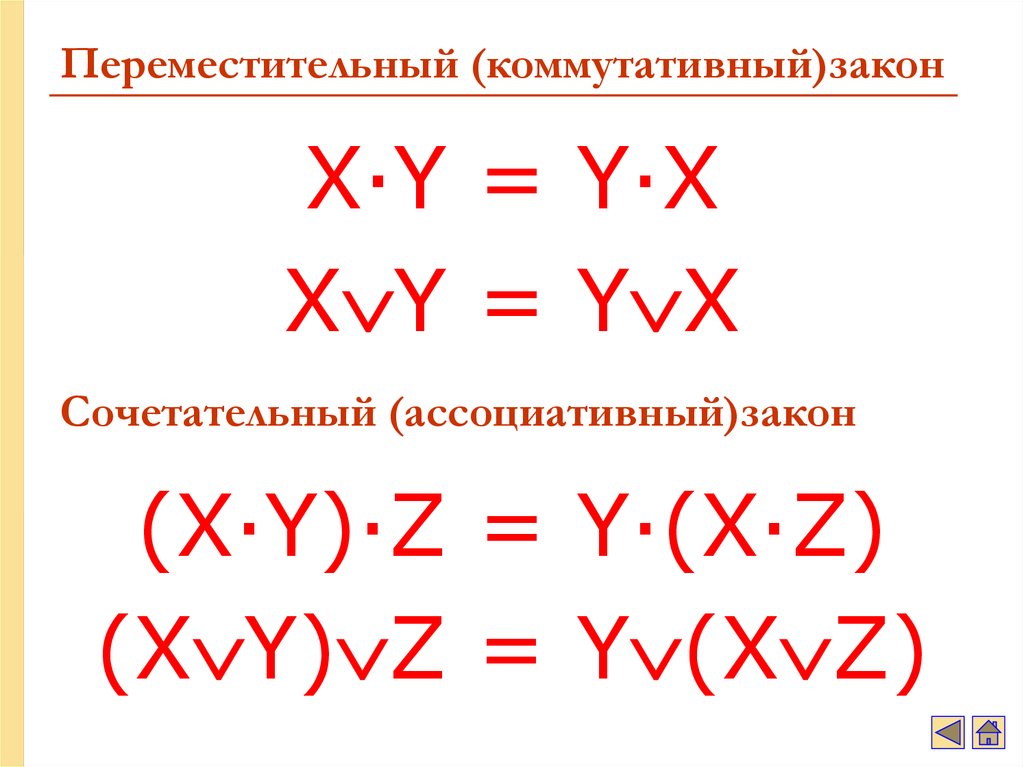




















































 Информатика
Информатика








