Теорема Эйлера, малая теорема Ферма; теорема Вильсона

1. Теорема Эйлера, малая теорема Ферма; теорема Вильсона

МБОУ-гимназия№ 13
Теорема Эйлера, малая
теорема Ферма; теорема
Вильсона
Выполнила: Апухтина Валерия
Руководитель Чистова Ирина Анатольевна
Учитель математики
п. Краснообск

2.

Цель:
1. Познакомиться с теоремами Эйлера, Ферма и теоремой Вильсона.
2. Рассмотреть примеры решений задач с помощью данных теорем
Содержание:
1.Теорема Эйлера
2.Доказательство теоремы Эйлера
3.Примеры решения задач по теореме Эйлера
4.Малая теорема Ферма
5.Примеры решения задач по теореме Ферма
6.Теорема Вильсона
7.Следствие
8.Доказательство
9.Примеры решения задач по теореме Вильсона
10.Литература

3. Теорема Эйлера

Теоре́ма Э́йлера в теории чисел гласит, что
Если a и m взаимно просты, то , где — функция
Эйлера
Частным случаем теоремы Эйлера при простом m
является малая теорема Ферма. В свою очередь,
теорема Эйлера является следствием теоремы
Лагранжа.
Доказательство
Пусть
— все различные натуральные
числа, меньшие m и взаимно простые с ним.
Рассмотрим всевозможные произведения xia для
всех i от 1 до .

4. Доказательство теоремы Эйлера

Поскольку a взаимно просто с m и xi взаимно просто с m, то и xia также
взаимно просто с m, то есть
для некоторого j.
Отметим, что все остатки xia при делении на m различны.
Действительно, пусть это не так, то есть существуют такие
, что
или
Так как a взаимно просто с m, то последнее равенство равносильно тому,
что
или
Это противоречит тому, что числа
модулю m.
попарно различны по

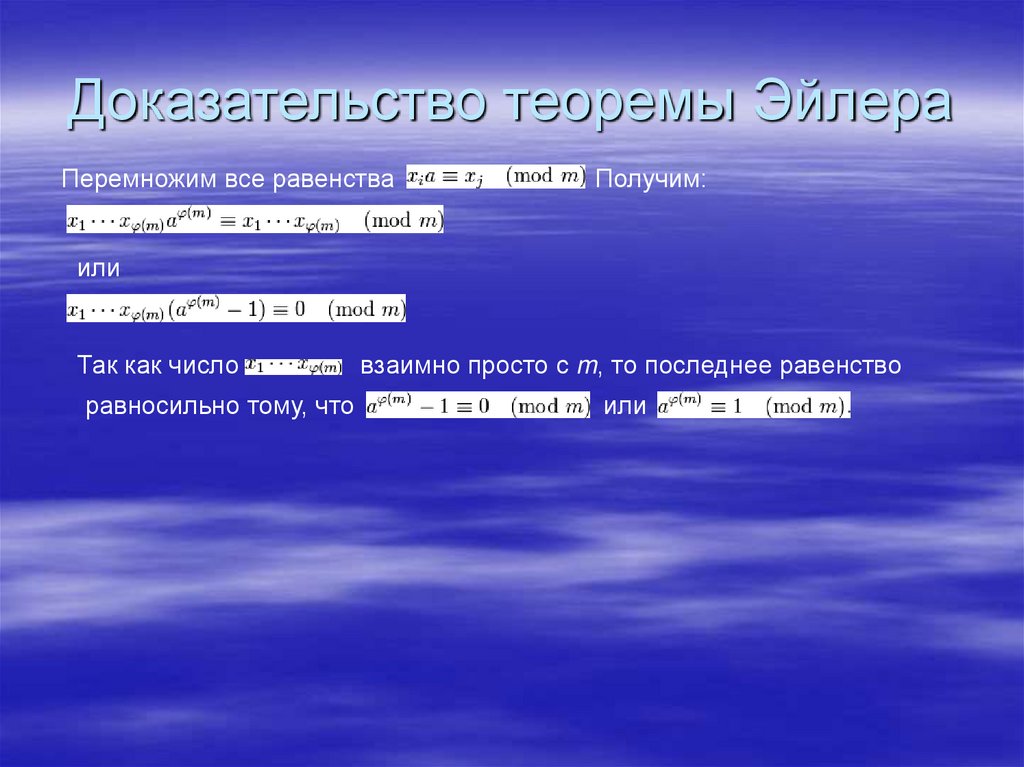
5. Доказательство теоремы Эйлера

Перемножим все равенства
Получим:
или
Так как число
равносильно тому, что
взаимно просто с m, то последнее равенство
или

6. Примеры решения задач по теореме Эйлера

1. Девятая степень однозначного числа оканчивается на 7. Найти это число.
Решение. a 9 º 7(mod 10) – это дано. Кроме того, очевидно, что (7, 10)=1 и ( a ,
10)=1. По теореме Эйлера, a j (10) º 1(mod 10). Следовательно, a 4 º 1(mod 10)
и, после возведения в квадрат, a 8 º 1(mod 10). Поделим почленно a 9 º
7(mod 10) на a 8 º 1(mod 10) и получим a º 7(mod 10). Это означает, что a=7.
2. Найти две последние цифры числа 243 402 .
Решение. Две последние цифры этого числа суть остаток от деления его на
100. Имеем: 243=200+43; 200+43 º 43(mod 100) и, возведя последнее
очевидное сравнение в 402-ую степень, раскроем его левую часть по биному
Ньютона (мысленно, конечно). В этом гигантском выражении все слагаемые,
кроме последнего, содержат степень числа 200, т.е. делятся на 100, поэтому
их можно выкинуть из сравнения, после чего понятно, почему 243 402 º 43
402 (mod 100). Далее, 43 и 100 взаимно просты, значит, по теореме Эйлера,
43 j (100) º 1(mod 100). Считаем:
j (100)= j (2 2 × 5 2 )=(10–5)(10–2)=40.

7. Примеры решения задач по теореме Эйлера

Имеем сравнение: 43 40 º 1(mod 100), которое немедленно возведем в
десятую степень и умножим почленно на очевидное сравнение,
проверенное на калькуляторе: 43 2 º 49(mod 100). Получим:
, следовательно, две последние цифры числа 243^ 402 суть 4 и 9 .

8. Малая теорема Ферма

Ма́лая теоре́ма Ферма́ — классическая теорема
теории чисел, которая утверждает что
Если p — простое число и целое a не делится на p, то
a p − 1 ≡ 1 (mod p) (или a p − 1 − 1 делится на p).Иная
формулировка:
Для любого простого p и целого a, (a p − a) делится на
p.
Примеры решений по теореме Ферма:
1. Какие числа являются элементами в Z14*?
Решение
Элементы – это 1, 3, 5, 9, 11 и 13.

9. Малая теорема Ферма (примеры решения задач)

2. Найдите результат 312 mod 11.
Решение
Здесь степень (12) и модуль (11) не соответствуют условиям теоремы
Ферма. Но, применяя преобразования, мы можем привести решение к
использованию малой теоремы Ферма.

10. Теорема Вильсона

Если p — простое, то выполняется сравнение
(p − 1)! + 1 ≡ 0(modp), (1.1)а если p — составное, то
(1.1) не выполняется.
Для доказательства нам потребуется вспомогательное
утверждение, которое интересно также и само по себе.
Лемма 1.1.1 Если НОД(a,b) = 1, то существуют целые
u,v, такие, что
au + bv = 1. (1.2)
Доказательство. Очевидно, достаточно доказать
утверждение для случая, когда a, b — натуральные
числа.
Нетривиальной частью доказательства является идея
индукции по сумме a + b. При a + b = 2 имеем a = b = 1 и
(1.2) выполняется с u = 1,v = 0. Пусть теорема верна для
всех a,b, таких что НОД(a,b) = 1, a + b < k, где k > 2.
Тогда, так как a + b > 2, НОД(a,b) = 1, то a ≠ b. Не теряя
общности можно считать, что a > b. Поскольку НОД(a −
b,b) = 1 и (a − b) + b = a < k, по индуктивному
предположению существуют целые x,y, такие, что
(a − b)x + by = 1,
или
ax + b(y − x) = 1.
Положив x = u,y − x = v, получим (1.2).

11. Теорема Вильсона (следствие)

Следствие 1.1.1 Если a > 1,b > 1, НОД(a,b) = 1, то для каждого k =
0, 1,… существуют единственные целые числа u, v, такие, что
выполняется
au − bv = 1,kb + 1 < u < (k + 1)b,k = 0, 1,… (1.3)
Доказательство. Существование u, v следует из леммы 1.1.1.
Докажем единственность. Предположим, от противного, что имеются
такие числа u′, v′, для которых u′ ≠ u, v′ ≠ v с условием kb + 1 < u′ < (k
+ 1)b и
au′− bv′ = 1. (1.4)Вычитая из (1.3) почленно (1.4) получим
a(u − u′) = b(v − v′).
Так как НОД(a,b) = 1, то (u − u′)⋮b, но
1 − b < u − u′ < b − 1,
следовательно, u − u′ = 0, и, поэтому, v − v′ = 0. Таким образом, u =
u′, v = v′ и получено противоречие.

12. Теорема Вильсона (доказательство)

Доказательство теоремы 1.1.1 Вильсона. Предположим p — простое, p > 3 (для
случаев p = 2, p = 3 утверждение теоремы не трудно проверить непосредственным
вычислением). Докажем, что все числа
2, 3,…,p − 2 (1.5)распадаются на пары чисел2 , произведение которых даёт при делении
на p остаток 1. Пусть q пробегает ряд (1.5), тогда по следствию из леммы 1.1.1 найдутся
единственные целые u,v, такие что qu − pv = 1,1 < u < p
Следовательно, множество чисел (1.5) можно разбить на такие пары (qi; qi¯), i = 1, 2,…,
(p − 3)∕2, для которых
qiqi¯ = pvi + 1,i = 1, 2,…, (p − 3)∕2 (1.6)Перемножая (1.6) по всевозможным значениям i
получим
(p − 2)! = pV + 1,
где V — некоторое натуральное число. После умножения обеих частей последнего
равенства на p − 1 имеем
(p − 1)! = p(p − 1)V + p − 1,
или
(p − 1)! + 1 = p(p − 1)V + 1,
то есть соотношение (1.1).
Пусть теперь p — составное, тогда оно имеет простой делитель p1, причём p1 < p и,
следовательно, (p − 1)!⋮p1. Тогда получим, что (p − 1)! + 1 не делится на p1 и, тем более,
на p.

13. Теорема Вильсона (примеры решения задач)

1. Доказать, что если простое число р представимо в виде 4n+1 , то существует
такое число х , что х 2 +1 делится на р .
Решение. Пусть р=4n+1 – простое число. По теореме Вильсона, (4n)!+1
делится на р . Заменим в выражении 1 × 2 × 3 × ... × (4n)+1 все множители
большие (p-1)/2=2n через разности числа р и чисел меньших (p-1)/2=2n .
Получим:
(p-1)!+1 = 1 × 2 × 3 × … × 2n × (p-2n)(p-2n+1) × … × (p-1) = (1 × 2 × 3 × … × 2n)[A
× p+(-1) 2n × 2n × (2n-1) × … × 2 × 1]+1 = A 1 p+(1 × 2 × 3 × … × 2n) 2 )+1 .
Так как это число делится на р , то и сумма (1 × 2 × 3 × … × 2n) 2 +1 делится на
р , т.е. x=(2n)!=((p-1)/2)!
2. Число 2 является квадратом по модулю 7 , т.к.
4 2 º 16 º 2(mod7). Значит, 2 - квадратичный вычет. (Сравнение x 2 º 2(mod7)
имеет еще и другое решение: 3 2 º 9 º 2(mod7).) Напротив, число 3 является
квадратичным невычетом по модулю 7 , т.к. сравнение x 2 º 3(mod7) решений не
имеет, в чем нетрудно убедиться последовательным перебором полной
системы вычетов: x = 0,1,2,3,4,5,6.

14. Литература:

•С. Г. Гиндикин Малая теорема Ферма // Квант. — 1972. — № 10.
•Э. Б. Винберг Малая теорема Ферма и ее обобщения // Математическое
просвещение. — 2008. — В. 12. — С. 43–53.
•Бухштаб А. А. Теория чисел, 2-е издание, М., 1966
•Трост Э. Простые числа, пер. с нем., М., 1959
•Виноградов И. М. Основы теории чисел. — 5 изд.. — М.-Л.: Гостехиздат,
1952.
•А. Н. Колмогоров. Математика — наука и профессия. М.: Наука, 1988.
•С. В. Житомирский. Архимед: Пособие для учащихся. М.:
Просвещение, 1981.
•Плутарх. Сравнительные жизнеописания. М.: Наука, 1994.
•М. Айгнер, Г. Циглер. Доказательства из Книги. Лучшие доказательства со
времён Евклида до наших дней. М.: Мир, 2006.
•Виноградов И. М. Основы теории чисел. М.: Наука, 1981.
•Чебышёв П. Л. Избранные труды. М.: изд. АН СССР, 1955.