Похожие презентации:
Зачётная система при подготовке к ЕГЭ по математике
1.
Зачётная системапри подготовке к
ЕГЭ по математике
2.
Цель урока:1
Повторение темы для проведения зачёта и
подготовки к ЕГЭ;
3.
Задачи урока:1
Закрепить и проверить знания при
решении базовых и профильных задач;
2
Вовлечь в активную деятельность
всех учащихся класса;
3
Развивать навыки коллективной работы
учащихся в сочетании с самостоятельной;
4.
Производнаяв заданиях ЕГЭ
5.
6.
«Уча других, мы учимся сами»Лицуй Анней Сенека (римский философ)
Хочешь научиться сам –
начни учить других!
7.
«Уча других, мы учимся сами»Лицуй Анней Сенека (римский философ)
Хочешь научиться сам –
начни учить других!
8.
Правила дифференцирования1
2
3
4
5
9.
Формулы дифференцирования10.
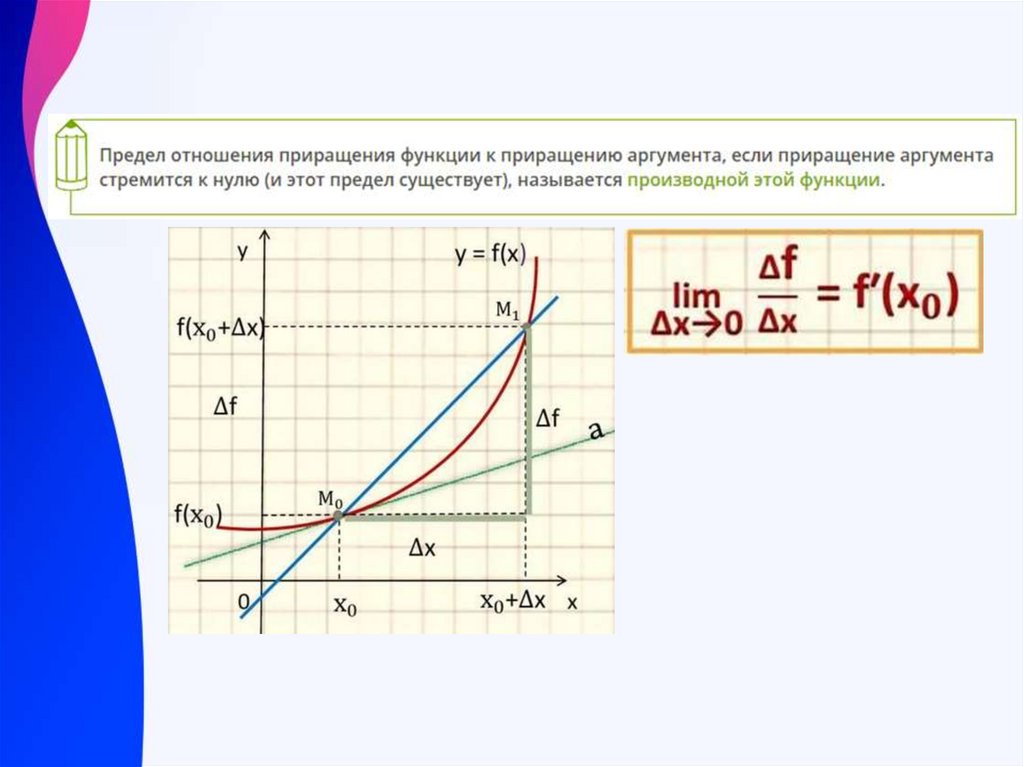
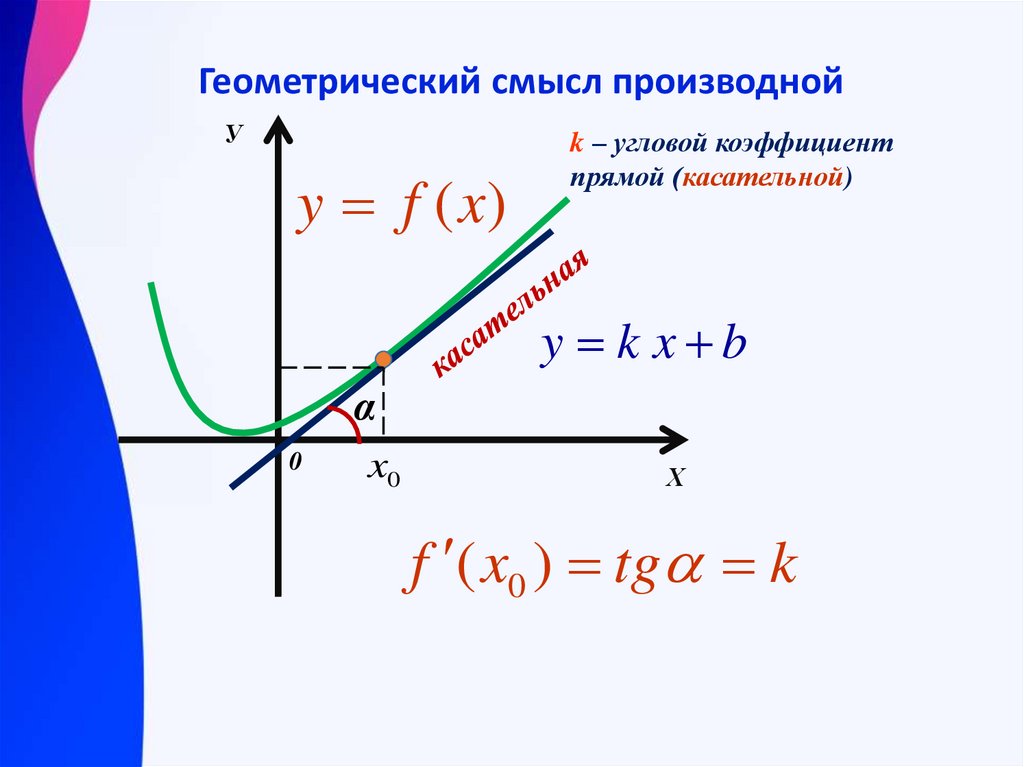
Геометрический смысл производнойУ
y f (x)
k – угловой коэффициент
прямой (касательной)
y k x b
α
0
x0
Х
f ( x0 ) tg k
11.
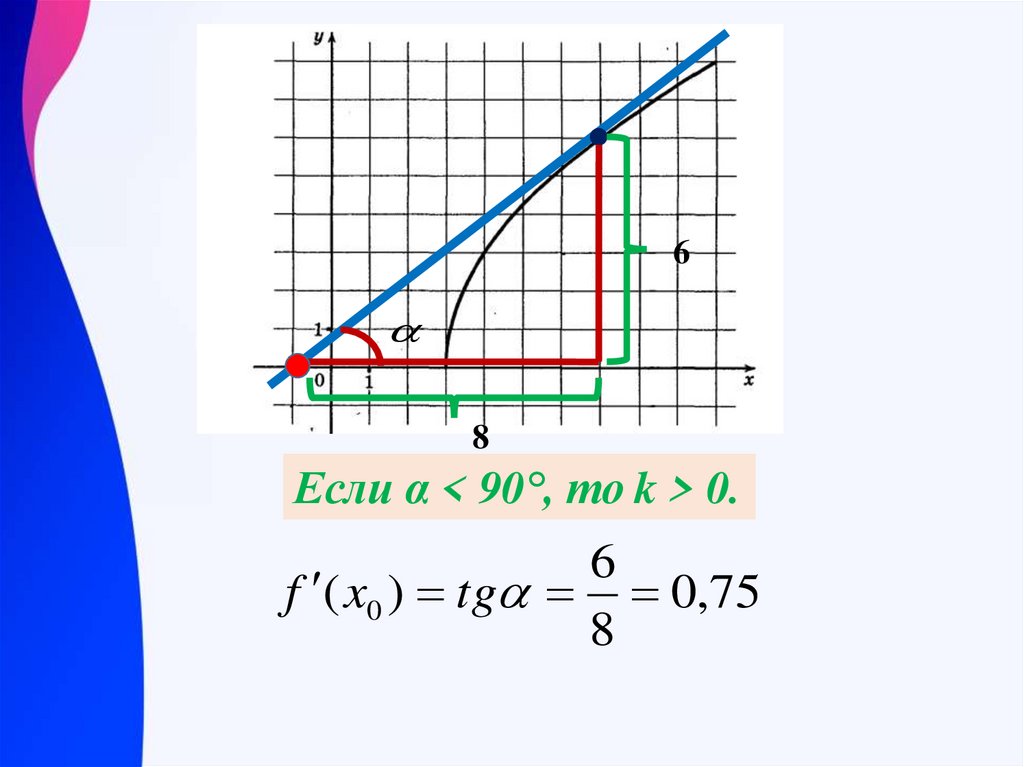
68
Если α < 90°, то k > 0.
6
f ( x0 ) tg 0,75
8
12.
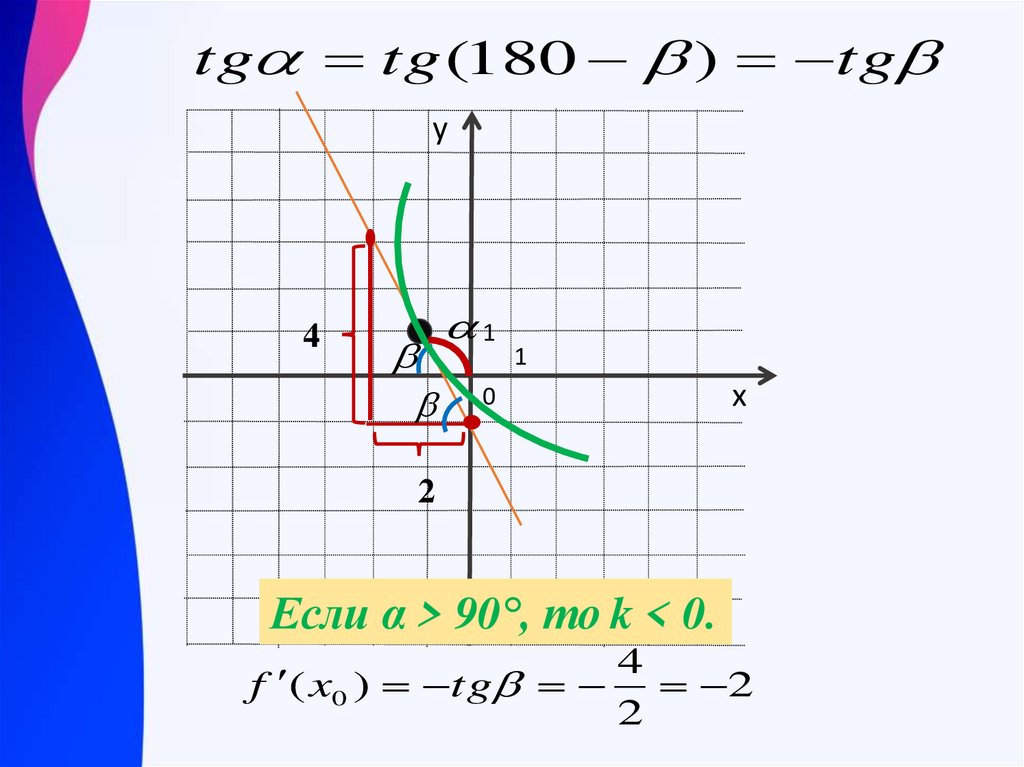
tg tg (180 ) tgу
4
1
1
х
0
2
Если α > 90°, то k < 0.
f ( x0 ) tg
4
2
2
13.
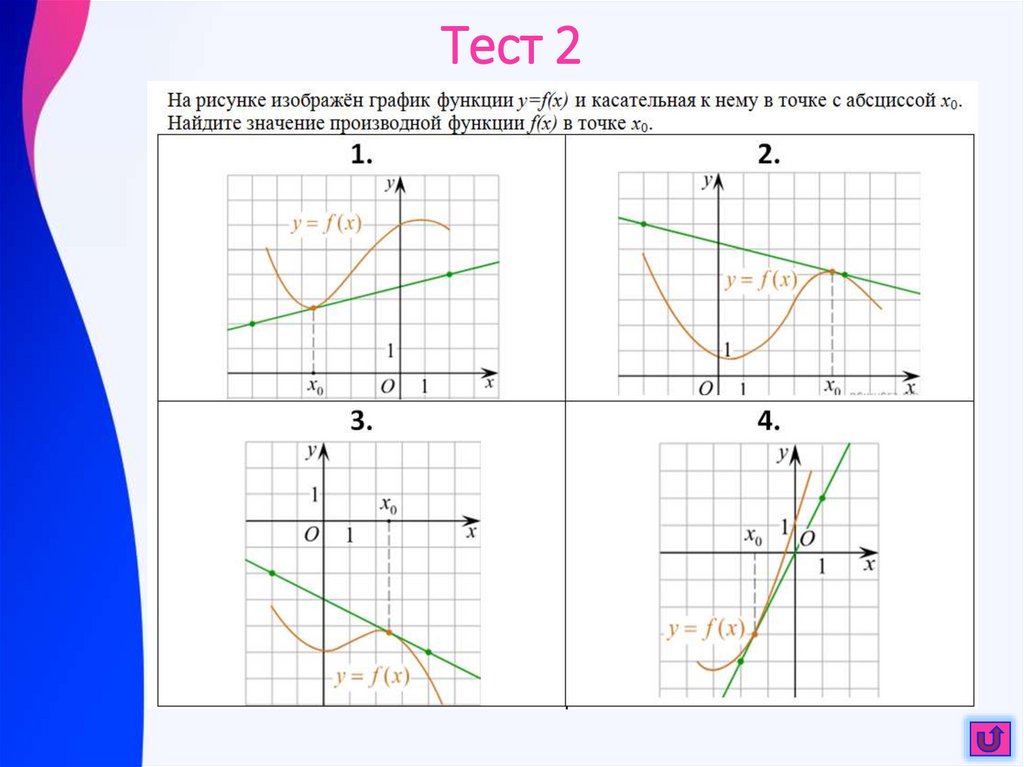
Тест 214.
Физический смысл производнойЕсли известен закон движения материальной
точки (тела) x(t) или s(t), то мгновенная
скорость в момент времени t вычисляется по
формуле v(t) = x(׳t) = s(׳t)
а ускорение a(t) = v(׳t)= x(׳׳t).
15.
Тест 316.
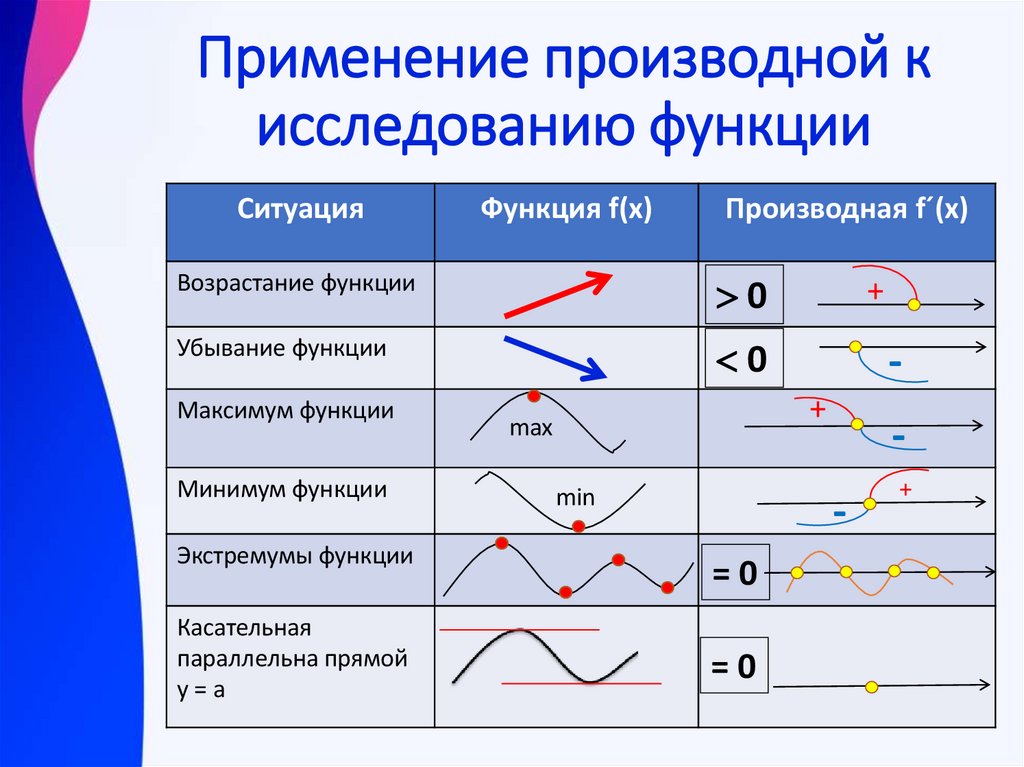
Применение производной кисследованию функции
Ситуация
Функция f(x)
Производная f´(x)
Возрастание функции
0
Убывание функции
0
Максимум функции
Минимум функции
Экстремумы функции
Касательная
параллельна прямой
у=а
+
+
max
min
-
=0
=0
+
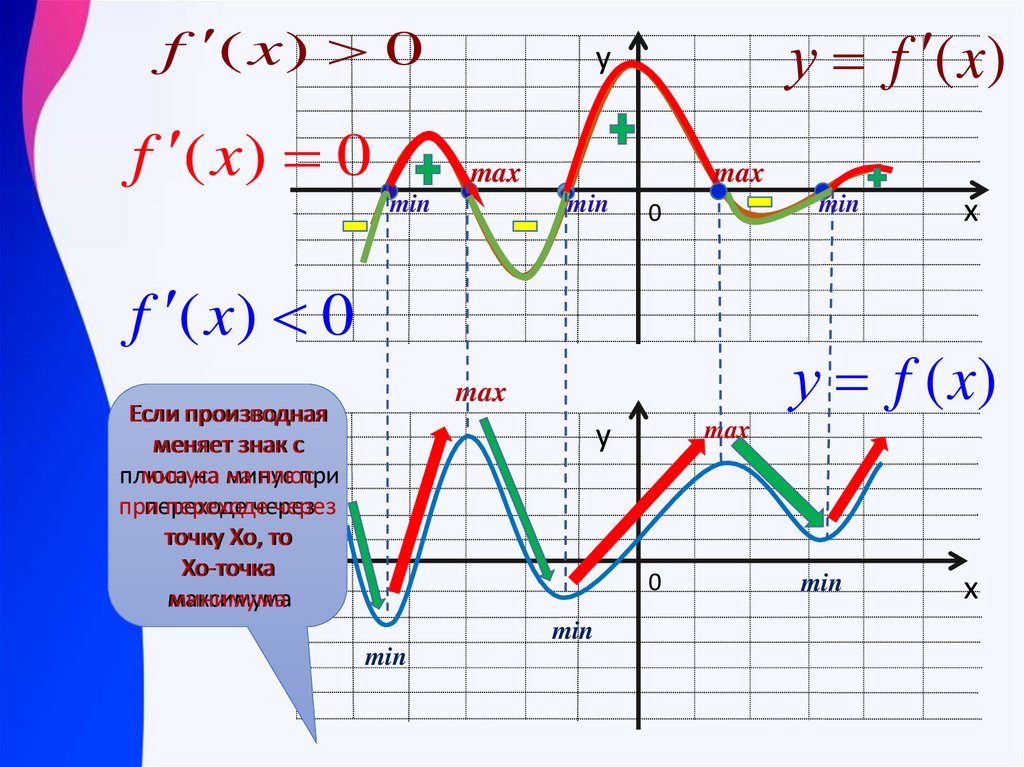
17.
f ( x ) 0f ( x) 0
у f (x)
у
max
min
max
min
min
0
f ( x) 0
у f (x)
max
Если производная
меняет знак с
плюса
минуса
на минус
на плюс
при
при
переходе
переходе
через
через
точку Хо, то
Хо-точка
максимума
минимума
у
max
0
min
min
х
min
х
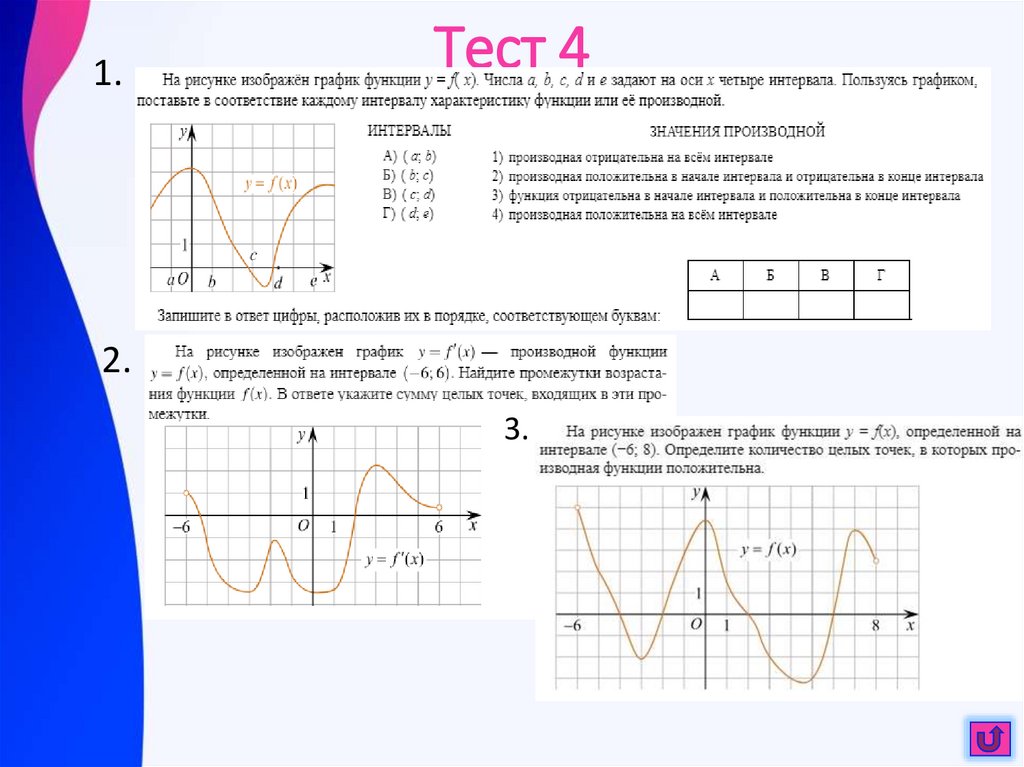
18.
1.Тест 4
2.
3.
19.
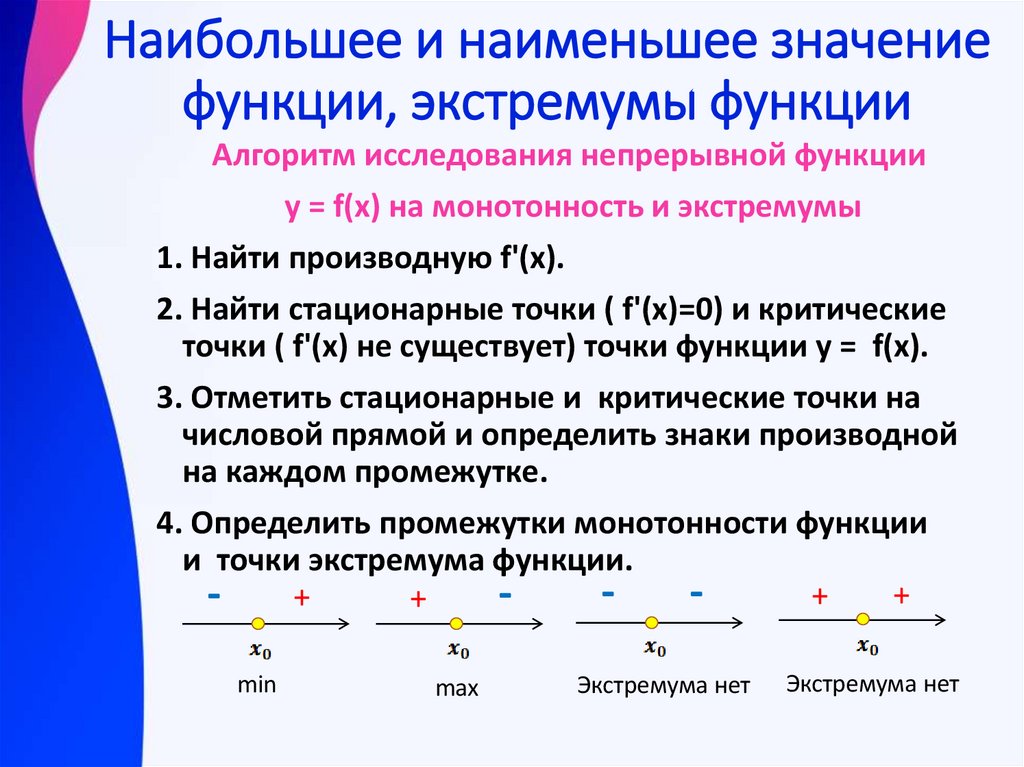
Наибольшее и наименьшее значениефункции, экстремумы функции
Алгоритм исследования непрерывной функции
y = f(x) на монотонность и экстремумы
1. Найти производную f'(x).
2. Найти стационарные точки ( f'(x)=0) и критические
точки ( f'(x) не существует) точки функции у = f(x).
3. Отметить стационарные и критические точки на
числовой прямой и определить знаки производной
на каждом промежутке.
4. Определить промежутки монотонности функции
и точки экстремума функции.
+
+
+
+
min
max
Экстремума нет
Экстремума нет
20.
Алгоритм нахождения наименьшего инаибольшего значений непрерывной функции
y = f(x) на отрезке [a;b]
1. Найти производную функции f′(x);
2. Найти стационарные и критические точки
функции, лежащие внутри отрезка [a;b];
3. Вычислить значения функции y= f(x) в точках,
отобранных на втором шаге, и в точках a и b;
выбрать среди этих значений наименьшее(
)
и наибольшее (
).













 Математика
Математика








