Похожие презентации:
Определение истинности составного высказывания
1.
2.
Определение истинностисоставного высказывания
3.
Логическое высказывание – это повествовательноепредложение, про которое можно однозначно сказать,
истинно оно или ложно.
Основными логическими операциями, определенными
над высказываниями, являются: инверсия, конъюнкция и
дизъюнкция.
4.
Логическиепеременные
A = 2+2 =4
B = Вчера жирафы летели
с севера на юг зигзагом
A=1
B=0
5.
Типы высказываний (по составу)Простые
Сложные (Составные)
6.
• Если высказывание А истинно,то не А – ложно, и наоборот.
• Высказывание А и В истинно тогда
и только тогда, когда истинны оба
высказывания А и В одновременно.
• Высказывание А или В ложно тогда
и только тогда, когда ложны оба
высказывания А и В одновременно.
7.
Инверсия8.
конъюнкция9.
дизъюнкция10.
Для какого из имён истинно высказывание:НЕ ((Первая буква согласная) ИЛИ (Последняя буква гласная))?
11.
Для какого из приведённых чисел истинно высказывание:НЕ (число < 20) И (число чётное)?
1. 21
2. 8
3. 36
4. 15
12.
Даны сложные высказывания.Запишите их с помощью знаков логических операций.
1. Данное число либо кратно, либо не кратно семи.
2. Минеральная вода может быть или газированной, или
негазированной.
3. Неверно, что сегодня выходной.
4. Мы поедем в Москву и побываем на Красной
площади.
5. Следующий урок или информатика, или физика.
13.
1. 7 – нечётное число.2. Лондон – столица Германии.
3. Если я не выучу уроки, то не получу хорошую оценку.
4. Сегодня пятница, и я не учусь.
5. Любой треугольник не имеет три угла и три стороны.
6. Если я не поставлю будильник ИЛИ не лягу пораньше, то просплю утро
7. Чтобы сохранить дружбу, нужно не быть честным и открытым друг с
другом.
8. Сегодня вторник или сегодня новый год.
14.
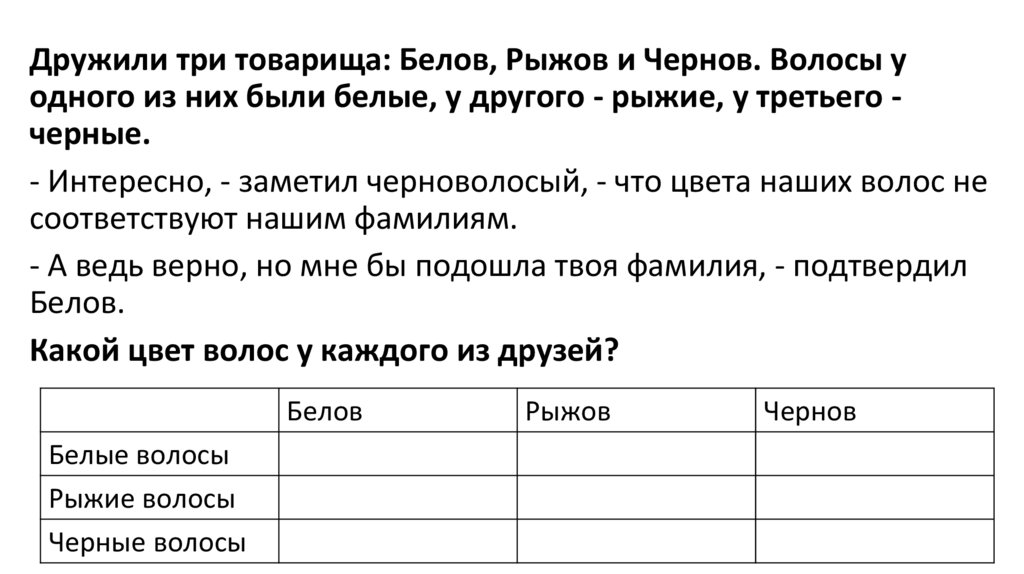
Дружили три товарища: Белов, Рыжов и Чернов. Волосы уодного из них были белые, у другого - рыжие, у третьего черные.
- Интересно, - заметил черноволосый, - что цвета наших волос не
соответствуют нашим фамилиям.
- А ведь верно, но мне бы подошла твоя фамилия, - подтвердил
Белов.
Какой цвет волос у каждого из друзей?
Белов
Белые волосы
Рыжие волосы
Черные волосы
Рыжов
Чернов
15.
• Логическое И - конъюнкция• Логическое ИЛИ - дизъюнкция
Домашнее задание: вопросы к параграфу 1.4 №2-7
(стр. 50-51)










 Информатика
Информатика








