Пифагор Самосский

1. Пифагор Самосский

ПИФАГОР
САМОССКИЙ
(ок. 580 – ок. 500 г. до н.э.)
1

2.

ПИФАГОРЕЙСКИЙ ОРДЕН –
школа философов и математиков.
1.Делай лишь то, что в последствии не омрачит
тебя и не заставит раскаиваться;
2.Не делай того, чего не знаешь, но
научись всему, что нужно знать;
3.Либо молчи, либо говори то,
то ценнее молчания;
4.Не закрывай глаза, когда
хочешь спать, не разобравши
всех своих поступков за день.
…… и др.
2

3.

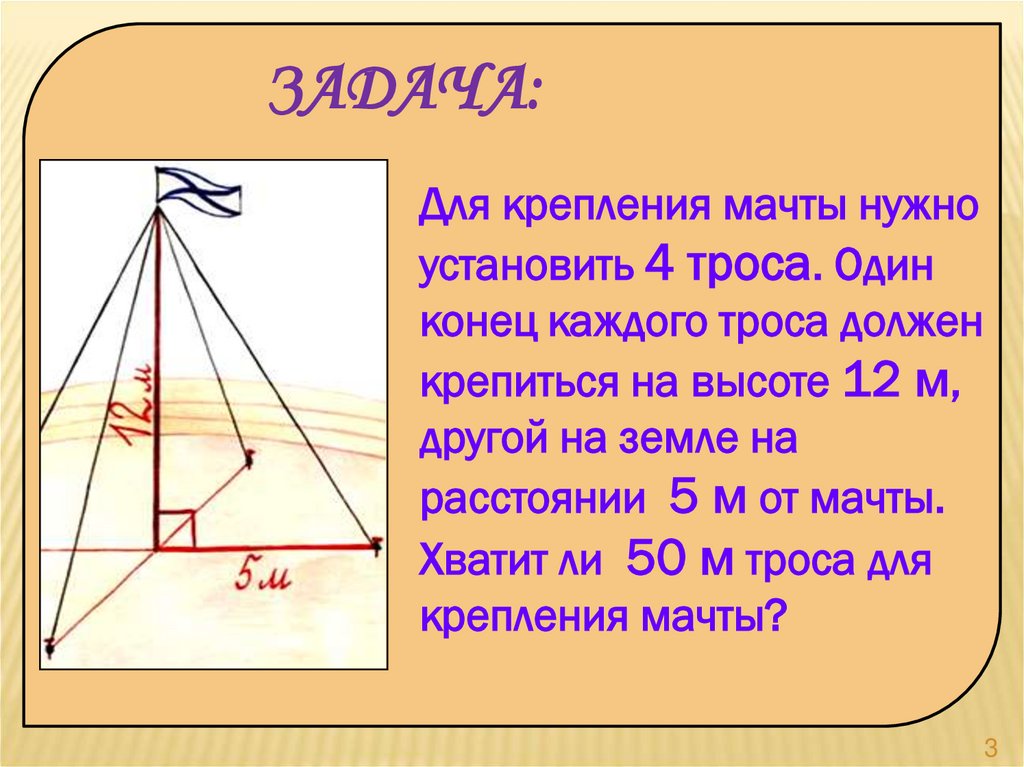
ЗАДАЧА:
Для крепления мачты нужно
установить 4 троса. Один
конец каждого троса должен
крепиться на высоте 12 м,
другой на земле на
расстоянии 5 м от мачты.
Хватит ли 50 м троса для
крепления мачты?
3

4.

Теорема ПИФАГОРА
В прямоугольном треугольнике квадрат
гипотенузы равен сумме квадратов
катетов.
4

5.

Теорема ПИФАГОРА в переводе с греческого,
латинского, немецкого и русского языков.
Латинский
перевод:
У
Евклида
(дословный
перевод):
В
Geometria
Culmonensis
(ок. 1400 г.):
В«Во
первом
русском
переводе:
всяком прямоугольном
треугольнике
«В
прямоугольном
треугольнике
квадрат
«Площадь
квадрата,
измеренного
по
«В
прямоугольных
треугольниках
квадрат
из
квадрат,
образованный
на
стороне,
стороны,
натянутой
над
прямым
углом,
длинной стороне,
столь жепрямому
велика, как
у
стороны,
противолежащей
углу,
натянутой
над прямым
углом, равен сумме
равен
квадратам
на
сторонах,
двух квадратов,
которыеизизмерены
по двум
равен
сумме
квадратов
сторон,
двух
квадратов,прямой
образованных
на двух
заключающих
угол».
сторонам его,прямой
примыкающим
к прямому
содержащих
угол».
сторонах, заключающих прямой угол».
углу».
5

6.

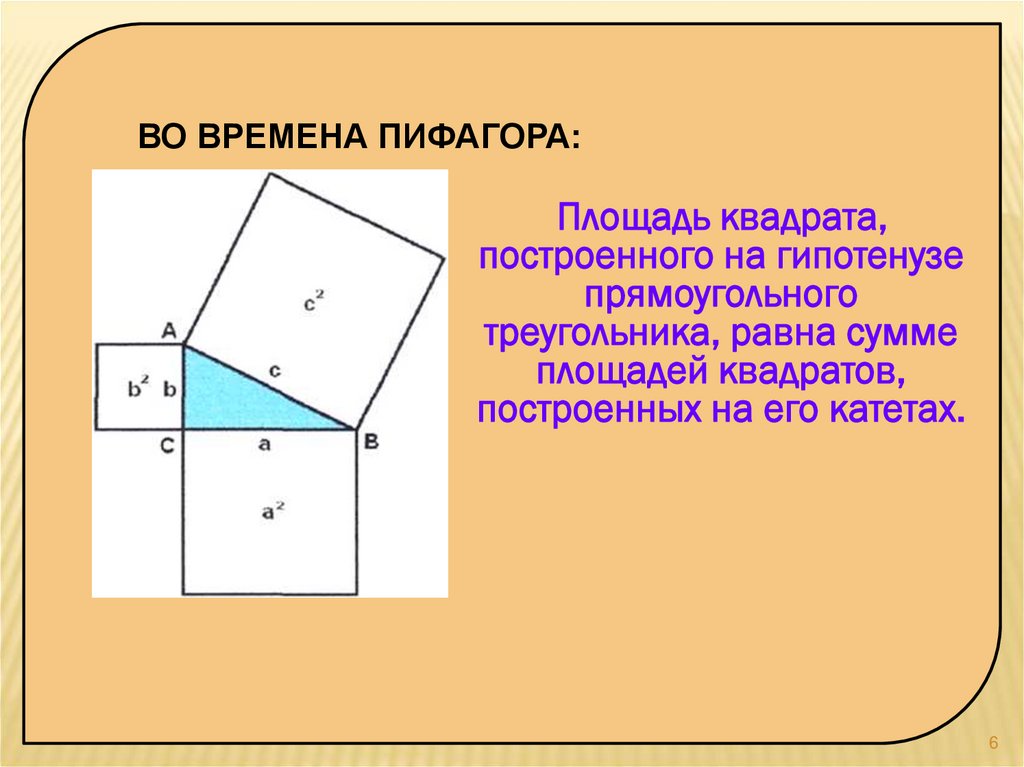
ВО ВРЕМЕНА ПИФАГОРА:
Площадь квадрата,
построенного на гипотенузе
прямоугольного
треугольника, равна сумме
площадей квадратов,
построенных на его катетах.
6

7.

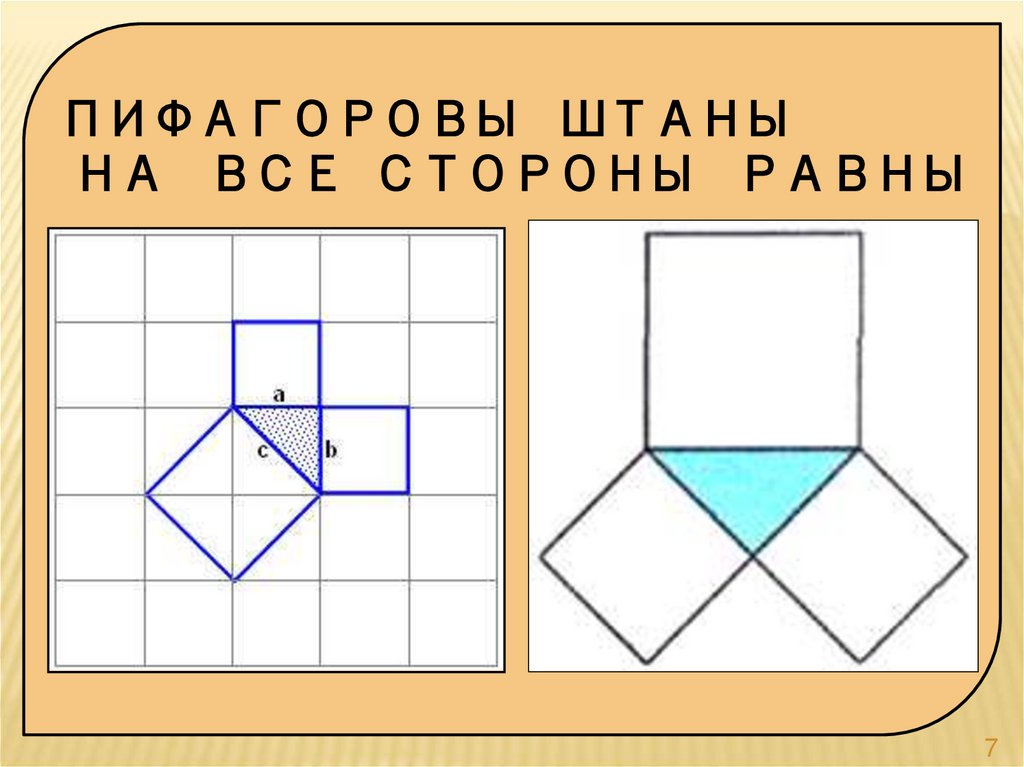
ПИФАГОРОВЫ ШТАНЫ
НА ВСЕ СТОРОНЫ РАВНЫ
7

8.

ШАРЖИ
8

9.

ТЕОРЕМА ПИФАГОРА
ТЕОРЕМА 100 БЫКОВ
МОСТ ОСЛОВ
ТЕОРЕМА НЕВЕСТЫ
9

10.

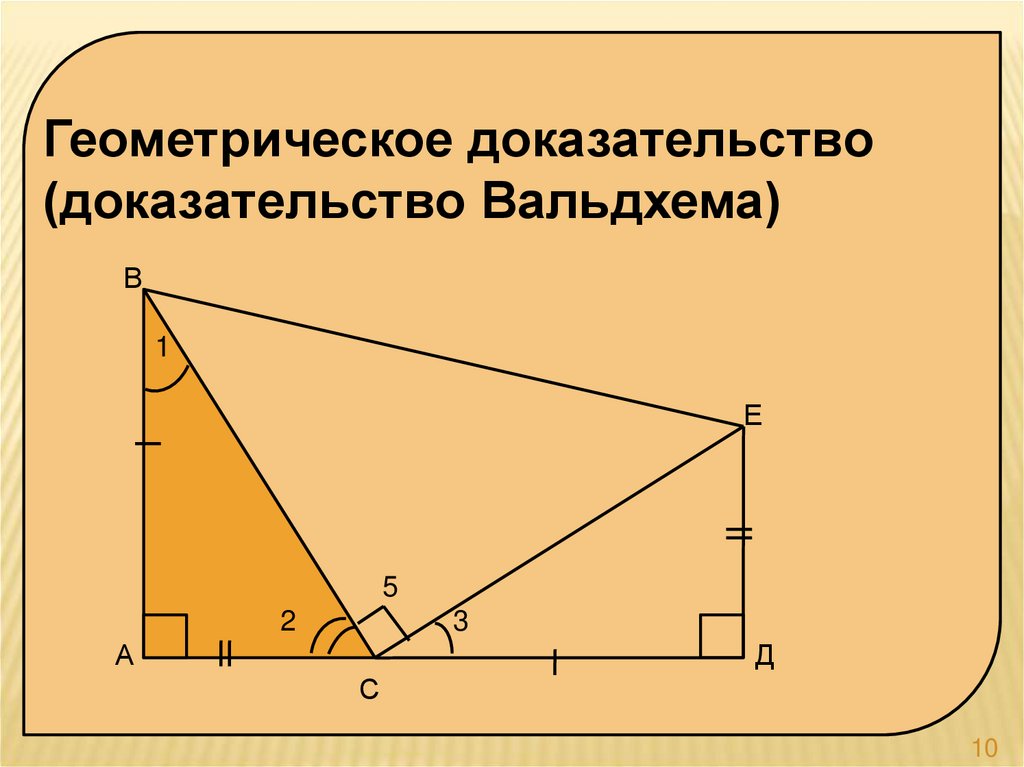
Геометрическое доказательство
(доказательство Вальдхема)
В
1
Е
5
2
3
А
Д
С
10

11.

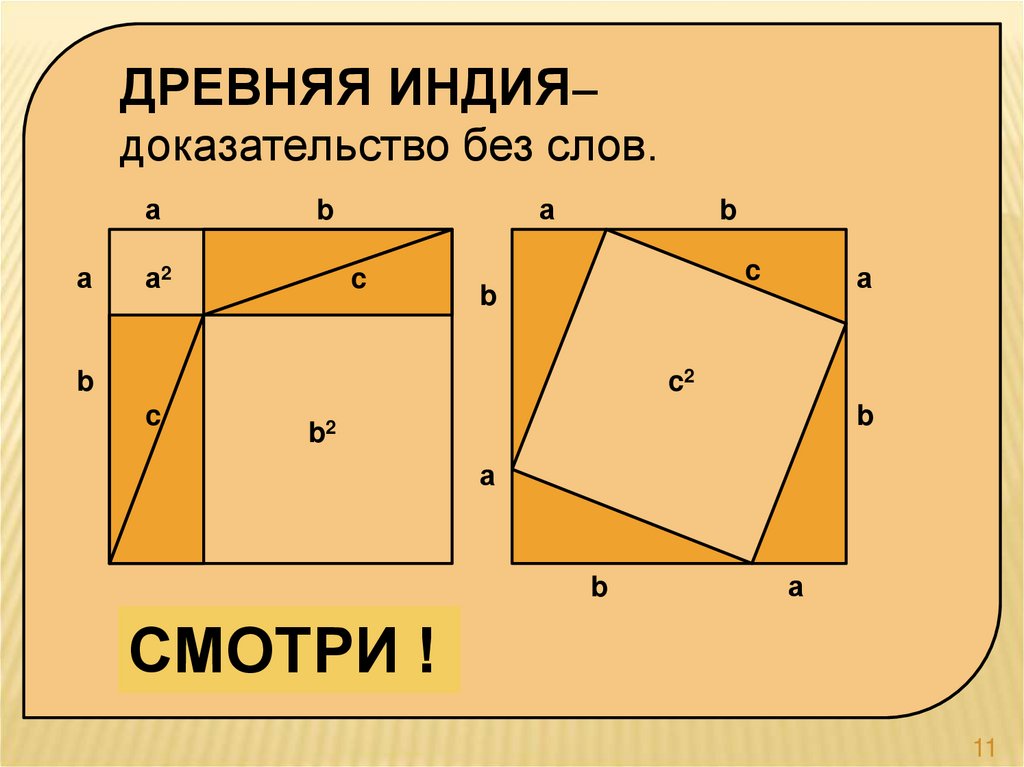
ДРЕВНЯЯ ИНДИЯ–
доказательство без слов.
а
а
а
b
а2
c
b
c
b
а
c2
b
c
b
b2
а
b
а
СМОТРИ !
11

12.

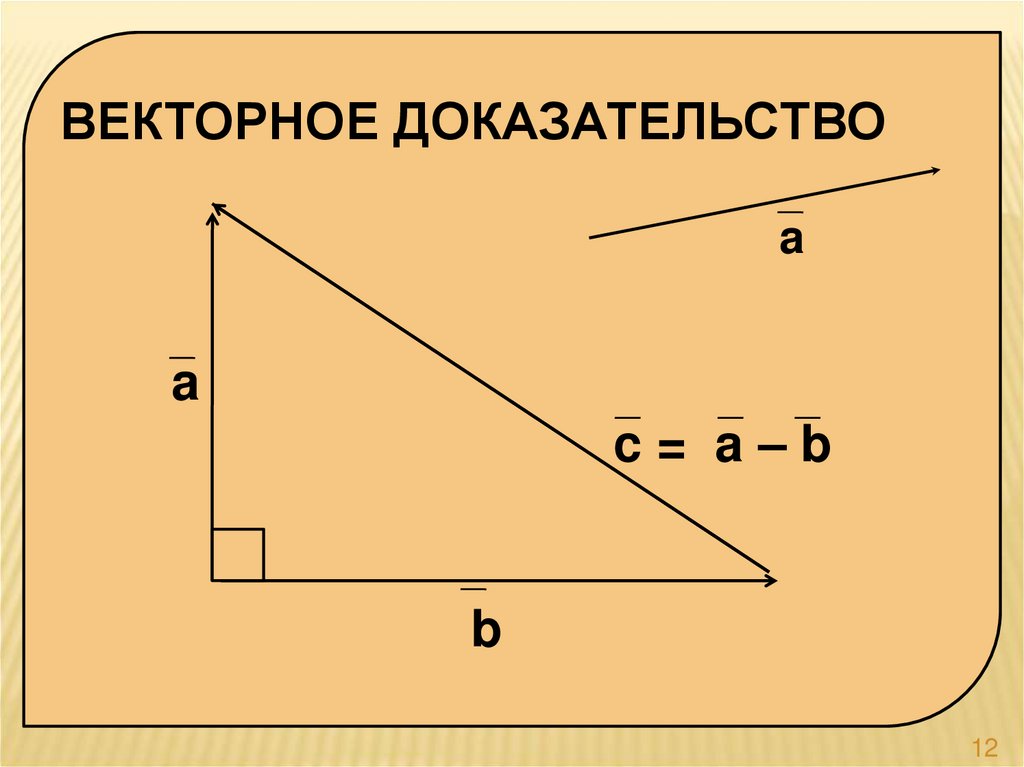
ВЕКТОРНОЕ ДОКАЗАТЕЛЬСТВО
a
a
c= a–b
b
12

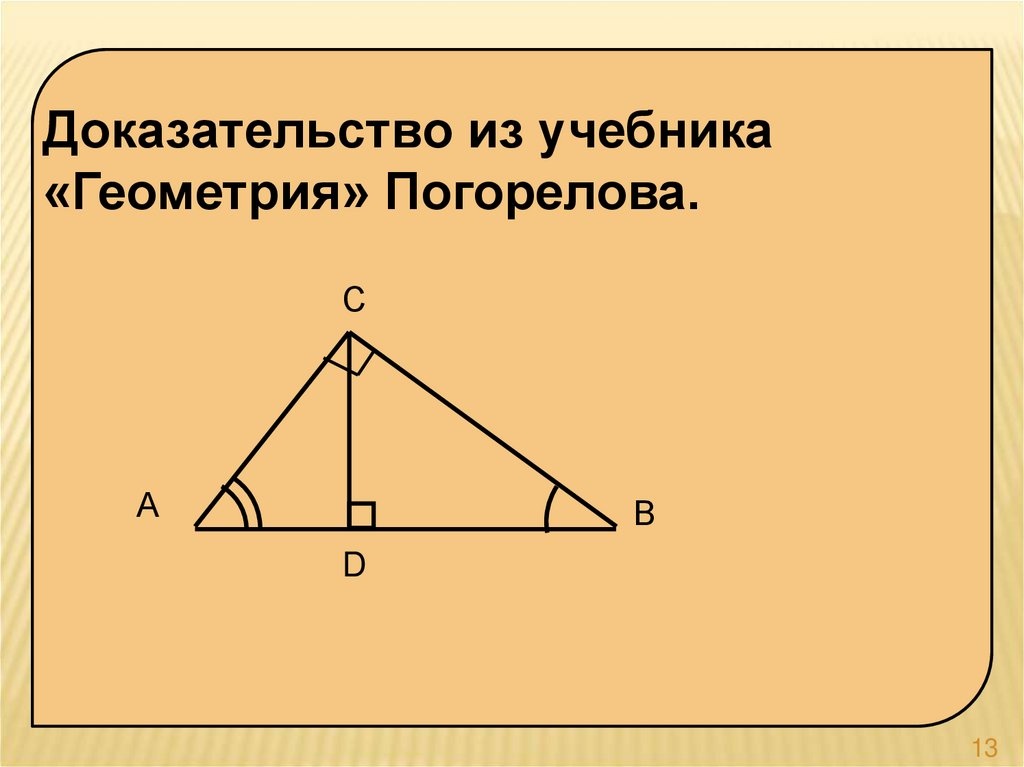
13.

Доказательство из учебника
«Геометрия» Погорелова.
С
А
В
D
13

14.

ТЕОРЕМА В СТИХАХ
Если дан нам треугольник
И притом с прямым углом,
То квадрат гипотенузы
Мы всегда легко найдём:
Катеты в квадрат возводим,
Сумму степеней находим –
И таким простым путём
К результату мы придём.
14

15.

Задача индийского математика XII века
БХАСКАРЫ
На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол
надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в этом месте
река
В четыре лишь фута была широка
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»
15

16.

Задача из учебника «АРИФМЕТИКА»
Лаврентия Магницкого
Случися некому человеку к
стене лестницу прибрати,
стены же тоя высота есть
117 стоп. И обреете лестницу
долготью 125 стоп. И ведати
хочет, колико стоп сея
лестницы нижний конец от
стены отстояти имать.
16

17.

ПОДВЕДЕНИЕ ИТОГОВ
УРОКА
17

18.

ДОМАШНЕЕ ЗАДАНИЕ
п 54, №484(а,д),
№487
18

19.

УРОК ЗАКОНЧЕН.
ДО СВИДАНИЯ!
19