Математика вокруг нас: золотая пропорция

1. «Математика вокруг нас: золотая пропорция»

Муниципальное общеобразовательное учреждение
«Средняя общеобразовательная школа п.Белоярский
Новобурасского района Саратовской области имени
Бабушкина А.М.»
«Математика вокруг нас:
золотая пропорция»
Выполнила:
учитель математики Лозе Елена Николаевна
1

2. Золотая пропорция в математике

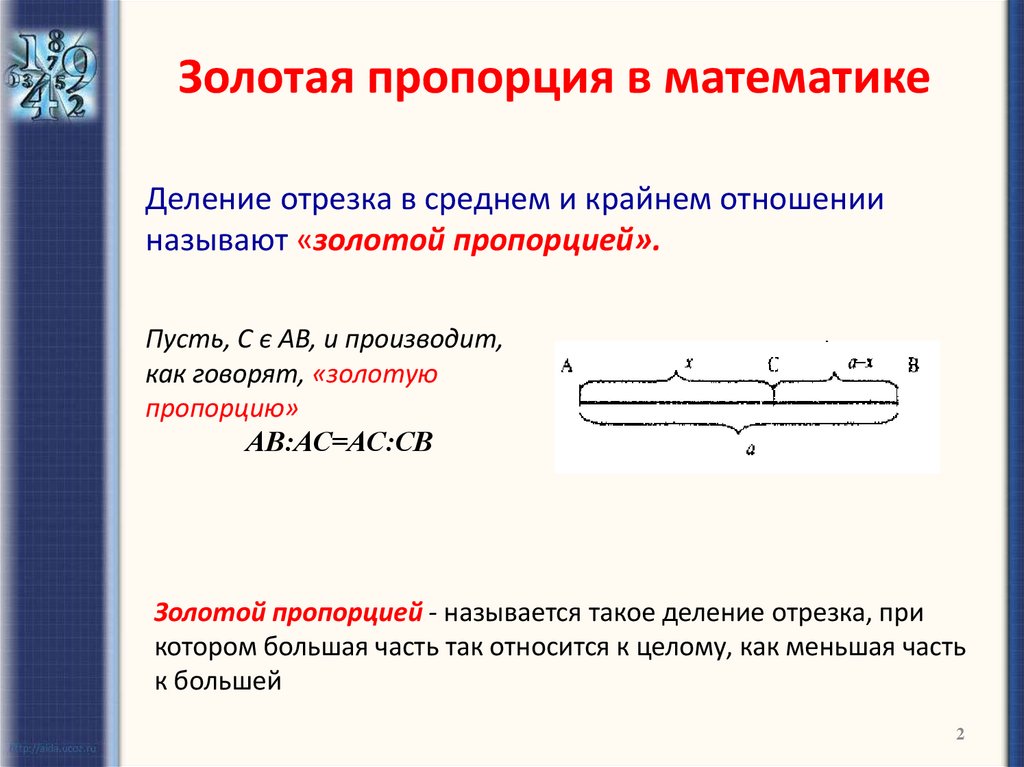
Деление отрезка в среднем и крайнем отношении
называют «золотой пропорцией».
Пусть, С є АВ, и производит,
как говорят, «золотую
пропорцию»
АВ:АС=АС:СВ
Золотой пропорцией - называется такое деление отрезка, при
котором большая часть так относится к целому, как меньшая часть
к большей
2

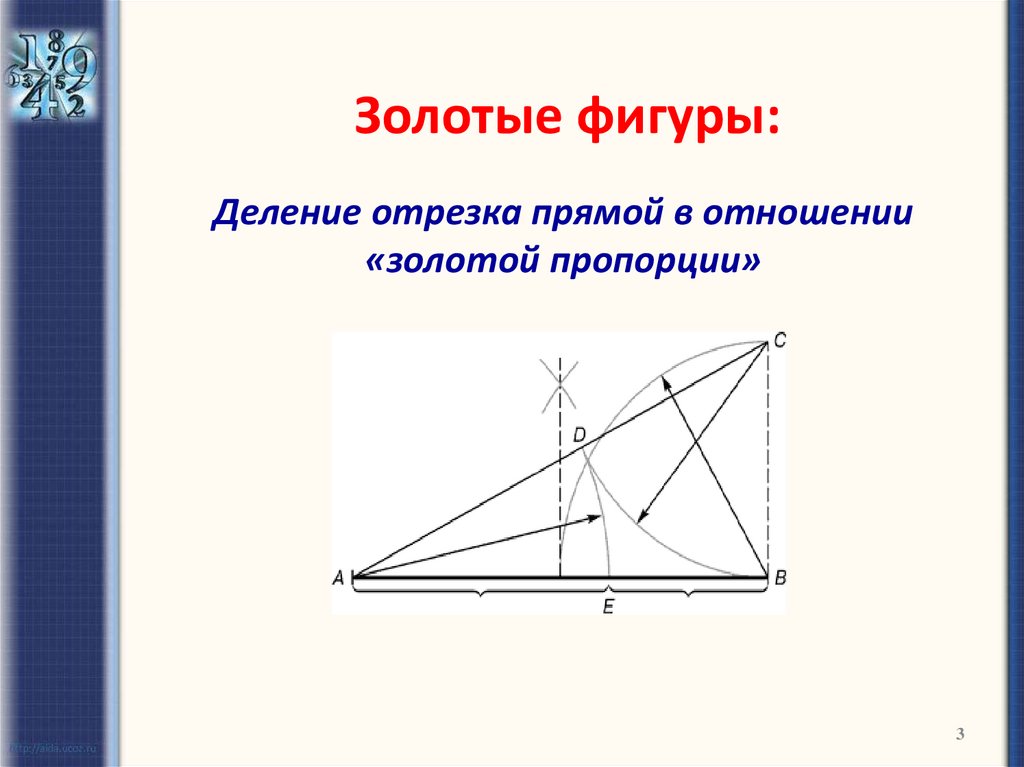
3. Золотые фигуры:

Деление отрезка прямой в отношении
«золотой пропорции»
3

4. Золотые фигуры:

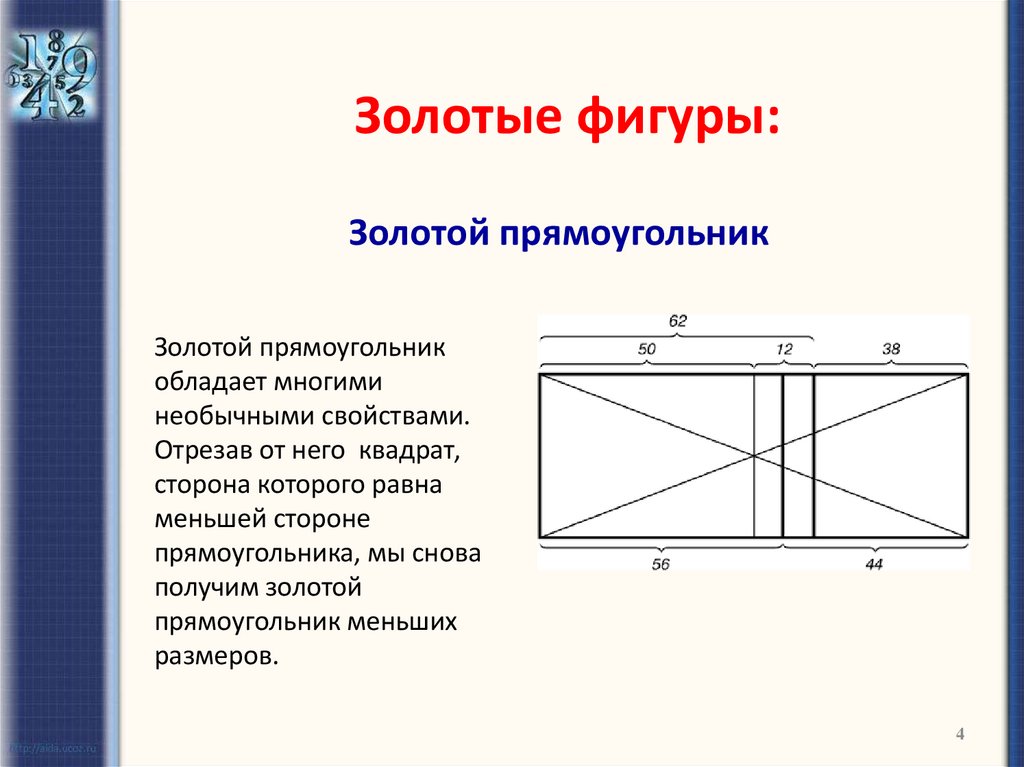
Золотой прямоугольник
Золотой прямоугольник
обладает многими
необычными свойствами.
Отрезав от него квадрат,
сторона которого равна
меньшей стороне
прямоугольника, мы снова
получим золотой
прямоугольник меньших
размеров.
4

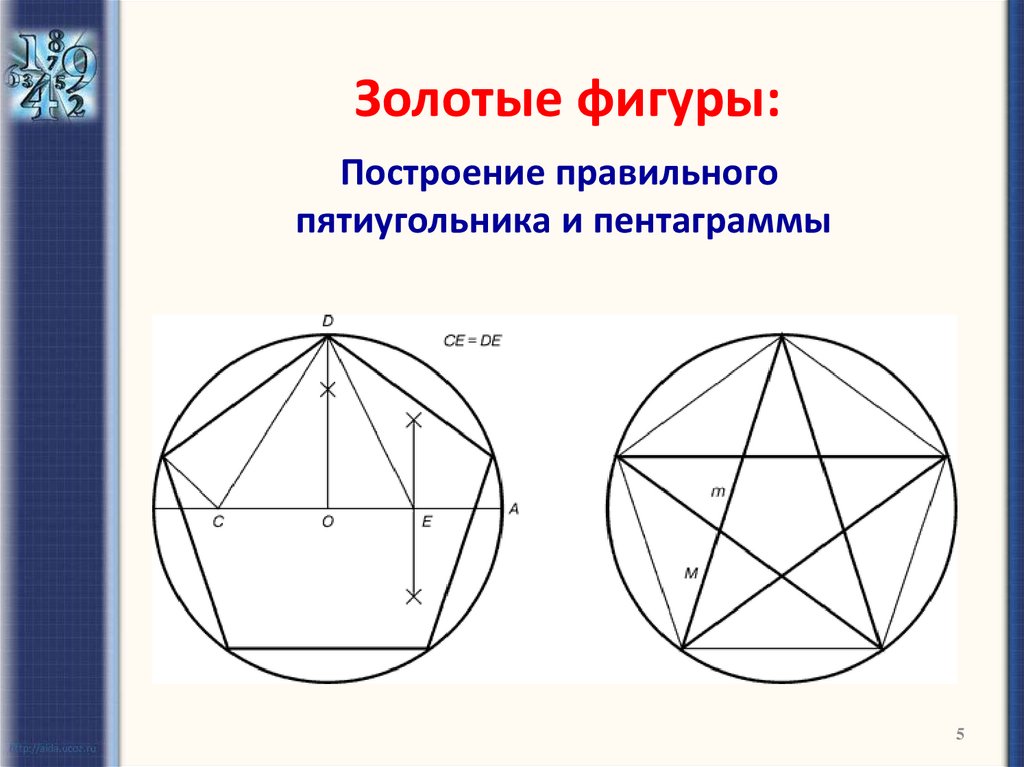
5. Золотые фигуры:

Построение правильного
пятиугольника и пентаграммы
5

6. Числа Фибоначчи

С Золотой пропорцией тесно связан ряд чисел Фибоначчи.
1,1,2,3,5,8,13,21,34,55,89 и т.д.
Если взять калькулятор и разделить
каждое из них на предыдущее, то
получиться:
1:1=1;
2:1=2;
3:2=1,5;
5:3=1,666666;
8:5=1,6;
13:8=1,625;
21:13=1,615384;…
1,618
6

7. Золотая пропорция в архитектуре

Парфенон — главный храм в
древних Афинах
• ширина Парфенона оценена
в 100 греческих футов (3089
см),
• высота Парфенона 61,8
• высота трех ступеней
основания и колонны – 38,2
• высота перекрытия и
фронтона – 23,6 футов.
Указанные размеры образуют
ряд золотой пропорции:
100 : 61,8 = 61,8 : 38,2 = 38,2
:23,6 1,6 = Ф
7

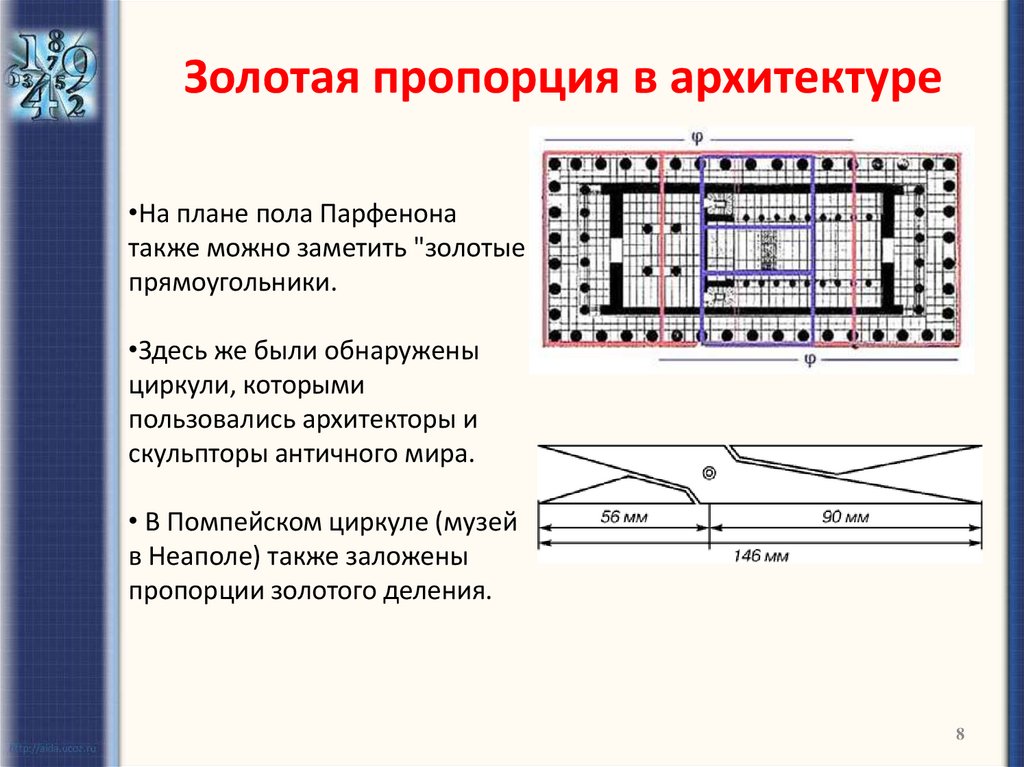
8. Золотая пропорция в архитектуре

•На плане пола Парфенона
также можно заметить "золотые
прямоугольники.
•Здесь же были обнаружены
циркули, которыми
пользовались архитекторы и
скульпторы античного мира.
• В Помпейском циркуле (музей
в Неаполе) также заложены
пропорции золотого деления.
8

9. Золотая пропорция в архитектуре

Среди грандиозных пирамид Египта особое место занимает
великая пирамида фараона Хеопса. Она самая крупная и
наиболее хорошо изученная. Чего только не находили в ее
пропорциях! Число «пи» и золотое сечение, число дней в году,
расстояние до Солнца, диаметр Земли.
9

10. Золотая пропорция в архитектуре

Золотая пропорция
в здании Большого театра Москвы.
Золотое соотношение мы можем увидеть и в
здании собора Парижской Богоматери
10

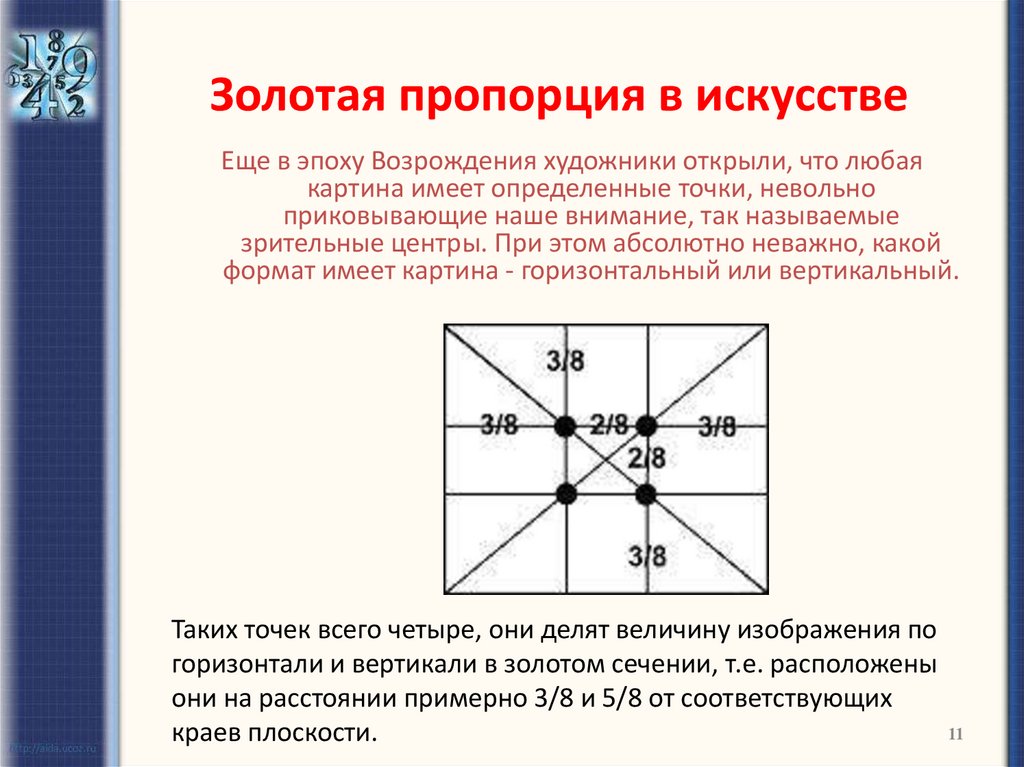
11. Золотая пропорция в искусстве

Еще в эпоху Возрождения художники открыли, что любая
картина имеет определенные точки, невольно
приковывающие наше внимание, так называемые
зрительные центры. При этом абсолютно неважно, какой
формат имеет картина - горизонтальный или вертикальный.
Таких точек всего четыре, они делят величину изображения по
горизонтали и вертикали в золотом сечении, т.е. расположены
они на расстоянии примерно 3/8 и 5/8 от соответствующих
11
краев плоскости.

12. Портрет Монны Лизы (Джоконды)

Портрет Монны Лизы
привлекает тем, что
композиция рисунка
построена на "золотых
треугольниках" (точнее на
треугольниках,
являющихся кусками
правильного звездчатого
пятиугольника).
12

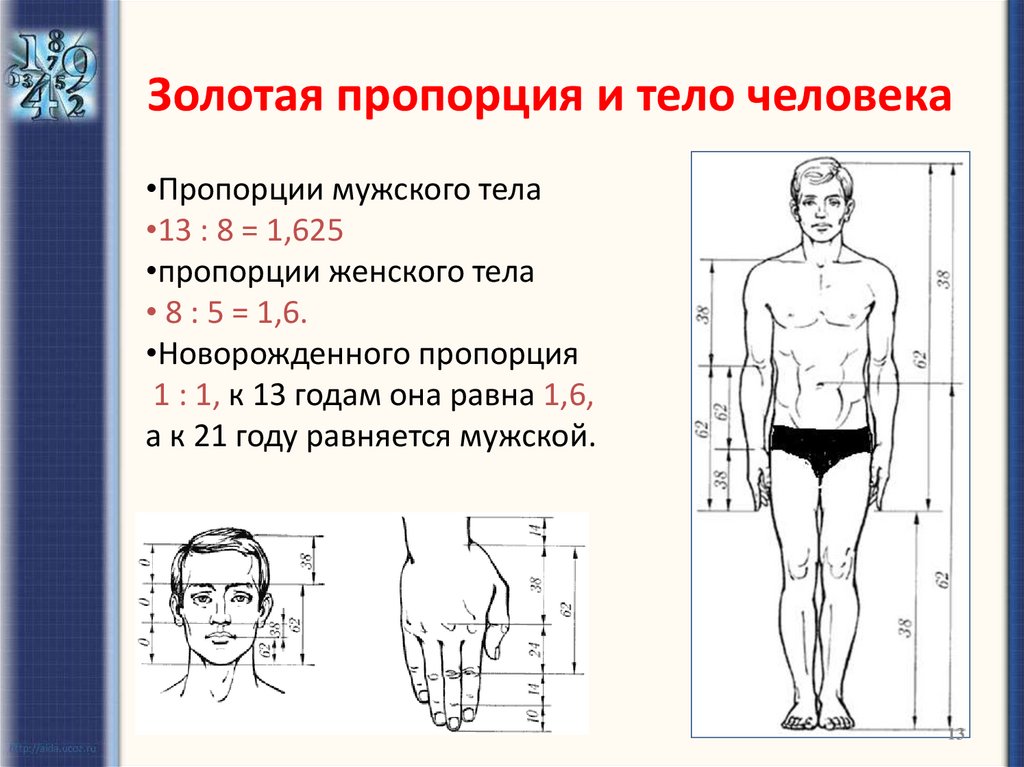
13. Золотая пропорция и тело человека

•Пропорции мужского тела
•13 : 8 = 1,625
•пропорции женского тела
• 8 : 5 = 1,6.
•Новорожденного пропорция
1 : 1, к 13 годам она равна 1,6,
а к 21 году равняется мужской.
13

14. Золотая пропорция в природе

Раковина закручена по спирали
Золотая пропорция в спирали Архимеда.
14

15. Золотая пропорция в природе

Выяснилось, что в
расположении листьев
на ветке, семян
подсолнечника, шишек
сосны проявляет себя
ряд Фибоначчи, а стало
быть, проявляет себя
закон золотой
пропорции.
15

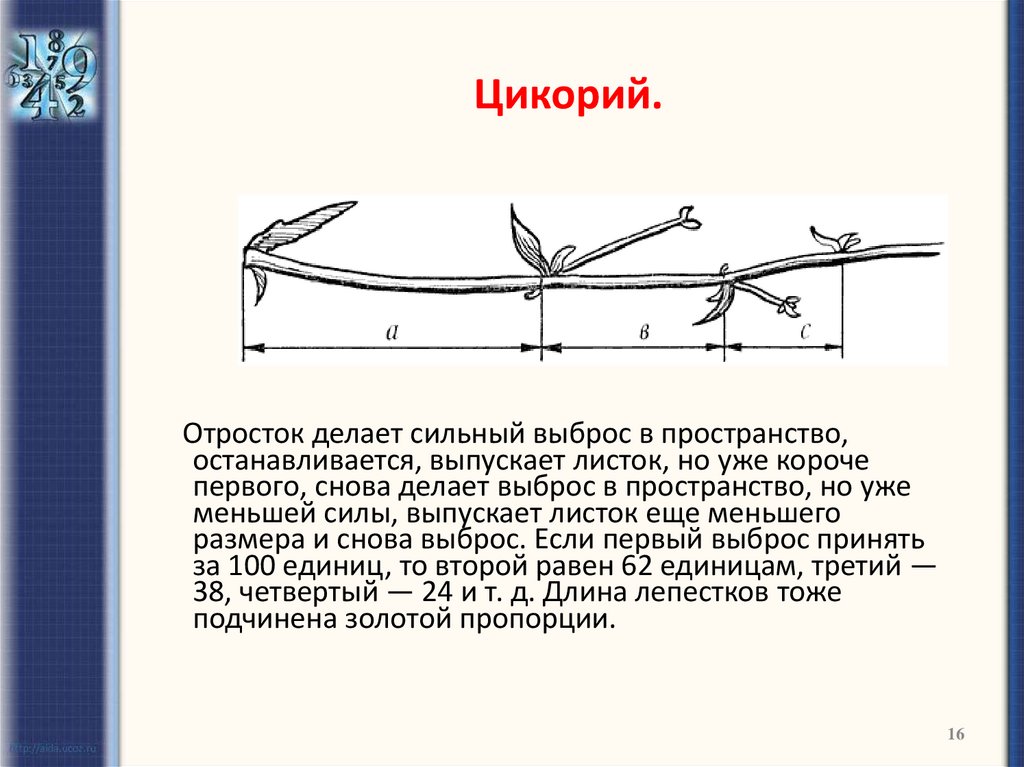
16. Цикорий.

Отросток делает сильный выброс в пространство,
останавливается, выпускает листок, но уже короче
первого, снова делает выброс в пространство, но уже
меньшей силы, выпускает листок еще меньшего
размера и снова выброс. Если первый выброс принять
за 100 единиц, то второй равен 62 единицам, третий —
38, четвертый — 24 и т. д. Длина лепестков тоже
подчинена золотой пропорции.
16

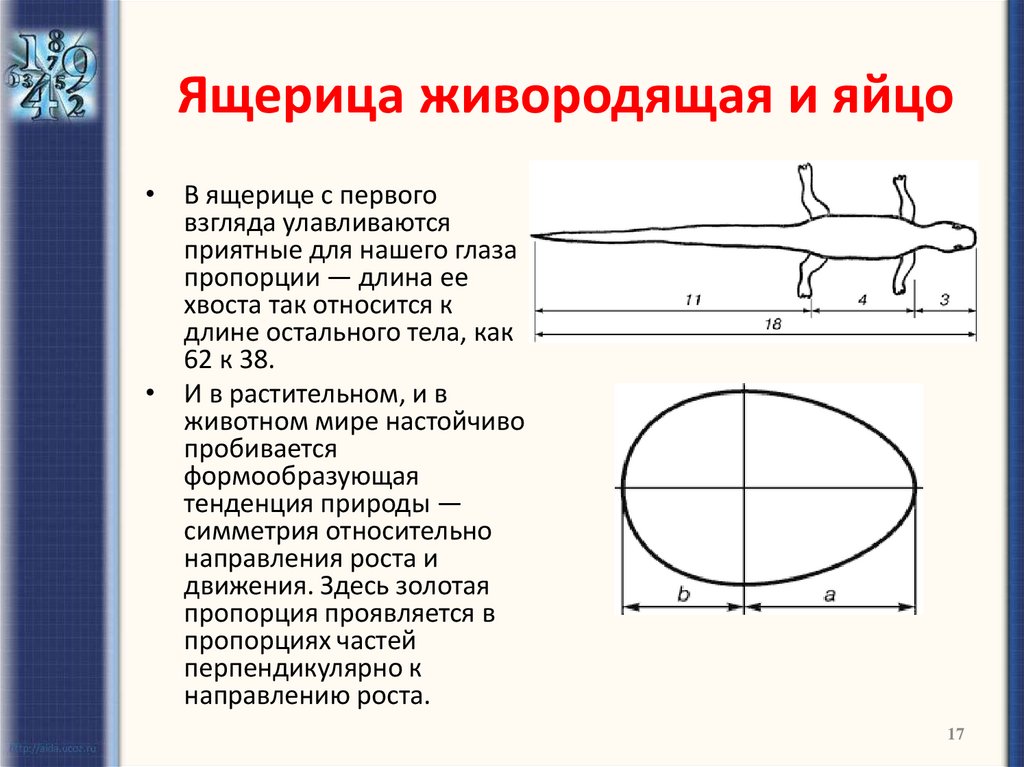
17. Ящерица живородящая и яйцо

• В ящерице с первого
взгляда улавливаются
приятные для нашего глаза
пропорции — длина ее
хвоста так относится к
длине остального тела, как
62 к 38.
• И в растительном, и в
животном мире настойчиво
пробивается
формообразующая
тенденция природы —
симметрия относительно
направления роста и
движения. Здесь золотая
пропорция проявляется в
пропорциях частей
перпендикулярно к
направлению роста.
17

18. Заключение

Принцип золотого сечения –
высшее проявление
структурного совершенства
целого и его частей в природе,
искусстве, науке и технике
18

19.

Библиография:
1.
Ковалев Ф.В. Золотое сечение в живописи/ Учебное пособие.-К., 1986.
2.
Мещеряков В.Т. Гармония и гармоническое отношение.-Л., 1976.
3.
Нафиков Н.Н. Гипотеза об истоке золотого сечения // Математика в
школе. М.: «Школа-Пресс», – 1994. – №3. – 96 с.
4.
Пидоу “Геометрия и искусство” – М., “Мир”, 1989
5.
Пичурин Л.Ф. За страницами учебника алгебры. – М.: «Просвещение»,
1990. – 222 с.
6.
Шевелев И.Ш., Марутаев М.А., Шмелев И.П. Золотое сечение/Три
взгляда на природу гармонии.-М., 1990.
7.
Шестаков В.П. Гармония как эстетическая категория.-М,. 1973. Журнал
“Математика в школе”, 1994, № 2, № 3
8.
http://netnotes.narod.ru
9.
http://photo-element.ru
10.
www.mavriz.ru
11.
www.konkurs.dnttm.ru
12.
www.isse.dnttm.ru
Н. Васютинский “Золотая пропорция” – М.,”Молодая гвардия”, 1990
19