Похожие презентации:
Нормальный закон распределения. Элементы математической статистики
1. Нормальный закон распределения. Элементы математической статистики
Лектор – к.п.н. Н.А. Ладнич2. План лекции
1. Нормальный закон распределения(закон Гаусса)
2. Свойства нормального
распределения
3. Законы распределения случайной величины
Законом распределения случайнойвеличины называют соответствие (связь)
между ее возможными значениями и
вероятностями их появления.
Закон распределения можно задать:
- таблично;
- аналитически (в виде формулы);
- графически.
Закон распределения полностью
характеризует случайную величину.
4.
Из законов распределения непрерывныхслучайных величин на практике чаще
используют:
• Нормальный закон распределения
(закон Гаусса) - рассматривается как
один из фундаментальных законов
природы
• Экспоненциальный закон
распределения (закон Больцмана)
5. «Нормальное» распределение или распределение Гаусса
Условия «нормального» распределения:1. Значения непрерывной случайной величины слабо
зависят от внешних факторов.
2. Значения непрерывной случайной величины
практически не зависят друг от друга.
3. Основное влияние на изменение случайной величины
– у внутренних факторов (причин, вызывающих
изменения).
Если условия выполняются, то:
- наиболее вероятной величиной распределения является
величина, равная М(Х);
- большинство значений случайной величины близки к М(Х);
- значения, далеко отстоящие от М(Х) имеют малую плотность
вероятности, т.е. встречаются в распределении редко.
6.
Нормальный закон выражаетприродные, естественные
закономерности
Например, при массовых исследованиях, для
однородных групп, распределение следующих
случайных величин подчиняются нормальному
закону:
- рост человека;
- вес;
- размер ступни;
- длина сосудов;
- большинство антропометрических признаков в
однородной популяции;
- и др.
7. Математическое выражение нормального закона распределения случайной величины
- математическое ожидание случайной величины;σ - среднее квадратическое отклонение
нормального распределения;
х - значение случайной величины;
f(х) - функция плотности вероятности;
е - основание натурального логарифма ( 2.72)
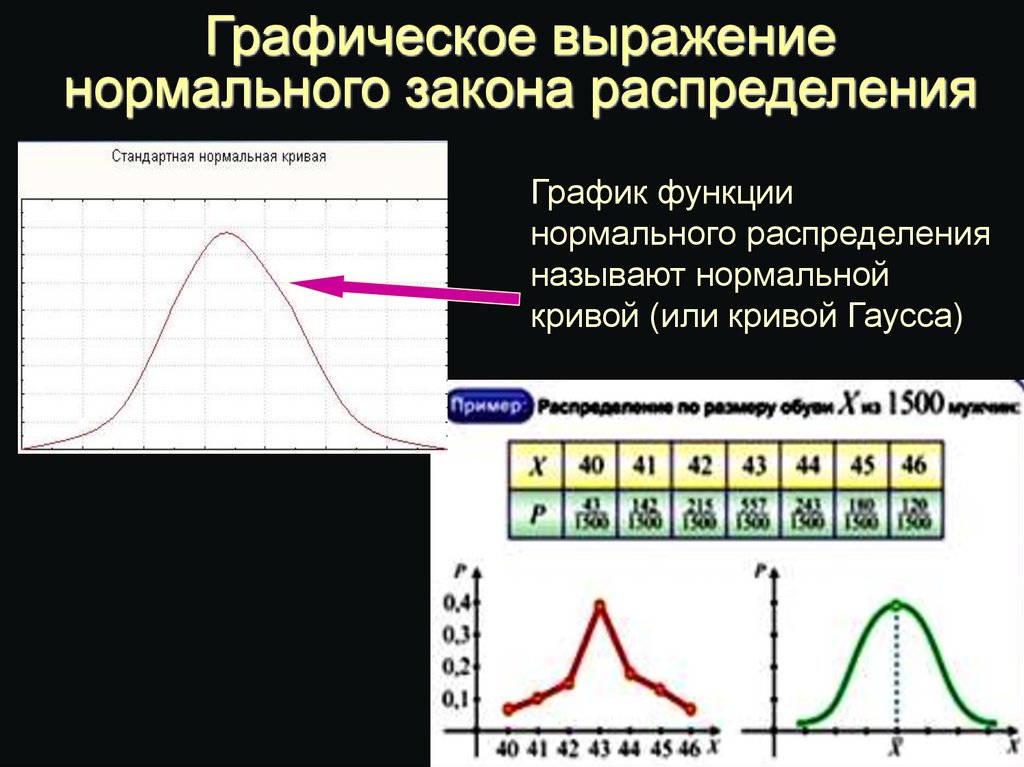
8. Графическое выражение нормального закона распределения
График функциинормального распределения
называют нормальной
кривой (или кривой Гаусса)
9.
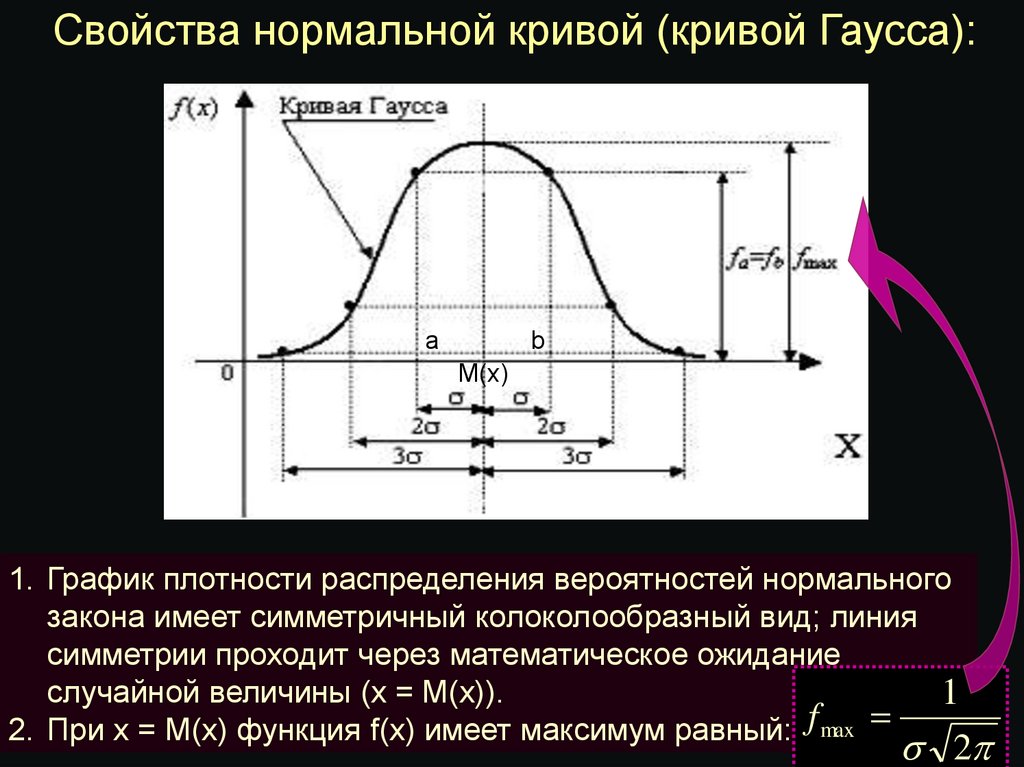
Свойства нормальной кривой (кривой Гаусса):a
b
М(х)
1. График плотности распределения вероятностей нормального
закона имеет симметричный колоколообразный вид; линия
симметрии проходит через математическое ожидание
случайной величины (х = М(х)).
1
2. При x = M(x) функция f(x) имеет максимум равный: f max
2
10.
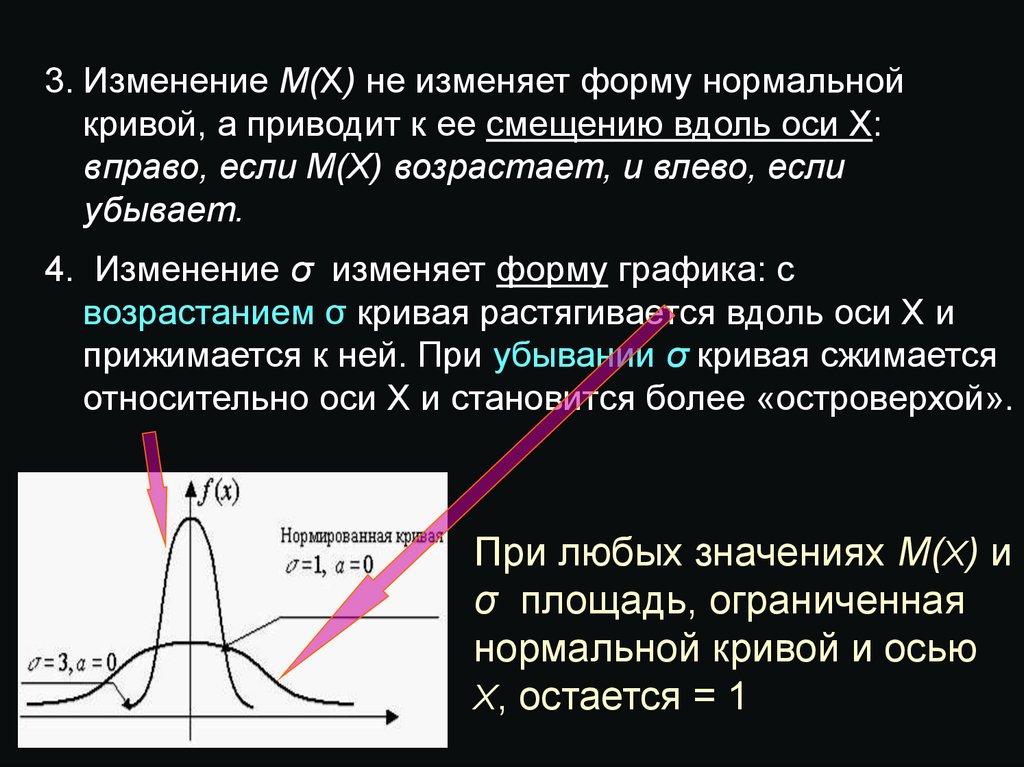
3. Изменение М(Х) не изменяет форму нормальнойкривой, а приводит к ее смещению вдоль оси X:
вправо, если М(Х) возрастает, и влево, если
убывает.
4. Изменение σ изменяет форму графика: с
возрастанием σ кривая растягивается вдоль оси X и
прижимается к ней. При убывании σ кривая сжимается
относительно оси X и становится более «островерхой».
При любых значениях М(Х) и
σ площадь, ограниченная
нормальной кривой и осью
X, остается = 1
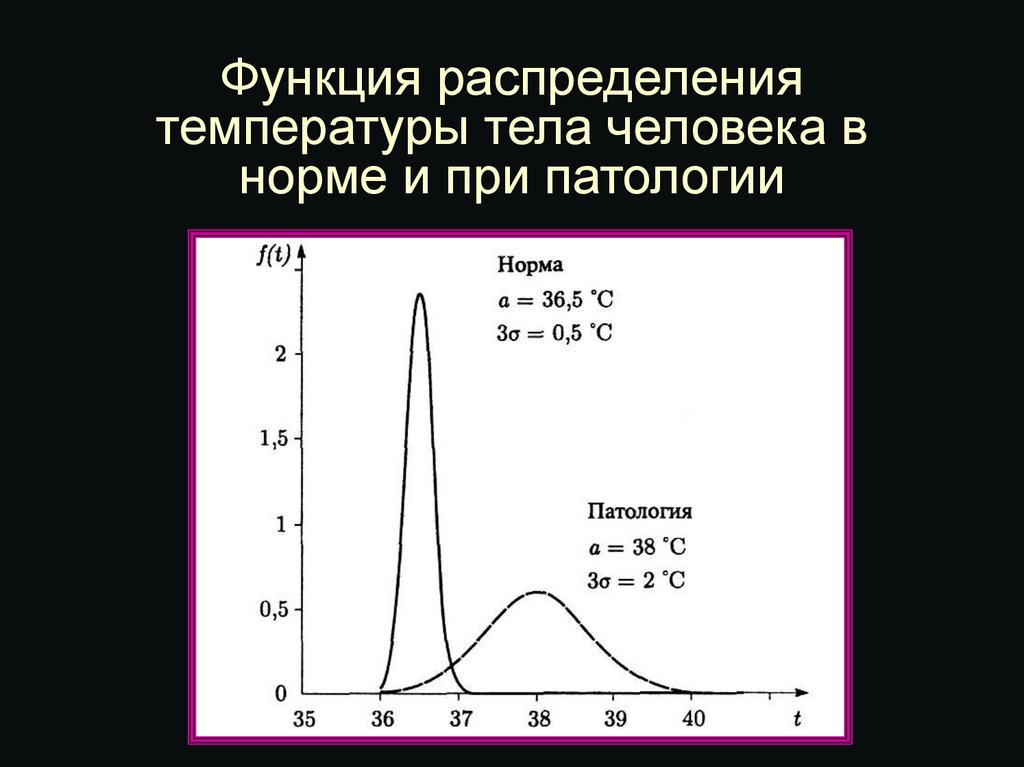
11. Функция распределения температуры тела человека в норме и при патологии
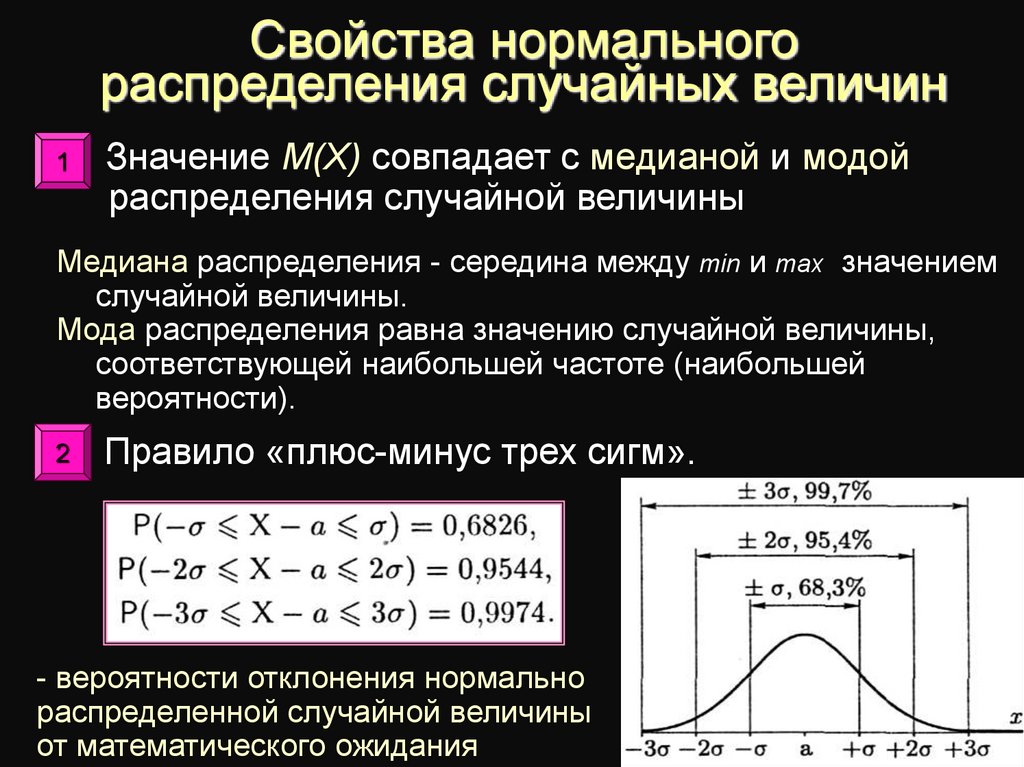
12. Свойства нормального распределения случайных величин
1. Значение М(X) совпадает с медианой и модой1
распределения случайной величины
Медиана распределения - середина между min и max значением
случайной величины.
Мода распределения равна значению случайной величины,
соответствующей наибольшей частоте (наибольшей
вероятности).
2
2.
Правило «плюс-минус трех сигм».
- вероятности отклонения нормально
распределенной случайной величины
от математического ожидания
13. Элементы математической статистики
Развитие политической арифметики и
государствоведения (демография, страховое
дело, торговля, здравоохранение и др.)
привело к появлению науки статистики.
Понятие «статистика» происходит от
латинского слова «status» (положение,
состояние, порядок явлений).
Математическая статистика — раздел
математики, посвященный математическим
методам обработки, систематизации и
использования статистических данных для
научных и практических выводов.
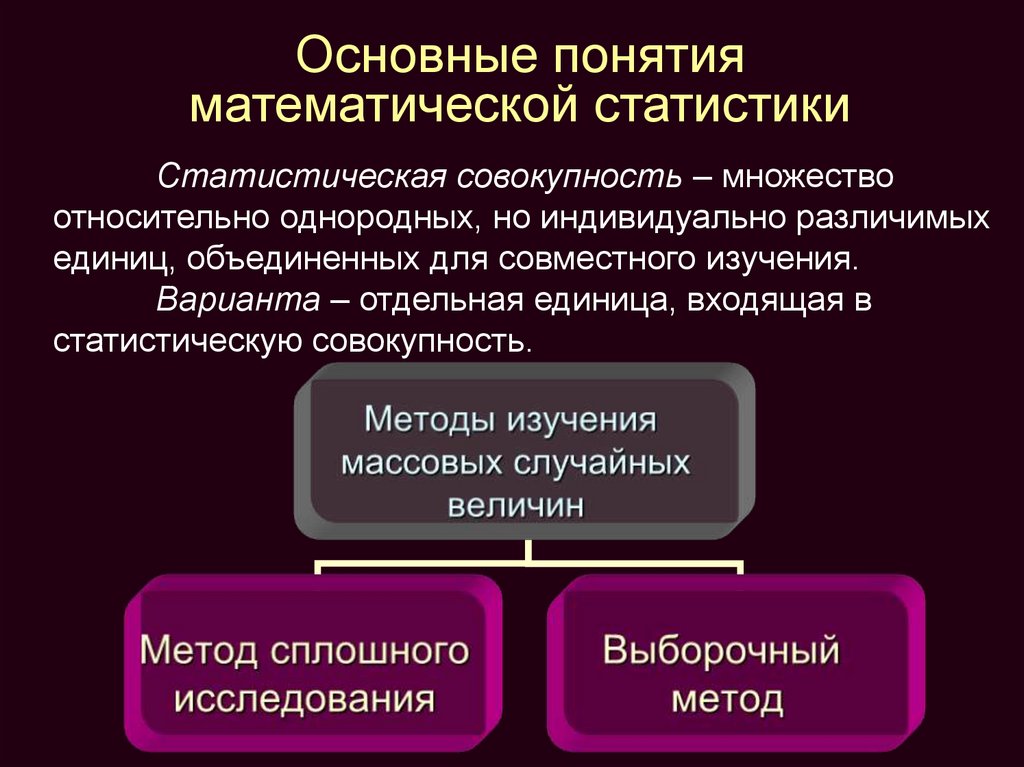
14. Основные понятия математической статистики
Статистическая совокупность – множествоотносительно однородных, но индивидуально различимых
единиц, объединенных для совместного изучения.
Варианта – отдельная единица, входящая в
статистическую совокупность.
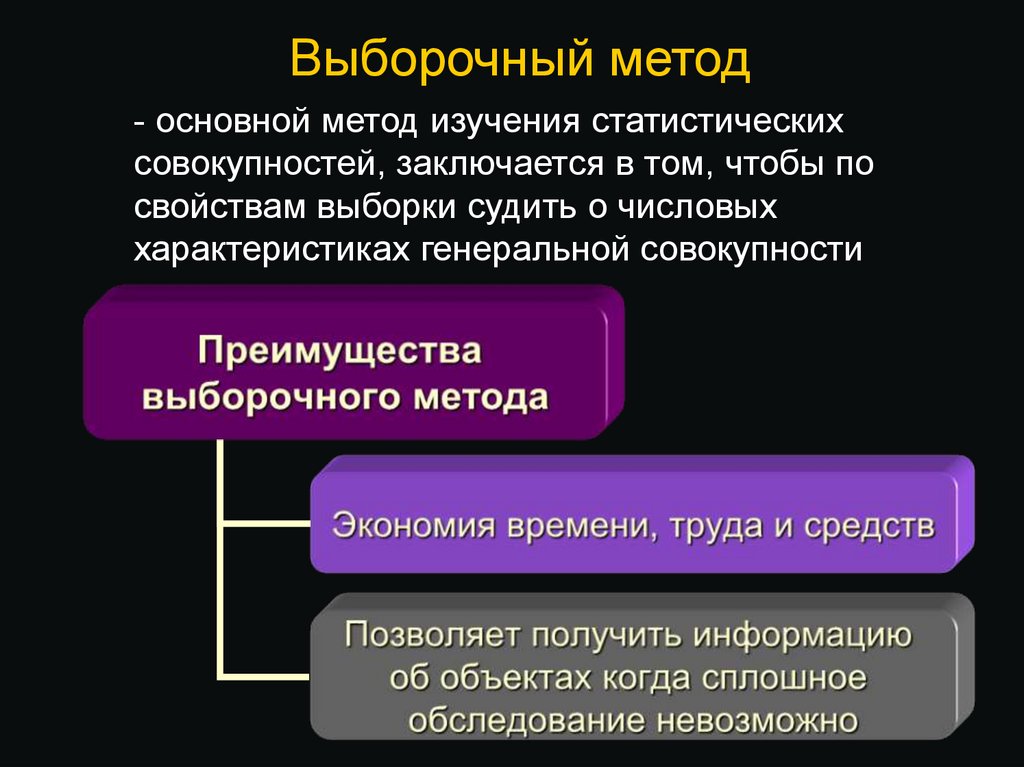
15. Выборочный метод
- основной метод изучения статистическихсовокупностей, заключается в том, чтобы по
свойствам выборки судить о числовых
характеристиках генеральной совокупности
16. Репрезентативность выборки
Свойства выборки должны соответствовать свойствамгенеральной совокупности, т.е. выборка должна быть
представительной или репрезентативной для данной
генеральной совокупности.
Условия
репрезентативности
выборки
Типичность
Объективность
17. Три способа оценки генеральной совокупности по выборочным данным
1 Точечный способ (выборочнаясредняя, выборочная дисперсия)
2 Интервальный (доверительный
интервал, уровень значимости)
3
Сравнительный (критерий
Стьюдента, критерий Фишера и др.)
18. Точечная оценка параметров генеральной совокупности по ее выборке
При неограниченном увеличенииобъема выборки точечные оценки
(выборочные) стремятся к истинным
значениям соответствующих
генеральных характеристик:










 Математика
Математика








