Функция және оның берілу тәсілдері. Функция графиктерін қарапайым түрлендіру

1. Сабақтың тақырыбы: Функция және оның берілу тәсілдері. Функция графиктерін қарапайым түрлендіру. Оқу мақсаты: -функция

анықтамасын және берілу тәсілдерін
беру
-функция графигіне түрлендірулер орындай алу
(параллель көшіру, сығу және созу);.

2.

«Кім жылдам?» ойыны бойынша өткен
материалдарды қайталау:
·Абсолют тұрақты шама дегеніміз ...
·Параметр дегеніміз ...
·Айнымалы шама дегеніміз ...
·Функция дегеніміз ...
·Функцияның анықталу облысы дегенміз
және оны қалай белгілейді?
·Функцияның мәндер жиыны дегенміз және
оны қалай белгілейді?

3.

Анықтама
Кез келген жағдайда, тек қана бір сандық мәнді ғана қабылдайтын
шаманы абсолют тұрақты шама деп атайды.
Шамалар тұрақты және айнымалы болып екіге бөлінеді.
Тұрақты шамалар:
абсолют тұрақты және параметр,
Айнымалылар:
тәуелді және тәуелсіз болып бөлінеді.
Анықтама
Берілген жағдайда ғана тұрақты, толық анықталған сандық мәнін сақтайтын
тұрақты шаманы параметр деп атайды.
Анықтама
Әртүрлі сандық мәндер қабылдайтын шаманы айнымалы шама деп атайды.
Анықтама
Х жиынындағы х-тің әрбір мәніне Y жиынның нықты бір мәнін сәйкес қоятын
ереже немесе заңдылық функция деп аталады.
Анықтама
f(x) функциясы белгілі бір мән қабылдайтын тәуелсіз айнымалының нақты
мәндер жиынын функцияның анықталу облысы D(f(x)), ал анықталу
облысынан алынған
әрбір тәуелсіз айнымалыға сәйкес табылған функцияның мәндерін оның
мәндер жиыны E(f(x)) деп атайды.

4.

Функцияның y=f(x), y=ϕ(x), y=g(x) және т.с.с. белгілейді,
мұндағы х – тәуелсіз айнымалы немесе функцияның
аргументі;
у – тәуелді айнымалы немесе функция.
Функцияның берілу тәсілдері:
1) кестелік тәсілдің ерекшелігі- аргументтің мәндеріне
сәйкес
2)графиктік тәсілдің ерекшелігі - көрнекілігінде
3) аналитикалық тәсіл функцияны толық зерттеуге
ыңғайлы.

5.

6.

7.

Функция графиктерін
түрлендіру

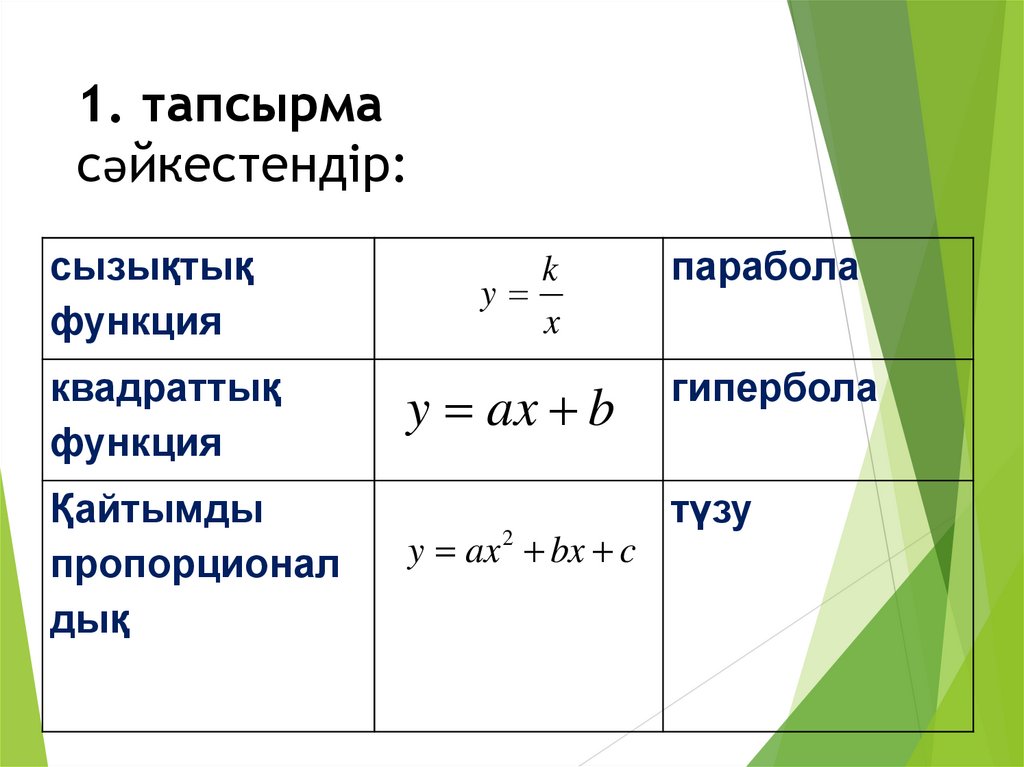
8. 1. тапсырма сәйкестендір:

сызықтық
функция
квадраттық
функция
Қайтымды
пропорционал
дық
k
y
x
парабола
y ax b
гипербола
y ax 2 bx c
түзу

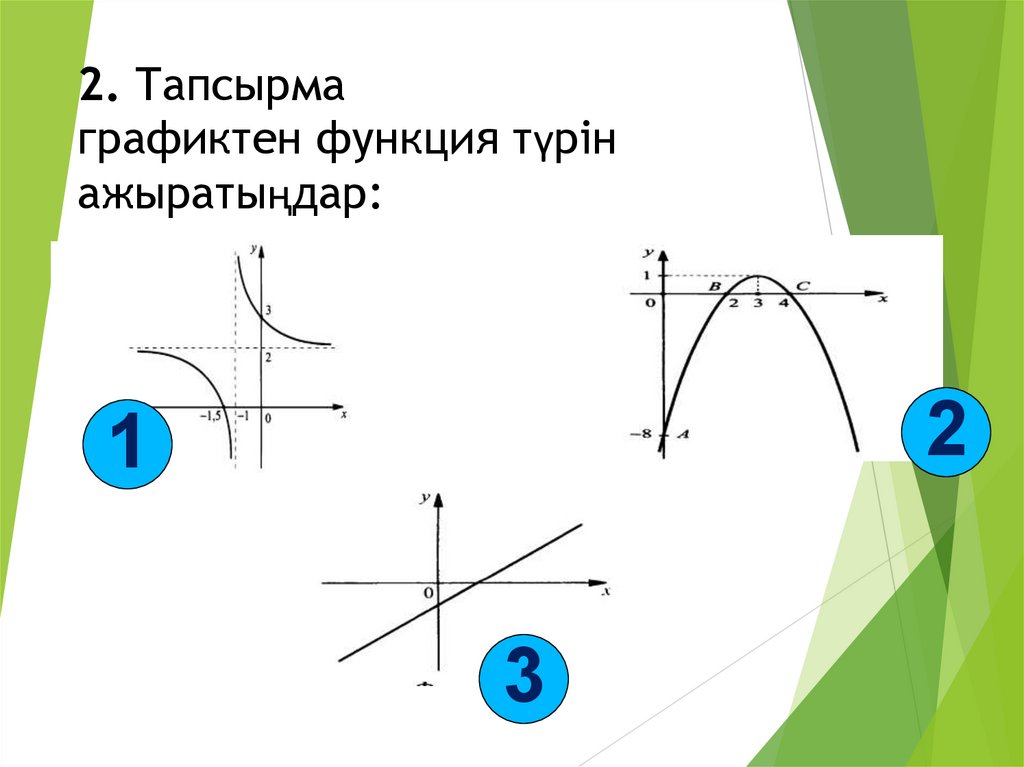
9. 2. Тапсырма графиктен функция түрін ажыратыңдар:

2
1
3

10. функция графигінің түрлендіруінің түрлерін қарастырайық:

y f (x )
функция графигінің түрлендіруінің
түрлерін қарастырайық:

11.

Функция
Функция графигін түрлендіру
1
y f x d
2
y f ( x b)
OX өсі бойымен параллель көшіру
b бірлікке оңға, егер b < 0, онда b
бірлікке солға, егер b > 0.
y kf (x)
Oy өсі бойымен созу OX өсіне
қарағанда k есе , егер k > 1, және сығу
1/k рет, егер 0 < k < 1.
4
y f (ax)
OX өсі бойымен сығу OY өсіне
қарағанда а есе, егер а > 1, және созу
1/а рет, егер 0 < а < 1.
5
y kf (ax b) d
3
OY өсі бойымен параллель көшіру
d бірлікке жоғары единиц , егер d>0,
және d бірлікке төмен , егер d<0.
Барлық 4 түрлендіру

12. 1. Параллель көшіру у өсі бойынша f(x)f(x)+d

1. Параллель көшіру у өсі бойынша
f(x) f(x)+d
y=f(x)+d функция графигі y=f(x) фунция графигінің
параллель көшіруі болып табылады егер у өсі
бойымен d>0 болғанда |d|-ға жоғары және d<0
төмен.

13. 2. Параллель көшіру х өсі бойынша f(x)f(x+b)

2. Параллель көшіру х өсі бойынша
f(x) f(x+b)
y=f(x+b) функция графигі y=f(x) функция
графигінің параллель көшіруі болып
табылады , егер х өсі бойымен |b| оңға b>0
және солға b<0 .

14. 3.Созу және сығу у өсі бойымен f(x)  kf(x), егер k>0

3.Созу және сығу у өсі бойымен
f(x) kf(x), егер k>0
k>1 y=kf(x) функция графигі y=f(x) функция графигінің у
өсі бойымен k есе созулуы.
0<k<1 y=kf(x) функция графигі y=f(x) функция
графигінің у өсі бойымен 1/k есе сығылу болады

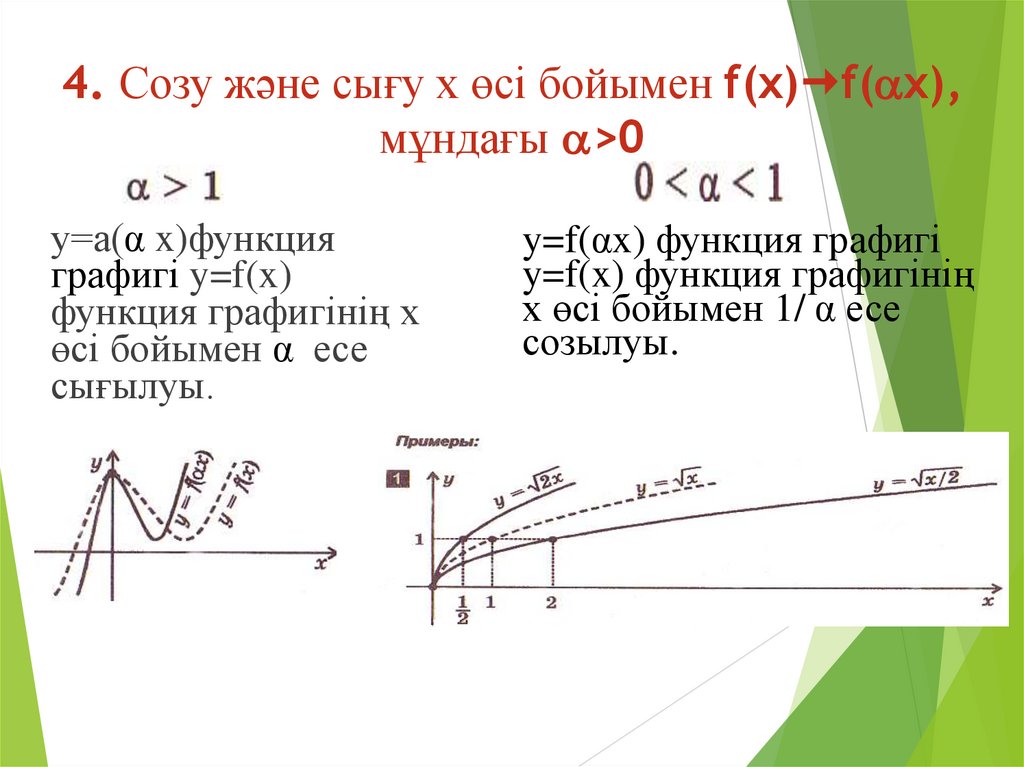
15. 4. Созу және сығу х өсі бойымен f(x)f(x), мұндағы >0

4. Созу және сығу х өсі бойымен f(x) f( x),
мұндағы >0
y=а(α x)функция
графигі y=f(x)
функция графигінің х
өсі бойымен α есе
сығылуы.
y=f(αx) функция графигі
y=f(x) функция графигінің
х өсі бойымен 1/ α есе
созылуы.

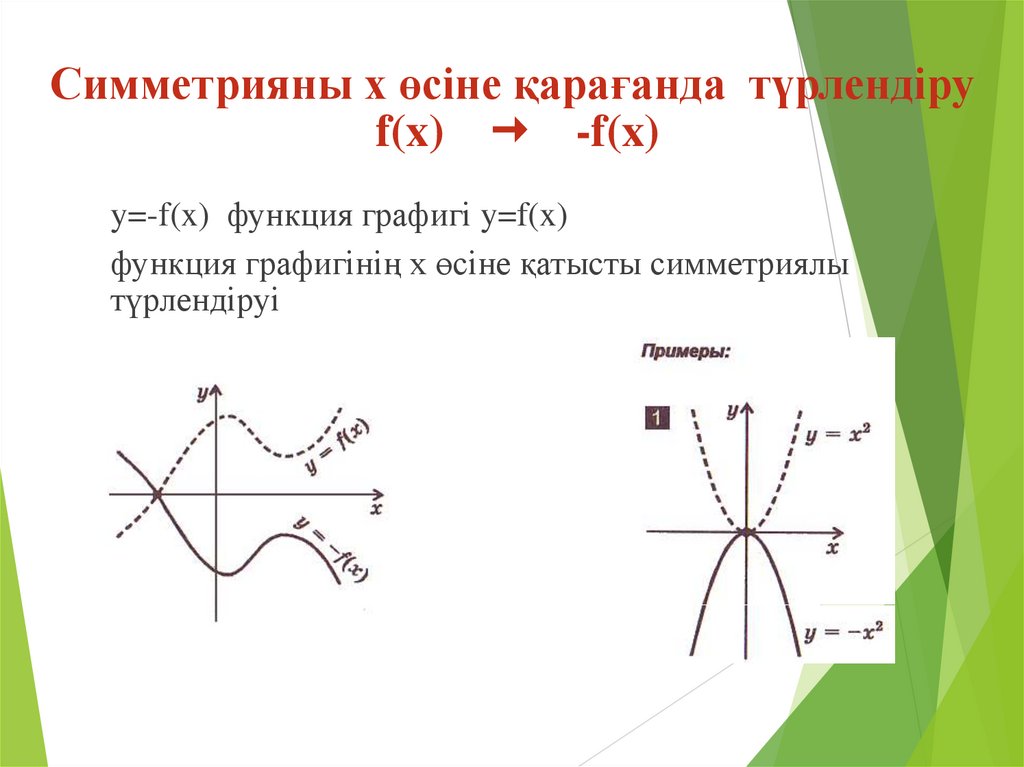
16. Симметрияны х өсіне қарағанда түрлендіру f(x)  -f(x)

Симметрияны х өсіне қарағанда түрлендіру
f(x) -f(x)
y=-f(x) функция графигі y=f(x)
функция графигінің х өсіне қатысты симметриялы
түрлендіруі

17. Симметрияны у өсіне қарағанда түрлендіру f(x)f(-x)

Симметрияны у өсіне қарағанда түрлендіру
f(x) f(-x)
y=f(-x) функция графигі y=f(x) функция
графигінің у өсіне қатысты симметриялы
түрлендіруі

18. №І. y=2x, y=2x+2, y=2x-1 функцияларының графигін салыңдар.

Үйге тапсырма:
«Функция» терминінің пайда болу тарихы
туралы (Готфрид, Лейбниц, И. Бернулли,
Н.И.Лобачевский, Дирихле) мәлімет
дайындаңдар.
№І. y=2x, y=2x+2, y=2x-1 функцияларының графигін
салыңдар.
№ІІ. y=x, y=x²-3, y=3x² функцияларының графигін
салыңдар.
А.Е.Әбілкасымова, З.Ә.Жұмағұлова «Алгебра және
анализ бастамалары», 10 сынып, 2019ж.