Механика. Термодинамика. Электричество и магнетизм

1. Курс физики в двух семестрах Семестр 1 «Механика. Термодинамика. Электричество и магнетизм.»

Лектор
Манилова Галина Васильевна
Доцент института ФПМ МИЭТ,
кандидат физико-математических наук

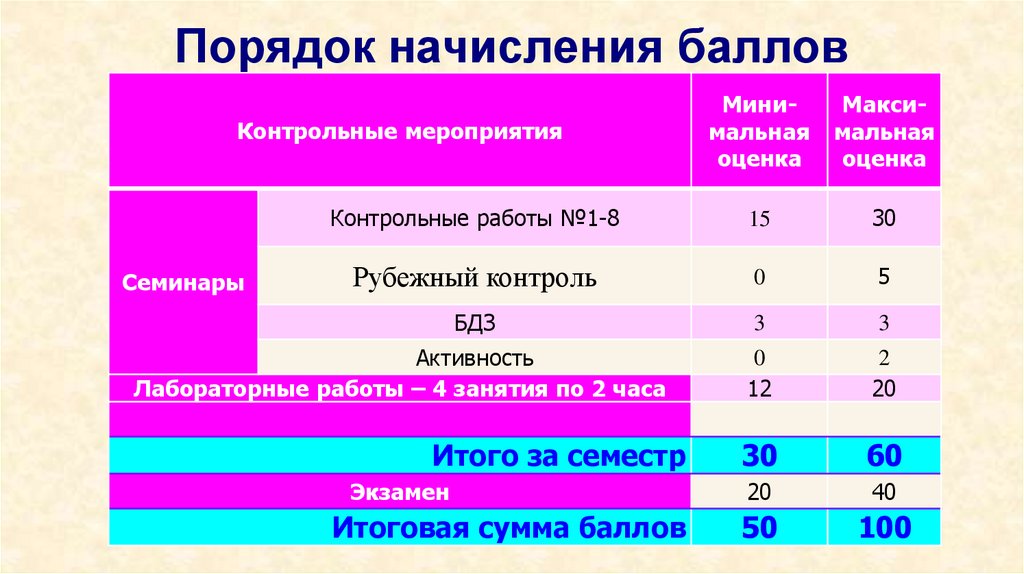
2. Порядок начисления баллов

Минимальная
оценка
Максимальная
оценка
Контрольные работы №1-8
15
30
Рубежный контроль
0
5
БДЗ
3
3
0
12
2
20
30
60
20
40
50
100
Контрольные мероприятия
Семинары
Активность
Лабораторные работы – 4 занятия по 2 часа
Итого за семестр
Экзамен
Итоговая сумма баллов

3. Литература Учебники

И1
И2 И3
И.Е.Иродов. Механика. Основные законы
И.Е.Иродов. Физика макросистем. Основные законы
И.Е.Иродов. Электромагнетизм. Основные законы

4. Литература Учебники

С1
С2
С3
И.В.Савельев. Механика. Курс общей физики.
И.В.Савельев. Молекулярная физика и термодинамика. Курс общей физики.
И.В.Савельев. Электричество и магнетизм. Курс общей физики.

5. Литература. Сборники задач

И.Е.Иродов.
Задачи по общей физике
М., Лаборатория базовых
знаний 2001
А.С.Овчинников
Механика и
молекулярная физика.
Сборник задач по
курсу «Общая физика»
И.Н.Горбатый
А.С.Овчинников
Электричество и магнетизм.
Сборник вопросов и задач по
физике

6. Литература. Тестовые задания

И.В.Федоренко
Механика. Молекулярная физика.
Сборник тестовых заданий по
физике

7. Модуль 1 Механика Лекция 1 Кинематика материальной точки

8. §1.1. Основные понятия

Механика – раздел физики, изучающий движение тел в пространстве и
во времени.
Свойства пространства:
Трехмерно
Однородно
Изотропно
Свойства времени:
Одномерно
Однородно
Направлено в одну сторону (может только увеличиваться)
Тело отсчета – тело, служащее для определения положения других тел.
Система отсчета – совокупность тела отсчета, связанных с ним
координат и синхронизованных между собой часов.

9. Классическая механика

Классическая (Ньютоновская) механика
V << c (c = 3·108 м/с); l >> 1 нм
1687 г.
Релятивистская механика
V~c
Квантовая механика
l < 100 нм
Эйнштейн, 1905 г.
Шредингер, Гейзенберг, 1925 г.
Релятивистская квантовая механика
V ~ c ; l < 100 нм
Дирак, 1928 г.

10. §1.1. Основные понятия

Кинематика – раздел механики, описывающий движение
тел, отвлекаясь от причин, его вызывающих.
Материальная точка – тело, размерами которого в
условиях данной задачи можно пренебречь.
Траектория
–
множество
точек
пространства,
пройденных материальной точкой в процессе движения.
Путь S – длина траектории.
Закон движения – функция времени, описывающая
положение материальной точки в пространстве.

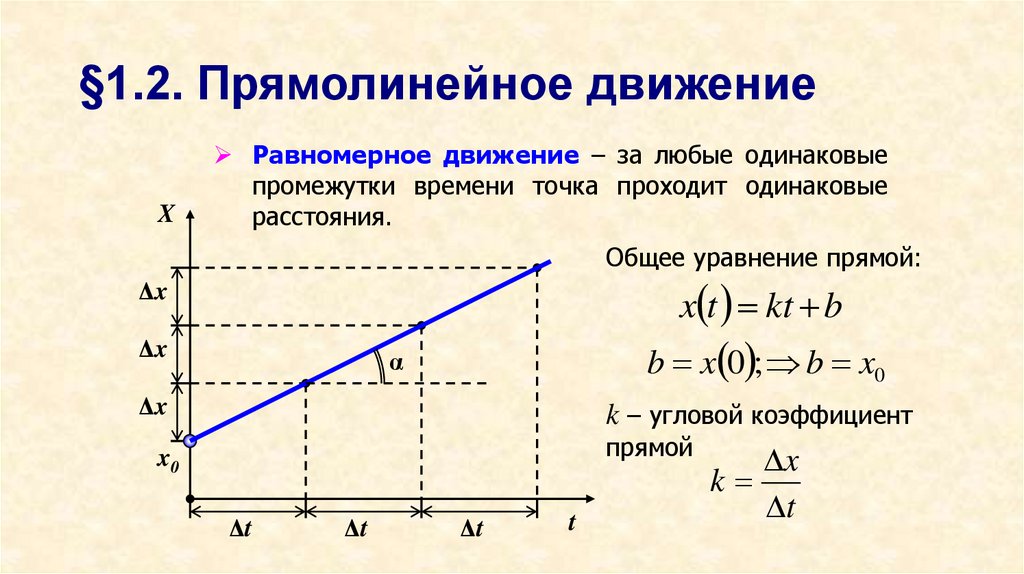
11. §1.2. Прямолинейное движение

X
Равномерное движение – за любые одинаковые
промежутки времени точка проходит одинаковые
расстояния.
Общее уравнение прямой:
x t kt b
Δx
Δx
b x 0 ; b x0
α
Δx
k – угловой коэффициент
прямой
x0
Δt
Δt
Δt
t
x
k
t

12. Прямолинейное равномерное движение

Скорость:
x
Vx
t
Закон движения прямолинейного
равномерного движения:
x t Vxt x0

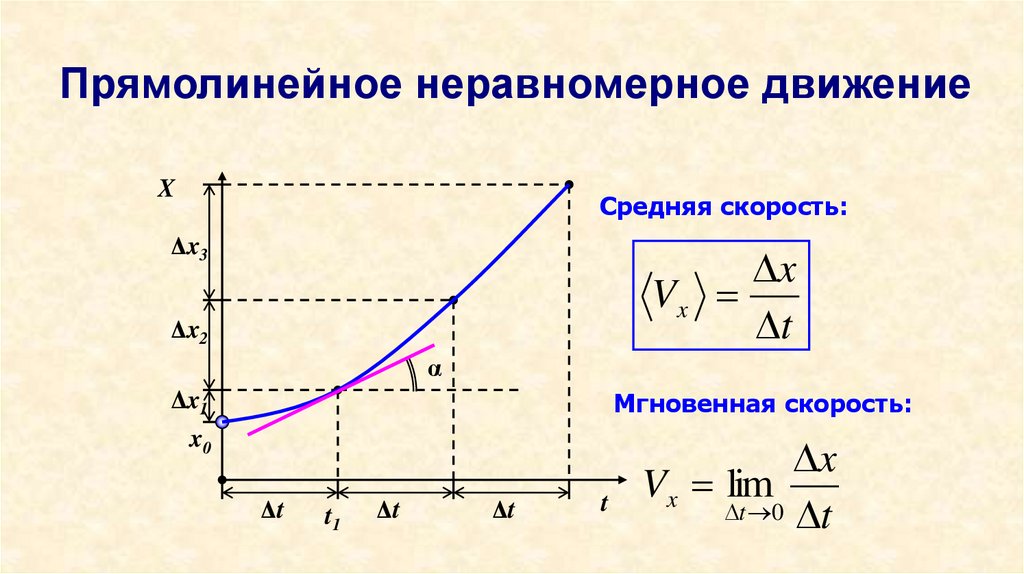
13. Прямолинейное неравномерное движение

X
Средняя скорость:
Δx3
x
Vx
t
Δx2
α
Δx1
x0
Мгновенная скорость:
Δt
t1
Δt
Δt
t
x
Vx lim
t 0 t

14. Скорость и ускорение

Скорость – производная координаты по времени.
Vx x x
dx
dt
dt – бесконечно малое приращение времени
dx – приращение координаты за время dt
Геометрический
смысл
скорости
(и
производной) – угловой коэффициент касательной к
графику функции координаты от времени
Ускорение – производная скорости по времени:
dVx
ax
dt

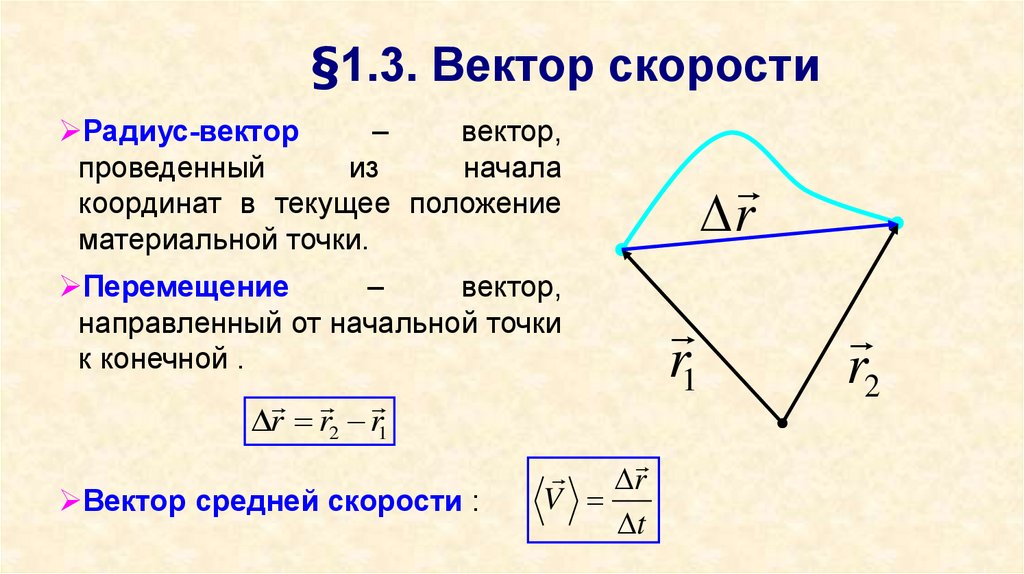
15. §1.3. Вектор скорости

Радиус-вектор
–
вектор,
проведенный
из
начала
координат в текущее положение
материальной точки.
Перемещение
–
вектор,
направленный от начальной точки
к конечной .
r r2 r1
Вектор средней скорости :
r
V
t
r
r1
r2

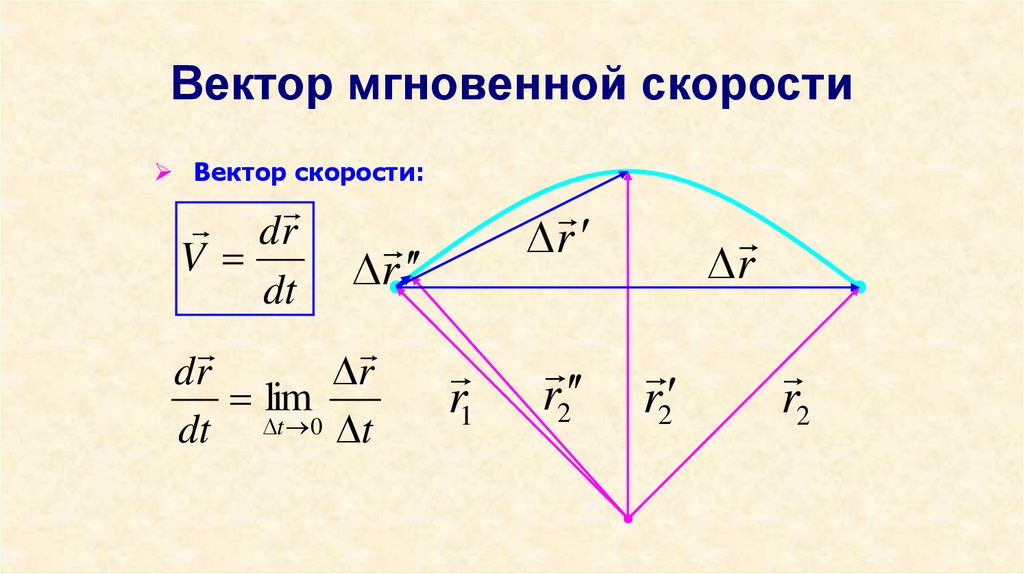
16. Вектор мгновенной скорости

Вектор скорости:
dr
V
r
dt
dr
r
lim
r
1
dt t 0 t
r
r2
r
r2
r2

17. Векторный способ

Свойства вектора мгновенной скорости
Всегда направлен по касательной к траектории
По модулю равен
пройденного пути:
производной
по
времени
от
dS
V
dt
Средние величины
Средний модуль скорости:
Модуль средней скорости:
S
r
V
V
V V
t
t
dV
a
Вектор ускорения:
dt

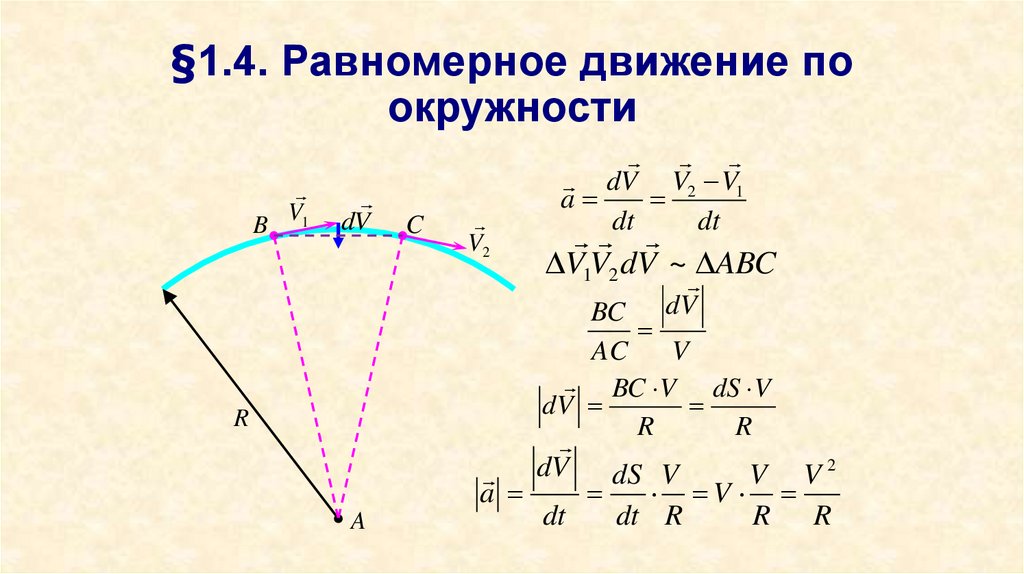
18. §1.4. Равномерное движение по окружности

B
V1
dV
C
V2
dV V2 V1
a
dt
dt
V1V2 dV ~ ABC
dV
R
A
BC
AC
V
BC V dS V
dV
R
R
dV dS V
V V2
a
V
dt
dt R
R R

19. Центростремительное ускорение

При
равномерном
движении
точки
по
окружности её вектор ускорения направлен к
центру окружности, равен по величине V2/R и
называется центростремительным.

20. §1.5. Тангенциальное и нормальное ускорение

Тангенциальная
траектории.
ось
направлена
по
касательной
к
- единичный вектор тангенциальной оси
Нормальная ось направлена перпендикулярно траектории.
n - единичный вектор нормальной оси
V V
n
dV d
dV
d
a
V
V
dt dt
dt
dt
V

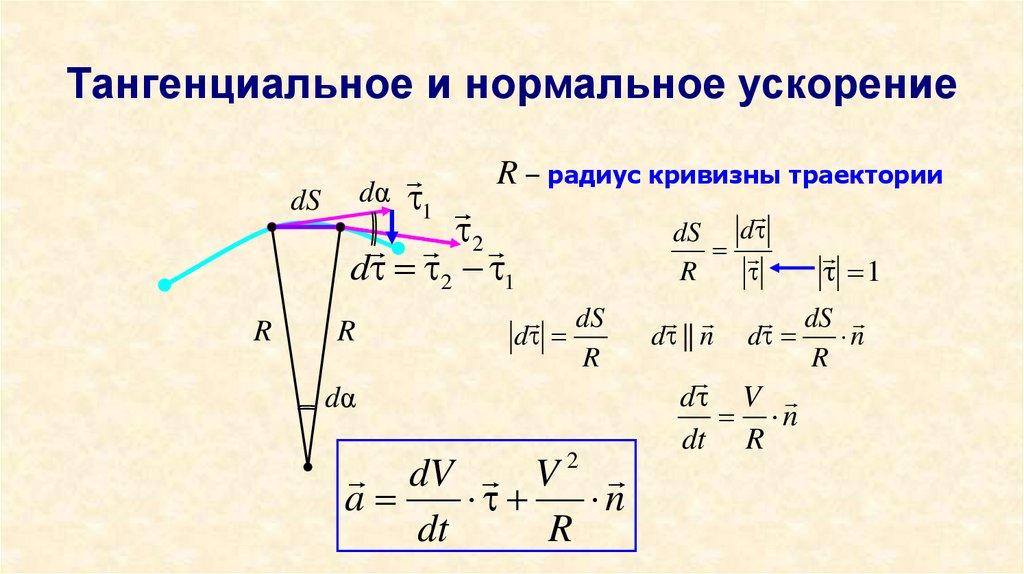
21. Тангенциальное и нормальное ускорение

dS
R
R – радиус кривизны траектории
1
dS d
R
dα
2
d 2 1
R
dS
d
R
dα
dV V 2
a
n
dt
R
d || n
1
dS
d
n
R
d V
n
dt R

22. Тангенциальное и нормальное ускорение

dV
a
– тангенциальное ускорение
dt
(касательное к траектории).
V2
an
n
R
–
нормальное
ускорение
(перпендикулярное касательной к
траектории).

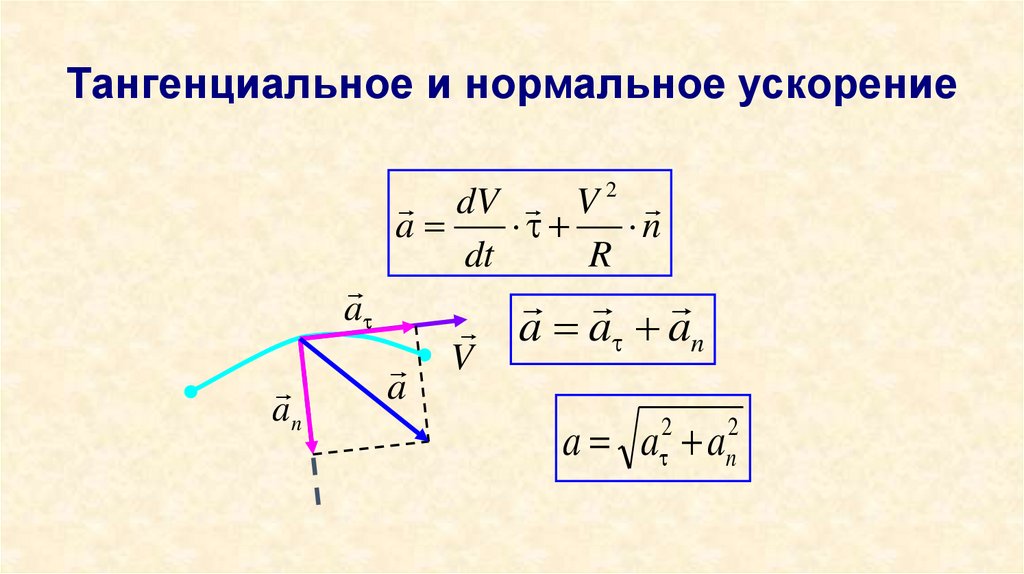
23. Тангенциальное и нормальное ускорение

a
an
dV V 2
a
n
dt
R
a
a a an
V
a a a
2
2
n

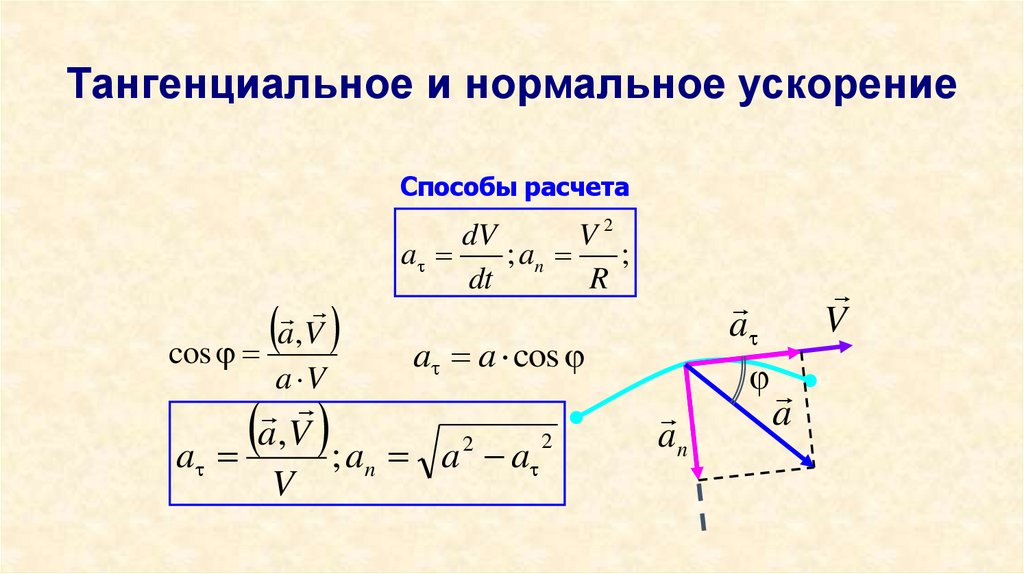
24. Тангенциальное и нормальное ускорение

Способы расчета
a,V
cos
a V
dV
V2
a
; an
;
dt
R
a a cos
a,V
2
2
a
; an a a
V
an
V
a
a

25. Тангенциальное и нормальное ускорение

Физический смысл:
Тангенциальное ускорение описывает изменение модуля
вектора скорости.
Пример: при равномерном движении V=const => aτ=0
Нормальное ускорение описывает изменение направления
вектора скорости.
Пример: при прямолинейном движении R→∞ => an=0

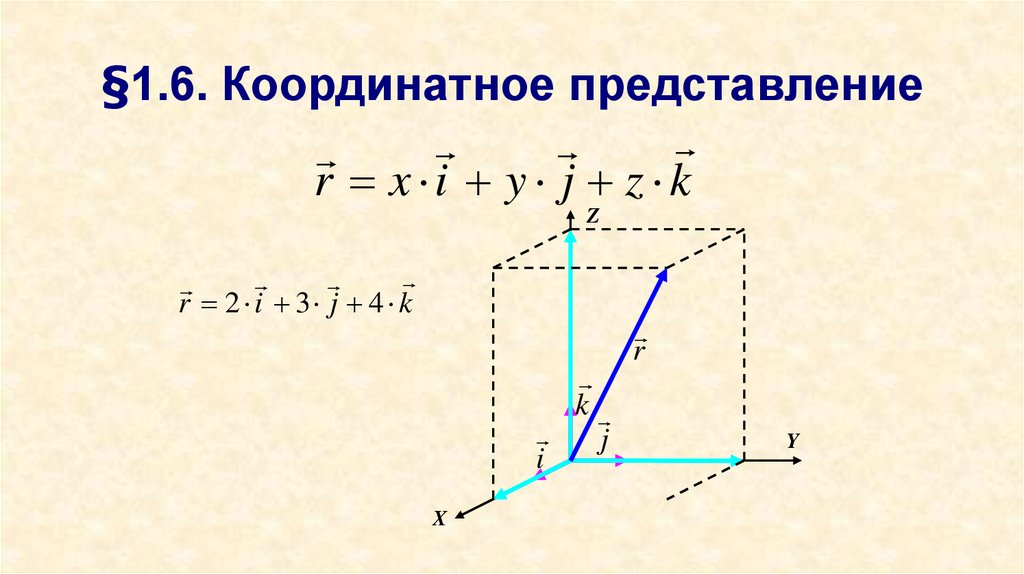
26. §1.6. Координатное представление

r x i y j z k
Z
r 2 i 3 j 4 k
k
j
i
X
r
Y

27. Координатное представление

dr
dV
ax i a y j az k ;
V
Vx i V y j Vz k ; a
dt
dt
dx
dy
dz
Vx ; V y ; Vz
dt
dt
dt
2
2
2
V V Vx Vy Vz
dVy
dVx
dVz
ax
; ay
; az
;
dt
dt
dt
2
2
2
a a ax a y az
dV
axVx a yVy azVz
a
,
V
a
или a
dt
V
V
2
2
V
an a 2 a
R
an

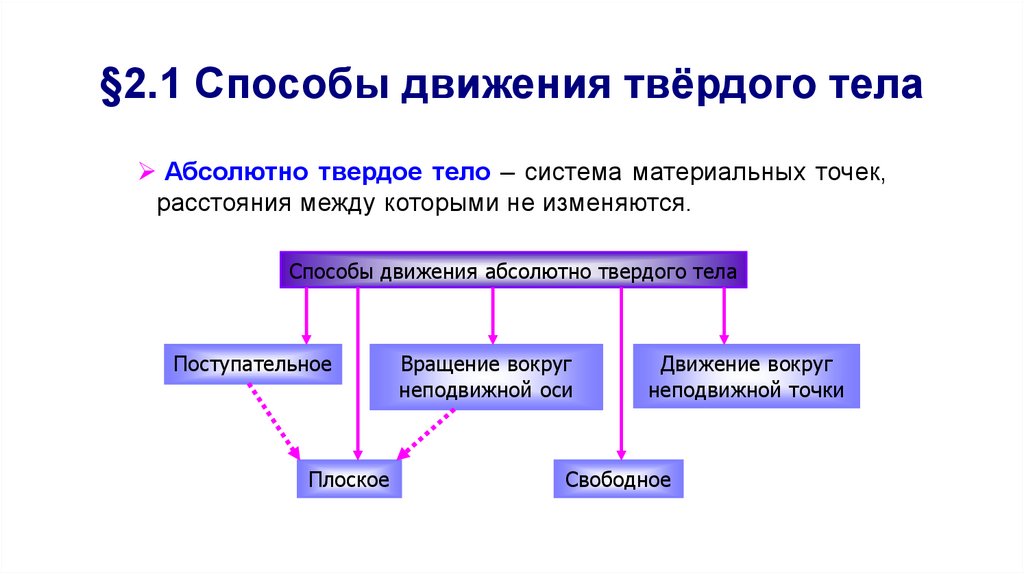
28. §2.1 Способы движения твёрдого тела

Абсолютно твердое тело – система материальных точек,
расстояния между которыми не изменяются.
Способы движения абсолютно твердого тела
Поступательное
Плоское
Вращение вокруг
неподвижной оси
Движение вокруг
неподвижной точки
Свободное

29. Поступательное движение

Движение
твердого
тела
называется
поступательным, если любая связанная с телом
прямая остается параллельной своему начальному
положению.
При поступательном движении все точки твердого
тела совершают за одинаковые промежутки времени
равные перемещения. Поэтому их скорости и
ускорения одинаковы.

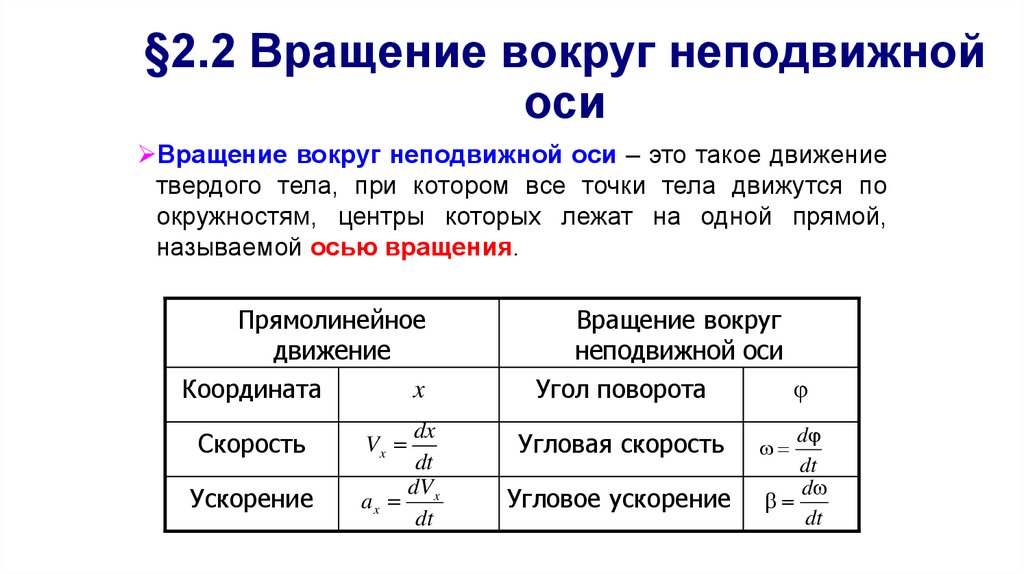
30. §2.2 Вращение вокруг неподвижной оси

Вращение вокруг неподвижной оси – это такое движение
твердого тела, при котором все точки тела движутся по
окружностям, центры которых лежат на одной прямой,
называемой осью вращения.
Прямолинейное
движение
x
Координата
Скорость
Ускорение
dx
dt
dV
ax x
dt
Vx
Вращение вокруг
неподвижной оси
φ
Угол поворота
Угловая скорость
Угловое ускорение
d
dt
d
dt

31. Вектор угловой скорости

Угловая скорость – вектор, численно равный углу
поворота твёрдого тела в единицу времени, направленный
вдоль оси вращения тела, причём это направление
определяется правилом правого винта.

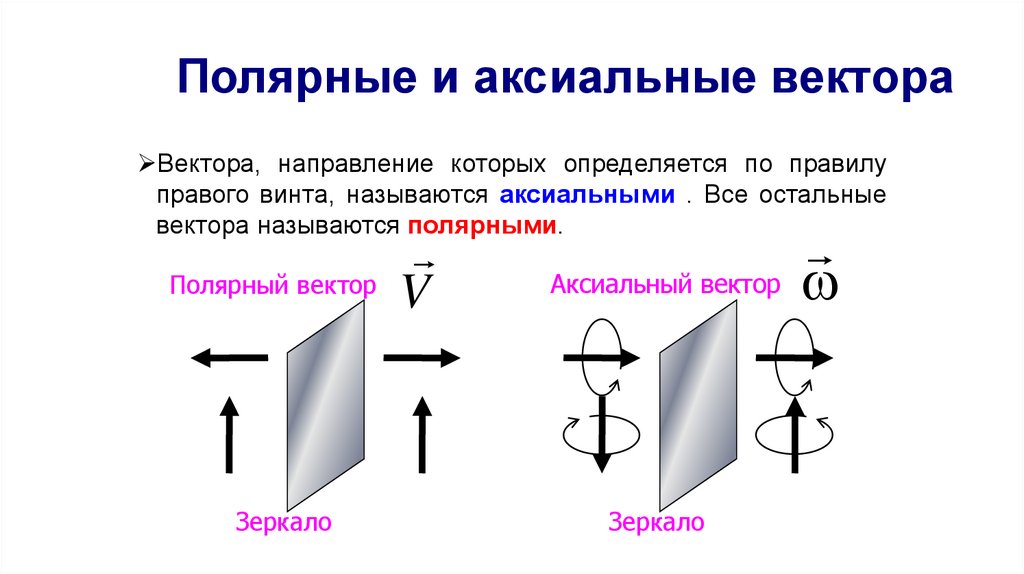
32. Полярные и аксиальные вектора

Вектора, направление которых определяется по правилу
правого винта, называются аксиальными . Все остальные
вектора называются полярными.
Полярный вектор
V
Зеркало
Аксиальный вектор
Зеркало

33. Вектор углового ускорения

Угловое ускорение –
производная по времени
скорости:
аксиальный
от вектора
d
dt
вектор,
угловой

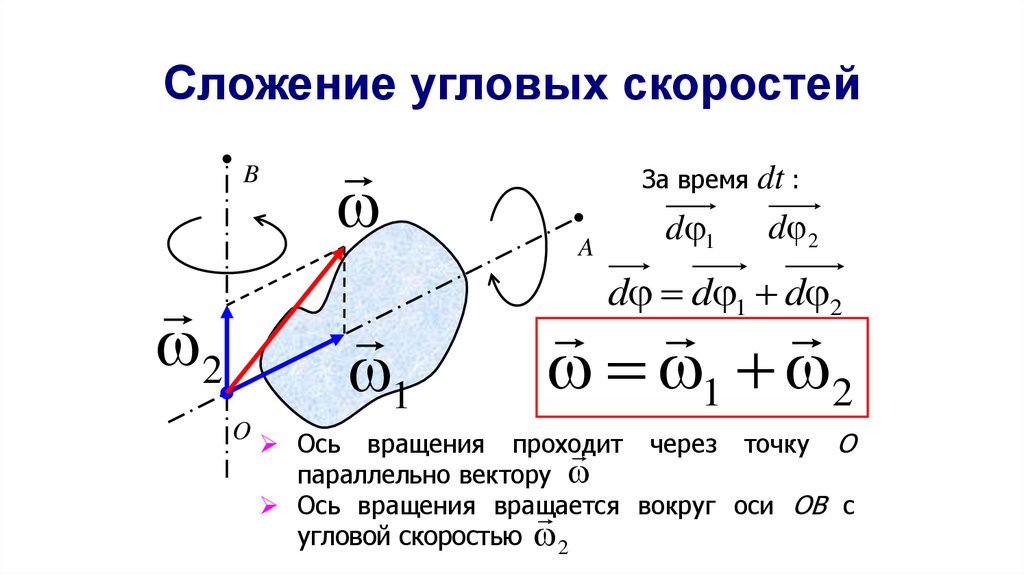
34. Сложение угловых скоростей

B
2
1
O
За время dt :
A
d 1
d 2
d d 1 d 2
1 2
Ось вращения проходит
через точку O
параллельно вектору
Ось вращения вращается
вокруг оси OB с
угловой скоростью 2

35. §2.3 Математический ликбез

36. Прямоугольный треугольник с бесконечно малым углом

c
a
0
b c sin
b atg
b
d
c
a
b
cosd 1
b cd ad
sin d tgd d

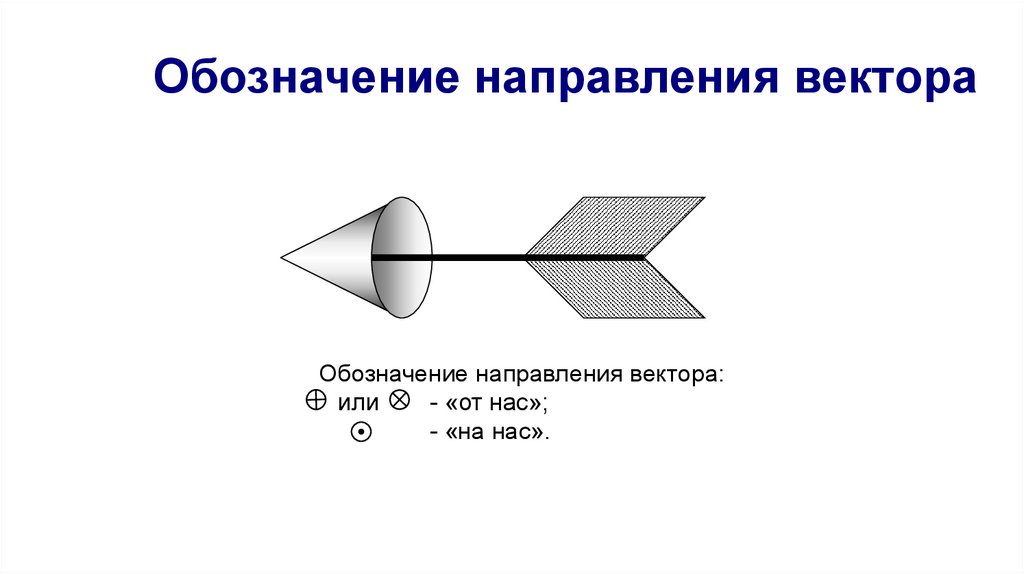
37. Обозначение направления вектора

Обозначение направления вектора:
или
- «от нас»;
- «на нас».

38. Скалярное произведение векторов

a ax i a y j az k
Пусть: даны вектора
b bx i by j bz k
угол между ними
Тогда:
Скалярным произведением векторов называется число:
a , b a b cos
В координатном представлении:
a, b axbx a y by az bz

39. Векторное произведение

Векторным произведением векторов называется
вектор:
[a , b ] c
1. c a b sin ;
2. c a; c b ; c плоскости ab
3. a , b , c правая тройка
i
В координатном представлении: c a x
bx
j
ay
by
k
az
bz

40. Как определить направление векторного произведения?

1. Мысленно с помощью параллельного переноса совместить
начала векторов.
2. Определить направление вращения: от первого вектора ко
второму по кратчайшему пути.
3. Поступательное движение винта при данном вращении
покажет направление результирующего вектора
c [a , b ]
c
a
b

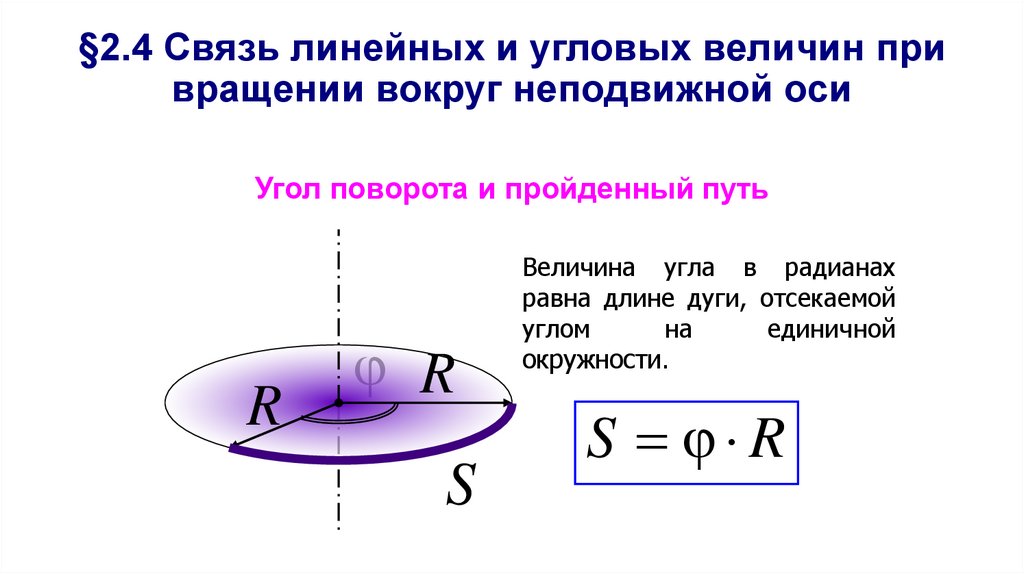
41. §2.4 Связь линейных и угловых величин при вращении вокруг неподвижной оси

Угол поворота и пройденный путь
R
R
S
Величина угла в радианах
равна длине дуги, отсекаемой
углом
на
единичной
окружности.
S R

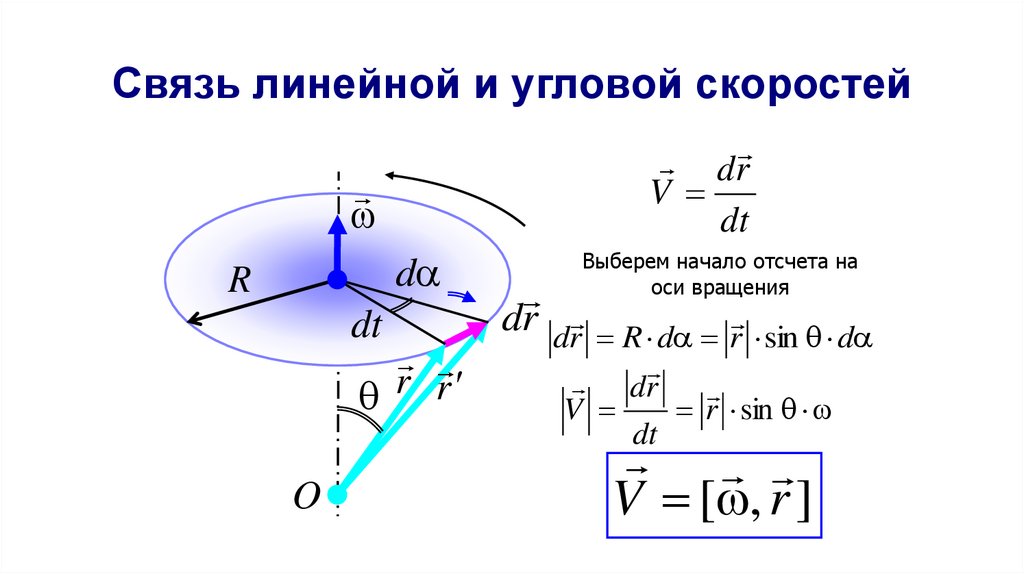
42. Связь линейной и угловой скоростей

dr
V
dt
d
R
dt
r r
O
Выберем начало отсчета на
оси вращения
dr dr R d r sin d
dr
V
r sin
dt
V [ , r ]

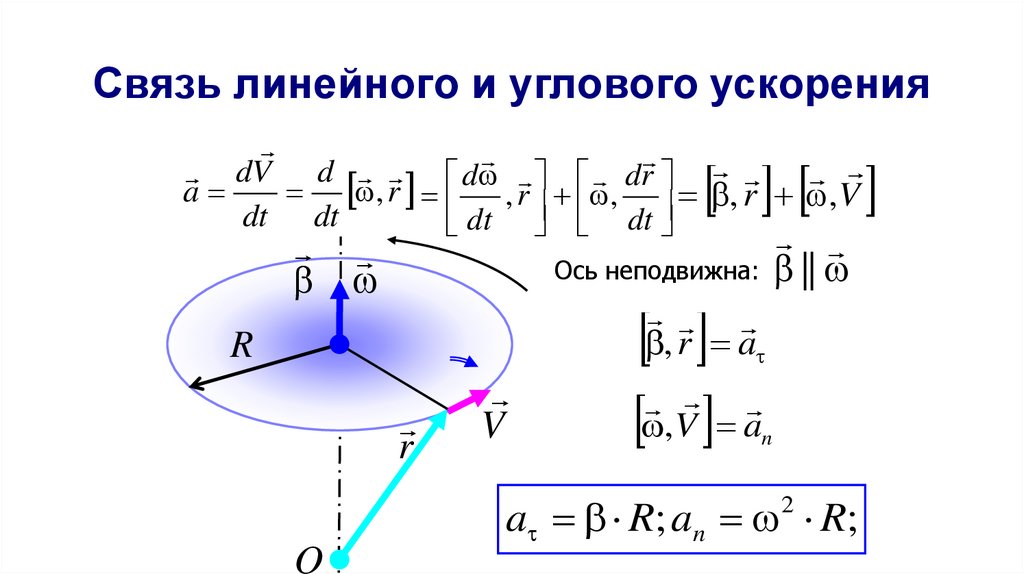
43. Связь линейного и углового ускорения

dV d d dr
a
, r
dt , r , dt , r , V
dt dt
Ось неподвижна: ||
R
r
O
V
, r a
,V an
a R; an 2 R;

44. Связь линейных и угловых величин при вращении вокруг неподвижной оси

Линейные величины
Путь
Вектор
скорости
Вектор
ускорения
S
Формула
связи
Угловые величины
S R
Угол
поворота
dr Вектор
V
V , r угловой
dt
скорости
Вектор
dV a R2
углового
a
a
R
n
dt
ускорения
d
dt
d
dt

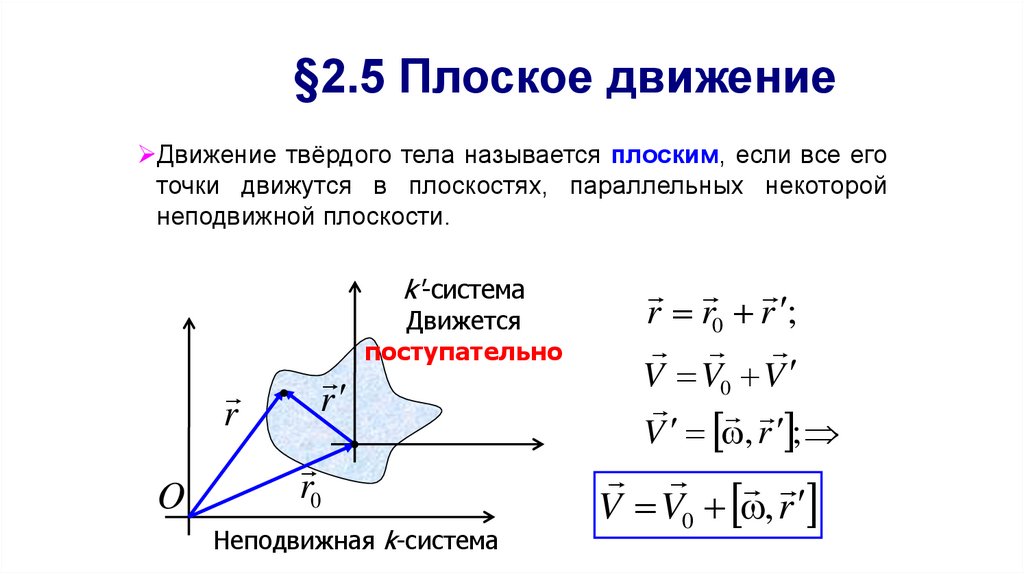
45. §2.5 Плоское движение

Движение твёрдого тела называется плоским, если все его
точки движутся в плоскостях, параллельных некоторой
неподвижной плоскости.
k'-система
r
O
r
Движется
поступательно
O
r0
Неподвижная k-система
r r0 r ;
V V0 V
V , r ;
V V0 , r

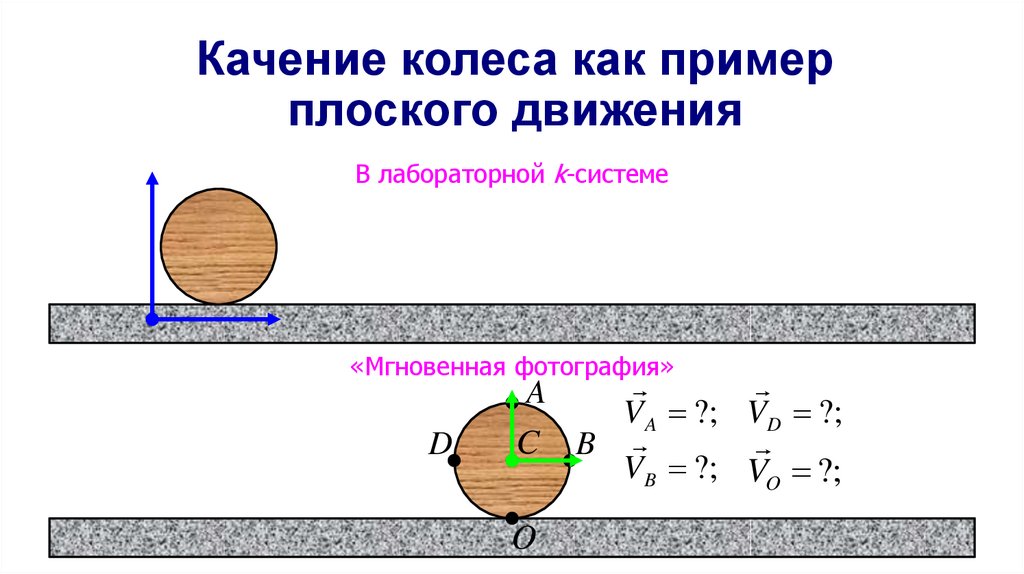
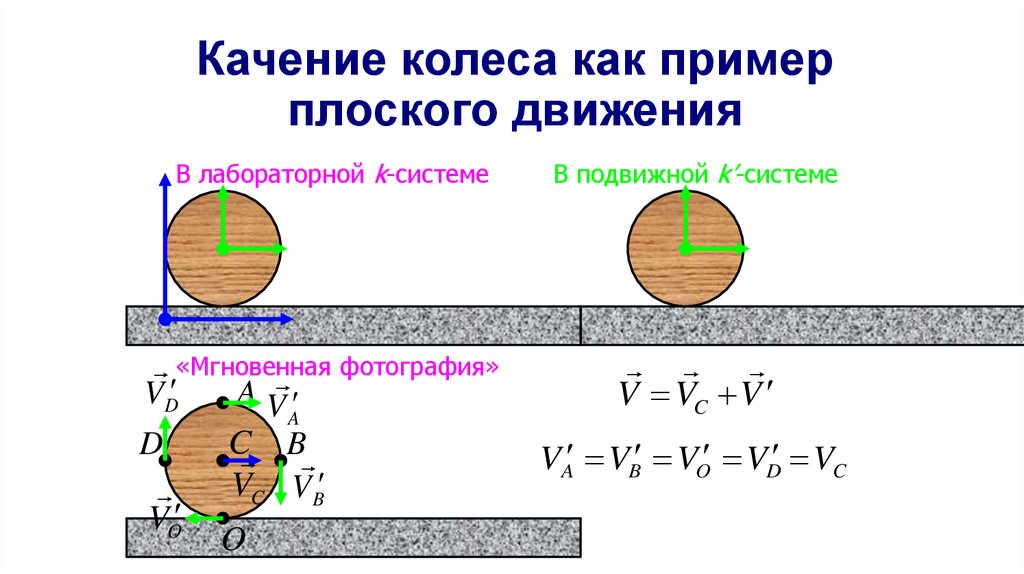
46. Качение колеса как пример плоского движения

В лабораторной k-системе
«Мгновенная фотография»
A
D
C
O
V A ?; VD ?;
B
VB ?; VO ?;

47. Качение колеса как пример плоского движения

В лабораторной k-системе
В подвижной k’-системе
«Мгновенная
фотография»
A V
VD
A
C B
D
VC VB
VO
O
V VC V
VA VB VO VD VC

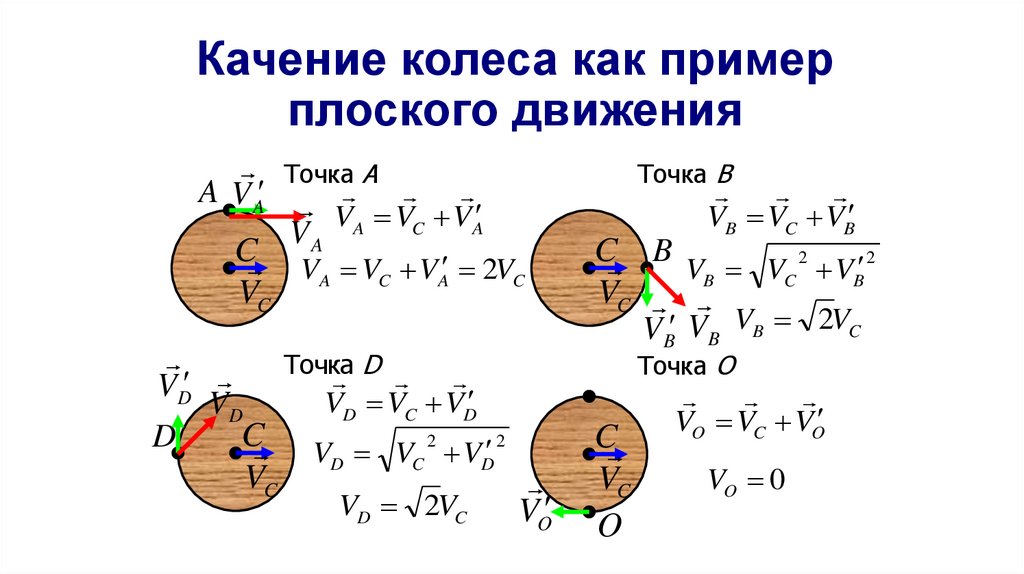
48. Качение колеса как пример плоского движения

Точка A
A V A
V A VA VC VA
C
VA VC VA 2VC
VC
Точка
D
VD
VD VC VD
VD
C V V 2 V 2
D
D
C
D
VC
VD 2VC
VO
Точка B
VB VC VB
C B
2
2
VB VC VB
VC
VB VB VB 2VC
Точка O
C
VC
O
VO VC VO
VO 0

49. Качение колеса как пример плоского движения

d
V VC V
dt
dVC
0; a a
dt
Ускорение точек направлено от обода к центру

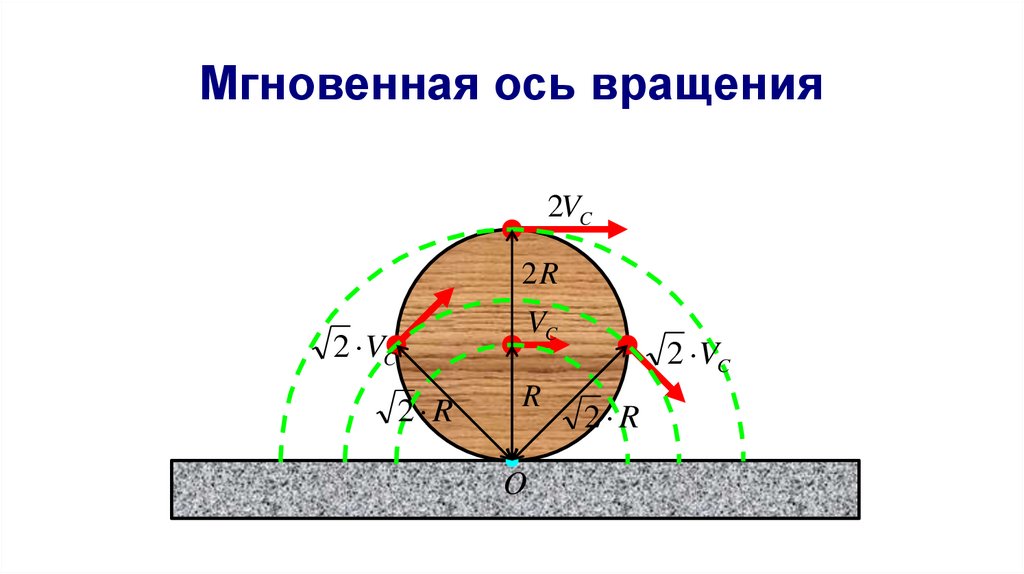
50. Мгновенная ось вращения

2VC
2R
VC
2 VC
2 R
R
O
2 VC
2 R

51. Свойства мгновенной оси вращения

Мгновенная ось вращения - прямая, проходящая
перпендикулярно плоскости движения через точку тела,
скорость которой в данный момент времени равна нулю.
Свойства
Движение твердого тела в данный момент времени
представляет собой чистое вращение вокруг этой оси
Положение мгновенной оси
временем
(и
относительно
лабораторной системы отсчета)
вращения
тела
и
меняется со
относительно
Мгновенная ось вращения может оказаться вне тела

52. §2.6 Число степеней свободы

Число степеней свободы – количество независимых
величин, необходимых для задания положения тела в
пространстве.
r x, y, z i=3
Вращение вокруг неподвижной оси
i=1
Плоское движение
r x, y , i=3
Вращение вокруг неподвижной точки , ,
i=3
Свободное движение
r x, y, z , , , i=6
Поступательное движение