Цель и задачи математики. Числа и вычисления. Тема 1.1

1.

«Математику уже затем учить
надо, что она ум в порядок
приводит»
Ломоносов Михаил Васильевич

2.

Тема 1.1
Цель и задачи математики
при освоении специальности
Базовые знания и умения по
математике в
профессиональной и в
повседневной деятельности

3.

Основная цель – научиться
учиться самостоятельно
1.
Развитие интеллектуальных способностей
2.
Подготовить себя к более лёгкому пониманию
и усвоению будущей профессии
3.
Развитие личностных качеств: честность,
ответственность, самостоятельность
4.
Научиться понимать то, что делаешь

4.

Базовые знания и умения по математике:
зачем нужны и где пригодятся разработчику ПО
1. Алгебра и логика:
Что это: Решение уравнений, логические операции, работа с булевой
алгеброй.
Зачем нужно: Для создания условий в коде, разработки алгоритмов и
структур данных.
Где пригодится: Написание кода, создание сложных логических
условий, отладка программ, разработка игр и приложений.
2. Дискретная математика:
Что это: Теория множеств, графов, комбинаторика.
Зачем нужно: Для работы с данными, структурирования информации,
построения графов и деревьев.
Где пригодится: Разработка баз данных, создание сложных алгоритмов,
работа с сетями и графами, разработка поисковых систем.

5.

Базовые знания и умения по математике:
зачем нужны и где пригодятся разработчику ПО
3. Линейная алгебра:
Что это: Работа с матрицами, векторами и линейными уравнениями.
Зачем нужно: Для обработки данных, графики, машинного обучения и
оптимизации.
Где пригодится: Разработка алгоритмов машинного обучения, 3Dграфики, компьютерного зрения.
4. Теория алгоритмов и вычислительная сложность:
Что это: Анализ и разработка алгоритмов, оценка их сложности.
Зачем нужно: Для создания эффективного и оптимизированного
программного кода.
Где пригодится: Оптимизация программ, разработка
высокопроизводительных систем, работа с большими данными.

6.

Базовые знания и умения по математике:
зачем нужны и где пригодятся разработчику ПО
5. Математический анализ:
Что это: Производные, интегралы, численные методы.
Зачем нужно: Для решения задач оптимизации, численного анализа,
работы с континуумом данных.
Где пригодится: Машинное обучение, анализ данных, обработка
сигналов.
6. Статистика и теория вероятностей:
Что это: Методы анализа данных, оценка вероятностей, распределение
данных.
Зачем нужно: Для работы с данными, прогнозирования, построения
моделей.
Где пригодится: Анализ больших данных, A/B тестирование,
предсказательная аналитика.

7.

Базовые знания и умения по математике:
зачем нужны и где пригодятся разработчику ПО
7. Числовые системы и теория чисел:
Что это: Двоичная, шестнадцатеричная системы, простые числа.
Зачем нужно: Для работы с низкоуровневым программированием,
криптографией.
Где пригодится: Разработка криптографических алгоритмов, систем
безопасности, работа с оборудованием.
Пример применения:
Создание эффективного алгоритма сортировки (алгебра и дискретная
математика) для оптимизации работы приложения.
В повседневной жизни это может быть планирование расходов на месяц
(арифметика).

8.

Базовые знания и умения по математике: зачем
нужны и где пригодятся графическому дизайнеру
1. Геометрия:
Что это: Формы, размеры и их взаимное расположение в
пространстве.
Зачем нужна: Для создания гармоничных и точных дизайнов, работы
с формами и пространством.
Где пригодится: В проектировании макетов, разработке логотипов,
создании пользовательских интерфейсов.
2. Теория цвета:
Что это: Взаимодействие цветов друг с другом, их влияние на
восприятие.
Зачем нужна: Для создания визуально привлекательных и
эффективных цветовых схем.
Где пригодится: В выборе палитр для веб-дизайна, иллюстраций,
печатных материалов.

9.

Базовые знания и умения по математике: зачем
нужны и где пригодятся графическому дизайнеру
3. Математика композиции:
Что это: Правила и принципы размещения элементов. Например,
золотое сечение, правило третей.
Зачем нужна: Для достижения баланса и эстетики в дизайне,
использования пропорций и симметрии.
Где пригодится: В создании макетов, постеров, интерфейсов, при
работе с типографикой.
4. Трансформации и анимации:
Что это: Способы изменения формы, размера или положения
объекта, а также создания движущихся изображений.
Зачем нужна: Для создания динамических и интерактивных элементов,
работы с движением и преобразованиями объектов.
Где пригодится: В разработке анимаций, веб-дизайне, создании
видеоэффектов.

10.

Базовые знания и умения по математике: зачем
нужны и где пригодятся графическому дизайнеру
5. Проектирование и планирование:
Что это: Организация и подготовка проекта - определение целей,
расчет времени и ресурсов.
Зачем нужна: Для эффективного использования пространства и
создания адаптивных дизайнов.
Где пригодится: В веб-дизайне, создании макетов для различных
устройств, в планировании проектов.
6. Статистика и анализ данных:
Что это: Сбор и интерпретация информации.
Зачем нужна: Для оценки эффективности дизайна, анализа
пользовательского опыта и принятия решений на основе данных.
Где пригодится: В A/B тестировании, анализе пользовательских
предпочтений, улучшении UX/UI.

11.

Базовые знания и умения по математике: зачем
нужны и где пригодятся графическому дизайнеру
Пример применения:
Создание веб-страницы с адаптивным дизайном (геометрия и
проектирование), использование цветовых моделей для
создания гармоничных палитр (теория цвета).
В повседневной жизни — использование пропорций для
планировки комнаты или составления меню на неделю.

12.

Базовые знания и умения по математике:
зачем нужны в повседневной жизни
Арифметика: Быстрое выполнение расчётов помогает в
управлении финансами, планировании покупок и
расчёте скидок.
Логическое мышление: Способствует принятию
обоснованных решений, решению проблем, расстановке
приоритетов, анализе сложных ситуаций.
Пропорции и масштабирование: Помогают в оценке и
планировании ресурсов, времени, пространственных
объектов.
Управление финансами: Знание базовой арифметики
необходимо для управления бюджетом, расчёта кредитов
и инвестиций.

13.

Тема 1.1
Действия над
положительными и
отрицательными числами,
модуль числа

14.

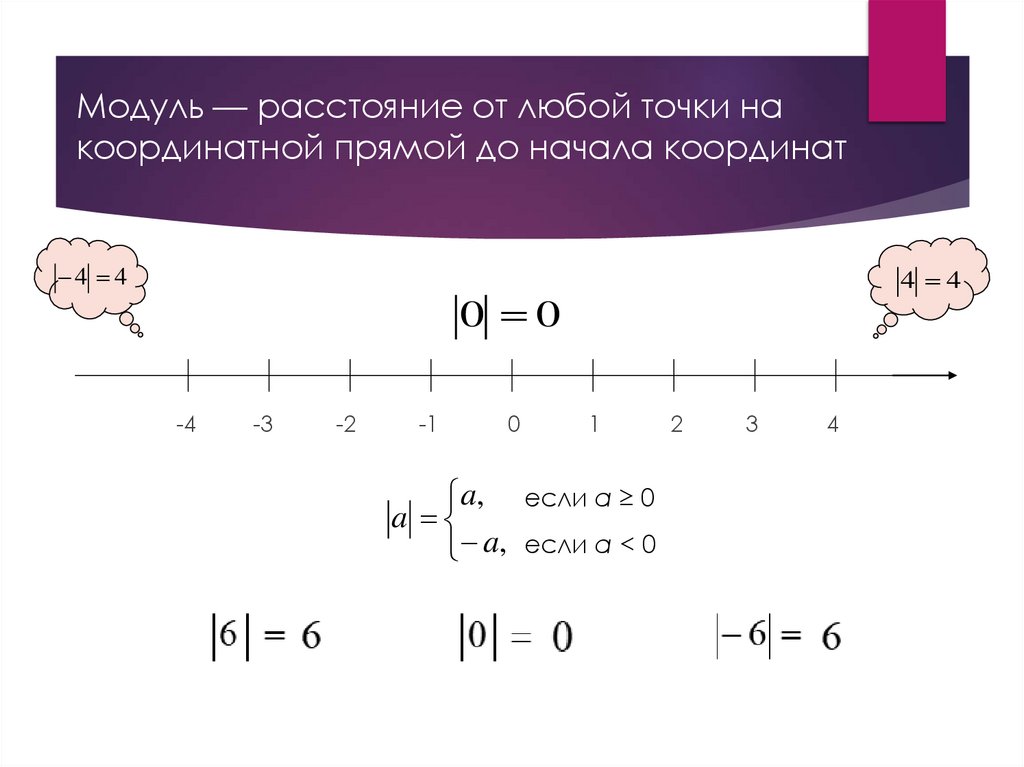
Модуль — расстояние от любой точки на
координатной прямой до начала координат
4 4
4 4
0 0
-4
-3
-2
-1
0
1
a, если а ≥ 0
a
a, если а < 0
2
3
4

15.

Чтобы сложить отрицательные числа
необходимо сложить их модули и перед
суммой поставить знак «–»
Чтобы сложить числа с разными знаками
необходимо из большего по модулю вычесть
меньшее и взять знак большего
( 12) ( 23) 35
16 42 58
( 12) 23 11
16 42 26

16.

При сложении противоположных чисел (и
слагаемых) всегда получается 0
( 2,5) 2,5 0
а–а=0
1
1
( 1 ) 1 0
4
4
4xy – 4xy = 0

17.

Раскрытие скобок
Если перед скобками стоит знак «+», то просто
опускаем скобки:
+ (- а + в – с) = - а + в – с
Если перед скобками стоит знак «-», то меняем
знак каждого слагаемого на противоположный:
- (- 5а + 4в – 7с) = + 5а - 4в + 7с

18.

В результате умножения (деления) двух чисел
с одинаковыми знаками получается
положительное число
В результате умножения (деления) двух чисел
с разными знаками получается
отрицательное число
2 3 6
( 2) ( 3) 6
6:2 3
( 6) : ( 2) 3
2 ( 3) 6
( 6) : 2 3
( 2) 3 6
6 : ( 2) 3

19.

Проверь себя
Ответы: а) 80;
б) -3;
1
в) 4 ;
3
г) -0,5.

20.

Тема 1.1
Действия с
обыкновенными и
десятичными дробями

21.

Для того, чтобы сложить две дроби, нужно
сначала привести их к общему
знаменателю, а затем выполнить сложение:
Заметим, что целая часть складывается и
вычитается отдельно.

22.

Для того, чтобы из одной дроби вычесть
другую, нужно сначала привести их к общему
знаменателю, а затем выполнить вычитание:

23.

Для того, чтобы перемножить две дроби,
нужно перемножить соответственно их
числители и знаменатели :
Заметим, что для умножения и деления
необходимо перевести в неправильные дроби.

24.

Для того, чтобы одну дробь разделить на
другую, нужно делимое умножить на дробь,
обратную делителю (вторая дробь переворачивается):

25.

Перевод дробей
Для перевода из
обыкновенной дроби в
десятичную делим
числитель на знаменатель:
Для перевода из десятичной
дроби в обыкновенную
записываем как слышим
(какой разряд – такой и знаменатель):

26.

Таблица удобных знаменателей
1
0,5
2
1
0,25
4
1
0,2
5
1
0,125
8
1
0,1
10
1
0,0625
16
1
0,05
20
1
0,04
25
1
0,03125
32
1
0,025
40
1
0,02
50
1
0,0125
80
1
0,01
100

27.

При сложении и вычитании десятичных дробей
записываем числа в столбик запятая под
запятой и производим вычисления.
При умножении десятичных дробей:
1)
умножить дроби, не обращая внимания на запятые;
2)
посчитать общее количество цифр после запятой в обеих
дробях и столько цифр справа в полученном числе
отделить запятой.

28.

При делении десятичных дробей:
1)
перенести запятую в делителе до образования
натурального числа;
2)
Выполнить деление.

29.

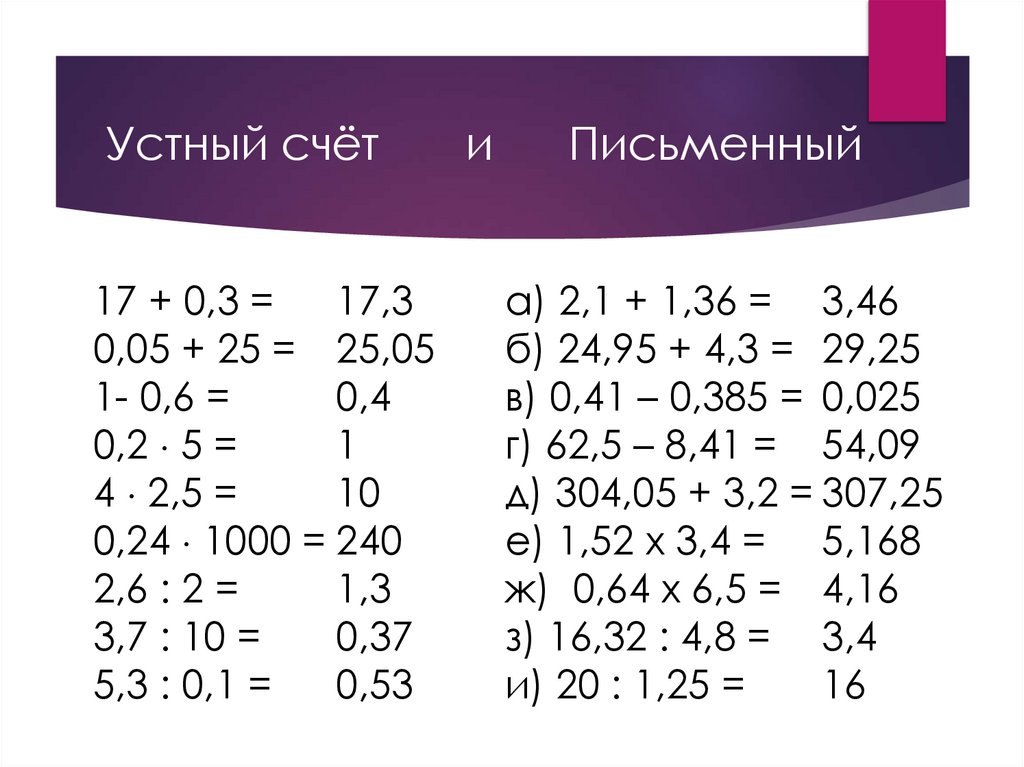
Устный счёт
17 + 0,3 =
17,3
0,05 + 25 = 25,05
1- 0,6 =
0,4
0,2 5 =
1
4 2,5 =
10
0,24 1000 = 240
2,6 : 2 =
1,3
3,7 : 10 =
0,37
5,3 : 0,1 =
0,53
и
Письменный
а) 2,1 + 1,36 = 3,46
б) 24,95 + 4,3 = 29,25
в) 0,41 – 0,385 = 0,025
г) 62,5 – 8,41 = 54,09
д) 304,05 + 3,2 = 307,25
е) 1,52 х 3,4 = 5,168
ж) 0,64 х 6,5 = 4,16
з) 16,32 : 4,8 = 3,4
и) 20 : 1,25 =
16

30.

Тема 1.1
Действия со степенями.
Стандартный вид числа.

31.

Стандартный вид числа представляет собой
число от 1 до 9 (в целой части) умноженное
на 10 в степени n

32.

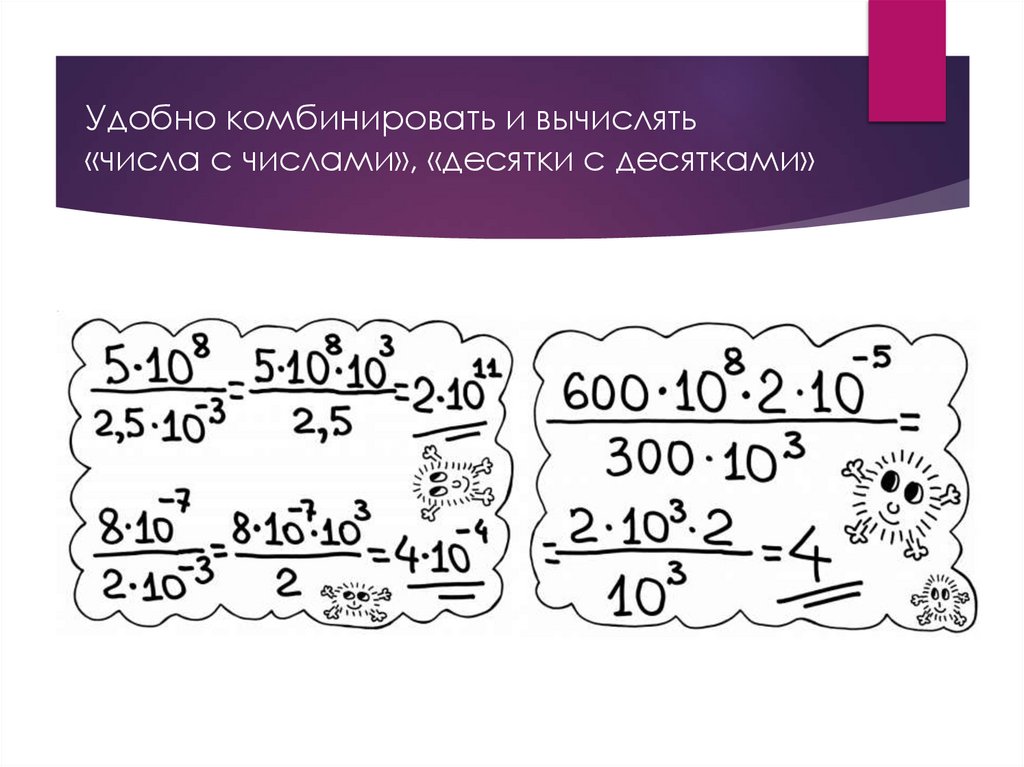
Удобно комбинировать и вычислять
«числа с числами», «десятки с десятками»

33.

Работа у доски:
Ответы: 1) 190; 2) 135; 3) 256; 4) 144;
5) 7/40=0,175; 6) 8,1; 7) 143/500=0,286;
8) 0,504; 9) 35807; 10) 0,0408.

34.

Задание по вариантам (кто быстрее)
x19
x 20
y11
y18
a 6n
7
9
81
a8n
17
25
16
7
1
12
13
2
36

35.

Тема 1.1
Формулы сокращённого
умножения
Преобразования
выражений

36.

Использование формул в
прямом направлении

37.

Использование формул в
обратном направлении

38.

Квадрат суммы трёх
слагаемых

39.

Треугльник Паскаля
Для возведения двучлена в степень выше третьей
быстрее всего будет воспользоваться треугольником
Паскаля или арифметическим треугольником.

40.

Преобразования выражений
2
5 2 n 1 n 3 n 1 2
x y x y
5
6
x y 2 x y 2
1сп : x y x y x y x y 2 x 2 y 4 xy
25 4 n 2 2 n
9 2n 2 4
x
y x 3n y n 2
x
y
36
25
2сп : x 2 2 xy y 2 x 2 2 xy y 2 4 xy
a 1 2 4 a 1 2 6 a 1 a 1
9a 2 10a 3
3x y x 3 y 2 xy
16 x 3 y 16 xy 3
x 2 x 2 2 x 4 x x 3 x 3
9x 8
5 x x 3 5 x 1 15 x 2 x 2
60 x 55
2
2
2
3

41.

Проверь себя

42.

Благодарю всех за работу!
Желаю всем счастья и
успехов в освоении
профессии!