Универсальная функция

1. Универсальная функция

2. Грамматика функций и данных в БНФ (форма Бэкуса-Наура)

атом ::= БУКВА конец_атома
конец_атома ::= пусто | БУКВА конец_атома |
ЦИФРА конец_атома
S-выражение ::= атом |
(S-выражение . S-выражение) |
(S-выражение )

3. Грамматика функций и данных в БНФ (форма Бэкуса-Наура)

идентификатор ::= атом
Идентификатор — это подкласс атомов,
применяемый при именовании неоднократно
используемых объектов программы — функций
и переменных.

4. Грамматика функций и данных в БНФ (форма Бэкуса-Наура)

форма ::= константа | переменная |
(функция аргумент ... ) |
(COND (форма форма)
(форма форма) ... )
константа ::= (QUOTE S-выражение) |
'S-выражение
переменная ::= идентификатор
аргумент::=переменная | константа | форма

5. Грамматика функций и данных в БНФ (форма Бэкуса-Наура)

вычислимое выражение (форма) -
данные, имеющие смысл как
выражения языка и приспособленные к
вычислению.

6. Грамматика функций и данных в БНФ (форма Бэкуса-Наура)

функция ::= название |
(LAMBDA список_переменных форма)|
(LABEL название функция)
список_переменных ::= (переменная ... )
название ::= идентификатор

7. Грамматика функций и данных в БНФ (форма Бэкуса-Наура)

Функция может быть введена с помощью лямбдавыражения, устанавливающего соответствие между
аргументами функции и связанными переменными,
упоминаемыми в теле ее определения (в
определяющей ее форме).
(LAMBDA (x)
(COND ((ATOM x) x) (T (CAR x) ) )
‘( (a k l j) (s j l j)))

8. Грамматика функций и данных в БНФ (форма Бэкуса-Наура)

Если функция рекурсивна, то следует объявить ее
имя с помощью специальной функции LABEL.
(LABEL first (LAMBDA (x)
(COND ((ATOM x) x)
(T (first (CAR x)) ) ) ) )
Используемая в дальнейшем DEFUN совмещает
эффекты LABEL и LAMBDA)

9. Универсальная функция

Универсальная функция —
это функция, которая может
вычислять значение любой
формы.

10. Основы рекурсии

Функция является рекурсивной,
если
в
ее
определении
содержится вызов самой этой
функции.

11. Списки строятся рекурсивно

Рекурсия в Лиспе основана на
математической теории рекурсивных
функций. Рекурсия хорошо подходит для
работы со списками, так как сами списки
могут состоять из подсписков, т.е. иметь
рекурсивное строение. Для обработки
рекурсивных структур совершенно
естественно использование рекурсивных
процедур.

12.

Списки можно определить с помощью
следующих правил Бэкуса-Наура:
список ::= NIL| (голова . хвост)
голова ::= атом | список
хвост ::= список

13.

Списки можно определить и в следующей
форме, которая подчеркивает
логическую рекурсивность
построения списков из атомов и
подсписков:
список -> NIL
список ->(элемент элемент ...)
элемент -> атом
элемент -> список
; рекурсия

14. Простая рекурсия

Мы будем говорить, что рекурсия простая,
если вызов функции встречается в
некоторой ветви лишь один раз.
Простой рекурсии в процедурном
программировании соответствует
обыкновенный цикл.

15.

Определим функцию КОПИЯ, которая
строит копию списка.
Копия списка логически идентична
первоначальному списку
(defun КОПИЯ (I)
( cond ( (null I) nil)
(t (cons (car l) (КОПИЯ (cdr (I))))))
Вызов: (копия'(a b с))
Результат: (А В С) ; логическая копия
(eq '(a b с) (копия '(a b с)))
NIL
; физически различные списки

16. Порядок следования ветвей в условном предложении для организации рекурсии существеннен

При определении порядка следования условий
основным моментом является то, что сначала
проверяются всевозможные условия
окончания, а затем ситуации, требующие
продолжения вычислений. При помощи
условий окончания последовательно
проверяются все особые случаи и
программируются соответствующие
результирующие выражения. На исключенные
таким образом случаи можно в последующем
не обращать внимания.

17. Правила записи рекурсивной функции

1. Терминальная ветвь необходима для окончания
рекурсивного вызова. Без терминальной ветви
рекурсивный вызов был бы бесконечным.
Терминальные ветви в теле функции пишутся в
начале.
2. После каждого вызова функцией самой себя,
рекурсия должна приближаться к терминальной
ветви. Всегда должна быть уверенность, что
рекурсивные вызовы ведут к терминальной ветви.

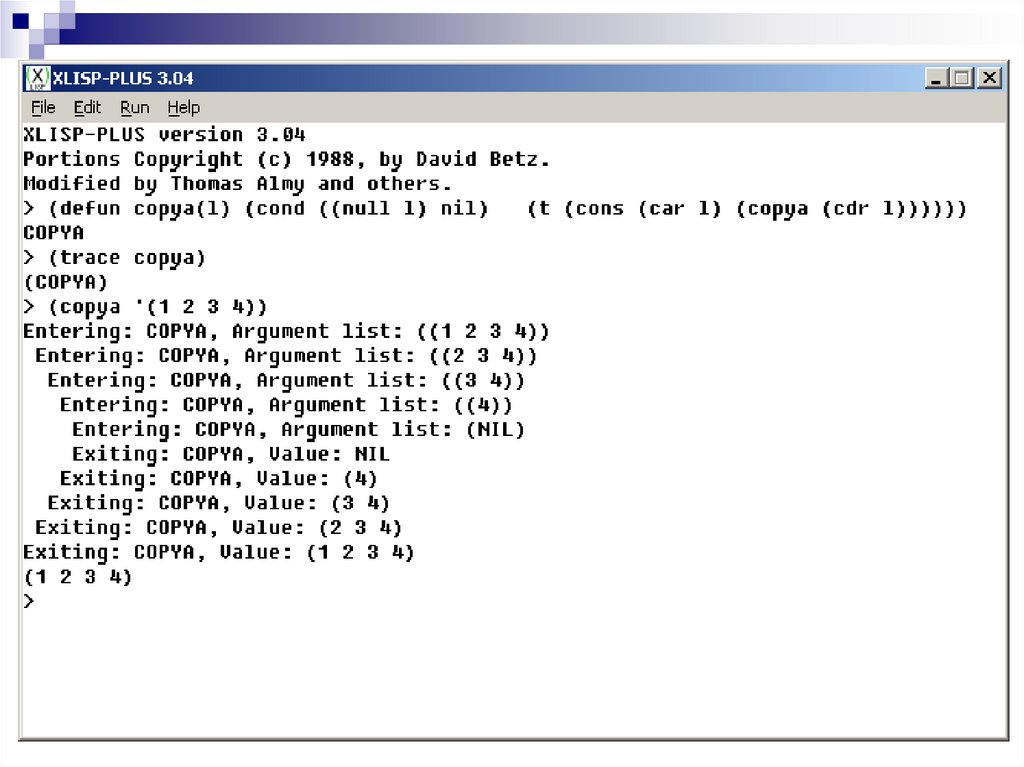
18.

Трассировка функции включается при
помощи директивы, которая в отличие от
обычных функций не вычисляет свой
аргумент.
(TRACE функция)
(trace копия)
Трассировку можно отменить аналогичной
по форме директивой UNTRACE.

19.

20. MEMBER проверяет, принадлежит ли элемент списку

Тело функции состоит из условного
предложения, содержащего три ветви.
Они участвуют в процессе вычислений в
зависимости от возникающей ситуации:
(DEFUN MEMBER1 (a S)
(cond ( (null S)
nil)
( (eql (car S) a) S)
(t (MEMBER1 a (cdr S)))
))

21. MEMBER проверяет, принадлежит ли элемент списку

Вызов:
(MEMBER1 'A '( S A F G J))
Результат: (A F G J)

22.

((null I) nil)
Аргумент - пустой список либо с самого начала,
либо потому, что просмотр списка окончен.
2.
((eql (car I) a) I)
Первым элементом является искомый элемент. В
качестве результата возвращается список, в
котором А - первый элемент.
3.
(t (MEMBER1 a (cdr l)))
Ни одно из предыдущих утверждений не верно: в
таком случае либо элемент содержится в хвосте
списка, либо вовсе не входит в список.
Эта задача аналогична первоначальной, только она
меньше по объему. Поэтому мы можем для ее
решения применить сам предикат к хвосту
списка.
1.

23. APPEND объединяет два списка

>(defun APPEND1 (x y)
(cond ((null x) y)
(t (cons (car x)
(APPEND1 (cdr x) y)))))
APPEND1

24.

Вызов: (append1 '(с л и) '(я н и е))
Результат (с л и я н и е)
Вызов (append1 '(а b) nil)
Результат (А В)
Вызов (APPEND1 '(1 2) 3)
Результат (1 2 . 3)

25. REMOVE удаляет элемент из списка

Все предыдущие определения функций
содержали лишь один рекурсивный
вызов.
Рассмотрим в качестве следующего
примера содержащую две рекурсивные
ветви встроенную функцию REMOVE

26.

(defun REMOVE1(а l)
(cond ((null l) nil)
((eql a (car l)) (REMOVE1 a (cdr l)))
(t (cons (car l)
(REMOVE1 a (cdr l))))))
(remove1 ’л '(с л о н))
(C О H)
(remove1 ‘b '(a ( s d (b c)) (b c))))
(A (В C))
(remove1 ‘(а b) '((а b) (с d)))
((А В) (СD))

27.

Список L сокращается путем удаления
всех идентичных А в смысле EQL
элементов (вторая ветвь) и копирования
в результирующий список (CONS)
остальных элементов (третья ветвь) до
тех пор, пока условие окончания (NULL)
не станет истинным. Результат
формируется в процессе возврата
аналогично функции APPEND1.

28. SUBSTITUTE заменяет все вхождения элемента

Функция SUBSTITUTE, заменяющая все
вхождения данного элемента СТАРЫЙ в
списке L на элемент НОВЫЙ, работает
подобно функции REMOVE. Замена
производится лишь на самом верхнем
уровне списка L, т.е. рекурсия
осуществляется только по хвостовой
части списка (в направлении CDR).

29.

>(defun SUBSTITUTE1 (новый старый l)
(cond ((null l) nil)
((eql старый (car l))
(cons новый
(SUBSTITUTE1 новый старый
(cdr l))))
(t (cons (car l)
(SUBSTITUTE1 новый старый
(cdr l))))))
(substitute1 'b 'x '(а х х а))
(А В В A)

30. REVERSE обращает список

В приведенных примерах мы
просматривали список в соответствии с
направлением указателей в списочных
ячейках слева направо. Но что делать,
если нужно обрабатывать список справа
налево, т.е. от конца к началу?

31.

Рассмотрим для примера функцию
REVERSE, которая также является
встроенной функцией Лиспа. REVERSE
изменяет порядок элементов в списке (на
верхнем уровне) на обратный.
Для обращения списка мы должны
добраться до его последнего элемента и
поставить его первым элементом
обращенного списка. Хотя нам
непосредственно конец списка не
доступен, можно, используя APPEND,
описать необходимые действия.

32.

>(defun REVERSE1 (l)
(cond ((null l) nil)
(t (append1 (REVERSE1 (cdr l)
(cons (car l) nil)))))
REVERSE1
>(reverse1 ‘(a b c))
(С В А)
>(reverse1 '((A B) (CD)))
((CD) (А В))

33.

Идея определения состоит в следующем:
берем первый элемент списка (CAR L),
делаем из него с помощью вызова (CONS
(CAR L) NIL) одноэлементный список и
объединяем его функцией APPEND с
перевернутым хвостом. Хвост списка
сначала обращается рекурсивным
вызовом (REVERSE1 (CDR L)).
Попробуем проследить, как происходит
такое обращение:
_(trace reverse1)

34. Использование вспомогательных параметров

Список является несимметричной
структурой данных, которая просто
проходится слева направо. Во многих
случаях для решения задачи более
естественны вычисления, производимые
справа налево.

35.

Например, то же переворачивание списка
было бы гораздо проще осуществить,
если бы был возможен
непосредственный доступ к последнему
элементу списка. Такое противоречие
между структурой данных и процессом
решения задачи приводит к трудностям
программирования и может служить
причиной неэффективности.

36.

Cоответствующий механизм можно легко
осуществить, используя вспомогательную
функцию, у которой нужные
вспомогательные переменные являются
параметрами. Тогда для функции
REVERSE мы получим такое
определение:

37.

>(defun reverse2 (l) (ПЕРЕНОС l nil))
REVERSE2
>(defun ПЕРЕНОС (l результат)
(cond ((null l) результат)
(t (ПЕРЕНОС (cdr l)
(cons (car l) результат)))))
ПЕРЕНОС

38.

Вспомогательная функция ПЕРЕНОС
рекурсивна по значению, так как
результирующим выражением ее тела
является либо непосредственно
рекурсивный вызов, либо готовое
значение. С помощью этой функции
элементы переносятся таким образом,
что на каждом шаге рекурсии очередной
элемент переходит из аргумента L в
аргумент РЕЗУЛЬТАТ.

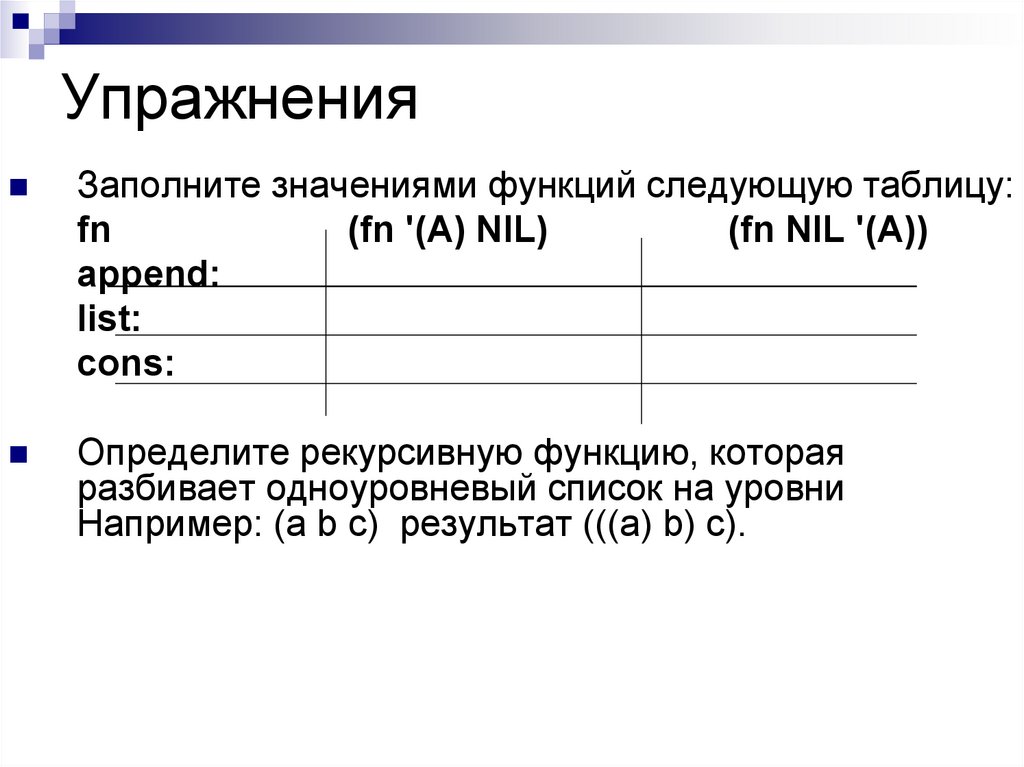
39. Упражнения

Заполните значениями функций следующую таблицу:
fn
(fn '(A) NIL)
(fn NIL '(A))
append:
list:
cons:
Определите рекурсивную функцию, которая
разбивает одноуровневый список на уровни
Например: (a b c) результат (((а) b) с).