Похожие презентации:
Таңдама тәсіл және оның нәтижелерін талдау
1.
Биостатистика және ғылыми зерттеу негіздері кафедрасыАға оқытушы Раманқұлова Алима Абдрамбекқызы
2.
1. Бас жиынтық (популяция) жәнетаңдама
2. Таңдама таралудың сандық
сипаттамалары
3. Бас жиынтықтың параметрлерінің
нүктелік және аралық бағалары
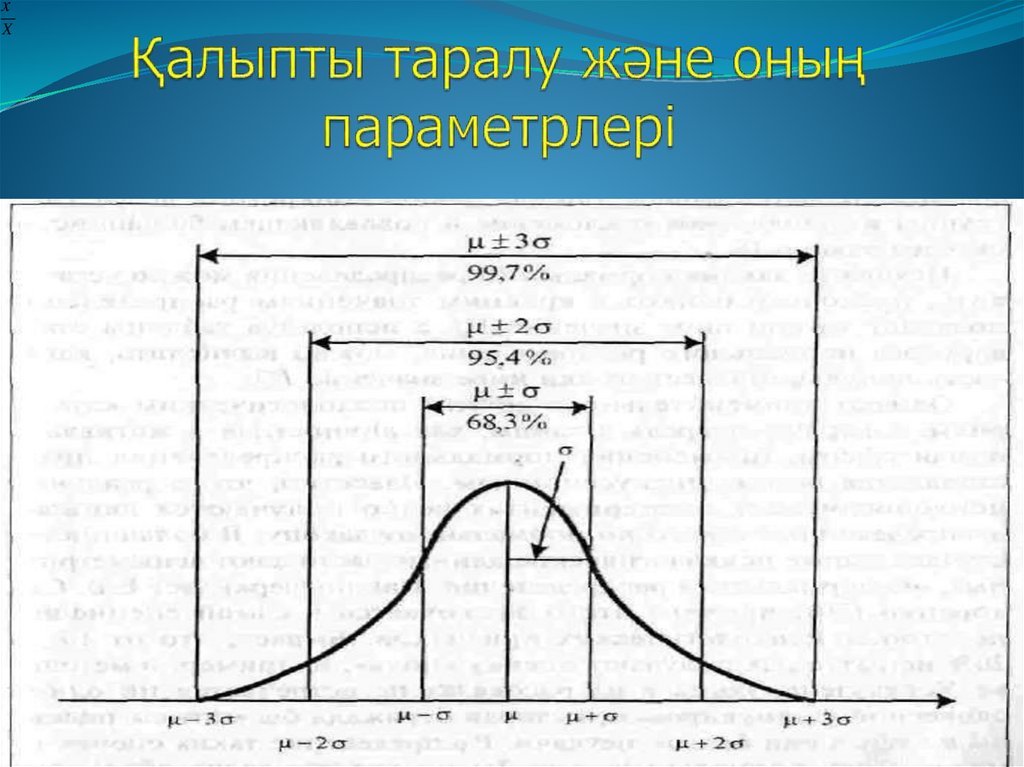
4. Қалыпты таралу және оның
параметрлері
3.
Қандай да бір сапалық немесе сандықбелгілермен сипатталатын нысандар жиыны
статистикалық жиынтық деп аталады.
Тексерілуге жататын (ең болмағанда, теория
жүзінде) барлық нысандардан тұратын
статистикалық жиынтық бас жиынтық (популяция)
деп аталады.
Бас жиынтықтан кездейсоқ түрде таңдалынып
алынған қандай да бір нысандар санынан тұратын
статистикалық жиынтық таңдама жиынтық
немесе жәй таңдама деп аталады.
4.
Таңдама жиынтықты зерттеу арқылыбарлық бас жиынтық жөнінде қорытынды
жасалынатын статистикалық зерттеу әдісі
таңдама әдіс деп аталады.
Таңдамаға қойылатын негізгі талап – бас
жиынтықтың қасиеттерін дұрыс бағалау,
яғни репрезентативті болу.
5.
бас жиынтықтан нысандарды таңдаукездейсоқ жүргізіледі,яғни нысандардың
әрқайсысының таңдалу мүмкіндігі бірдей;
таңдамадағы бақылаулар нәтижелері бір
бірінен тәуелсіз;
барлық нақты шарттарды есепке ала
отырып таңдама көлемін дұрыс анықтау.
6.
жиынтықтағы белгінің өлшенген мәніварианта, ал өсу ретімен орналастырылған
варианталар тізбегі варияциялық қатар деп
аталады.
Варианталар мен олардың кездесу
жиіліктері арасындағы сәйкестік таңдаманың
статистикалық таралуы деп аталады.
7.
таңдаманың есептеуді қажет етпейтінсандық сипаттамалары мода және медиана
болып табылады.
Мода – таңдамада ең үлкен жиілікке
сәйкес келетін варианта.
Медиана – вариациалық қатарды тең екіге
бөлетін варианта.
8.
таңдама орта:k
x
n x
i
i 1
i
n
таңдама стандарттық ауытқу:
k
s
n ( x x)
i 1
i
i
n 1
2
9.
Еркіндік дәрежесінің саны – бұл таңдамақұрамындағы еркін өзгеріп отыратын
бірліктер саны.
df = n-1, мұндағы n – таңдама көлемі.
10.
Сенім аралығы – бұл ішінде популяцияның ақиқатпараметрі жататын, әдетте біз 95% сенімді болатын
мәндер ауқымы. Параметрдің нақты мәнінің осы
ауқымның шекараларынан шығып кету ықтималдығы
1–0,95=0,05 (5%)-дан аспайды. Сенім ықтималдығын
толықтыратын шаманы әдетте α деп белгілейді және
оны мәнділік деңгейі деп атайды.
Белгілі
таңдама
көрсеткіштері
негізінде
бас
жиынтықтың параметрлері жөнінде сенімді пікір айту
үшін жеткілікті деп саналатын ықтималдықтар сенім
ықтималдықтары деп аталады.
11.
Медицинада қабылданған сенімықтималдықтары:
Р=0,95 (95%)
Р=0,99 (99%)
Сәйкес мәнділік деңгейлері:
α =1-0,95=0,05 (5%)
α =1-0,99=0,01 (1%)
12.
( х t SE; х t SE)мұндағы
tα- Стьюдент
коэффициенті.
орта мәннің стандарттық қатесі:
SE
s
n
13.
Үлкен стандарттық қате бағаның дәлеместігін көрсетеді, ал кіші стандарттық қате
бағаның дәлдігін көрсетеді.
Егер таңдама көлемі ұлғайса және
деректердің шашылуы аз болса, онда
стандарттық қате азаяды, яғни біз дәлірек
баға аламыз.
14.
Стандарттық ауытқу деректердің мәндеріндегіқұбылмалылықты бейнелейді және ол деректер
жиынындағы өзгергіштікті анықтау қажет болғанда
көрсетілуі тиіс.
Стандарттық қате таңдама ортаның дәлдігін
бейнелейді және ол деректер жиынындағы орта
мәнді анықтау қажет болғанда көрсетілуі тиіс.
15.
ҚазҰМУ студенттерінің артериялық қысымыАйталық, біз университеттің 100 студенттерінің
арасында систолалық артериялық қысымдарын 2016ж.
қаңтар айында өлшедік делік.
Осы зерттеудің деректері негізінде біз
университеттің барлық студенттерінің систолалық
артериялық қысымдарының орта мәні үшін 95% сенім
аралығын бағалағымыз келеді.
Нәтижелері:
x̄=121 .3; s= 12 .9
16.
SE ( x )12,9
12,9
1,29
10
100
121,3 2 1,3
(118,7; 123,9)
17.
18.
19.
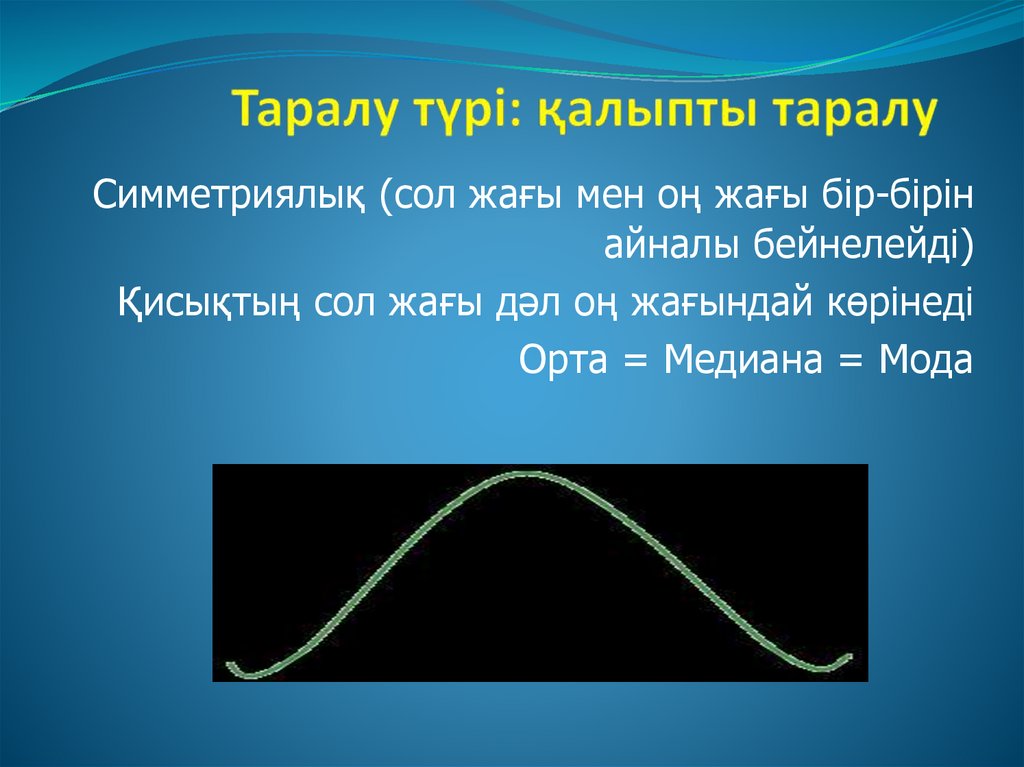
Симметриялық (сол жағы мен оң жағы бір-бірінайналы бейнелейді)
Қисықтың сол жағы дәл оң жағындай көрінеді
Орта = Медиана = Мода
20.
Johann CarlFriedrich Gauß
1777 - 1855
20
21.
Қалыпты таралуx
22.
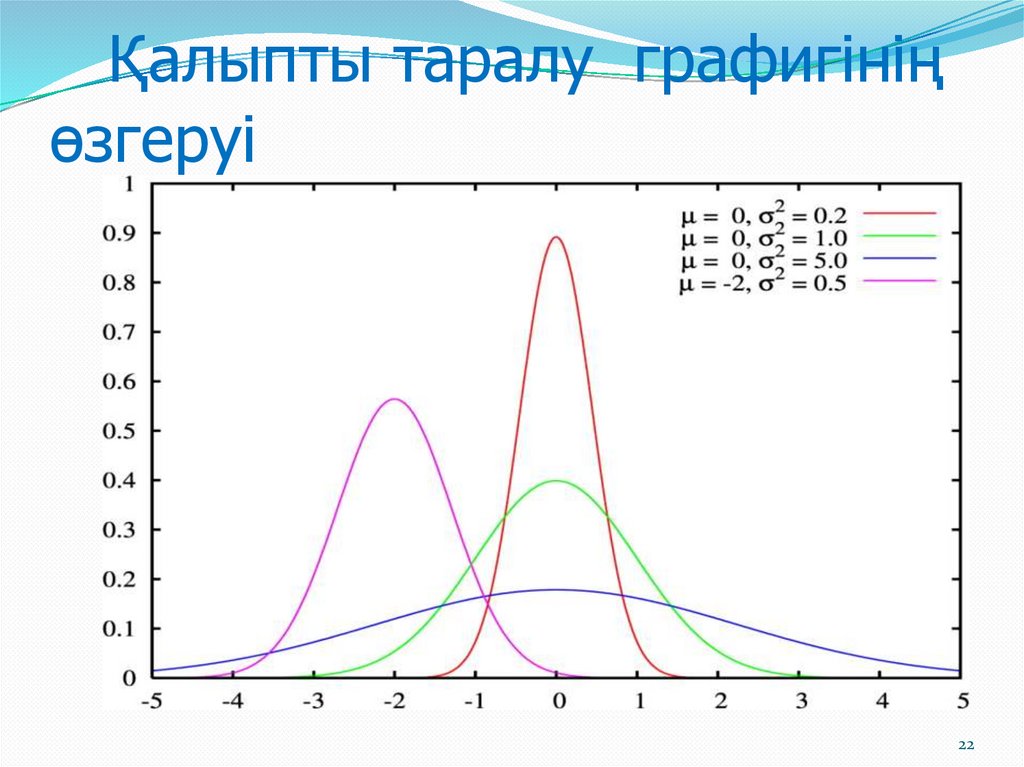
Қалыпты таралу графигініңөзгеруі
22
23.
- барлық мәндердің 68,26%, ±s аралығындажатады
(орта мәннен ±1
ортаквадраттық ауытқу);
-барлық мәндердің 95,44%, ±2s аралығында
жатады
( орта мәннен ±2 орта квадраттық ауытқулар);
-барлық мәндердің 99,73%, ±3s аралығында
жатады
(орта мәннен ±3 орта
квадраттық ауытқулар).
24.
xX
25.
Сандық сипаттамалардың теңдігі (орта мән, мода жәнемедиана өз ара тең) ;
- орта мәннен ауытқудың симметриялылығы;
- қисық астындағы жалпы аудан 1 ге тең;
- қисықтың ұштары екі бағытта да абцисса осіне
үздіксіз жақындай отырып, алайда ешқашан онымен
жанаспай шексіздікке ұмтылады.
- қисықтың түрі бас жиынтықтың орта квадраттық
ауытқуымен анықталады;
- орта квадраттық ауытқуы аз таралуға жіңішке,
жоғары созылған қисықтар, ал орта квадраттық
ауытқуы үлкен таралуға жазыңқы қисықтар сәйкес
келеді.
26.
Әдебиет:1. Раманқұлова А.А. Биологиялық статистика. Оқу
құралы.-Алматы. 2015
2. Лукьянова Е.А. Медицинская статистика. – М:
Изд. РУДН, 2002.
3. Медик В.А., Токмачев М.С., Фишман Б.Б.
Теоретическая статистика//Статистика в
медицине и биологии. В 2-х томах / Под. ред.
проф. Ю.М Комарова. Т.1. – М.: Медицина,
2000.
4. Гланц С. Медико-биологическая статистика. –
М.: Практика, 1999.
5. Рокицкий П.Ф. Биологическая статистика. –
Высшая школа, 1973.















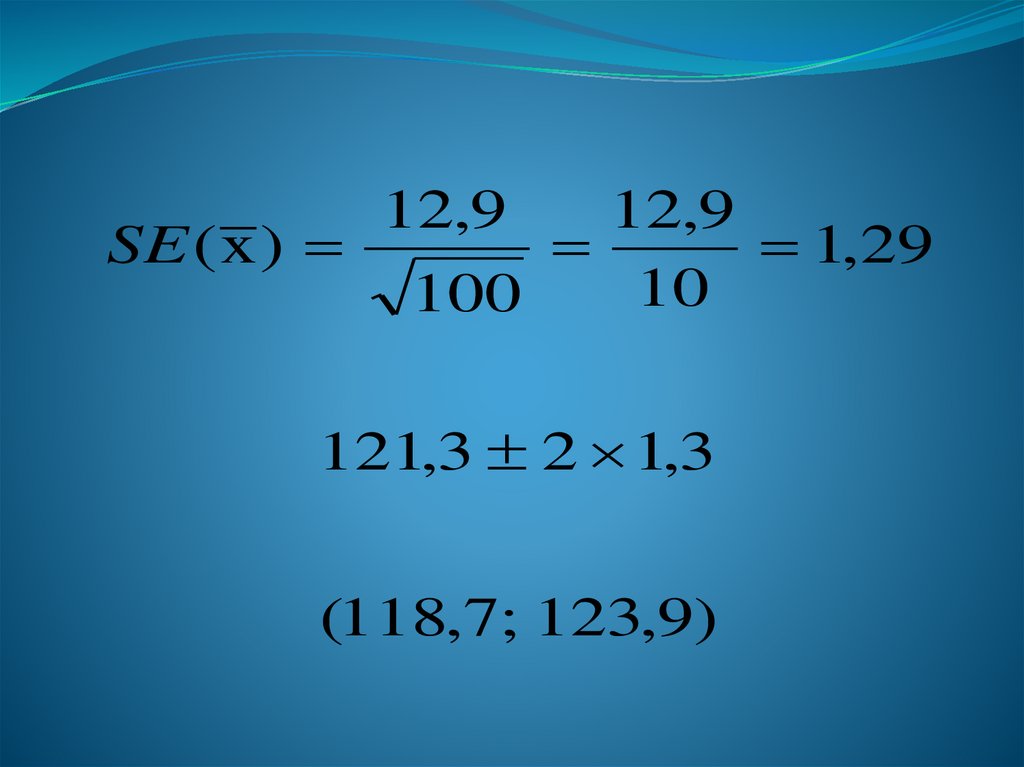







 Математика
Математика








