Многозначные логики

1.

Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«Ижевский государственный технический университет
имени М. Т. Калашникова»
Кафедра «АСОИУ»
Курс «Неклассические логики»
Тема «Многозначные логики»
Автор Исенбаева Е.Н., старший преподаватель
Ижевск
2014

2. МНОГОЗНАЧНЫЕ ЛОГИКИ

Многозначная логика — тип формальной
логики, в которой допускается более двух
истинностных значений для высказываний.
Первые многозначные логики построили
независимо друг от друга польский логик
Я. Лукасевич в 1920 г. и американский логик
Э. Пост в 1921 г.
Курс «Неклассические логики»
Тема «Многозначные логики»
2

3. Ян Лукасевич

Ян Лукасевич (1878 — 1956)
польский логик. Лукасевичу
принадлежат основополагающие
работы в области многозначной
логики, а также ряд исследований
по построению и аксиоматизации
систем пропозициональной
логики, модальной логики,
разработке оригинальной
логической (бесскобочной)
символики.
Курс «Неклассические логики»
Тема «Многозначные логики»
3

4. Трёхзначная логика Лукасевича

Я. Лукасевичем предложил трехзначную
логику, основанную на предположении, что
высказывания бывают истинными, ложными
и возможными, или неопределенными.
Все законы трехзначной логики Лукасевича
оказались также законами и классической
логики; обратное, однако, не имело места.
Курс «Неклассические логики»
Тема «Многозначные логики»
4

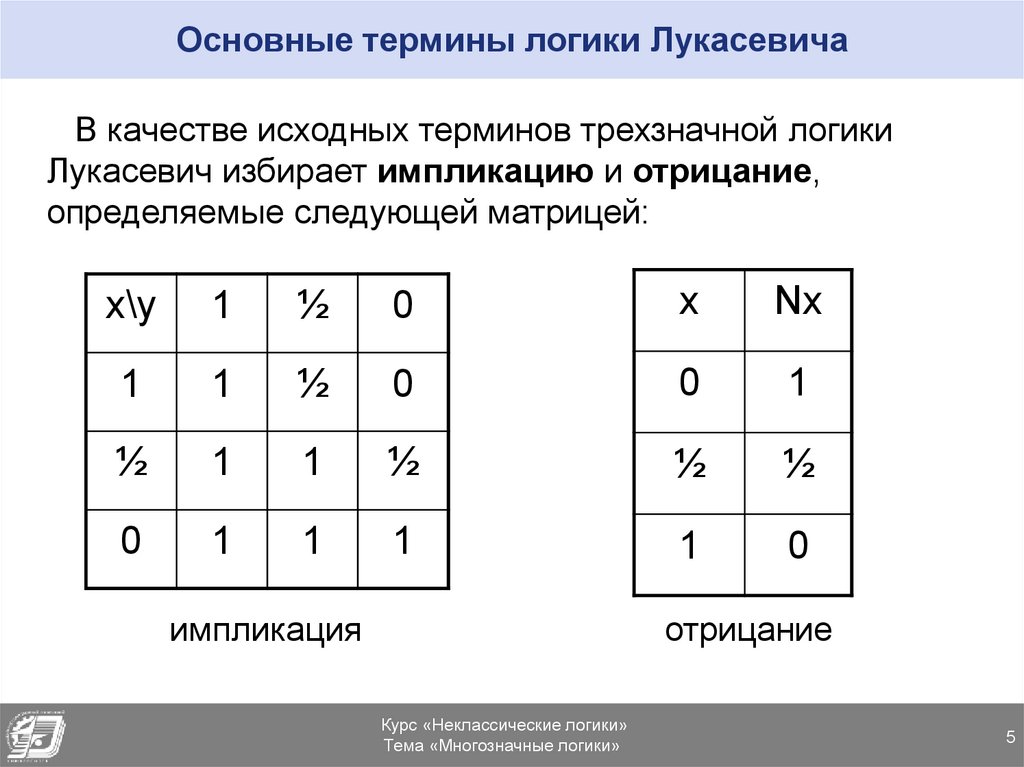
5. Основные термины логики Лукасевича

В качестве исходных терминов трехзначной логики
Лукасевич избирает импликацию и отрицание,
определяемые следующей матрицей:
x\y
1
½
0
x
Nx
1
1
½
0
0
1
½
1
1
½
½
½
0
1
1
1
1
0
импликация
отрицание
Курс «Неклассические логики»
Тема «Многозначные логики»
5

6. Конъюнкция

Конъюнкция определяется как минимум значения
аргументов. [Kxy] = min ([x], [y])
x\y
1
½
0
1
1
½
0
½
½
½
0
0
0
0
0
Конъюнкция выражается через импликацию и
отрицание следующим образом:
Курс «Неклассические логики»
Тема «Многозначные логики»
6

7. Дизъюнкция

Дизъюнкция определяется как минимум значения
аргументов. [Axy] = max ([x], [y])
x\y
1
½
0
1
1
1
1
½
1
½
½
0
1
½
0
Дизъюнкция выражается через импликацию и
отрицание следующим образом:
Курс «Неклассические логики»
Тема «Многозначные логики»
7

8. Эквивалентность

x\y
1
½
0
1
1
½
0
½
½
1
½
0
0
½
1
Эквивалентность выражается через импликацию и
отрицание следующим образом:
Курс «Неклассические логики»
Тема «Многозначные логики»
8

9. Тавтологиями НЕ являются

Закон непротиворечия
Закон исключенного третьего
Отрицание закона непротивореция
Отрицание закона исключенного
третьего
• Закон modus tollens
Курс «Неклассические логики»
Тема «Многозначные логики»
9

10. Тавтологиями являются

Правило снятия двух отрицаний
Все правила де Моргана
Правило контрапозиции
Все тавтологии логики Лукасевича являются
тавтологиями в двухзначной логике, но
обратное неправильно.
Курс «Неклассические логики»
Тема «Многозначные логики»
10

11. Область применения:

1. Для проектирования оболочек экспертных систем
(как механизм вывода экспертных систем).
2. Построение теории «правдоподобных» выводов.
3. Описание событий, связанных с человеческой
деятельностью.
4. Для подтверждения определенных философских
идей.
5. Предсказание вероятностных будущих событий.
6. Например, для моделирования распространения
лесного пожара (и других «стихийных» событий).
Курс «Неклассические логики»
Тема «Многозначные логики»
11

12. Эмиль Пост

Эмиль Пост (1897 — 1954) —
американский математик и
логик; один из основателей
многозначной логики (1921);
основные труды по
математической логике:
алгебра Поста, классы Поста
функций алгебры логики;
предложил абстрактную
вычислительную машину —
машину Поста.
Курс «Неклассические логики»
Тема «Многозначные логики»
12

13. Многозначная система Поста

В многозначной системе Поста среди значений
истинности t1 t2, ..., tm (m≥2) значение t1
соответствует истине, a tm – лжи.
Операции дизъюнкции и отрицания у Поста
являются основными операциями.
Пост вводит два вида отрицания (N1x и N2х)
соответственно называемые циклическим и
симметричным. Они определяются путем матриц и
посредством равенств.
Курс «Неклассические логики»
Тема «Многозначные логики»
13

14. Циклическое отрицание

x
N1x
Первое отрицание определяется
системой равенств:
1
2
2
3
•[N1x] = [x] +1, при [x] < m-1
3
4
…
…
n-2
n-1
n-1
n
n
1
•[N1x] = 1, при [x] = m
Курс «Неклассические логики»
Тема «Многозначные логики»
14

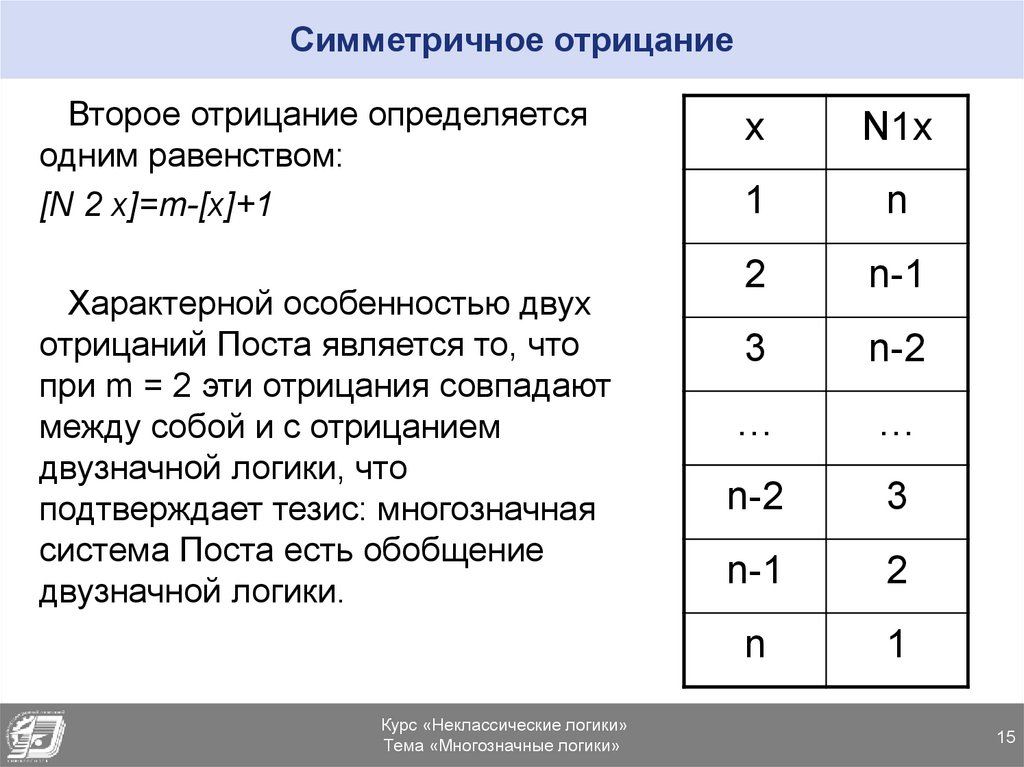
15. Симметричное отрицание

Второе отрицание определяется
одним равенством:
[N 2 x]=m-[x]+1
Характерной особенностью двух
отрицаний Поста является то, что
при m = 2 эти отрицания совпадают
между собой и с отрицанием
двузначной логики, что
подтверждает тезис: многозначная
система Поста есть обобщение
двузначной логики.
Курс «Неклассические логики»
Тема «Многозначные логики»
x
N1x
1
n
2
n-1
3
n-2
…
…
n-2
3
n-1
2
n
1
15

16. Конъюнкция

Конъюнкция определяется как минимум значения
аргументов. [Kxy] = min ([x], [y])
Построим таблицу истинности для конъюнкции
при m = 3.
x\y 1
2
3
1
1
2
3
2
2
2
3
3
3
3
3
Курс «Неклассические логики»
Тема «Многозначные логики»
16

17. Дизъюнкция

Дизъюнкция определяется как минимум значения
аргументов. [Axy] = max ([x], [y])
Построим таблицу истинности для дизъюнкции
при m = 3.
x\y 1
2
3
1
1
1
1
2
1
2
2
3
1
2
3
Курс «Неклассические логики»
Тема «Многозначные логики»
17

18. Эквивалентность

Построим таблицу истинности для
эквивалентности при m = 3.
x\y
1
2
3
1
1
2
3
2
1
2
2
3
1
1
1
Курс «Неклассические логики»
Тема «Многозначные логики»
18

19. Область применения:

1) теория автоматических устройств
2) теоретическое программирование
3) формализация высказываний, истинное
значение которых не зависит от контекста
4) анализ парадоксов
5) проблемы информационного поиска
Курс «Неклассические логики»
Тема «Многозначные логики»
19

20. Аренд Гейтинг

Аренд Гейтинг (1898 — 1980)
— голландский математик и
логик. Исследования
посвящены основаниям
математики. Один из
виднейших представителей
интуиционизма, опубликовал
работу с изложением
формальных правил
интуиционистской логики
высказываний.
Курс «Неклассические логики»
Тема «Многозначные логики»
20

21. Трёхзначная логика Гейтинга

Трехзначная логика Гейтинга это
часть
многозначной
логики.
Она
охватывала лишь часть классической
формальной логики.
Класс функций в логике Гейтинга
задается
суперпозицией
следующих
исходных функций:→, ˅, &.
Курс «Неклассические логики»
Тема «Многозначные логики»
21

22. Отрицание

По Гейтингу 1 – истинна, 0 – ложь, ½ неопределенность.
Отрицание можно задать системой уравнений
или таблицей истинности.
x
Nx
Курс «Неклассические логики»
Тема «Многозначные логики»
0
1
½
0
1
0
22

23. Импликация

Импликацию тоже можно задать системой
уравнений и таблицей истинности.
x\y
1
½
0
1
1
½
0
½
1
1
0
0
1
1
1
Курс «Неклассические логики»
Тема «Многозначные логики»
23

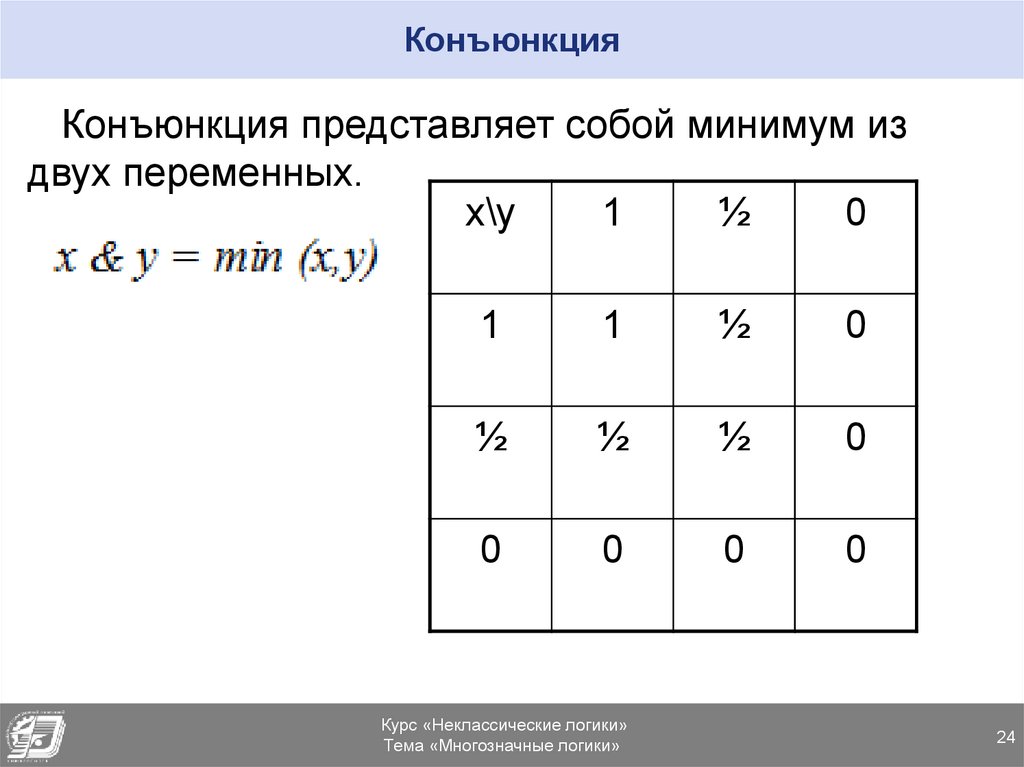
24. Конъюнкция

Конъюнкция представляет собой минимум из
двух переменных.
x\y
1
½
0
1
1
½
0
½
½
½
0
0
0
0
0
Курс «Неклассические логики»
Тема «Многозначные логики»
24

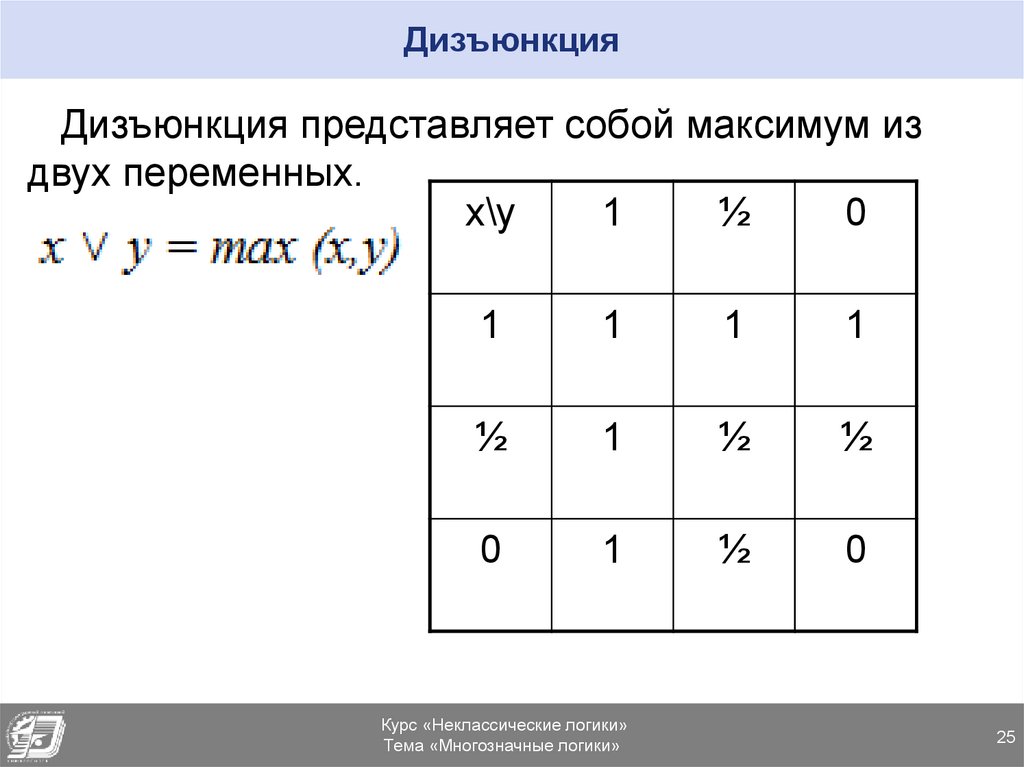
25. Дизъюнкция

Дизъюнкция представляет собой максимум из
двух переменных.
x\y
1
½
0
1
1
1
1
½
1
½
½
0
1
½
0
Курс «Неклассические логики»
Тема «Многозначные логики»
25

26. Законы, действующие в логике Гейтинга

Тавтологиями не являются:
• Закон непротиворечия
• Закон исключенного третьего
• Отрицание закона исключенного третьего
• Отрицание закона непротиворечия
Тавтологиями являются:
• Закон исключенного четвертого
• Правила де Моргана
Курс «Неклассические логики»
Тема «Многозначные логики»
26

27. Область применения:

1) решение логико-философских проблем
квантовой механики
2) методологический анализ концепций
пространства и времени
3) Задание семантики абстрактных
математических пространств
Курс «Неклассические логики»
Тема «Многозначные логики»
27

28.

СПАСИБО ЗА ВНИМАНИЕ
© ФГБОУ ВПО ИжГТУ имени М.Т. Калашникова, 2014
© Исенбаева Елена Насимьяновна, 2014