Синхронные машины. Цикл лекций в курсе «Электрические машины»

1.

Синхронные
машины
Цикл лекций в курсе «Электрические
машины»

2.

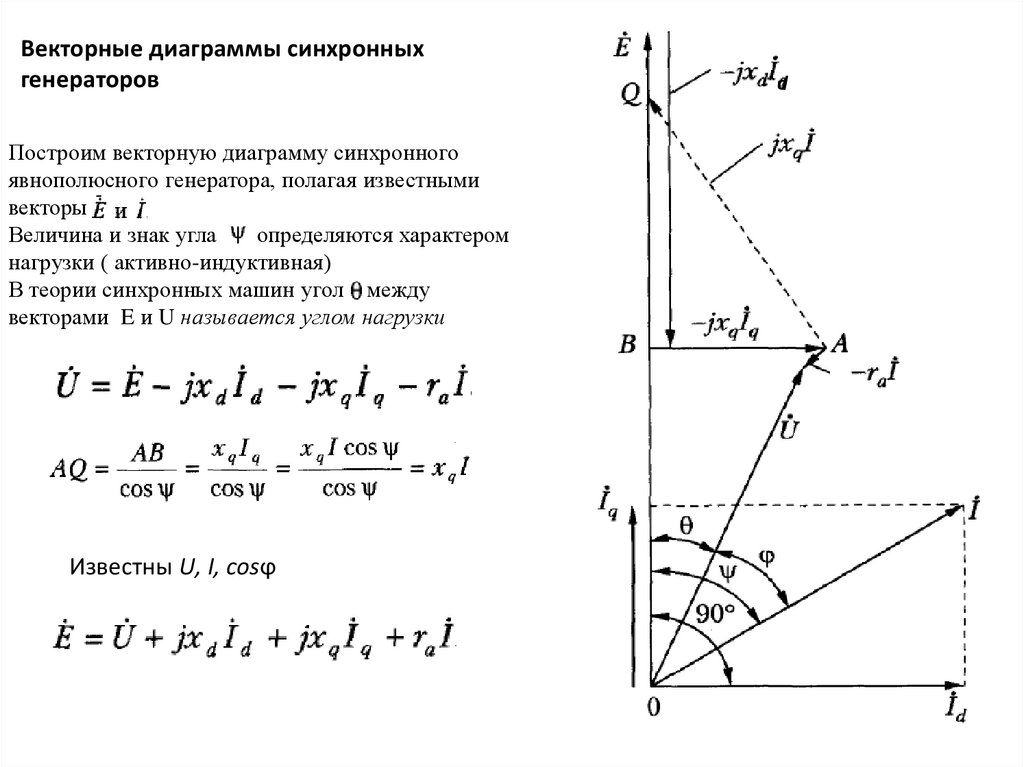
Векторные диаграммы синхронных
генераторов
Построим векторную диаграмму синхронного
явнополюсного генератора, полагая известными
векторы
Величина и знак угла
определяются характером
нагрузки ( активно-индуктивная)
В теории синхронных машин угол между
векторами E и U называется углом нагрузки
Известны U, I, cosϕ
d

3.

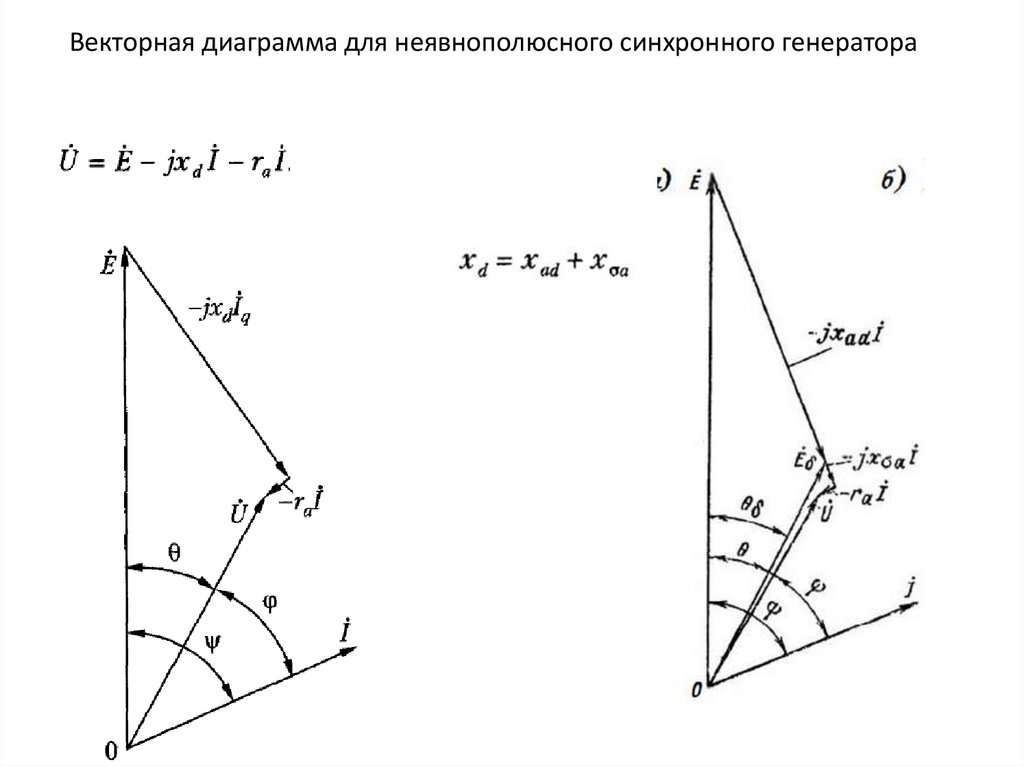
Векторная диаграмма для неявнополюсного синхронного генератора

4.

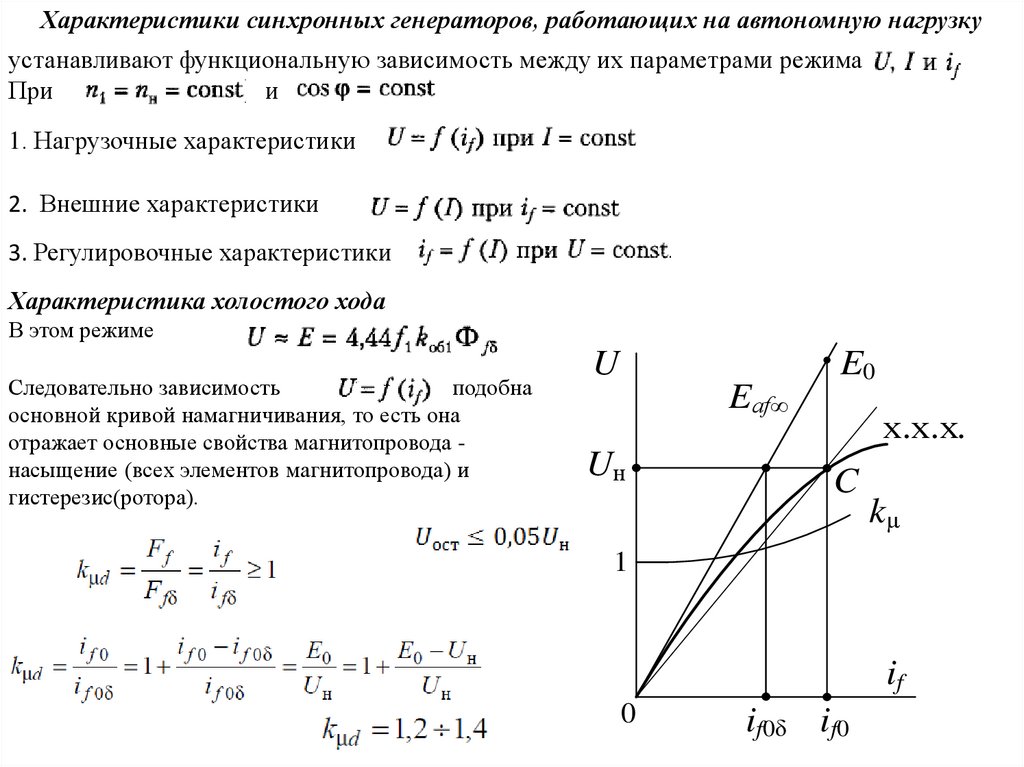
Характеристики синхронных генераторов, работающих на автономную нагрузку
устанавливают функциональную зависимость между их параметрами режима
При
и
1. Нагрузочные характеристики
2. Внешние характеристики
3. Регулировочные характеристики
Характеристика холостого хода
В этом режиме
Следовательно зависимость
подобна
основной кривой намагничивания, то есть она
отражает основные свойства магнитопровода насыщение (всех элементов магнитопровода) и
гистерезис(ротора).
U
Eaf∞
Uн
E0
х.х.х.
C
kμ
1
if
0
if0δ if0

5.

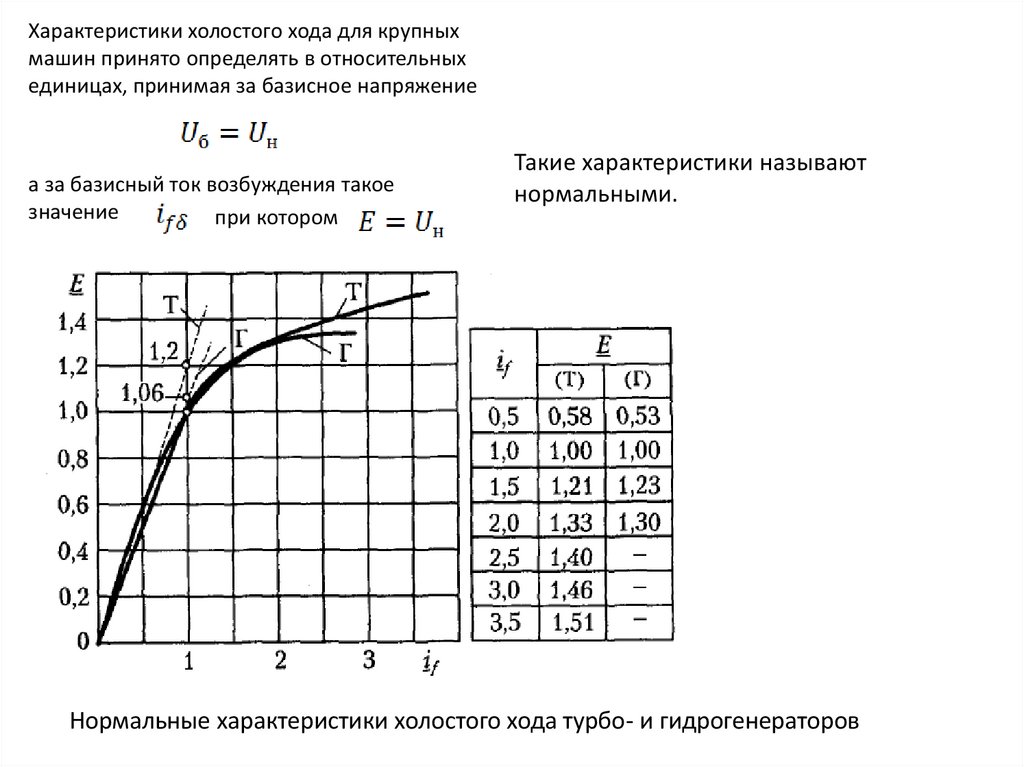
Характеристики холостого хода для крупных
машин принято определять в относительных
единицах, принимая за базисное напряжение
а за базисный ток возбуждения такое
значение
при котором
Такие характеристики называют
нормальными.
Нормальные характеристики холостого хода турбо- и гидрогенераторов

6.

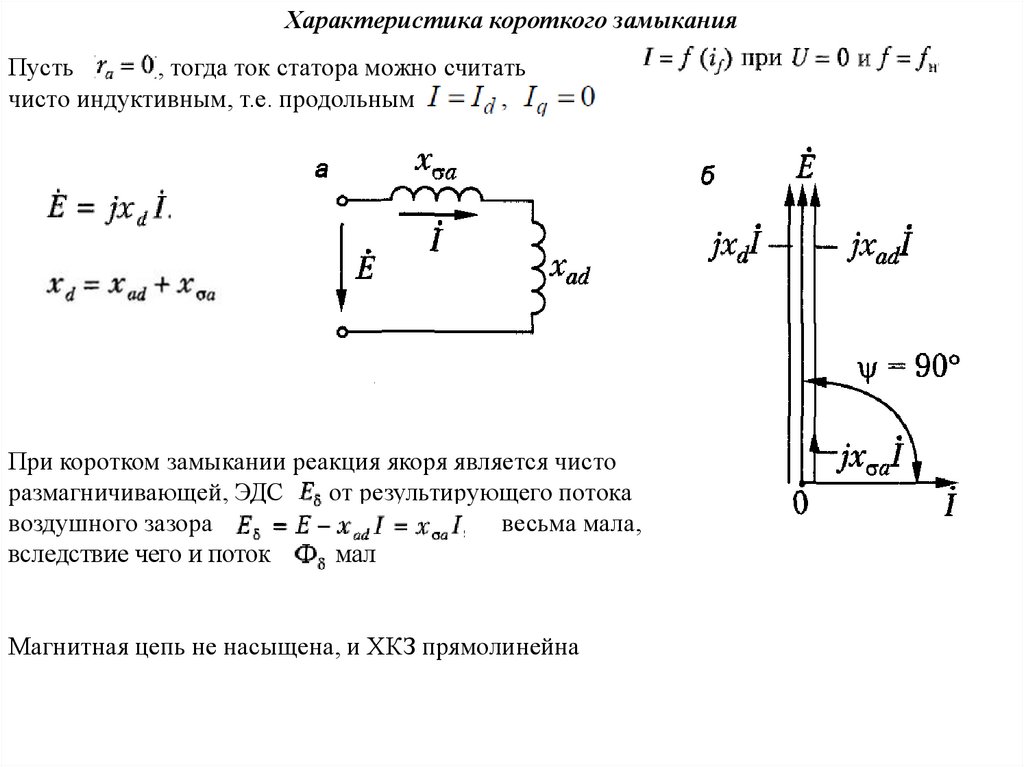
Характеристика короткого замыкания
Пусть
, тогда ток статора можно считать
чисто индуктивным, т.е. продольным
При коротком замыкании реакция якоря является чисто
размагничивающей, ЭДС
от результирующего потока
воздушного зазора
весьма мала,
вследствие чего и поток
мал
Магнитная цепь не насыщена, и ХКЗ прямолинейна

7.

Опытное определение
Обычно находят ненасыщенное значение этого сопротивления
насыщенного значения для каждой машины вполне определенно.
которое, в отличие от
Определим при одном и том же токе возбуждения (ОА)
ненасыщенной ХХХ и ток I по ХКЗ
по спрямленной
Насыщенное значение,
соответствующее данной ЭДС
получим при

8.

Отношение короткого замыкания (ОКЗ)
это отношение установившегося тока короткого замыкания, определенного при таком токе
возбуждения , при котором в режиме холостого хода
, к номинальному
току якоря :
В соответствии с рис.
,
где
- насыщенное значение
продольного синхронного
сопротивления, соответствующее
У многих машин
, то есть
Из подобия треугольников
значение ОКЗ, определяет предельную нагрузку, которую способен нести генератор при
установившемся режиме работы, причем чем больше ОКЗ, тем больше предельная
нагрузка

9.

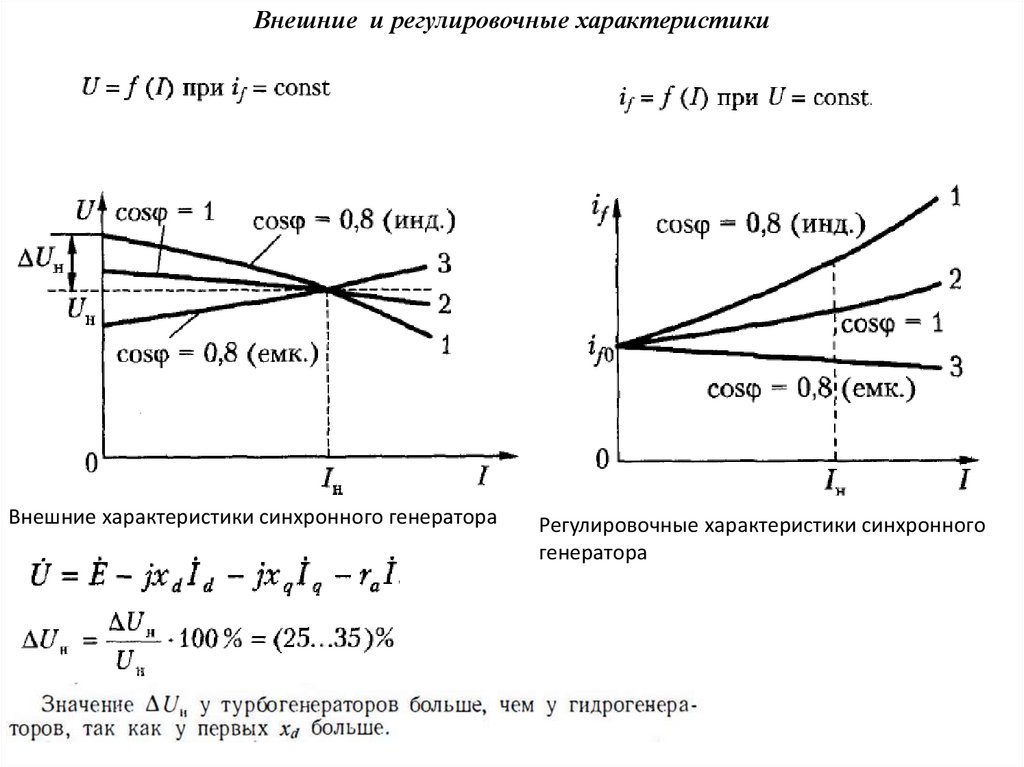
Внешние и регулировочные характеристики
Внешние характеристики синхронного генератора
Регулировочные характеристики синхронного
генератора

10.

Из семейства нагрузочных характеристик, определяемых для различных значений
наибольший практический интерес представляет характеристика при
=0, называемая
индукционной.
В режиме индукционной характеристики ток якоря I является продольным
Зависимость
идентична основной
кривой намагничивания машины
,
если МДС F ad приведена к обмотке возбуждения
и выражена в масштабе тока возбуждения.
Зависимость
будет идентична
характеристике холостого хода
под
подразумевается результирующая МДС,
выраженная в масштабе тока возбуждения.

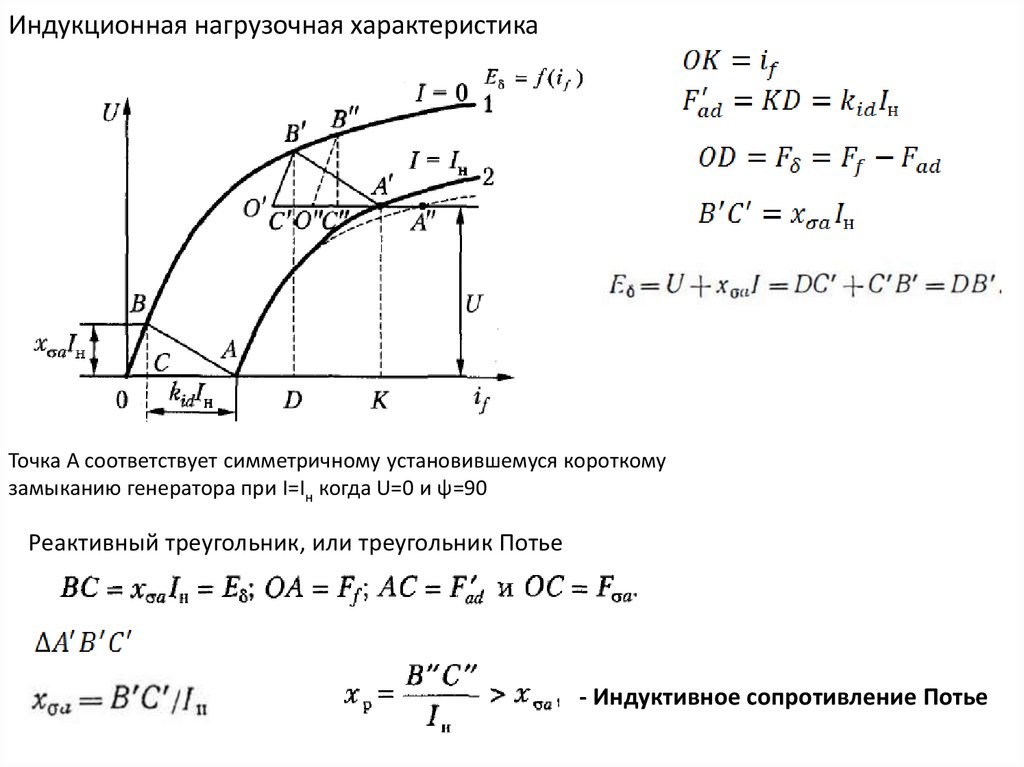
11.

Индукционная нагрузочная характеристика
Точка А соответствует симметричному установившемуся короткому
замыканию генератора при I=Iн когда U=0 и ψ=90
Реактивный треугольник, или треугольник Потье
- Индуктивное сопротивление Потье

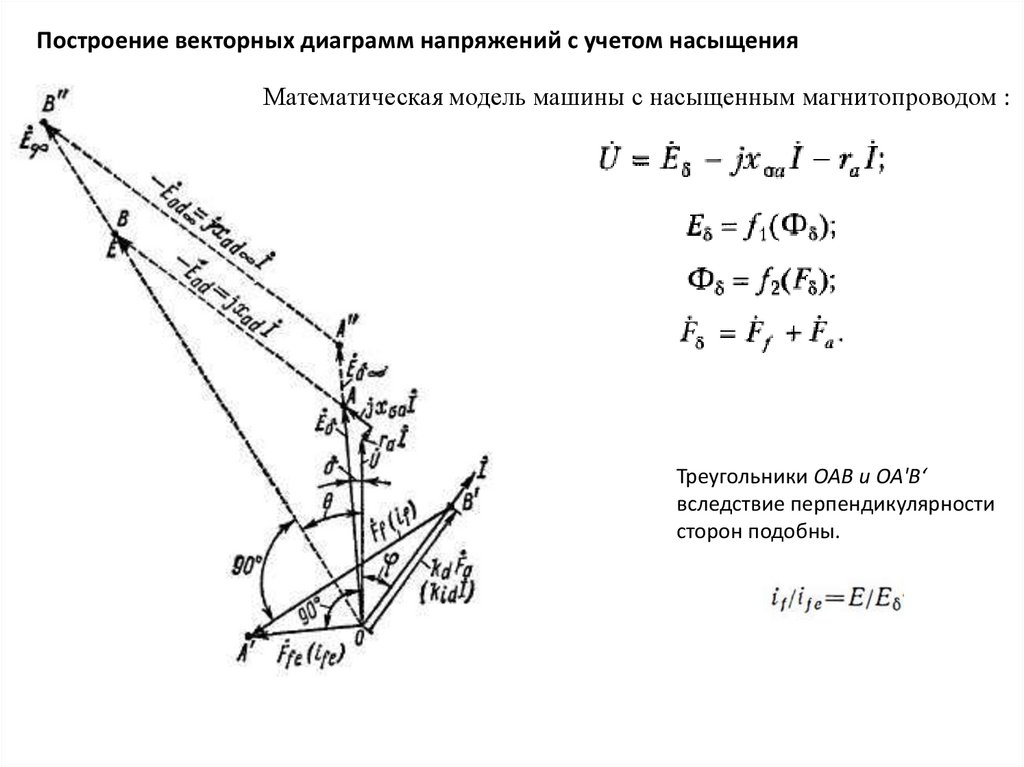
12.

Построение векторных диаграмм напряжений с учетом насыщения
Математическая модель машины с насыщенным магнитопроводом :
Треугольники ОАВ и ОА'В‘
вследствие перпендикулярности
сторон подобны.

13.

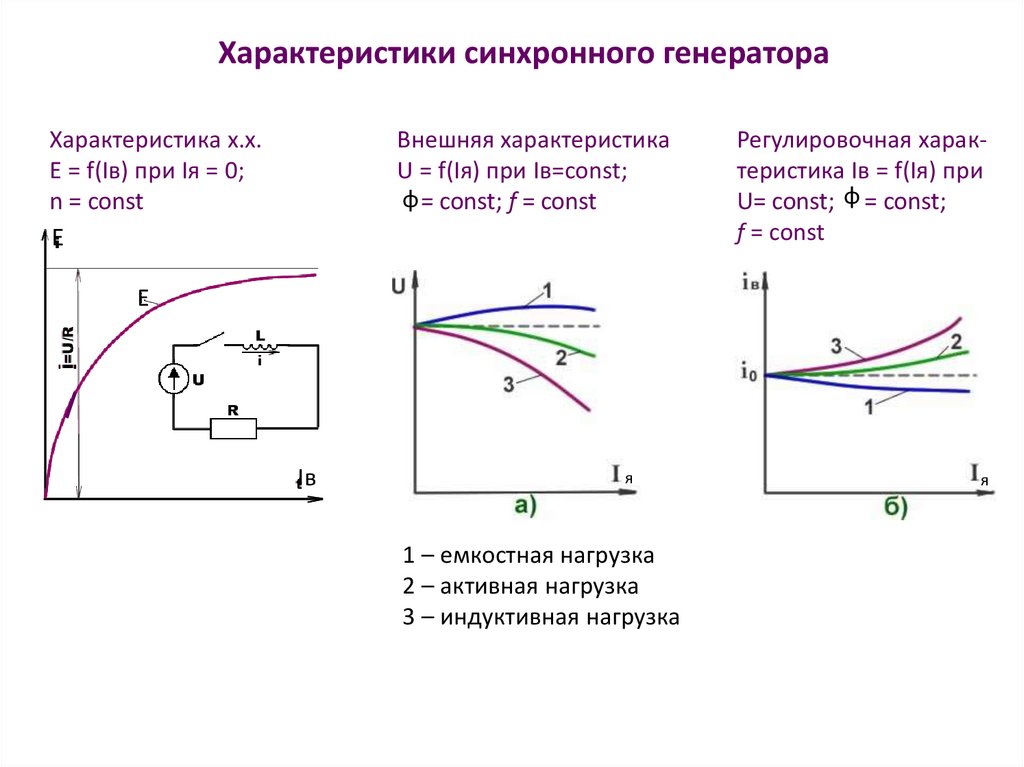
Характеристики синхронного генератора
Характеристика х.х.
E = f(Iв) при Iя = 0;
n = const
Е
Внешняя характеристика
U = f(Iя) при Iв=const;
φ = const; f = const
Регулировочная характеристика Iв = f(Iя) при
U= сonst; φ = сonst;
f = const
Е
Iв
я
1 – емкостная нагрузка
2 – активная нагрузка
3 – индуктивная нагрузка
я

14.

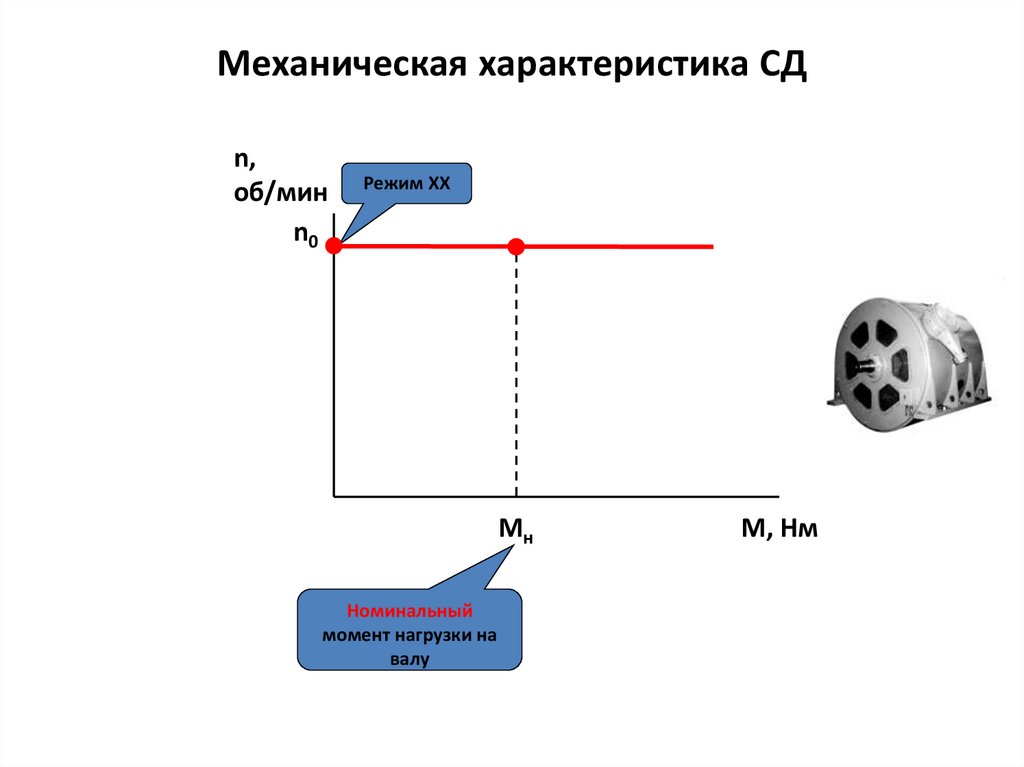
Механическая характеристика СД
n,
об/мин
n0
Режим ХХ
Мн
Номинальный
момент нагрузки на
валу
М, Нм

15.

• ЭЛЕКТРОМАГНИТНЫЙ ПЕРЕХОДНЫЙ
ПРОЦЕСС
В ЭЛЕКТРИЧЕСКИХ МАШИНАХ

16.

• Аналитическое исследование электромагнитного переходного
процесса в электрических машинах представляет достаточно сложную
задачу.
• Для её упрощения вводится ряд допущений:
• учитывается только периодическая слагающая тока статора;
• скорость ротора считается неизменной и равной ;
• рассматривается синхронная машина, работающая отдельно от
других источников питания;
• трансформаторные ЭДС принимаются равными нулю, вследствие
того, что обобщённые векторы потоков изменяются медленно.
• Таким образом, в дальнейшем рассматривается в известной мере
идеализированная машина. Это вносит погрешности в оценку
отдельных величин. Однако, как показывают сопоставления
полученных величин с экспериментальными данными, обычно
погрешности находятся в допустимых для практических расчётов
пределах.

17.

ЭЛЕКТРОМАГНИТНЫЙ ПЕРЕХОДНЫЙ ПРОЦЕСС
В ЭЛЕКТРИЧЕСКИХ МАШИНАХ
1. Уравнения синхронной машины в фазных
координатах

18.

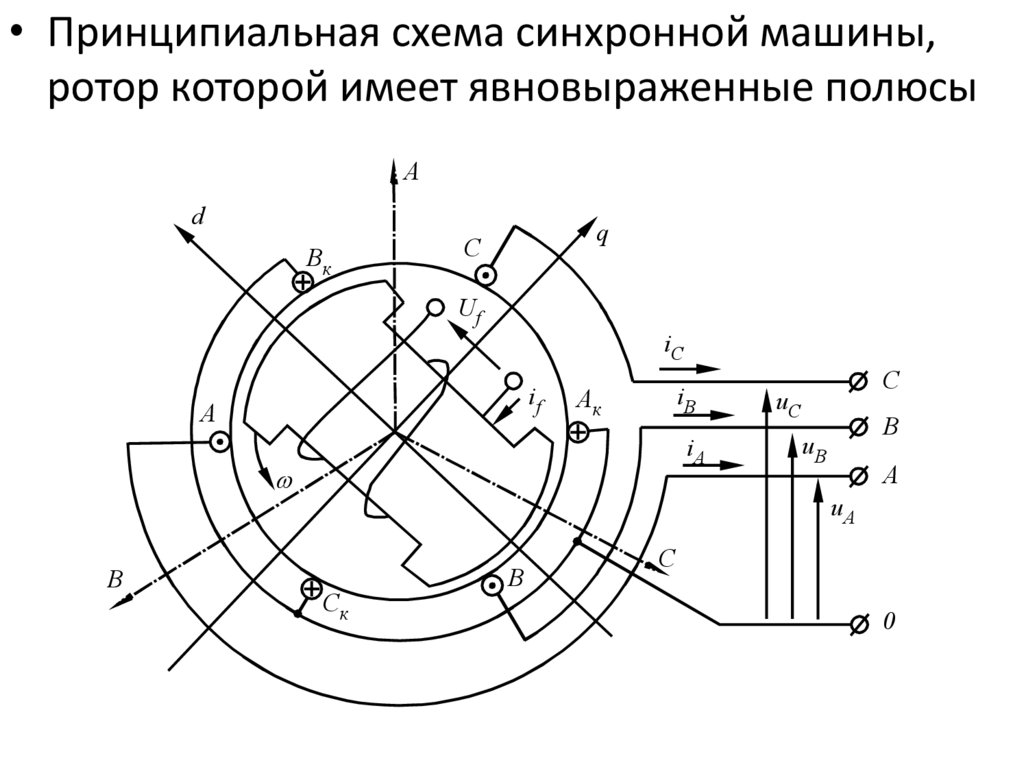
• Принципиальная схема синхронной машины,
ротор которой имеет явновыраженные полюсы
A
d
Bк
q
C
Uf
iC
if
A
iB
Aк
iA
B
C
uC
B
uB
A
uA
Cк
B
C
0

19.

• Дифференциальные уравнения для каждой из
обмоток синхронной машины
d A
Ri A u A
dt
d B
RiB u B
dt
d C
RiC uC
dt
d f
Rf if u f
dt
(5.1)
где R , R f - активные сопротивления контуров каждой фазы цепи
возбуждения соответственно,
• A , B , C , f
- результирующие потокосцепления обмоток
статора и обмотки возбуждения соответственно,
• u A , u B , uC , u f
- напряжения на зажимах соответствующих
обмоток.

20.

• При принятых допущениях выражения для
потокосцеплений представляют линейные
зависимости.
• Так для потокосцепления фазы ,
A LAiA M AB iB M AC iC M Af i f
L A - индуктивность фазы А ;
• где
• M AB , M AC , M Af
- взаимные индуктивности фазы А с фазами
В и С, и обмоткой возбуждения (индекс f ) соответственно.
• Аналогично
f M fA iA M fB iB M fCiC L f i f
• где L f - индуктивность обмотки возбуждения.
• Необходимо отметить, что по принципу взаимности .
M AB M BA
M Af M fA
и т.д

21.

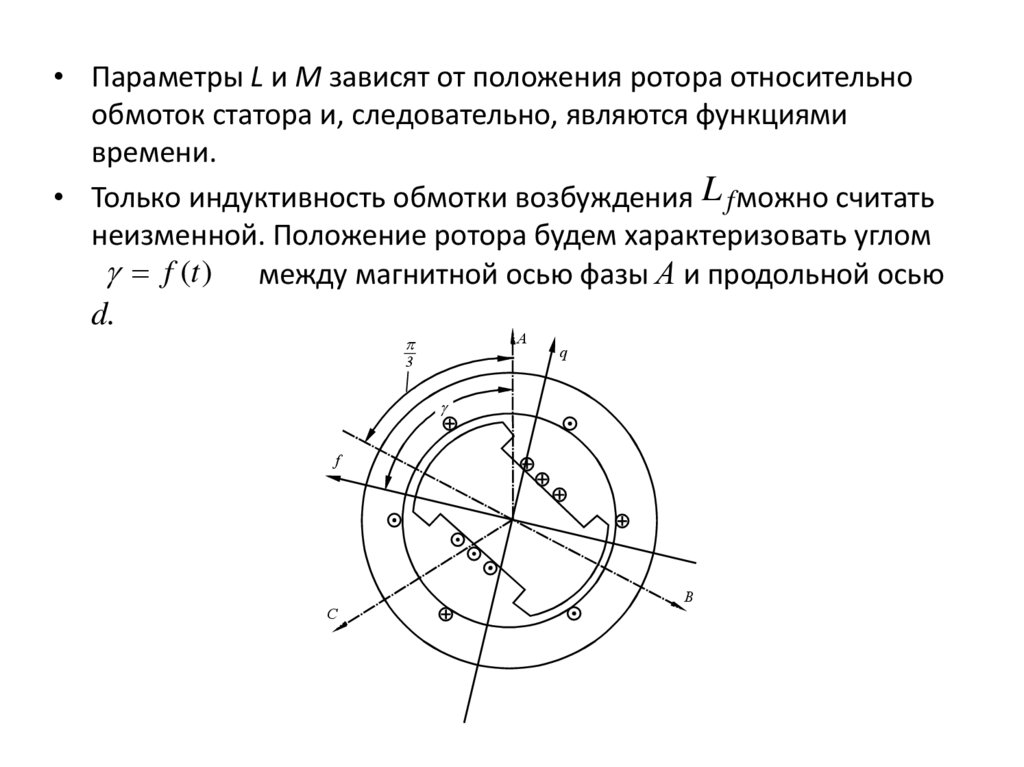
• Параметры L и M зависят от положения ротора относительно
обмоток статора и, следовательно, являются функциями
времени.
• Только индуктивность обмотки возбуждения L f можно считать
неизменной. Положение ротора будем характеризовать углом
f (t ) между магнитной осью фазы А и продольной осью
d.
A
3
q
f
C
B

22.

• Синусоидальность наводимых в статоре ЭДС
указывает на гармонический закон изменения
взаимных индуктивностей между обмоткой
возбуждения и каждой из фазных обмоток.
• Так, например, для фазы А,
M Af M fA M d cos
• где M d - максимальное значение
взаимоиндукции при совпадении магнитных
осей обмоток статора и ротора.
• Изменение индуктивностей фазных обмоток и
взаимных индуктивностей между ними
обусловлены вращением явнополюсного
ротора, поскольку при этом меняется
сопротивление магнитным потокам, которые
определяют данные величины.

23.

• Изменение магнитных потоков происходит
гармонически
, так как при повороте
T сTпериодом
2
ротора на 180о повторяется предыдущий цикл
изменения магнитного сопротивления.
• Так, например, индуктивность фазы А определяется
выражением,
LA l0 l2 cos 2
• взаимная индуктивность между обмотками фаз А и В,
1
M AB m0 m2 cos 2 / 3
• где l0 ,m - постоянные составляющие соответствующих
индуктивностей;
• l2 m
, 2- амплитуды вторых гармоник соответствующих
индуктивностей.
0

24.

ЭЛЕКТРОМАГНИТНЫЙ ПЕРЕХОДНЫЙ ПРОЦЕСС
В ЭЛЕКТРИЧЕСКИХ МАШИНАХ
• Аналогично могут быть записаны выражения
для L и M остальных обмоток.
• Таким образом, коэффициенты в уравнениях
системы (5.1) являются переменными, что
значительно усложняет её решение.
• (Дифференциальные уравнения с
переменными коэффициентами называются
параметрическими; аналитическое решение
имеют только немногие из них).

25.

ЭЛЕКТРОМАГНИТНЫЙ ПЕРЕХОДНЫЙ ПРОЦЕСС
В ЭЛЕКТРИЧЕСКИХ МАШИНАХ
• 2. Обобщённый вектор трёхфазной системы и
замена переменных синхронной машины

26.

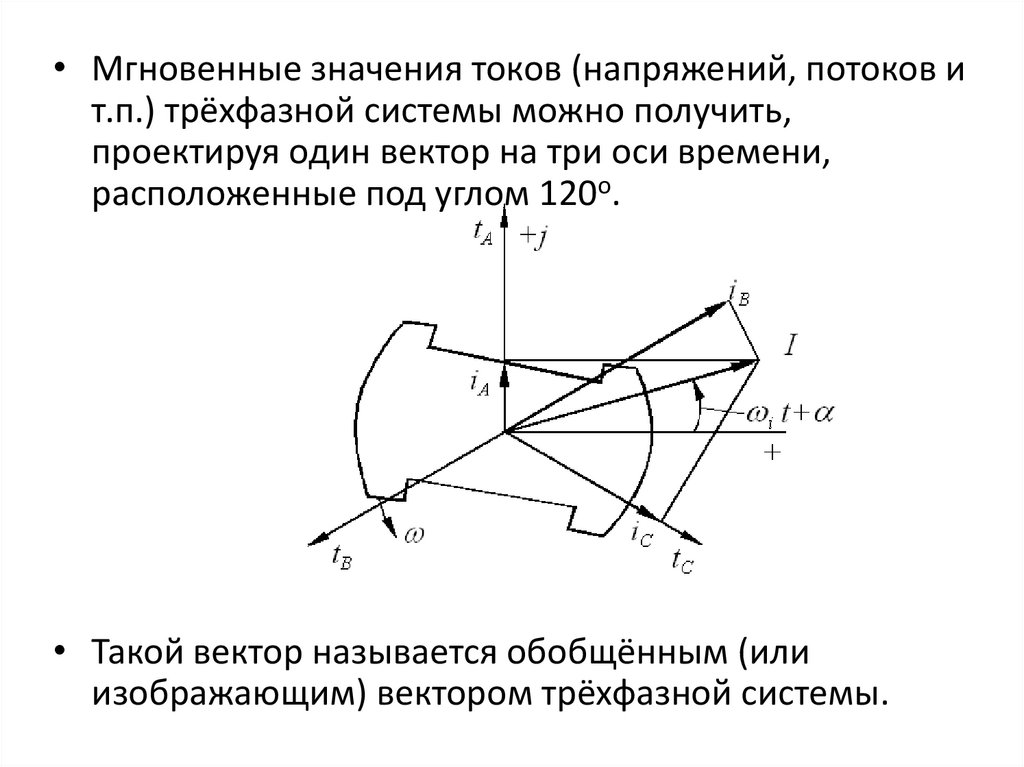
• Мгновенные значения токов (напряжений, потоков и
т.п.) трёхфазной системы можно получить,
проектируя один вектор на три оси времени,
расположенные под углом 120о.
• Такой вектор называется обобщённым (или
изображающим) вектором трёхфазной системы.

27.

• Замена фазных переменных величин обобщённым вектором
позволяет разложить его на продольную (d) и поперечную (q)
составляющие.
• Оси d,q,0 образуют декартову систему координат,
вращающуюся вместе с ротором.
• Переход от неподвижной фазной системы координат A, B, C к
вращающейся, жестко связанной с ротором системы d,q,0 был
впервые предложен Блонделем для установившегося
режима.
• Такой подход был распространён Парком Р.Х. на переходный
режим. Это позволяет параметрическую систему уравнений
(5.1) свести к системе дифференциальных уравнений с
постоянными коэффициентами, что упрощает её решение.

28.

• Величина обобщённого вектора может быть
определена исходя из следующих равенств
i A I sin i t ,
iB I sin i t / 3 ,
iC I sin i t / 3 ,
(5.2)
i
• где
- угловая скорость обобщённого вектора
I, которая в переходном режиме может
отличаться от угловой скорости вращения
,
,ротора
- начальный угол обобщённого
вектора относительно оси, перпендикулярной
оси обмотки A.

29.

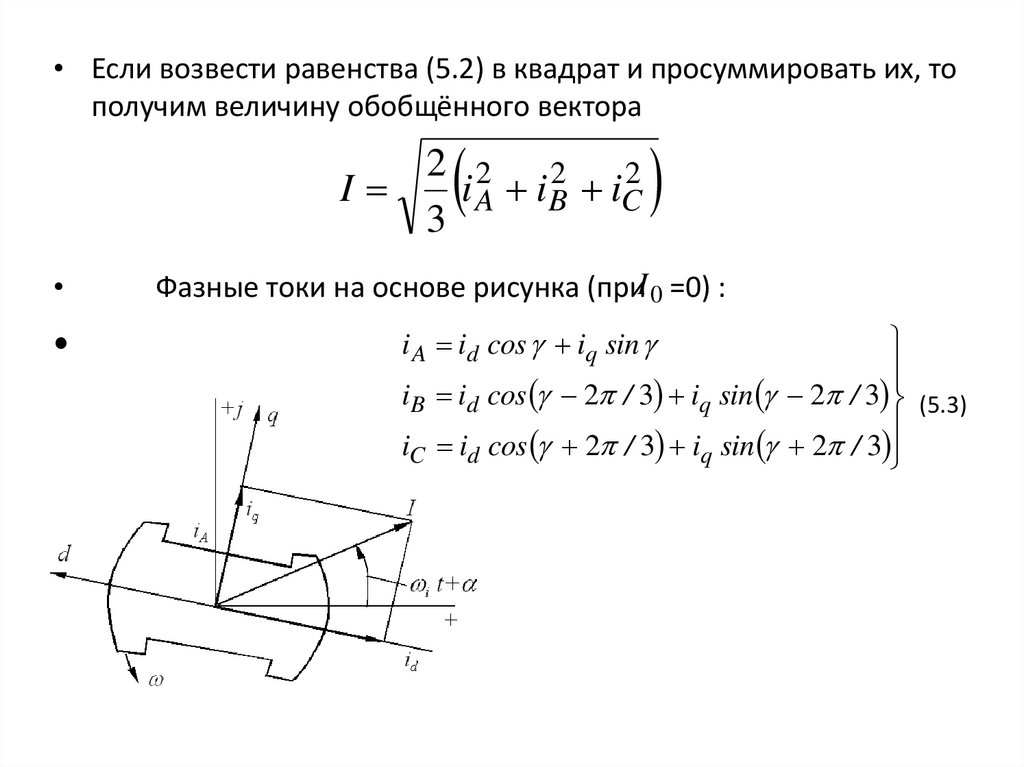
• Если возвести равенства (5.2) в квадрат и просуммировать их, то
получим величину обобщённого вектора
2 2 2 2
I
i A iB iC
3
Фазные токи на основе рисунка (приI 0 =0) :
iB id cos 2 / 3 iq sin 2 / 3 (5.3)
iC id cos 2 / 3 iq sin 2 / 3
i A id cos iq sin

30.

ЭЛЕКТРОМАГНИТНЫЙ ПЕРЕХОДНЫЙ ПРОЦЕСС
В ЭЛЕКТРИЧЕСКИХ МАШИНАХ
• 3. Уравнения Парка для синхронной машины

31.

• В уравнение для фазы обмотки статора (из (5.1))
d A
RiA u A
dt
• подставим выражения для фазных величин (
), выраженные через обобщённые векторы в , i , u
продольной и поперечной осях ротора (из 5.3))
A d cos q sin
i A id cos iq sin
u A ud cos uq sin
• С помощью этой подстановки заменим фазные
переменные обобщёнными. После
дифференцирования и преобразования получим
d q
d d
d
d
u
Ri
cos
u
Ri
d
q
d
q
d
q sin 0
dt
dt
dt
dt
(5.4)

32.

• Равенство (5.4) может быть удовлетворено при любом значении
, только при условии, что каждое выражение в скобках
тождественно равно нулю.
• Приравнивая выражения в скобках к нулю, получим два
уравнения.
• Добавим к полученным уравнениям уравнение для обмотки
возбуждения из системы (5.1), получим систему уравнений
синхронной машины при отсутствии в роторе демпферных
контуров
d d
d
q
Rid u d
dt
dt
d q
d
d
Riq u q
dt
dt
d f
Rf if u f
dt
(5.5)

33.

• Полученные уравнения называются уравнениями
Парка.
• Они выражают теорию двух реакций обмоток статора
синхронной машины и характеризуют переходный
процесс в ней.
• Входящие в систему дифференциальные уравнения
имеют постоянные коэффициенты.
d d
• Слагаемые dt
d q
, dt представляют ЭДС
трансформации, так как наводятся в обмотках статора
и ротора благодаря изменению потокосцеплений.
• Трансформаторные ЭДС наводятся в переходном
режиме, в стационарном режиме они отсутствуют.

34.

d
• Слагаемые, содержащие dt , представляют собой ЭДС вращения
(резания), которые наводятся в обмотках статора благодаря
вращающемуся полю.
В обмотках ротора в стационарном режиме эти ЭДС отсутствуют,
так как не создают в них изменяющегося потока. В переходном
режиме происходит перемещение обобщённого вектора потока
относительно ротора и в его обмотках наводятся ЭДС
скольжения.
Потокосцепления d и q включают потоки рассеяния обмоток
статора.
Полные синхронные индуктивности Ld Lad L , Lq Laq L
При принятом положительном направлении потока из ротора в
статор результирующее потокосцепление можно выразить через
обобщённые векторы токов ротора и статора
d Lad i f Ld id , q Lq iq