Стереометрия (многогранники). Игра «Назови фигуру»

1.

СТЕРЕОМЕТРИЯ
(МНОГОГРАННИКИ)

2.

ИГРА «НАЗОВИ ФИГУРУ»

3.

4.

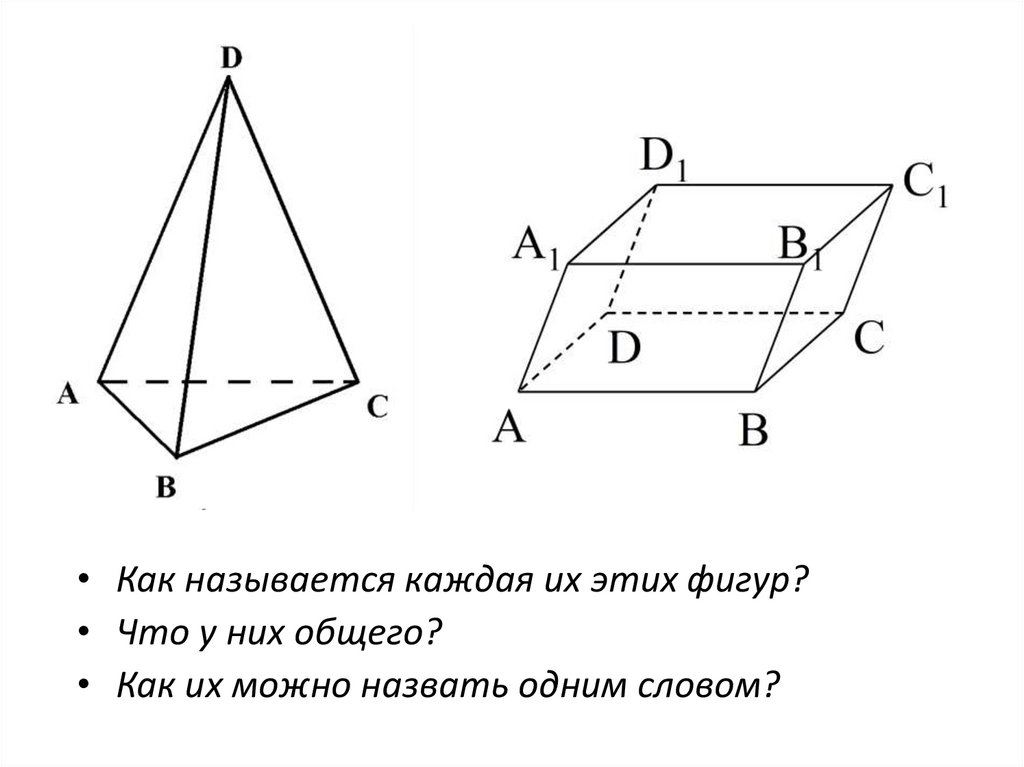
• Как называется каждая их этих фигур?
• Что у них общего?
• Как их можно назвать одним словом?

5.

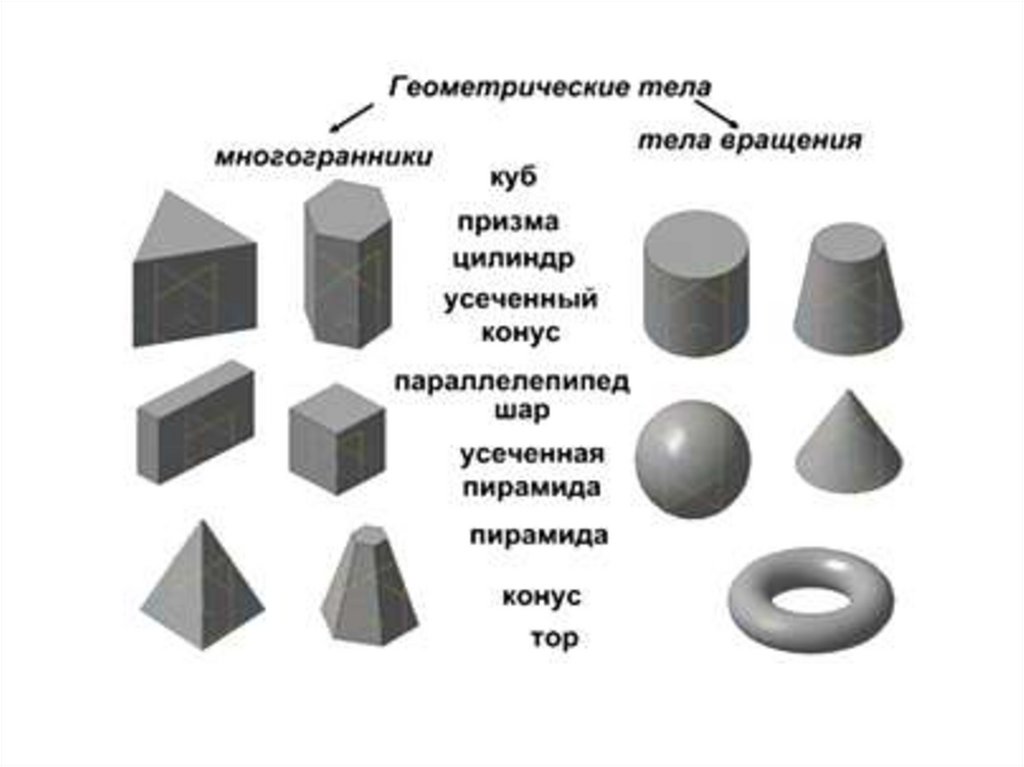
МНОГОГРАННИКИ

6.

Понятие многогранника
Попробуем сами сформулировать определение…
Опр.: МНОГОГРАННИК – поверхность, составленная
из многоугольников и ограничивающая некоторое
геометрическое тело.
*(само тело тоже называется многогранником)

7.

Виды многогранников насчитывают не один десяток представителей,
отличающихся количеством и формой граней.

8.

9.

10.

Многие строения
в окружающем
нас мире имеют
форму
многогранников
или состоят из
нескольких
разных
многогранников

11.

Пирамида Хеопса
Памятник относится
к эпохе Древнего
царства (IV
династия).
Построена
племянником
фараона Хеопса
Хемиуном.
Поэтому для лучшей сохранности,
эксплуатации и моделирования здания
нужно изучить свойства многогранников.

12.

Многие многогранники изобрёл не
человек, а создала природа в виде
кристаллов:
Поваренная и каменная соль
Горный
хрусталь
Кристаллы
льда

13.

Кристаллы кварца
Кристаллы граната

14.

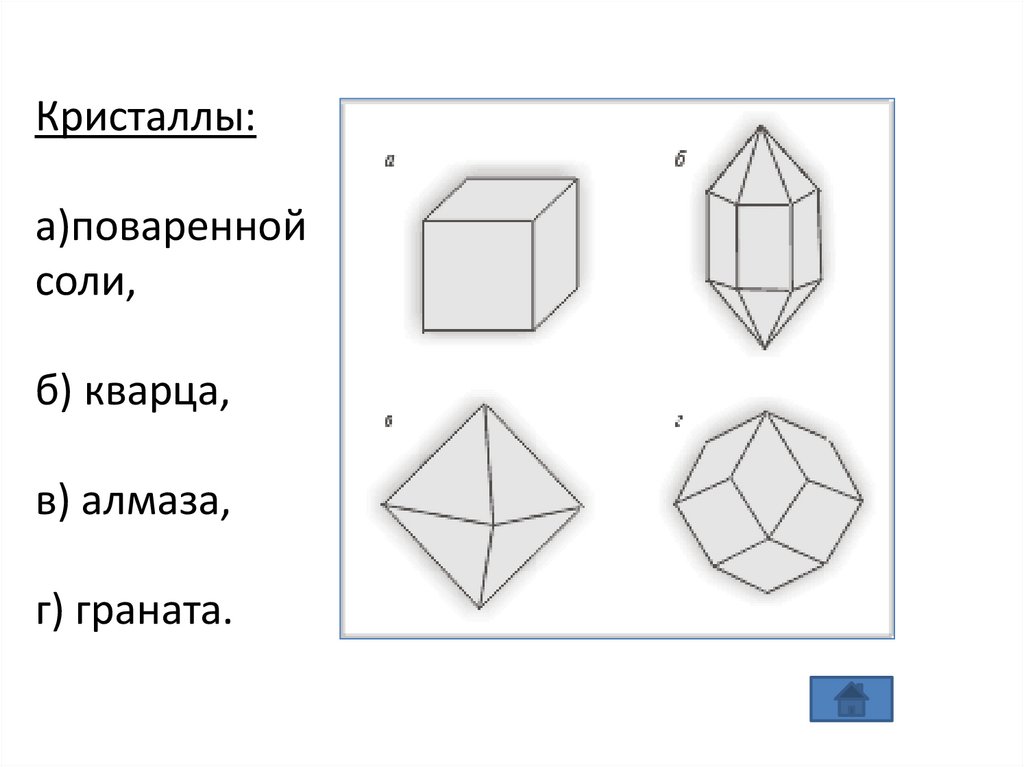
Кристаллы:
а)поваренной
соли,
б) кварца,
в) алмаза,
г) граната.

15.

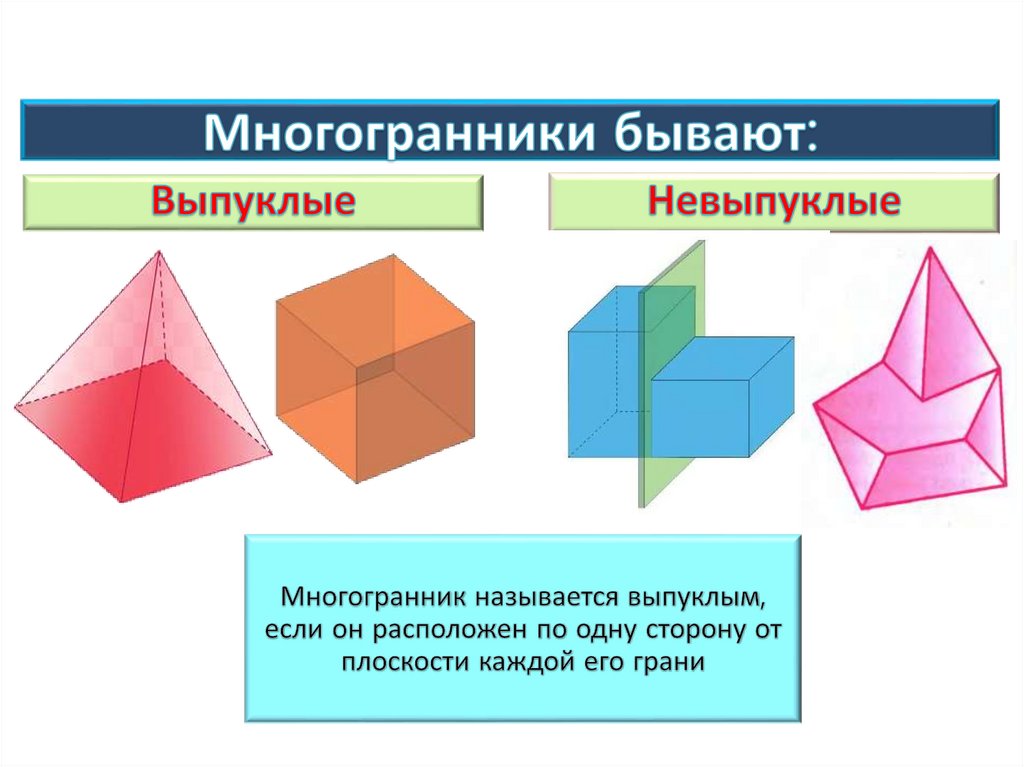
Многогранники делятся на:
• Выпуклые
Многогранник называется выпуклым, если он расположен
по одну сторону от плоскости каждой его грани.
*Грани выпуклого многогранника являются выпуклыми
многоугольниками;
** В выпуклом многограннике сумма всех плоских углом
при каждой его вершине меньше 3600 .
• Невыпуклые

16.

17.

Выберем выпуклые и невыпуклые

18.

Общие свойства многогранников:
Все они имеют 3 неотъемлемых компонента:
грани – многоугольники, из которых составлен
многогранник;
ребра – стороны граней многогранника;
вершины – концы ребер.
Каждое ребро многоугольника соединяет две, и только две
грани, которые по отношению друг к другу являются
смежными.

19.

Из чего состоит поверхность многогранника?
Из многоугольников .
Значит грани многогранника – многоугольники.
В данном случае: Δ ASD, ΔASB, ΔDSC, ΔBSC,
четырехугольник ABCD
S
D
A
C
B

20.

Что такое многоугольник?
Это плоская фигура, образованная замкнутым
рядом прямолинейных отрезков.
Прямолинейные отрезки – это рёбра, а концы
рёбер – вершины многогранника.
Назовите вершины и рёбра многогранника.
S
D
A
C
B

21.

Отрезок, соединяющий 2 несоседние вершины
одной грани, называется диагональю грани, а
отрезок, соединяющий 2 вершины, не
принадлежащие одной грани, - это диагональ
многогранника.
C1
D1
A1
B1
D
A
C
B

22.

Многоугольники, из которых составлен многогранник, называются
его гранями. Например, АА1D1A (перечислите остальные)
Стороны граней называются рёбрами (AD,
DC, перечислите остальные), а концы рёбер
–
вершинами
(А,
В, перечислите
остальные) многогранника.
Отрезок, соединяющий две вершины , не
принадлежащие одной грани, называется
диагональю (DB1, перечислите остальные)
многогранника.

23.

Еще немного определений
Отрезок, соединяющий 2 вершины , не принадлежащие
одной грани называется
диагональю многогранника;
Плоскость по обе стороны от которой расположены точки
многогранника, называется
секущей плоскостью;
Общая часть многогранника и секущей плоскости называется
сечением многогранника

24.

Куб
Куб – правильный многогранник, каждая
грань которого представляет собой
квадрат. Все ребра куба равны.
Куб является частным случаем
параллелепипеда и призмы.
Sполн 6a 2
V Sосн h a
d a 3
3

25.

Теорема Эйлера
Леонард Эйлер (1707 - 1783)
Th: В любом выпуклом многограннике сумма
числа граней и числа вершин больше числа
ребер на 2.
Г+В–Р=2

26.

ПРИЗМА

27.

Определение
Опр.: ПРИЗМА - многогранник, составленный из
двух равных n- угольников, расположенных в
параллельных плоскостях, и n параллелограммов

28.

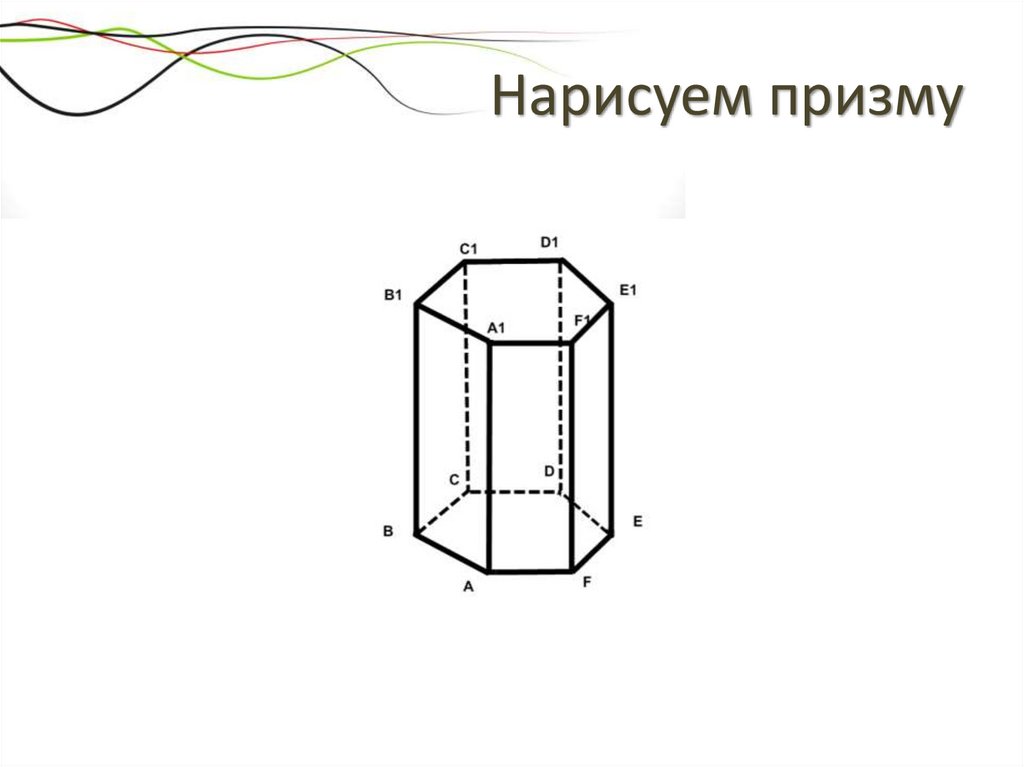
Нарисуем призму

29.

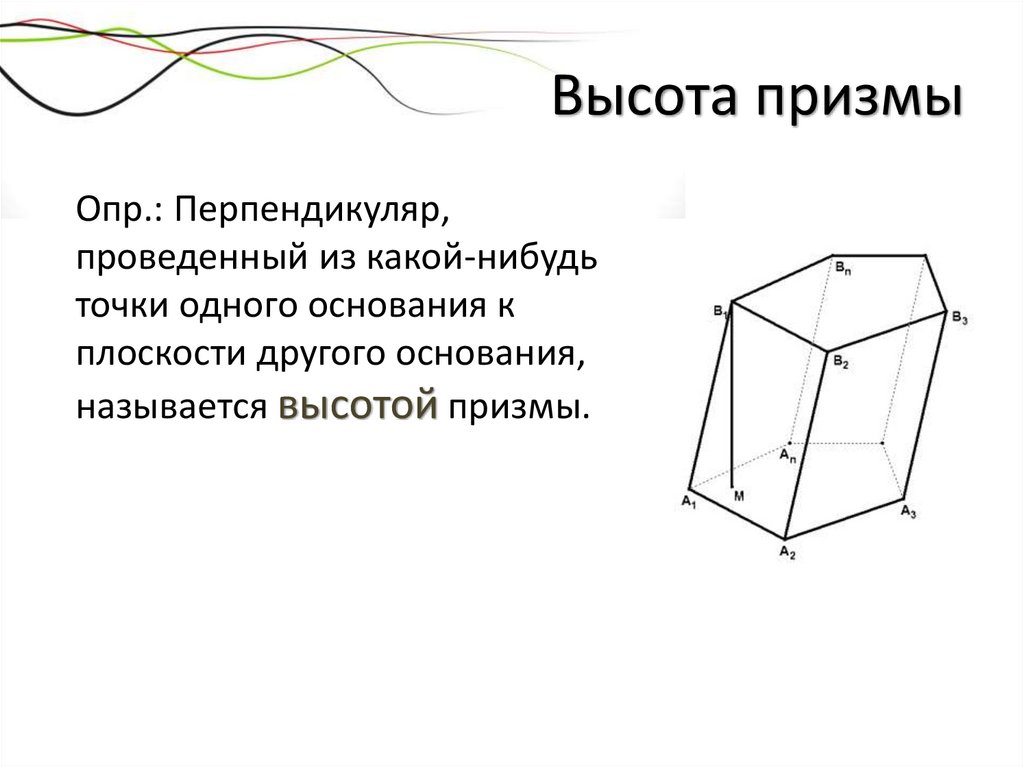
Высота призмы
Опр.: Перпендикуляр,
проведенный из какой-нибудь
точки одного основания к
плоскости другого основания,
называется высотой призмы.

30.

НАЗВАНИЕ
ОПРЕДЕЛЕНИЕ
Основания
Две
грани,
являющиеся
конгруэнтными многоугольниками,
лежащими
в
параллельных
плоскостях
Боковые грани
Все грани, кроме оснований. Каждая
боковая грань обязательно является
параллелограммом
Боковые рёбра
Общие стороны боковых граней
Высота
Перпендикуляр, проведённый из
какой-нибудь
точки
одного
основания к плоскости другого
основания
Диагональ
Отрезок, соединяющий две вершины
призмы, не принадлежащие одной
грани
ОБОЗНАЧЕНИЕ
(заполни
самостоятельно см.
рисунок)

31.

Призмы делятся на
ПРЯМЫЕ и НАКЛОННЫЕ
Призма называется прямой, если ее
боковые ребра перпендикулярны к
основаниям, в противном случае –
наклонной.

32.

Правильные призмы
Опр.: Прямая призма называется правильной,
ее основание – правильный многоугольник

33.

34.

35.

Многогранник, составленный из n –угольника и n
треугольников, называется пирамидой.
реугольная пирамида –
Четырехугольная пирамида
Шестиугольная пирамид
Тетраэдр

36.

37.

Пирамида называется
правильной, если её
основание –
правильный
многоугольник, а
отрезок, соединяющий
вершину пирамиды с
центром основания,
является её высотой

38.

Площадь поверхности

39.

Изображение многогранников на
рисунках
• Все грани куба являются квадратами. Противоположные стороны
квадратов параллельны и равны. Это свойство сохранится при
изображении.
• Изобразим ближнюю к нам грань в виде квадрата, верхнюю грань –
в виде произвольного параллелограмма (см. рис.). Мы получили
уже три ребра, исходящих из одной точки. Все остальные ребра
будут изображены параллельными и равными одному из них, т.е.
дальше все получится автоматически.

40.

Изображение многогранников на
рисунках
• Изображаем
правую
грань,
сохраняя
параллельность
соответствующих ребер.
• Остальные ребра при
рассматривании куба с
этой точки нам не
видны. Их изображают
пунктирами (см. рис.).

41.

Изображение многогранников на
рисунках
Итак, еще раз, самое главное:
• Параллельные ребра куба должны быть
параллельны и равны друг другу на
изображении;
• Все ребра куба равны, но непараллельные
ребра на рисунке могут быть неравными;
• Все углы граней куба прямые. Но на рисунке
некоторые остались прямыми, другие
изображены острыми или тупыми.

42.

Изображение многогранников на
рисунках
Зная, как нарисовать куб,
несложно
понять,
как
нарисовать прямоугольный
параллелепипед
–
достаточно
заменить
квадрат передней грани на
прямоугольник и дальше
пропорционально изменить
длины
соответствующих
ребер (см. рис.).

43.

Изображение многогранников на
рисунках
• Изобразим теперь произвольную
призму. Верхнее и нижнее
основания призмы – равные
многоугольники.
Причем
соответствующие стороны у них
параллельны.
• Изображаем
два
равных
многоугольника ровно один над
другим, если призма прямая, и
со
сдвигом,
если
призма
наклонная (см. рис.).

44.

Верхнее основание нам видно
целиком, поэтому мы изображаем
его
целиком
сплошными
линиями.
Невидимые боковые
ребра и стороны нижнего основания
изображаем
пунктиром.
Все
боковые ребра призмы параллельны
друг другу, это должно выполняться
и для рисунка (см. рис.).

45.

Перейдем теперь к пирамидам и начнем с
треугольной. В основании пирамиды лежит
треугольник. В треугольнике нет параллельных
сторон, поэтому основание можно изобразить
любым треугольником. В качестве вершины можно
выбрать любую точку сверху и соединить её с
вершинами треугольника в основании. Невидимое
ребро делаем пунктирным. Чаще всего основание
пирамиды располагают к нам вершиной, но иногда и
наоборот (см. рис. ). Главное не повернуть пирамиду
таким образом, чтобы два ребра оказались очень
близко или вообще совпали.

46.

В
четырехугольной
пирамиде
нужно
учитывать, что если в основании есть
параллельные стороны, то на рисунке они
должны остаться параллельными. Так, если в
основании квадрат, то мы изображаем
параллелограмм. При этом, глядя на уже
готовый рисунок, нам не удастся понять, что
на самом деле лежит в основании – квадрат,
прямоугольник, ромб или произвольный
параллелограмм (см. рис.). Поэтому в
описании
фигуры
нужно
делать
соответствующее пояснение.

47.

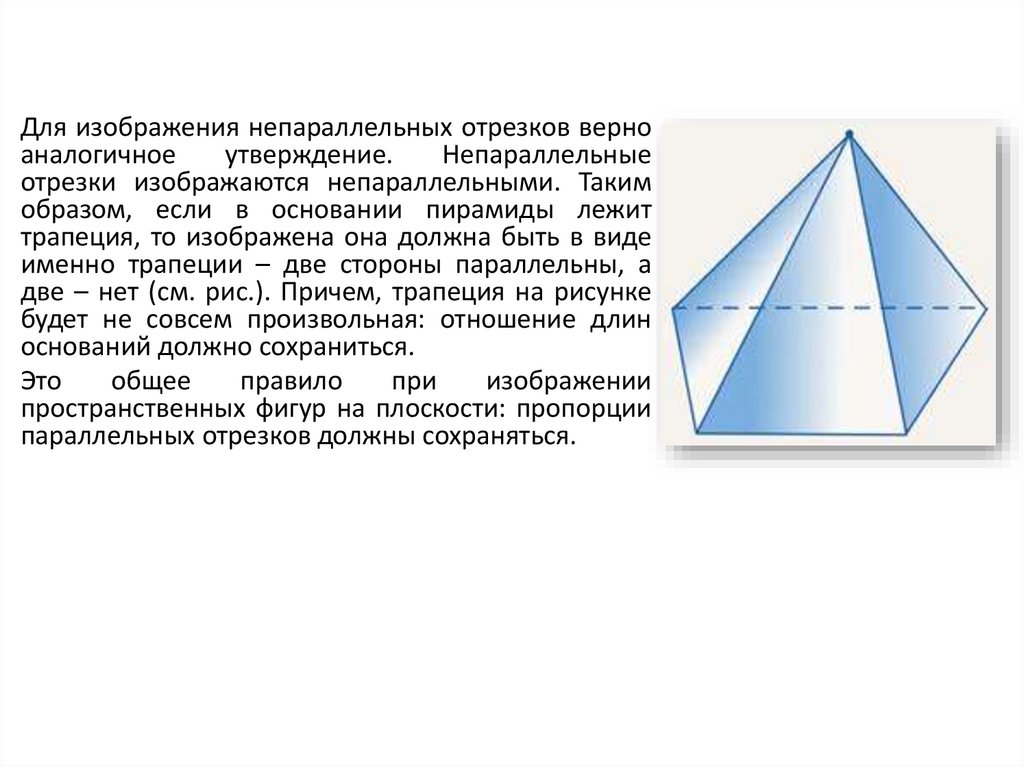
Для изображения непараллельных отрезков верно
аналогичное
утверждение.
Непараллельные
отрезки изображаются непараллельными. Таким
образом, если в основании пирамиды лежит
трапеция, то изображена она должна быть в виде
именно трапеции – две стороны параллельны, а
две – нет (см. рис.). Причем, трапеция на рисунке
будет не совсем произвольная: отношение длин
оснований должно сохраниться.
Это
общее
правило
при
изображении
пространственных фигур на плоскости: пропорции
параллельных отрезков должны сохраняться.

48.

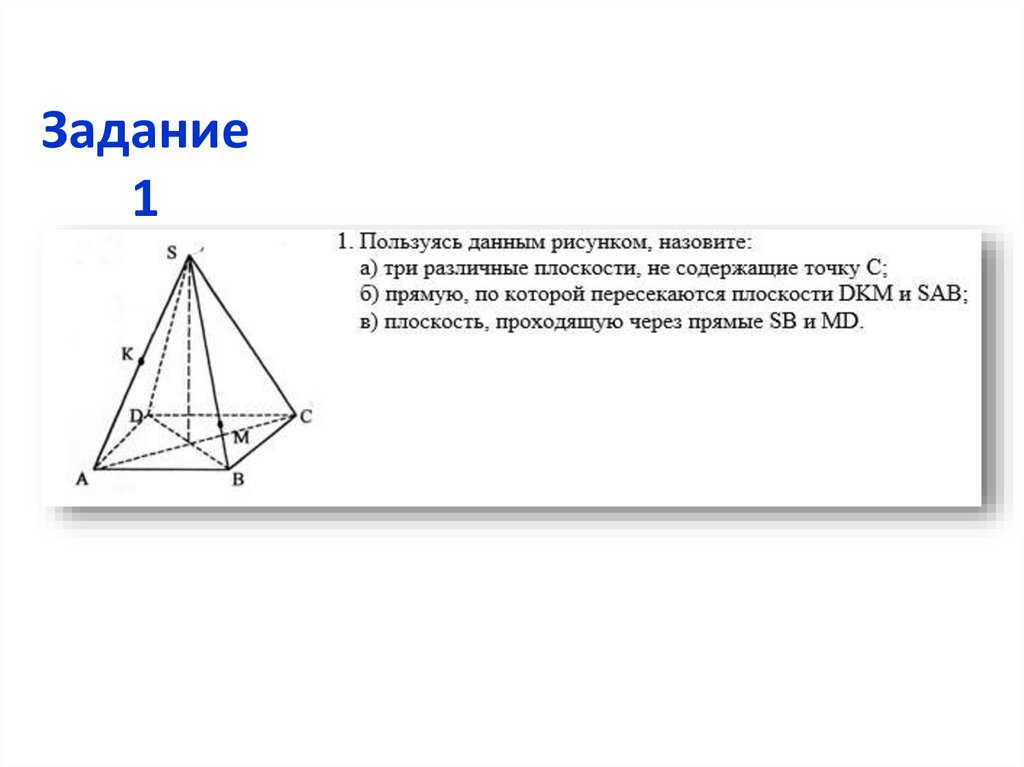
Задание
1

49.

Задание 2

50.

Задание
3
Пользуясь изображением, запишите:
1) точки, которые принадлежат плоскости грани АВС;
2) точки которые не лежат в плоскости грани АВС;
3) общие точки плоскостей граней АВС и АВS;
4) прямую пересечения плоскостей граней АВС и SВС;
5) плоскость, которая проходит через прямые АВ и
ВС;
6) плоскость, которая не содержит прямых АВ и ВС.

51.

Домашнее задание