Похожие презентации:
Задание свойств материала. Начинаем с модуля Engineering Data. Лопатка компрессора
1.
ПрактикаЛопатка компрессора
2.
Исходные данные• Частота вращения 10200 об/мин
• Температура на входе 200оС
• Температура на выходе 250оС
• Материал лопатки: титановый сплав (ВТ6,
ВТ8)
• Распределение давлений представлено
далее
3.
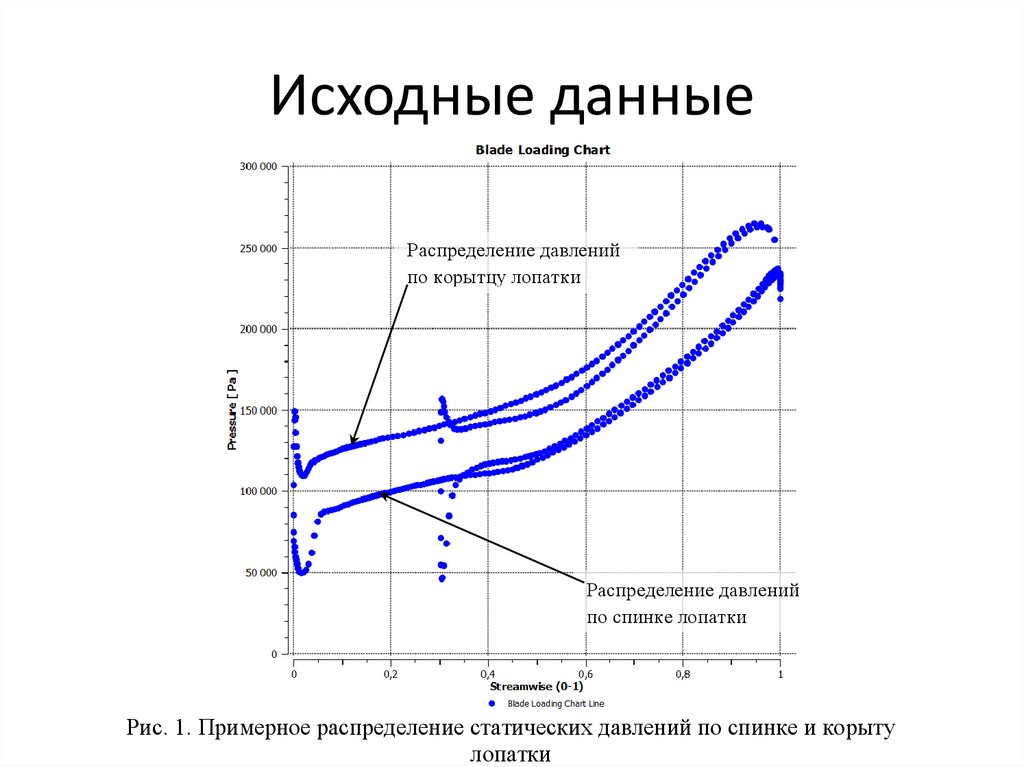
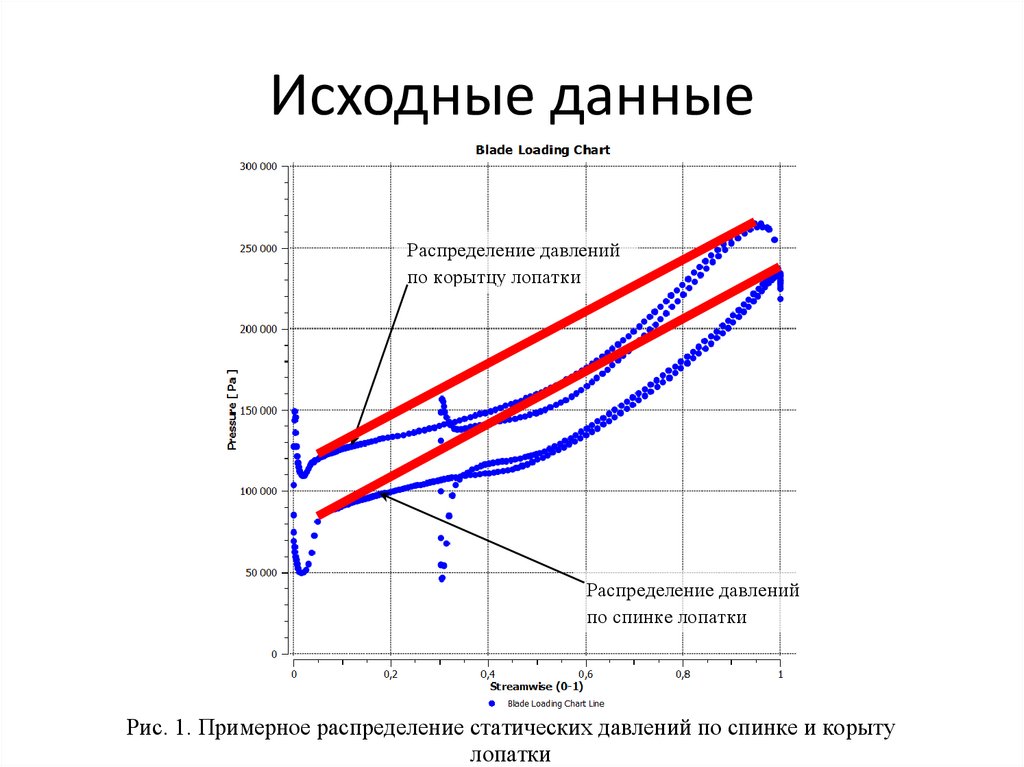
Исходные данныеРаспределение давлений
по корытцу лопатки
Распределение давлений
по спинке лопатки
Рис. 1. Примерное распределение статических давлений по спинке и корыту
лопатки
4.
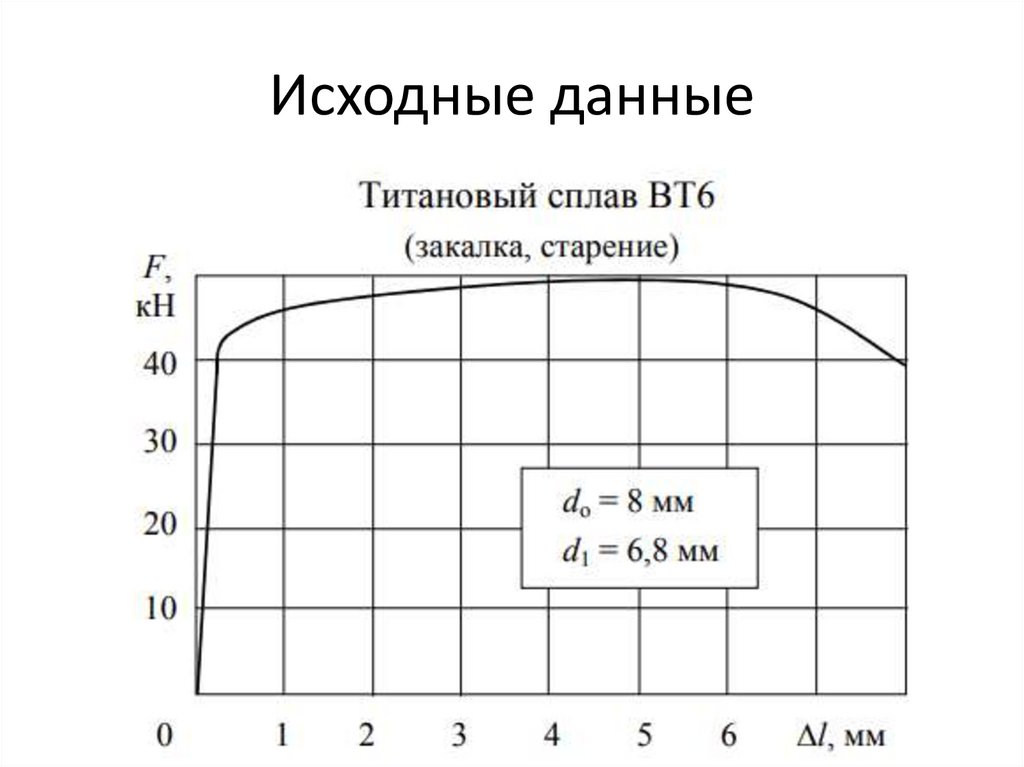
Исходные данные5.
Обработка диаграммы деформированияl0,2 l0 0,002 40 0,002 0,08 мм 1,06 ммг
6
0,0753
79,67
40000
Н
kF
795, 4
50, 29
мм
F0,2 53,59 795, 4 42625 Н
kl
0,2
F0,2
A0
42625
849 МПа
50, 2
d 02 3,14 82
A0
50, 2 мм 2
4
4
F l0
40000 40
E
138,8 ГПа
A0 l 50, 2 3,05 0,0753
6.
Зависимость свойств материала от температуры7.
Зависимость свойств материала от температурыдо обработки
оС
T
кгс/мм2
E
mu
20
12500
300 10548,48
350
10200
400
10100
*10^6
кгс/мм2 кгс/мм2 кгс/мм2 1/оС
G
sigma02 sigmav
alpha
0,32 4734,848
105
115
8,4
0,32 3995,638
75
87
9,8
0,32 3863,636
72
86
9,95
0,32 3825,758
60
82
10,1
после обработки
оС
T
ГПа
E
20
300
350
400
ro
ГПа
G
mu
122,6
103,5
100,1
99,1
4430 кг/м3
0,32
0,32
0,32
0,32
*10^6
МПа
МПа
1/оС
sigma02 sigmav
alpha
46,4
1030
1128
8,4
39,2
736
853
9,8
37,9
706
844
9,95
37,5
589
804
10,1
8.
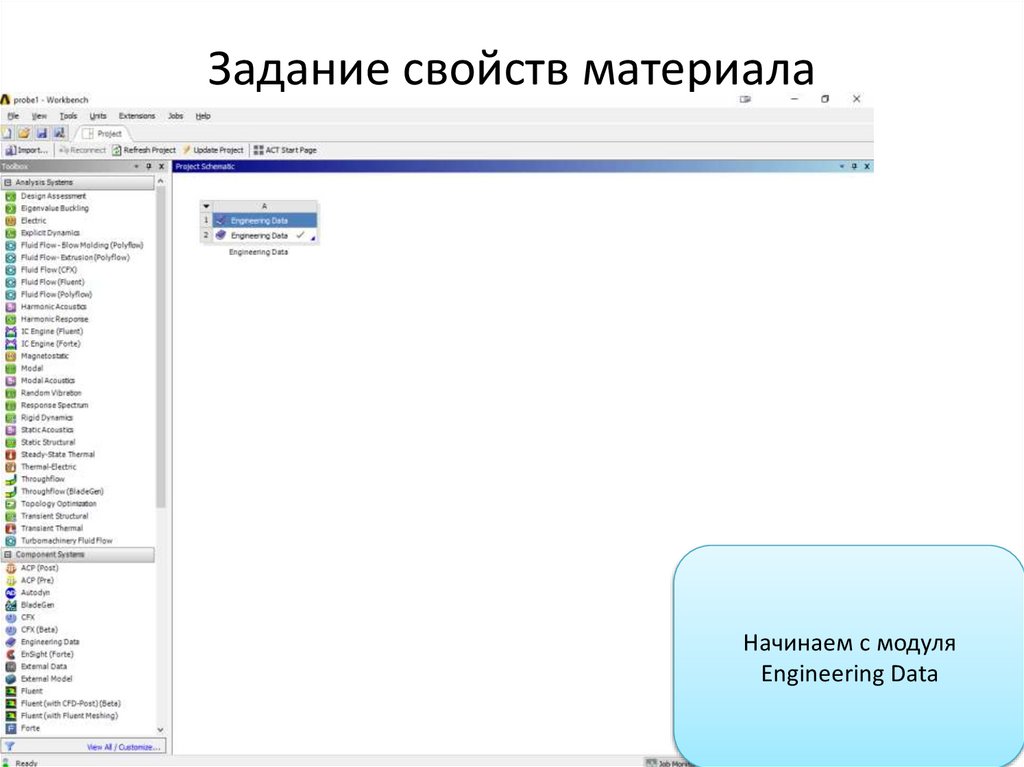
Задание свойств материалаНачинаем с модуля
Engineering Data
9.
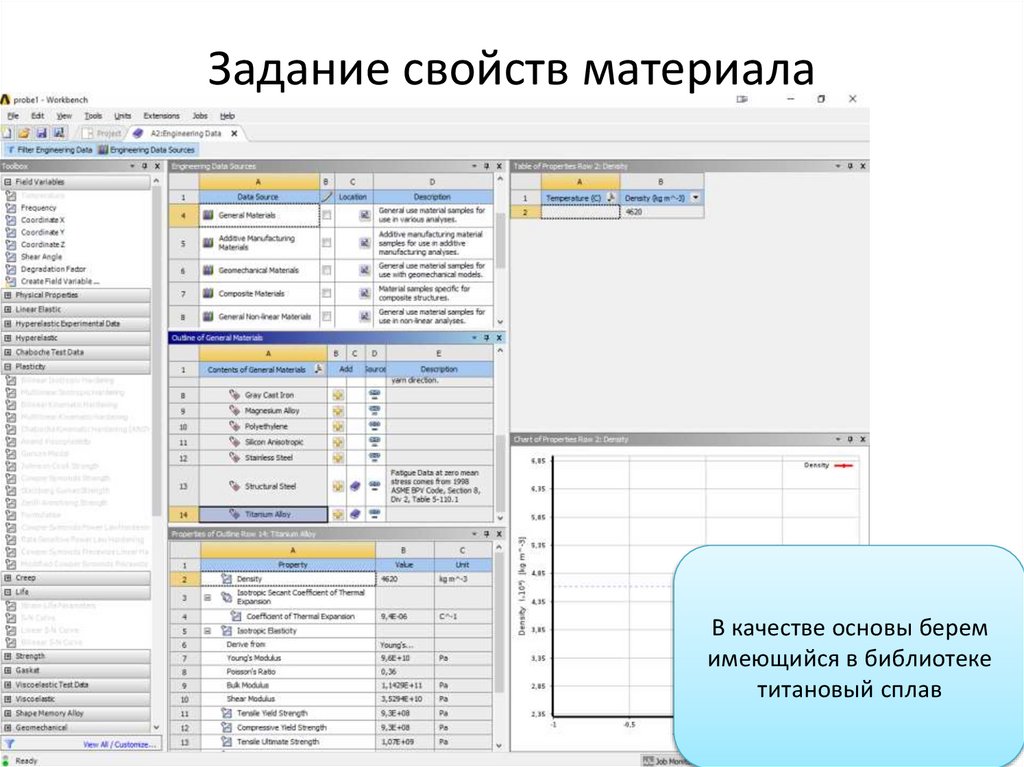
Задание свойств материалаВ качестве основы берем
имеющийся в библиотеке
титановый сплав
10.
Задание свойств материалаСоздаем копию
добавленного материала с
помощью опции Duplicate
11.
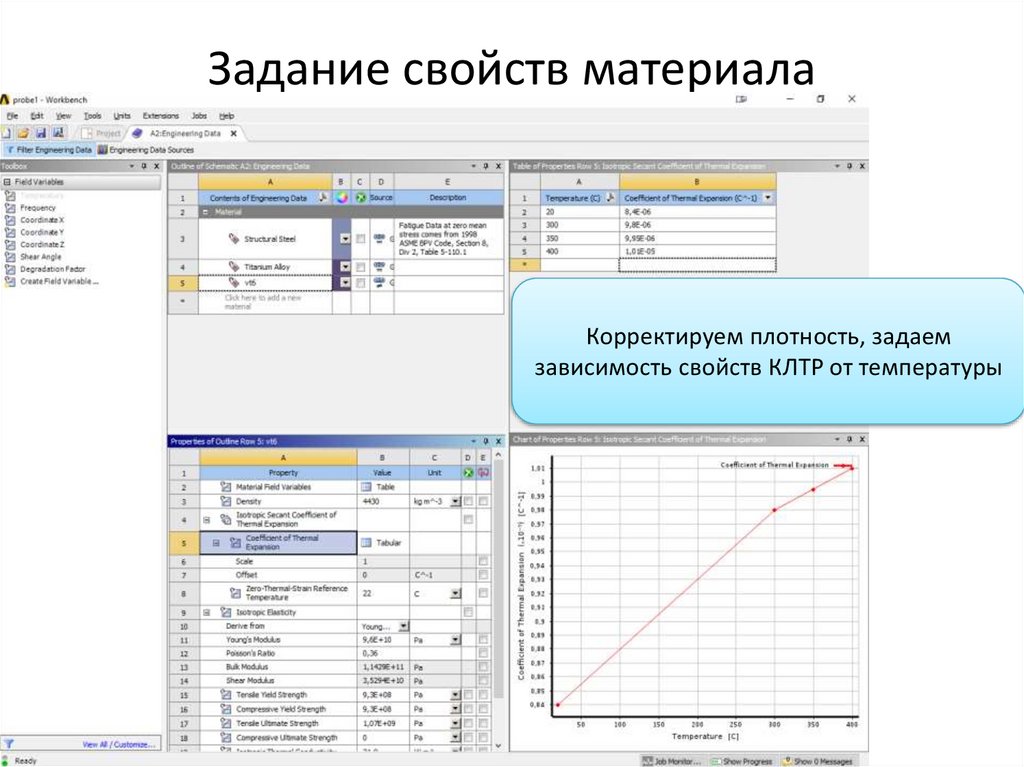
Задание свойств материалаКорректируем плотность, задаем
зависимость свойств КЛТР от температуры
12.
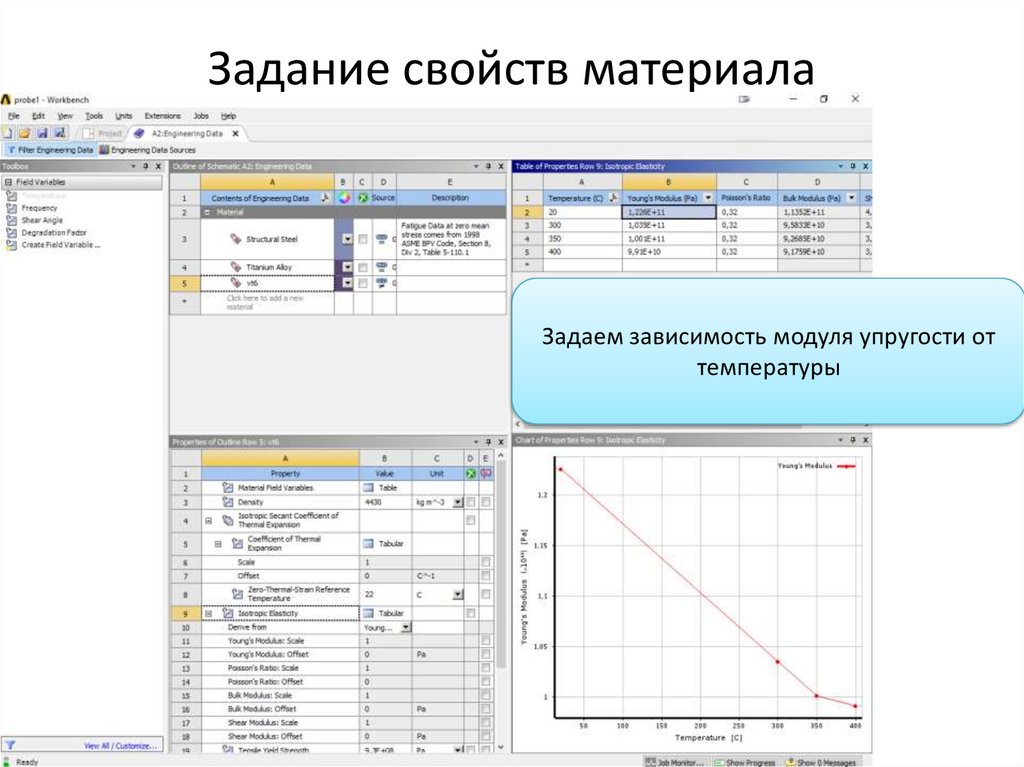
Задание свойств материалаЗадаем зависимость модуля упругости от
температуры
13.
Работа с модельюИмпортируем геометрию
14.
Работа с модельюПодавляем ненужную в данной задаче
геометрию диска, оставляем лишь лопатку
15.
Работа с модельюПереходим к созданию сетки
16.
Работа с модельюПолучена нормальная сетка со
следующими параметрами:
method – hex dominant
resolution = 7
17.
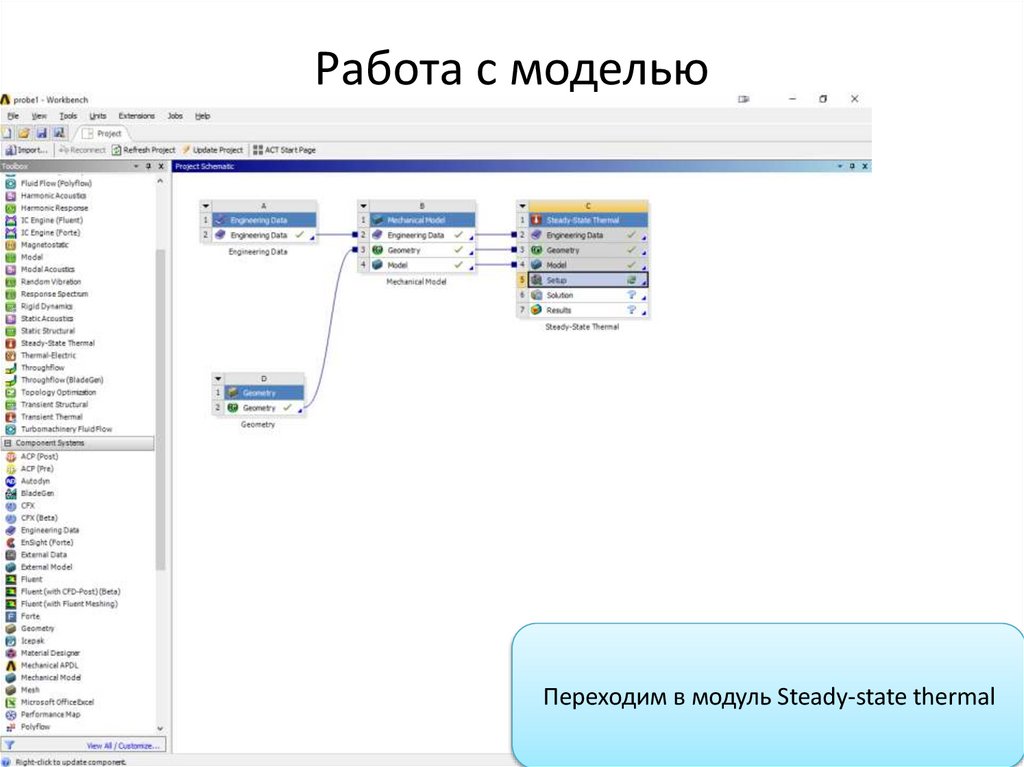
Работа с модельюПереходим в модуль Steady-state thermal
18.
Работа с модельюНазначаем нужный материал
19.
Работа с модельюУказываем температуры на входе и выходе
из рабочего колеса
20.
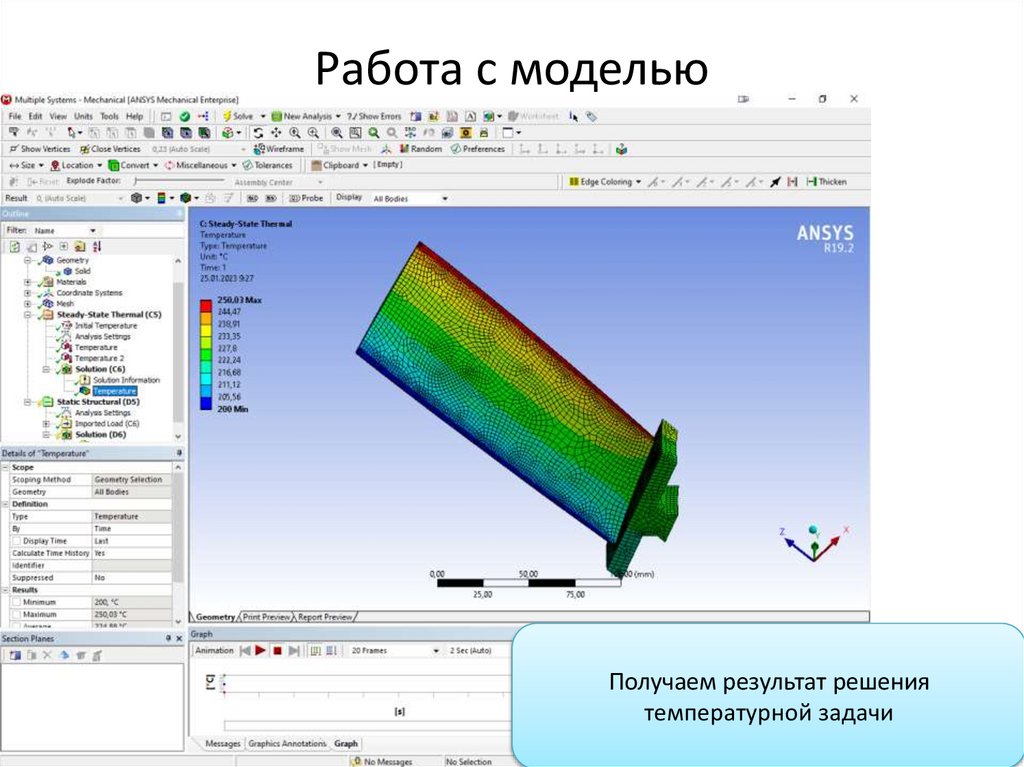
Работа с модельюПолучаем результат решения
температурной задачи
21.
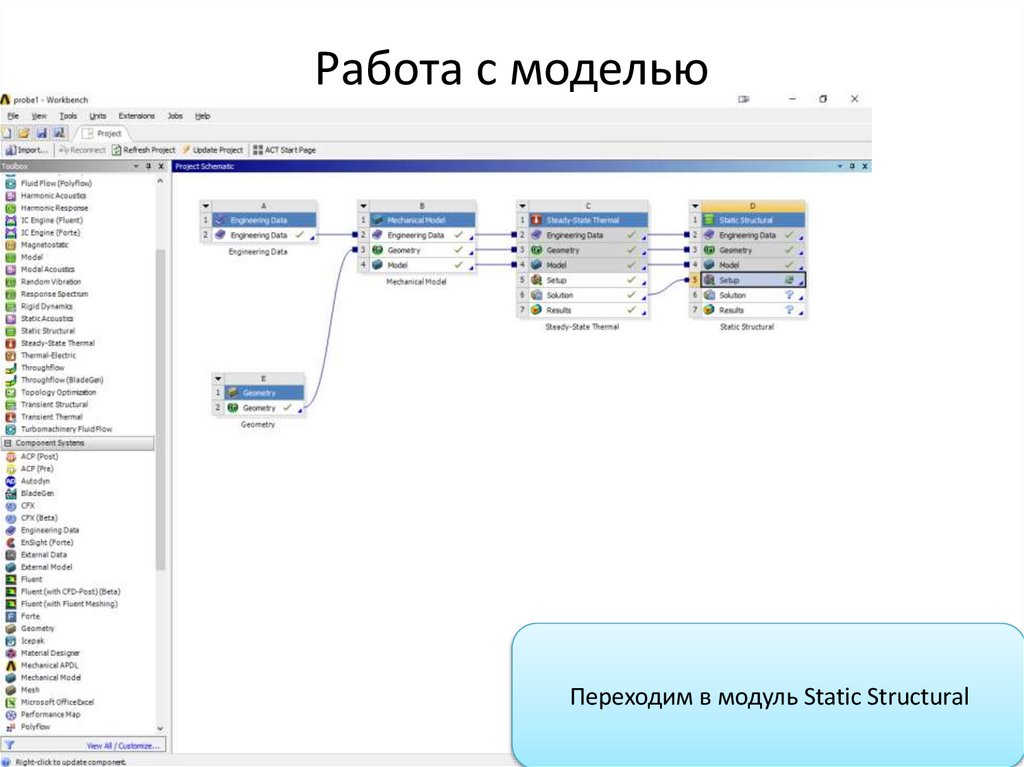
Работа с модельюПереходим в модуль Static Structural
22.
Линейно-упругая постановказадачи
23.
Работа с модельюЗадаем следующие граничные условия:
Угловая скорость 10200 об/мин
Жесткое закрепление по контактным поверхностям хвостовика
Линейное распределение давлений по поверхностям корытца и спинки
лопатки
24.
Работа с модельюПри прикладывании давлений на основе анализа имеющегося графика
давлений делаем следующие допущения:
Давления распределены линейно
Давления задаем в виде функции p=x*a-b+c
25.
Работа с модельюРекомендации по определению коэффициентов a,b и с:
1. Сначала задать функцию давления как p=x*1, записать минимальное и
максимальное давление по полученному распределению pmin_1 и pmax_1
соответственно;
2. по исходному графику распределения давлений определить, какие значения
давления требуются: pmin_need и pmax_need
3. Рассчитать коэффициент a:
p
a
p
max, need
max,1
pmin,need
pmin,1
4. Теперь задать функцию давления в виде p=x*a, записать минимальное давление
по полученному распределению pmin_а, это и будет коэффициент b:
b pmin,a
5. Коэффициент с равен минимальному требуемому давлению pmin_need:
c pmin,need
26.
Исходные данныеРаспределение давлений
по корытцу лопатки
Распределение давлений
по спинке лопатки
Рис. 1. Примерное распределение статических давлений по спинке и корыту
лопатки
27.
Анализ результатовПолученное решение по деформациям
28.
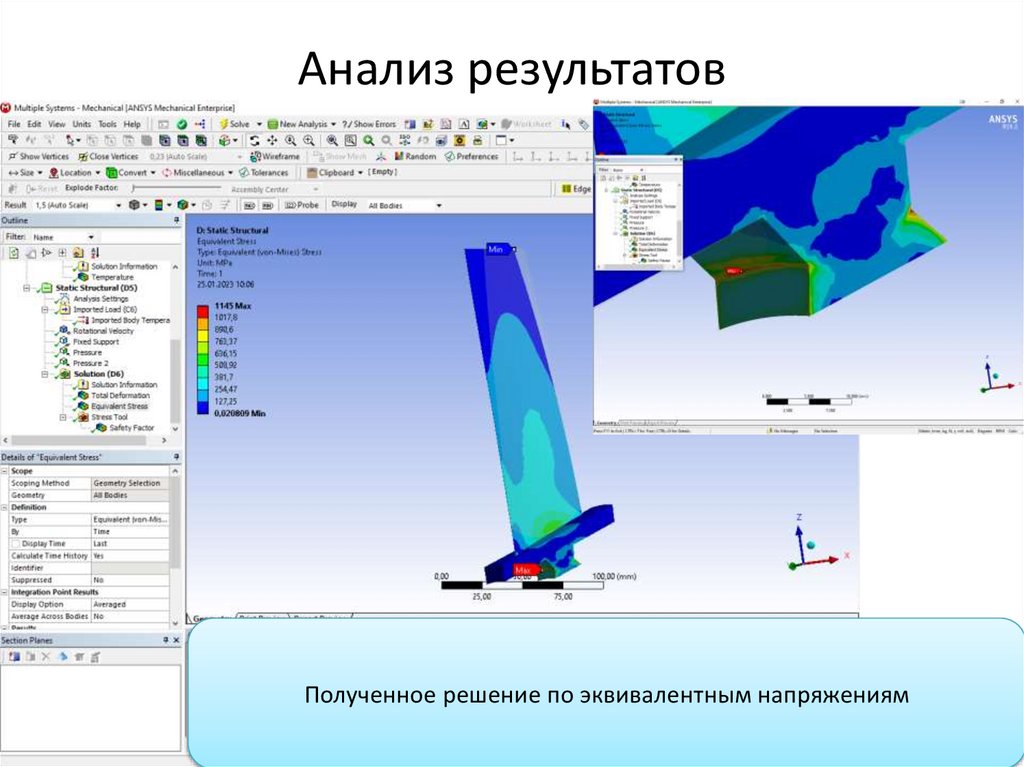
Анализ результатовПолученное решение по эквивалентным напряжениям
29.
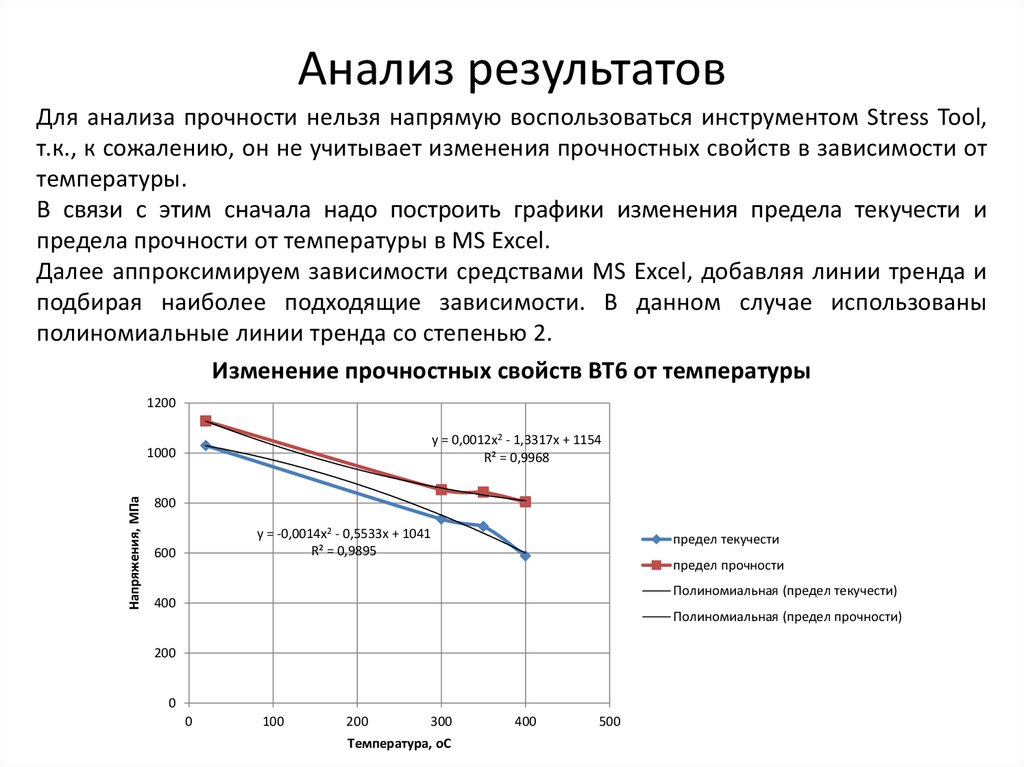
Анализ результатовДля анализа прочности нельзя напрямую воспользоваться инструментом Stress Tool,
т.к., к сожалению, он не учитывает изменения прочностных свойств в зависимости от
температуры.
В связи с этим сначала надо построить графики изменения предела текучести и
предела прочности от температуры в MS Excel.
Далее аппроксимируем зависимости средствами MS Excel, добавляя линии тренда и
подбирая наиболее подходящие зависимости. В данном случае использованы
полиномиальные линии тренда со степенью 2.
Изменение прочностных свойств ВТ6 от температуры
1200
y = 0,0012x2 - 1,3317x + 1154
R² = 0,9968
Напряжения, МПа
1000
800
y = -0,0014x2 - 0,5533x + 1041
R² = 0,9895
600
предел текучести
предел прочности
Полиномиальная (предел текучести)
400
Полиномиальная (предел прочности)
200
0
0
100
200
300
Температура, оС
400
500
30.
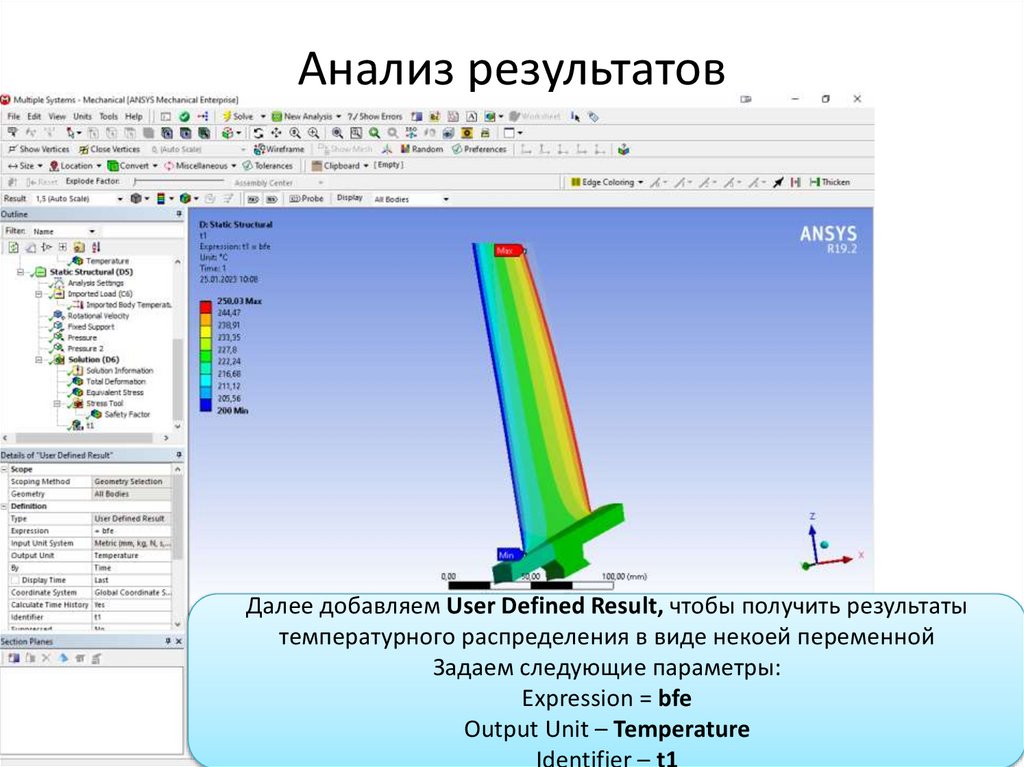
Анализ результатовДалее добавляем User Defined Result, чтобы получить результаты
температурного распределения в виде некоей переменной
Задаем следующие параметры:
Expression = bfe
Output Unit – Temperature
Identifier – t1
31.
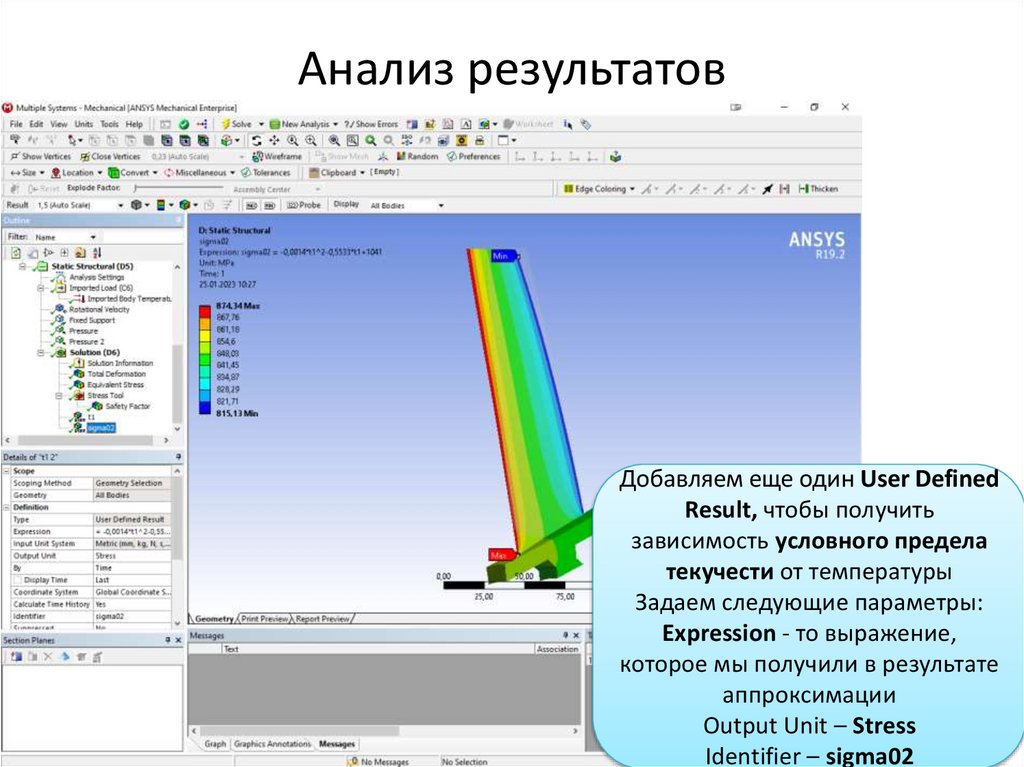
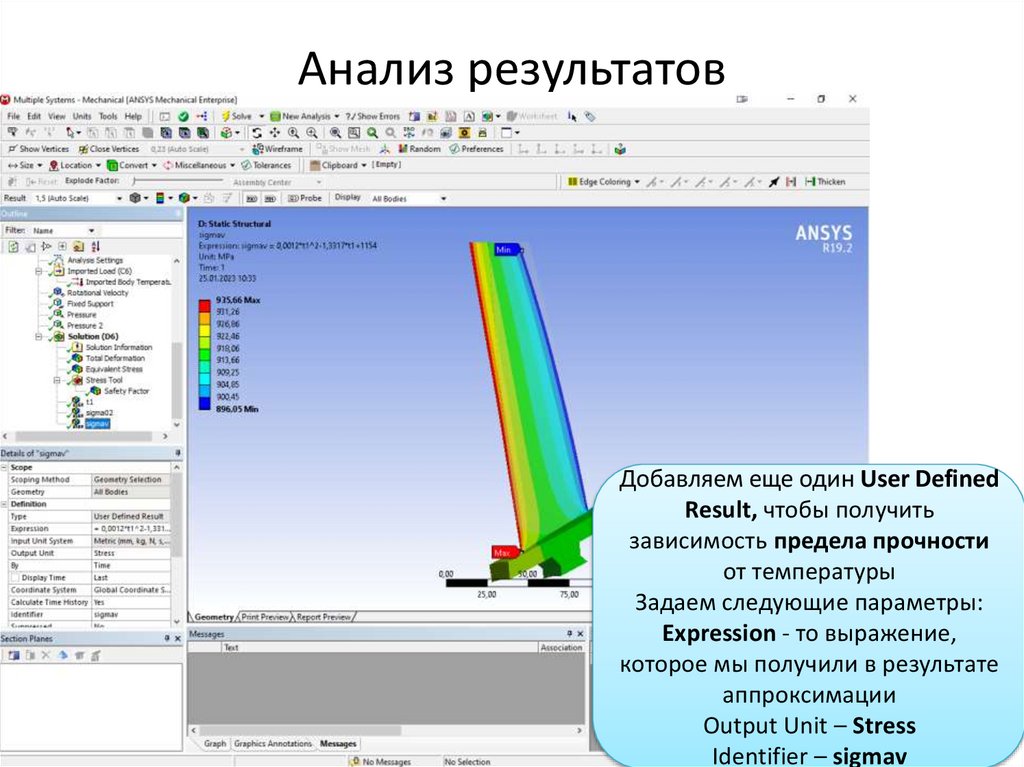
Анализ результатовДобавляем еще один User Defined
Result, чтобы получить
зависимость условного предела
текучести от температуры
Задаем следующие параметры:
Expression - то выражение,
которое мы получили в результате
аппроксимации
Output Unit – Stress
Identifier – sigma02
32.
Анализ результатовДобавляем еще один User Defined
Result, чтобы получить
зависимость предела прочности
от температуры
Задаем следующие параметры:
Expression - то выражение,
которое мы получили в результате
аппроксимации
Output Unit – Stress
Identifier – sigmav
33.
Анализ результатовЧтобы получить коэффициент
запаса прочности по
условному пределу
текучести, необходимо ввести
следующее выражение:
Expression = sigma02/seqv
Output Unit – Stress
Анализируем полученные
результаты
34.
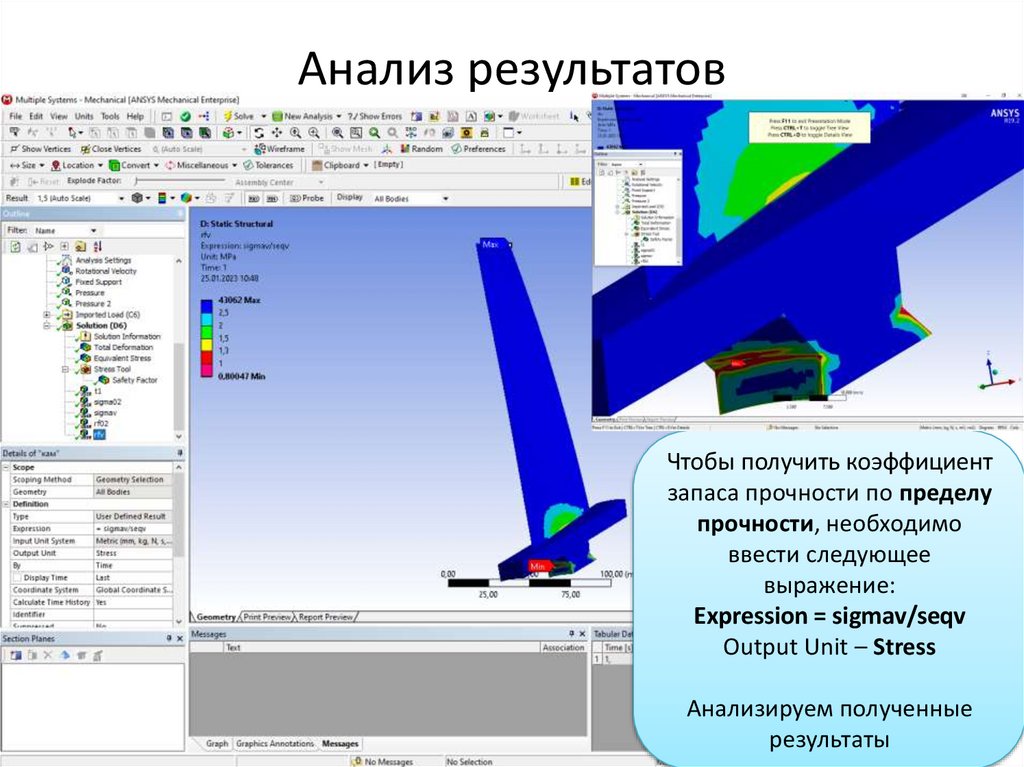
Анализ результатовЧтобы получить коэффициент
запаса прочности по пределу
прочности, необходимо
ввести следующее
выражение:
Expression = sigmav/seqv
Output Unit – Stress
Анализируем полученные
результаты
35.
Упруго-пластическая (билинейная)постановка задачи
36.
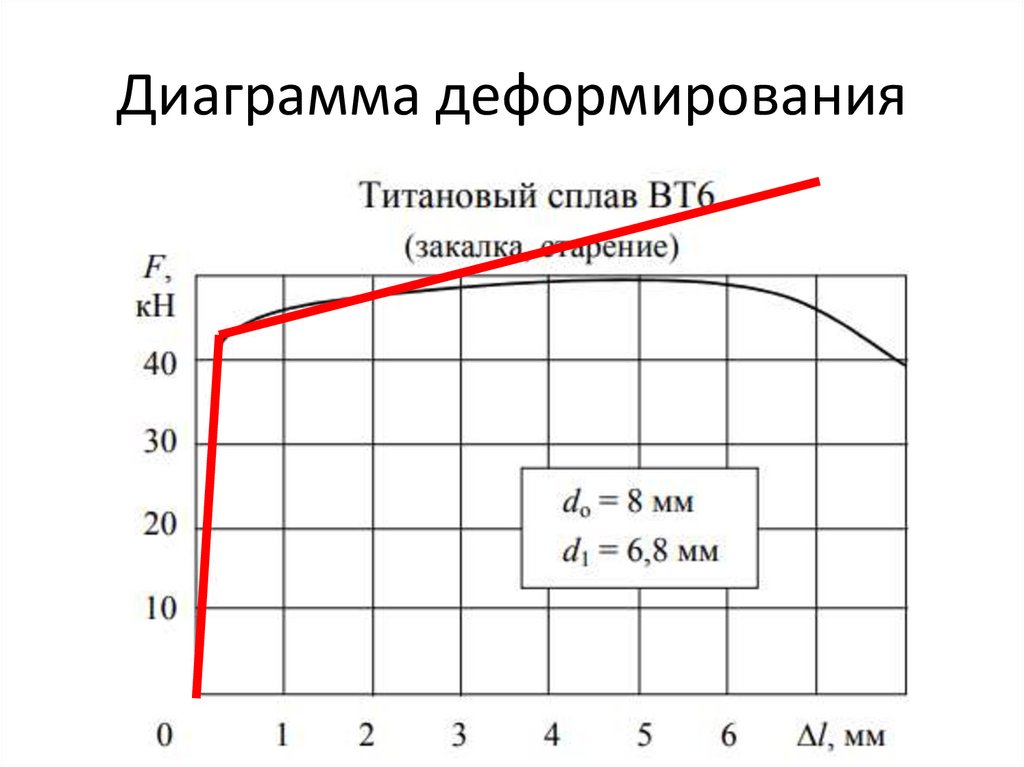
Диаграмма деформирования37.
Диаграмма деформированияДиаграмма деформирования ВТ6
60
40
30
20
10
0
0
2
4
6
8
10
деформация, мм
Диаграмма деформирования ВТ6
1200
1000
Напряжение, МПа
Усилие, кН
50
800
600
400
200
0
0
0,05
0,1
0,15
относительная деформация
0,2
0,25
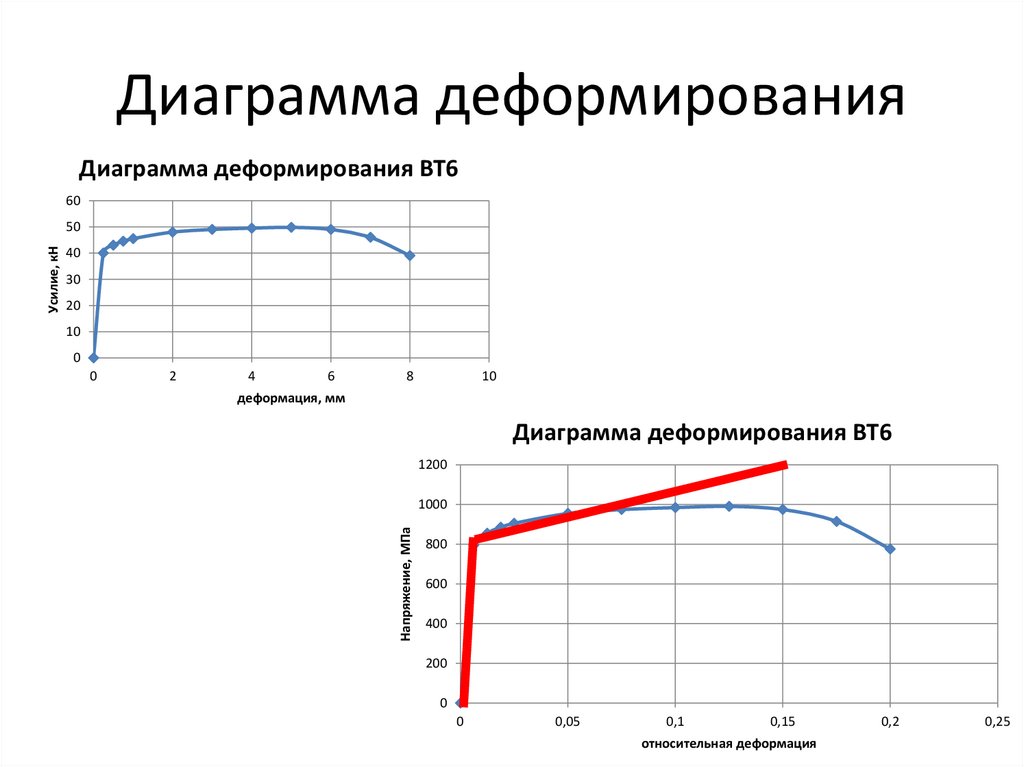
38.
Диаграмма деформированияДиаграмма деформирования ВТ6
60
40
30
20
10
0
0
2
4
6
8
10
деформация, мм
Диаграмма деформирования ВТ6
1200
1000
Напряжение, МПа
Усилие, кН
50
800
600
400
200
0
0
0,05
0,1
0,15
относительная деформация
0,2
0,25
39.
Создание модели материала40.
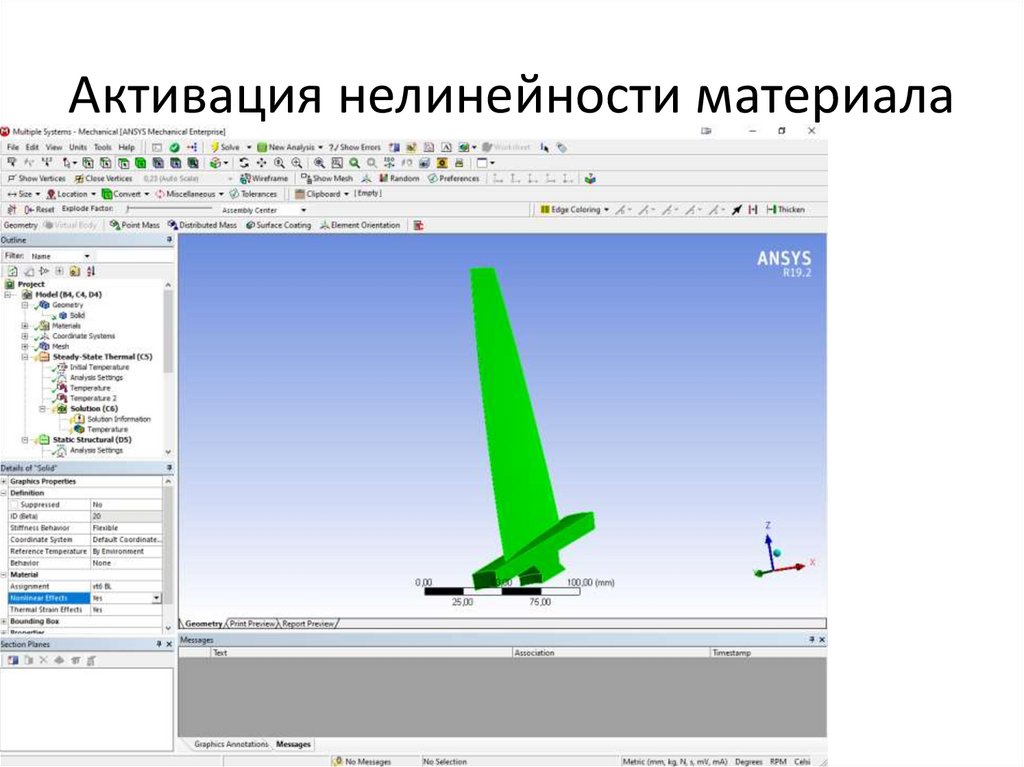
Активация нелинейности материала41.
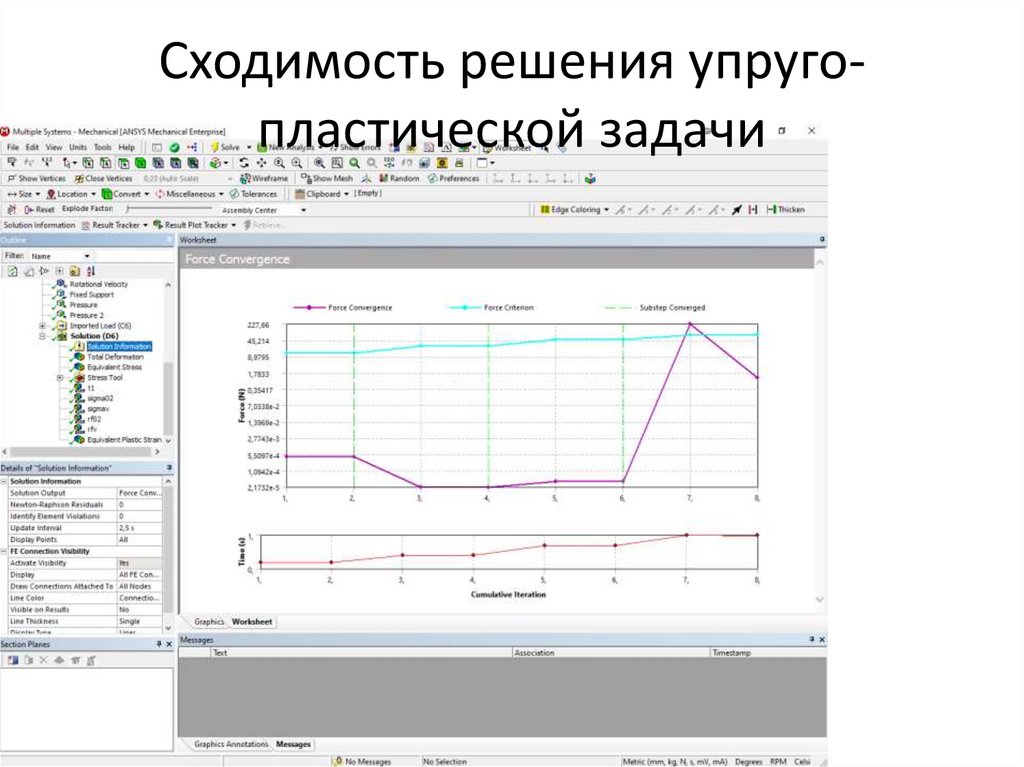
Сходимость решения упругопластической задачи42.
Анализ результатовКартина распределения
пластических деформаций
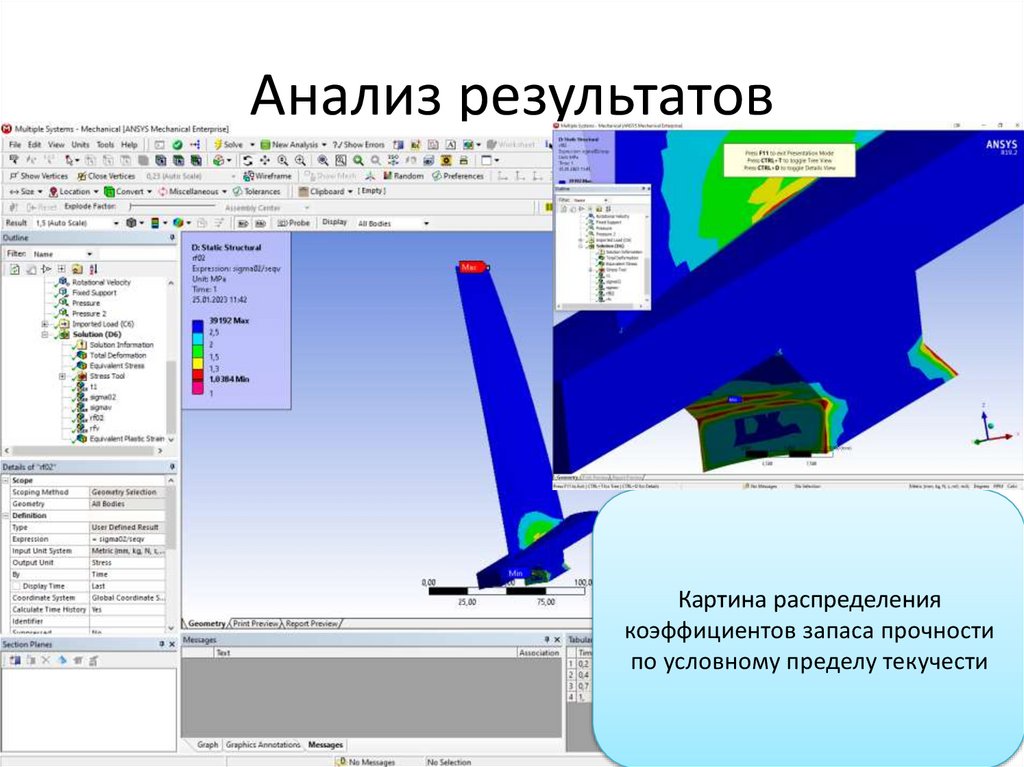
43.
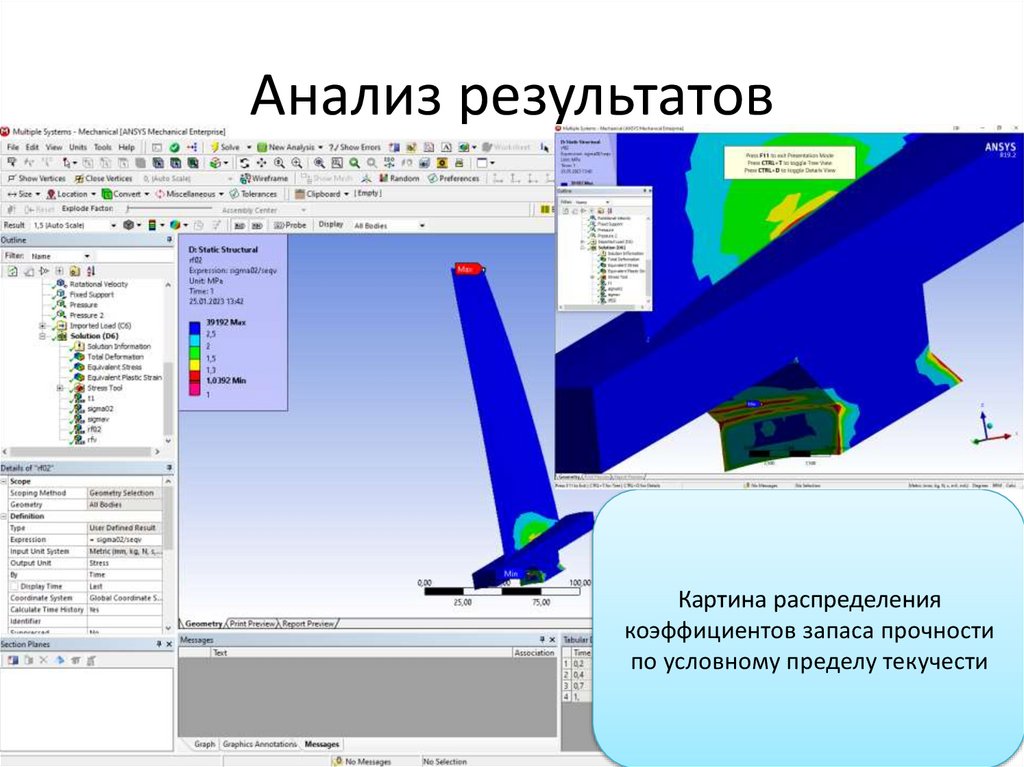
Анализ результатовКартина распределения
коэффициентов запаса прочности
по условному пределу текучести
44.
Упруго-пластическая(мультилинейная) постановка
задачи
45.
Создание модели материала46.
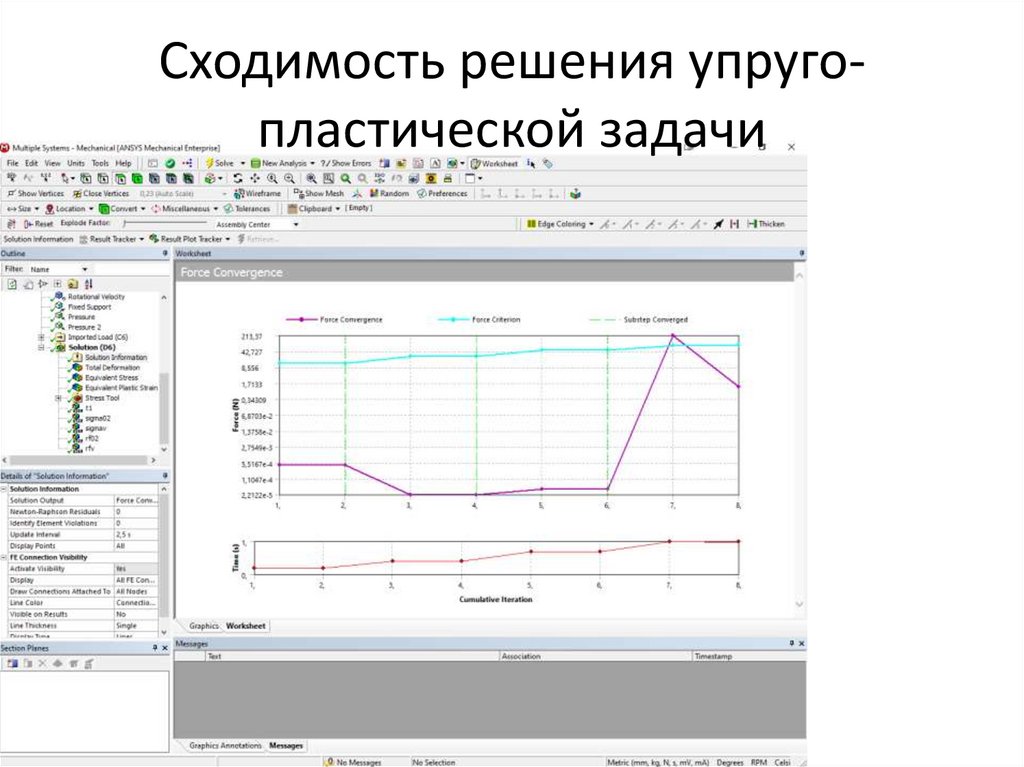
Сходимость решения упругопластической задачи47.
Анализ результатовКартина распределения
пластических деформаций
48.
Анализ результатовКартина распределения
коэффициентов запаса прочности
по условному пределу текучести
49.
Задание для самостоятельнойработы
Провести конструкторскую проработку лопатки компрессора средствами ANSYS
Design Modeler или ANSYS SpaceClaim с целью повышения прочности лопатки

























 Программное обеспечение
Программное обеспечение