Похожие презентации:
Параллельные прямые в пространстве
1.
12.
ОпределениеДве прямые в пространстве называются
параллельными, если
1) они лежат в одной плоскости и
2) не пересекаются
b
a
Показать (1)
2
3.
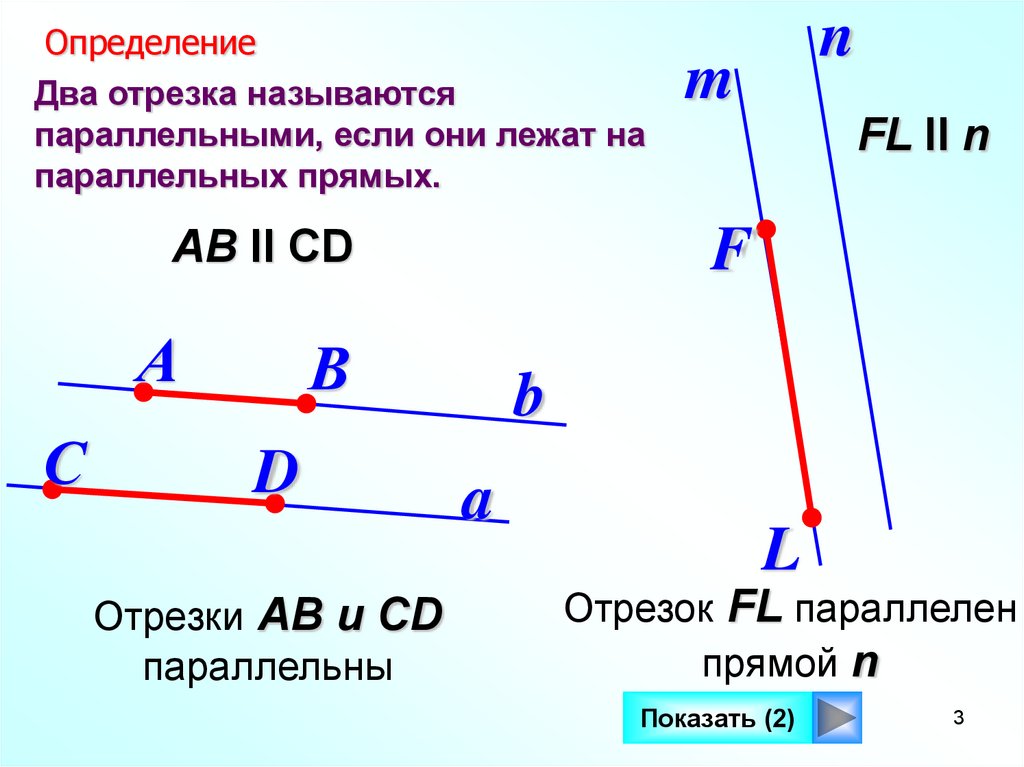
ОпределениеДва отрезка называются
параллельными, если они лежат на
параллельных прямых.
АВ II СD
А
С
Отрезки АВ и СD
параллельны
m
FL II n
F
В
D
n
b
a
L
Отрезок FL параллелен
прямой n
Показать (2)
3
4.
№ 17.Точки М, N, P и Q – середины отрезков BD, CD, AB и АС.
РMNQP - ?
D
M
N
В
А
P
Q
С
4
5.
ТеоремаЧерез любую точку пространства, не лежащую на
данной прямой, проходит прямая, параллельная
данной, и притом только одна.
Прямая и не лежащая
на ней точка определяют плоскость
М
b
a
Показать (2)
5
6.
ЛеммаЕсли одна из двух параллельных прямых
пересекает данную плоскость, то и другая
прямая пересекает данную плоскость.
a
b
М
?
Показать (2)
6
7.
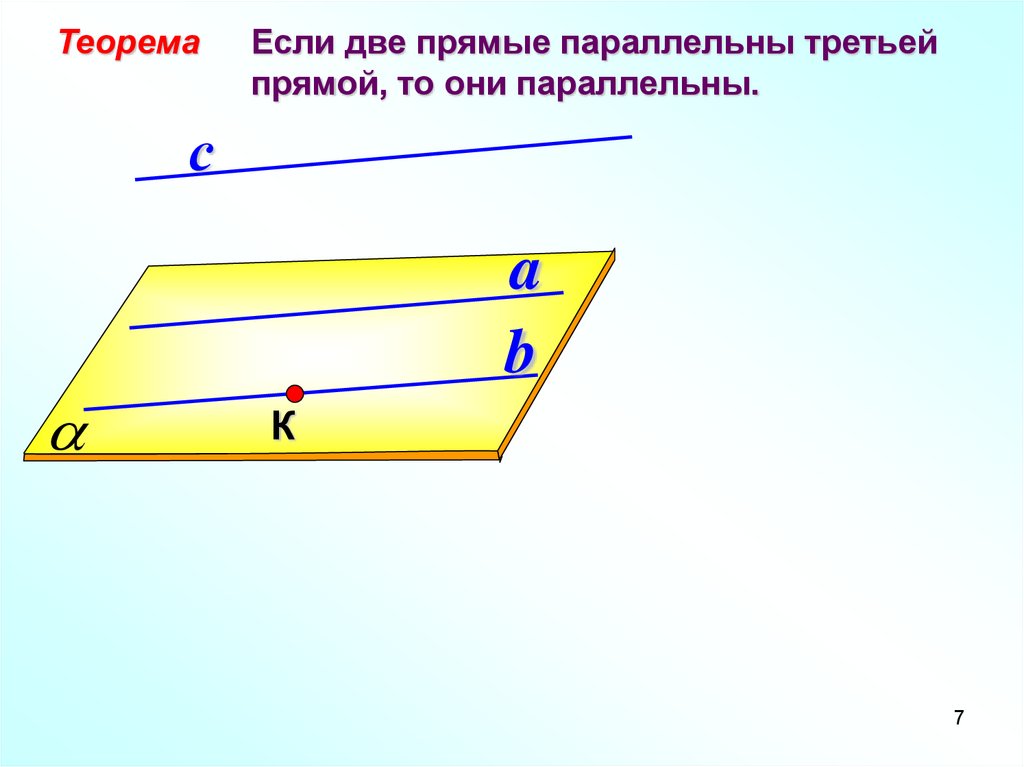
ТеоремаЕсли две прямые параллельны третьей
прямой, то они параллельны.
с
a
b
К
7
8.
Треугольник АВС и квадрат АEFC не лежат в однойплоскости. Точки К и М – середины отрезков АВ и ВС
соответственно.
Докажите, что КМ II EF.
Найдите КМ, если АЕ=8см.
В
M
K
С
А
8см
F
Е
8
9.
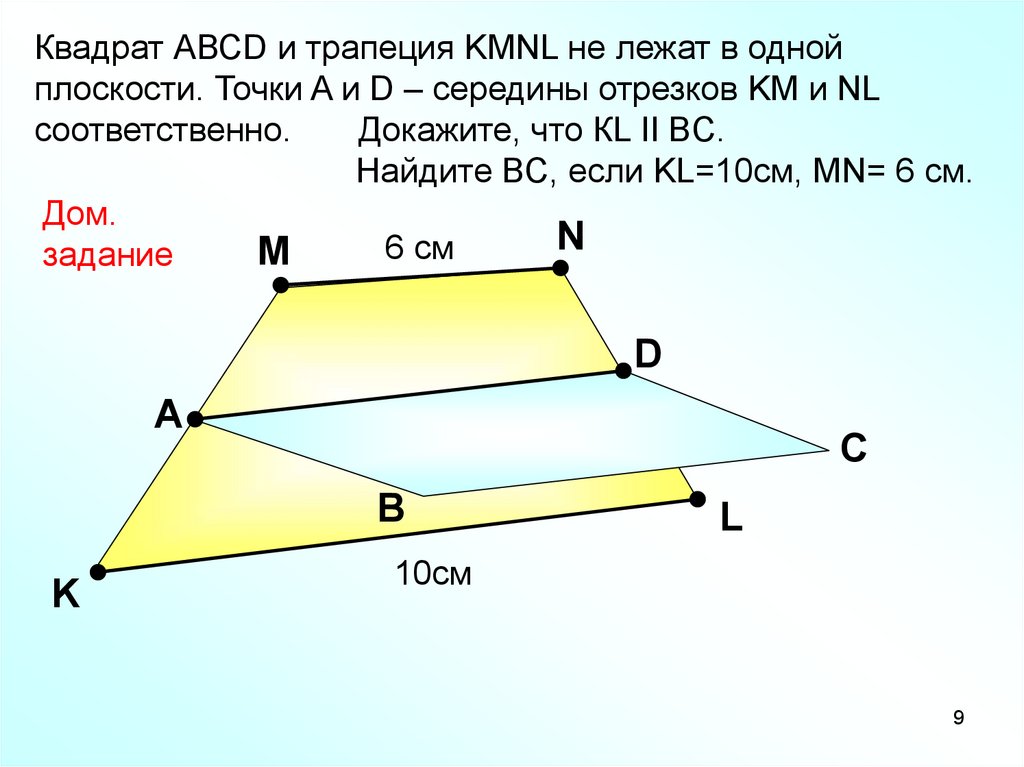
Квадрат АВСD и трапеция KMNL не лежат в однойплоскости. Точки A и D – середины отрезков KM и NL
соответственно.
Докажите, что КL II BC.
Найдите BC, если KL=10см, MN= 6 см.
Дом.
N
6 см
M
задание
D
А
В
K
С
С
L
10см
9
10.
11.
Наглядное представление о прямой, параллельнойплоскости, дают натянутые троллейбусные или
трамвайные провода – они параллельны плоскости земли.
a II
а
12.
а13.
аb
14.
Назовите прямые, параллельные данной плоскостиС1
D1
А1
В1
D
А
С
В
15.
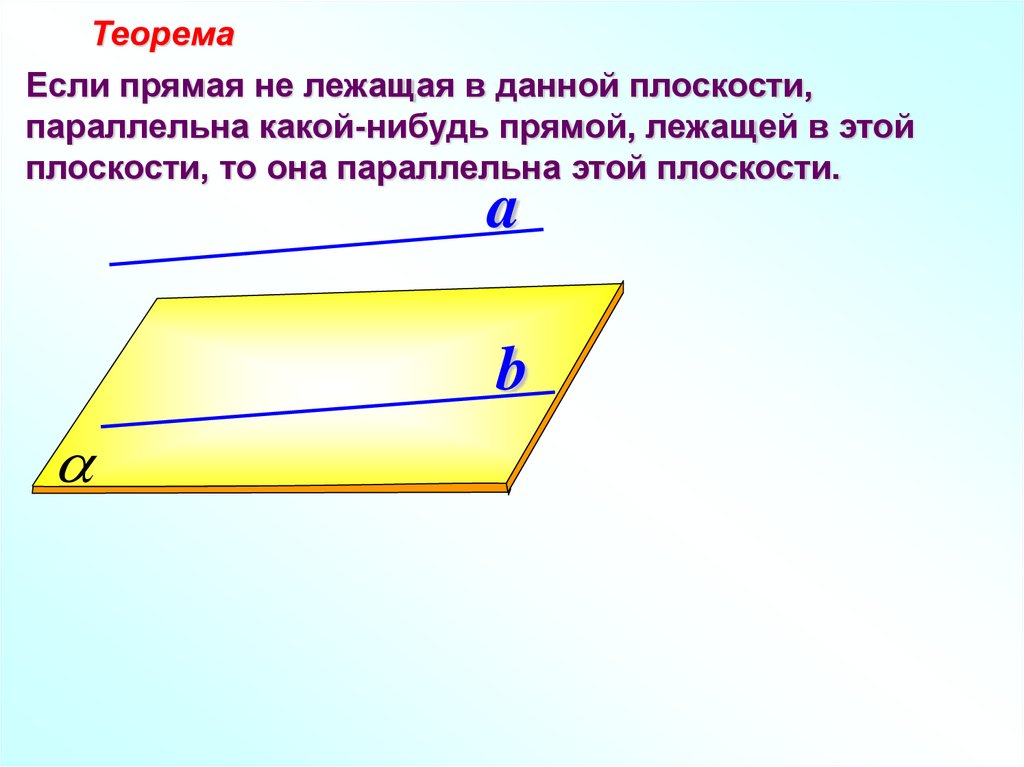
ТеоремаЕсли прямая не лежащая в данной плоскости,
параллельна какой-нибудь прямой, лежащей в этой
плоскости, то она параллельна этой плоскости.
a
b
16.
Плоскость проходит через основание АD трапецииАВСD. Точки Е и F - середины отрезков АВ и СD
соответственно. Докажите, что EF II
В
С
Е
F
A
D
17.
Плоскость проходит через сторону АС треугольника АВС.Точки D и E - середины отрезков АВ и BC соответственно.
Докажите, что DE II
В
D
E
A
С
18.
РDB – треугольник. А и N – середины сторон ВD и ВРсоответственно.
Докажите, что РD II
В
A
N
D
Р
19.
Плоскость проходит через середины боковых сторон АВ иСD трапеции АВСD – точки М и N.
B
Дом.
задание
M
С
N
A
D
Докажите, что АD II .
Найдите ВС, если АD=10 см, MN= 8 см.
20.
21.
ОпределениеДве плоскости
называются
параллельными, если
они не пересекаются.
II
22.
23.
24.
25.
Признак параллельности двух плоскостейЕсли две пересекающиеся прямые одной плоскости
параллельны двум пересекающимся прямым другой
плоскости, то эти плоскости параллельны.
а1
b1
а
M
b
Признак 1
26.
Признак параллельности двух плоскостейЕсли две пересекающиеся прямые m и n плоскости
параллельны плоскости , то плоскости
и параллельны.
m
M
n
Признак 2
27.
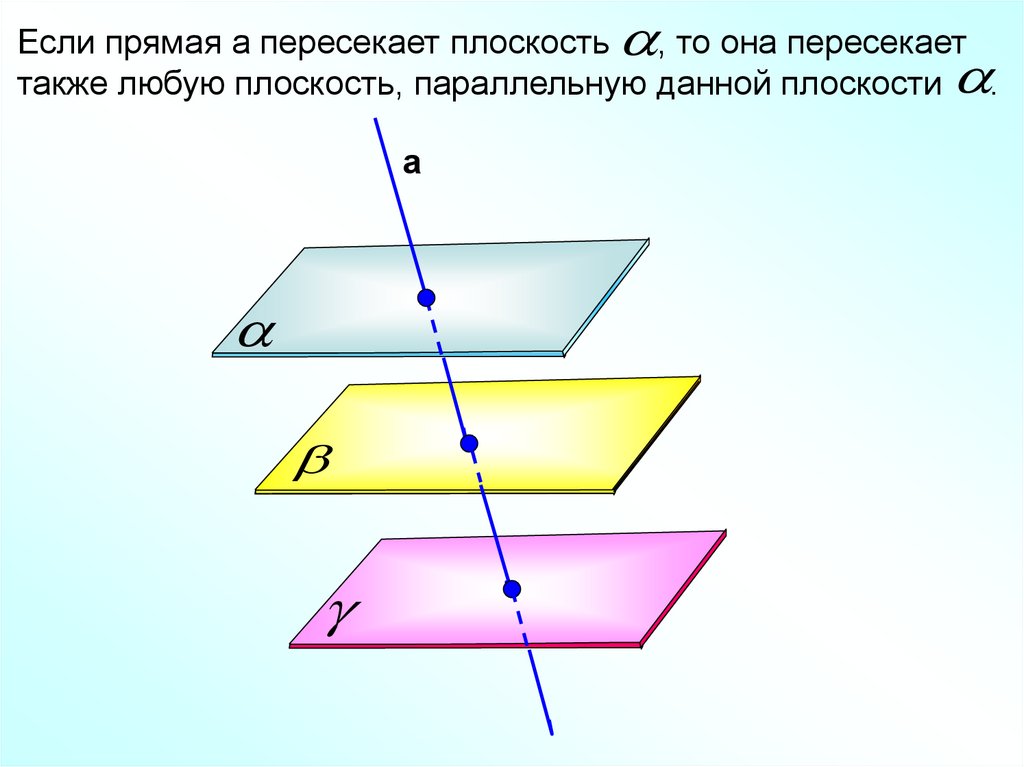
Если прямая а пересекает плоскость , то она пересекаеттакже любую плоскость, параллельную данной плоскости .
а
28.
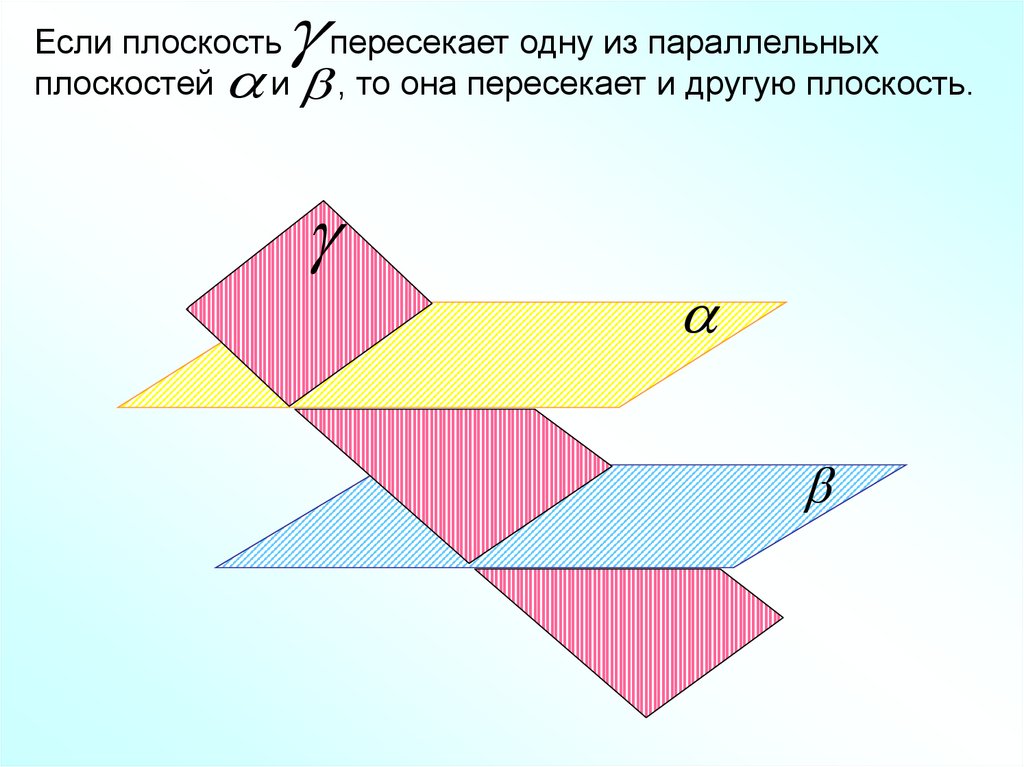
Если плоскость пересекает одну из параллельныхплоскостей
и , то она пересекает и другую плоскость.
29.
№60Признак параллельности трех плоскостей
Если две плоскости
и параллельны плоскости
то плоскости
и параллельны.
,
Признак 3
30.
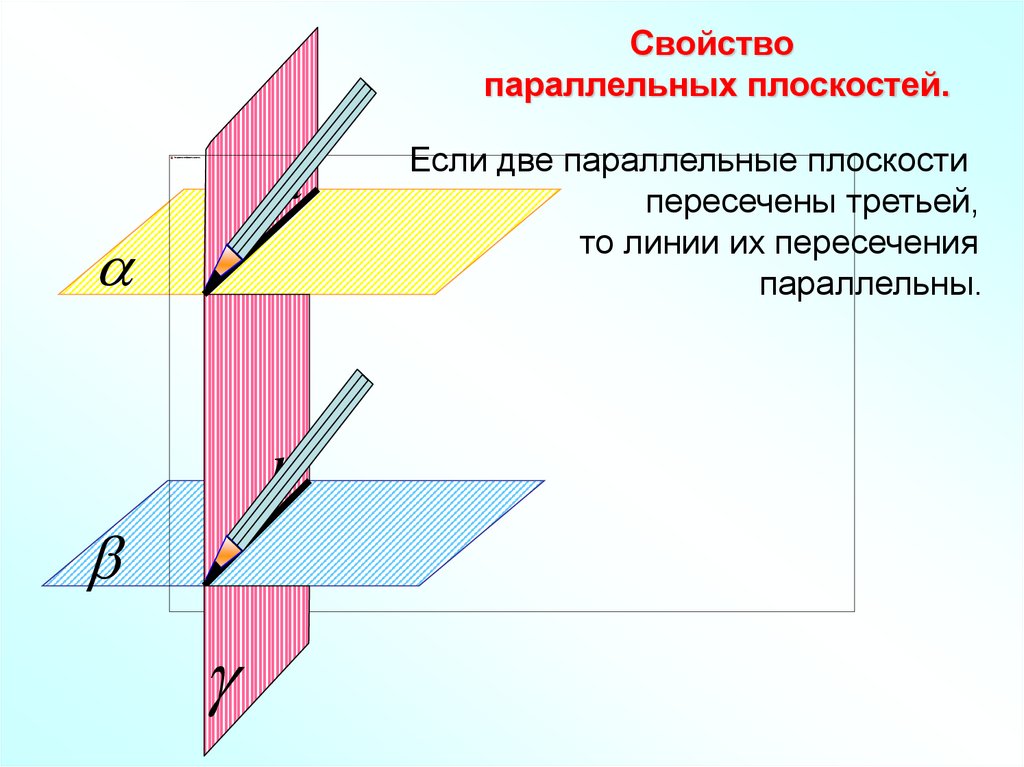
Свойствопараллельных плоскостей.
а
b
Если две параллельные плоскости
пересечены третьей,
то линии их пересечения
параллельны.
31.
Свойствопараллельных плоскостей.
С
а
А
Отрезки параллельных прямых,
заключенные между
параллельными плоскостями,
равны.
АВ = СD
D
В
b























 Математика
Математика








