Похожие презентации:
Нечеткая логика
1.
Федеральное государственное бюджетное образовательное учреждениевысшего профессионального образования
«Ижевский государственный технический университет
имени М. Т. Калашникова»
Кафедра «АСОИУ»
Курс «Неклассические логики»
Тема «Нечеткая логика»
Автор Исенбаева Е.Н., старший преподаватель
Ижевск
2014
2. ВВЕДЕНИЕ
Математическая теория нечетких множеств (fuzzysets) и нечеткая логика (fuzzy logic) являются
обобщениями классической теории множеств и
классической формальной логики. Основной
причиной появления новой теории стало наличие
нечетких и приближенных рассуждений при
описании человеком процессов, систем, объектов.
Курс «Неклассические логики»
Тема «Нечеткая логика»
2
3. ПЕРИОДЫ РАЗВИТИЯ НЕЧЕТКИХ СИСТЕМ
• Первый период характеризуется развитиемтеоретического аппарата нечетких множеств.
• Во втором периоде появляются первые практические
результаты в области нечеткого управления
сложными техническими системами. Одновременно
стало уделяться внимание вопросам
построения экспертных систем, построенных на
нечеткой логике, разработке нечетких контроллеров.
• Наконец, в третьем периоде появляются пакеты
программ для построения нечетких экспертных
систем, а области применения нечеткой логики
заметно расширяются.
Тема «Нечеткая логика»
Курс «Неклассические логики»
3
4. ОТЛИЧИЕ ОТ КЛАССИЧЕСКОЙ ЛОГИКИ
Как известно, классическая логика оперирует толькос двумя значениями: истина и ложь. Однако этими
двумя значениями довольно сложно представить
(можно, но громоздко) большое количество реальных
задач. Поэтому для их решения был разработан
специальный математический аппарат, называемый
нечеткой логикой. Основным отличием нечеткой
логики от классической является наличие не только
двух классических состояний (значений), но и
промежуточных:
F = {0…1}
Курс «Неклассические логики»
Тема «Нечеткая логика»
4
5. МАТЕМАТИЧЕСКИЙ АППАРАТ
Характеристикой нечеткого множества выступаетфункция принадлежности. Обозначим через
– степень принадлежности к нечеткому множеству C,
представляющей собой обобщение понятия
характеристической функции обычного множества.
Тогда нечетким множеством С называется множество
упорядоченных пар вида
[0,1].
Значение
=0 означает отсутствие
принадлежности к множеству, 1 – полную
принадлежность.
Курс «Неклассические логики»
Тема «Нечеткая логика»
5
6. МАТЕМАТИЧЕСКИЙ АППАРАТ
Для описания нечетких множеств вводятсяпонятия нечеткой и лингвистической переменных.
Нечеткая переменная описывается набором
(N,X,A), где N – это название переменной, X –
универсальное множество (область рассуждений),
A – нечеткое множество на X.
Значениями лингвистической переменной
могут быть нечеткие переменные, т.е.
лингвистическая переменная находится на более
высоком уровне, чем нечеткая переменная.
Курс «Неклассические логики»
Тема «Нечеткая логика»
6
7. МАТЕМАТИЧЕСКИЙ АППАРАТ. ПРИМЕР
Формализуем неточное определение "горячий чай". Вкачестве x (область рассуждений) будет выступать шкала
температуры в градусах Цельсия. Очевидно, что она будет
изменяется от 0 до 100 градусов. Нечеткое множество для
понятия "горячий чай" может выглядеть следующим образом:
C={0/0; 0/10; 0/20; 0,15/30; 0,30/40; 0,60/50; 0,80/60; 0,90/70;
1/80; 1/90; 1/100}.
Так, чай с температурой 60ºС принадлежит к множеству
"Горячий" со степенью принадлежности 0,80. Для одного
человека чай при температуре 60ºС может оказаться горячим,
для другого – не слишком горячим. В этом проявляется
нечеткость задания соответствующего множества.
Курс «Неклассические логики»
Тема «Нечеткая логика»
7
8. МЕТОДЫ ПОСТРОЕНИЯ ФУНКЦИЙ ПРИНАДЛЕЖНОСТИ
Существует значительное количествометодов построения по экспертным
оценкам функций принадлежности
нечеткого множества m А(х).
Выделяют две группы методов: прямые
и косвенные методы.
Курс «Неклассические логики»
Тема «Нечеткая логика»
8
9. МЕТОДЫ ПОСТРОЕНИЯ ФУНКЦИЙ ПРИНАДЛЕЖНОСТИ
Прямые методы характеризуются тем, что экспертнепосредственно задает правила определения значений
функции принадлежности
, характеризующей элемент
х. Эти значения согласуются с его предпочтениями на
множестве элементов Х следующим образом:
1. для любых , Î Х
тогда и только
тогда, когда предпочтительнее , т.е. в большей степени
характеризуется свойством А;
2. для любых , Î Х
тогда и только
тогда, когда и безразличны относительно свойства А.
Курс «Неклассические логики»
Тема «Нечеткая логика»
9
10. МЕТОДЫ ПОСТРОЕНИЯ ФУНКЦИЙ ПРИНАДЛЕЖНОСТИ
В косвенных методах значения функции принадлежностивыбираются таким образом, чтобы удовлетворить заранее
сформулированным условиям. Экспертная информация является
только исходной информацией для дальнейшей обработки.
Дополнительные условия могут налагаться как на вид получаемой
информации, так и на процедуру обработки.
Наиболее часто используемые косвенные методы построения
функций принадлежности:
1. Построение функций принадлежности на основе парных
сравнений;
2. Построение функций принадлежности с использованием
статистических данных;
3. Построение функций принадлежности на основе экспертных
оценок;
4. Параметрический подход к построению функций
принадлежности;
5. Построение функции принадлежности на основе ранговых
оценок.
Курс «Неклассические логики»
Тема «Нечеткая логика»
10
11. ТИПОВЫЕ ФОРМЫ КРИВЫХ ДЛЯ ЗАДАНИЯ ФУНКЦИЙ ПРИНАДЛЕЖНОСТИ
Существует свыше десятка типовых формкривых для задания функций
принадлежности. Наибольшее
распространение получили: треугольная,
трапецеидальная и гауссова функции
принадлежности.
Курс «Неклассические логики»
Тема «Нечеткая логика»
11
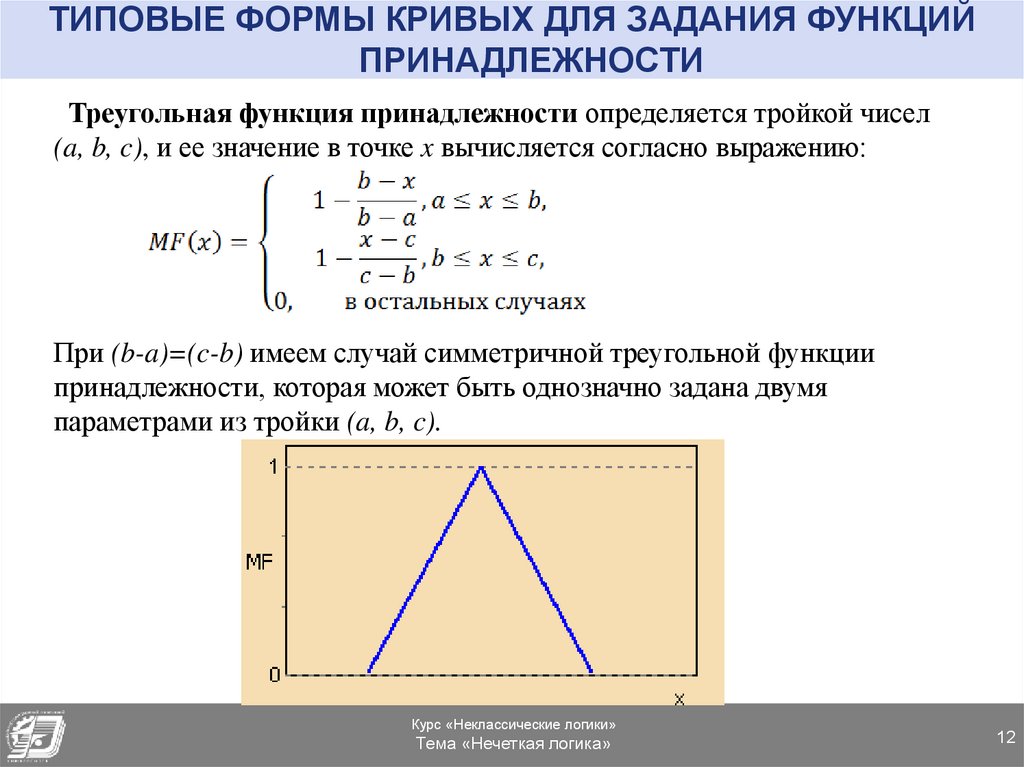
12. ТИПОВЫЕ ФОРМЫ КРИВЫХ ДЛЯ ЗАДАНИЯ ФУНКЦИЙ ПРИНАДЛЕЖНОСТИ
Треугольная функция принадлежности определяется тройкой чисел(a, b, c), и ее значение в точке x вычисляется согласно выражению:
При (b-a)=(c-b) имеем случай симметричной треугольной функции
принадлежности, которая может быть однозначно задана двумя
параметрами из тройки (a, b, c).
Курс «Неклассические логики»
Тема «Нечеткая логика»
12
13. ТИПОВЫЕ ФОРМЫ КРИВЫХ ДЛЯ ЗАДАНИЯ ФУНКЦИЙ ПРИНАДЛЕЖНОСТИ
Аналогично для задания трапецеидальной функции принадлежностинеобходима четверка чисел (a, b, c, d):
При (b-a)=(d-c) трапецеидальная функция принадлежности принимает
симметричный вид.
Курс «Неклассические логики»
Тема «Нечеткая логика»
13
14. ТИПОВЫЕ ФОРМЫ КРИВЫХ ДЛЯ ЗАДАНИЯ ФУНКЦИЙ ПРИНАДЛЕЖНОСТИ
Функция принадлежности гауссова типа описывается формулойи оперирует двумя параметрами. Параметр c обозначает центр
нечеткого множества, а параметр σ отвечает за крутизну функции.
Курс «Неклассические логики»
Тема «Нечеткая логика»
14
15. ОПЕРАЦИИ НАД НЕЧЕТКИМИ МНОЖЕСТВАМИ
Для нечетких множеств, как и для обычных, определеныосновные логические операции. Самыми основными,
необходимыми для расчетов, являются пересечение и
объединение.
Пересечением нечетких множеств
называется нечеткое множество
с функцией принадлежности
для каждого
.
Объединение нечетких множеств А и В –
нечеткое множество
, определенное
функцией принадлежности
для каждого
.
Курс «Неклассические логики»
Тема «Нечеткая логика»
15
16. ОПЕРАЦИИ НАД НЕЧЕТКИМИ МНОЖЕСТВАМИ
Дополнением нечеткого множестваназывается нечеткое множество с функцией
принадлежности
для каждого
.
Концентрация нечеткого множества
обозначается CON(A) и определяется как
для каждого
.
Разбавление нечеткого множества
обозначается DIL(A) и определяется как
для каждого
.
Курс «Неклассические логики»
Тема «Нечеткая логика»
16
17. ПРИМЕРЫ НЕЧЕТКИХ МНОЖЕСТВ
Пусть E = {0,1,2,..,10}, M =[0,1]. Нечеткое множество "несколько" можноопределить следующим образом: "несколько" =
0,5/3+0,8/4+1/5+1/6+0,8/7+0,5/8; его характеристики: высота = 1,
носитель={3,4,5,6,7,8}, точки перехода - {3,8}.
Пусть E = {0,1,2,3,...,n,...}. Нечеткое множество "малый" можно определить:
Курс «Неклассические логики»
Тема «Нечеткая логика»
17
18. ПРИМЕРЫ НЕЧЕТКИХ МНОЖЕСТВ
Пусть E = {1,2,3,...,100} и соответствует понятию "возраст", тогда нечеткоемножество "молодой" может быть определено с помощью
m «молодой»(x) =
Нечеткое множество "молодой" на универсальном множестве E' ={Иванов,
Петров, Сидоров,...} задается с помощью функции принадлежности
m"молодой"(x) на E = {1,2,3,..100} (возраст), называемой по отношению к E'
функцией совместимости, при этом:
m"молодой"(Сидоров):= m"молодой"(x), где x - возраст Сидорова.
Курс «Неклассические логики»
Тема «Нечеткая логика»
18
19. ПРИМЕРЫ НЕЧЕТКИХ МНОЖЕСТВ
Пусть E = {Запорожец, Жигули, Мерседес,....} - множество марокавтомобилей, а E' = [0,¥) - универсальное множество "стоимость", тогда на
E' мы можем определить нечеткие множества типа: "для бедных", "для
среднего класса", "престижные", с функциями принадлежности типа:
Имея эти функции и зная стоимости автомобилей из E в данный момент
времени, мы тем самым определим на E' нечеткие множества с этими же
названиями.
Курс «Неклассические логики»
Тема «Нечеткая логика»
19
20. ПРИМЕРЫ НЕЧЕТКИХ МНОЖЕСТВ
Так, например, нечеткое множество "для бедных", заданное науниверсальном множестве E = {Запорожец, Жигули, Мерседес,....} выглядит
следующим образом:
Аналогично можно определить Нечеткое множество "скоростные",
"средние", "тихоходные" и т.д.
Курс «Неклассические логики»
Тема «Нечеткая логика»
20
21. НЕЧЕТКИЙ ЛОГИЧЕСКИЙ ВЫВОД
Основой для проведения операции нечеткого логическоговывода является база правил, содержащая нечеткие
высказывания в форме "Если-то" и функции принадлежности
для соответствующих лингвистических термов. При этом
должны соблюдаться следующие условия:
• Существует хотя бы одно правило для каждого
лингвистического терма выходной переменной.
• Для любого терма входной переменной имеется
хотя бы одно правило, в котором этот терм
используется в качестве предпосылки (левая часть
правила).
В противном случае имеет место неполная база нечетких
правил.
Курс «Неклассические логики»
Тема «Нечеткая логика»
21
22. НЕЧЕТКИЙ ЛОГИЧЕСКИЙ ВЫВОД. ПРИМЕР
Пусть в базе правил имеется m правил вида:R1: ЕСЛИ x1 это A11 … И … xn это A1n, ТО y это B1
…
Ri: ЕСЛИ x1 это Ai1 … И … xn это Ain, ТО y это Bi
…
Rm: ЕСЛИ x1 это Ai1 … И … xn это Amn, ТО y это Bm,
где xk , k=1..n – входные переменные; y – выходная
переменная; Aik – заданные нечеткие множества с
функциями принадлежности.
Результатом нечеткого вывода является четкое
значение переменной y* на основе заданных четких
значений xk , k=1..n.
Курс «Неклассические логики»
Тема «Нечеткая логика»
22
23. НЕЧЕТКИЙ ЛОГИЧЕСКИЙ ВЫВОД
В общем случае механизм логического вывода включаетчетыре этапа:
• введение нечеткости (фазификация),
• нечеткий вывод,
• композиция и приведение к четкости, или дефазификация.
Курс «Неклассические логики»
Тема «Нечеткая логика»
23
24. НЕЧЕТКИЙ ЛОГИЧЕСКИЙ ВЫВОД. МЕХАНИЗМ МАМДАНИ
Механизм Мамдани включает в себя следующую последовательность действий:1. Процедура фазификации: определяются степени истинности, т.е. значения
функций принадлежности для левых частей каждого правила (предпосылок). Для
базы правил с m правилами обозначим степени истинности как
2. Нечеткий вывод. Сначала определяются уровни "отсечения" для левой части
каждого из правил:
Далее находятся «усеченные» функции принадлежности:
3. Композиция, или объединение полученных усеченных функций, для чего
используется максимальная композиция нечетких множеств:
где MF(y) – функция принадлежности итогового нечеткого множества
4. Дефазификация, или приведение к четкости. Существует несколько методов
дефазификации. Например, метод среднего центра, или центроидный метод:
Геометрический смысл такого значения – центр тяжести для кривой MF(y).
Курс «Неклассические логики»
Тема «Нечеткая логика»
24
25. НЕЧЕТКИЙ ЛОГИЧЕСКИЙ ВЫВОД. МЕХАНИЗМ МАМДАНИ
Схема нечеткого вывода по Мамдани для двух входных переменных и двухнечетких правил R1 и R2.
Курс «Неклассические логики»
Тема «Нечеткая логика»
25
26. НЕЧЕТКИЙ ЛОГИЧЕСКИЙ ВЫВОД. АЛГОРИТМ ЦУКАМОТО
Формально алгоритм Цукамото может быть определен следующим образом:• Формирование базы правил систем нечеткого вывода.
• Фаззификация входных переменных.
• Агрегирование подусловий в нечетких правилах продукций. Для нахождения
степени истинности условий всех правил нечетких продукций используются
парные нечеткие логические операции. Те правила, степень истинности условий
которых отлична от нуля, считаются активными и используются для
дальнейших расчетов.
• Активизация подзаключений в нечетких правилах продукций. Осуществляется
аналогично алгоритму Мамдани, после чего находятся обычные (не нечеткие)
значения всех выходных лингвистических переменных в каждом из
подзаключений активных правил нечетких продукций. В этом случае значение
выходной лингвистической переменной в каждом из под заключений
находится как решение уравнения:
где q – общее количество подзаключений в базе правил.
Курс «Неклассические логики»
Тема «Нечеткая логика»
26
27. НЕЧЕТКИЙ ЛОГИЧЕСКИЙ ВЫВОД. АЛГОРИТМ ЦУКАМОТО
•Аккумуляция заключений нечетких правил продукций. Фактическиотсутствует, поскольку расчеты осуществляются с обычными действительными
числами .
•Дефаззификация выходных переменных. Используется модифицированный
вариант в форме метода центра тяжести для одноточечных множеств:
где n – общее количество активных правил нечетких продукций, в подзаключениях которых присутствует выходная лингвистическая переменная .
Курс «Неклассические логики»
Тема «Нечеткая логика»
27
28. ПРИМЕНЕНИЕ
В результате объединения нескольких технологий искусственного интеллектапоявился специальный термин – "мягкие вычисления", который ввел Л. Заде в
1994 году. В настоящее время мягкие вычисления объединяют такие области
как: нечеткая логика, искусственные нейронные сети, вероятностные
рассуждения и эволюционные алгоритмы. Они дополняют друг друга и
используются в различных комбинациях для создания гибридных
интеллектуальных систем.
Нечеткие нейронные сети. Такие сети осуществляют выводы на основе
аппарата нечеткой логики, однако параметры функций принадлежности
настраиваются с использованием алгоритмов обучения нейронных сетей.
Поэтому для подбора параметров таких сетей применим метод обратного
распространения ошибки, изначально предложенный для обучения
многослойного персептрона. Для этого модуль нечеткого управления
представляется в форме многослойной сети. Нечеткая нейронная сеть, как
правило, состоит из четырех слоев: слоя фазификации входных переменных,
слоя агрегирования значений активации условия, слоя агрегирования нечетких
правил и выходного слоя.
Курс «Неклассические логики»
Тема «Нечеткая логика»
28
29. ПРИМЕНЕНИЕ
Адаптивные нечеткие системы. Алгоритмы обученияадаптивных нечетких систем относительно трудоемки и сложны по
сравнению с алгоритмами обучения нейронных сетей, и, как
правило, состоят из двух стадий:
1. Генерация лингвистических правил;
2. Корректировка функций принадлежности.
Первая задача относится к задаче переборного типа, вторая – к
оптимизации в непрерывных пространствах. При этом возникает
определенное противоречие: для генерации нечетких правил
необходимы функции принадлежности, а для проведения
нечеткого вывода – правила. Кроме того, при автоматической
генерации нечетких правил необходимо обеспечить их полноту и
непротиворечивость. Значительная часть методов обучения
нечетких систем использует генетические алгоритмы.
Курс «Неклассические логики»
Тема «Нечеткая логика»
29
30. ПРИМЕНЕНИЕ
Нечеткие запросы. Нечеткие запросы к базам данных –перспективное направление в современных системах
обработки информации. Данный инструмент дает
возможность формулировать запросы на естественном
языке, например: "Вывести список недорогих
предложений о съеме жилья близко к центру города", что
невозможно при использовании стандартного механизма
запросов. Для этой цели разработана нечеткая
реляционная алгебра и специальные расширения языков
SQL для нечетких запросов.
Курс «Неклассические логики»
Тема «Нечеткая логика»
30
31. ПРЕИМУЩЕСТВА НЕЧЕТКИХ СИСТЕМ
•возможность оперировать нечеткими входными данными: например,непрерывно изменяющиеся во времени значения (динамические задачи),
значения, которые невозможно задать однозначно (результаты
статистических опросов, рекламные компании и т.д.);
возможность нечеткой формализации критериев оценки и сравнения:
оперирование критериями "большинство", "возможно", преимущественно" и
т.д.;
•возможность проведения качественных оценок как входных данных,
так и выходных результатов: вы оперируете не только значениями данных,
но и их степенью достоверности (не путать с вероятностью!) и ее
распределением;
•возможность проведения быстрого моделирования сложных
динамических систем и их сравнительный анализ с заданной степенью
точности: оперируя принципами поведения системы, описанными fuzzyметодами, вы во-первых, не тратите много времени на выяснение точных
значений переменных и составление описывающих уравнений, во-вторых,
можете оценить разные варианты выходных значений.
Курс «Неклассические логики»
Тема «Нечеткая логика»
31
32.
СПАСИБО ЗА ВНИМАНИЕ© ФГБОУ ВПО ИжГТУ имени М.Т. Калашникова, 2014
© Исенбаева Елена Насимьяновна, 2014































 Информатика
Информатика








