Сортировки 1 курс плюс алг.слож

1. Квадратичные и эффективные сортировки

2. Алгоритмическая сложность

2

3. Оценка производительности алгоритмов

Для оценки производительности алгоритмов
можно использовать разные подходы.
Самый бесхитростный - просто запустить
каждый алгоритм на нескольких задачах и
сравнить время исполнения.
Другой способ - оценить время исполнения
через символ O(n)
3

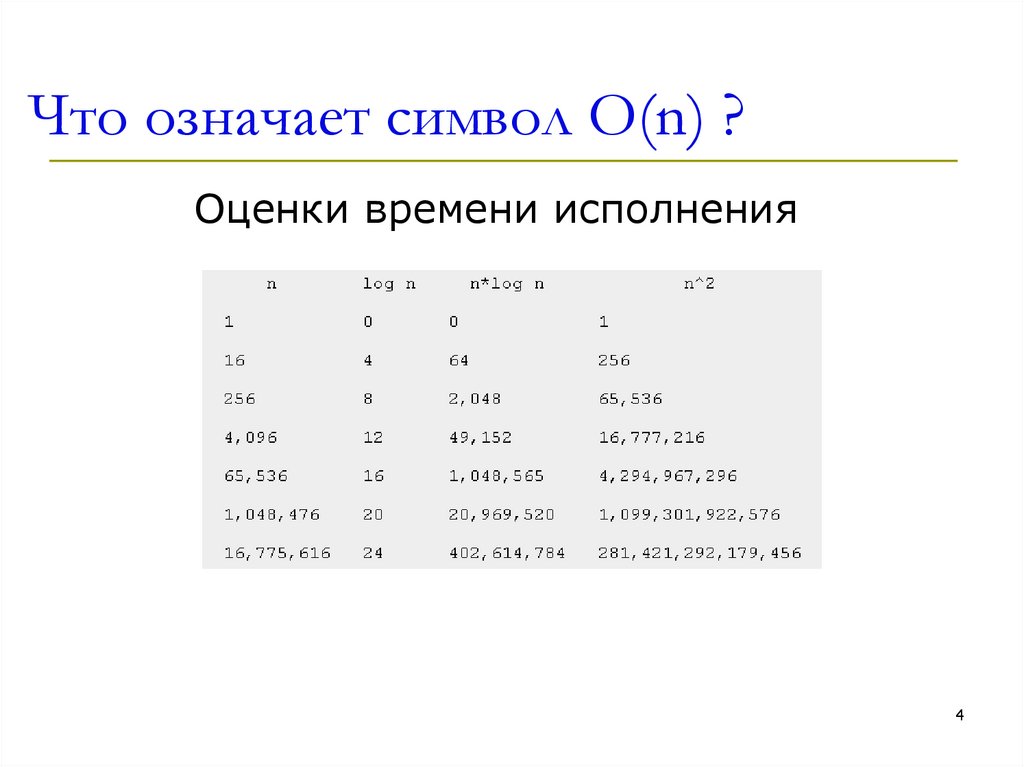
4. Что означает символ O(n) ?

Оценки времени исполнения
4

5. Что означает символ O(n) ?

Если оба алгоритма, например, O ( n*log n ), то это отнюдь
не значит, что они одинаково эффективны.
Символ О не учитывает константу, то есть первый может
быть, скажем в 1000 раз эффективнее. Это значит лишь
то, что время (или требуемая память или что-либо еще,
что надо оценить) возрастает приблизительно c такой же
скоростью, как функция n*log n
Если в программе одна функция выполняется O(n) раз например, умножение, а сложение - O(n^2) раз, то общая
сложность - O(n^2), так как n^2 возрастает быстрее.
5

6. Про O(n) видео от Сириуса

https://youtu.be/Snyn7EqHJME
https://youtu.be/5P-I6RSQGtY (логарифм)
6

7. Квадратичные алгоритмы сортировки

Список, примеры, время
выполнения

8. Некоторые сортировки

Пирамидальная
Быстрая
Пирамидальная
Слиянием
Пузырьком + модификации
Вставками
Шелла
Выбором
Топологическая
Быстрая с составными ключами
…

9. Сортировка выбором

Находим наибольший элемент в массиве и
ставим его на первое место, затем находим
наибольший элемент из оставшихся и
ставим его на второе место и т.д. Таким
образом, в решении имеется циклfor(i = 0; i
< n -1; ++i), внутри которого находится
наибольший элемент средиA[i],A[i+1],
...,A[n-1], который устанавливается на
местоA[i].
9

10. Сортировка выбором

11. Сортировка пузырьком

Осуществляется проход по массиву от
начала к концу, и если два соседних
элемента стоят в неверном порядке, то они
переставляются в правильном порядке. В
результате минимальный элемент массива
окажется на последнем месте. Повторим эту
процедуру еще несколько раз, чтобы
поставить все элементы на свои места.
11

12. Сортировка пузырьком

13. Сортировка вставками

В каждый произвольный момент начальная
часть массива уже отсортирована. В
решении имеется цикл for(i = 1; i < n; ++i),
внутри которого в предположении, что
элементы массива A[0],A[1], ...,A[i-1]уже
отсортированы, элемент A[i]добавляется в
отсортированную часть. Для этого
находится позиция, в которую необходимо
вставить элемент A[i], затем
осуществляется циклический сдвиг
фрагмента уже отсортированной части.
13

14. Cортировка вставками

15. Быстрая сортировка

Выберем случайным образом какой-то элемент х и
просмотрим массив, двигаясь слева направо, пока не найдем
аi больший x, а затем справа налево, пока не найдем аi
меньший х. Поменяем их местами и продолжим процесс
просмотра с обменом, пока просмотры не встретятся где-то в
середине массива. В результате массив разделится на две
части: левую - с ключами, меньшими х и правую - с ключами,
большими х. Этот шаг называется разделением. Х - центром.
К получившимся частям рекурсивно применяем ту же
процедуру. В результате получается очень эффективная
сортировка.
Среднее быстродействие O(nlogn), но возможен случай таких
входных данных, на которых алгоритм будет работать за
O(n^2) операций.
15

16. Сравнение времени квадратичных сортировок

Коричневая: сортировка
пузырьком
синяя: шейкер-сортировка;
розовая: сортировка
выбором
желтая: сортировка
вставками
голубая: сортировка
вставками со сторожевым
элементом
фиолетовая: сортировка
Шелла

17. Эффективные сортировки

18. Распределяющая сортировка: Для массивов

1.
2.
3.
4.
Общее быстродействие O(k(n+s)) [s
иногда не учитывают вовсе]
Реализация со временным массивом
O(n), [Radix Sort] Реализация без
временного массива O(logn) [Radix
Exchange Sort]
Реализация со временным массивом
устойчивая, Реализация без временного
массива неустойчивая.
Hеестественное поведение
18

19. Распределяющая сортировка: Для списков

1.
2.
3.
4.
Общее быстродействие O(k(n+s)) [s
иногда не учитывают]
Дополнительной памяти не требуется,
так как реорганизовывать список можно
просто через указатели
Устойчивая сортировка
Hеестественное поведение
19

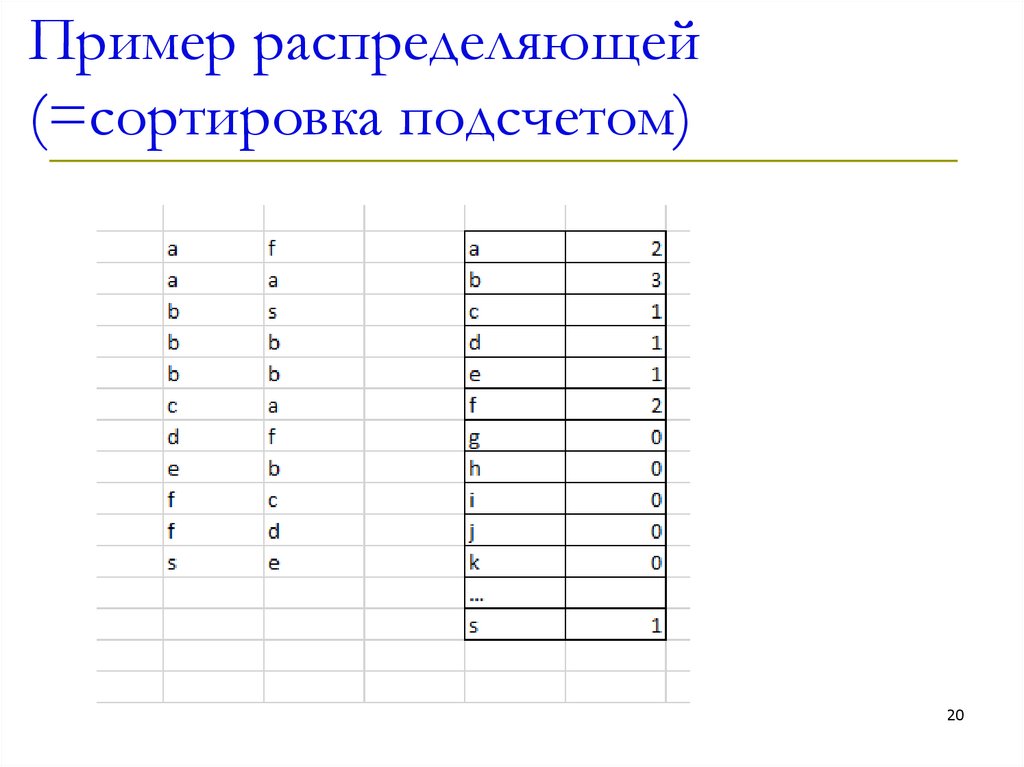
20. Пример распределяющей (=сортировка подсчетом)

20

21. Сортировка слиянием

22. Сортировка слиянием

23. Сравнение разных сортировок

Сравнение по 4 параметрам

24. Охарактеризуем сортировки по четырем параметрам:

1.
Время сортировки
2.
Память - дополнительные затраты памяти,
зависящие от размера массива.
3.
Устойчивость - устойчивая сортировка не
меняет взаимного расположения равных
элементов
4.
Естественность поведения - эффективность
метода при обработке уже отсортированных,
или частично отсортированных данных

25. Распределяющая сортировка: Для массивов

1.
Общее быстродействие O(k(n+s))
2.
Реализация со временным массивом
O(n), реализация без временного
массива O(logn)
3.
Реализация со временным массивом
устойчивая, без него неустойчивая
4.
Hеестественное поведение

26. Распределяющая сортировка: Для списков

1.
Общее быстродействие O(k(n+s))
2.
Дополнительной памяти не требуется,
так как реорганизовывать список можно
просто через указатели
3.
Устойчивая сортировка
4.
Hеестественное поведение

27. Сортировка двоичным деревом

1.
Общее быстродействие O(nlogn)
2.
Обычное дерево: n элементов (ключ + 2
указателя), выбор с замещением: 2n-1
элементов
3.
Устойчивости нет
4.
Поведение неестественно

28. Quicksort - быстрая сортировка

1.
Общее быстродействие O(nlogn)
2.
Итерационный вариант требует log n
памяти, рекурсивный - O(n)
3.
Устойчивости нет
4.
Поведение неестественно

29. Heapsort - пирамидальная сортировка

1.
Общее быстродействие всегда O(nlogn)
2.
Сортировка 'на месте'
3.
Устойчивости нет
4.
Поведение неестественно

30. Mergesort - сортировка слиянием

1.
Общее быстродействие - O(nlogn)
2.
O(n)
3.
Устойчивая
4.
Hа практике используются реализации с
естественным поведением

31. Рекомендации по выбору сортировки

Малые массивы/списки - менее 20
элементов => InsertSort
Большие массивы => QuickSort,
Heapsort
Длинные списки/файлы => MergeSort
Если количество возможных различных
ключей ненамного больше их общего
числа - то наибыстрейшей будет
распределяющая сортировка

32. Создание большого набора данных

33. Предварительная работа

Сгенерировать в цикле
набор случайных чисел.
Количество 108, диапазон
0-106
Сохранить в файл
1 Гб информации

34. Основная работа

Реализовать в коде на выбор 2
сортировки:
Пузырьком или вставками
MergeSort или QuickSort или
Пирамидальная
Применить, засечь время исполнения
Записать упорядоченный набор в новые
файлы

35. Результаты проверки

Время исполнения на 108, диапазон 0-106
пузырьком 7-8 секунд
QuickSort менее 1 секунды
O(n2)
Распределяющая сортировка? O(n)
MergeSort? O(n*logn)
Пирамидальная?

36. Литература

Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К.
Алгоритмы: построение и анализ, 2-е
издание.стр. 110 М.: Издательский дом
"Вильямс", 2005. ISBN 5-8459-0857-4
Кнут Д. Искусство программирования. — 3-е изд.
— М.: Вильямс, 2007. — Т. 2. Получисленные
алгоритмы. — 832 с. — ISBN 0-201-89684-2.
https://neerc.ifmo.ru/wiki/index.php?title=Мастертеорема
http://algolist.ru/olimp/sor_prb.php
https://habr.com/ru/post/281675/