c48f44771f9643c2839efd9fae3b9111

1. ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ

2.

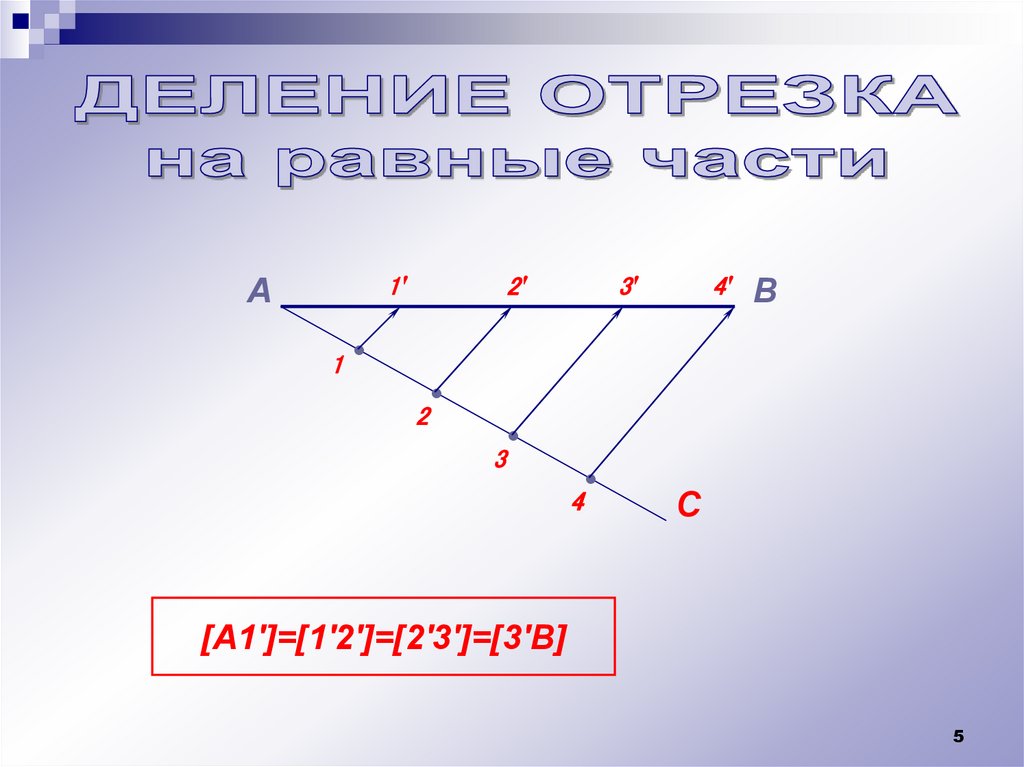
Проведение перпендикуляров
Деление отрезка на равные части;
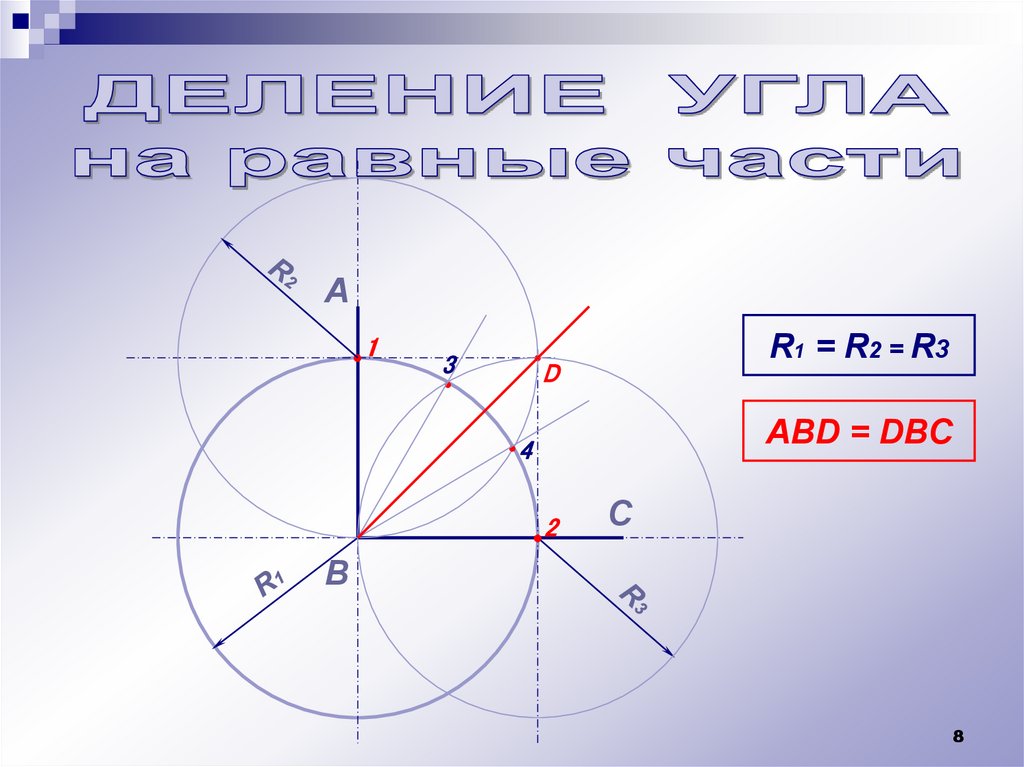
Деление угла и дуги на равные части;
Деление окружностей на равные части;
Нахождение центра дуги;
Создание орнамента
Сопряжения
2

3.

Геометрические построения - это
способ решения задачи, при
котором ответ получают
графическим путем. Построения
выполняют чертежными
инструментами при максимальной
точности и аккуратности работы,
так как от этого зависит
правильность решения.
Условия задач и вспомогательные
построения выполняют тонкими
сплошными линиями.

4.

Графический способ решения
геометрических задач на плоскости
при помощи чертежных
инструментов
4

5.

А
1'
2'
1
2
3'
4'
В
3
4
С
[А1']=[1'2']=[2'3']=[3'В]
5

6.

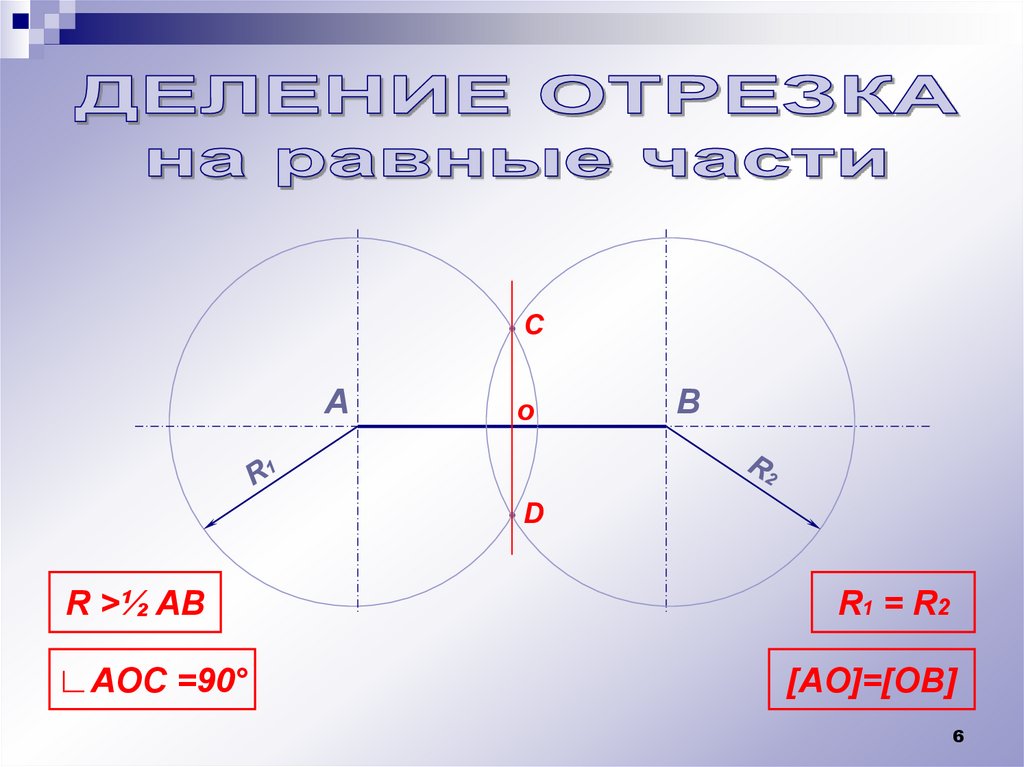
•С
А
o
В
D
R >½ AB
R1 = R2
∟AOC =90°
[AO]=[OB]
6

7.

А
•1
R1 = R2 = R3
3
α=β=γ
•4
•2
С
В
7

8.

А
•1
R1 = R2 = R3
3
D
ABD = DBC
•4
•2
С
В
8

9. Геометрические построения

Тема урока:
«Деление окружности
на равные части»

10.

Приемы деления окружности на равные
части человек использовал с
незапамятных времен. Например,
превращение колеса из сплошного диска
в обод со спицами поставило человека
перед необходимостью распределить
спицы в колесе равномерно. Выполняя
изображение такого колеса, люди
искали точные способы с помощью
чертежных инструментов.

11.

С делением окружности неразрывно связано
построение правильных многоугольников. Они
встречаются в древнейших орнаментах у всех
народов. Люди уже тогда
оценивали их красоту.

12.

Кроме того, они видели эти фигуры
в природе. Например, пятиугольник
встречается в очертаниях
минералов, плодов, в форме
некоторых морских животных,

13.

шестиугольник встречается в
очертаниях цветов,
просматривается в пчелиных сотах
и т.д.

14.

Иоганн Кеплер
(1571- 1630)
Правильный шестиугольник явился
предметом исследования великого
немецкого астронома и математика
Иоганна Кеплера (1571-1630), о
котором он рассказывает в своей
книге «Новогодний подарок, или о
шестиугольных снежинках».

15.

Рассуждая о причинах того, почему
снежинки имеют шестиугольную форму,
он отмечает: «…плоскость можно
покрыть без зазоров лишь следующими
фигурами: равносторонними
треугольниками, квадратами и
правильными шестиугольниками. Среди
этих фигур правильный шестиугольник
покрывает большую площадь»

16.

17.

Строительство
В «Десяти книгах о зодчестве»
римского архитектора Витрувия
(жившего примерно в 63-14 гг. до н. э.)
говорится, что городские стены
должны иметь в плане вид
правильного многоугольника, а башни
крепости «следует делать круглыми
или многоугольными, ибо
четырехугольник скорее разрушается
осадными орудиями»

18.

Планировка городов, которую
предлагал Витрувий представляла
собой защиту от 8 главных ветров и 16
второстепенных.. для построения
восьмиугольника Витрувий предлагал
применить деления пополам сторон
квадрата, вписанного в окружность.

19.

В строительстве широко применяли
деление окружности на равные части.
Одним из примеров может служить
величественный памятник готической
архитектуры – Нотр–Дам де Пари или
Собор Парижской Богоматери (30 метров
в длину, 108 – в ширину) который
находится в Париже, на острове Сити.
Его строили 94 года. Фасад Собора
украшает удивительный витраж 18 века.
Этот витраж в архитектуре называется
«роза». Диаметр розы собора Собор
Парижской Богоматери12 метров 90 см.

20. Архитектура

Собор Парижской
Богоматери

21.

Альбрехт Дюрер
(1471-1528).
Одним из наиболее известных ученых,
занимавшихся геометрическими
построениями, был великий художник и
математик Альбрехт Дюрер (1471-1528),
который посвятил им значительную
часть своей книги «Руководства…». Он
предложил правила построения
правильных многоугольников с 3, 4,
5…16-ю сторонами. Методы деления
были не универсальны, в каждом
конкретном случае используется
индивидуальный прием

22. Орнаменты и узоры

23. «Правильные многоугольники в природе»

24.

В декоративно-прикладном
искусстве дизайнеры, ювелиры с
успехом применяли деление
окружности, создавая прекрасные
произведения: ордена, медали,
монеты, ювелирные изделия

25.

26. Ордена и медали

27.

28.

29.

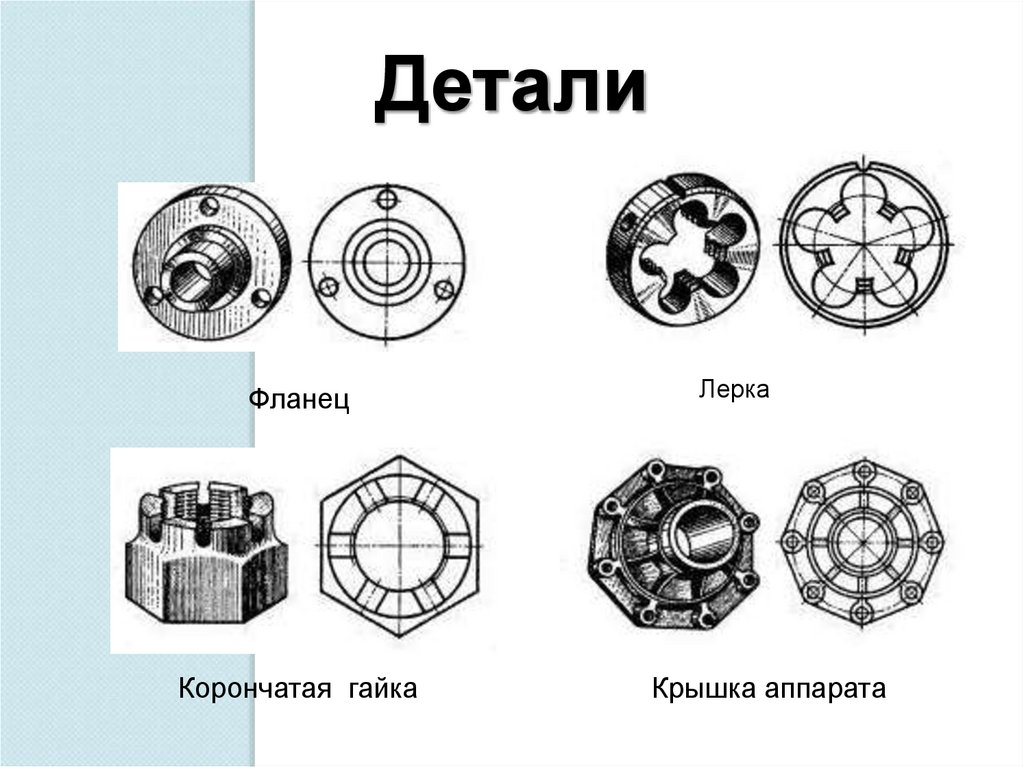
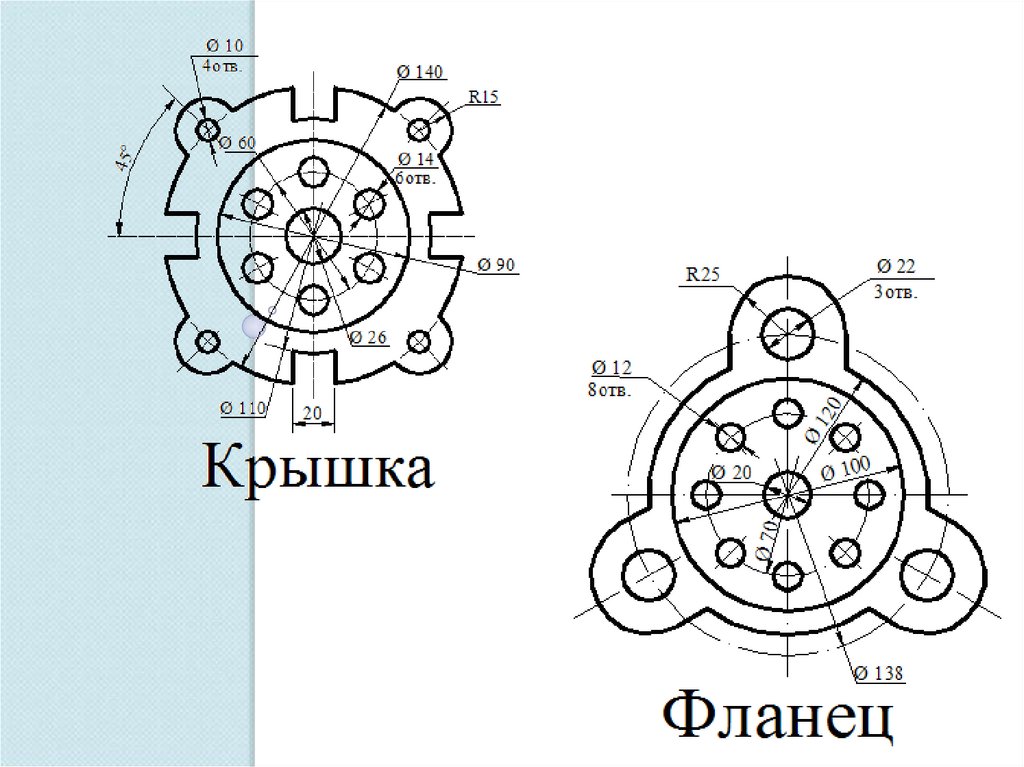
Детали
Фланец
Корончатая гайка
Лерка
Крышка аппарата

30.

31.

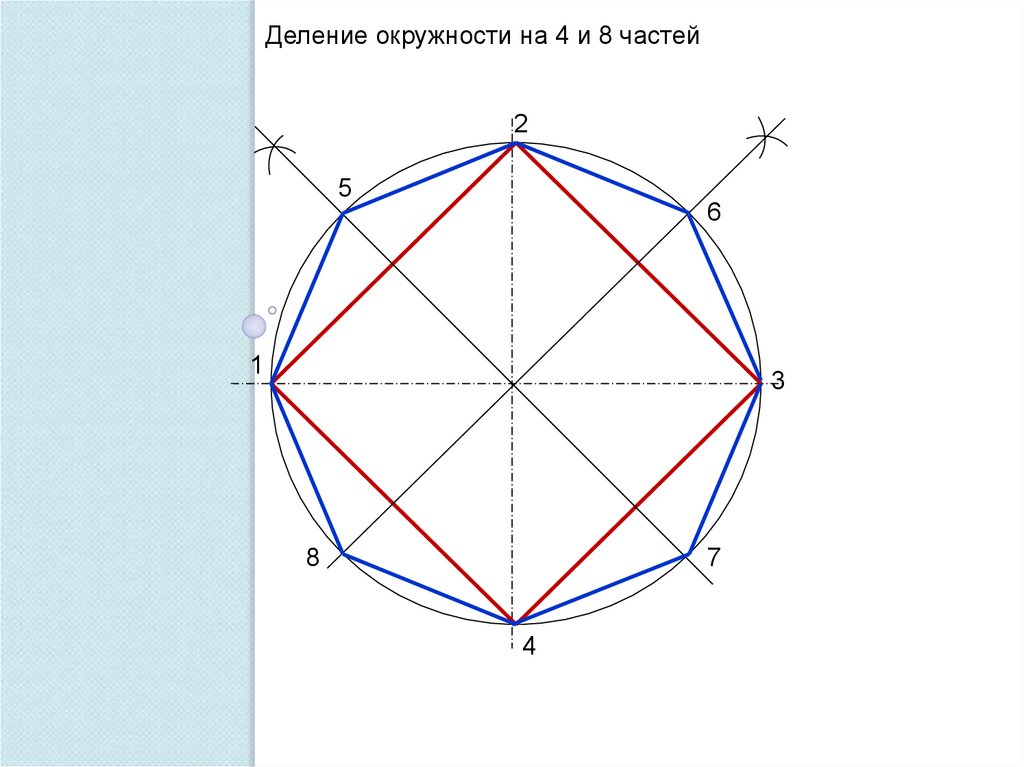
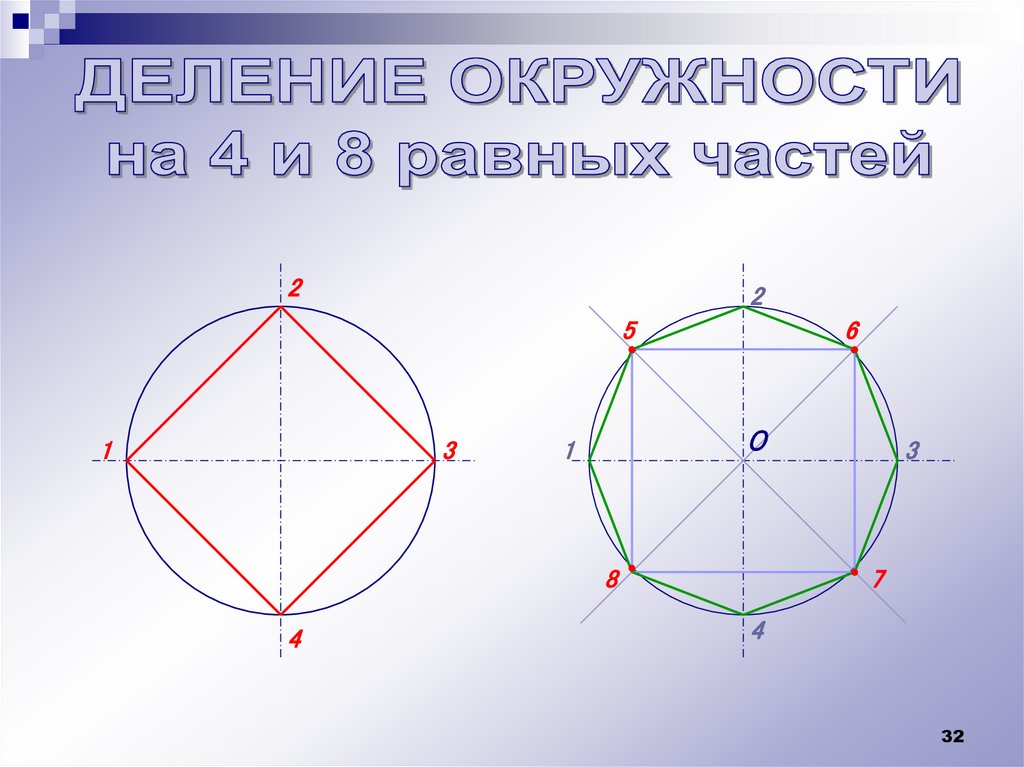
Деление окружности на 4 и 8 частей
2
5
6
1
3
8
7
4

32.

2
2
5
6
1
3
О
1
8
4
3
•7
4
32

33.

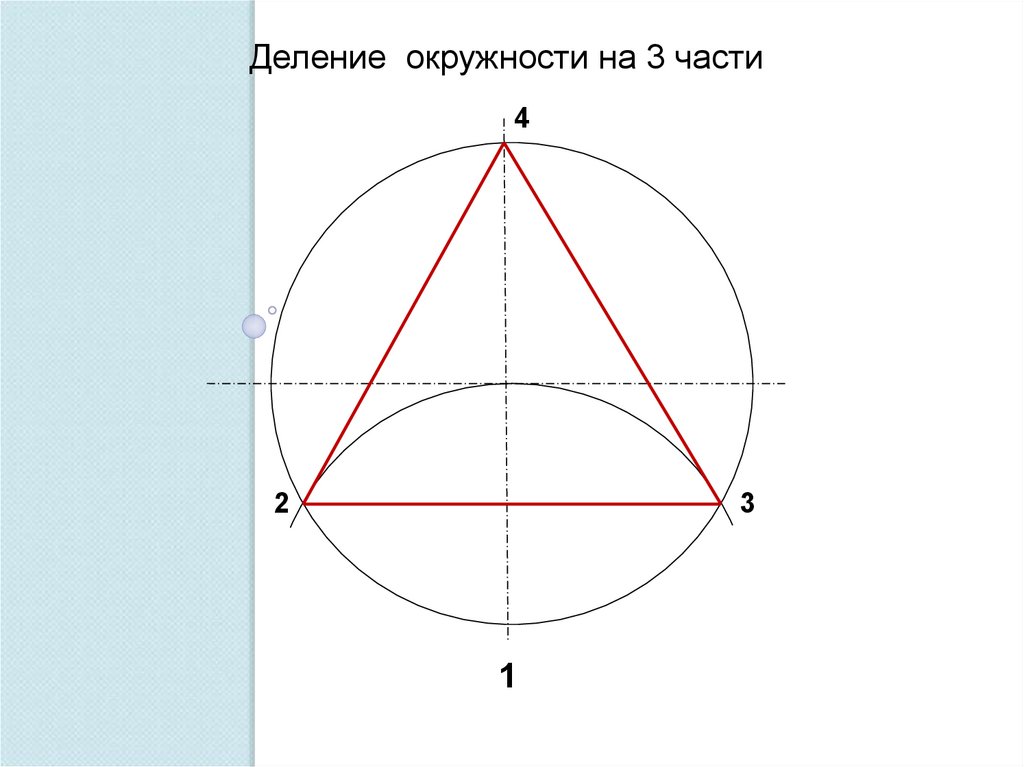
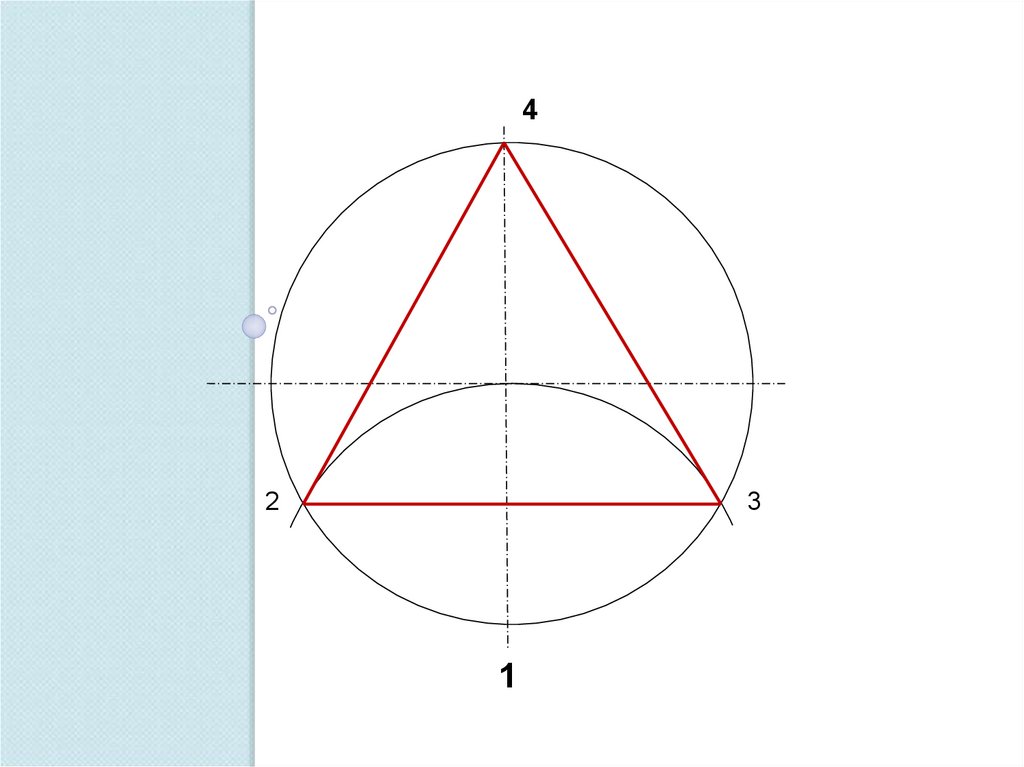
Деление окружности на 3 части
4
2
3
1

34.

4
2
3
1

35.

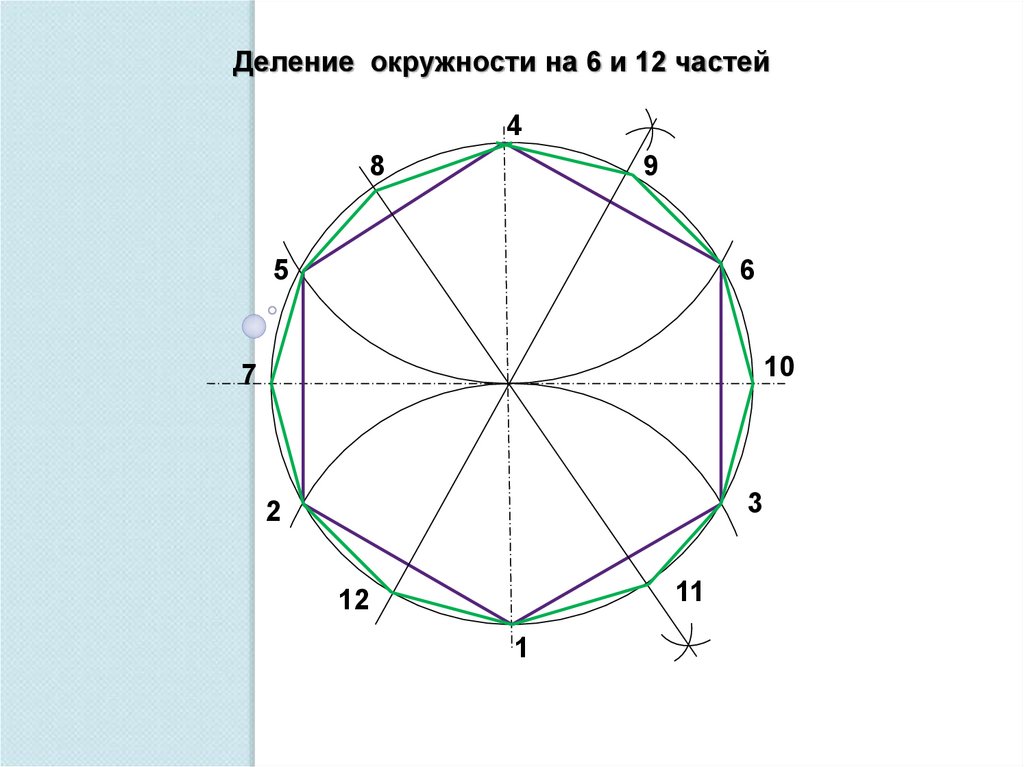
Деление окружности на 6 и 12 частей
4
8
9
5
6
10
7
3
2
11
12
1

36.

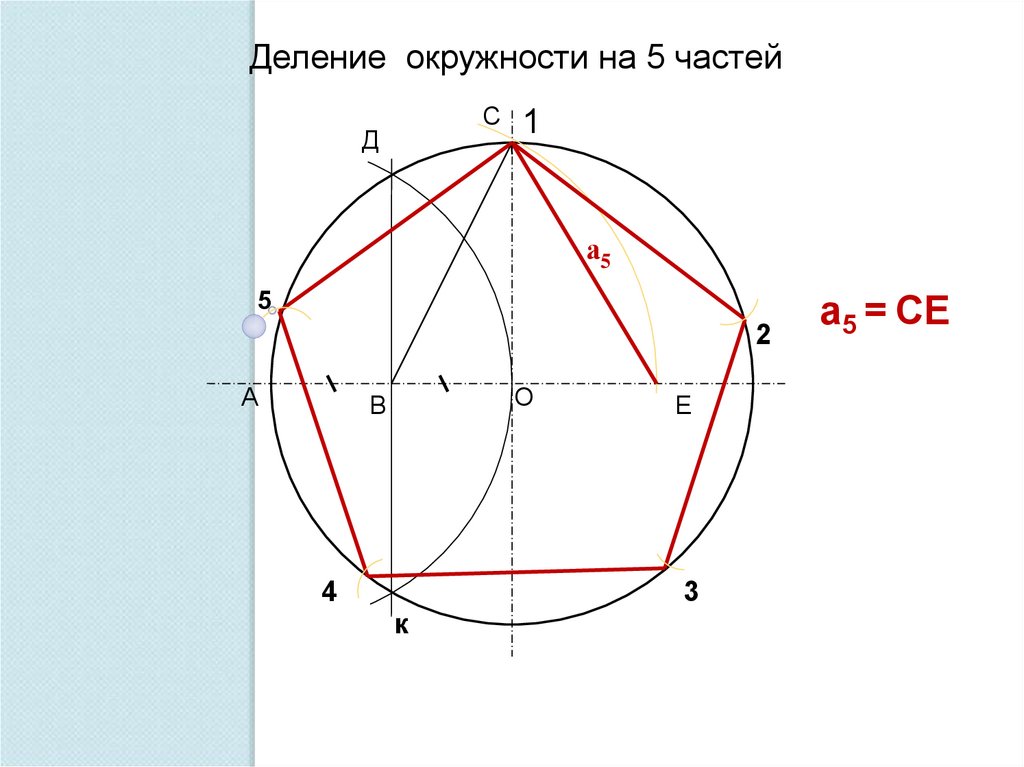
Деление окружности на 5 частей
С
Д
1
а5
5
2
А
О
В
4
Е
3
к
а5 = СЕ

37.

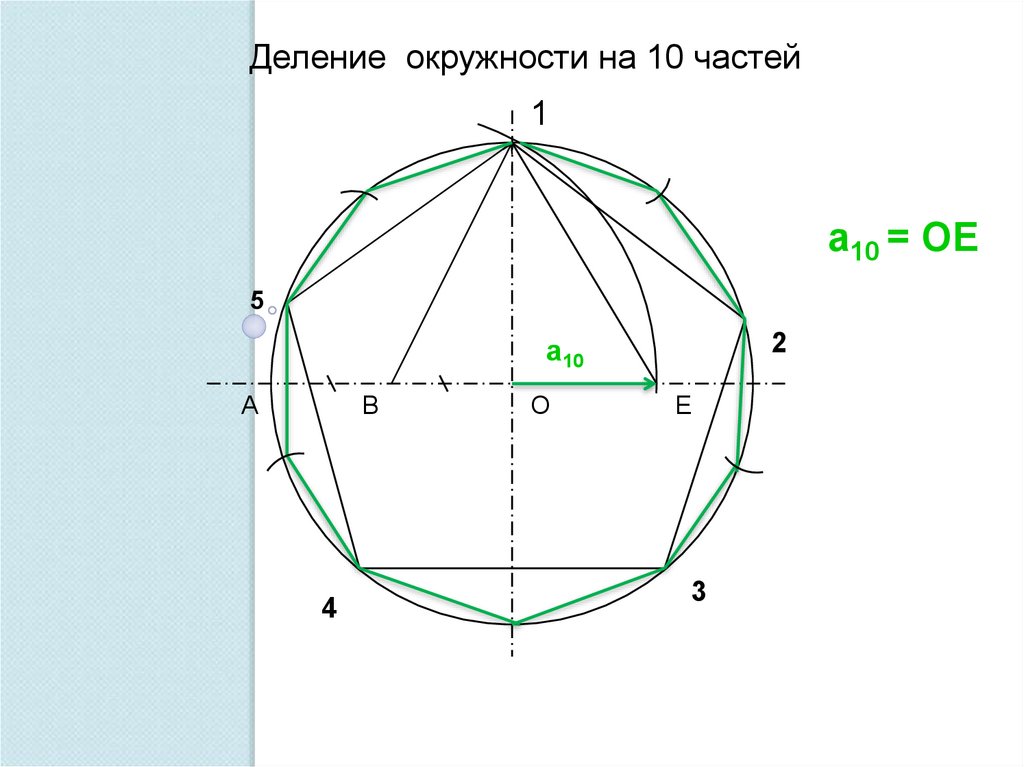
Деление окружности на 10 частей
1
а10 = ОЕ
5
2
а10
А
В
4
О
Е
3

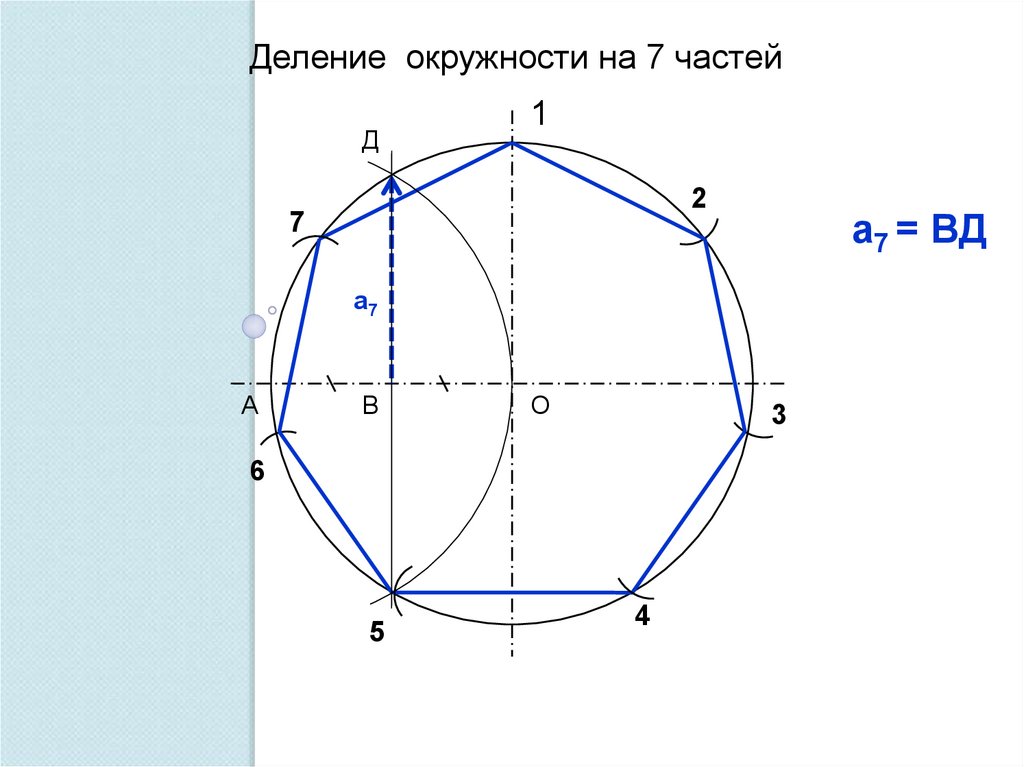
38.

Деление окружности на 7 частей
Д
1
2
7
а7 = ВД
а7
А
В
О
3
6
5
4

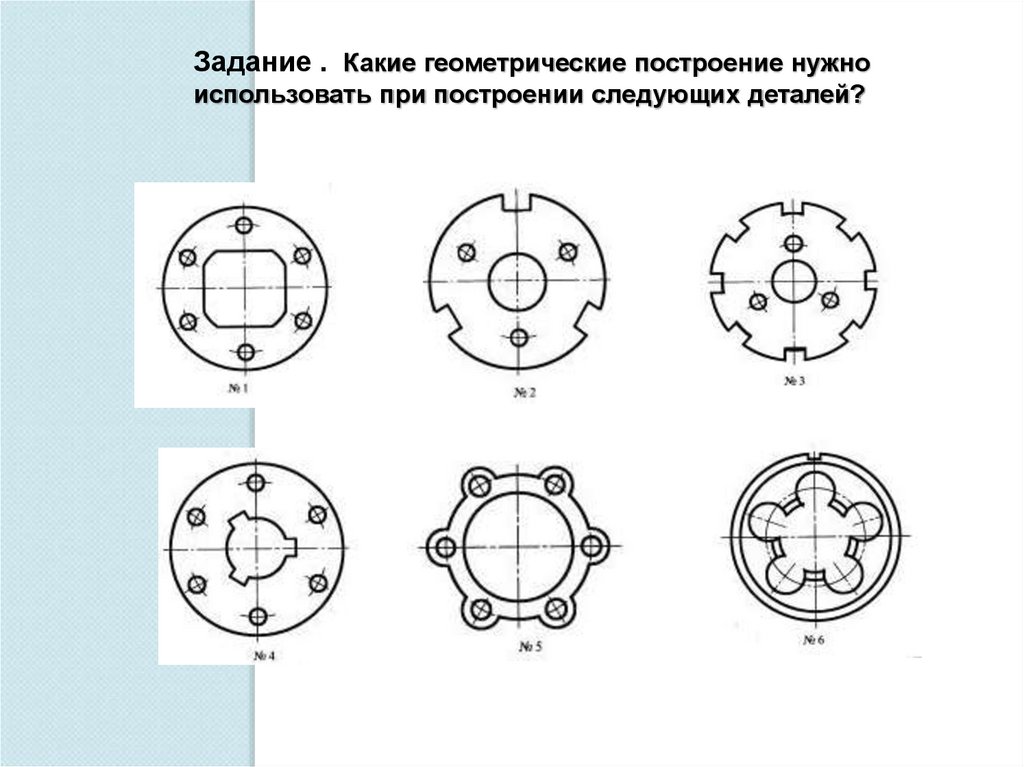
39.

Задание . Какие геометрические построение нужно
использовать при построении следующих деталей?

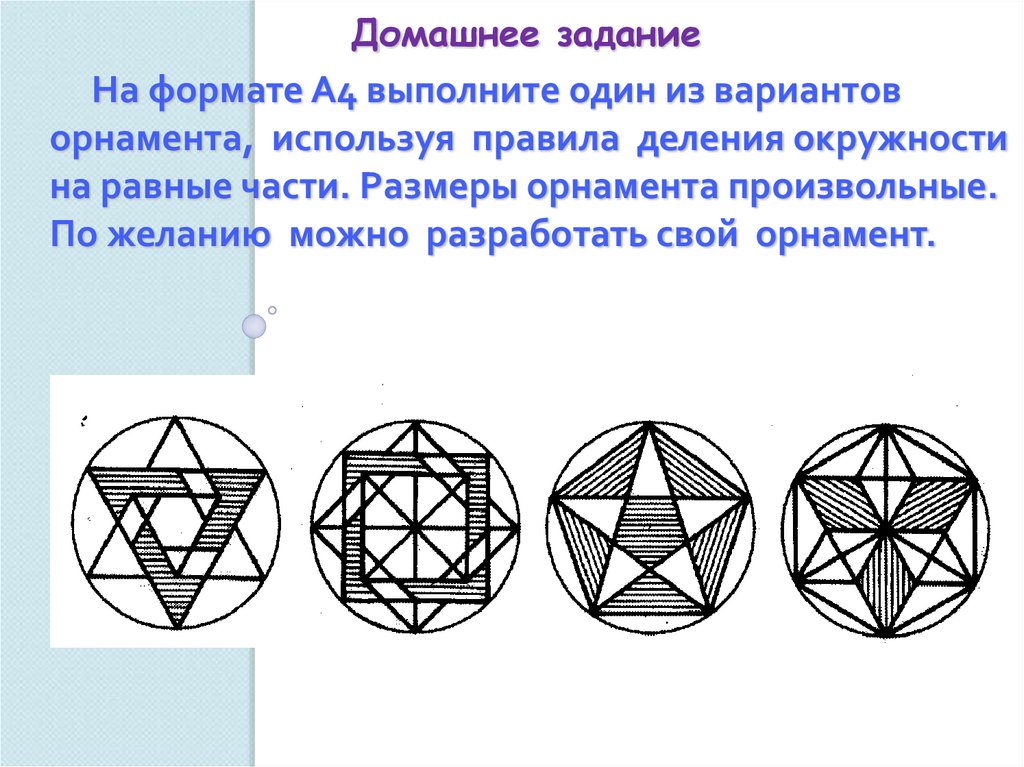
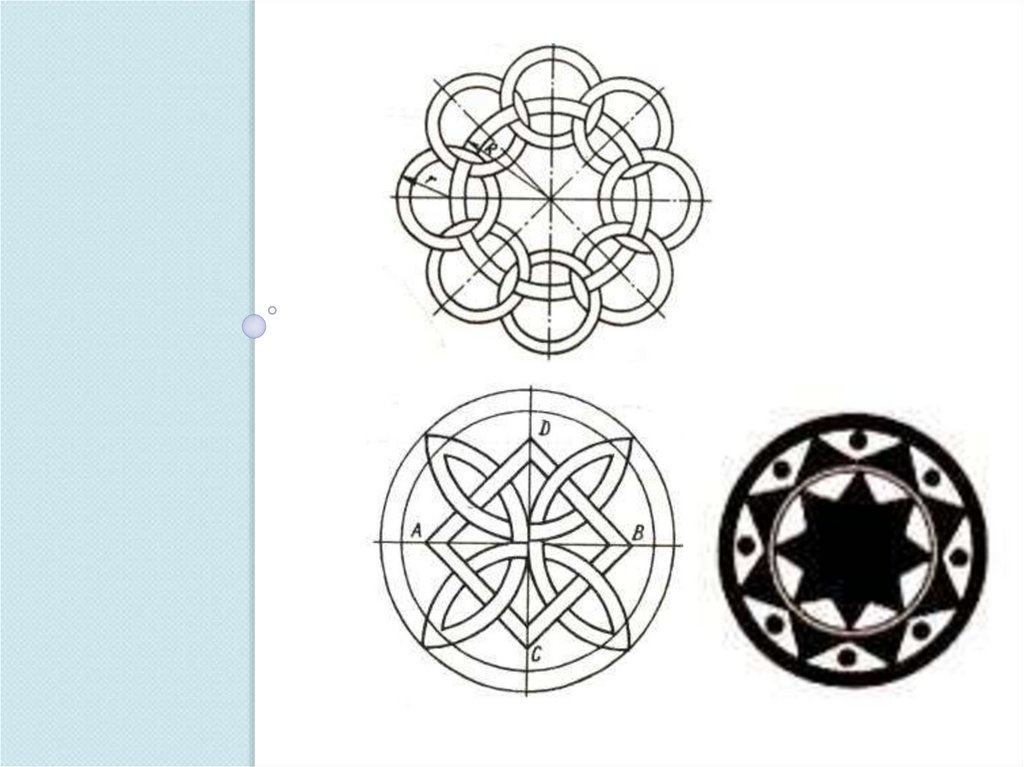
40. Домашнее задание

На формате А4 выполните один из вариантов
орнамента, используя правила деления окружности
на равные части. Размеры орнамента произвольные.
По желанию можно разработать свой орнамент.