Алгебра логики. Основные логические операции. Логические элементы

1. Алгебра логики. Основные логические операции. Логические элементы

2.

1. ОСНОВЫ ЛОГИКИ
Логика - это наука о формах и способах мышления
Мышление осуществляется через:
– понятия;
– высказывания;
– умозаключения.
Понятие - это форма мышления, которая выделяет
существенные признаки предмета или класса предметов,
позволяющие отличать их друг от друга
Пример: Прямоугольник - геометрическая фигура у которой все
углы прямые
Высказывание - это повествовательное предложение в
котором что-либо утверждается или отрицается. Это
формулировка своего понимания окружающего мира
Пример: Париж – столица Франции

3.

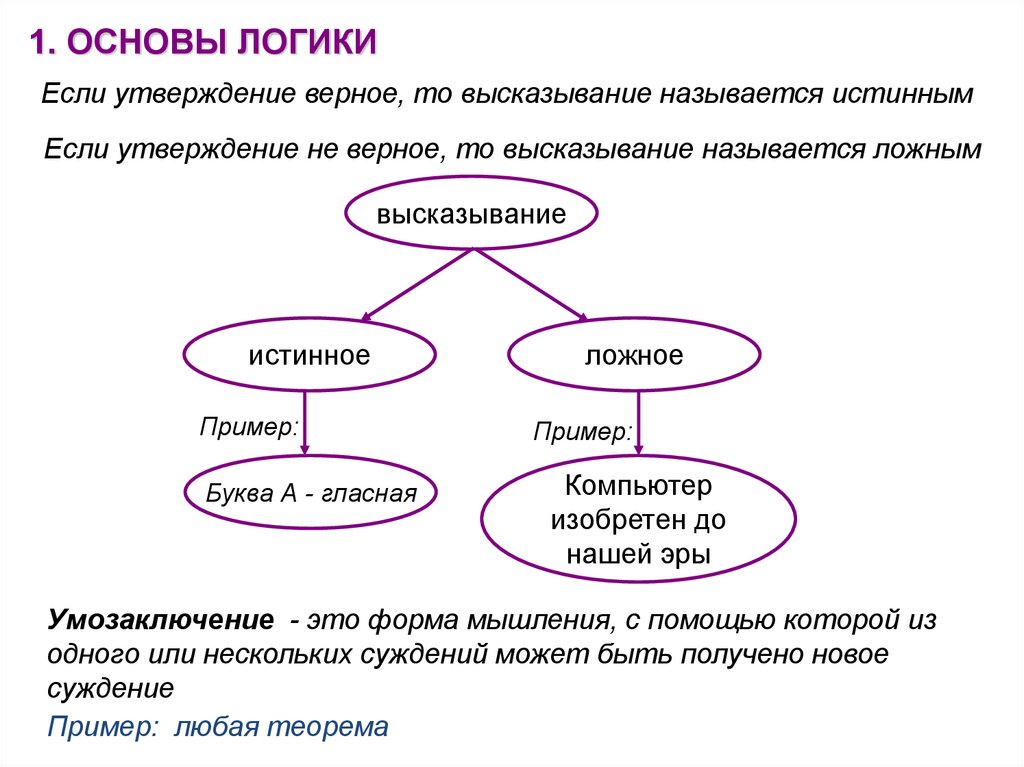
1. ОСНОВЫ ЛОГИКИ
Если утверждение верное, то высказывание называется истинным
Если утверждение не верное, то высказывание называется ложным
высказывание
истинное
ложное
Пример:
Пример:
Буква А - гласная
Компьютер
изобретен до
нашей эры
Умозаключение - это форма мышления, с помощью которой из
одного или нескольких суждений может быть получено новое
суждение
Пример: любая теорема

4.

2. АЛГЕБРА ЛОГИКИ
Алгебра логики – это наука об операциях, которые выполняются
над высказываниями
Основные понятия алгебры логики
Логическая переменная – это простое высказывание,
содержащее только одну мысль.
Обозначение: латинская буква (А, В, Х …)
Значение: ИСТИНА (1) или ЛОЖЬ (0)
Логическая функция – это составное высказывание,
которое содержит несколько простых мыслей, соединенных
между собой с помощью логических операций
Логические операции – логическое действие

5.

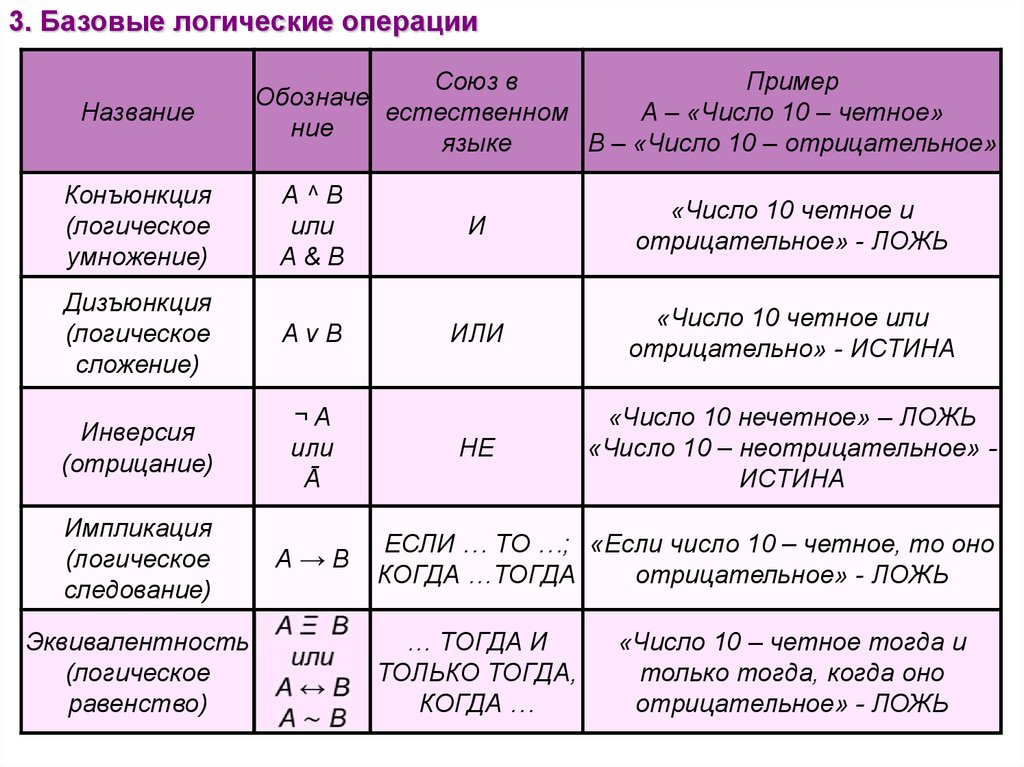
3. Базовые логические операции
Название
Союз в
Пример
Обозначе
естественном
А – «Число 10 – четное»
ние
языке
В – «Число 10 – отрицательное»
Конъюнкция
(логическое
умножение)
А^B
или
A&B
И
«Число 10 четное и
отрицательное» - ЛОЖЬ
Дизъюнкция
(логическое
сложение)
AvB
ИЛИ
«Число 10 четное или
отрицательно» - ИСТИНА
Инверсия
(отрицание)
¬A
или
Ā
НЕ
«Число 10 нечетное» – ЛОЖЬ
«Число 10 – неотрицательное» ИСТИНА
Импликация
(логическое
следование)
А→В
Эквивалентность
(логическое
равенство)
ЕСЛИ … ТО …; «Если число 10 – четное, то оно
КОГДА …ТОГДА
отрицательное» - ЛОЖЬ
… ТОГДА И
ТОЛЬКО ТОГДА,
КОГДА …
«Число 10 – четное тогда и
только тогда, когда оно
отрицательное» - ЛОЖЬ

6. Задание: Записать в виде логического выражения следующее высказывание: «Летом Петя поедет в деревню и, если будет хорошая

3. Базовые логические операции
Задание: Записать в виде логического выражения следующее
высказывание: «Летом Петя поедет в деревню и, если будет
хорошая погода, то он пойдет на рыбалку»
Это составное высказывание состоит из простых
высказываний:
А - «Петя поедет в деревню»
В - «Будет хорошая погода»
С - «Он пойдет на рыбалку»
Записываем высказывание в виде логического выражения,
учитывая порядок действий
F = A & (B → C)
Если составное высказывание (логическую функцию) выразить в виде
формулы, в которую войдут логические переменные и знаки логических
операций, то получится ЛОГИЧЕСКОЕ ВЫРАЖЕНИЕ

7.

Законы алгебры логики
A A
A&B A B
A B A&B
A B A& B
A B A B
A B A B & A B
A B A & B A & B

8.

Законы алгебры логики
A & A B A
A A&B A
A & A B A & B
A A&B A B
A 1 1;
A 0 A;
A & 1 A; A & 0 0;
A&A 0
A A 1
A A A;
A&A A

9.

Законы алгебры логики
Законы коммутативности:
A&B B&A
A B B A
Законы ассоциативности:
A B C A B C A B C
A & B & C A & B & C A & B & C
Законы дистрибутивности:
A & B C A & B A & C
A B & C A B & A C

10. Порядок выполнения логических операций:

3. Базовые логические операции
Порядок выполнения логических операций:
• Действия в скобках
• Инверсия
• Конъюнкция
• Дизъюнкция
• Импликация
• Эквивалентность

11.

ФИЗИЧЕСКИЕ ПРИНЦИПЫ РАБОТЫ КОМПЬЮТЕРА.
ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
Была установлена связь между формой представления информации в
ЭВМ в двоичной системе счисления и алгеброй логики
Схемы процессора и внутренней памяти построены на схемах, которые
называются логическими элементами или вентилями.
Характерной особенностью работы вентилей является то,
что они обрабатывают сигналы двух уровней: 0 и 1

12.

1. Логический элемент НЕ
Логический элемент НЕ называют инвертером или логическим
отрицанием.
Соответствует логической операции – инверсия
Имеет один входной сигнал и один выходной
Сигнал на выходе элемента всегда противоположен сигналу на
входе
Условно обозначается:
A
1
A
Таблица истинности:
вход
выход
0
1
1
0

13.

2. Логический элемент ИЛИ
Логический элемент ИЛИ называют логическим сложением
Соответствует логической операции – дизъюнкция
Имеет два входных сигнала и один выходной
Имеет значение 1 на выходе тогда и только тогда, когда хотя бы
один из сигналов на входе равен 1
Условно обозначается:
A
B
1
A B
Имеет значение 0 на выходе тогда
и только тогда, когда оба значения
сигналов на входе равны 0
Таблица истинности:
вход 1
А
вход 2
B
Выход
A B
0
0
1
0
1
0
0
1
1
1
1
1

14.

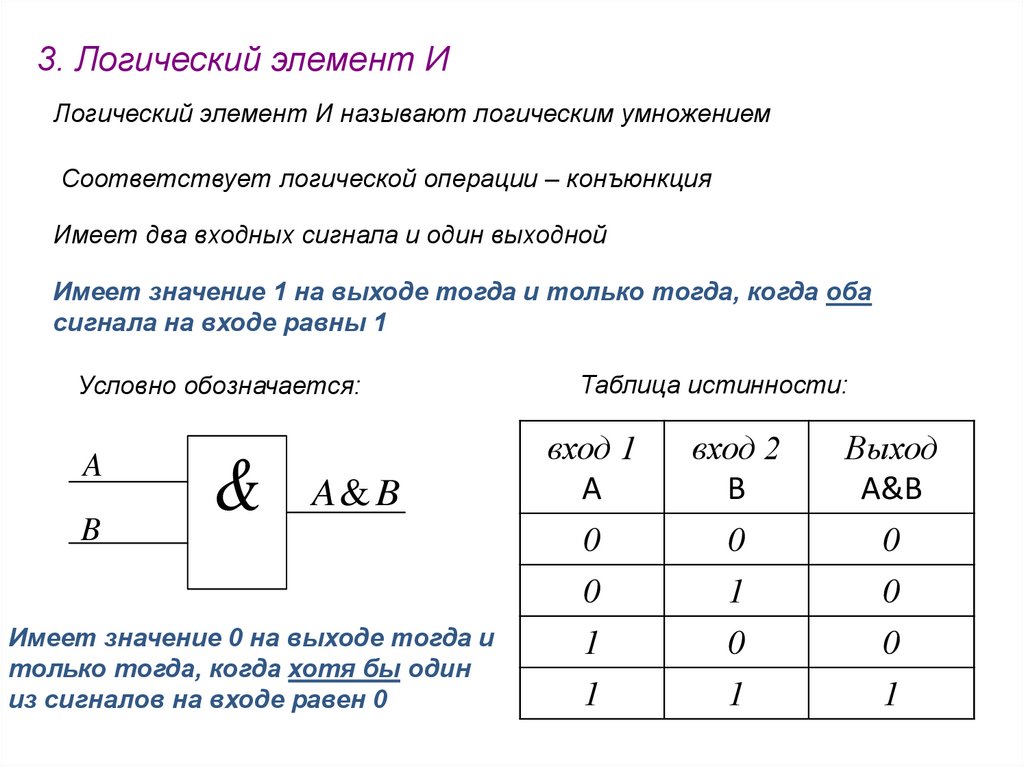
3. Логический элемент И
Логический элемент И называют логическим умножением
Соответствует логической операции – конъюнкция
Имеет два входных сигнала и один выходной
Имеет значение 1 на выходе тогда и только тогда, когда оба
сигнала на входе равны 1
Условно обозначается:
A
B
& A& B
Имеет значение 0 на выходе тогда и
только тогда, когда хотя бы один
из сигналов на входе равен 0
Таблица истинности:
вход 1
А
вход 2
B
Выход
А&B
0
0
0
0
1
1
1
0
1
0
0
1

15.

Для удобства разработчиков ЭВМ были созданы совмещенные элементы,
которые реализуют функции двух элементов
4. Логический элемент ИЛИ - НЕ
Логический элемент ИЛИ-НЕ называют логическим отрицанием сложения
Соответствует логической операции – инверсия дизъюнкции
Имеет два входных сигнала и один выходной
Условно обозначается:
Таблица истинности:
A
вход 1
А
вход 2
B
0
0
1
1
0
1
0
1
B
1
A B
Имеет значение 1 на выходе тогда и
только тогда, когда оба сигнала на
входе равны 0
Имеет значение 0 на выходе тогда и
только тогда, когда хотя бы один
из сигналов на входе равен 1
Выход
A B
1
0
0
0

16.

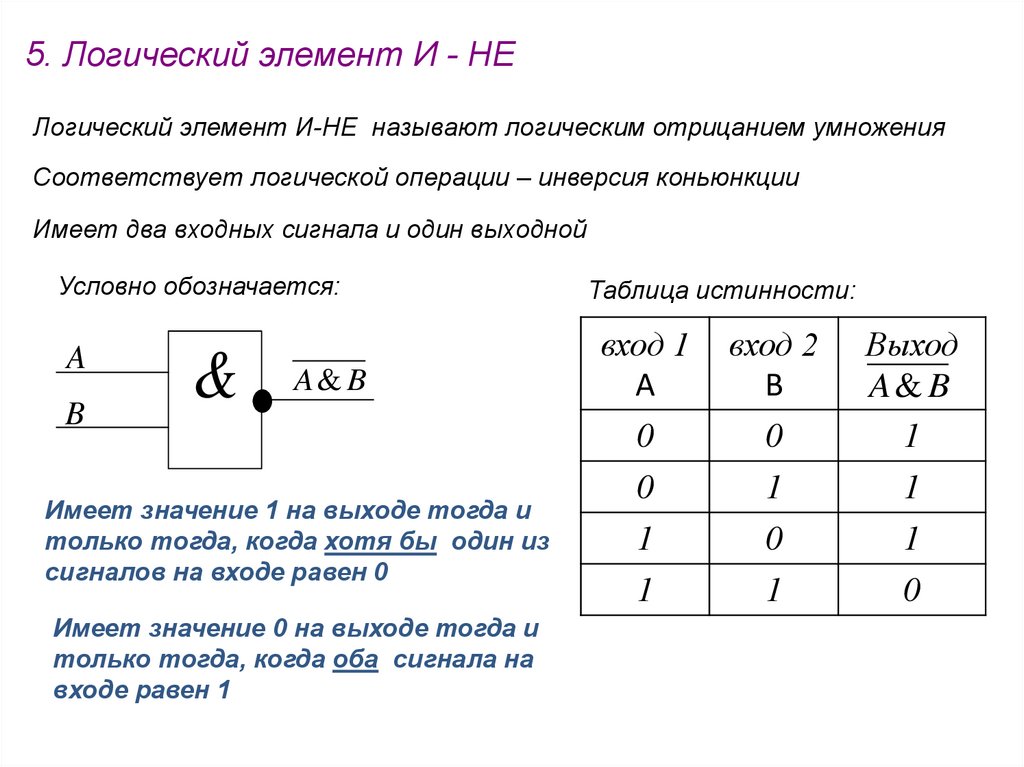
5. Логический элемент И - НЕ
Логический элемент И-НЕ называют логическим отрицанием умножения
Соответствует логической операции – инверсия коньюнкции
Имеет два входных сигнала и один выходной
Условно обозначается:
Таблица истинности:
A
вход 1
А
вход 2
B
0
0
1
1
0
1
0
1
B
&
A& B
Имеет значение 1 на выходе тогда и
только тогда, когда хотя бы один из
сигналов на входе равен 0
Имеет значение 0 на выходе тогда и
только тогда, когда оба сигнала на
входе равен 1
Выход
A& B
1
1
1
0