Lecture_5_2024 (1)

1. РЕАКТОРЫ С НЕПОДВИЖНЫМ СЛОЕМ КАТАЛИЗАТОРА

Инженерная химия каталитических процессов

2. Процесс на пористом зерне катализатора

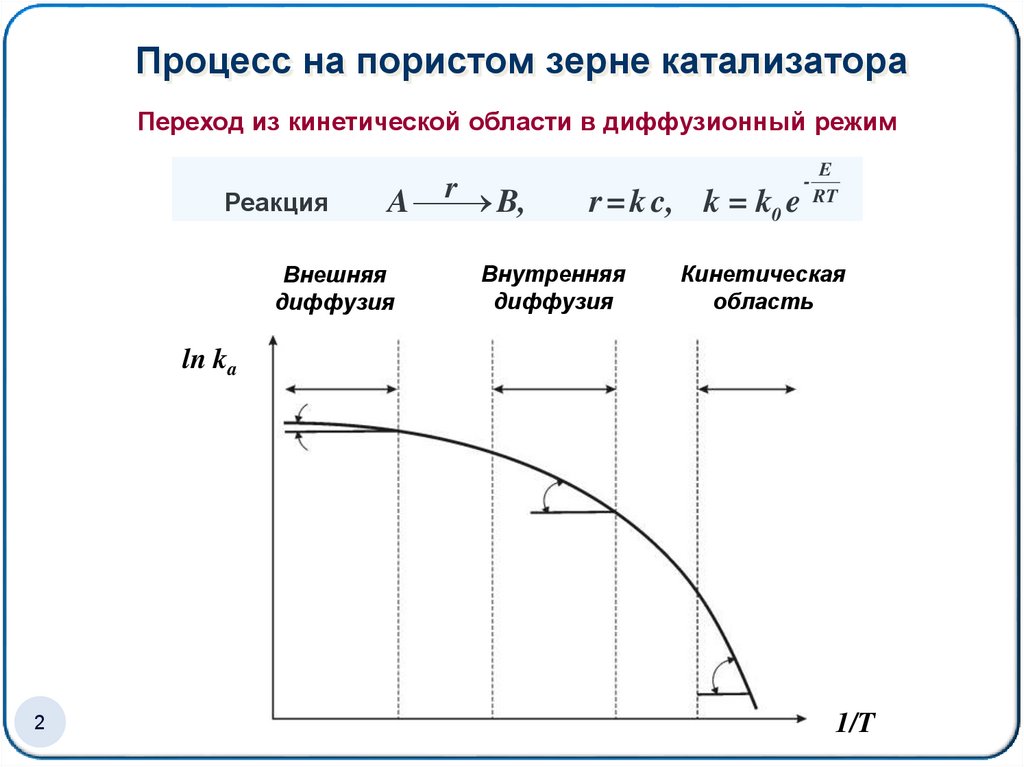
Переход из кинетической области в диффузионный режим
Реакция
r B,
A
Внешняя
диффузия
r = k c, k = k0 e
Внутренняя
диффузия
-
E
RT
Кинетическая
область
ln ka
2
1/T

3.

Процесс на пористом зерне катализатора
Характеристики наблюдаемой скорости реакции
Область протекания процесса
Параметр
Энергия активации
Кинетическая
Внутридиффузионная
Внешнедиффузионная
Еа = Е
Еа Е / 2
Еа 3 – 10 кдж/моль
( T 1,5)
Наблюдаемая
константа
скорости реакции
3
ka = k
ka ~ k ( 1/ ) ka ~ k out ( )
Влияние скорости
газового потока
нет
нет
u 0,65
Влияние размера
зерна
нет
есть
есть

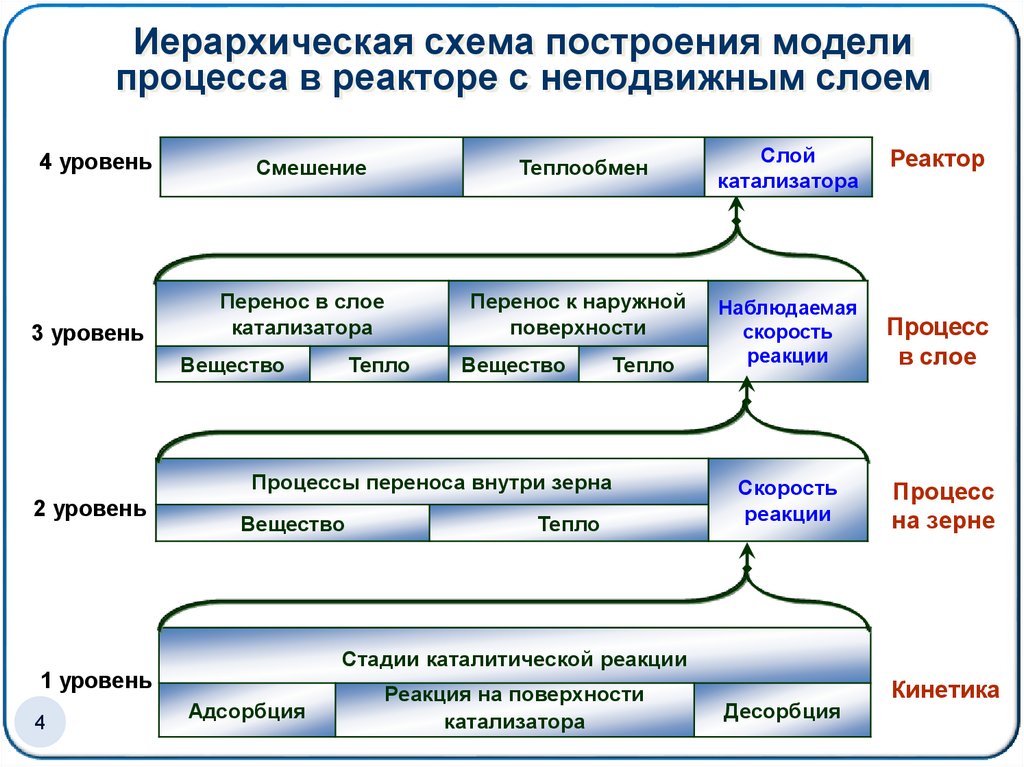
4. Иерархическая схема построения модели процесса в реакторе с неподвижным слоем

4 уровень
Смешение
Теплообмен
3 уровень
Перенос в слое
катализатора
Перенос к наружной
поверхности
Вещество
Тепло
Вещество
Тепло
Процессы переноса внутри зерна
2 уровень
Вещество
Реактор
Наблюдаемая
скорость
реакции
Процесс
в слое
Скорость
реакции
Процесс
на зерне
Стадии каталитической реакции
1 уровень
4
Тепло
Слой
катализатора
Адсорбция
Реакция на поверхности
катализатора
Десорбция
Кинетика

5.

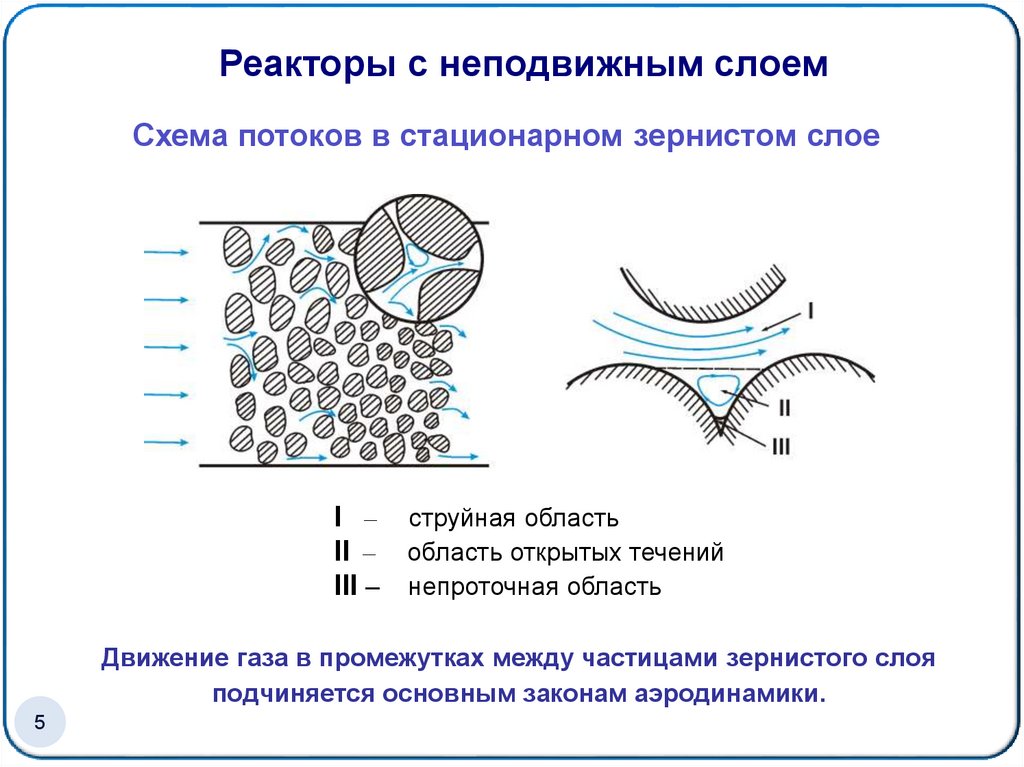
Реакторы с неподвижным слоем
Схема потоков в стационарном зернистом слое
I – струйная область
II – область открытых течений
III – непроточная область
Движение газа в промежутках между частицами зернистого слоя
подчиняется основным законам аэродинамики.
5

6. Характеристики зернистого слоя

Пористость
in - доля объема пористого зерна катализатора, занятая пустотами
in
Порозность
Vg
Vp
(порами)
cм
cм3
3
Vg - объем пор в грануле зерна
V p - объем зерна
- доля объема слоя, не занятая зернистыми элементами
Vg
Vb
м
м3
3
Vg - объем пустот между зернистыми
элементами, через который
проходит газовый поток,
V b - объем зернистого слоя
(газ + зерна)
Доля сечения слоя, пронизываемого потоком газа, в среднем, также равна
Вид упаковки
Шары
6
Порозность
[ м2/ м2].
0,33-0,5 0,4
Цилиндры
0,4
Кубы
0,4
Кольца
0,55-0,65
dp / Dc 0,01

7. Характеристики зернистого слоя

Плотность зернистого элемента (кажущаяся плотность)
p ( 1 in ) m
г
cм3
p
particle density
m – плотность материала (истинная плотность)
Насыпная плотность
(material density)
b
b ( 1 ) p
г
cм3
bulk density
p – плотность зерен твердой фазы
Удельная поверхность зерен Sp - отношение внешней поверхности
зерна S к его объему Vp
S
Sp
Vp
Удельная поверхность зернистого слоя Sb - суммарная внешняя
поверхность зерен в единице объема слоя
Sb S p (1 ) ;
7
c м2
c м3
4 R 2p
для шара
3
c м2
Sb
(1 )
(1 ) 3
3
(4 / 3) R p
Rp
c м

8.

Характеристики зернистого слоя
Газ проходит через зернистый слой по каналам сложного сечения
(поровым каналам)
Эквивалентный диаметр порового канала dpe
d pe
- для каналов некруглого сечения
4
4
Sb
Sp ( 1 )
- для слоя шаров одинакового диаметра
Sb
6
( 1 );
dp
d pe
4
dp;
6 (1 )
0 ,4;
d pe
dp
0 ,5
Средняя линейная скорость u - отношение объемного расхода газа U
к площади сечения слоя Sc
u
U
Sc
c м ( м)
c ек ( superficial velocity )
Скорость скольжения потока относительно зерен
8
U
ue
Sc
ue-
( interstitial velocity )

9. Аэродинамика стационарного зернистого слоя

Движение газа в промежутках между частицами зернистого слоя подчиняется
основным законам аэродинамики.
Критерий Рейнольдса (отношение сил инерции к силам вязкости) - является
основным параметром, определяющим гидродинамические свойства газового
потока :
Re
ud
u - линейная (средняя) скорость, cм/сек;
d - линейный размер, определяющий характер течения газа в системе, cм;
- кинематическая вязкость, cм2/ сек
В аэродинамике рассматривают два предельных случая:
- при обтекании крыла самолета, лопасти турбины и т.д. поток газа
является внешним по отношению к граничным поверхностям.
- при течении газа по трубам и каналам поток течет внутри поверхностей,
на которых задаются граничные условия.
Движение газового потока через зернистый слой - смешанная задача
9

10.

Аэродинамика стационарного зернистого слоя
1. Внешняя задача. При подходе к анализу течения газа, когда оно носит характер
обтекания, в качестве линейного размера берется размер исходных элементов
слоя – диаметр зерна dp. Такой подход оправдан для рыхлых зернистых слоев с
высокой порозностью.
2. Внутренняя задача. Поток газа течет через зернистый слой по проходам
сложного сечения. Характеристический размер – эквивалентный диаметр
порового канала dpe:
Ree
для шара
ue d pe
;
Ree
4
;
Re
6 (1 )
Ree
4
Re
Sb d p
0 ,33 0 ,5;
Ree
1 1,4
Re
Ламинарный режим – движение газа за счет переноса молекул газа, в основном,
посредством диффузии. Граница устойчивости ламинарного движения
Re = 1000 – 1300
Турбулентный режим - движение газа в результате конвективного перемешивания
во внутренней части газового потока
10
Re 1500
Реактор с неподвижным слоем катализатора - ламинарный режим течения
потока реакционной смеси

11.

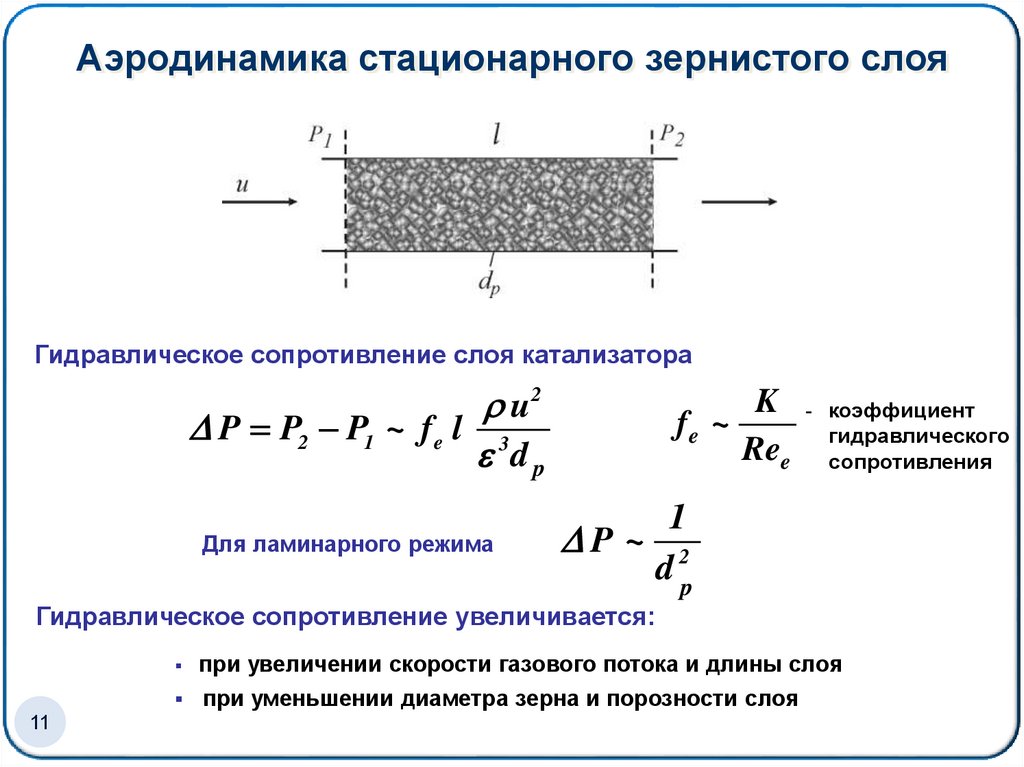
Аэродинамика стационарного зернистого слоя
Гидравлическое сопротивление слоя катализатора
u2
P P2 P1 ~ f e l 3
dp
Для ламинарного режима
K - коэффициент
fe ~
Ree гидравлического
сопротивления
1
P~ 2
dp
Гидравлическое сопротивление увеличивается:
11
при увеличении скорости газового потока и длины слоя
при уменьшении диаметра зерна и порозности слоя

12.

Аэродинамика стационарного зернистого слоя
Оптимальные размеры и форма зерен катализатора
Диаметр зерна. При уменьшении диаметра зерна:
- уменьшаются расходы на катализатор за счет снижения влияния внутренней
диффузии;
- возрастают расходы на преодоление гидравлического сопротивления.
Порозность слоя. Наиболее резко P зависит от доли свободного объема слоя:
- доля свободного объема
0,35
0,5
0,6
- относительное уменьшение
гидравлического сопротивления
1
3,0
5,0
Форма зерен
При низких давлениях оптимальная форма зерен – кольца с тонкими
стенками – большой свободный объем слоя и большое отношение
наружной поверхности зерна к его объему (малый эквивалентный диаметр)
При высоких давлениях – стоимость единицы контактного объема выше
стоимости расходов на преодоление гидравлического сопротивления и
оптимальной формой является шар или цилиндр с плотной упаковкой.
12

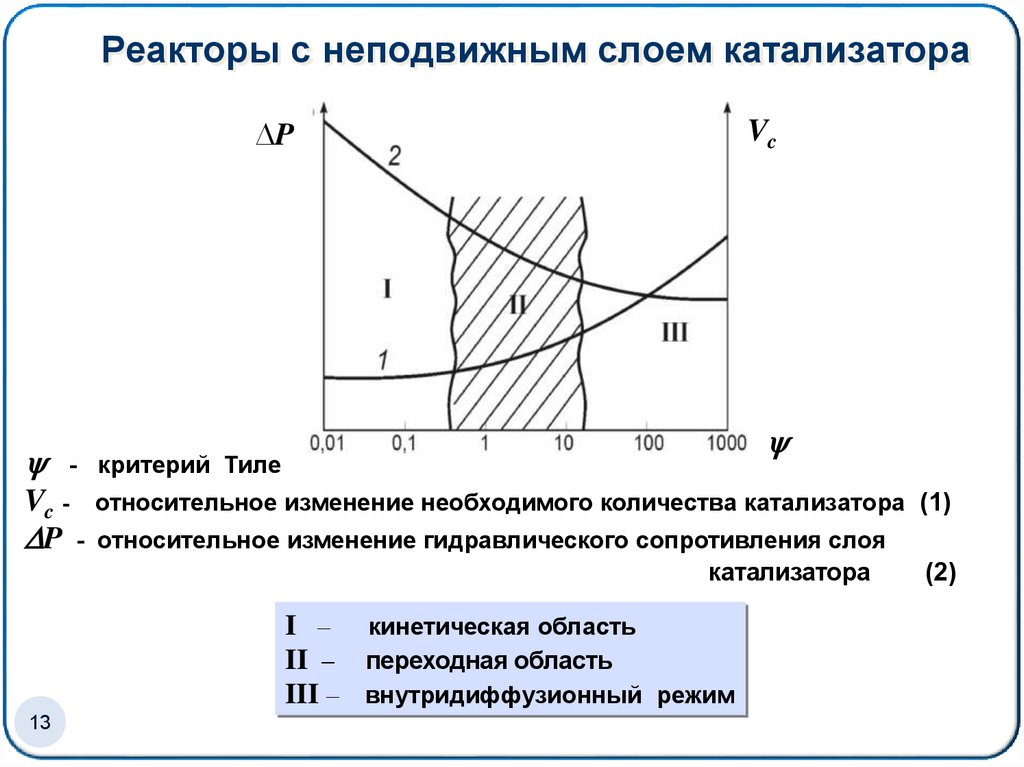
13. Реакторы с неподвижным слоем катализатора

∆P
Vc
- критерий Тиле
Vc - относительное изменение необходимого количества катализатора (1)
P - относительное изменение гидравлического сопротивления слоя
катализатора
I – кинетическая область
II – переходная область
III – внутридиффузионный режим
13
(2)

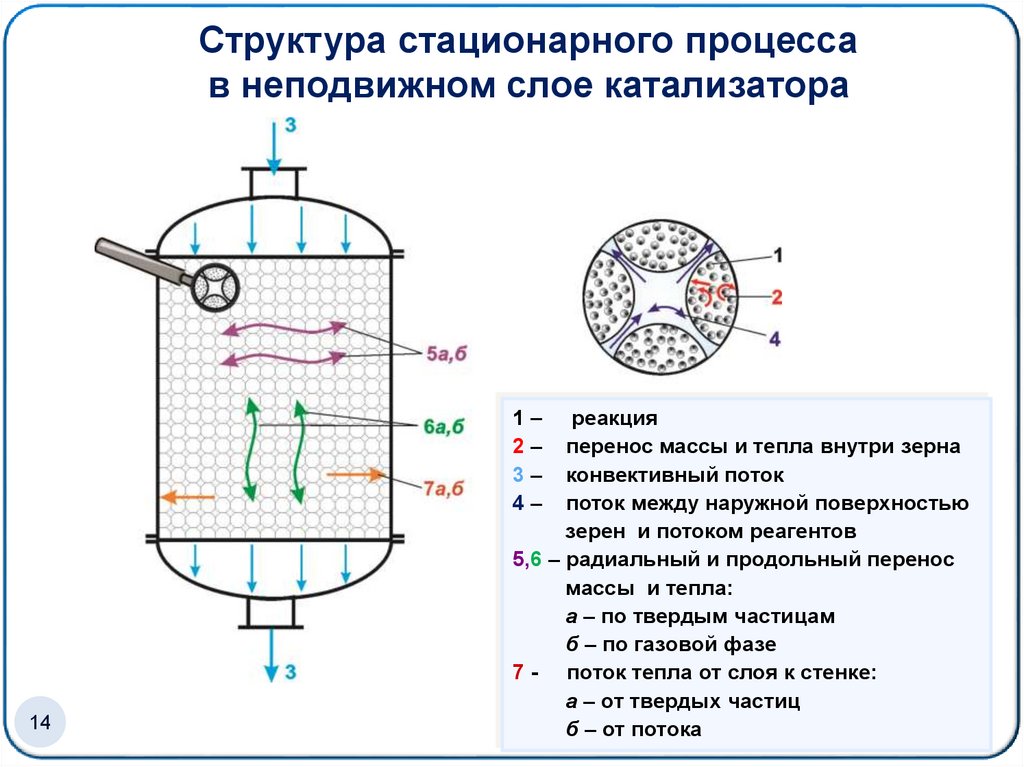
14.

Структура стационарного процесса
в неподвижном слое катализатора
1–
2–
3–
4–
14
реакция
перенос массы и тепла внутри зерна
конвективный поток
поток между наружной поверхностью
зерен и потоком реагентов
5,6 – радиальный и продольный перенос
массы и тепла:
а – по твердым частицам
б – по газовой фазе
7 - поток тепла от слоя к стенке:
а – от твердых частиц
б – от потока

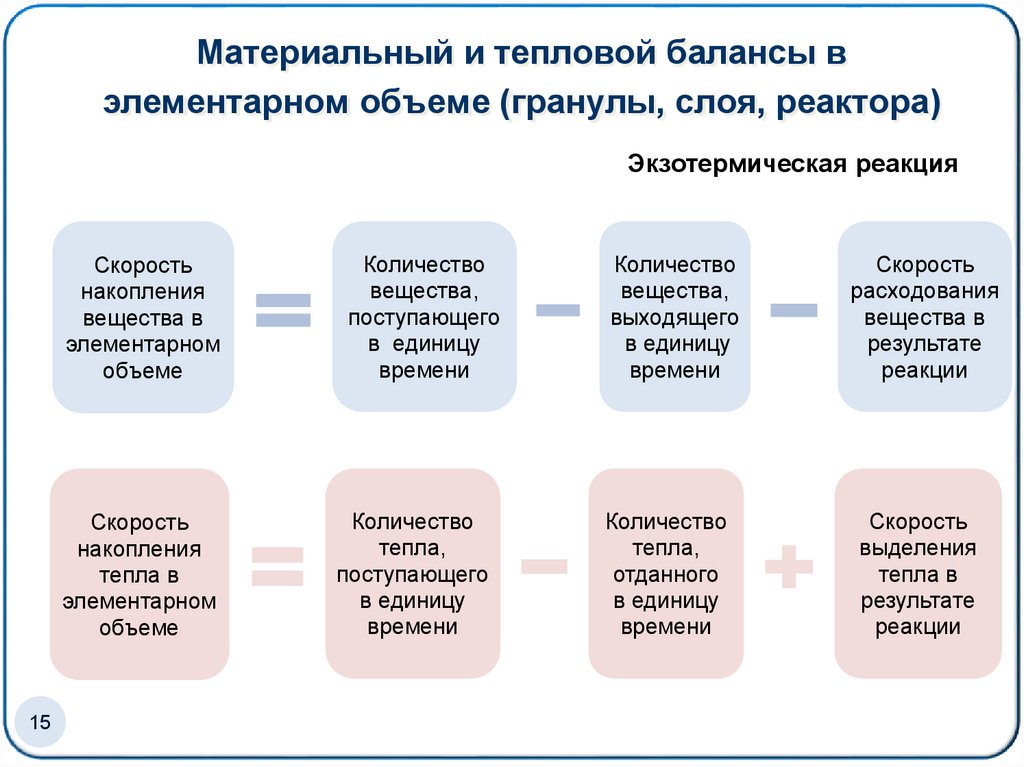
15. Материальный и тепловой балансы в элементарном объеме (гранулы, слоя, реактора)

Экзотермическая реакция
15
Скорость
накопления
вещества в
элементарном
объеме
Количество
вещества,
поступающего
в единицу
времени
Количество
вещества,
выходящего
в единицу
времени
Скорость
расходования
вещества в
результате
реакции
Скорость
накопления
тепла в
элементарном
объеме
Количество
тепла,
поступающего
в единицу
времени
Количество
тепла,
отданного
в единицу
времени
Скорость
выделения
тепла в
результате
реакции

16. Уравнения материального и теплового баланса в каталитическом реакторе

Исходные соотношения математической модели слоя катализатора:
- уравнения общего материального баланса по каждому компоненту в газовой
фазе,
- уравнения теплового баланса по каждой из фаз отражают скорость реакции и скорости процессов переноса массы и тепла
в слое, которые появляются в результате возникновения градиентов
концентраций и температур
Слой катализатора рассматривается как однородная среда и вводятся обобщенные характеристики слоя.
Степень детализации зависит от цели исследований, от того, на какие вопросы
необходимо получить ответ.
Простейшие модели реактора с неподвижным слоем– модели реакторов с
режимами ИВ и ИС используются:
- при описании данных кинетических экспериментов в лабораторных реакторах;
16
- при выявлении принципиально новых, более эффективных способов
осуществления процесса;
- для определения оптимальных условий;
- для проверки адекватности более детальных и сложных моделей.

17. Реакторы непрерывного действия

Режим идеального вытеснения (ИВ):
При протекании каталитической реакции в неподвижном слое градиенты
концентраций и температур обусловлены только конвективным потоком.
Скорости остальных процессов переноса гораздо выше скоростей реакции и
не оказывают заметного влияния на профили концентраций и температур.
dl
U, co
U, c
c+∆c
c
dVc
Реакция А В
Т = соnst
r - скорость расходования А,
Sc – площадь сечения слоя
Материальный баланс:
c
c
dVc U c - U (c
dVc ) - r dVc ;
t
Vc
c
c
-u r ;
t
l
17
t 0
U
u; dVc Sc dl
Sc
c ( l ) c * ; l 0 c co

18. Реакторы непрерывного действия

Реакция А В, r = k c
Режим идеального вытеснения (ИВ):
Т = соnst
dc
- k c;
d
t
c co e
с, сout
cо
k
r kc n
n1 n2
Критерий Дамкелера – К = k ,
(соотношение скорости реакции, объема
катализатора и скорости конвективного
переноса вещества)
n1
n2
l ( )
18
0: c c0 ;
Vc l
U u
Характерное время конвективного
переноса вещества ─
Профиль концентраций реагента А от длины реактора c и зависимость
выходной концентрации реагента А cout от времени контакта подобны.

19. Реакторы непрерывного действия

Режим идеального смешения (ИС):
Газовый поток проходит через неподвижный слой катализатора, в результате
дополнительных воздействий реализуется режим, при котором концентрации
реагентов постоянны по высоте слоя.
U, сo
Реакция А В
Т = соnst
L
dc
Vc
U (co c ) Vc r
dt
t 0
c c
U, с
Уравнение материального баланса получено сразу для всего объема
катализатора, т.к. градиент концентраций существует только на входе в реактор.
19

20. Реакторы непрерывного действия

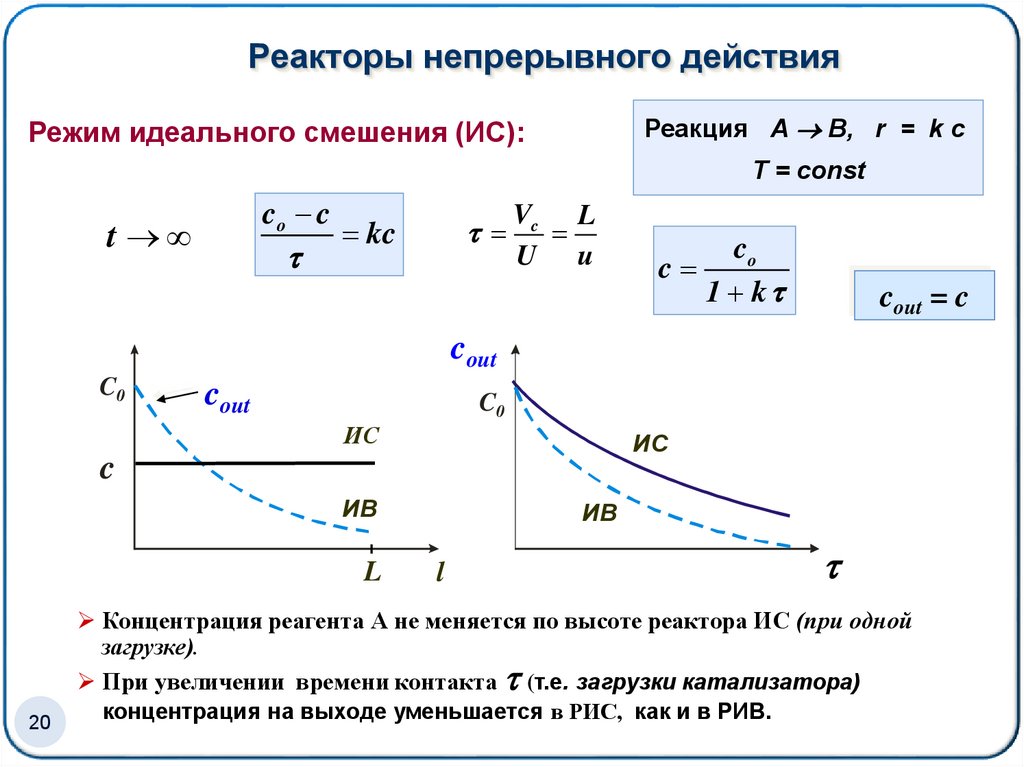
Реакция А В, r = k c
Режим идеального смешения (ИС):
Т = соnst
co c
t
kc
Vc L
U u
c
co
1 k
cout = c
cout
C0
cout
C0
ИС
ИС
c
ИВ
L
ИВ
l
Концентрация реагента А не меняется по высоте реактора ИС (при одной
загрузке).
При увеличении времени контакта (т.е. загрузки катализатора)
20
концентрация на выходе уменьшается в РИС, как и в РИВ.

21. Реакторы непрерывного действия

Реакция А В, r = k c
Реактор идеального вытеснения
dc
kc
d
c co e k
dx
k (1 x )
d
x 1 e k
Реактор идеального смешения
c co
k c
co
c
1 k
x
k (1 x )
k
x
1 k
Т = соnst
Качественные закономерности, полученные для
моделей ИВ и ИС при
протекании реакции 1-го
порядка, справедливы и для
более сложной кинетики
Количество превращенного
вещества в реакторах ИВ и ИС
зависит от одного параметра –
критерия Дамкелера
К = k
21

22.

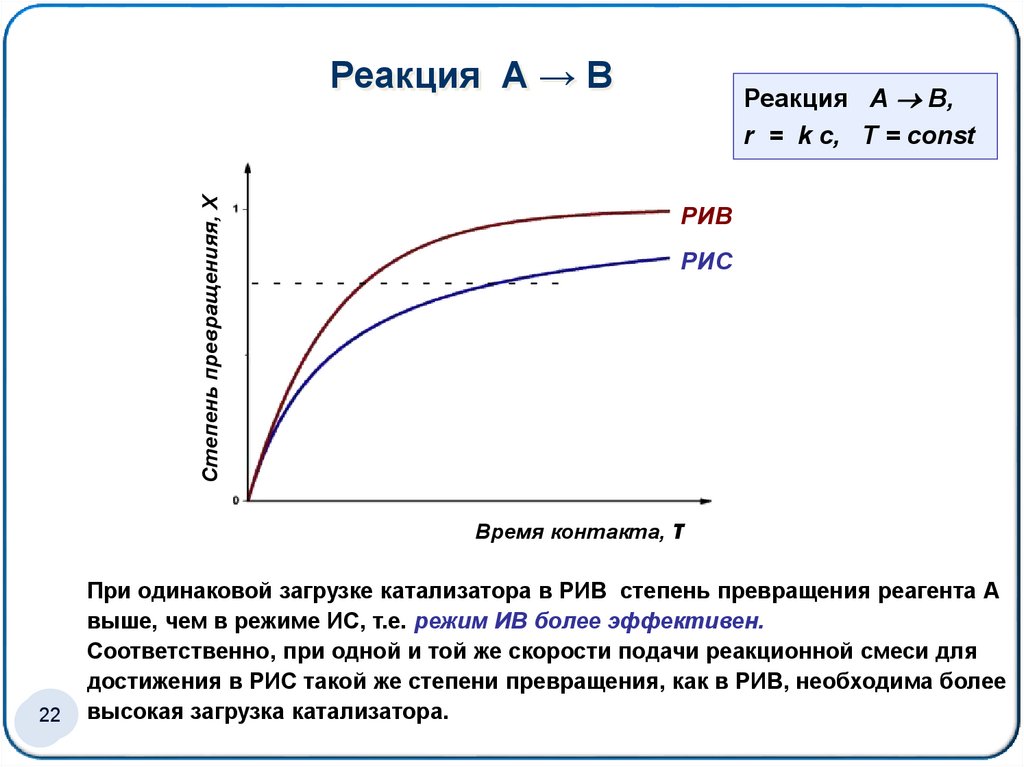
Степень превращенияя, X
Реакция А → В
Реакция А В,
r = k c, Т = соnst
РИВ
- - - - - - - - - - - - - - -
РИС
Время контакта, τ
22
22
При одинаковой загрузке катализатора в РИВ степень превращения реагента А
выше, чем в режиме ИС, т.е. режим ИВ более эффективен.
Соответственно, при одной и той же скорости подачи реакционной смеси для
достижения в РИС такой же степени превращения, как в РИВ, необходима более
высокая загрузка катализатора.

23.

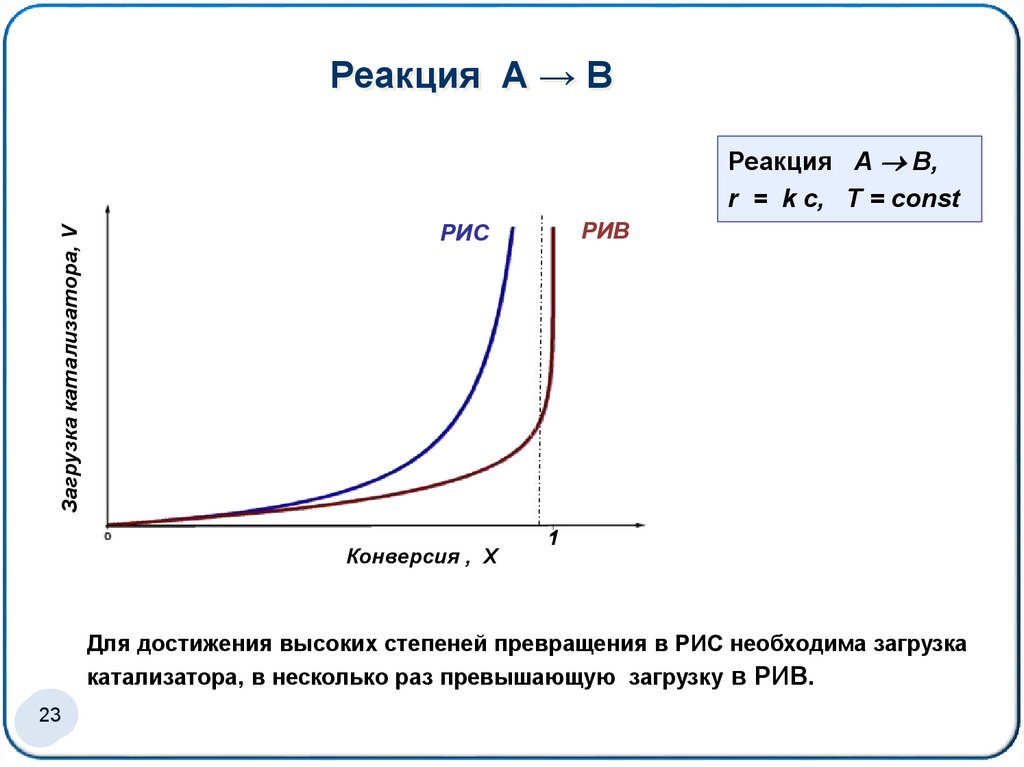
Реакция А → В
Загрузка катализатора, V
Реакция А В,
r = k c, Т = соnst
РИВ
РИС
Конверсия , Х
1
Для достижения высоких степеней превращения в РИС необходима загрузка
катализатора, в несколько раз превышающую загрузку в РИВ.
23
23

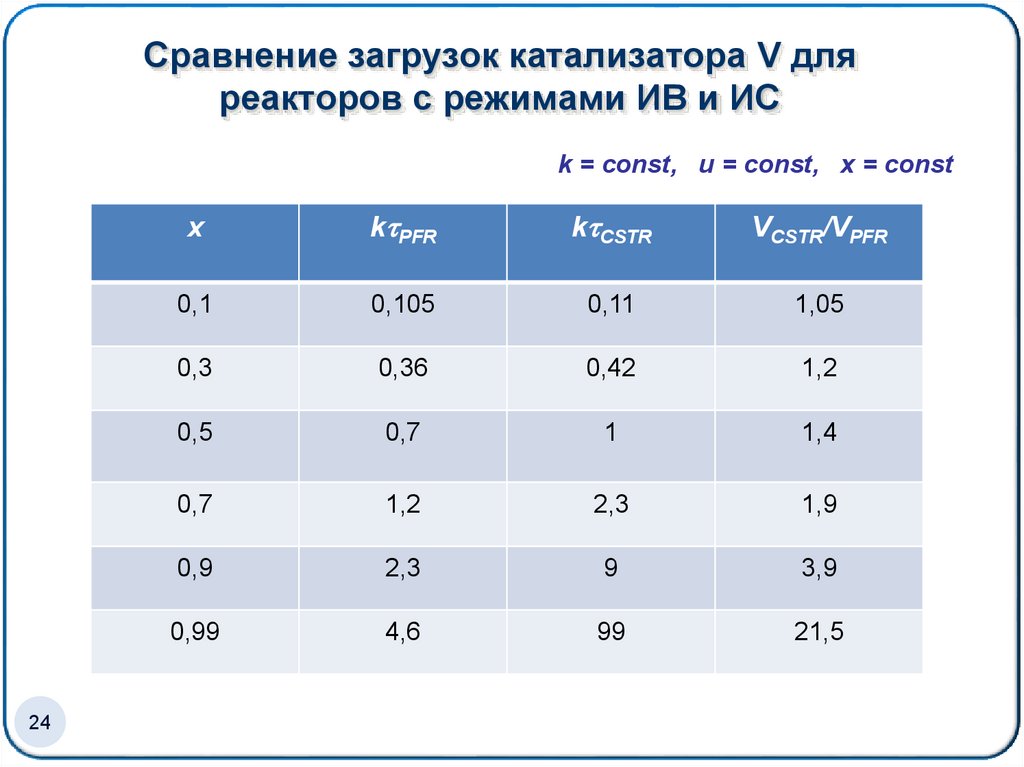
24. Сравнение загрузок катализатора V для реакторов с режимами ИВ и ИС

k = const, u = const, x = const
24
x
k PFR
k CSTR
VCSTR/VPFR
0,1
0,105
0,11
1,05
0,3
0,36
0,42
1,2
0,5
0,7
1
1,4
0,7
1,2
2,3
1,9
0,9
2,3
9
3,9
0,99
4,6
99
21,5

25. Реактор идеального вытеснения

Cложная реакция
r1
T = const
r2
A B C
d cA
k1 c A
d
d cB
k1 c A - k2 c B
d
r1 = k1 cA, r2 = k2 cB
В безразмерном виде:
0:
x
c A c A0 , cB 0
dx
d k1 ( 1 - x )
d EB k ( 1 - x ) - k E
1
1
B
d
cB
EB
c A0
0:
x 0, E B 0
Максимальный выход ЕB равен:
d EB
0;
d
25
E max
1
k1 ( 1 )
c A0 - c A
c A0
ln ;
E B max 1
k2
k1

26. Реактор идеального смешения

Cложная реакция
c A0 c A
cB
r1
r2
A B C
T = const
r1 = k1 cA, r2 = k2 cB
k1 c A
В безразмерном виде:
c A0 - c A
x
c A0
k1 c A - k 2 c B
x
k1 ( 1 - x )
EB k ( 1 - x ) - k E
1
1
B
EB
k1
x
1 k1
EB
k1
( 1 k1 ) ( 1 k1 )
cB
c A0
k2
k1
Максимальный выход ЕB равен:
26
d EB
0;
d
B max
1
k1
;
E B max
1
(1 )2

27.

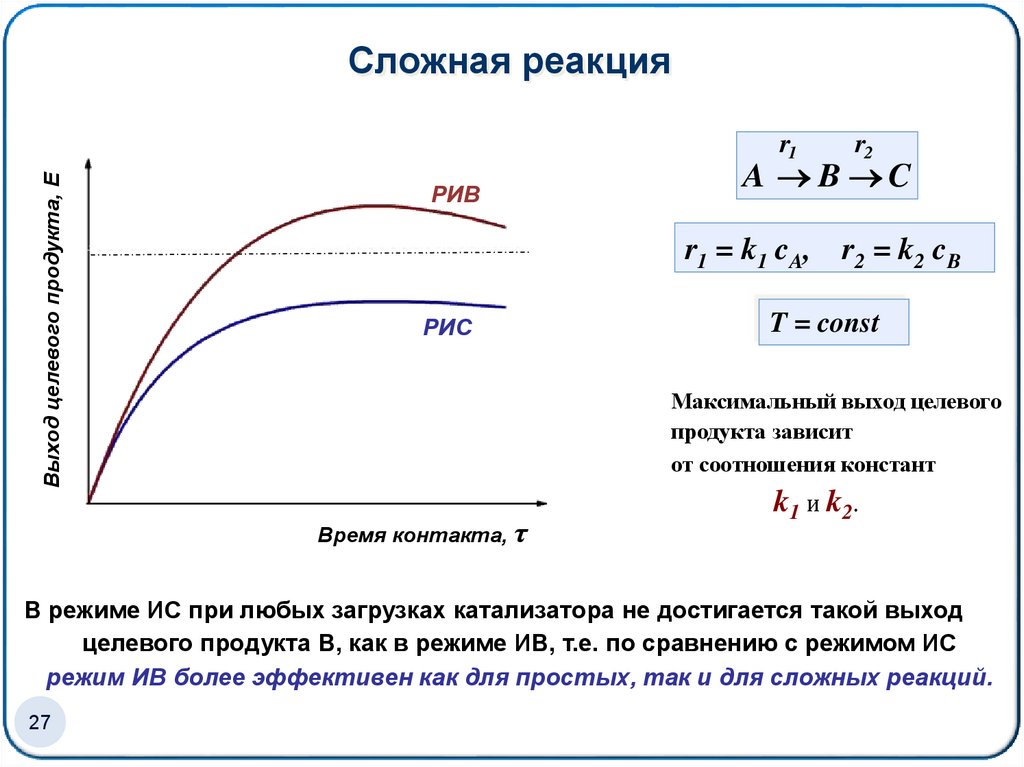
Сложная реакция
Выход целевого продукта, Е
r1
РИВ
A B C
r1 = k1 cA,
РИС
r2
r2 = k2 cB
T = const
Максимальный выход целевого
продукта зависит
от соотношения констант
Время контакта, τ
k1 и k2.
В режиме ИС при любых загрузках катализатора не достигается такой выход
целевого продукта B, как в режиме ИВ, т.е. по сравнению с режимом ИС
режим ИВ более эффективен как для простых, так и для сложных реакций.
27

28.

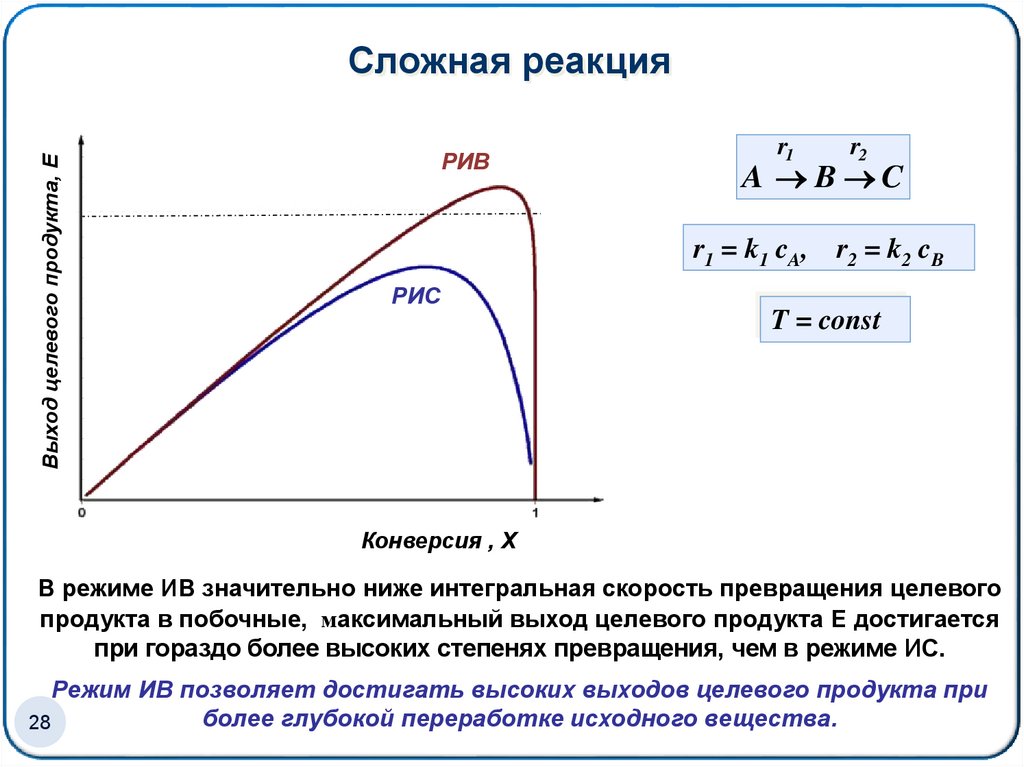
Выход целевого продукта, Е
Сложная реакция
РИВ
r1
r2
A B C
r1 = k1 cA, r2 = k2 cB
РИС
T = const
Конверсия , Х
В режиме ИВ значительно ниже интегральная скорость превращения целевого
продукта в побочные, максимальный выход целевого продукта Е достигается
при гораздо более высоких степенях превращения, чем в режиме ИС.
Режим ИВ позволяет достигать высоких выходов целевого продукта при
более глубокой переработке исходного вещества.
28

29. Проточный реактор идеального вытеснения

Реакция А В
Материальный баланс
c
t
-U
c
-r
Vc
r =r kck c; ,
E
k k e RT
-
0
Тепловой баланс
C gVg C c Vc ( 1 - ) T
T
C
U
Qr r
g
Vc
Vc
t
Граничные условия
l 0 : c c0 , T T0
t 0: c l c* l , T l T * l
c
T - f ( t, Vg, Vc, U, Cg, Cc, T0, c0, k0, E, Qr )
29
11 параметров

30. Проточный реактор идеального cмешения

Материальный баланс
Vc
dc
U (co c ) Vc r
dt
Реакция А В
r =r kck c; ,
E
k k e RT
-
0
Тепловой баланс
dT
Vg C g Vc Cc (1 ) dt U C g T0 - T QrVc r
t 0: c c* , T T *
время, сек
со, с – концентрации вещества A на входе в реактор и в реакторе,
объемные доли
Tо, T – температура реакционной смеси на входе в реактор и в
реакторе, oK
r–
скорость расходования реагента A, моль/м3 сек
Qr –
тепловыделение реакции, кдж/моль
U–
скорость подачи газа, м3/сек
Vg,Vc – объем газовой фазы и cлоя катализатора в реакторе, м3
Cg,Cc– теплоемкость газовой фазы и катализатора, дж/м3град
t -
30

31. Уравнения материального и теплового баланса в реакторе с неподвижным слоем

Cлой катализатора представляет собой неоднородную систему из двух фаз:
- твердые частицы;
- промежутки между ними, по которым движется газ.
Исходные соотношения математической модели слоя:
- уравнения материального баланса по каждому компоненту в газовой фазе,
- уравнения теплового баланса по каждой из фаз.
В слое возникают градиенты концентраций и температур, обусловленные
протеканием реакции и процессами тепло- и массопереноса, такими как:
1.
2.
3.
4.
5.
31
Конвективный поток
Внутренняя диффузия
Внешняя диффузия
Продольный и радиальный перенос массы и тепла
Теплопередача через стенку реактора
Для описания процессов продольного и радиального переноса
массы и тепла используются также законы Фика и Фурье

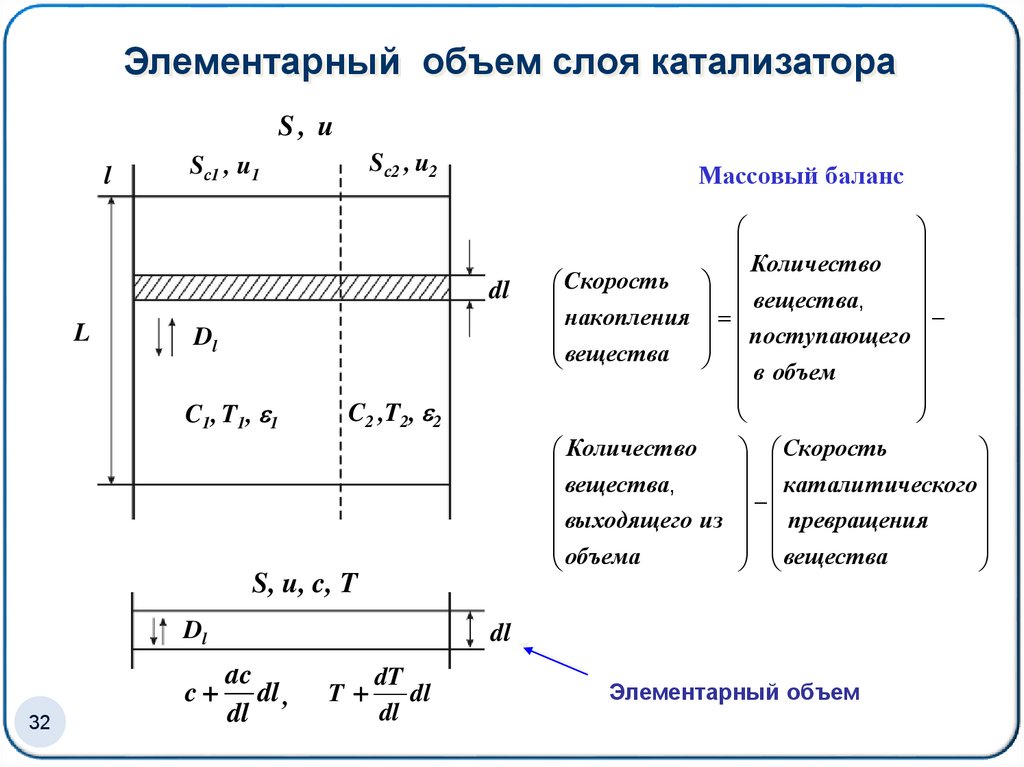
32.

Элементарный объем слоя катализатора
S, u
l
Sс2 , u2
Sс1 , u1
Массовый баланс
dl
L
Dl
C1, T1, 1
C2 ,T2, 2
S, u, c, T
Dl
c
32
Количество
Cкорость
вещества,
накопления поступающего
вещества
в объем
Количество
Скорость
вещества
,
каталитического
выходящего из превращения
объема
вещества
dl
dc
dl ,
dl
T
dT
dl
dl
Элементарный объем

33. Диффузионная модель неподвижного слоя

Допущения:
- Протекает простая реакция без изменения объема при
стационарных усл.
- Скорость внешней диффузии гораздо выше, чем скорость
реакции, слой рассматривается как квазигомогенная среда,
т.е. катализатор имеет ту же температуру, что и газ.
- Cкорость переноса массы и тепла по радиусу слоя велика,
т.е. концентрация вещества и температуры постоянны по
радиусу слоя
33

34. Квазигомогенная модель реактора с неподвижным слоем

Учет аксиальной диффузии
Без учета внешней и радиальной диффузии и без
отвода тепла, стационарные условия, т.е. t
d 2c
dc
Dl 2 u
r c,T 0
dl
dl
d 2T
dT
l 2 ucg
Qr r c,T 0
dl
dl
Граничные условия
(условия Данквертса)
l 0
Dl - эффективный коэффициент
l -
продольной диффузии
эффективный коэффициент
продольной теплопроводности
l L
dc
Dl
u ( c c0 )
dl
dT
u c0 T T0
dl
dc dT
0
dl
dl
Процессы в слое катализатора –
3 уровень иерархической схемы
34

35. Квазигомогенная модель реактора с неподвижным слоем

С учетом радиальной диффузии и отвода тепла
2 c 1 c
2 c
c
Dl 2 Dr
u
r
c
,
T
0
l
l
rc rc rc
2T 1 T
2T
T
l 2 r 2
uc
Qr r c,T 0
g
l
rc rc
l
rc
Dr - эффективный
коэффициент
радиальной
диффузии
r - эффективный
коэффициент
радиальной
теплопроводности
Граничные условия
l 0
l L
35
c
c T
rc 0
0
u ( c c0 )
l
rc rc
T
c
l
u c0 T T0 rc 1
0
l
rc
c T
T
0
r
F Tc T
l l
rc
Dl

36. Характерные времена процессов массо- переноса в слое катализатора

Характерные времена процессов массопереноса в слое катализатора
Процесс
Реакция
- превращение
вещества
- дезактивация
катализатора
Выражение
1
r
k
rd
Внутренняя диффузия
- масса
Dp
Внешняя диффузия
- масса
Неподвижный слой
продольная диффузия
- масса
радиальная диффузия
- масса
L2
τ =
D
Псевдоожиженный слой
- массообмен
36
Характерное время
(time scale)
Порядок величин
1
kd
R2p
De
1
Sbc
10-1 – 10 сек
103 – 105сек
10-1 – 10 сек
10-2 – 10–1 сек
100 – 103 сек
Rc2
τr =
Dr
1
10-1 – 10 сек
100 – 101 сек