Похожие презентации:
Простые числа
1.
2.
3.
ЭвклидС древних времен известно,
что во множестве
натуральных чисел
встречаются числа, которые
делятся только на 1 и на
само число. Такие числа
назвали простыми.
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,
12 13, 14, 15, 16, 17, 18, 19,
20, 21, 22, 23, 24, 25, 26,
27,…
4.
Небольшую «коллекцию»простых чисел нам поможет
составить старинный способ,
придуманный еще в 3 веке
до н.э. Эратосфеном Киренским,
хранителем знаменитой
Александрийской библиотеки
5.
6.
РешетоЭратосфена
7.
Д. X. Лемер8.
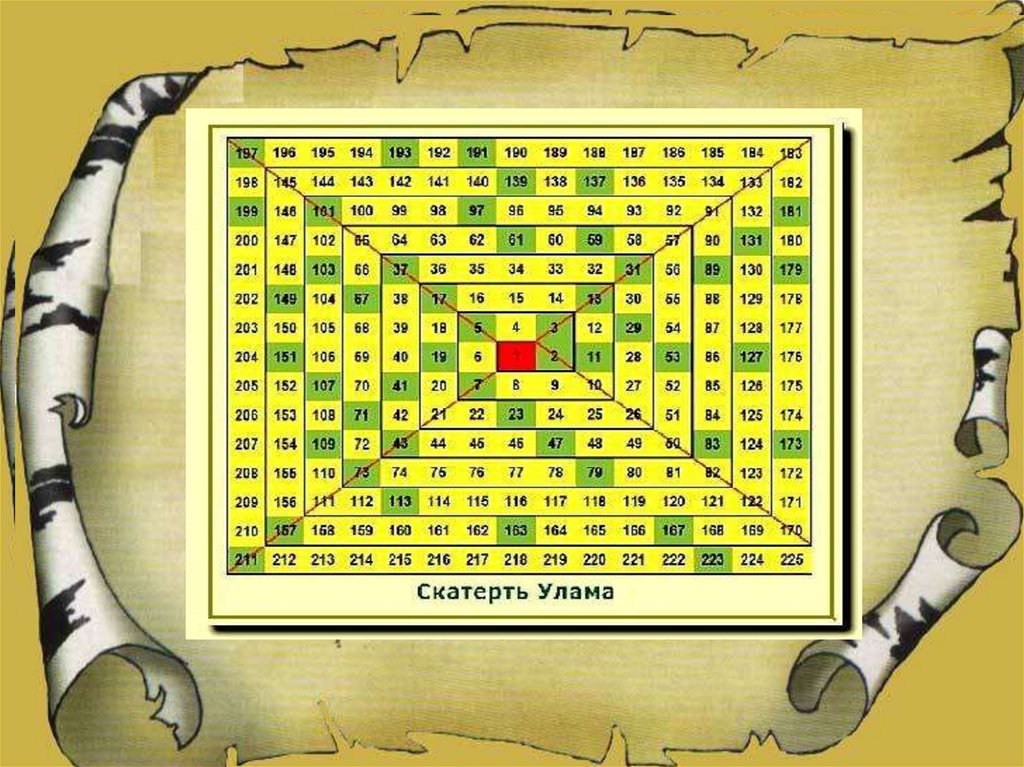
Станислав Мартин Улам(1909-1984)
Американский математик,
поляк по происхождению.
Открыл свойство простых
чисел, которое получило
название «Скатерть
Улама»
В Научно-исследовательской
лаборатории Лос-Аламоса были
получены все простые числа до
100 000 000.
9.
В Научно-исследовательскойлаборатории Лос-Аламоса были
получены все простые числа до
100 000 000.
10.
11.
12.
Непростые задачиНепростые задачи
с простыми
с простыми
числами
числами
13.
Задача №1Простое число умножили на само себя и отняли 8.
В результате получили 41.Запишите это число
7
14.
Задача №2.Составьте таблицы простых чисел для чисел
От 1 до 100
2, 3, 5, 7, 11, 13, 17, 19,
23, 29, 31, 37, 41, 43,
47, 53, 59, 61, 67, 71,
73, 79, 83, 89, 97
.
15.
Задача №3В разные времена математики пытались найти
формулу, которая позволяла бы вычислять простые
числа. Так, Леонард Эйлер указал формулу:
p = x * x – x + 41, позволяющую вычислять сорок
одно простое число, если х = 0, 1, 2… 40. С помощью
этой формулы найдите пять простых чисел.
p = простое число; х = натуральное число от нуля
до сорока.
16.
Задача №4Ваня задумал простое трехзначное число
все цифры которого различны. На какую
цифру оно может оканчиваться ,если его
последняя цифра равна сумме первых
двух
7
17.
Задача №5Как Вы считаете, какие числа
называются БЛИЗНЕЦАМИ и приведите
примеры таких чисел
18.
Числа-близнецы – это простыечисла, находящиеся на расстоянии
друг от друга в одно составное
число.
Примеры:
17 и 19
1997 и 1999
1301 и 1303…
19.
Задача №6.а) Кто и когда впервые разделил числа
на чётные и нечётные, простые и
составные?
б) Как Вы думаете, как учёные пришли
к этому открытию?
в) Могло ли случиться так, что простые
числа так и не были открыты?
20.
а) Пифагорб) методом наблюдения
в)нет
21.
Задача №7.Числа р и р + 15 простые. Найдите
все такие р.
Ответ: 2
22.
Задача №8.Сколько существует простых
чисел р, таких ,что числа р









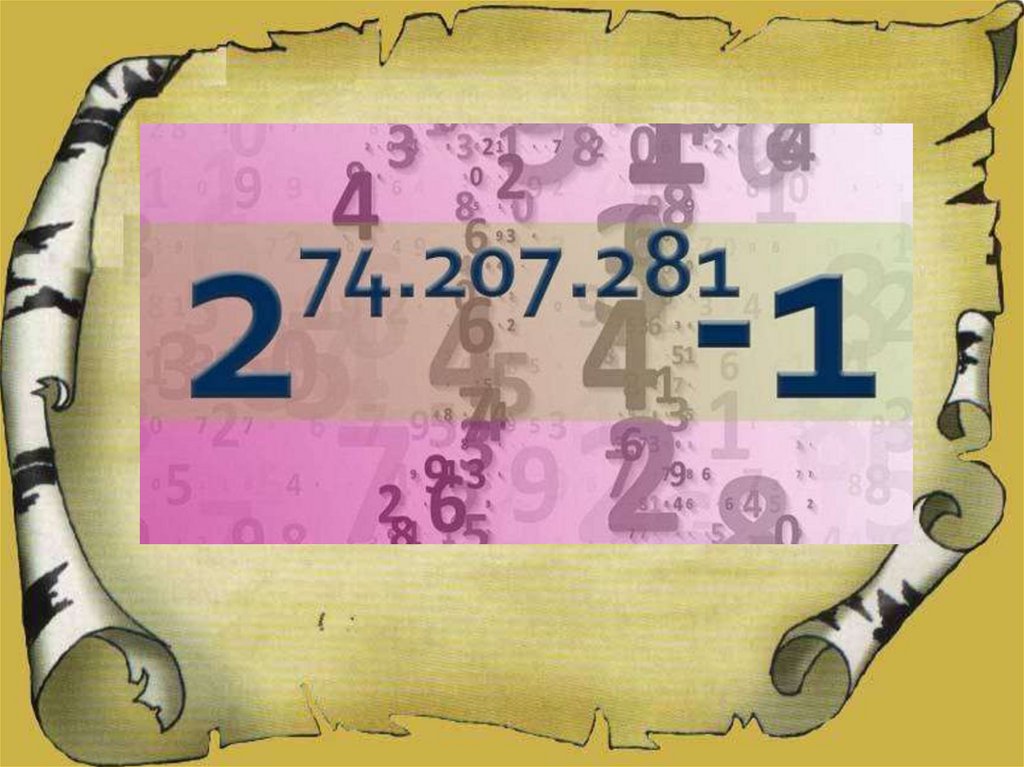















 Математика
Математика








